Идеальный газ физика формулы: Давление идеального газа, теория и онлайн калькуляторы - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Идеальный газ, все формулы и примеры

Это газ, который состоит из материальных точек, имеющих конечную массу, но не имеющих объема. Данные частицы не могут взаимодействовать на расстоянии. Столкновения частиц идеального газа описываются при помощи законов абсолютно упругого соударения шаров. Следует отметить, что имеются в виду законы столкновения именно шаров, так как точечные частицы испытывают только лобовые столкновения, которые не могут изменять направления скоростей на разные углы.

Идеальный газ существует только в теории. В реальной жизни он не может существовать в принципе, так как точечные молекулы и отсутствие их взаимодействия на расстоянии аналогично их существованию вне пространства, то есть их не существованию. Ближе всех по своим свойствам к модели идеального газа приближаются газы при малом давлении (разреженные газы) и (или) высокой температуре. Модель идеального газа подходит для изучения методов исследования систем многих частиц, знакомства с соответствующими понятиями.

В промежутках между столкновениями молекулы идеального газа движется по прямым. Законы столкновений и соударений о стенки сосудов, в которых находится газ, известны. Следовательно, если знать положения и скорости всех частиц идеального газа в какой-то момент времени, то можно найти их координаты и скорости в любой другой момент времени. Эта информация наиболее полно описывает состояние системы частиц. Однако количество частиц столь велико, что динамическое описание системы многих частиц непригодно для теории и бесполезно для практики. Это означает, что для изучения систем многих частиц информация должна быть обобщена, и ее относят не к отдельным частицам, а к их большим совокупностям.

Давление идеального газа

При помощи модели идеального газа удалось качественно и количественно объяснить давление газа на стенки сосуда, в котором он находится. Газ оказывает давление на стенки сосуда потому, что его молекулы взаимодействуют со стенками как упругие тела по законам классической механики. Количественно давление (p) идеального газа получили равным:

где — средняя кинетическая энергия поступательного движения молекул газа; — концентрация молекул газа (N – число молекул газа в сосуде; V – объем сосуда).

Законы идеальных газов

Идеальным называют газы, которые строго подчиняются законам Бойля – Мариотта и Гей – Люссака.

Закон Бойля – Мариотта. Для постоянной массы (m) идеального газа при постоянной температуре (T) произведение давления (p) газа на его объем (V) является постоянной величиной для любых состояний рассматриваемого вещества:

Закон Гей-Люссака. Для постоянной массы газа при неизменном давлении выполняется соотношение:

В поведении реальных газов наблюдают отступления от законов Бойля — Мариотта и Гей-Люссака, и эти отступления различны для разных газов.

Для идеального газа выполняется закон Шарля. Который говорит о том, что для постоянной массы газа, при постоянном объеме, отношение давления газа к температуре, не изменяется:

Для связи параметров идеального газа, часто используют уравнение состояния, которое носит имена двух ученых Клапейрона и Менделеева:

где — молярная масса газа; – универсальная газовая постоянная.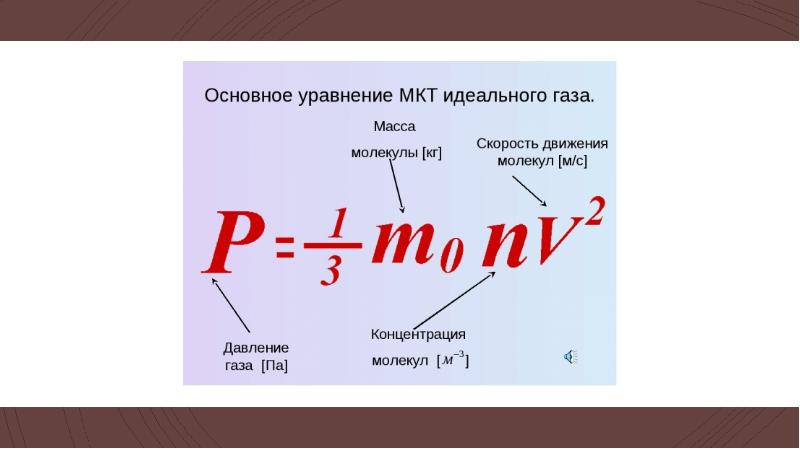

Закон Дальтона. Давление смеси идеальных газов (p) равно сумме парциальных давлений () рассматриваемых газов:

При этом уравнение состояния смеси идеальных газов имеет вид (2), как будто газ является химически однородным.

Примеры решения задач

Идеальный газ. Уравнение состояния идеального газа. Изопроцессы.

Идеальный газ, уравнение состояния идеального газа, его температура и давление, объем… список параметров и определений, которыми оперируют в соответствующем разделе физики, можно продолжать достаточно долго. Сегодня мы поговорим как раз на эту тему.

Что рассматривается в молекулярной физике?

Основным объектом, который рассматривается в этом разделе, является идеальный газ. Уравнение состояния идеального газа было получено с учетом нормальных условий окружающей среды, и об этом мы поговорим немного позднее. Сейчас давайте подойдем к этой “проблеме” издалека.

Допустим, у нас есть некоторая масса газа. Ее состояние можно определить при помощи трех параметров термодинамического характера. Это, конечно же, давление, объем и температура. Уравнением состояния системы в этом случае будет формула связи между соответствующими параметрами. Она выглядит таким образом: F (p, V, T) = 0.

Вот здесь мы впервые потихоньку подбираемся к появлению такого понятия, как идеальный газ. Им называется газ, в котором взаимодействия между молекулами пренебрежимо малы. Вообще в природе такого не существует. Однако любой сильно разреженный газ близок к нему. От идеального мало чем отличаются азот, кислород и воздух, находящиеся в нормальных условиях. Чтобы записать уравнение состояния идеального газа, мы можем использовать объединенный газовый закон. Получим: pV/T = const.

Связанное понятие № 1: закон Авогадро

Он может рассказать нам о том, что если мы возьмем одинаковое количество молей абсолютно любого случайного газа и поставим их в одинаковые условия, среди которых температура и давление, то газы займут одинаковый объем. В частности, опыт проводился при нормальных условиях. Это означает, что температура была равна 273,15 Кельвинам, давление – одной атмосфере (760 миллиметров ртутного столба или же 101325 Паскалей). При таких параметрах газ занял объем равный 22,4 литра. Следовательно, мы можем говорить о том, что для одного моля любого газа соотношение числовых параметров будет величиной постоянной. Именно поэтому было принято решение этой цифре дать обозначение буквой R и назвать ее универсальной газовой постоянной. Таким образом, она равняется 8,31. Размерность Дж/моль*К.

Идеальный газ. Уравнение состояния идеального газа и манипуляции с ним

Давайте попробуем переписать формулу. Для этого запишем его в таком виде: pV = RT. Далее совершим нехитрое действие, умножим обе части уравнения на произвольное количество молей. Получим pVu = uRT. Примем во внимание тот факт, что произведение молярного объема на количество вещества есть просто объем. Но ведь количество молей одновременно будет равняться частному массы и молярной массы. Именно так выглядит уравнение Менделеева-Клапейрона. Оно дает четкое понятие о том, какую систему образует идеальный газ. Уравнение состояния идеального газа примет вид: pV = mRT/M.

Выведем формулу для давления

Давайте проведем еще некоторые манипуляции с полученными выражениями. Для этого правую часть уравнения Менделеева-Клапейрона умножим и разделим на число Авогадро. Теперь внимательно смотрим на произведение количества вещества на число Авогадро. Это есть не что иное, как общее число молекул в газе. Но в то же время отношение универсальной газовой постоянной к числу Авогадро будет равно постоянной Больцмана. Следовательно, формулы для давления можно записать таким образом: p = NkT/V или p = nkT. Здесь обозначение n это концентрация частиц.

Процессы идеального газа

В молекулярной физике существует такое понятие, как изопроцессы. Это термодинамические процессы, которые имеют место в системе при одном из постоянных параметров. При этом масса вещества также должна оставаться постоянной. -1 и носит название “коэффициент объемного расширения”. Мы можем подставить температуру как по шкале Цельсия, так и по шкале Кельвина. В последнем случае получим формулу V = Voat.

Постоянным остается объем

Это второй закон Гей-Люссака, более часто называемый законом Шарля. Выглядит он так: p/T = const. Есть и другая формулировка: p = po (1 + at). Преобразования могут быть проведены в соответствии с предыдущим примером. Как можно видеть, законы идеального газа иногда бывают достаточно похожими друг на друга.

Постоянным остается температура

Если температура идеального газа остается величиной постоянной, то мы можем получить закон Бойля-Мариотта. Он может быть записан таким образом: pV = const.

Связанное понятие № 2: парциальное давление

Допустим, у нас имеется сосуд с газами. Это будет смесь. Система находится в состоянии теплового равновесия, а сами газы между собой не реагируют. Здесь N будет обозначать общее количество молекул. N1, N2 и так далее, соответственно, количество молекул в каждом из компонентов имеющейся смеси. Возьмем формулу давления p = nkT = NkT/V. Ее можно раскрыть для конкретного случая. Для двухкомпонентной смеси формула примет вид: p = (N1 + N2) kT/V. Но тогда получится, что общее давление будет суммироваться из частных давлений каждой смеси. А значит, оно будет иметь вид p1 + p2 и так далее. Это и будут парциальные давления.

Для чего это нужно

Полученная нами формула указывает на то, что давление в системе оказывается со стороны каждой группы молекул. Оно, кстати, не зависит от других. Этим воспользовался Дальтон при формулировании закона, названного впоследствии в его честь: в смеси, где газы не реагируют между собой химически, общее давление будет равно сумме парциальных давлений.

Богданов К.Ю. – учебник по физике для 10 класса

§ 24. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ЗАКОН АВОГАДРО

Уравнение состояния идеального газа связывает между собой три его макроскопические характеристики – занимаемый газом объём, его давление и температуру.

В §23 мы вывели формулу, связывающую давление идеального газа, p, концентрацию молекул в нём, n, и его абсолютную температуру, Т:

p = nkT , (24.1)

где k – постоянная Больцмана. Однако в большинстве случаев пользоваться формулой (24.1) неудобно, т.к. величина

n, как правило, неизвестна, а мы лишь знаем, какой это газ и какой объём он занимает. Чтобы в этих случаях формулой (24.1) было пользоваться проще, преобразуем её следующим образом. Пусть газ, состоящий из N молекул, находится в сосуде объёмом V. Тогда концентрация, n молекул равна:

где m и n – масса и количество вещества, содержащееся в газе с молярной массой M и объёмом V, а N_A – число Авогадро (см.

19.1 и 19.2). Подставляя (24.2) в (24.1), получаем:

Произведение kN_A обозначают буквой R и называют универсальной (молярной) газовой постоянной, которая равна 8,31 Дж/(моль^.К). Заменяя kN_A на R в формуле (24.3), получаем:

Уравнение (24.4) называют уравнением состояния идеального газа

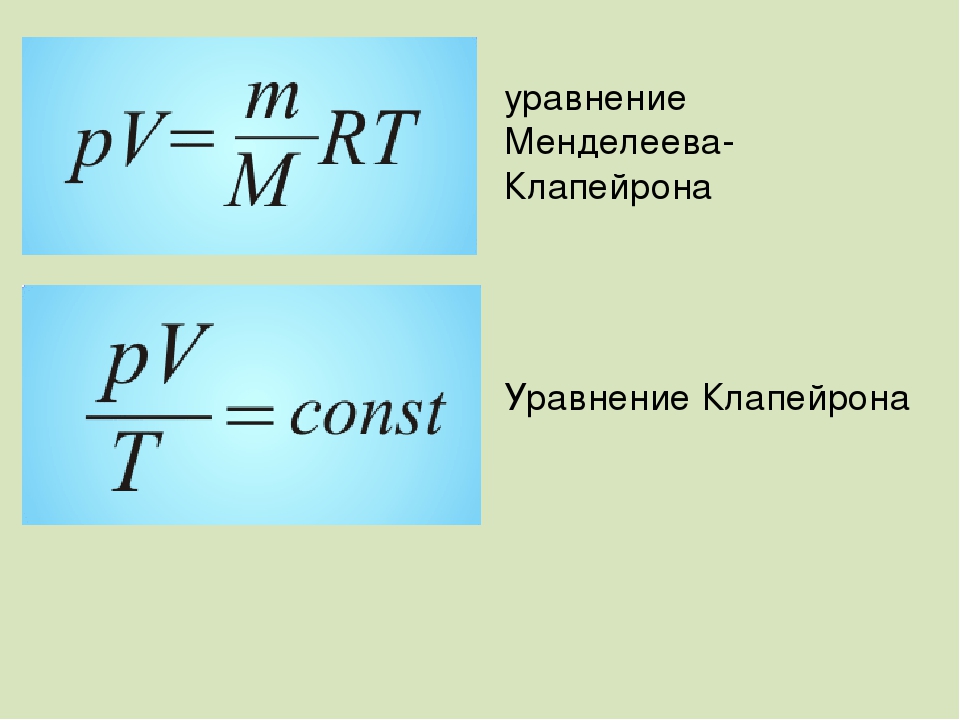
или уравнением Менделеева-Клапейрона, названным в честь русского учёного Д.И. Менделеева и французского физика Б. Клапейрона. Формула (24.4) определяет взаимозависимость трёх макроскопических характеристик данной массы газа, определяющих его состояние, – давления, объёма и температуры.

Уравнение Менделеева-Клапейрона позволяет вычислить одну из пяти переменных (p, V, m, M и T), если значения остальных четырёх известны. Можно, например, найти молярную массу, М газа, т.е. определить его относительную молекулярную массу, если измерить его давление, объём, массу и температуру.

Из уравнения (24.4) следует, что если данная масса газа находится в состоянии 1, в котором её давление, объём и температуры равны p₁, V₁ и T₁, соответственно, а потом переходит в состояние 2 (см. рис. 24а), в котором её давление, объём и температуры становятся равными p₂, V₂ и T₂, то:

Уравнение (24. 5), называемое уравнением Клапейрона, позволяет вычислить значение одной из макроскопических характеристик газа в состоянии 2, если остальные две известны.

Возьмём одинаковое число молей n двух разных газов (А и Б). Пусть эти газы имеют одинаковую температуру T₀ и давление p₀. Тогда из уравнения (24.4) следует, что объёмы этих газов, V_А и V_Б, тоже равны:

Таким образом, при одинаковых давлении и температуре равные объёмы различных газов содержат одинаковое количество вещества, т.е. молекул. Этот вывод называют законом Авогадро. Из закона Авогадро и формулы (24.6) следует, что при нормальных условиях, т.е. при температуре 0^оС (Т₀=273 К) и нормальном атмосферном давлении (p₀=101325 Па), газ, взятый в количестве 1 моль, занимает объём 0,0224 м³ или 22,4 литра (см. рис. 24б).

Вопросы для повторения:

· Сформулируйте уравнение Менделеева-Клапейрона. Для каких газов оно справедливо?

· Как связана универсальная газовая постоянная с постоянными Больцмана и Авогадро?

· Сформулируйте закон Авогадро.

· Какие объёмы занимает один, два и три моля идеального газа при нормальных условиях?

Рис. 24. (а) – связь между параметрами газа в двух его состояниях; (б) – связь между параметрами одного моля газа при нормальных условиях.

Основное уравнение МКТ (молекулярно-кинетической теории). Давление идеального газа | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Согласно модели идеального газа молекулы все время находятся в беспорядочном движении, сталкиваются между собой и со стенками сосуда, в котором пребывают. В момент столкновения молекулы со стенкой она действует на нее с силой, импульс которой, согласно второму закону Ньютона, равняется изменению ее импульса (количества движения):

F̅t = Δ(m͞v). Это значит, что изменение модуля импульса всех молекул ΣΔ(mv_i) при ударе равнозначно действию усредненного значения силы F̅ в течение времени t. Это суммарное действие молекул вызывает давление газа, которое по определению равно p = F / S.

Давление газа вызывают удары о стенку сосуда большого количества молекул, передающих ему импульс.

Рассмотрим идеальный газ, который находится в сосуде объемом V. Для простоты расчетов выберем его в форме параллелепипеда (рис. 1.15). Пусть в нем находится N молекул массой m₀ каждая; их концентрация равна n = N / V. Поскольку молекулы движутся беспорядочно (условие динамического хаоса для идеального газа), то достаточно определить давление на одну из стенок, поскольку на другие стенки молекулы будут создавать такое же давление. Для простоты изложения сначала будем считать, что все они имеют одинаковые скорости V.

Представим отдельный слой газа, перпендикулярный координатной плоскости ZY. В силу хаотичности движения количество молекул, влетающих в этот слой справа, равняется количеству молекул, вылетающих из него слева. Очевидно, что и те и другие передают данному слою импульс: влетающие слева (рис. 1.16) несут импульс m₀v_x, где v_x — проекция скорости на ось Х; вылетающие из него выносят импульс —m₀v_x, в целом передавая ему импульс 2m₀v_x. Итак, со стороны всех молекул Z, влетающих в отдельный слой, стенка получает импульс 2Zm₀v_x.

Рис. 1.15. Передача молекул газа импульса стенке сосуда

Рис.

1.16. Упругий удар молекулы в стенку

Количество молекул Z, которые сталкиваются со стенкой площадью S за время t, можно определить по их концентрации в объеме отдельного слоя: Z = nv_xtS, где n — концентрация молекул. Поскольку к стенке долетают лишь те молекулы, которые имеют положительную проекцию скорости на ось X (v_x > 0), то их количество будет составлять половину от числа молекул, пересекающих плоскость отдельного слоя газа:

Z = nv_xtS / 2.

Итак, со стороны всех молекул, находящихся в отдельном слое, стенка получает общий импульс:

F_xt = 2 • nv_xtSm₀v_x / 2.

Разделив левую и правую части равенства на St, получим:

F_x / S = p = nm₀v²_x.

Предположения, что скорости всех молекул одинаковы, было сделано с целью упрощения вывода уравнений. На самом же деле диапазон их значений довольно широк — от 0 до определенного максимального значения v_max. Поэтому в предыдущем уравнении для определения давления газа правильнее будет брать средний квадрат проекции скорости v_x. Тогда оно будет иметь вид:

p = nm₀v̅²_х.

Понятно, что аналогичные соображения будут справедливы для стенок, лежащих в других координатных плоскостях:

p = nm₀v̅²_y,

p = nm₀v̅²_z.

Средний квадрат скорости имеет смысл среднестатистического значения скорости. Материал с сайта http://worldofschool.ru

Очевидно, что вследствие хаотического движения молекул v̅²_x = v̅²_y = v̅²_z. По математическому определению средний квадрат скорости равен v̅² = (v̅²_x + v̅²_y + v̅²_z). Отсюда v̅²_x = (1 / 3) • v̅². Подставив это выражение в уравнение p = nm₀v̅²_х, получим окончательное уравнение для определения давления идеального газа:

p = (1 / 3) • nm₀v̅².

Эта формула является основным уравнением молекулярно-кинетической теории (МКТ) идеального газа, которое определяет связь между макропараметром термодинамической системы — давлением идеального газа и характеристиками его микроскопического состояния. Таким образом, оно определяет давление газа как статистическую величину посредством микропараметров системы — концентрации, массы и скорости молекулы.

Поскольку nm₀ = ρ, где ρ — плотность газа, основное уравнение молекулярно-кинетической теории идеального газа будет иметь еще и такой вид:

p = (1 / 3) • ρv̅².

Основное уравнение MKT является мостиком между двумя подходами в толковании тепловых явлений и процессов — термодинамическим и молекулярно-кинетическим.

На этой странице материал по темам:

Доклал оснлвное ураанение молекулярно кинетической теории газоы кратко
Идеальный газ лекция основное уравнение мкт
Как изменяется импульс слоя газа за счет молекул вылетающих в него
Решебник физики мкт

Вопросы по этому материалу:

Чем объясняется давление газа в МКТ?
Как изменяется импульс слоя газа за счет молекул, влетающих в него?
От чего зависит количество молекул в отдельном слое?
Какой смысл имеет средний квадрат скорости?
Почему мы используем понятие среднего квадрата скорости?
Почему уравнение давления идеального газа называют основным уравнением МКТ?

Идеальный газ.

Основное уравнение молекулярно-кинетической теории.

Идеальный газ

Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.

Параметры состояния газа

Давление, температура и объем – параметры состояния газа. Или их называют макропараметрами. Температура – внешняя характеристика скоростей частиц газа. Давление – внешняя характеристика соударений со стенками, например, сосуда. Объем – место, куда заключены частицы газа. Газ занимает весь предоставленный ему объем. Существуют еще внешние параметры, например тела или поля, действующие на газ из вне.

Микропараметры (маленькие, внутренние характеристики) газа – это параметры, которые мы не можем оценить без специальных экспериментов, например, скорость и направление движения каждой молекулы газа.

Состояние термодинамической системы, когда все ее параметры при неизменных внешних условиях не изменяются со временем, называют равновесным.

Основное уравнение молекулярно-кинетической теории

Уравнение связывает микропараметры и макропараметры (давление, объем и температуру) идеального газа.

Рассмотрим идеальный газ, который находится в кубическом сосуде. Каждая молекула упруго сталкивается со стенкой сосуда, при этом изменятся ее импульс. Столкновение всех молекул со стенкой на макроуровне ощущается как давление газа на сосуд. В формулах будут присутствовать средние значения, потому что какая-то молекула движется быстрее, какая-то помедленнее, для того, чтобы оценить примерную скорость, будем брать средние значения.

Основное уравнение мкт имеет вид

Средний квадрат скорости молекул

Средняя квадратичная скорость v_кв молекул это квадратный корень из среднего квадрата скорости

Средняя кинетическая энергия молекул

Можно вывести формулы

Температура

Это макропараметр, который характеризует способность тел к теплопередаче. Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.

Температура характеризует интенсивность движения частиц, поэтому связана со средней кинетической энергией частиц. Из опыта известно, что средняя кинетическая энергия молекул не зависит от вида газа и определяется температурой.

Связь между температурами по шкале Цельсия и по шкале Кельвина

Калькулятор уравнения состояния идеального газа

Уравнение идеального газа — это простая формула, которая связывает основные параметры любого газообразного вещества. По сути, уравнение идеального газа представляет собой квинтэссенцию всех газовых законов.

Математические модели и идеальный газ

Простыми словами идеальный газ представляет собой математическую модель газообразного вещества, которая не учитывает взаимодействие между молекулами. В целом математические модели используются для построения рабочих научных теорий в области физики, химии или математики. К таким моделям относятся математический маятник, материальная точка, ньютоновская жидкость, и, естественно, идеальный газ. Такие модели не осуществимы на практике, но принятые допущения позволяют изучать реальные физические явления с математической точностью. К примеру, в материальной точке пренебрегают размером, но сохраняют ее массу. В идеальном газе пренебрегают силами сопротивления для изучения преобразования энергии из одного вида в другой.

На крайне малых расстояниях, когда молекулярные частицы практически сталкиваются, между ними возникают значительные силы отталкивания. Одновременно с этим на больших расстояниях наблюдаются слабые силы притяжения. В газах в нормальных условиях постоянно наблюдается явление, когда молекулы ударяются друг о друга. Идеальный же газ полностью игнорирует взаимодействие молекул, и так как частицы ведут себя как упругие шарики, в математической модели газа тепловая и кинетическая энергия эквиваленты благодаря отсутствию каких-либо потерь. Кроме того, в математической модели идеального газа размеры молекулярных частиц пренебрежительно малы по сравнению с расстоянием между ними. Для идеального газа справедливы следующие законы.

Основные газовые законы

Любой газ имеет 4 главных характеристики: объем V, давление P, температура T и количество вещества n. Эти параметры связаны между собой основными газовыми законами.

Закон Бойля-Мариотта утверждает, что при T = const произведение объема и давления не изменяется, следовательно, P×V = const. Из этого следует, что изменение одного параметра вызывает обратно пропорциональное изменение другого. Газовые реакции, протекающие при статической температуре, носят название изотермических.

Закон Шарля устанавливает, что при V = const отношение давления газа к его температуре не изменяется: P/T = const. Из формулы следует, что изменение одной характеристики сопровождается прямо пропорциональным изменением другой. Химические реакции с сохранением объемов носят название изохорических.

Закон Гей-Люссака гласит, что при P = const соотношение объема газообразного вещества к его температуре также постоянно: V/T = const. Это означает, что изменение одной величины вызывает прямо пропорциональное изменение другой. Тепловые процессы, которые протекают при статическом давлении, называются изобарическими.

Закон Авогадро утверждает, что в равных объемах газообразных веществ при одинаковых температуре и давлении содержится одинаковое число молекул n. Таким образом, при всех равных параметрах, количество моль двух газов также одинаково.

Закон идеального газа

Если взять все перечисленные законы и объединить их в одну элегантную формулу, то мы получим уравнение идеального газа, который связывает все параметры вещества и иллюстрирует относительное изменение этих величин. Математически закон идеального газа, который также носит название уравнения Менделеева-Клапейрона, записывается так:

Р × V = n × R × T,

где R — универсальная газовая постоянная, которая эквивалентна работе расширения/сжатия одного моля идеального газа в изобарическом процессе при изменении температуры на 1 кельвин.

В международной системе СИ газовая константа равна R = 8,3144 Дж/моль×К. В этом случае для правильных расчетов требуется давление выражать в паскалях, а объем — в кубических метрах. Для упрощения расчетов газовая константа выражается как R = 0,0821 л×атм/моль×К. В этом случае объем газа выражается в литрах, давление — в атмосферах, количество вещества — в моль, а температура — кельвинах.

Так как температура обычно выражается в градусах Цельсия, а все расчеты необходимо производить в кельвинах, мы напоминаем формулу для перевода значений из одной шкалы в другую:

T= t + T0,

где t — температура в градусах Цельсия, T0 — температура абсолютного нуля, равная -273 градуса.

Абсолютный нуль — это температура, при которой молекулы любого химического вещества теряют способность двигаться. Газообразные вещества при температуре -273 градуса теряют весь свой объем, однако в рамках термодинамики точка неподвижности молекул на практике недостижима.

Пример использования уравнения идеального газа

Вычисление молей

Пусть у нас есть баллон кислорода объемом V= 50 л, под давлением P = 1 атмосфера и при температуре 25 градусов Цельсия. Требуется узнать количество вещества, которое содержится в баллоне. Для этого воспользуемся уравнением Менделеева-Клапейрона и выразим из него количество вещества n:

n = P × V / R × T

Теперь необходимо перевести температуру по шкале Кельвина T = 25 + 273 = 298 К и подставить значения в формулу:

n = 1 × 50 / 0,0821 × 298 = 2,04

Таким образом, в баллоне объемом 50 л содержится 2,04 моль кислорода. Интересно, что справочное значение объема 1 моля идеального газа при нормальных условиях составляет 22,41 л, что приблизительно соответствует условию задачи, так как в нашем случае температура в баллоне несколько выше нормальной.

Наша программа позволяет вычислить любой неизвестный параметр из уравнения Менделеева-Клапейрона в случае, если заданы 3 любые величины. Для этого требуется ввести значения в соответствующие ячейки и кликнуть кнопку «Рассчитать», после чего в пустой ячейке отобразится искомое значение. Напоминаем, что указывать температуру следует в кельвинах для корректного расчета параметров при минусовой температуре.

Заключение

Изучение свойств идеального газа — неотъемлемая часть любого курса химии. Наш калькулятор пригодится школьникам и студентам начальных курсов для проверки заданий на тему «Идеальный газ».

12.4: Закон идеального газа – Physics LibreTexts

цели обучения

Опишите, как был получен закон идеального газа.

Закон идеального газа – это уравнение состояния гипотетического идеального газа (иллюстрация приведена в). В идеальном газе нет взаимодействия молекулы с молекулой, и допускаются только упругие столкновения. Это хорошее приближение к поведению многих газов во многих условиях, хотя у него есть несколько ограничений. Впервые он был сформулирован Эмилем Клапейроном в 1834 году как комбинация закона Бойля и закона Чарльза.

Атомы и модули в газе : Атомы и молекулы в газе обычно широко разделены, как показано. Поскольку силы между ними на таких расстояниях довольно малы, они часто описываются законом идеального газа.

Эмпирический вывод

Закон Бойля гласит, что давление P и объем V данной массы ограниченного газа обратно пропорциональны:

\ [\ mathrm {P∝ \ dfrac {1} {V},} \]

, в то время как закон Чарльза гласит, что объем газа пропорционален абсолютной температуре T газа при постоянном давлении

\ [\ mathrm {V∝T.} \]

Объединив два закона, мы получим

\ [\ mathrm {\ dfrac {PV} {T} = C,} \]

, где C – постоянная величина, прямо пропорциональная количеству газа n (представляющая количество молей).

Коэффициент пропорциональности – это универсальная газовая постоянная R, то есть \ (\ mathrm {C = nR} \).

Отсюда и закон идеального газа

\ [\ mathrm {PV = nRT} \]

Эквивалентно его можно записать как \ (\ mathrm {PV = NkT} \),

где k – постоянная Больцмана, а N – количество молекул.

(Поскольку N = nN _A, вы можете видеть, что \ (\ mathrm {R = N_ {Ak}} \), где N _A – число Авогадро. 2}} {3V},} \]

где P – давление, N – количество молекул, m – масса молекулы, v – скорость молекул, V – объем газа.2}} \]

Изотермы

Изотермический процесс – это изменение системы, в которой температура остается постоянной: \ (\ mathrm {ΔT = 0} \).

цели обучения

Укажите условия, при которых могут происходить изотермические процессы.

Изотермический процесс – это изменение системы, в которой температура остается постоянной: ΔT = 0. Обычно это происходит, когда система находится в контакте с внешним тепловым резервуаром (термостатом), и изменение происходит достаточно медленно, чтобы позволить системе для постоянной адаптации к температуре резервуара за счет теплообмена.Напротив, адиабатический процесс происходит, когда система не обменивается теплом с окружающей средой (Q = 0). Другими словами, в изотермическом процессе значение ΔT = 0, но Q ≠ 0, а в адиабатическом процессе ΔT ≠ 0, но Q = 0.

Для идеального газа произведение PV (P: давление, V: объем) является постоянным, если газ находится в изотермических условиях (закон Бойля). Согласно закону идеального газа, значение постоянной равно NkT, где N – количество молекул газа, а k – постоянная Больцмана.

Это означает, что выполняется \ (\ mathrm {p = \ frac {NkT} {V} = \ frac {Constant} {V}} \).

Семейство кривых, генерируемых этим уравнением, показано на графике, представленном на. Каждая кривая называется изотермой. Такие графики называются индикаторными диаграммами – они впервые использовались Джеймсом Ваттом и другими для мониторинга эффективности двигателей. Температура, соответствующая каждой кривой на рисунке, увеличивается от левого нижнего угла к правому верхнему.

Изотермы идеального газа : Несколько изотерм идеального газа на фотоэлектрической диаграмме.{V_B} PdV.} \]

(Это уравнение получено в нашем Атоме для «Постоянного давления» в соответствии с кинетической теорией. Обратите внимание, что \ (\ mathrm {P = \ frac {F} {A}} \). Это определение согласуется с нашим определением работы как силы умножить на расстояние.)

Для изотермического обратимого процесса этот интеграл равен площади под соответствующей изотермой давление-объем и обозначен синим цветом in для идеального газа. Опять же, применяется \ (\ mathrm {P = \ frac {nRT} {V}} \), и если T является постоянным (поскольку это изотермический процесс), мы имеем:

Работа, выполненная газом во время расширения : Синяя область представляет «работу», совершаемую газом во время расширения для этого изотермического изменения.{V_B} \ dfrac {NkT} {V} dV} \\ & \ mathrm {= NkT \ ln \ dfrac {⁡V_B} {V_A}.} \ End {align} \]

По соглашению, работа определяется как работа, которую система выполняет в своей среде. Если, например, система расширяется поршнем, движущимся в направлении силы, приложенной внутренним давлением газа, то работа считается положительной. Поскольку эта работа выполняется за счет использования внутренней энергии системы, в результате внутренняя энергия уменьшается. И наоборот, если окружающая среда воздействует на систему так, что ее внутренняя энергия увеличивается, эта работа считается отрицательной (подробности о внутренней энергии см. В нашем Атоме «Внутренняя энергия идеального газа»).

Постоянное давление

Изобарический процесс – это термодинамический процесс, в котором давление остается постоянным (при постоянном давлении работа, выполняемая газом, равна \ (\ mathrm {PΔV} \)).

цели обучения

Опишите поведение одноатомного газа во время изобарических процессов.

При определенных ограничениях (например, давлении) газы могут расширяться или сжиматься; в зависимости от типа ограничения конечное состояние газа может измениться. Например, идеальный газ, который расширяется при постоянной температуре (так называемый изотермический процесс), будет существовать в другом состоянии, чем газ, который расширяется при постоянном давлении (так называемый изобарический процесс).Этот Атом обращается к изобарическому процессу и коррелированным терминам. Мы обсудим изотермический процесс в следующем атоме.

Изобарический процесс

Изобарный процесс – это термодинамический процесс, в котором давление остается постоянным: \ (\ mathrm {ΔP = 0} \). Для идеального газа это означает, что объем газа пропорционален его температуре (исторически это называется законом Чарльза). Давайте рассмотрим случай, когда газ действительно воздействует на поршень при постоянном давлении P, обратившись к Рис. 1 в качестве иллюстрации.Поскольку давление постоянно, прилагаемая сила постоянна, а выполненная работа выражается как W = Fd, где F (= PA) – сила, прикладываемая к поршню со стороны давления, а d – смещение поршня. Следовательно, работа, совершаемая газом (Вт), равна:

\ [\ mathrm {W = PAd} \]

Поскольку изменение объема цилиндра равно его площади поперечного сечения A, умноженной на смещение d, мы видим, что Ad = ΔV, изменение объема. Таким образом,

\ [\ mathrm {W = PΔV} \]

(как видно на рис. 2 – изобарный процесс).Примечание: если ΔV положительно, то W положительно, что означает, что работа выполняется газом во внешнем мире. Используя закон идеального газа \ (\ mathrm {PV = NkT (P = const)} \),

Рис. 2 : График зависимости давления от объема для постоянного или изобарного процесса. Площадь под кривой равна работе, совершаемой газом, поскольку W = PΔV.

\ [\ mathrm {W = NkΔT} \]

(уравнение 1) для идеального газа, претерпевающего изобарический процесс.

Одноатомный газ

Согласно первому закону термодинамики,

\ [\ mathrm {Q = ΔU + W} \]

(Ур.2), где W – работа, совершаемая системой, U – внутренняя энергия, Q – тепло. Закон гласит, что тепло, передаваемое системе, действительно работает, но также изменяет внутреннюю энергию системы. Так как,

\ (\ mathrm {U = \ frac {3} {2} NkT} \) для одноатомного газа, мы получаем \ (\ mathrm {ΔU = \ frac {3} {2} NkΔT} \)

(уравнение 3; подробности о внутренней энергии см. В нашем Атоме «Внутренняя энергия идеального газа»). Используя уравнения 1 и 3, уравнение. 2 можно записать как:

\ (\ mathrm {Q = \ frac {5} {2} NkΔT} \) для одноатомного газа в изобарическом процессе.

Удельная теплоемкость

Удельная теплоемкость при постоянном давлении определяется следующим уравнением:

\ (\ mathrm {Q = ncPΔT} \)

Здесь n – количество частиц в газе, выраженное в молях. Отметив, что \ (\ mathrm {N = N_An} \) и \ (\ mathrm {R = kN_A} \) _{(N _A: число Авогадро, R: универсальная газовая постоянная), мы получаем:}

\ (\ mathrm {c_P = \ frac {5} {2} kN_A = \ frac {5} {2} R} \) для одноатомного газа.

Решение проблем

С помощью закона идеального газа мы можем вычислить давление, объем или температуру, а также количество молей газа при идеальных термодинамических условиях.

цели обучения

Определите шаги, используемые для решения уравнения идеального газа.

Закон идеального газа – это уравнение состояния гипотетического идеального газа. Это хорошее приближение к поведению многих газов во многих условиях, хотя у него есть несколько ограничений. Он наиболее точен для одноатомных газов при высоких температурах и низких давлениях.

Закон идеального газа имеет вид:

\ [\ mathrm {PV = nRT,} \]

, где R – универсальная газовая постоянная, и с ее помощью мы можем найти значения давления P, объема V, температуры T или числа молей n при определенных идеальных термодинамических условиях . Обычно вам дается достаточно параметров, чтобы вычислить неизвестное. Вариации уравнения идеального газа могут помочь легко решить проблему. Вот несколько общих советов.

Закон идеального газа также может иметь форму:

\ [\ mathrm {PV = NkT,} \]

где N – количество частиц в газе, а k – постоянная Больцмана.

Для решения уравнения идеального газа:

Запишите всю информацию, которую вы знаете о газе.
При необходимости преобразуйте известные значения в единицы СИ.
Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную.
Подставьте известные значения в уравнение. Вычислить неизвестную переменную.

Помните, что общее уравнение газа применимо только в том случае, если молярное количество газа фиксировано. Например, если газ смешан с другим газом, вам, возможно, придется применить уравнение отдельно для отдельных газов.

Пример

Представим, что грузовая шина в начале пути имеет объем 30 000 см ³ и внутреннее давление 170 кПа.Температура шины составляет 16 C. К концу поездки объем шины увеличился до 32000 см ³, а температура воздуха внутри шины составляет 40 ^∘ C. Что такое давление в шинах в конце пути?

Давление в шинах : Давление в шинах может значительно измениться во время эксплуатации автомобиля. В основном это связано с изменением температуры воздуха в шинах.

Решение:

Шаг 1.Запишите всю информацию, которую вы знаете о газе: P ₁ = 170 кПа и P ₂ неизвестно. V ₁ = 30 000 см ³ и V ₂ = 32 000 см ³. T ₁ = 16 C и T ₂ = 40 ^∘ C.

Шаг 2. Преобразуйте известные значения в единицы СИ, если необходимо: Здесь температуру необходимо перевести в Кельвины. Следовательно, T ₁ = 16 + 273 = 289 K, T ₂ = 40 + 273 = 313 K

Шаг 3.Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную: Мы можем использовать общее уравнение газа для решения этой проблемы: \ (\ mathrm {\ frac {P_1V_1} {T_1} = \ frac {P_2V_2} {T_2} } \).

Следовательно, \ (\ mathrm {P_2 = \ frac {P_1 \ times V_1 \ times T_2} {T_1 \ times V_2}} \).

Шаг 4. Подставьте известные значения в уравнение. Вычислить неизвестную переменную:

\ [\ mathrm {P_2 = \ dfrac {170 \ times 30 000 \ times 313} {289 \ times 32 000} = 173 \; кПа} \]

Давление в шине в конце пути 173 кПа.

Обратите внимание, что на шаге 2 мы не удосужились преобразовать значения объема в м ³. На шаге 4 давление появляется как в числителе, так и в знаменателе. В этом случае преобразование не требовалось.

Число Авогадора

Число молекул в молье называется числом Авогадро (N _A) и определяется как 6,02x 10 ²³ моль ^-1.

цели обучения

Объясните связь между числом Авогадро и родинкой.

При измерении количества вещества иногда проще работать с единицей измерения, отличной от количества молекул. Моль (сокращенно моль) – основная единица Международной системы единиц (СИ). Он определяется как любое вещество, содержащее столько атомов или молекул, сколько содержится ровно в 12 граммах (0,012 кг) углерода-12. Фактическое количество атомов или молекул в одном моль, по признанию итальянского ученого Амедео Авогадро, называется постоянной Авогадро (N _A) .

Амадео Авогадро : Амедео Авогадро (1776–1856). Он установил, что соотношение между массами одного и того же объема разных газов (при одинаковой температуре и давлении) соответствует соотношению между их соответствующими молекулярными массами.

Число Авогадро (N) обозначает количество молекул в одной грамм-молекуле кислорода. Это указывает на количество вещества, а не на независимое измерение.В 1811 году Амедео Авогадро впервые предположил, что объем газа (при заданном давлении и температуре) пропорционален количеству атомов или молекул, независимо от природы газа (т. Е. Это число универсально и не зависит от типа газа). газ). В 1926 году Жан Перрен получил Нобелевскую премию по физике, в основном за его работу по определению постоянной Авогадро (несколькими различными методами). Значение постоянной Авогадро, N _A, оказалось равным 6,02 × 10 ²³ моль ^-1.{−1}.} \]

Измерение N

Определение N _A имеет решающее значение для расчета массы атома, поскольку последняя получается делением массы моля газа на постоянную Авогадро. В своем исследовании броуновского движения в 1905 году Альберт Эйнштейн предположил, что эта постоянная может быть определена на основе величин, наблюдаемых в броуновском движении. Впоследствии идея Эйнштейна была подтверждена, что привело к первому определению N _A в 1908 году в результате экспериментальной работы Жана Батиста Перрена.

Абсолютная температура

Абсолютная температура – это наиболее часто используемая термодианмическая единица измерения температуры и стандартная единица измерения температуры.

цели обучения

Опишите взаимосвязь между абсолютной температурой и кинетической энергией.

Термодинамическая температура – это абсолютная мера температуры. Это один из основных параметров термодинамики и кинетической теории газов. Термодинамическая температура – это «абсолютная» шкала, потому что это мера фундаментального свойства, лежащего в основе температуры: ее нулевая или нулевая точка («абсолютный ноль») – это температура, при которой частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее.То есть они имеют минимальное движение, сохраняя только квантово-механическое движение, как показано на рисунке.

График зависимости давления от температуры : График зависимости давления от температуры для различных газов, поддерживаемых в постоянном объеме. Обратите внимание, что все графики экстраполируются к нулевому давлению при одной и той же температуре

В самом простом случае, «температура» возникает из кинетической энергии случайных движений составляющих материальных частиц, таких как молекулы или атомы, как показано на.Поэтому разумно выбрать абсолютный ноль, при котором все классическое движение прекращается, в качестве точки отсчета (T = 0) нашей температурной системы. Используя шкалу абсолютных температур (система Кельвина), которая является наиболее часто используемой термодинамической температурой, мы показали, что средняя поступательная кинетическая энергия (KE) частицы в газе имеет простую связь с температурой:

Поступательное движение гелия : Реальные газы не всегда ведут себя в соответствии с идеальной моделью при определенных условиях, таких как высокое давление.Здесь размер атомов гелия относительно их расстояния показан в масштабе при давлении 1950 атмосфер.

\ [\ mathrm {\ bar {KE} = \ dfrac {3} {2} тыс. Т.} \]

Обратите внимание, что это уравнение не выглядело бы так элегантно, если бы вместо него использовалась шкала Фаренгейта.

Шкала Кельвина

Кельвин (или «абсолютная температура») – это стандартная термодинмическая единица измерения температуры. Это одна из семи основных единиц Международной системы единиц (СИ), которой присвоен символ единицы K.По международному соглашению единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой Венской стандартной средней океанской воды (вода с определенной смесью изотопов водорода и кислорода). Абсолютный ноль, минимально возможная температура, определяется как 0 K и −273,15 ° C. Тройная точка воды определяется точно как 273,16 K и 0,01 ° C.

Ключевые моменты

Закон идеального газа был получен эмпирическим путем путем объединения закона Бойля и закона Чарльза.2}.} \)
Изотермические процессы обычно происходят, когда система находится в контакте с внешним тепловым резервуаром (тепловой ванной), и изменение происходит достаточно медленно, чтобы позволить системе постоянно приспосабливаться к температуре резервуара посредством теплообмена.
Для идеального газа согласно закону идеального газа \ (\ mathrm {PV = NkT, PV} \) остается постоянным в результате изотермического процесса. Кривая на диаграмме P-V, порожденная уравнением \ (\ mathrm {PV = const} \), называется изотермой.
Для изотермического обратимого процесса работа, совершаемая газом, равна площади под соответствующей изотермой давление-объем. Он задается как \ (\ mathrm {W_A \ rightarrow B = NkT \ ln \ frac {⁡V_B} {V_A}} \).
Газы могут расширяться или сжиматься при определенных ограничениях. В зависимости от ограничения конечное состояние газа может измениться.
Тепло, передаваемое системе, работает, но также изменяет внутреннюю энергию системы. В изобарическом процессе для одноатомного газа тепло и изменение температуры удовлетворяют следующему уравнению: \ (\ mathrm {Q = \ frac {5} {2} NkΔT} \).
Для одноатомного идеального газа удельная теплоемкость при постоянном давлении равна \ (\ mathrm {\ frac {5} {2} R} \).
Запишите всю информацию, которую вы знаете о газе, и при необходимости преобразуйте известные значения в единицы СИ.
Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную, и подставьте известные значения в уравнение. Затем вычислите неизвестную переменную.
Общее уравнение газа применимо только в том случае, если молярное количество газа фиксировано.
Авогадро предположил, что равные объемы газа при одинаковом давлении и температуре содержат равное количество молекул, независимо от типа газа.
Постоянная Авогадро – это коэффициент масштабирования между макроскопическими и микроскопическими (атомный масштаб) наблюдениями за природой. Он обеспечивает связь между другими физическими константами и свойствами.
Альберт Эйнштейн предположил, что число Авогадро можно определить на основе величин, наблюдаемых в броуновском движении.Впервые числовая апертура была измерена Жаном Батистом Перреном в 1908 году.
Температура возникает из кинетической энергии случайных движений компонентов материи, таких как молекулы или атомы. Следовательно, в качестве точки отсчета разумно выбрать абсолютный ноль, при котором все классическое движение прекращается.
Согласно международному соглашению, единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой стандартизованной воды.
При абсолютном нуле частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее.Они сохраняют минимальное квантово-механическое движение.

Ключевые термины

моль : В Международной системе единиц – основная единица количества вещества; количество вещества системы, которая содержит столько же элементарных объектов, сколько атомов в 12 г углерода-12. Символ: мол.
идеальный газ : гипотетический газ, молекулы которого не взаимодействуют друг с другом и подвергаются упругому столкновению друг с другом и со стенками контейнера.
Число Авогадро : количество составляющих частиц (обычно атомов или молекул) в одном моль данного вещества. Он имеет размеры обратного моля и его значение равно 6.02214129 · 1023 моль-1
адиабатический : Происходит без увеличения или уменьшения тепла.
внутренняя энергия : сумма всей энергии, присутствующей в системе, включая кинетическую и потенциальную энергию; эквивалентно, энергия, необходимая для создания системы, за исключением энергии, необходимой для перемещения ее окружения.
первый закон термодинамики : Вариант закона сохранения энергии: изменение внутренней энергии замкнутой системы равно количеству тепла, подаваемого в систему, за вычетом количества работы, выполняемой системой на его окрестности.
удельная теплоемкость : Отношение количества тепла, необходимого для повышения температуры единицы массы вещества на единицу градуса, к количеству тепла, необходимому для повышения температуры той же массы воды на такое же количество.
Единицы СИ : Международная система единиц (сокращенно СИ от французского: Le Système international d’unités). Это современная форма метрической системы.
газовая постоянная : Универсальная постоянная R, которая появляется в законе идеального газа (PV = nRT), полученная из двух фундаментальных констант, постоянной Больцмана и числа Авогадро (R = NAk).
Постоянная Фарадея : Величина электрического заряда на моль электронов.
Броуновское движение : Случайное движение взвешенных в жидкости частиц, возникающее в результате столкновения этих частиц с отдельными молекулами жидкости.
абсолютный ноль : самая низкая из возможных температур: ноль по шкале Кельвина и приблизительно -273,15 ° C и -459,67 ° F. Полное отсутствие тепла; температура, при которой движение всех молекул прекратится.
Международная система единиц : (СИ): Стандартный набор основных единиц измерения, используемый в мировой научной литературе.
Венский стандарт для средней океанической воды : Стандарт, определяющий стандартизованный изотопный состав воды.

ЛИЦЕНЗИИ И АТРИБУЦИИ

CC ЛИЦЕНЗИОННЫЙ КОНТЕНТ, ПРЕДЫДУЩИЙ РАЗДЕЛ

CC ЛИЦЕНЗИОННОЕ СОДЕРЖАНИЕ, СПЕЦИАЛЬНЫЙ АТРИБУЦИЯ

идеальный газ. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/ideal_gas . Лицензия : CC BY-SA: Attribution-ShareAlike
Закон об идеальном газе. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Ideal_gas_law%23Empirical . Лицензия : CC BY-SA: Attribution-ShareAlike
Номер Авогадро. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Avogadro’s%20number . Лицензия : CC BY-SA: Attribution-ShareAlike
моль. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/mole . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
идеальный газ. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/ideal_gas . Лицензия : CC BY-SA: Attribution-ShareAlike
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY-SA: Attribution-ShareAlike
Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/internal-energy . Лицензия : CC BY-SA: Attribution-ShareAlike
адиабатический. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/adiabatic . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Закон об идеальном газе.4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
Изобарический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isobaric_process . Лицензия : CC BY-SA: Attribution-ShareAlike
первый закон термодинамики. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/the%20first%20law%20of%20thermodynamics . Лицензия : CC BY-SA: Attribution-ShareAlike
удельная теплоемкость. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/specific_heat . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы.5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
идеальный газ. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/ideal_gas . Лицензия : CC BY-SA: Attribution-ShareAlike
Закон об идеальном газе. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Ideal_gas_law . Лицензия : CC BY-SA: Attribution-ShareAlike
Бесплатный проект научных текстов для старших классов, Тепловые свойства и идеальные газы: закон идеального газа и общее уравнение газа. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39086/latest/ . Лицензия : CC BY: Attribution
Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/si-units . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http: // cnx.org / content / m42216 / latest / . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
Шина. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Tire . Лицензия : CC BY: Attribution
Броуновское движение. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/Brownian_motion . Лицензия : CC BY-SA: Attribution-ShareAlike
Константа Авогадро. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Avogadro_constant%23Measurement . Лицензия : CC BY-SA: Attribution-ShareAlike
Броуновское движение. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Brownian_motion . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Закон об идеальном газе.17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
Постоянная Фарадея. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Faraday%20constant . Лицензия : CC BY-SA: Attribution-ShareAlike
газовая постоянная. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/gas_constant . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы.5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
Шина. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Tire . Лицензия : CC BY: Attribution
Авогадро Амедео. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Avogadro_Amedeo.jpg . Лицензия : CC BY-SA: Attribution-ShareAlike
абсолютный ноль. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/absolute_zero . Лицензия : CC BY-SA: Attribution-ShareAlike
Термодинамическая температура. Предоставлено : Википедия. Расположен по адресу: : en.Wikipedia.org/wiki/Thermodynamic_temperature . Лицензия : CC BY-SA: Attribution-ShareAlike
Международная система единиц. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/International%20System%20of%20Units . Лицензия : CC BY-SA: Attribution-ShareAlike
Венский стандарт средней океанской воды. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/Vienna_Standard_Mean_Ocean_Water . Лицензия : CC BY-SA: Attribution-ShareAlike
Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Изотермический процесс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы.5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
Шина. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Tire . Лицензия : CC BY: Attribution
Авогадро Амедео. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Avogadro_Amedeo.jpg . Лицензия : CC BY-SA: Attribution-ShareAlike
OpenStax College, Температура. 28 апреля 2014 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42214/latest/ . Лицензия : CC BY: Attribution
Кинетическая теория. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Kinetic_theory . Лицензия : Общественное достояние: неизвестно Авторские права

идеального газа | химия и физика

идеальный газ , также называемый идеальный газ , газ, который по физическому поведению соответствует определенной идеализированной связи между давлением, объемом и температурой, называемой общим законом газа.Этот закон является обобщением, содержащим как закон Бойля, так и закон Чарльза как частные случаи и гласит, что для заданного количества газа произведение объема v и давления p пропорционально абсолютной температуре t ; то есть в форме уравнения p v = k t , в котором k является константой. Такое соотношение для вещества называется его уравнением состояния, и его достаточно, чтобы описать его грубое поведение.

Общий газовый закон может быть выведен из кинетической теории газов и основан на предположении, что (1) газ состоит из большого числа молекул, которые находятся в беспорядочном движении и подчиняются законам движения Ньютона; 2) объем молекул пренебрежимо мал по сравнению с объемом, занимаемым газом; и (3) никакие силы не действуют на молекулы, кроме как во время упругих столкновений пренебрежимо малой продолжительности.

Подробнее по этой теме

газ: Идеальный газ

Уравнение состояния идеального газа может быть выведено путем расчета давления, вызванного молекулярными ударами о стенку контейнера.Внутренний …

Хотя ни один газ не обладает такими свойствами, поведение реальных газов довольно точно описывается общим газовым законом при достаточно высоких температурах и низких давлениях, когда относительно большие расстояния между молекулами и их высокие скорости преодолевают любое взаимодействие. Газ не подчиняется уравнению, когда условия таковы, что газ или любой из составляющих его газов в смеси находится вблизи точки конденсации, температуры, при которой он сжижается.

Общий газовый закон может быть записан в форме, применимой к любому газу, в соответствии с законом Авогадро, если константа, определяющая количество газа, выражается через количество молекул газа.Для этого в качестве единицы массы используется грамм-моль; то есть молекулярная масса, выраженная в граммах. Уравнение состояния n грамм-моля идеального газа может быть записано как p v / t = n R , в котором R называется универсальной газовой постоянной. Эта константа была измерена для различных газов в почти идеальных условиях высоких температур и низких давлений, и было обнаружено, что она имеет одинаковое значение для всех газов: R = 8.314472 джоулей на моль-кельвин.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас Закон об идеальном газе

| Протокол

Вывод закона об идеальном газе

Газы – это фундаментальное состояние вещества. Газ – это совокупность молекул, между молекулами которых находится значительное расстояние. Из-за такого расстояния бесцветные газы невидимы для человеческого глаза и изучаются с помощью четырех измеряемых параметров: давления (P), объема (V), количества молей (n) и температуры (T).Закон идеального газа – это математическое уравнение, которое связывает все эти параметры. Это комбинация нескольких разных законов, описывающих поведение газов.

В 1662 году Роберт Бойль подтвердил предыдущее открытие, связавшее давление газа с его объемом. Закон Бойля гласит, что давление газа обратно пропорционально его объему, если температура и количество молей газа остаются постоянными.

Закон Бойля может быть расширен для расчета нового давления или объема газа, если известны начальное давление и объем.

В 1780-х годах неопубликованная работа французского ученого Жака Шарля была признана французским ученым Жозефом Луи Гей-Люссаком за описание прямой зависимости между объемом и температурой газа.

Закон Чарльза позволяет нам рассчитать новый объем или температуру газа, если начальный объем и температура известны, а давление и количество молей постоянны.

Жозеф Луи Гей-Люссак расширил закон Шарля, связав давление и температуру.Закон Гей-Люссака устанавливает, что давление газа в замкнутом пространстве прямо пропорционально его температуре.

Следовательно, если изменение применяется к газу с постоянным объемом и числом молей, новое давление или температура могут быть рассчитаны, если известны начальное давление и температура.

Наконец, в 1811 году Амедео Авогадро предложил прямую пропорциональность между объемом газа и количеством присутствующих молей.

Закон описывает, как равные объемы двух газов с одинаковой температурой и давлением содержат одинаковое количество молекул.

Все эти соотношения вместе образуют закон идеального газа, впервые предложенный Эмилем Клапейроном в 1834 году как способ объединения этих законов физической химии. Закон идеального газа учитывает давление (P), объем (V), моль газа (n) и температуру (T) с добавленной константой пропорциональности, постоянной идеального газа (R). Универсальная газовая постоянная R равна 8,314 Дж · К ^-1 моль ^-1.

Допущения закона об идеальном газе

Закон идеального газа предполагает, что газы ведут себя идеально, что означает, что они соответствуют следующим характеристикам: (1) столкновения, происходящие между молекулами, являются упругими и их движение происходит без трения, что означает, что молекулы не теряют энергию; (2) общий объем отдельных молекул на величину меньше, чем объем, который занимает газ; (3) между молекулами и их окружением отсутствуют межмолекулярные силы; (4) молекулы постоянно находятся в движении, а расстояние между двумя молекулами значительно больше, чем размер отдельной молекулы.В результате всех этих предположений идеальный газ не мог бы образовывать жидкость при комнатной температуре.

Однако, как мы знаем, многие газы переходят в жидкое состояние при комнатной температуре и, следовательно, имеют отклонения от идеального поведения. В 1873 году Йоханнес Д. Ван дер Ваальс модифицировал закон идеального газа, чтобы учесть размер молекулы, межмолекулярные силы и объем, которые определяют реальные газы.

В уравнении Ван-дер-Ваальса параметры a и b являются константами, которые могут быть определены экспериментально и различаются от одного газа к другому.Параметр a будет иметь большие значения для газов с сильными межмолекулярными силами (например, вода) и меньшие значения для газов со слабыми межмолекулярными силами (например, инертные газы). Параметр b представляет объем, который занимает 1 моль молекул газа; таким образом, когда b уменьшается, в результате увеличивается давление.

Метод Дюма

Изобретенный Жаном Батистом Андре Дюма, метод Дюма использует закон идеального газа для исследования проб газа.Закон идеального газа включает закон Авогадро, согласно которому количество молей двух проб газа, занимающих один и тот же объем, одинаково при постоянном давлении и температуре. Это соотношение позволяет методу Дюма рассчитать молярную массу неизвестной пробы газа.

Для этого используется трубка Дюма. Трубка Дюма представляет собой удлиненную стеклянную колбу с длинной капиллярной шейкой. Перед экспериментом измеряют объем и массу трубки. Затем в трубку Дюма помещается небольшое количество летучего соединения.Летучие соединения имеют высокое давление пара при комнатной температуре и испаряются при низких температурах. Таким образом, когда трубка Дюма, содержащая летучую жидкость, помещается в кипящую воду, жидкость испаряется и вытесняет воздух из трубки, и трубка заполняется только паром. Когда трубку вынимают из водяной бани и оставляют при комнатной температуре, пар снова конденсируется в жидкость. Поскольку масса сохраняется, масса жидкости в трубке равна массе газа в трубке.Используя известные массу и объем газа, а также известные температуру водяной бани и комнатное давление, можно рассчитать моль и, следовательно, молекулярную массу газа, используя закон идеального газа.

Здесь сделаны три допущения: (1) пар действует идеально, (2) объем трубки не меняется в зависимости от комнатной температуры и рабочей температуры, и (3) газ и водяная баня находятся в тепловом состоянии. равновесие.

Список литературы

Коц, Дж.К., Трейхель-младший, П.М., Таунсенд, Дж. Р. (2012) Химия и химическая реакционная способность. Белмонт, Калифорния: Брукс / Коул, Cengage Learning.
Гей-Люссак, Ж. Л. (1809). Воспоминания о соединении газообразных веществ друг с другом. Mémoires de la Société d’Arcueil, Vol. 2, 207.
Ван дер Ваальс, доктор медицины (1967). Уравнение состояния газов и жидкостей. Нобелевские лекции по физике. Elsevier: Амстердам, стр. 254-265.
Сильдерберг, М.С. (2009). Химия: молекулярная природа вещества и изменения . Бостон, Массачусетс: Макгроу Хилл.

13.3 Закон идеального газа – College Physics

Рис. 13.16 Воздух внутри воздушного шара, летящего над Путраджайей, Малайзия, горячее окружающего воздуха. В результате воздушный шар испытывает подъемную силу, толкающую его вверх. (Источник: Кевин По, Flickr)

В этом разделе мы продолжаем исследовать термическое поведение газов.В частности, мы исследуем характеристики атомов и молекул, из которых состоят газы. (Большинство газов, например азот, размер 12 N2N2 {N rSub {размер 8 {2}}} {}, и кислород, размер O2O2 12 {O rSub {размер 8 {2}}} {}, состоят из двух или Мы будем в первую очередь использовать термин «молекула» при обсуждении газа, потому что этот термин также может быть применен к одноатомным газам, таким как гелий.)

Газы легко сжимаются. Мы можем увидеть доказательства этого в Таблице 13.2, где вы заметите, что у газов наибольших коэффициента объемного расширения .Большие коэффициенты означают, что газы расширяются и сжимаются очень быстро при изменении температуры. Кроме того, вы заметите, что большинство газов расширяются с той же скоростью или имеют такой же размер ββ 12 {β} {}. Это поднимает вопрос, почему все газы должны действовать почти одинаково, когда жидкости и твердые тела имеют сильно различающиеся скорости расширения.

Ответ кроется в большом разделении атомов и молекул в газах по сравнению с их размерами, как показано на рис. 13.17. Поскольку атомы и молекулы находятся на большом расстоянии друг от друга, силами между ними можно пренебречь, кроме случаев, когда они сталкиваются друг с другом во время столкновений.Движение атомов и молекул (при температурах, значительно превышающих температуру кипения) происходит быстро, так что газ занимает весь доступный объем, и газы расширяются быстро. Напротив, в жидкостях и твердых телах атомы и молекулы расположены ближе друг к другу и весьма чувствительны к силам между ними.

Рис. 13.17 Атомы и молекулы в газе обычно широко разделены, как показано. Поскольку силы между ними на этих расстояниях довольно слабы, свойства газа больше зависят от количества атомов в единице объема и температуры, чем от типа атома.

Чтобы получить некоторое представление о том, как давление, температура и объем газа связаны друг с другом, рассмотрим, что происходит, когда вы закачиваете воздух в изначально спущенную шину. Объем шины сначала увеличивается прямо пропорционально количеству впрыскиваемого воздуха без значительного увеличения давления в шине. Как только шина расширилась почти до своего полного размера, стенки ограничивают объемное расширение. Если продолжать закачивать в него воздух, давление возрастает. Давление будет еще больше увеличиваться, когда автомобиль движется, а шины двигаются.Большинство производителей указывают оптимальное давление в шинах для холодных шин. (См. Рисунок 13.18.)

Рис. 13.18 (a) Когда воздух нагнетается в спущенную шину, его объем сначала увеличивается без значительного увеличения давления. (b) Когда шина заполнена до определенной точки, стенки шины сопротивляются дальнейшему расширению, и давление увеличивается с увеличением количества воздуха. (c) Когда шина накачана, ее давление увеличивается с температурой.

При комнатной температуре столкновениями между атомами и молекулами можно пренебречь.В этом случае газ называется идеальным газом, и в этом случае соотношение между давлением, объемом и температурой задается уравнением состояния, называемым законом идеального газа.

Закон об идеальном газе

Согласно закону идеального газа,

PV = NkT, PV = NkT, размер 12 {ital “PV” = ital “NkT”} {}

13,18

, где размер PP 12 {P} {} – абсолютное давление газа, размер VV 12 {V} {} – объем, который он занимает, размер NN 12 {N} {} – количество атомов и молекул в газе. , а размер ТТ 12 {T} {} – его абсолютная температура.Константа kk размером 12 {k} {} называется постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844–1906) и имеет значение

. k = 1,38 × 10–23 Дж / К. k = 1,38 × 10–23 Дж / К. размер 12 {k = 1 “.” “38” умножить на 10 “rSup {size 8 {-” 23 “}}” J “/ K} {}

13,19

Закон идеального газа можно вывести из основных принципов, но первоначально он был выведен из экспериментальных измерений Чарльза ‘(объем, занимаемый газом, пропорционален температуре при фиксированном давлении) и из закона Бойля (что для фиксированной температуры продукт PVPV размером 12 {курсив “PV”} {} является константой).В модели идеального газа объем, занимаемый его атомами и молекулами, составляет ничтожную долю от размера VV 12 {V} {}. Закон идеального газа описывает поведение реальных газов в большинстве условий. (Обратите внимание, например, что размер NN 12 {N} {} – это общее количество атомов и молекул, независимо от типа газа.)

Давайте посмотрим, как закон идеального газа согласуется с поведением заполнения шины, когда она накачивается медленно и температура постоянна. Сначала давление PP размером 12 {P} {} по существу равно атмосферному давлению, а объем VV размером 12 {V} {} увеличивается прямо пропорционально количеству атомов и молекул NN размером 12 {N} {} положить в шину.Как только объем шины остается постоянным, уравнение PV = NkTPV = NkT размер 12 {ital “PV” = ital “NkT”} {} предсказывает, что давление должно увеличиваться пропорционально числу N атомов и молекул.

Пример 13.6

Расчет изменений давления из-за изменений температуры: давление в шинах

Предположим, шина вашего велосипеда полностью накачана с абсолютным давлением 7,00 × 105 Па 7,00 × 105 Па размером 12 {7 “.” “00” умножить на “10” rSup {размер 8 {5}} “Па”} {} (манометрическое давление чуть ниже 90.0 фунтов / дюйм 290,0 фунтов / дюйм2, размер 12 {“90” “.” 0` “фунт / дюйм” rSup {размер 8 {2}}} {}) при температуре 18,0ºC18,0ºC размер 12 {“18” “.” 0 ° C} {}. Какое давление будет после того, как его температура повысится до 35,0 ° C 35,0 ° C размер 12 {“35” “.” 0 ° C} {}? Предположим, что нет заметных утечек или изменений объема.

Стратегия

Давление в шине меняется только из-за изменения температуры. Сначала нам нужно определить, что мы знаем и что мы хотим знать, а затем определить уравнение, которое нужно решить для неизвестного.

Нам известно начальное давление P0 = 7,00 × 105 ПаP0 = 7,00 × 105 Па, начальная температура T0 = 18.0ºCT0 = 18.0ºC, а конечная температура Tf = 35,0ºCTf = 35,0ºC. Мы должны найти последнее давление PfPf. Как мы можем использовать уравнение PV = NkTPV = NkT? Поначалу может показаться, что дано недостаточно информации, потому что объем VV и число атомов NN не указаны. Что мы можем сделать, так это использовать уравнение дважды: P0V0 = NkT0P0V0 = NkT0 и PfVf = NkTfPfVf = NkTf. Если мы разделим PfVfPfVf – пользователем P0V0P0V0 мы можем придумать уравнение, которое позволяет нам решить для PfPf.

PfVfP0V0 = NfkTfN0kT0PfVfP0V0 = NfkTfN0kT0

13.20

Так как объем постоянный, VfVf size 12 {V rSub {size 8 {f}}} {} и V0V0 size 12 {V rSub}} {0} размер 8 {0} то же самое, и они уравновешиваются. То же самое верно для NfNf размера 12 {N rSub {size 8 {f}}} {} и N0N0 размера 12 {N rSub {size 8 {0}}} {} и размера kk 12 {k} {}, которые является константой. Следовательно,

PfP0 = TfT0.PfP0 = TfT0. размер 12 {{{P rSub {размер 8 {f}}} больше {P rSub {размер 8 {0}}}} = {{T rSub {размер 8 {f}}} больше {T rSub {размер 8 {0 }}}} “.”} {}

13,21

Затем мы можем изменить это, чтобы решить для PfPf размером 12 {P rSub {size 8 {f}}} {}:

Pf = P0TfT0, Pf = P0TfT0, размер 12 {P rSub {размер 8 {f}} = P rSub {размер 8 {0}} {{T rSub {размер 8 {f}}} больше {T rSub {размер 8 { 0}}}},} {}

13,22

, где температура должна быть в единицах кельвина, поскольку T0T0 размер 12 {T rSub {размер 8 {0}}} {} и TfTf размер 12 {T rSub {size 8 {f}}} {} являются абсолютными температурами.

Решение

1.Преобразование температуры из Цельсия в Кельвин.

T0 = 18,0 + 273 K = 291 KTf = 35,0 + 273 K = 308 KT0 = 18,0 + 273 K = 291 KTf = 35,0 + 273 K = 308 Kalignl {stack { размер 12 {T rSub {size 8 {0}} = left (“18” “.” 0+ “273” right) “K” = “291 K”} {} # T rSub {size 8 {f}} = left (“35” “.” 0+ “273” right) “K” = “308 K” {} }} {}

13,23

2. Подставьте известные значения в уравнение.

Pf = P0TfT0 = 7,00 × 105 Па308 K291 K = 7,41 × 105 ПаPf = P0TfT0 = 7,00 × 105 Па308 K291 K = 7,41 × 105 Па, размер 12 {P rSub {размер 8 {f}} = P rSub {размер 8 {0}} { {T rSub {size 8 {f}}} больше {T rSub {size 8 {0}}}} = 7 дюймов.”” 00 “умножить на” 10 “rSup {размер 8 {5}}” Па “влево ({{” 308 K “} больше {” 291 K “}} справа) = 7”. “” 41 “умножить на” 10 ” rSup {размер 8 {5}} «Па»} {}

13,24

Обсуждение

Конечная температура примерно на 6% выше исходной температуры, поэтому конечное давление также примерно на 6% больше. Обратите внимание, что абсолютное давление и абсолютная температура должны использоваться в законе идеального газа.

Установление соединений: домашний эксперимент – охлаждение воздушного шара

Надуйте баллон при комнатной температуре.Оставьте надутый баллон в холодильнике на ночь. Что происходит с воздушным шаром и почему?

Пример 13.7

Расчет количества молекул в кубическом метре газа

Сколько молекул содержится в типичном объекте, таком как газ в шине или вода в напитке? Мы можем использовать закон идеального газа, чтобы дать нам представление о том, насколько велик типичный размер NN 12 {N} {}.

Рассчитайте количество молекул в кубическом метре газа при стандартной температуре и давлении (STP), которое определяется как 0ºC0ºC размером 12 {0 ° C} {} и атмосферном давлении.

Стратегия

Поскольку давление, объем и температура заданы, мы можем использовать закон идеального газа PV = NkTPV = NkT, размер 12 {курсив “PV” = курсив “NkT”} {}, чтобы найти размер NN 12 {N} {} .

Решение

1. Определите известные.

T = 0 ° C = 273 KP = 1,01 × 105 ПаВ = 1,00 м3k = 1,38 × 10–23 Дж / KT = 0 ° C = 273 KP = 1,01 × 105 ПаВ = 1,00 м3k = 1,38 × 10–23 Дж / К

13,25

2 • Определите неизвестное: количество молекул, размер NN 12 {N} {}.

3.Измените закон идеального газа, чтобы решить для NN размером 12 {N} {}.

PV = NkTN = PVkTPV = NkTN = PVkTalignl {стек { размер 12 {ital “PV” = ital “NkT”} {} # размер 12 {N = {{ital “PV”} больше {ital “kT”}}} {} }} {}

13,26

4. Подставьте известные значения в уравнение и решите для размера NN 12 {N} {}.

N = PVkT = 1,01 · 105 Па · 1,00 м · 31,38 · 10−23 Дж / K273 K = 2,68 · 1025 молекул N = PVkT = 1,01 · 105 Па · 1,00 м31,38 · 10−23 Дж / K273 K = 2,68 · 1025 размер молекул 12 {N = {{ital “PV”} over {ital “kT”}} = {{left (1 “.”” 01 “умножить на” 10 “rSup {размер 8 {5}}” Па “справа) влево (1”. “” 00 м “rSup {размер 8 {3}} справа)} над {левым (1”. “.” “38” умножить на “10” rSup {размер 8 {- “23”}} “J / K” справа) влево (“273 K” справа)}} = 2 “.” “68” умножить на “10” rSup {size 8 {“25”}} “” молекулы “} {}

13,27

Обсуждение

Это число, несомненно, велико, учитывая, что газ – это в основном пустое пространство. Размер NN 12 {N} {} огромен даже в небольших объемах. Например, 1 см31 см3 размером 12 {1 “см” rSup {размер 8 {3}}} {} газа на STP имеет 2.68 × 10192,68 × 1019 размер 12 {2 “.” “68” ´ “10” rSup {размер 8 {“19”}}} {} молекул в нем. Еще раз отметим, что размер NN 12 {N} {} одинаков для всех типов или смесей газов.

Молей и число Авогадро

Иногда при измерении количества вещества удобно работать с единицей, отличной от молекул. Моль (сокращенно моль) определяется как количество вещества, которое содержит столько атомов или молекул, сколько атомов содержится ровно в 12 граммах (0,012 кг) углерода-12.Фактическое количество атомов или молекул в одном моле называется числом Авогадро (NA) (NA) размером 12 {\ (N rSub {size 8 {A}} \)} {} по признанию итальянского ученого Амедео Авогадро (1776–1776 гг.) 1856 г.). Он разработал концепцию мола, основываясь на гипотезе о том, что равные объемы газа при одинаковом давлении и температуре содержат равное количество молекул. То есть количество не зависит от типа газа. Эта гипотеза подтвердилась, и значение числа Авогадро составляет

. NA = 6.02 × 1023 моль −1. NA = 6,02 × 1023 моль − 1. размер 12 {N rSub {размер 8 {A}} = 6 дюймов ». “02” умножить на “10” rSup {размер 8 {“23”}} “” моль “rSup {размер 8 {- 1}}”. ” } {}

13.28

№ Авогадро

Одна родинка всегда содержит 6,02 × 10236,02 × 1023 размером 12 {6 “.” “02” ´ “10” rSup {size 8 {“23”}}} {} частиц (атомов или молекул), независимо от элемента или вещества. Моль любого вещества имеет массу в граммах, равную его молекулярной массе, которую можно вычислить из атомных масс, указанных в периодической таблице элементов.

NA = 6,02 × 1023 моль − 1NA = 6,02 × 1023 моль − 1, размер 12 {N rSub {size 8 {A}} = 6 “.” “02” умножить на “10” rSup {размер 8 {“23”}} “” моль “rSup {размер 8 {- 1}}} {}

13,29

Рисунок 13.19 Насколько велика родинка? На макроскопическом уровне один крот мячей для настольного тенниса покроет Землю на глубину около 40 км.

Проверьте свое понимание

Активным ингредиентом таблетки тайленола является 325 мг ацетаминофена (C8H9NO2) (C8H9NO2) размером 12 {\ (C rSub {размер 8 {8}} H rSub {размер 8 {9}} «NO» rSub {размер 8 { 2}} \)} {}.Найдите количество активных молекул парацетамола в одной таблетке.

Решение

Сначала нам нужно вычислить молярную массу (массу одного моля) ацетаминофена. Для этого нам нужно умножить количество атомов каждого элемента на атомную массу элемента.

(8 моль углерода) (12 г / моль) + (9 моль водорода) (1 г / моль) + (1 моль азота) (14 г / моль) + (2 моль кислорода) (16 г / моль) = 151 г (8 моль углерода) (12 г / моль) + (9 моль водорода) (1 г / моль) + (1 моль азота) (14 г / моль) + (2 моль кислорода) (16 г / моль) = 151 г

13.30

Затем нам нужно посчитать количество молей в 325 мг.

325 мг 151 грамм / моль1 грамм 1000 мг = 2,15 × 10-3 моль325 мг 151 грамм / моль1 грамм 1000 мг = 2,15 × 10-3 моль

13,31

Затем используйте число Авогадро для расчета количества молекул.

N = 2,15 · 10−3моль 6,02 · 1023молекул / моль = 1,30 · 1021молекул N = 2,15 · 10−3моль 6,02 · 1023молекул / моль = 1,30 · 1021 размер молекулы 12 {N = слева (2 “.” 15 “раз” 10 “rSup {размер 8 {- 3}}” “молей” справа) слева (6 “.” “02” умножить на “10” rSup {размер 8 {“23″}} `” молекул / моль “справа) = 1″ .”” 30 “умножить на” 10 “rSup {размер 8 {” 21 “}}” “молекул”} {}

13,32

Пример 13,8

Расчет молей на кубический метр и литров на моль

Рассчитайте: (а) количество молей в 1,00 м31,00 м3 размером 12 {1 “.” “00” “m” rSup {size 8 {3}}} {} газа на СТП, и (b) количество литров газа на моль.

Стратегия и решение

(a) Нас просят найти количество молей на кубический метр, и из примера 13.7 мы знаем, что количество молекул на кубический метр в STP равно 2.68 × 10252,68 × 1025 размер 12 {2 “.” “68” ´ “10” rSup {размер 8 {“25”}}} {}. Количество молей можно найти, разделив количество молекул на число Авогадро. Пусть nn размер 12 {n} {} обозначает количество молей,

нмоль / м3 = Nмолекул / м 36,02 × 1023молекул / моль = 2,68 × 1025молекул / м36,02 × 1023молекул / моль = 44,5моль / м3.нмоль /m3=Nmolecules/m36.02 × 1023molecules/mol=2.68 ×1025molecules/m36.02 ×1023molecules/mol=44.5mol/m3. размер 12 {n` “моль / м” rSup {размер 8 {3}} = {{N` “молекул / м” rSup {размер 8 {3}}} больше {6 “.”” 02 “умножить на” 10 “rSup {размер 8 {” 23 “}}` “молекул / моль”}} = {{2 “.” “68” умножить на “10” rSup {размер 8 {“25”}} “” молекул / м “rSup {размер 8 {3}}} больше {6”. “” 02 “умножить на” 10 “rSup {размер 8 {” 23 “}}” “молекул / моль”}} = “44” “.” 5` “моль / м” rSup {размер 8 {3}} “.”} {}

13,33

(b) Использование значения, полученного для количества молей в кубическом метре, и преобразование кубических метров в литров, получаем

103 л / м 344,5 моль / м3 = 22,5 л / моль. 103 л / м 344,5 моль / м3 = 22,5 л / моль. размер 12 {{{left (“10″ rSup {размер 8 {3}} `” L / m “rSup {size 8 {3}} right)} больше {44″.”5`” моль / м “rSup {size 8 {3}}}} =” 22 “”. “5`” л / моль “”. “} {}

13,34

Обсуждение

Это значение очень близко к принятому значению 22,4 л / моль. Небольшая разница связана с ошибками округления, вызванными использованием трехзначного ввода. Опять же, это число одинаково для всех газов. Другими словами, он не зависит от газа.

(Средняя) молярная масса воздуха (приблизительно 80% N2N2 размер 12 {N rSub {размер 8 {2}}} {} и 20% O2O2 размер 12 {O rSub {размер 8 {2}}} {} составляет M = 28.8 г. M = 28,8 г. размер 12 {M = “28” “.” 8 “г” “.” } {} Таким образом, масса одного кубометра воздуха составляет 1,28 кг. Если гостиная имеет размеры 5 м × 5 м × 3 м, 5 м × 5 м × 3 м, размер 12 {5 “м” умножить на “5 м” умножить на “3 м”} {} масса воздуха внутри комната 96 кг, что является типичной массой человека.

Проверьте свое понимание

Плотность воздуха при стандартных условиях (P = 1 атм (P = 1 атм, размер 12 {\ (P = 1 “атм”} {} и T = 20ºC) T = 20ºC) размер 12 {T = “20” ° C \ )} {} составляет 1,28 кг / м 31,28 кг / м3 размер 12 {1 “.”” 28 “” кг / м “rSup {размер 8 {3}}} {}. При каком давлении плотность 0,64 кг / м3 30,64 кг / м3 размер 12 {0”. “” 64 кг / м “rSup {size 8 {3}}} {} если температура и количество молекул остаются постоянными?

Решение

Лучший способ подойти к этому вопросу – подумать о том, что происходит. Если плотность упадет до половины от исходного значения и никакие молекулы не потеряны, объем должен удвоиться. Если мы посмотрим на уравнение PV = NkTPV = NkT size 12 {ital “PV” = ital “NkT”} {}, мы увидим, что когда температура постоянна, давление обратно пропорционально объему.Следовательно, если объем увеличится вдвое, давление должно упасть до половины от исходного значения, и Pf = 0,50 атм. Pf = 0,50 атм. размер 12 {P rSub {size 8 {f}} = 0 “.” «50» «банкомат» «. } {}

Закон идеального газа, переформулированный с использованием молей

Очень распространенное выражение закона идеального газа использует число молей, размер nn 12 {n} {}, а не количество атомов и молекул, размер NN 12 {N} { }. Начнем с закона идеального газа,

. PV = NkT, PV = NkT, размер 12 {ital “PV” = ital “NkT”} {}

13,35

, умножьте и разделите уравнение на число Авогадро NANA size 12 {N rSub {size 8 {A}}} {}.Это дает

PV = NNANAkT.PV = NNANAkT. размер 12 {ital “PV” = {{N} over {N rSub {size 8 {A}}}} N rSub {size 8 {A}} ital “kT” “.” } {}

13,36

Обратите внимание, что n = N / NAn = N / NA размер 12 {n = N / N rSub {размер 8 {A}}} {} – это количество родинок. Мы определяем универсальную газовую постоянную R = NAkR = NAk size 12 {R = N rSub {size 8 {A}} k} {} и получаем закон идеального газа в молях.

Закон идеального газа (в молях)

Закон идеального газа (в молях):

PV = nRT.PV = nRT. размер 12 {ital “PV” = ital “nRT”} {}

13,37

Числовое значение размера 12 RR {R} {} в единицах СИ составляет

R = NAk = 6,02 × 1023 моль − 11,38 × 10−23Дж / K = 8,31Дж / моль⋅K.R = NAk = 6,02 × 1023 моль − 11,38 × 10−23Дж / K = 8,31Дж / моль⋅K. размер 12 {R = N rSub {размер 8 {A}} k = левый (6 дюймов. “02” умножить на “10” rSup {размер 8 {“23”}} “” моль “rSup {размер 8 {- 1 }} справа) слева (1 “.” “38” умножить на “10” rSup {размер 8 {- “23”}} `” J / K “справа) = 8″. ” “31” Дж / “моль” cdot K} {}

13,38

В других единицах,

R = 1.99 кал / моль⋅KR = 0,0821 л⋅атм / моль⋅K.R = 1,99 кал / моль⋅KR = 0,0821 л⋅атм / моль⋅K.alignl {stack { размер 12 {R = 1 “.” “99” “кал / моль” cdot K} {} # размер 12 {R “= 0” “.” “0821 л” cdot “атм / моль” cdot K “.” } {} }} {}

13,39

Вы можете использовать любое значение размера RR 12 {R} {}, наиболее подходящее для конкретной задачи.

Пример 13.9

Расчет количества молей: газ в шине велосипеда

Сколько молей газа содержится в велосипедной шине объемом 2,00 × 10–3 м3 (2.00 л), 2,00 × 10–3 м3 (2,00 л), размер 12 {2 “.” “00” ´ “10” rSup {размер 8 {+ – 3}} “m” rSup {размер 8 {3}} \ (2 “.” “00 L” \),} {} давление 7,00 × 105 Па7 .00 × 105 Па, размер 12 {7 “.” “00” ´ “10” rSup {размер 8 {5}} “Па”} {} (манометрическое давление чуть менее 90,0 фунтов / дюйм 290,0 фунтов / дюйм2, размер 12 {“90” “.” 0 “фунтов / дюйм “rSup {size 8 {2}}} {}), и при температуре 18,0ºC18,0ºC размер 12 {” 18 “”. ” 0 ° C} {}?

Стратегия

Определите известные и неизвестные и выберите уравнение для решения неизвестного.В этом случае мы решаем закон идеального газа, PV = nRTPV = nRT size 12 {ital “PV” = ital “nRT”} {}, для числа моль nn размера 12 {n} {}.

Решение

1. Определите известные.

P = 7,00 × 105 ПаВ = 2,00 × 10–3 м3 T = 18,0 ° C = 291 KR = 8,31 Дж / моль⋅KP = 7,00 × 105 ПаВ = 2,00 × 10–3 м3T = 18,0 ° C = 291 KR = 8,31Дж / моль⋅Kalignl {stack { размер 12 {P = 7 “.” “00” умножить на “10” rSup {размер 8 {5}} “Па”} {} # V = 2 “.” «00» умножить на «10» rSup {размер 8 {- 3}} «m» rSup {размер 8 {3}} {} # Т = “18” “.” 0 ° C = “291 K” {} # R = 8 дюймов.”” 31 “” Дж / моль “кдот K {} }} {}

13,40

2. Перепишите уравнение, чтобы найти размер nn 12 {n} {}, и подставьте известные значения.

n = PVRT = 7,00 × 105Па2,00 × 10−3м38,31Дж / моль⋅K291 K = 0,579мольн = PVRT = 7,00 × 105Па2,00 × 10−3м38,31Дж / моль⋅K291 K = 0,579мольалигнл {стек { размер 12 {n = {{ital “PV”} больше {ital “RT”}} = {{слева (7 “.” “00” умножить на “10” rSup {size 8 {5}} “” Pa “справа) left (2 “.” 00 раз “10” rSup {размер 8 {- 3}} `m rSup {size 8 {3}} right)} over {left (8″. “” 31 “` “Дж / моль” cdot K справа) слева (“291” “K” справа)}}} {} # “” = “0” “.”” 579 “` “моль” {} }} {}

13.41

Обсуждение

Наиболее удобный выбор для размера RR 12 {R} {} в этом случае – 8,31 Дж / моль⋅К, 8,31 Дж / моль⋅К, размер 12 {8 “”. “31” “Дж / моль” cdot “K”} {}, потому что известные нам величины выражены в единицах СИ. Давление и температура получены из начальных условий в примере 13.6, но мы получили бы тот же ответ, если бы использовали окончательные значения.

Закон идеального газа можно рассматривать как еще одно проявление закона сохранения энергии (см. Сохранение энергии).Работа, выполняемая с газом, приводит к увеличению его энергии, увеличению давления и / или температуры или уменьшению объема. Эту повышенную энергию также можно рассматривать как увеличенную внутреннюю кинетическую энергию с учетом атомов и молекул газа.

Закон идеального газа и энергия

Давайте теперь исследуем роль энергии в поведении газов. Когда вы накачиваете велосипедную шину вручную, вы выполняете работу, многократно прилагая силу на расстоянии. Эта энергия идет на повышение давления воздуха внутри шины и повышение температуры насоса и воздуха.

Закон идеального газа тесно связан с энергией: единицы измерения с обеих сторон – джоули. Правая часть закона идеального газа в PV = NkTPV = NkT, размер 12 {ital “PV” = ital “NkT”} {} – это NkTNkT, размер 12 {ital “NkT”} {}. Этот термин примерно соответствует количеству поступательной кинетической энергии атомов или молекул NN размером 12 {N} {} при абсолютной температуре TT размером 12 {T} {}, как мы формально увидим в «Кинетической теории: атомное и молекулярное объяснение давления». и температура. Левая часть закона идеального газа – это PVPV размером 12 {ital “PV”} {}, который также имеет единицы измерения в джоулях.Из нашего исследования жидкостей мы знаем, что давление – это один из видов потенциальной энергии на единицу объема, поэтому давление, умноженное на объем, является энергией. Важным моментом является то, что в газе есть энергия, связанная как с его давлением, так и с его объемом. Энергия может быть изменена, когда газ выполняет работу по мере расширения – это мы исследуем в разделе «Методы теплопередачи и теплопередачи» – аналогично тому, что происходит в бензиновых или паровых двигателях и турбинах.

Стратегия решения проблем: Закон об идеальном газе

Шаг 1 Изучите ситуацию, чтобы определить, что речь идет об идеальном газе.Большинство газов почти идеальны.

Шаг 2 Составьте список того, какие количества указаны или могут быть выведены из проблемы, как указано (определить известные количества). Преобразуйте известные значения в соответствующие единицы СИ (K для температуры, Па для давления, м3 м3 размером 12 {m rSup {size 8 {3}}} {} для объема, молекул для размера NN 12 {N} {} и молей для nn размер 12 {n} {}).

Шаг 3 Определите, что именно необходимо определить в проблеме (определите неизвестные количества).Письменный список полезен.

Шаг 4 Определите, известно ли количество молекул или количество молей, чтобы решить, какую форму закона идеального газа использовать. Первая форма – PV = NkTPV = NkT размером 12 {ital “PV” = ital “NkT”} {} и включает в себя размер NN 12 {N} {}, количество атомов или молекул. Вторая форма – PV = nRTPV = nRT размером 12 {ital “PV” = ital “nRT”} {} и включает размер nn 12 {n} {}, количество молей.

Шаг 5 Решите закон идеального газа для количества, которое необходимо определить (неизвестное количество).Вам может потребоваться соотношение конечных состояний к начальным состояниям, чтобы исключить неизвестные количества, которые остаются фиксированными.

Шаг 6 Подставьте известные величины вместе с их единицами измерения в соответствующее уравнение и получите численные решения с указанием единиц. Обязательно используйте абсолютную температуру и абсолютное давление.

Шаг 7 Проверьте ответ, чтобы узнать, разумен ли он: имеет ли он смысл?

Проверьте свое понимание

Жидкости и твердые вещества имеют плотность примерно в 1000 раз больше, чем газы.Объясните, как это означает, что расстояния между атомами и молекулами в газах примерно в 10 раз больше, чем размер их атомов и молекул.

Решение

Атомы и молекулы в твердых телах и жидкостях расположены близко друг к другу. В газах они разделены пустым пространством. Таким образом, газы имеют меньшую плотность, чем жидкости и твердые тела. Плотность – это масса на единицу объема, а объем связан с размером тела (например, сферы) в кубе. Таким образом, если расстояние между атомами и молекулами увеличивается в 10 раз, то занимаемый объем увеличивается в 1000 раз, а плотность уменьшается в 1000 раз.

Закон об идеальном газе

При изучении поведения газов в замкнутых пространствах полезно ограничиться изучением идеальных газов. Идеальные газы – это теоретические модели реальных газов, в которых используется ряд основных предположений, упрощающих их изучение. Эти допущения включают рассмотрение газа как состоящего из множества частиц, которые беспорядочно перемещаются в контейнере. Частицы, в среднем, находятся далеко друг от друга, и они не оказывают друг на друга силы, если они не вступают в контакт при упругом столкновении.

При нормальных условиях, таких как стандартная температура и давление, большинство газов ведут себя так же, как идеальный газ. Тяжелые газы, а также газы при очень низких температурах или очень высоких давлениях не так хорошо моделируются идеальным газом.

Закон об идеальном газе связывает давление, объем, количество частиц и температуру идеального газа в одном уравнении, и его можно записать разными способами.

В этом уравнении P – давление газа (в паскалях), V – объем газа (в кубических метрах), n – количество молей газа, N – количество молекул газа, R – универсальная газовая постоянная, равная 8.31 Дж / моль · К (что также составляет 0,08206 л · атм / моль · К), kB – постоянная Больцмана (1,38 × 10 ^-23 Дж / К), а T – температура в Кельвинах. Чтобы преобразовать молекулы в моль, вы можете использовать число Авогадро (N0 = 6,02 × 10 ^-23 молекул / моль):

Обратите внимание, что Паскаль, умноженный на кубический метр, равен ньютон-метру или Джоуля. Кроме того, постоянная Больцмана – это постоянная закона идеального газа, деленная на число Авогадро.

Вопрос: Сколько молей идеального газа эквивалентно 3.01 × 10 ²⁴ молекул?
Ответ:
Вопрос: Найдите количество молекул в 0,4 моля идеального газа.
Ответ:
Вопрос: Сколько молей газа содержится в баллоне с углекислым газом объемом 0,3 м ³, выдерживаемом при температуре 320 К и давлении 1 × 10 ⁶ Паскалей?
Ответ:
Вопрос: Кубический метр углекислого газа при комнатной температуре (300K) и атмосферном давлении (101,325 Па) сжимается до объема 0.1 м ³ и выдерживали при температуре 260К. Какое давление сжатого углекислого газа?
Ответ: Поскольку количество молей газа постоянно, вы можете упростить уравнение идеального газа до закона комбинированного газа, установив соотношение начального давления, объема и температуры, равное конечному давлению, объему и температуре.
Поскольку вам известны все величины в этом уравнении, кроме конечного давления, вы можете напрямую вычислить конечное давление.
Вопрос: Один моль газообразного гелия находится внутри воздушного шара. Какое давление внутри воздушного шара, когда воздушный шар поднимается до точки в атмосфере, где температура составляет -12 ° C, а объем воздушного шара составляет 0,25 кубических метра?
Ответ: Сначала вы должны перевести температуру из градусов Цельсия в Кельвины.
Затем вы можете использовать закон идеального газа для определения давления внутри воздушного шара.

Также довольно просто найти полную внутреннюю энергию идеального газа. Напомним, что средняя кинетическая энергия частиц идеального газа описывается формулой:

Полная внутренняя энергия идеального газа может быть найдена умножением средней кинетической энергии частиц газа на количество частиц (N) в газе. Следовательно, внутреннюю энергию газа можно рассчитать по формуле:

Вопрос: Найдите внутреннюю энергию 5 молей кислорода при температуре 300К.
Ответ:
Вопрос: Какова температура 20 молей аргона с полной внутренней энергией 100 кДж?
Ответ:

Закон идеального газа – AP Physics 2

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Закон об идеальном газе – Викиверситет

Закон об идеальном газе – это знаменитое уравнение, которое преподают всем студентам-химикам:

PV = NRT {\ displaystyle PV = NRT \,}

, который описывает поведение «идеального» газа.Различные его части также известны как закон Чарльза , закон Бойля , закон Гей-Люссака или закон Авогадро .

Формулировка этого закона сыграла решающую роль в развитии атомной теории (то есть осознании того, что материя действительно состоит из атомов), а также в развитии термодинамики.

Этот «закон» долгое время был всего лишь экспериментальным наблюдением, без какого-либо научного понимания того, почему он истинен.Только в середине 1800-х годов с появлением кинетической теории газов она получила прочную теоретическую основу. Эта теоретическая основа выходит за рамки данной статьи.

В формуле PV = NRT {\ displaystyle PV = NRT \,}:

P – давление газа. В единицах СИ это измеряется в паскалях или ньютонах силы на квадратный метр площади. («Стандартное атмосферное давление на уровне моря» составляет около 101 000 паскалей или 101 килопаскалей.100 кПа также известно как 1 бар , а давление часто описывается как миллибар . На барометрах, откалиброванных по ртути, 100 кПа составляет 29,5 дюймов (750 миллиметров) ртутного столба, поэтому стандартное атмосферное давление составляет 29,8 дюйма.)
V – объем в кубических метрах.
T – температура в Кельвинах. То есть абсолютная температура . Кельвин или абсолютная температура – это температура по Цельсию плюс 273,15.
N – количество газа в молях.Моль определяется как число Авогадро (6,022 x 10 ²³) частиц. Это число выбрано таким образом, чтобы 1 моль любого атома или молекулы, измеренный в граммах, был равен атомному весу всех атомов, содержащихся в молекуле. Например, хлор представляет собой двухатомную молекулу, Cl ₂. Атомный вес хлора составляет 35,45, поэтому 1 моль молекул Cl ₂ весит 70,9 грамма.

R – универсальная газовая постоянная , которая заставляет все это работать.{3})} {(моль) (Кельвин)}}}

что является

8,314 Джоуля (моль) (Кельвин) {\ displaystyle 8.314 \ {\ frac {Джоуль} {(моль) (Кельвин)}}}

Различные части закона были открыты в несколько этапов несколькими людьми, проводившими тщательные эксперименты в 17 ^-м, 18 ^-м и 19 ^-м веках. Это применимо только к «идеальным» газам (см. Обсуждение этого вопроса в газах и газовых законах), но обычные газы достаточно близки к идеальному поведению, чтобы эксперименты были плодотворными.

Анимация, показывающая соотношение между давлением и объемом, когда количество и температура остаются постоянными.

Закон Бойля , сформулированный около 1662 года Робертом Бойлем (1627–1691), гласит, что при постоянной температуре объем, занимаемый данным количеством газа, обратно пропорционален давлению. Интуитивно понятно, что поршень на баллоне с газом «пружинит» – он сопротивляется попыткам его толкнуть.

PV = что-то, что зависит от температуры для данного количества данного газа {\ displaystyle PV = {\ textrm {something}} \ \ {\ textrm {that}} \ \ {\ textrm {зависит}} \ \ {\ textrm {on}} \ \ {\ textrm {temperature}} \ \ {\ textrm {for}} \ \ {\ textrm {a}} \ \ {\ textrm {given}} \ \ {\ textrm {amount}} \ \ {\ textrm {of}} \ \ {\ textrm {a}} \ \ {\ textrm {given}} \ \ {\ textrm {gas}} \,}

Анимация, демонстрирующая взаимосвязь между объемом и температурой.

Закон Гей-Люссака , сформулированный около 1802 года Жозефом Луи Гей-Люссаком (1778-1850), гласит, что при постоянном давлении объем, занимаемый данным количеством газа, прямо пропорционален температуре.

Этот закон иногда называют законом Чарльза , после более ранней формулировки того же принципа около 1787 года Жаком Шарлем (1746-1823).

Интуитивно понятно, что когда газ нагревается, он расширяется. Это потребовало переопределения шкалы температур, чтобы добиться пропорциональности.Эта шкала температур теперь называется шкалой Кельвина или абсолютной температуры . Температура Кельвина на 273,15 градуса выше, чем температура Цельсия или Цельсия. Закон Гей-Люссака подразумевает, что, если бы газ можно было охладить до абсолютного нуля (0 ° Кельвина или -273,15 ° Цельсия), его объем упал бы до нуля. На практике вещество перестает быть газом до того, как будет достигнута эта точка.

Соединяя закон Бойля и закон Гей-Люссака, получаем:

PVT = то, что зависит от типа и количества газа {\ displaystyle {\ frac {PV} {T}} = {\ textrm {something}} \ \ {\ textrm {that}} \ \ {\ textrm {зависит}} \ \ {\ textrm {on}} \ \ {\ textrm {the}} \ \ {\ textrm {type}} \ \ {\ textrm {and}} \ \ {\ textrm {количество}} \ \ {\ textrm {of}} \ \ {\ textrm {gas}} \,}

Правая часть этого уравнения явно пропорциональна количеству газа, измеренному в граммах, например, поскольку два грамма занимают вдвое больший объем, чем один грамм, при прочих равных условиях.

Примерно в 1811 году Амедео Авогадро (1776-1856) сделал замечательное открытие: если количество газа измеряется в реальном количестве молекул, существует только одна константа – она не зависит от типа газа. Это основано на атомной теории, сформулированной около 1803 года Джоном Дальтоном (1766-1844), согласно которой материя состоит из молекул и атомов и что масса данного атома пропорциональна его атомному весу – мера, которая была отработана. к тому времени многие элементы в зависимости от их химического состава.Это означало, что если количество газа измеряется в единицах, кратных его атомному весу, существует только одна константа. Количество газа (или любого другого вещества), вес которого в граммах равен его атомному или молекулярному весу, называется моль (или, возможно, грамм-моль , чтобы прояснить, как взвешиваются предметы) и является определенное количество атомов или молекул. Это число , число Авогадро , которое теперь принято равным 6,022 x 10 ²³.

Раньше число Авогадро не было достоверно известно.По сути, это мера того, насколько малы атомы – число атомов водорода Авогадро весит 1,008 грамма (его атомный вес). Было просто известно, что атомы чрезвычайно малы, и, следовательно, число Авогадро чрезвычайно велико. Но закон идеального газа и химические законы определенных пропорций и множественных пропорций, которые привели к теории атома, не зависели от знания фактического значения.

Собирая все вместе, получаем:

PV = NRT {\ displaystyle PV = NRT \,}

где N – количество молей газа, то есть количество молекул, деленное на число Авогадро, или, что то же самое, масса в граммах, деленная на молекулярную массу. R – универсальная газовая постоянная:

R = 8,314 Дж (моль) (Кельвин) {\ displaystyle R = 8,314 \ {\ frac {Джоуль} {(моль) (Кельвин)}}}

В лаборатории это обычное дело использовать «стандартную температуру и давление» (STP) в качестве начального приближения. Это температура 273,15 ° Кельвина, или 0 ° Цельсия, и давление 101,325 килопаскалей, или 760 миллиметров ртутного столба. При таком предположении объем одного моля газа равен:

V = RTP = 8.{3} = 22,4 \ L}

Итак, на СТП 39,95 грамма (его атомная масса) аргона занимает 22,4 литра.

Это конкретное значение газовой постоянной на самом деле является артефактом выбора числа Авогадро, которое является артефактом способа измерения атомных весов. Мы можем разделить газовую постоянную на число Авогадро, получив более фундаментальное значение «на молекулу» вместо значения «на моль». Это называется постоянной Больцмана, обычно обозначаемой k .{-23} \ {\ frac {Джоуль} {Кельвин}}}

Выраженный таким образом, закон идеального газа имеет вид

PV = nkT {\ displaystyle PV = nkT \,}

, где n – количество молекул, а k – постоянная Больцмана. Принято считать, что n в нижнем регистре считает молекулы, а N в верхнем регистре – моль.

Постоянная Больцмана играет важную роль в термодинамике и статистической механике.

Теплоемкость или удельная теплоемкость вещества – это количество тепловой энергии, которое требуется для повышения его температуры на некоторую величину. Его часто измеряют в Джоулях на градус (Цельсия или Кельвина) на количество вещества. Хотя общая тема теплоемкости вещества выходит далеко за рамки данной статьи, есть несколько вещей, которые можно сказать об этом в контексте закона идеального газа.

Количество вещества может быть измерено в граммах, что означает, что единицей теплоемкости является Джоуль (грамм) (Кельвин) {\ displaystyle {\ frac {Джоуль} {(грамм) (Кельвин)}}}.Для веществ, которые имеют четкое представление о том, что составляет молекулу, моль, возможно, является лучшим выбором в качестве единицы вещества. Измеренная таким образом единица теплоемкости – Джоуль (моль) (Кельвин) {\ displaystyle {\ frac {Джоуль} {(моль) (Кельвин)}}}. Это та же размерность, что и у универсальной газовой постоянной R , что означает, что теплоемкость вещества может быть выражена как кратное R .

Для газов имеет значение, поддерживается ли объем постоянным («теплоемкость при постоянном объеме», обозначается C _v) или давление остается постоянным («теплоемкость при постоянном давлении», обозначается C _p ).Для жидкостей или твердых тел изменение объема незначительно, поэтому практически не имеет значения.

Вот несколько примеров, все при разумных температурах и давлениях:

Вещество	C, в Джоулях (граммах) (Кельвинах) {\ displaystyle {\ frac {Joules} {(граммах) (Кельвинах)}}}	C, в Джоулях (моль) (Кельвин) {\ displaystyle {\ frac {Джоуль} {(моль) (Кельвин)}}}	C, кратное R
Гелий	C _p = 5.19	C _p = 20,78	C _p = 2,5 R
	С _против = 3,12	C _против = 12,47	C _v = 1,5 R
Неон	C _p = 1,03	C _p = 20,78	C _p = 2,5 R
	C _против = 0,618	C _против = 12,47	C _v = 1.5 р
Аргон	C _p = 0,52	C _p = 20,78	C _p = 2,5 R
	C _против = 0,312	C _против = 12,47	C _v = 1,5 R
Азот	C _p = 1,04	С _п = 29,1	С _п = 3,5 R
	C _v =.742	С _против = 20,8	C _v = 2,5 R
Кислород	C _p = 0,918	C _p = 29,39	C _p = 3,53 R
	C _против = 0,659	С _против = 21,1	C _v = 2,53 R
Хлор	C _p = 0,478	С _п = 33,9	C _p = 4.08 R
	C _против = 0,361	С _против = 25,6	C _v = 3,08 R
Аммиак (газ, 40 ° C)	С _п = 2,12	С _р = 36,0	C _p = 4,33 R
	C _против = 1,63	C _против = 27,7	C _v = 3,33 R
Гексафторид серы	C _p = 5.52	С _п = 806	C _p = 97 R
	C _против = 5,47	С _против = 798	C _v = 96 R
Литий	С = 3,57	С = 24,8	С = 2,98 Р
Алюминий	C = 0,897	С = 24,2	С = 2,91 Р
Медь	С =.385	C = 24,47	С = 2,94 Р
Утюг	C = 0,412	C = 25,09	С = 3,02 Р
Сера	C = 0,709	C = 22,75	С = 2,73 Р
Уран	С = 0,116	С = 27,7	С = 3,33 р
Вода (жидкость, комнатная температура)	С = 4,184	C = 75,3	С = 9.06 R
Пар (100 ° C)	C _p = 2,02	С _п = 36,4	C _p = 4,38 R
	С _против = 1,56	С _против = 28,1	C _v = 3,38 R

Тот факт, что для многих веществ теплоемкость невероятно просто кратна R , объясняется кинетической теорией и статистической механикой и выходит за рамки данной статьи.Однако существует простая связь между C _p и C _v для любого газа, который подчиняется закону идеального газа.

Поскольку R = 8,314 Дж на моль-Кельвин, можно проверить, что третий столбец в приведенной выше таблице всегда в 8,314 раза больше четвертого столбца. Поскольку отношение моля к грамму является молекулярной массой, можно проверить, что в третьей колонке всегда умножена молекулярная (не атомная) масса второй колонки. Например, молекулярная масса хлора (Cl ₂) равна 70.9, поэтому 33,9 = 0,478 × 70,9.

калорий – единица энергии, равная 4,184 джоулей. Это делает теплоемкость жидкой воды равной 1 калории на грамм-Кельвина. килокалорий (или «большая калория», написанная с заглавной буквы C) в 1000 раз больше, или 4184 Джоуля. Теплоемкость жидкой воды составляет 1 калорию на килограмм-кельвин. Калорийность, используемая при измерении питательных веществ, – это калория с высоким содержанием С.

Связь между C

_p и C _v [править | править код]

Поскольку объем газа может легко измениться, необходимо тщательно определять теплоемкость.«Теплоемкость при постоянном объеме» (C _v) – это количество тепловой энергии, которое требуется для повышения температуры пробы газа на некоторую величину при сохранении постоянного объема. Когда вводится тепловая энергия, температура и давление повышаются. «Теплоемкость при постоянном давлении» (C _p) измеряется при поддержании постоянного давления. Когда вводится тепловая энергия, температура и объем увеличиваются.

Предположим, что некоторое количество Q _v тепловой энергии вводится в баллон с газом, заставляя его поддерживать постоянным.К ΔT температура повысится, а давление повысится. Никаких механических работ производиться не будет, так как поршень не двигается. Отношение тепловой энергии на моль к повышению температуры составляет C _v :

Qv = NCvΔT {\ displaystyle Q_ {v} = NC_ {v} \ Delta {} T}

Теперь предположим, что вместо этого вводится количество Q _p тепловой энергии, удерживая постоянное давление. То есть поршень может двигаться свободно и имеет фиксированный вес. Q _p настроен таким образом, чтобы повышение температуры было таким же. На этот раз газ совершит механическую работу, равную длине хода поршня, умноженной на силу. Сила – это просто давление, умноженное на площадь поршня, поэтому

ΔE = lF = lPA {\ displaystyle \ Delta {} E = lF = lPA}

Но lA = ΔV {\ displaystyle lA = \ Delta {} V}, изменение объема, поэтому

ΔE = PΔV {\ displaystyle \ Delta {} E = P \ Delta {} V}

Сейчас

Δ (PV) = PΔV + VΔP {\ displaystyle \ Delta {} (PV) = P \ Delta {} V + V \ Delta {} P}

Но ΔP = 0 {\ displaystyle \ Дельта {} P = 0} в этом случае, поэтому

ΔE = PΔV = Δ (PV) = NRΔT {\ displaystyle \ Delta {} E = P \ Delta {} V = \ Delta {} (PV) = NR \ Delta {} T}

Но для сохранения энергии требуется, чтобы тепловая энергия во втором случае была на ΔE {\ displaystyle \ Delta {} E} больше, чем тепловая энергия в первом случае, поэтому

Qp − Qv = ΔE = NRΔT = N (CP − Cv) ΔT {\ displaystyle Q_ {p} -Q_ {v} = \ Delta {} E = NR \ Delta {} T = N (C_ {P } -C_ {v}) \ Delta {} T}

Итак

Cp = Cv + R {\ displaystyle C_ {p} = C_ {v} + R}

Из приведенной выше таблицы видно, что это соотношение сохраняется для всех (идеальных) газов, даже тех , нравиться Гексафторид серы, обладающий необычно большой теплоемкостью.

Идеальный газ, все формулы и примеры

Давление идеального газа

Законы идеальных газов

Примеры решения задач

Идеальный газ. Уравнение состояния идеального газа. Изопроцессы.

Что рассматривается в молекулярной физике?

Связанное понятие № 1: закон Авогадро

Идеальный газ. Уравнение состояния идеального газа и манипуляции с ним

Выведем формулу для давления

Процессы идеального газа

Постоянным остается объем

Постоянным остается температура

Связанное понятие № 2: парциальное давление

Для чего это нужно

Богданов К.Ю. – учебник по физике для 10 класса

Доклал оснлвное ураанение молекулярно кинетической теории газоы кратко

Идеальный газ лекция основное уравнение мкт

Как изменяется импульс слоя газа за счет молекул вылетающих в него

Решебник физики мкт

Чем объясняется давление газа в МКТ?

Как изменяется импульс слоя газа за счет молекул, влетающих в него?

От чего зависит количество молекул в отдельном слое?

Какой смысл имеет средний квадрат скорости?

Почему мы используем понятие среднего квадрата скорости?

Почему уравнение давления идеального газа называют основ­ным уравнением МКТ?

Идеальный газ.

Идеальный газ

Параметры состояния газа

Основное уравнение молекулярно-кинетической теории

Температура

Калькулятор уравнения состояния идеального газа

Математические модели и идеальный газ

Основные газовые законы

Закон идеального газа

Пример использования уравнения идеального газа

Вычисление молей

Заключение

12.4: Закон идеального газа – Physics LibreTexts

Эмпирический вывод

Изотермы

Постоянное давление

Изобарический процесс

Одноатомный газ

Удельная теплоемкость

Решение проблем

Пример

Число Авогадора

Измерение N

Абсолютная температура

Шкала Кельвина

Ключевые моменты

Ключевые термины

идеального газа | химия и физика

| Протокол

13.3 Закон идеального газа – College Physics

Закон об идеальном газе

Пример 13.6

Расчет изменений давления из-за изменений температуры: давление в шинах

Стратегия

Решение

Обсуждение

Установление соединений: домашний эксперимент – охлаждение воздушного шара

Пример 13.7

Расчет количества молекул в кубическом метре газа

Стратегия

Решение

Обсуждение

Молей и число Авогадро

№ Авогадро

Проверьте свое понимание

Решение

Пример 13,8

Расчет молей на кубический метр и литров на моль

Стратегия и решение

Обсуждение

Проверьте свое понимание

Решение

Закон идеального газа, переформулированный с использованием молей

Закон идеального газа (в молях)

Пример 13.9

Почему уравнение давления идеального газа называют основным уравнением МКТ?