Идеальный газ формулы физика: Ошибка 403 — доступ запрещён

Идеальный газ – Wikiwand

• ВведениеИдеальный газ
• История
• Классический идеальный газМолекулярно-кинетическая теория идеального газаТермическое уравнение состояния и термические коэффициенты идеального газаСмесь идеальных газовСовершенный газ (гидроаэромеханика)ТеплоёмкостьЭнтропия и термодинамические потенциалы
• Применение теории идеального газаФизический смысл температуры газаРаспределение БольцманаАдиабатический процессСкорость звука
• Квантовый идеальный газФерми-газБозе-газ
• Идеальный газ в гравитационном поле
• Пределы применимости теории идеального газа
• См. также
• Комментарии
• Примечания
• Литература

Уважаемый Wikiwand AI, давайте упростим задачу, просто ответив на эти ключевые вопросы:

Перечислите основные факты и статистические данные о %d0%98%d0%b4%d0%b5%d0%b0%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9 %d0%b3%d0%b0%d0%b7?

Кратко изложите эту статью для 10-летнего ребёнка

ПОКАЗАТЬ ВСЕ ВОПРОСЫ

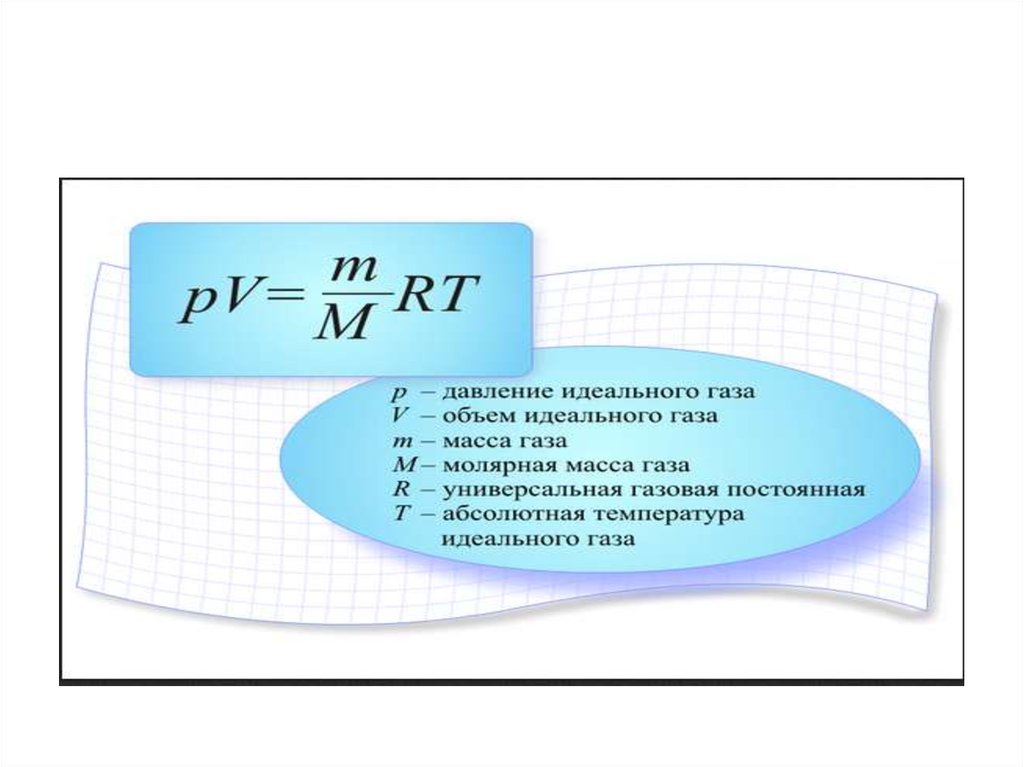
Идеа́льный газ — теоретическая модель, широко применяемая для описания свойств и поведения реальных газов при умеренных давлениях и температурах. В этой модели, во-первых, предполагается, что составляющие газ частицы не взаимодействуют друг с другом, то есть их размеры пренебрежимо малы, поэтому в объёме, занятом идеальным газом, нет взаимных неупругих столкновений частиц. Частицы идеального газа претерпевают столкновения только со стенками сосуда. Второе предположение: между частицами газа нет дальнодействующего взаимодействия, например, электростатического или гравитационного. Дополнительное условие упругих столкновений между молекулами и стенками сосуда в рамках молекулярно-кинетической теории приводит к термодинамике идеального газа .

Статья является частью одноименной серии.
Термодинамика
Уравнение состояния Идеальный газ Термодинамические величины Термодинамические потенциалы Термодинамические циклы Фазовые переходы
См. также «Физический портал»

В различных расширенных моделях идеального газа предполагается, что частицы имеют внутреннюю структуру и протяжённые размеры, что можно представить частицы в виде эллипсоидов или сфер, соединённых упругими связями (например, двухатомные молекулы). Представление частиц газа в виде многоатомных молекул приводит к возникновению дополнительных степеней свободы, что побуждает учитывать энергию не только поступательного, но и вращательно-колебательного движения частиц, а также не только центральные, но и нецентральные столкновения частиц[1].

Модель широко применяется для решения задач термодинамики газов и аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с достаточной для практических расчётов точностью хорошо описывается моделью идеального газа.

В случае очень больших давлений требуется применение более точных уравнений состояния реальных газов, например, полуэмпирического уравнения Ван-дер-Ваальса, в котором учитывается притяжение между молекулами и их конечные размеры.

При очень высоких температурах молекулы реальных газов могут диссоциировать на составляющие их атомы, или атомы могут ионизироваться с отщеплением электронов. Поэтому в случаях высоких давлений и/или температур уравнения состояния идеального газа применимы только с некоторыми допущениями, либо неприменимы совсем.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и подчиняются статистике Максвелла — Больцмана),

квазиклассический идеальный газ[2] (для которого — в отличие от классического идеального газа — не выполняется закон равномерного распределения энергии по степеням свободы[3][4]) и квантовый идеальный газ (его свойства определяются законами квантовой механики и описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).

С термодинамической точки зрения различие между классическим и квазиклассическим идеальными газами состоит в следующем. Теплоёмкость классического идеального газа не зависит от температуры и однозначно задана геометрией молекулы газа[5], которая тем самым определяет вид калорического уравнения состояния газа.

Классические идеальные газы с одинаковой геометрией молекул подчиняются одному и тому же калорическому уравнению состояния. Теплоёмкость квазиклассического идеального газа зависит от температуры[6][K 1], причём эта зависимость индивидуальна для каждого газа; соответственно каждый квазиклассический идеальный газ описывается своим собственным калорическим уравнением состояния. Очень часто — в том числе и в данной статье, — когда различия между классическим и квазиклассическим приближениями не играют роли, термин «классический идеальный газ» рассматривают как синоним выражения « неквантовый идеальный газ». При макроскопическом подходе идеальными классическими и квазиклассическими газами называют гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состояния Клапейрона[11][12] (Клапейрона — Менделеева[13][12]). Иногда дополнительно указывают, что для классического идеального газа справедлив закон Джоуля[14][15][16][17]. Термодинамика утверждает, что закон Джоуля выполняется для любого флюида с уравнением состояния вида pT=f(V){\displaystyle {\frac {p}{T}}=f(V)} или pV=f(T){\displaystyle pV=f(T)}, где p{\displaystyle p} — давление, T{\displaystyle T} — абсолютная температура и V{\displaystyle V} — объём (см.

[18][19][20]). Поэтому, давая дефиницию классическому идеальному газу, упоминать о законе Джоуля необязательно. С другой стороны, если рассматривать данный закон как обобщение экспериментальных данных, то изложение макроскопической теории классического идеального газа требует привлечения только самых элементарных сведений из термодинамики.

Популярность модели «идеальный газ» в учебных курсах термодинамики обусловлена тем обстоятельством, что результаты, получаемые с помощью уравнения Клапейрона, представляют собой не слишком сложные математические выражения и обычно допускают простой аналитический и/или графический анализ поведения входящих в них величин. Квазиклассическое приближение используют для вычисления термодинамических функций газов по их молекулярным данным[21][22][23].

Физика Идеальный газ в молекулярно-кинетической теории. Основное уравнение молекулярно-кинетической теории

Материалы к уроку

• 28. Идеальный газ в молекулярно-кинетической теории. Основное уравнение молекулярно-кинетической теории.doc

  58 KBСкачать

• 28. Идеальный газ в молекулярно-кинетической теории. Основное уравнение молекулярно-кинетической теории.ppt

  20.79 MBСкачать

Конспект урока

    Известно, что частицы в газах, в отличие от жидкостей и твердых тел, располагаются друг относительно друга на расстояниях, существенно превышающих их собственные размеры. В этом случае взаимодействие между молекулами пренебрежимо мало и кинетическая энергия молекул много больше энергии межмолекулярного взаимодействия. Для выяснения наиболее общих свойств, присущих всем газам, используют упрощенную модель реальных газов – идеальный газ.

Идеальный газ имеет отличия от реального газа.
1. Частицы идеального газа – сферические тела очень малых размеров, практически материальные точки.
2. Между частицами отсутствуют силы межмолекулярного взаимодействия.
3. Соударения частиц являются абсолютно упругими.
Молекулярно-кинетическая теория рассматривает идеальный газ как модель, в которой не учитывается взаимодействие частиц и их собственный объем. Частицы непрерывно хаотично двигаются. Соударение частиц происходит по закону упругого взаимодействия. 
Состояние идеального газа и процессы, проходящие в нем, будут определяться количеством частиц (молекул), из которых состоит газ, и их микроскопическими параметрами или микропараметрами. К таким параметрам относятся: масса, диаметр, скорость, энергия.
    Однако состояние газов можно охарактеризовать физическими величинами, относящимися не к каждой молекуле, а ко всему газу в целом.  Если состояние газа не меняется, то не меняются и эти параметры.  
Температура, объем, давление принято называть макроскопическими параметрами или макропараметрами состояния газа.
   Реальные разреженные газы действительно ведут себя подобно идеальному газу. Используя модель идеального газа, объясним происхождение давления газа. Вследствие теплового движения, частицы газа время от времени ударяются о стенки сосуда. При каждом ударе молекулы действуют на стенку сосуда с некоторой силой. Складываясь друг с другом, силы ударов отдельных частиц образуют некоторую силу давления, постоянно действующую на стенку. Чем больше частиц содержится в сосуде, тем чаще они будут ударяться о стенку сосуда, и тем большей будет сила давления, а значит и давление. Чем быстрее движутся частицы, тем сильнее они ударяют в стенку сосуда.
 Проведем опыт: толкнем мяч, он начнет двигаться, затем ударится о стенку. Если мяч катится медленно, то он при ударе подействует на стенку с меньшей силой, если толкнем мяч сильнее, то он будет двигаться быстро и удар о стенку будет сильнее.

 
Проведем другой опыт. Возьмем 2 мяча разного размера и толкнем с одинаковой силой, мы увидим, что сила удара большого мяча больше. Следовательно, чем больше масса частицы, тем больше сила удара. 
Посмотрите, как перемешиваются шары в игре «Спортлото». Чем быстрее двигаются шары, тем чаще они ударяют о стенки. Также и частицы газа, чем быстрее они двигаются, тем чаще они ударяются о стенки сосуда. 
Рассмотрим поведение газа в закрытом сосуде. Манометр показывает давление газа. Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с некоторой силой. В результате беспорядочных ударов о стенку давление быстро меняется со временем. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади поверхности его чувствительного элемента – мембраны. Несмотря на небольшие изменения давления, среднее значение давления практически оказывается вполне определенной величиной, так как ударов о стенку очень много, а массы молекул очень малы.
 Для вычисления среднего давления надо знать среднюю скорость молекул (точнее, среднее значение квадрата скорости), которая зависит от движения всех частиц.
Но невозможно проследить за движением всех молекул, из которых состоит газ. Их слишком много, и двигаются они по очень сложным траекториям. Но нам не нужно знать, как двигается каждая молекула. Выясним, к какому результату приводит движение всех молекул газа. Молекулы участвуют в беспорядочном (тепловом) движении, поэтому скорость любой молекулы может оказаться как очень большой, так и очень малой. Направление движения молекул постоянно меняется при их столкновениях друг с другом.
Скорости отдельных молекул могут быть любыми, однако среднее значение модуля этих скоростей вполне определенное. Точно так же рост учеников в классе неодинаков, но его среднее значение – определенное число. Чтобы это число найти, надо сложить рост отдельных учеников и разделить эту сумму на число учащихся.
Обозначим модули скоростей отдельных молекул газа через в1, в2, в3 и так далее.  
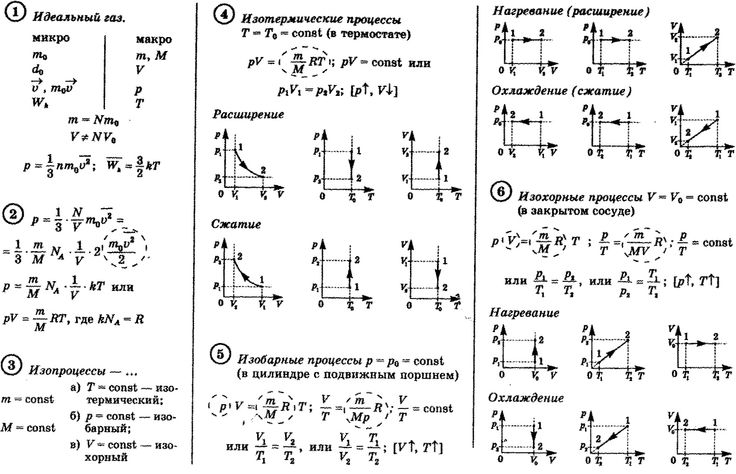
Так как в дальнейшем нам понадобится среднее значение не самой скорости, а квадрата скорости. От этой величины зависит средняя кинетическая энергия молекул. Средняя кинетическая энергия молекул имеет очень большое значение во всей молекулярно-кинетической теории.
Среднее значение квадрата скорости 
равно сумме квадратов скоростей всех молекул, деленной на  число молекул в газе. 
Скорость – векторная величина, и молекулы двигаются в сосуде в различных направлениях, поэтому мы должны учитывать, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат ОХ, ОY, ОZ. Поэтому
В в квадрате равно сумме В икс в квадрате, В игрек в квадрате, В зет в квадрате.
Средние значения величин В икс в квадрате, В игрек в квадрате, В зет в квадрате можно определить с помощью формул, подобных формуле под номером один (1).  Между средним значением квадрата проекции скорости Вэ и средними значениями квадратов проекций существует такое же соотношение, как соотношение в формуле под номером 2.
Это равенство справедливо для каждой молекулы. Сложив такие равенства для отдельных молекул и разделив обе части полученного уравнения на число молекул, мы получим В среднее в квадрате равно сумме В икс в квадрате среднее, В игрек в квадрате среднее, В зет в квадрате среднее.
Так как направления трех осей ОХ, ОY и OZ вследствие беспорядочного движения молекул равноправны, средние значения квадратов проекций скорости равны друг другу,    подставим в формулу. Тогда для среднего квадрата проекции скорости получим, что средний квадрат проекции скорости равен 1/3 среднего квадрата самой скорости, где множитель 1/3 (1 к трем) появляется вследствие трехмерности пространства и соответственно существования трех проекций у любого вектора.
Скорости молекул беспорядочно меняются, но средний квадрат скорости вполне определенная величина.
Основное уравнение молекулярно-кинетической теории газов. Справедливость этого уравнения была экспериментально доказана в XIX в. , после чего началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.
В этом уравнении можно увидеть зависимость давления газа от средней кинетической энергии его молекул.  
Вычислим давление газа на стенку CD сосуда ABCD площадью S, перпендикулярную координатной оси OX.
Каждая молекула обладает своим импульсом. При ударе молекулы о стенку ее импульс изменяется. Так как модуль скорости молекул при ударе не меняется, то ∆р=2*m0V0x. дельта пэ равно 2 эм нулевое на Вэ нулевое по икс.
Согласно второму закону Ньютона, изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен дельта пэ равно 2 эм нулевое на Вэ нулевое по икс.
Молекул много, и каждая из них передает стенке при столкновении такой же импульс. За секунду они передадут стенке импульс,  где Z – число столкновений всех молекул со стенкой за это время. Число прямо пропорционально концентрации молекул,  скорости молекул. Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой. Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Число столкновений молекул со стенкой пропорционально площади поверхности стенки. В среднем только половина всех молекул движется к стенке, так как другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с равно половине произведения количества молекул на площадь стенок на  скорость и полный импульс, переданный стенке за 1 с, равен произведению массы молекулы на их количество  на площадь стенок S на квадрат скорости.
Согласно второму закону Ньютона изменение импульса любого тела за единицу времени равно действующей на него силе.   Учтем, что не все молекулы имеют одно и то же значение квадрата скорости. В действительности средняя за секунду сила, действующая на стенку, пропорциональна среднему квадрату скорости. 
Согласно формуле, получается. 
В тоже время давление равно отношению силы к площади поверхности.
Следовательно, получаем: давление газа прямо пропорционально концентрации частиц, массе частицы и квадрату скорости частицы. Это и есть основное уравнение молекулярно-кинетической теории газов.
Эта формула связывает макроскопическую величину – давление, которое может быть измерено манометром,  с микроскопическими величинами, характеризующими молекулы: их массой, скоростью хаотичного движения.
Зависимость давления идеального газа от концентрации и от средней кинетической энергии частиц выражается основным уравнением молекулярно-кинетической теории идеального газа.
Если через  обозначить среднюю кинетическую энергию поступательного движения молекулы, то уравнение можно записать в виде пэ равно две трети эн умноженное на е кинетическое.
Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.
Основное уравнение молекулярно- кинетической теории идеального газа можно преобразовать и найти зависимость давления от плотности газа. Концентрация молекул равна числу молекул в единице объема, а кинетическая энергия равна половине произведения массы на квадрат скорости, подставим эти формулы в основную и   получим, что давление газа равно ⅓ произведения плотности газа и среднего квадрата скорости.

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

Закон идеального газа | Определение, формула и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Britannica Beyond
  Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Факты и сопутствующий контент

Уравнение идеального газа – GeeksforGeeks

Термометр с заполненной жидкостью колбой на одном конце, наиболее часто используемыми жидкостями являются ртуть, толуол, спирт, пентан, креозот, показывают разные показания для температур, отличных от фиксированных, из-за их различного расширения. характеристики. С другой стороны, термометр, использующий газ, показывает те же показания для температуры. Неважно, какой тип газа используется. Эксперименты показывают, что все газы расширяются одинаково при малых плотностях.

Давление (P), объем (V) и температура (T), где T = t + 273,15, а t — температура в °C, являются переменными, которые объясняют поведение данного количества (массы) газа. Закон идеального газа, также известный как универсальное газовое уравнение, представляет собой состояние уравнения для гипотетического идеального газа. Несмотря на свои недостатки, закон идеального газа дает хорошее приближение к поведению многих газов в различных ситуациях. Бенуа Поль Эмиль Клапейрон предложил закон идеального газа в 1834 году как смесь эмпирического закона Шарля, закона Бойля, закона Авогадро и закона Гей. Люссака.

Уравнение идеального газа

Законы идеального газа представляют собой комбинацию наблюдений Бойля в семнадцатом веке и Чарльза в восемнадцатом веке.

Закон Бойля: Давление газа обратно пропорционально объему газа для данного количества газа при фиксированной температуре, т.е. при постоянной температуре отношение между давлением и объемом количества газа можно записать как

П ∝ 1 / В

или

PV = константа

, где P — давление, а V — объем.

Закон Шарля: Объем газа прямо пропорционален температуре газа для данного фиксированного количества газа, поддерживаемого при постоянном давлении, т.е. при постоянной температуре соотношение между объемом и температурой количества газа может быть записано как, 

В ∝  T

или  

В / T = константа

, где T — температура.

Эти два закона применимы к газам с низкой плотностью и могут быть объединены в одно соотношение. Стоит отметить, что

PV = константа  

и

V/T = константа

Для определенного количества газа тогда

15 PV/T также должно быть константой.

Это можно сформулировать в более общей форме, применимой к любому количеству любого газа с низкой плотностью, а не просто к определенному количеству этого газа. Это соотношение описывает закон идеального газа и известно как уравнение идеального газа .

Это может быть выражено как

PV / T = nR

или

PV = nRT

, где n
0 9015 универсальное число молей газа. газовая постоянная.

Примечание: Универсальная газовая постоянная (R) имеет значение 8,314 кДж/моль в системе СИ.

Его также можно сформулировать в более общей форме, применимой к любому количеству любого газа с низкой плотностью, а не просто к определенному количеству этого газа.

Вывод уравнения идеального газа

Пусть P — давление газа, V — объем газа, T — температура.

Согласно закону Бойла,

P ∝ 1/V

или

V ∝ 1/P …… (1)

V ∝ 1/P …… (1)

V ∝ 1/P …0128

Согласно закону Чарльза,

В. ∝ T …… .. (2)

Согласно закону Авогадро,

Когда P и T постоянные, объем газа продовольен количеству. моль газа, т.е.

V ∝ N ……. (3)

Сравните уравнения (1), (2) и (3) как значение 8,314 Дж/моль-К

Абсолютная температура

Термодинамическая температура — другое название абсолютная температура . При этой температуре термодинамическая энергия системы минимальна. Абсолютная температура равна нулю по Кельвину или -273 °C, широко известная как 9.0150 абсолютный ноль . Скорость частиц газа останавливается при температуре абсолютного нуля. Это означает, что частицы газа на самом деле не движутся. При абсолютном нуле объем газа равен нулю. В результате объем газа измеряется его абсолютным нулем.

Температура имеет прямую зависимость от давления и объема, т. е.

PV ∝ T  

Эта зависимость позволяет использовать газ для определения температуры в газовом термометре с постоянным объемом.

Таким образом, при постоянном объеме отношение можно записать как  

P ∝ T , а температура считывается в терминах давления с помощью газового термометра постоянного объема.

Прямая линия выходит из графика зависимости давления от температуры.

При постоянном объеме график Давление в зависимости от температуры газа с низкой плотностью  

Наблюдения за реальными газами отличаются от значений, ожидаемых законом идеального газа при низких температурах. Однако зависимость является линейной в широком диапазоне температур, и кажется, что если бы газ оставался газом, давление падало бы до нуля при понижении температуры. Экстраполяция прямой на ось дает абсолютный минимум температуры идеального газа. Абсолютный ноль определяется как температура – ​​273,15 градуса по Цельсию. Температурная шкала Кельвина, часто известная как абсолютная шкала температуры, основана на абсолютном нуле.

Та же самая абсолютная нулевая температура на графике зависимости давления от температуры и экстраполяции линий для газов с низкой плотностью.

В температурной шкале Кельвина за нуль точек принимается –273,15 °C, то есть 0 K. В температурных системах Кельвина и Цельсия размер единицы одинаков. Таким образом, отношение между ними может быть выражено как

T = t + 273,15

, где t — температура в °C

Примеры задач  

Задача 1: Какой объем занимают 2,34 грамма углекислого газа при STP?

Решение:

Дано,

Вес (м) углекислого газа 2,34 грамма.

При СТП температура 273,0 К.

Давление 1,00 атм.

Универсальная газовая постоянная (R) имеет значение 0,08206 л атм моль¯ ¹ K¯ ¹ .

Выражение для количества молей:

n = m/M

, где n — количество молей, m — вес, а M — молярная масса вещества.

Молярная масса диоксида углерода 44,0 г моль¯ ¹ .

SO, значение N можно рассчитать как,

N = 2,34 г / 44,0 г MOL¯ ¹

= 0,0532 моль

Согласно уравнению идеального газа,

PV = NR

. уравнение,

V = nRT / P

Подстановка всех значений,

В = [0,0532 моль) (0,08206 л атм моль¯1 К¯1) (273,0 К)] / 1,00 атм

   = 1,19 л

. Определить количество молей аргона и массу аргона в образце.

Решение:

Дано,

Объем (V) газообразного аргона составляет 56,2 литра.

При СТП температура 273,0 К.

Давление 1,00 атм.

Молярная масса газообразного аргона 390,948 г/моль.

Согласно уравнению идеального газа,

PV = nRT

Преобразуя уравнение,

n = PV / RT

Подставив все значения в приведенное выше уравнение,

n = [(1,00 л) (56,2 л) ) ] / [ (0,08206 л атм моль¯1 K¯1) (273,0 K)]

  = 2,50866 моль

Выражение для числа молей:

m = нМ

Подставляя все значения в приведенное выше уравнение,

м = (2,50866 моль) × (39,948 г/моль) 

   = 100 г

Решение:

Дано,

Объем (V) газа неона составляет 12,30 литров.

Давление 1,95 атм.

Количество молей 0,654 моля.

Согласно уравнению идеального газа

PV = nRT

Преобразование уравнения,

T = PV / nR

Подстановка всех значений в приведенное выше уравнение,

T = [(1,95 атм) × (12,30 л)] / [(0,654 моль) × (0,08206 л атм моль¯ ¹ K¯ ¹ )]

   = 447 K

Задача 4: вывести уравнение идеального газа?

Решение:

Пусть P — давление газа, V — объем газа, T — температура.

Согласно закону Бойла,

P ∝ 1/V

или

V ∝ 1/P …… (1)

В зависимости ……..(2) 

Согласно закону Авогадро,

Когда P и T постоянны, объем газа пропорционален количеству молей газа, т.е.

В. ∝ N ……. (3)

Сравнение уравнения (1), (2) и (3) как,

В ∝ NT/P

V ∝ NT/P

V ∝ NT/P

.