В цилиндре под поршнем находится идеальный одноатомный газ.Формулы А и Б позволяют рассчитать значения физических величин, характеризующихсостояние газа. Физика 18530
Задание 18530
В цилиндре под поршнем находится идеальный одноатомный газ. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих состояние газа. Использованы обозначения: p – давление; V – объём; – средняя кинетическая энергия молекул; ν – количество вещества.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФОРМУЛЫ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ||
| А) | 1) | средняя кинетическая энергия молекул | |
| Б) | 32pVNAE¯к | 2) | количество вещества |
| 3) | давление | ||
| 4) | объём |
42
Задание 17560 Задание 17663 Задание 17768 Задание 18243 Задание 18416 Задание 18530 Задание 18824 Задание 18869 Задание 18997 Задание 22488
Теоретическая физика.
Т. V. Статистическая физика. Теоретическая физика. Т. V. Статистическая физика.
ОглавлениеПРЕДИСЛОВИЕНЕКОТОРЫЕ ОБОЗНАЧЕНИЯ ГЛАВА I. ОСНОВНЫЕ ПРИНЦИПЫ СТАТИСТИКИ § 1. Статистическое распределение § 2. Статистическая независимость § 4. Роль энергии § 5. Статистическая матрица § 6. Статистическое распределение в квантовой статистике § 7. Энтропия § 8. Закон возрастания энтропии ГЛАВА II. 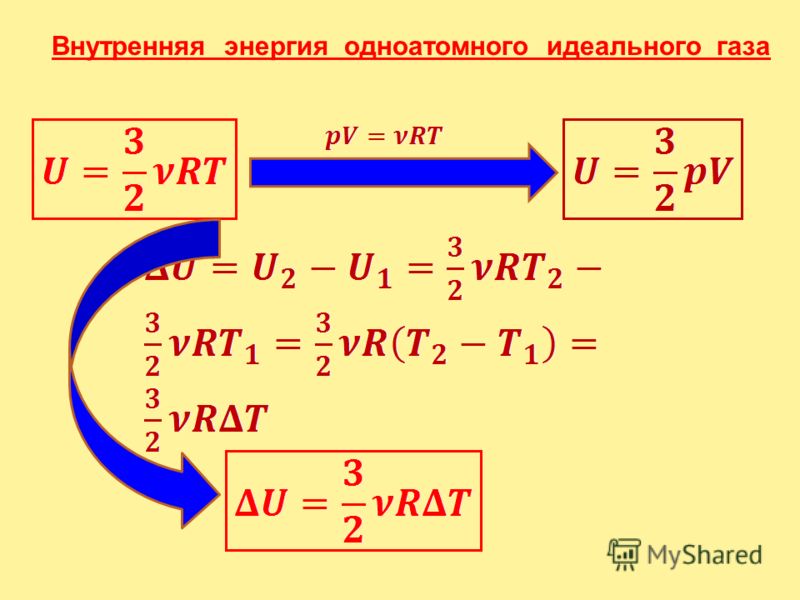 ТЕРМОДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ§ 9. Температура § 10. Макроскопическое движение § 11. Адиабатический процесс § 12. Давление § 13. Работа и количество тепла § 14. Тепловая функция § 15. Свободная энергия и термодинамический потенциал § 16. Соотношения между производными термодинамических величин § 17. Термодинамическая шкала температуры § 18. Процесс Джоуля — Томсона § 19. Максимальная работа § 21. Термодинамические неравенства § 22. Принцип Ле-Шателье § 23. Теорема Нериста § 24. Зависимость термодинамических величин от числа частиц § 25. Равновесие тела во внешнем поле § 26. Вращающиеся тела § 27. Термодинамические соотношения в релятивистской области ГЛАВА III. РАСПРЕДЕЛЕНИЕ ГИББСА § 28. Распределение Гиббса § 29. Распределение Максвелла Задачи § 30. Распределение вероятностей для осциллятора § 31. Свободная энергия в распределении Гиббса Задачи § 32.  Термодинамическая теория возмущений§ 34. Распределение Гиббса для вращающихся тел § 35. Распределение Гиббса с переменным числом частиц § 36. Вывод термодинамических соотношений из распределения Гиббса ГЛАВА IV. ИДЕАЛЬНЫЙ ГАЗ § 37. Распределение Больцмана § 38. Распределение Больцмана в классической статистике Задачи § 39. Столкновения молекул Задачи § 40. Неравновесный идеальный газ § 41. Свободная энергия больцмановского идеального газа § 42. Уравнение состояния идеального газа Задачи § 43. Идеальный газ с постоянной теплоемкостью Задачи § 44. Закон равнораспределения § 43. Одноатомный идеальный газ § 46. Одноатомный газ. Влияние электронного момента § 48. Двухатомный газ с молекулами из одинаковых атомов. Вращение молекул § 49. Двухатомный газ. Колебания атомов § 50. Двухатомный газ. Влияние электронного момента § 51.  Многоатомный газ§ 52. Магнетизм газов Задачи ГЛАВА V. РАСПРЕДЕЛЕНИЯ ФЕРМИ И БОЗЕ § 53. Распределение Ферми § 54. Распределение Бозе § 55. Неравновесные ферми- и бозе-газы § 56. Ферми- и бозе-газы элементарных частиц § 57. Вырожденный электронный газ § 58. Теплоемкость вырожденного электронного газа § 61. Релятивистский вырожденный электронный газ Задачи § 62. Вырожденный бозе-газ Задача § 63. Черное излучение ГЛАВА VI. ТВЕРДЫЕ ТЕЛА § 64. Твердые тела при низких температурах § 65. Твердые тела при высоких температурах § 66. Интерполяционная формула Дебая § 67. Тепловое расширение твердых тел § 68. Сильно анизотропные кристаллы § 69. Колебания кристаллической решетки § 70. Плотность числа колебаний § 71. Фононы. § 72. Операторы рождения и уничтожения фононов § 73. Отрицательные температуры ГЛАВА VII. НЕИДЕАЛЬНЫЕ ГАЗЫ § 74. Отклонение газов от идеальности  Разложение по степеням плотности§ 76. Формула ван-дер-Ваальса § 77. Связь вириального коэффициента с амплитудой рассеяния § 78. Термодинамические величины классической плазмы § 79. Метод корреляционных функций § 80. Термодинамические величины вырожденной плазмы ГЛАВА VIII. РАВНОВЕСИЕ ФАЗ § 81. Условия равновесия фаз § 82. Формула Клапейрона — Клаузиуса § 83. Критическая точка § 84. Закон соответственных состояний ГЛАВА IX. РАСТВОРЫ § 85. Системы с различными частицами § 86. Правило фаз § 87. Слабые растворы § 88. Осмотическое давление § 89. Соприкосновение фаз растворителя Задачи § 91. Выделение тепла и изменение объема при растворении § 92. Растворы сильных электролитов § 93. Смесь идеальных газов § 94. Смесь изотопов § 95. Давление пара над концентрированным раствором § 96. Термодинамические неравенства в растворах § 97. Кривые равновесия § 98.  Примеры диаграмм состояния§ 99. Пересечение особых кривых поверхности равновесия § 100. Газ и жидкость ГЛАВА X. ХИМИЧЕСКИЕ РЕАКЦИИ § 101. Условие химического равновесия § 102. Закон действующих масс § 103. Теплота реакции § 104. Ионизационное равновесие § 105. Равновесие по отношению к образованию пар ГЛАВА XI. СВОЙСТВА ВЕЩЕСТВА ПРИ ОЧЕНЬ БОЛЬШИХ ПЛОТНОСТЯХ § 106. Уравнение состояния вещества при больших плотностях § 107. Равновесие тел с большой массой § 108. Энергия гравитирующего тела § 109. Равновесие нейтронной сферы ГЛАВА XII. ФЛУКТУАЦИИ § 110. Распределение Гаусса § 111. Распределение Гаусса для нескольких величин § 112. Флуктуации основных термодинамических величин Задачи § 113. Флуктуации в идеальном газе § 114. Формула Пуассона § 115. Флуктуации в растворах § 116. Пространственная корреляция флуктуаций плотности Задачи § 118.  Корреляция флуктуаций во времени§ 119. Временная корреляция флуктуаций нескольких величин § 120. Симметрия кинетических коэффициентов § 121. Диссипативная функция § 122. Спектральное разложение флуктуаций § 123. Обобщенная восприимчивость § 124. Флуктуационно-диссипационная теорема § 125. Флуктуационно-диссипационная теорема для нескольких величин § 126. Операторное выражение обобщенной восприимчивости § 127. Флуктуации изгиба длинных молекул ГЛАВА XIII. СИММЕТРИЯ КРИСТАЛЛОВ § 128. Элементы симметрии кристаллической решетки § 129. Решетка Бравэ § 130. Кристаллические системы § 131. Кристаллические классы § 132. Пространственные группы § 133. Обратная решетка § 134. Неприводимые представления пространственных групп § 135. Симметрия относительно обращения времени § 136. Свойства симметрии нормальных колебаний кристаллической решетки § 137. Структуры с одно- и двумерной периодичностью § 138. Корреляционная функция в двумерных системах § 139.  Симметрия по ориентации молекул§ 140. Нематические и холестерические жидкие кристаллы § 141. Флуктуации в жидких кристаллах ГЛАВА XIV. ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА И КРИТИЧЕСКИЕ ЯВЛЕНИЯ § 142. Фазовые переходы второго рода § 143. Скачок теплоемкости § 144. Влияние внешнего поля на фазовый переход § 145. Изменение симметрии при фазовом переходе второго рода § 146. Флуктуации параметра порядка § 147. Эффективный гамильтониан § 148. Критические индексы § 149. Масштабная инвариантность § 150. Изолированные и критические точки непрерывного перехода § 151. Фазовый переход второго рода в двумерной решетке § 152. Ван-дер-ваальсова теория критической точки § 153. Флуктуационная теория критической точки ГЛАВА XV. ПОВЕРХНОСТИ § 154. Поверхностное натяжение § 155. Поверхностное натяжение кристаллов § 156. Поверхностное давление § 157. Поверхностное натяжение растворов § 158. Поверхностное натяжение растворов сильных электролитов § 159.  Адсорбция§ 160. Смачивание § 161. Краевой угол § 162. Образование зародышей при фазовых переходах § 163. Невозможность существования фаз в одномерных системах |
Q4Q Идеальный одноатомный газ в начале… [БЕСПЛАТНОЕ РЕШЕНИЕ]
Q4Q Идеальный одноатомный газ в начале… [БЕСПЛАТНОЕ РЕШЕНИЕ] | StudySmarterВыберите язык
Предлагаемые языки для вас:
Немецкий (DE)
Дойч (Великобритания)
Европа
- английский (DE)
- английский (Великобритания)
К4К
Проверено экспертами
Найдено: Страница 603
Перейти к главе
Самые популярные вопросы для учебников по физике
Изобретатель утверждает, что изобрел четыре двигателя, каждый из которых работает между резервуарами с постоянной температурой при 400 и 300 К .
Данные по каждому двигателю за рабочий цикл следующие: двигатель А, QH=200 Дж, QL=175 Дж и Вт = 40 Дж ; двигатель B, QH=500 Дж, QL=-200 Дж и Вт = 400 Дж ; двигатель C, QH=600 Дж, QL=-200 Дж и Вт = 400 Дж ; двигатель D, QH=100 Дж, QL=-90 Дж и Вт = 10 Дж . Какие из первого и второго законов термодинамики (если вообще) нарушает каждый двигатель?
2,0 моль двухатомный газ, первоначально нагретый до 300 K , подвергается следующему циклу: он (1) нагревается при постоянном объеме до 800 K , (2) затем ему дают изотермически расшириться до исходного давления, (3) затем сжимается при постоянном давлении до исходного состояния. Предполагая, что молекулы газа не вращаются и не колеблются, найдите (а) чистую энергию, переданную газу в виде тепла, (б) чистую работу, совершаемую газом, и (в) эффективность цикла. CENGAGE PHYSICS АНГЛИЙСКИЙ-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ И ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ-Субъективный РЕКЛАМА Ab Padhai karo bina ads ke Khareedo DN Pro и dekhorukisi sari видео бина! Ответить Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах. Стенограмма hello kaun sa вопрос один моль идеального одноатомного газа подвергается процессу P равен Альфе t-критерий для половины Где Альфа постоянная найдите работу совершаемую газом Если температура увеличится на 50 К и также молярная удельная теплоемкость газа Сурья найти работу, совершенную газом, если его температура увеличилась на 50 К и задан удельный вес отношения к другим давление равно альфа оно возведено в степень половина уравнения идеального газа лихорадка равна нрт общество значение мощности справочника Альфа в два раза мы будем равны нрт отсюда объем будет равен Анне на Альфе дихао половина и дифференцируя обе стороны получим давай будет равен 1 на 2 и на Альфа мощность минус половина X обязан поддерживать это ваше уравнение номер один работы, проделанной для любого процесса, задается в виде интеграла e x dawai ok учитывая соотношение температуры лихорадки как Альфа в 10 поднимите в степень наполовину и мы рассчитали для истины из уравнение того, что составляет полчаса на Альфе в степени минус половина умноженной на пошлину, так что отсюда люцерна аннулируется, ее мощность 35 – из аннулирована, а на 2 – константа выйдет из интегрирования с w будет равно nro с учетом интеграла Duty от t2t плюс Delta T правильная работа будет равна 1 при 2 в Delta T количество молей равно одному Я хочу, чтобы приложение Delta TV было указано как 50 Sukanya Waqt Bhi request 225 are или что мы можем сказать 25 в 8,31, что будет равно 20 7,75 драгоценных камней, это будет проделанная работа, теперь мы должны рассчитать молярную удельную теплоемкость при удельный вес газа из первого закона термодинамики вы равен Delta up p w для еще одного можно написать что он будет равен см в Delta T где она молярная теплоемкость в Delta вы будете CVT Delta T + спецодежда рассчитанная так как наш после 2 X Delta T A Delta T был отменен запрос СР дается как при 1 минус 1 + 1 на 2 принимая за общее что получится если она будет близка к нашей в единицу при х минус 1 + 1 при 2 отсюда она будет равна 8. Видео по теме Один моль идеального одноатомного газа подвергается процессу p=αT1/2, где α — константа. 10966189 Идеальный одноатомный газ подвергается процессу, при котором его давление обратно пропорционально его температуре. а) Рассчитайте молярную удельную теплоемкость процесса. б) Найдите работу, совершаемую двумя молями газа при изменении температуры от Т_1 до Т_2. 10966193 Один моль идеального одноатомного газа подвергается процессу, как показано на рисунке. Найдите молярную удельную теплоемкость газа в этом процессе. 11797033 Один моль идеального одноатомного газа подвергается процессу p=αT1/2 , где a – константа. Работа, совершаемая газом при повышении его температуры на 50К, равна 50Rx. 13078410 Один моль идеального одноатомного газа подвергается процессу P=αT1/2, где α постоянная . Если молярная теплоемкость газа равна βR1 при R = газовой постоянной, то найти значение β. 32498940 Идеальный одноатомный газ совершает процесс, в котором его внутренняя энергия зависит от его объема как 69129622 В термодинамическом процессе два моля одноатомного идеального газа подчиняются PV–2=константе. Если температура газа увеличивается с 300 К до 400 К, то найдите работу, совершаемую газом (где R – универсальная газовая постоянная) 268001653 Один моль одноатомного идеального газа совершает процесс ArarrB , как на данной P-V диаграмме . Удельная теплоемкость этого процесса равна 278676350 В термодинамическом процессе два моля одноатомного идеального газа подчиняются PV–2=константе. 642769792 Text Решение Идеальный одноатомный газ совершает процесс, при котором его давление обратно пропорционально его температуре. изменяется от T1 до T2 642769842 Text Solution Идеальный двухатомный газ подвергается процессу, в котором его внутренняя энергия относится к объемам как U = alpha sqrt(V ), где a – постоянная величина. а) Найти работу, которую совершает газ, и количество теплоты, которое необходимо передать этому газу, чтобы увеличить его внутреннюю энергию на 100 Дж. б) Найти молярную удельную теплоемкость газа 9.0005 642769846 Text Solution Один моль идеального одноатомного газа подвергается процессу p=αT1/2, где α — константа. 
9(1//2), где альфа — константа. а) Найдите работу, которую совершит газ, если его температура увеличится на 50 К. б) Кроме того, найдите молярную удельную теплоемкость газа.
2 в Гамма + 1 / Gaon -18 HD спасибо
а) Найдите работу, которую совершит газ, если его температура увеличится на 50К.
(b) Также найдите молярную удельную теплоемкость газа.
R — газовая постоянная.
Найдите значение х.
U=a√V [где a — константа]
(a) найти работу, совершаемую газом, и теплоту, переданную газу, для увеличения его внутренней энергии на 200 Дж.
(b) найти молярную удельную теплоемкость газа для этого процесса .
(-1//2), где alpha – константа. а) Найдите работу, которую совершит газ, если его температура увеличится на 50 К. б) Найдите также молярную удельную теплоемкость газа.
а) Найдите работу, которую совершит газ, если его температура увеличится на 50К.
(b) Также найдите молярную удельную теплоемкость газа.