Инерция и инертность тела,сила инерции при поступательном движении, момент инерции при вращении. Первый закон Ньютона
Явление, которому посвящена наша сегодняшняя беседа, встречается в разных жизненных ситуациях. Мы с удовольствием его используем, учитываем и частенько ругаем.
Речь пойдет об инерции. Постараемся разобраться, что скрывается за этим названием.
Что же такое инерция
Наблюдая полёт копья, брошенного рукой атлета, падение всадника через голову споткнувшейся лошади; созерцая камни, веками неподвижно лежащими на одних и тех же местах — греческие мыслители задумывались, что общего в этих явлениях?
На пути их познания Аристотелем было введено понятие инерции, что дословно означает «бездействие». Эти размышления греческого философа об инерции получили продолжение в опытах Г. Галилея. Он делает вывод о том, что если на тело не действуют другие тела, то скорость тела не изменяется. Спустя несколько веков эти выводы дополнил и обобщил в своих трудах Исаак Ньютон.
Данная им формулировка явления инерции известна как I закон Ньютона.
«Инерция — это физическое явление сохранения скорости тела постоянной, если на него не действуют другие тела или их действие скомпенсировано».
Это означает, что, благодаря инерции, тела, находящиеся в покое, продолжают покоиться, а движущиеся продолжают свое движение, пока на них не окажут воздействие внешние силы.
Например, автомобиль может находиться в покое в двух случаях, если на горизонтальном участке дороги его двигатель выключен, либо его двигатель включен, но силы сопротивления уравновесили силу тяги двигателя, т. е. скомпенсировали её.
Теперь вернемся к нашему всаднику, перелетающему через голову споткнувшейся лошади. Лошадь, споткнувшись, резко теряет скорость, а невезучий всадник… по инерции продолжает движение.
По этой же причине при ДТП водитель, пренебрегающий ремнями безопасности, получает удар о лобовое стекло.
Почему, поскользнувшись при ходьбе, мы падаем назад? Тело по инерции сохраняет прежнюю скорость, а ноги на скользком участке быстренько «убегают» вперед.
Формула силы инерции
Количественной характеристикой явления инерции является сила инерции.
Для расчета этой силы используют формулу:
Fин= — ma
где:
- Fин — сила инерции;
- m — масса тела;
- a — ускорение.
Знак минус указывает на то, что сила инерции противодействует силе, вызвавшей изменение скорости тела.
Понятие инертности в физике
Итак, инерция — это физическое явление. С ним тесно связано еще одно понятие — инертность. Под инертностью в физике понимают свойства тел противодействовать мгновенному изменению направления или скорости движения.
Любое тело не может мгновенно изменить свою скорость, однако, одни тела это делают быстрее, другие — медленнее. Для остановки гружёного и порожнего самосвалов, движущихся с одинаковой скоростью, требуется разное время.
Это происходит потому, что тело с большей массой более инертно, и ему на изменение скорости требуется больше времени. То есть мерой инертности в физике является масса тела.
Инертные люди, инертные газы
Термин «инертный» широко используется в химии. Он относится к химическим элементам, которые при обычных условиях не вступают в химические реакции. Например, благородные газы аргон, ксенон и др.
Этот термин может быть применен и к поведению человека. Инертные люди отличаются равнодушием к окружающему миру. Они противятся любым переменам, как в их собственной судьбе, так и в работе. Они ленивы и безынициативны.
Инертность вращающихся объектов
Все приведенные ранее примеры относились к поступательно движущимся телам. А как же быть с вращающимися объектами? Скажем, с вентилятором, с маховиком в двигателе внутреннего сгорания или детской игрушке. Ведь после выключения электрического вентилятора его лопасти ещё некоторое время по инерции продолжают крутиться.
Насколько тела инертны во время вращения определяет момент инерции. Он зависит от массы тела, его геометрических размеров и расстояния до оси вращения. Изменение этого расстояния влияет на скорость вращения тела. Это используют спортсмены — фигуристы, поражая зрителей продолжительным вращением с изменением скорости.
Специальные расчёты позволяют определить оптимальные размеры механизма и допустимую скорость вращения, чтобы не допустить разрыва вращающихся частей.
Т.е. момент инерции во вращательном движении играет ту же роль, что и масса при поступательном движении. Но в отличие от массы момент инерции можно изменять, как это делают фигуристы — то широко разводя руки, то прижимают их к груди.
Инерция вокруг нас
Именно это явление используют:
- для сбрасывания ртутного столбика в медицинском термометре и выбивания пыли из ковров;
- для продолжения движения после разбега на коньках, лыжах, велосипеде;
- для экономии горючего при езде на автомобиле;
- в принципе работы артиллерийских детонаторов и т.
 д.
д.
Это лишь небольшая часть из всех применений инерции. Но не следует забывать о возможной опасности, которую таит это явление природы. Надпись на заднем борту грузовика «Водитель, сохраняй дистанцию», напоминает, что транспорт мгновенно остановить нельзя.
И при торможении впереди едущего автомобиля, следующая за ним машина, остановиться мгновенно не может. По этой же причине категорически запрещено перебегать дорогу перед движущимся транспортом.
Теперь вы легко ответите на вопрос, почему при торможении автомобилей обязательно включается задний красный свет, почему при повороте водитель обязательно сбрасывает скорость.
В спортзале и на катке, в цирке и в мастерской — инерция сопровождает нас всюду. Присмотритесь.
Автор: Драчёва Светлана Семёновна
Если это сообщение тебе пригодилось, буда рада видеть тебя в группе ВКонтакте. А ещё — спасибо, если ты нажмёшь на одну из кнопочек «лайков»:
Вы можете оставить комментарий к докладу.
Инерция – это… Что такое Инерция?
Ине́рция (от лат. inertia —
Формулировка
Существование явления инерции в классической механике постулируется Первым законом Нью́тона, который также называется Зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»:
Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Современная формулировка закона:
Существуют такие системы отсчёта, относительно которых материальная точка при отсутствии внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.
Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными. Проявлением неинерциальности в них является возникновение фиктивных сил, называемых «силами инерции».
История
Древнегреческие учёные, судя по дошедшим до нас сочинениям, размышляли о причинах совершения и прекращения движения. В «Физике» Аристотеля (IV век до н. э.) приводится такое рассуждение о движении в пустоте
| Никто не сможет сказать, почему [тело], приведенное в движение, где-нибудь остановится, ибо почему оно скорее остановится здесь, а не там? Следовательно, ему необходимо или покоиться, или двигаться до бесконечности. |
Однако сам Аристотель считал, что пустота в природе не может существовать, и в другом его труде, «Механике», утверждается[2]:
Движущееся тело останавливается, если сила, его толкающая, прекращает свое действие. |
Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Естественное противодействие внешних сил (сил трения, сопротивления воздуха и т. п.) движению толкаемого тела при этом не учитывалось. Поэтому Аристотель связывал неизменность скорости движения любого тела с неизменностью прилагаемой к нему силы.
Только через два тысячелетия Галилео Галилей (1564—1642) смог исправить эту ошибку Аристотеля. В своем труде «Беседы о двух новых науках» он писал[2]:
| …скорость, однажды сообщенная движущемуся телу, будет строго сохраняться, поскольку устранены внешние причины ускорения или замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время, как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно |
Это суждение нельзя вывести непосредственно из эксперимента, так как невозможно исключить все внешние влияния (трение и т. п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то, при движении по горизонтальной плоскости, у тела нет причин ускоряться или замедляться, и оно должно пребывать в состоянии равномерного движения или покоя.
п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то, при движении по горизонтальной плоскости, у тела нет причин ускоряться или замедляться, и оно должно пребывать в состоянии равномерного движения или покоя.
Таким образом, Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считал Аристотель и его последователи. Это открытие Галилея вошло в науку как Закон инерции. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). В современном виде закон инерции сформулировал Декарт. Ньютон включил закон инерции в свою систему законов механики как первый закон.
Смежные понятия
Принцип относительности Галилея: во всех инерциальных системах отсчёта все механические процессы протекают одинаково (если начальные условия для всех тел одинаковы). В системе отсчёта, приведенной в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчёта (условно — «покоящейся»), все процессы протекают точно так же, как и в покоящейся системе.
Следует отметить, что понятие инерциальной системы отсчёта — абстрактная модель, то есть некий идеальный объект, рассматриваемый вместо реального объекта (примерами абстрактной модели служат абсолютно твердое тело или нерастяжимая невесомая нить). Реальные системы отсчёта всегда связаны с каким-либо объектом или объектами, и соответствие реально наблюдаемого движения тел в таких системах с результатами расчётов будет неполным. В то же время точность подобной абстракции в земных условиях весьма велика и ограничивается лишь величиной искривления пространства-времени, которое было предсказано в рамках общей теории относительности (1915 год) и впервые зафиксировано в 1919 году при исследовании отклонения света в гравитационном поле Солнца.
Инертность — свойство тела в большей или меньшей степени препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии на него внешних сил. Мерой инертности в физике выступает инертная масса.
См. также
Литература
Примечания
Что такое инерция?
Тела не могут самостоятельно приходить в движение или изменять его направление, для этого необходимо воздействие внешней силы. Такое противодействие изменениям называется инерцией, которая просто означает, что тела, находящиеся в покое, остаются в покое, а движущиеся — в движении, пока на них не окажут воздействие внешние силы.
Например, после выключения электрического вентилятора колесо с лопастями продолжает какое-то время быстро вращаться и лишь потом замедляет свой ход и останавливается. Если бы не было трения в подшипниках и аэродинамического сопротивления, колесо вращалось бы неограниченное время и после выключения вентилятора. Однако после того как колесо остановится, оно уже не сможет снова начать самостоятельно вращаться. Для того чтобы вентилятор начал работать, необходима внешняя сила,
Однако после того как колесо остановится, оно уже не сможет снова начать самостоятельно вращаться. Для того чтобы вентилятор начал работать, необходима внешняя сила,
в данном случае электродвигатель. Стремление всех тел сохранять состояние движения или покоя объясняет, почему пассажиры, стоящие в проходе поезда, начинают падать назад или вперед в те моменты, когда поезд трогается или останавливается (рисунки сверху и снизу).
С тех пор как греческий философ Аристотель более 2000 лет назад ввел понятие инерции, многие великие мыслители ломали себе голову над ее смыслом. В 1635 году итальянский физик Галилео Галилей выполнил серию экспериментов с шарами, скатывающимися по наклонной плоскости, что позволило ученому впервые сформулировать понятие инерции в современном ее понимании. Основываясь на работах Галилея, Исаак Ньютон обобщил свои наблюдения в области инерции в первый из трех законов механики, носящих его имя.
Покоящиеся тела
Как показано на рисунке над текстом, пассажиры были застигнуты врасплох, когда поезд начал движение, и они начинают падать назад. Диаграмма справа показывает, что силу, препятствующую падению пассажиров, передает ручной ремень, в то время как сила тяжести держит их на месте. Пассажиры реагируют на ускорение так, как будто невидимая сила тянет их назад.
Диаграмма справа показывает, что силу, препятствующую падению пассажиров, передает ручной ремень, в то время как сила тяжести держит их на месте. Пассажиры реагируют на ускорение так, как будто невидимая сила тянет их назад.
Движущиеся тела
Когда движущийся поезд замедляет свой ход, его тормоза создают силу, направленную противоположно направлению движения {голубая стрелка). Так как на пассажиров, стоящих внутри поезда, тормозящая сила не действует, они продолжают движение и начинают падать вперед. Сила, передаваемая через ручной ремень, и сила тяжести останавливают падение пассажиров. Резкое торможение поезда создает у пассажиров ощущение, что какая-то сила толкает их вперед.
Эксперимент Галилея
Наблюдая за шарами, перекатывающимися по наклонным плоскостям, Галилей правильно сформулировал понятие инерции. При отсутствии трения, замедляющего движение тел, шарик, скатывающийся по наклонной плоскости, продолжал бы качение вверх по другой наклонной плоскости {верхний рисунок) до тех пор, пока его кинетическая энергия (энергия движения) не была бы полностью израсходована на преодоление силы тяжести. В среднем примере шарик перемещается вдоль второй наклонной плоскости дальше, чем в верхнем, так как вторая наклонная плоскость не столь крута. Галилей сделал вывод, что если бы угол наклона второй наклонной плоскости стал бы еще меньше, шарик прокатился бы еще дальше, прежде чем уступить силе тяжести. А если бы вторая плоскость была бы горизонтальной, как в нижнем примере, сила тяжести не влияла бы на движение и шарик катился бы вечно.
В среднем примере шарик перемещается вдоль второй наклонной плоскости дальше, чем в верхнем, так как вторая наклонная плоскость не столь крута. Галилей сделал вывод, что если бы угол наклона второй наклонной плоскости стал бы еще меньше, шарик прокатился бы еще дальше, прежде чем уступить силе тяжести. А если бы вторая плоскость была бы горизонтальной, как в нижнем примере, сила тяжести не влияла бы на движение и шарик катился бы вечно.
Примеры инерции в физике
Определение и общие принципы инерции
Основная задача механики – это исследование движения тел относительно избранной системы отсчета и установка причин, которые определяют характер движения. Следует установить, в каких условиях тело перемещается по прямой линии, а в каких его траекторией является кривая, когда тело движется с постоянной скоростью, когда имеет ускорение.
Эксперимент устанавливает, что если тела взаимодействуют, то характер движения тел изменяется. Например, тело падает, при соприкосновении с Землей оно остановится или изменит направление своего движения на противоположное (подпрыгнет). Находящееся в покое, по отношению к Земле, тело самостоятельно никогда не станет перемещаться само, оно начнет движение только под действием другого тела.
Находящееся в покое, по отношению к Земле, тело самостоятельно никогда не станет перемещаться само, оно начнет движение только под действием другого тела.
Следует заметить, что вывод о том, что взаимодействие тел ведет к изменению их скорости перемещения. Так, Аристотель считал, что само движение возможно только во взаимодействии с другими телами. Причиной ошибки служило то, что Земля в то время считалась неподвижным центром Вселенной. Состояние покоя относительно Земли считалось естественным, а движение вынужденным состоянием, для которого необходимо воздействие внешних сил.
К концу XIV века проблема движения была актуализирована, так как развивалась артиллерия, и следовало объяснить законы движения снарядов. Кроме этого появилась гелиоцентрическая система Коперника, в которой центром Вселенной стало Солнце, а Земля – это рядовая планета, вращающаяся вокруг него. Возник вопрос: что толкает Землю и другие планеты, заставляя двигаться миллиарды лет? Требовало объяснения тот факт, что люди не чувствуют вращения Земли и оторвавшись от Земли человек опустится в ту же точку, откуда, например, подпрыгнул.
Первое верное, но неполное решение проблемы представил Галилей. Идея мысленного эксперимента с телом, на которое не воздействуют никакие тела, дала возможность ученому выдвинуть гипотезу инерциального движения тела. Галилей был прав, когда предположил, что по инерции тело может двигаться равномерно и прямолинейно, но ошибся, когда решил, что тело может двигаться равномерно по окружности.
Закон инерции
Закон инерции окончательно сформулировал Ньютон (первый закон Ньютона): Если на тело не действуют другие тела, то скорость его перемещения не изменяется по модулю и направлению (тело движется равномерно и прямолинейно или покоится).
Движение по инерции – это перемещение по кратчайшему пути, в свободном пространстве кратчайшим расстоянием между двумя точками является прямая. Если мы утверждаем, что тело находится в покое, то покой считать абсолютным нельзя. Это состояние тела только относительно отдельной системы отсчета, которая сама движется относительно других тел.
В результате существования инерции, подпрыгнув вверх в вагоне мы опустимся на тоже место. Стоя на полу вагона, перемещающегося с постоянной скоростью, мы обладаем такой же скоростью. Подпрыгнув вверх, мы сохраним горизонтальную скорость без изменения, так как в направлении горизонта на нас не действуют другие тела. Следовательно, за момент прыжка мы проходим по горизонтали такой же путь, как и вагон, и возвращаемся в туже точку, с которой мы совершили прыжок. Аналогично можно рассмотреть наше движение вместе с Землей.
По инерции перемещаются тела, которые бросили. Бросая камень, мы сообщаем ему некоторую скорость в момент броска. В том случае, если бы сопротивления воздуха и силы притяжения к Земле не было бы, то камень мог бы двигаться по инерции без изменения скорости по модулю и направлению бесконечно долго.
Если заставить тело скользить по поверхности, то чем более гладкая поверхность, тем медленнее уменьшает скорость тело. На гладком льду тело скользит долго, не изменяя скорость. Трение можно уменьшить до минимума (почти до нуля) если использовать воздушную подушку (струю воздуха, которая будет поддерживать тело над поверхностью, вдоль которой идет движение).
Трение можно уменьшить до минимума (почти до нуля) если использовать воздушную подушку (струю воздуха, которая будет поддерживать тело над поверхностью, вдоль которой идет движение).
Подведем итоги. Инерцией называют явление, при котором скорость тела остается неизменной, если на него не действуют другие тела или их действие взаимно компенсируются. Inertia — от латинского бездеятельность, косность.
Явление инерции становится очевидным тогда, когда изменяется величина или направление скорости движения. Так, при уменьшении скорости движения автомобиля, особенно, если это происходит резко, водитель и пассажиры отклоняются вперед, продолжая движение. Если резко затормозить при езде на велосипеде, то можно перелететь через его руль вперед. Инерция – это свойство материи, все тела обладают свойством инерции.
Если любое тело вывести из состояния покоя, то после прекращения воздействия на него, оно будет двигаться по инерции. Явление инерции проявляется повсюду.
Примеры решения задач на инерцию
Гипотезы о преодолении инерции и ее природе / Хабр
Каждый день мы сталкиваемся с явлением инерции. Имея различное высокотехнологичное оборудование, человечество так и не научилось преодолевать хотя бы на малую величину, влияние инерции. В данной статье анализируются гипотезы о возможном преодолении, ликвидации инерции, а также о ее природе.
Имея различное высокотехнологичное оборудование, человечество так и не научилось преодолевать хотя бы на малую величину, влияние инерции. В данной статье анализируются гипотезы о возможном преодолении, ликвидации инерции, а также о ее природе.
Сначала подберемся к понятию инерции: инерция — это свойство, которое проявляет масса, пытаясь сохранить свое состояние движения при ускорениях и смене направления движения (как в случае с центробежной силой). Причем инерционность тела растет не только при увеличении массы, но и при увеличении протяженности тела в пространстве, вспомним формулы момента инерции:
Из формулы видно, что, к примеру, для диска, инерционность диска будет увеличиваться с увеличением как массы m, так и его радиуса R. Если говорить проще, то цилиндр, массой 10000 кг и радиусом 1 метр, будет трудно раскрутить и остановить так же как диск массой 1 кг и радиусом 100 метров.
Существуют различные мнения об природе инерции, которые местами противоречат друг другу. Известен парадокс Маха, в котором утверждается, что инерция (центробежная сила) никогда не будет проявляться для вращающегося тела, если не будет других тел во Вселенной, кроме как этого вращающегося тела. Реальность такого парадокса поддерживается теорией относительности А. Эйнштейна. Также эта теория утверждает, что инерционность одной массы будет зависеть от расстояния до других масс, и чем это расстояние больше, тем меньше будет инерция тела удаленного от других масс (цитата: “Поэтому если я удалю какую-нибудь массу на достаточно большое расстояние от всех других масс Вселенной, то инерция этой массы должна стремиться к нулю.” стр. 605 «Вопросы космологии и общая теория относительности.» А. Эйнштейн Собрание научных трудов. — М.: Наука, 1965. — Т. 1). Но неизвестны такие опытные данные, которые согласовались бы с этой точкой зрения, также не представляется осуществимым на опыте реализации, парадокса Маха, одиноко вращающегося тела во Вселенной. Существуют точки зрения, что сил инерции вообще не существуют, и это математическая фикция, у нас в стране это известно под спором академиков А.
Известен парадокс Маха, в котором утверждается, что инерция (центробежная сила) никогда не будет проявляться для вращающегося тела, если не будет других тел во Вселенной, кроме как этого вращающегося тела. Реальность такого парадокса поддерживается теорией относительности А. Эйнштейна. Также эта теория утверждает, что инерционность одной массы будет зависеть от расстояния до других масс, и чем это расстояние больше, тем меньше будет инерция тела удаленного от других масс (цитата: “Поэтому если я удалю какую-нибудь массу на достаточно большое расстояние от всех других масс Вселенной, то инерция этой массы должна стремиться к нулю.” стр. 605 «Вопросы космологии и общая теория относительности.» А. Эйнштейн Собрание научных трудов. — М.: Наука, 1965. — Т. 1). Но неизвестны такие опытные данные, которые согласовались бы с этой точкой зрения, также не представляется осуществимым на опыте реализации, парадокса Маха, одиноко вращающегося тела во Вселенной. Существуют точки зрения, что сил инерции вообще не существуют, и это математическая фикция, у нас в стране это известно под спором академиков А. Ю. Ишлинского и Л.И. Седова (на фотографии ниже, как раз они, статьи затрагивающие этот спор: тут и тут).
Ю. Ишлинского и Л.И. Седова (на фотографии ниже, как раз они, статьи затрагивающие этот спор: тут и тут).
Споры происходили и в более поздние времена, известна дискуссия на эту тему в советских научно-технических изданиях Л.Г. Ливенсона и Г.К. Суслова в 1936-1937 годах.
Одним из примеров о разном понимании фиктивности или реальности сил инерции могут послужить эти две цитаты известных ученых:
А.Н. Матвеев «Механика и теория относительности» 1976 г.:
«Являются ли силы инерции реальными силами? Они реальны в том же смысле, в каком являются реальными ускорения, для описания которых они введены. Они реальны также и в более глубоком смысле: при рассмотрении физических явлений можно указать конкретные физические последствия действия сил инерции. Например, в вагоне поезда силы инерции могут привести к увечьям пассажиров, т.е. к весьма реальному и осязаемому результату».
Н.В.Гулиа «Инерция» 1982 г.:
«Все силы инерции – силы нереальные, необходимые нам лишь для облегчения тех или иных задач механики. Ни в коем случае нельзя их считать реальными силами и приписывать им свойства и действия физических сил».
Ни в коем случае нельзя их считать реальными силами и приписывать им свойства и действия физических сил».
Также похожие споры встречаются и в современности, подобное столкновение, двух точек зрения о фиктивности или реальности сил инерции представлены в теме этого физического форума. И тем не менее, даже среди тех кто выступает за реальность силы инерции и толкования её физической причины — нет общего согласия. Однако, есть общие точки соприкосновения, она гласит, что инерция тела вызывается физической средой, которая существует во всем материальном пространстве, которая сопротивляется ускорению и смене направления движущейся массы.
Одна из них утверждает, что такая среда, которая ответственна не только за инерцию, но и из-за распространения света, должна иметь собственную массу, то есть это среда упругая, по типу некоторых эфирных гипотез 19-20 веков, примером такого представления может служить воззрения, известного теоретика массового эфира В.А. Ацюковского, в своей работе (Эфиродинамические основы электромагнетизма, стр. 21) он выводит примерную массу частички элемента эфира “амера” как кг, количество таких частичек-амеров в кубометре пространства выводит . Резюмирую такие рассуждения можно сказать что подход массового эфира не раскрывает причину наблюдения инерции у массы, объявляя саму причину массой, даже если очень маленькой. То есть даже если принять что инерция у нас возникает из-за амеров, то возникает вопрос по каким причинам происходит инерция у самих амеров раз у них тоже есть масса и они могут вращаться (образуя вихри) и соударяться друг о друга? Также это рождает и другие парадоксы и несоответствия опытным данным. К примеру, известный опыт Майкельсона, по обнаружению ветра такой массовой всепроницающей среды, ветер не был обнаружен. Еще в качестве примера одного из них, можно привести формулы моментов для центрифуг при вентиляционных потерях из-за сопротивления упругой среды (статический момент) и при динамическом (инерционном) моменте.
21) он выводит примерную массу частички элемента эфира “амера” как кг, количество таких частичек-амеров в кубометре пространства выводит . Резюмирую такие рассуждения можно сказать что подход массового эфира не раскрывает причину наблюдения инерции у массы, объявляя саму причину массой, даже если очень маленькой. То есть даже если принять что инерция у нас возникает из-за амеров, то возникает вопрос по каким причинам происходит инерция у самих амеров раз у них тоже есть масса и они могут вращаться (образуя вихри) и соударяться друг о друга? Также это рождает и другие парадоксы и несоответствия опытным данным. К примеру, известный опыт Майкельсона, по обнаружению ветра такой массовой всепроницающей среды, ветер не был обнаружен. Еще в качестве примера одного из них, можно привести формулы моментов для центрифуг при вентиляционных потерях из-за сопротивления упругой среды (статический момент) и при динамическом (инерционном) моменте.
Статический момент, сопротивление движению упругой (массовой) среды+механические потери, вычисляется по формуле:
— коэффициент вентиляционных потерь, зависит от плотности среды
— момент трения в подшипниках
— угловая скорость
Динамический (инерционный) момент рассчитывается по формуле:
где
— момент инерции
— угловая скорость
— время разгона
Из формул видим, что природа сопротивления упругой среды, имеет другую природу, нежели чем получаем при ускорениях. Упругая среда сопротивляется квадратично, в зависимости от скорости вращения, то есть чем больше скорость, тем больше сопротивляется «инерция» если брать упруго-эфирную точку зрения, но никакой квадратичной зависимости от скорости вращения не наблюдается для тел где наблюдается инерция. То есть получаем, что гипотеза упругого эфира не способна объяснять такое явление как инерция. Тем не менее В.А. Ацюковский предлагает способы по уменьшению инерции если ускоряющиеся тела “продувать эфиром“, такой продув автор предлагает делать “с помощью аннигиляции эфирных вихрей“, но не встречено объяснение как создать такие вихри.
Упругая среда сопротивляется квадратично, в зависимости от скорости вращения, то есть чем больше скорость, тем больше сопротивляется «инерция» если брать упруго-эфирную точку зрения, но никакой квадратичной зависимости от скорости вращения не наблюдается для тел где наблюдается инерция. То есть получаем, что гипотеза упругого эфира не способна объяснять такое явление как инерция. Тем не менее В.А. Ацюковский предлагает способы по уменьшению инерции если ускоряющиеся тела “продувать эфиром“, такой продув автор предлагает делать “с помощью аннигиляции эфирных вихрей“, но не встречено объяснение как создать такие вихри.
Другая точка зрения, которая также поддерживает мысль о причине инерции, как проявлении всепроницаемой, но именно безмассовой среды, это структура вакуума А.В. Рыкова (из ОИФЗ РАН). Гипотеза спорная, хоть и не противоречит известному опыту Майкельсона и другим опытам, в которых упругий, массовый эфир вызывает несоответствия опытным данным. Гипотеза получила положительные рецензии, академика РАН д.ф-м.н. В.Н. Страхова (прочитать его рецензию можно тут) и к.ф-м.н. вед. науч. сотрудника РНЦ «Курчатовский институт», одного из разработчиков самой мощной взорванной бомбы в истории человечества Царь-бомбы, Ю.Н. Смирнова (с ним удалось поговорить лично, прочитать его рецензию можно тут). Гипотеза выведена на основании факта рождения пар масс элементарных частиц при гамма-излучении в вакууме вблизи атома ядра или частицы, то есть все массы рождаются из этой среды при определенной энергии от 1,022 МэВ и выше, а также факта токов смещения в вакууме, наличия одного заряда ( Кл) для всех элементарных частиц независимо от массы.
Гипотеза получила положительные рецензии, академика РАН д.ф-м.н. В.Н. Страхова (прочитать его рецензию можно тут) и к.ф-м.н. вед. науч. сотрудника РНЦ «Курчатовский институт», одного из разработчиков самой мощной взорванной бомбы в истории человечества Царь-бомбы, Ю.Н. Смирнова (с ним удалось поговорить лично, прочитать его рецензию можно тут). Гипотеза выведена на основании факта рождения пар масс элементарных частиц при гамма-излучении в вакууме вблизи атома ядра или частицы, то есть все массы рождаются из этой среды при определенной энергии от 1,022 МэВ и выше, а также факта токов смещения в вакууме, наличия одного заряда ( Кл) для всех элементарных частиц независимо от массы.
Если коротко, среда состоит из электрических безмассовых зарядов “+” и “-” и магнитного потока между ними. При движении, известные массовые частицы и античастицы двигаются по этим зарядам, приобретая тем самым волнообразное движение, длина волны которых считается по формуле де Бройля:
Магнитный поток сопротивляется ускорению частиц и смене направления движения частиц, не дает сразу перепрыгнуть частицам с одной амплитуды движения в зарядовой решетке на другую или сделать моментально поворот в этой решетке.
Автор теории отрицает кварки (кстати, кварки так и не получены в свободном состоянии) считает нейтрон состоящим из электрона и протона. Нейтрино, считает безмассовым своеобразным магнитоэлектрическим излучением (не электромагнитным) частота которого превышает Гц, высчитывает скорость гравитации выше скорости света в 3576,055 раз, не считает что в черной дыре встает время, а нераспространение в ней света, трактует как отсутствие среды для него, по аналогии как вакуум не имеет среды для распространения звука. За кварки, нейтрино и расчет скорости гравитации с помощью усовершенствованных установок Майкельсона, которая в этих расчетах равна скорости света (достоверность этого опыта вызывает споры в научном сообществе) получены Нобелевские премии.
Гипотеза Рыкова предлагает идеи о преодолении инерции, гипотетически, гамма-излучение деформирует среду отвечающую за инерцию и уменьшает ее величину. Видео представляет упрощенно такой опыт:
Упрощенное видео, является вольной трактовкой идей автора по прочитанному в его книге, видео делалось без согласования с автором, пока писалась статья автор гипотезы умер.

Немного пояснений к видео: вокруг тела, на котором мы наблюдаем в обычных условиях явление инерции, создан «кокон» из гамма-лучей некой энергии, автор указывал на вероятность наблюдения эффекта уменьшения величины инерции от выбора частоты гамма-излучения. Также высказана гипотеза об уменьшении инерции с помощью переменного магнитного поля и вращательных ускорений.
Более подробное описание с формулами у автора таких предположений в его книге «Вакуум и вещество Вселенной», глава «Возможные практические технологии», стр. 136.
Вдобавок по темеМной был сделан фильм в котором рассматривается гипотеза Рыкова о строении среды Вселенной и история взглядов на такой вопрос, в 2011 году, на киностудии Леннаучфильм.
О фильме, как вопиющем примере псевдонауки, писала
Газета.ру, однако, при этом серьезно переврав об утверждениях сделанных в фильме:
1) Неверно указано представление Анатолия Рыкова о структуре вакуума:
«структура вакуума представляет собой кристаллическую решетку из элементарных частиц, связанных между собой силами электричества».
В фильме говорится что структура вакуума наоборот безмассовая и это очень важная черта этой теории.
2) Неверно представлена информация данная в фильме:
«векторы электрических и магнитных полей («магнитные» потоки) в кристалле вакуума были параллельны, а не перпендикулярны друг другу».
Про это вообще не говорится и не показывается в фильме.
3) «Фильм «Структура вакуума»… вызвавших массу гневных откликов в научном сообществе» — не совсем так, часть научного сообщества одобрительно отозвалась о фильме, а часть научного сообщества была «гневной».
4) Искажена степень наук ученого чья гипотеза рассматривается в фильме: «Этот двадцатиминутный ролик был посвящен гипотезе кандидата наук из Института физики Земли».
Кандидата физико-математических наук правильно.
После резонанса в СМИ, я стал лауреатом молодежной премии правительства Санкт-Петербурга за научно-популярное кино.
Нельзя здесь обойти популярное поле
Хиггса. Согласно этой гипотезе, существует всепроницающее вакуумное поле Хиггса, и при ускорениях масс — это поле создает инерцию массы. Более подробно про эту гипотезу можно почитать
Согласно этой гипотезе, существует всепроницающее вакуумное поле Хиггса, и при ускорениях масс — это поле создает инерцию массы. Более подробно про эту гипотезу можно почитать
,
тут(статьи
И.П. Иванова) и
тут(статья
Э.Э. Боосаи др.). Гипотеза Питера Хиггса, о всепроницающем поле, которое порождает инерцию, напоминает высказывание
Анри Пуанкаре:
«Инерцией обладает не материя, а эфир; он один оказывает сопротивление движению».Только «эфир» Хиггса не является светоносным. В гипотезе Хиггса, не встречено, как это поле воздействует на массу
при смене направления движения, когда тоже проявляется инерция. Также не встречено гипотез согласующихся с механизмом Хиггса, о возможности преодоления инерции.
Достаточно широко встречаются также и различные полумистические описания, о летающей тарелке преодолевающей инерционное сопротивление на якобы тайных знаниях Тесла, но в этих писаниях на мой взгляд почти рандомно перебираются различные физические термины, то есть крайне некорректно.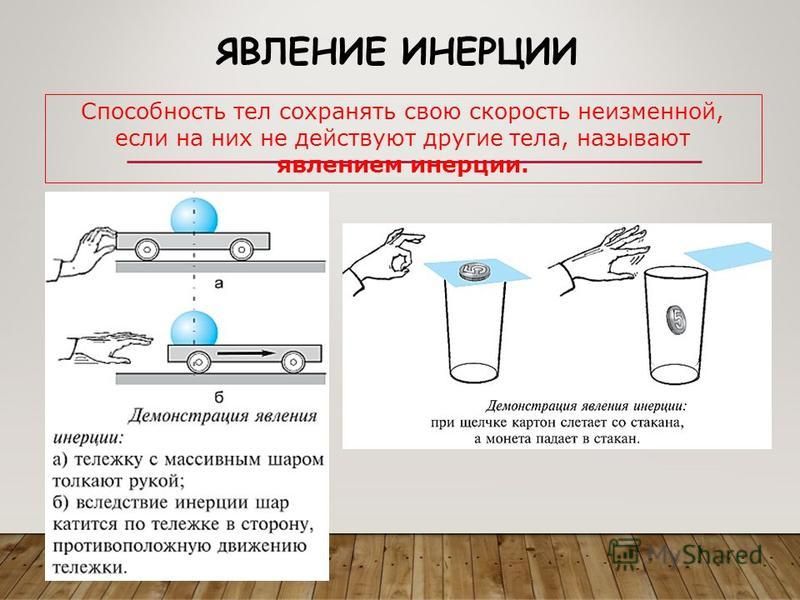
Также встречаются статьи в различных источниках, и даже в серьезных изданиях типа письма в ЖТФ, в которых утверждается, что создана установка (к примеру установки: Дж. Серла, В.С. Гребенникова, В.В. Рощина и С.М. Година) на которой испытатели достигли небывалых эффектов в уменьшении инерции/гравитации/веса, но потом по каким-то причинам установка утрачена, новую, повторяющую достигнутые эффекты, почему-то не удается/не удалось сделать, свидетелей таких небывалых эффектов единицы, а документальные доказательства выглядят малоубедительно, что наводит подозрения о блефе.
Возможность преодоления инерции важна для осуществления старинных мечтаний человечества о межзвездных путешествиях, то что даже если человечество научится получать большие скорости перемещения, то одним из негативных факторов сдерживающий такие перемещения, могут стать очень сильные перегрузки, возникающие по причине инерции, которые воздействуют на материал космического корабля и его пассажиров.
Ресурсы с которых были использованы изображения:
1. Объясните назначение ремней безопасности в автомобиле
2. Момент инерции
3. Александр Юльевич Ишлинский
6. Инертность. Масса. Инерция. Сила. Законы Ньютона.
6. Инертность. Масса. Инерция. Сила. Законы Ньютона. | физика
Инертность – свойство разных тел по разному изменять свою скорость под действием одной и той же силы. (большая инертность у того, у кого изменения меньше за единицу времени)
– это свойство всех тел оказывать “сопротивление” при любых попытках изменить его скорость как по модулю, так и по направлению.
Масса (m) – скалярная физическая величина, мера инертности тела; измеряется в килограммах (кг). свойства:
- масса системы тел = сумма масс отдельных частей этой системы.
- масса системы тел, не обменивающихся веществом с окружением, – величина постоянная, и не изменяется при движении этой системы.
- ~~ отношение масс двух тел обратно отношению их ускорений ( m1 / m2 = a2 / a1 ) ~~
Инерция – свойство тела сохранять свою скорость, при отсутствии действия на него других тел.
Сила (F{век}) – мера взаимодействия тел, в результате которого тела деформируются или приобретают ускорение; измеряется в ньютонах (Н).
– величина, характеризующая действия одного тела на
другое.
Силы:
- Гравитационные
- Электрические
Законы Ньютона
Первый закон Ньютона – существуют такие системы отсчёта, называемые инерциальными, в которых тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела, или их действие скомпенсировано.
Второй закон Ньютона – ускорение, с которым движется тело, прямо пропорционально приложенной силе, и обратно пропорционально его массе: a{век} = F{век} / m, где F{век} – сила или результирующая всех сил, действующих на тело.
Третий закон Ньютона – силы, с которыми взаимодействуют тела, направлены в противоположенные стороны вдоль одной прямой, равны по модулю, имеют одинаковую физическую природу, приложены к разным телам(F1{век} = -F2{век}) время их действия одинаково.
Второй закон Ньютона в импульсной форме – изменение импульса равно изменению действующей на тело силы: Δp{век} = F{век}Δt
|
Глава 2. ЧТО ТАКОЕ ИНЕРЦИЯ Куда залетит копьеЧерез двадцать строк вас ждет сообщение еще об одном чуде природы. Чтобы легче понять его, сделаем физкультурную разминку — займемся метанием копья. Я разбежался по зеленому полю стадиона, сосредоточил волю в резком броске — и копье летит вперед. Дальше, выше!.. Ниже… Упало. Далеко оно пролетело? Для нашей космической эры — не очень. Если метров на 100, значит, я мировой рекордсмен. А хорошо бы закинуть копье прочь от стадиона, километров этак за сто, за тысячу, вообще куда-нибудь в бездну Вселенной. Как вы думаете, много силы надо иметь для этого? Да почти совсем не надо. Здесь мы и столкнулись с очередным чудом природы. Для неискушенного в физике человека оно, пожалуй, еще удивительнее, чем чудеса тяготения, действующего через пустоту, и одинаковой ускоренности падающих тел. Ведь загадка тяготения видна сразу, постоянство земного ускорения легко заметить по упавшим с карниза сосулькам. А неуничтожимость начатого движения никак не увидишь: все в нашем мире, где невозможно «убрать с дороги» Землю и воздух, тормозится и падает. Древние мудрецы думали поэтому, что движение брошенного камня происходит потому, что его проталкивает вперед воздух, окружающая среда. Так же, как удав проталкивает проглоченного кролика. Хитро? Не очень. При таком объяснении совсем непонятно, почему же копье, летящее в воздухе, тормозится. В действительности разогнанное копье летит само, если не встречает помех, летит, ничем не подталкиваемое, как угодно далеко — по прямой линии, с постоянной скоростью. Но все-таки почему бы копью, летящему в пустоте вдалеке от планет и звезд, не остановиться вдруг или, наоборот, разогнаться, свернуть по дуге, завертеться по какой-нибудь спирали, кувыркнуться? Что заставляет его держаться прямого пути, сохранять скорость? Постепенно сложилось такое мнение. Копью, как и любому другому физическому телу, присуще свойство инерции, которое и олицетворяет это универсальное стремление всех тел к сохранению покоя или равномерного прямого движения. Копью «все равно», покоится оно или движется. Оба состояния для него равноценны. И благодаря своей инерции оно бережно хранит каждое. В фразах, которые вы только что прочитали, изложен знаменитый закон инерции. Надеюсь, вы не в претензии, что я обращаюсь с Землей, как футболист с мячом: захотел и отбросил ее, чтобы «не мешала». Ради удобства рассуждений и наглядности ученые нередко устраивают подобные «мысленные эксперименты». Значит, и нам с вами они не запрещены. Итак, мы откинули Землю вместе с ее любопытным умением придавать вес всему, что пребывает рядом. Поэтому наше летящее по инерции копье не будет ничего весить: тяжести-то неоткуда взяться, нет того, что заставляло бы наше копье давить на опору. Вес тела вдали от Земли, если верить Кеплеру, равен нулю. Ну, а если мы теперь вернем Землю и поставим ее где-нибудь подле летящего копья так, чтобы оно попало в зону земного притяжения, — приобретет тогда наше копье вес? Новичка тянет сказать: да, приобретет. Как только Земля водворена на место, копье начнет на нее падать — двигаться в направлении ее центра. Кроме того, оно будет продолжать по инерции лететь вперед, ибо появление Земли не сможет отменить первоначальный толчок, в свое время пославший копье по прямому пути. Получается совмещение двух движений. Копье будет сразу и лететь вперед (прямо и с постоянной скоростью) и отвесно падать в направлении к Земле (с ускорением свободного падения). В первом движении вес копья равен нулю. Во втором движении, которое только и добавилось из-за возвращения Земли, вес копья тоже равен нулю, ибо падающие тела не имеют тяжести. Займемся сложением: нуль плюс нуль равно нулю. Вывод: несмотря на возвращение Земли, свободно брошенное копье продолжает оставаться невесомым. Падает вверхНеожиданное известие: не только прославленные космонавты, но и остальные люди, в том числе читатели этой книжки (как и всех остальных), некоторую часть своей жизни проводят в состоянии невесомости. Пусть Земля где-то в стороне. Копье брошено и летит в определенном направлении, например вправо, точно по строке, которую вы сейчас читаете. Берем в руки Землю и помещаем ее перед летящим копьем — так, чтобы центр планеты находился на прямой линии, продолжающей вправо ту же строку. Что произойдет с копьем? Направление его движения не изменится. Путь останется таким же прямым, как и без Земли. Только из равномерного полет превратится в ускоренный. Получится нечто вроде обыкновенного отвесного падения, но с большей начальной скоростью, а потому более быстрое, хоть и с прежним ускорением. И, разумеется, копье останется невесомым (ибо, напоминаю, складывая нули, получаем нуль). Случай второй. Подносим Землю с противоположной стороны — помещаем ее центр слева от копья на прежней линии. Теперь копье сперва будет лететь, как и раньше, вперед (от Земли), но не равномерно, а замедленно (потому что Земля тянет его назад), потом замедлится настолько, что на мгновение остановится (в этот момент полностью исчезнет скорость, сообщенная копью первоначальным толчком), и тут же двинется назад, к Земле, в обычном отвесном падении. Опять, по известной вам причине, копье останется невесомым, несмотря на то что некоторое время оно двигалось не к Земле, а от Земли — падало вверх! — и на бесконечно малое мгновение останавливалось, когда меняло направление. Гагарин или Брумель?Перекидка планеты вовсе не обязательна. И не трогая ее, можно прийти к тем же заключениям. Вы стоите на стадионе и бросаете вверх все то же копье, если оно вам еще не надоело. Во время взмаха оно ускоряется, а вылетев из рук, участвует сразу в двух движениях: равномерном, направленном вверх (точно таком же, как если бы не было Земли), и ускоренном, направленном вниз — отвесном падении. Тут тяготение включается не с запозданием (что мы делали раньше из соображений наглядности), а сразу после разгона. Результат же прежний: едва копье вырвалось из ваших рук, оно потеряло вес. Если, конечно, пренебречь сопротивлением воздуха. Можно закинуть копье не вверх, а куда-нибудь вбок, под углом к вертикали — опять после толчка будет сложение прямолинейного равномерного движения по инерции с отвесным падением. Многим кажется странным, что брошенный камень теряет вес тотчас после вылета из руки. Легче согласиться, что он невесом во время движения вниз. Но интуиция подводит. И вверх и вниз брошенное тело летит, не имея ни грамма веса. Все, что вы подбрасываете — камни, палки, пятаки, мячи, самих себя (когда прыгаете), — после броска пребывает в свободном падении и потому невесомо (разумеется, до тех пор, пока можно не считаться с сопротивлением воздуха). И поскольку прыжки случаются довольно часто в вашей жизни (я уж не говорю о бесконечных падениях, особенно в младенческом возрасте), эту часть жизни вы находитесь в состоянии невесомости. По той же причине Валерий Брумель, я думаю, был в невесомости больше, чем Юрий Гагарин. Если Брумель ежедневно совершал десять тренировочных прыжков длительностью по полторы секунды каждый (это соответствует двухметровой высоте прыжка), то за десять лет (за вычетом воскресений) он был в невесомости примерно пятнадцать часов. Впрочем, и Гагарин спортсмен. И он прыгал, бегал, упражнялся на батуте. К тому же он старше Брумеля. Так что, возможно, Гагарин и тут первый. Опровергаем фантастовНе стоит в сотый раз журить за ошибку Жюля Верна, который в романе «Из пушки на Луну» уверял, что невесомость в снаряде наступит где-то в середине пути между Землей и Луной (когда-де уравновесятся притяжения Земли и Луны). Теперь вину приписывают ученому-консультанту знаменитого фантаста: консультант- то обязан был знать, что на самом деле невесомость должна была наступить тотчас по вылете снаряда из жерла пушки. Но, видимо, по этому примеру, а также и по собственной инициативе писатели-фантасты сочинили затем массу небылиц про невесомость. Например, «падая на чужую планету, звездолетчики всем своим существом чувствовали ее могучее тяготение». Или «двигатели умолкли, ракета удалялась от Земли, и постепенно все вещи становились легче». Даже теперь, в разгар космической эры, про невесомость то и дело говорят опрометчивые вещи. Многие ваши друзья, читатель, считают, что наши космонавты были невесомы потому, что оказались далеко от Земли. Ручаюсь, что по крайней мере человек шесть из десяти думают в таком роде (сам проверял!). В действительности и космонавты в своих кораблях-спутниках падали. Ракета-носитель настолько сильно разогнала корабль-спутник, что когда он был отпущен ракетой и перешел в свободное падение, то, сворачиваемый к Земле тяготением, не успевал упасть на нее. Движение корабля по инерции, направленное всегда вперед вдоль касательной к криволинейной орбите, было очень быстрым — около восьми километров в секунду. Вот и кружился корабль вокруг планеты, совершая виток за витком. Падал и не мог упасть! Алексей Леонов, который выбрался из корабля в космос, тоже падал и не мог упасть. В космосе он даже не отстал от корабля и не опередил его по той же самой причине, по которой маленькая сосулька не отстала в падении от большой и не опередила ее. Будь скорость космического корабля больше одиннадцати километров в секунду, он, падая, улетел бы прочь от Земли. При шестнадцати километрах в секунду ушел бы даже из Солнечной системы! Ванна невесомости Теперь вы можете без всяких хлопот исполнить старый замысел Уэллса — избавить человека от веса. Если под руками нет космической ракеты и корабля-спутника, надо попросить человека подпрыгнуть, только и всего. Так, правда, он освободится от тяжести ненадолго. Лучше посадить его в самолет и попросить пилота, чтобы тот забрался повыше, разогнался вверх и резко снизил тягу двигателей — чтобы она преодолевала только сопротивление воздуха. В этом режиме самолет полетит по «баллистической кривой» — сначала поднимется с замедлением, а потом будет ускоренно опускаться. Движение самолета будет таким, как если бы у Земли отсутствовала атмосфера. Произойдет полная имитация свободного падения в безвоздушной среде. Если самолет высотный и достаточно быстроходный, а летчик опытный, каждый баллистический прыжок продлится довольно долго — минуту, а то и больше. Именно таким способом проходят тренировку космонавты, чтобы подготовиться к многодневной невесомости космического полета. В самолетах устраивают «ванны невесомости» — просторные кабины, где удобно парить в воздухе, кувыркаться, отталкиваясь от мягких стенок, в критических случаях хвататься за поручни — и все это без риска с непривычки натворить бед на каком-нибудь пульте. Ванну эту я сейчас использую, с вашего разрешения, не по прямому назначению: пусть она побудет боксерским рингом. Зачем боксеру вес?Какой-нибудь рекордсмен-сверхтяжеловес, позабывший чудесные школьные годы, наверное, обидится на этот вопрос. Он убежден, что вес ему совершенно необходим— чтобы тяжелыми были кулаки, весомыми удары. Предложите этому боксеру лишиться веса, и он, я думаю, пошлет вас в нокдаун. Все же проявите такт и постарайтесь зазвать в ванну невесомости даже не одного спортсмена, а двух, да еще разных весовых категорий. Если вам это удастся, сделайте эксперимент — упросите боксеров, ради интересов научной популяризации, провести небольшой показательный бой. И вот в ванне невесомости дерутся два боксера, тяжеловес и легковес. Лучше сказать, бывший тяжеловес и бывший легковес. Теперь они оба «ничегоневесы», ибо вес каждого равен нулю. Казалось бы, весовые категории спортсменов выравнены, шансы на победу одинаковые. Но присмотримся к бою. Довольно быстро боксеры освоились с необычной обстановкой. Им уже не мешает отсутствие верха и низа, невозможность опираться на ноги. Опытные спортсмены применились к невесомости и азартно дерутся. Бывший легковес подвижен и быстр. Так и сыплет свингами по неповоротливому и спокойному бывшему тяжеловесу. Тот не спешит. Удары его неторопливы. Но какой эффект от каждого! Боковой крюк — и легковес (бывший) завертелся, как волчок. Могучий апперкот — и бывший легковес мчится к потолку, отскакивает от него мячиком. Бывший тяжеловес, несмотря на свою невесомость, буквально давит бывшего легковеса. И за его явным преимуществом вы, не дождавшись конца раунда, прекращаете бой. Произошло доказательство того, что вес боксеру совсем не обязателен. Бывший тяжеловес победил, сбросив все свои килограммы! Почему же? Может быть, у победителя лучше развиты мышцы? Это нетрудно проверить. После боя, отходив обессилевшего легковеса (а лучше, разумеется, до боя, чтобы оба спортсмена были свежими), вы даете им по эспандеру — пусть посоревнуются в растягивании тугой резины. И выясняется, что оба они могут растянуть эспандер одинаковое число раз. Значит, мышцы у них развиты одинаково. Ради строгости допустим, что, кроме того, вы проверили быстроту их спортивной реакции, стратегические навыки, тактические приемы, опыт, даже, если хотите, умственные способности. Во избежание придирок, оговоримся еще одним невероятным условием: наши боксеры дрались в рыцарских латах и поэтому с одинаковой болезненностью переносили удары равной силы (дабы не давать легковесу преимущества, известного по стихотворной строке из «Василия Теркина»: «Хорошо, что легок телом, отлетел, а то б конец. Так, буквально все качества боксеров, кроме веса, оказались как будто одинаковыми. А во время боя равным — нулевым — был и вес. В чем же, в конце концов, было преимущество бывшего тяжеловеса? Его преимущество — в инерции, в том самом свойстве сохранять покой или прямолинейное равномерное движение, которое положено Ньютоном в основу механики. Инерция ведь у разных тел разная. Больше инерция — значит, тело медленнее реагирует на толчок или напор, а если уж движется, то крепко держит скорость и быстрее рушит преграды. Об этом и свидетельствовала картина боксерского боя. Бывший тяжеловес посылал удары, от которых бывший легковес вертелся, кувыркался и отскакивал. Наоборот, от весьма сильных наскоков бывшего легковеса противник только слегка покачивался. После боя нельзя было сказать традиционное «победил сильнейший» (оба одинаково сильны). В невесомости не годились и слова «победил тяжелейший». Надо было объявить: «Победил инерционнейший». Разумеется, печальный исход поединка можно было предотвратить, если бы вы не ограничились лишением боксеров веса, а еще и заранее учли инерцию каждого из них. Можно было измерить инерцию до боя? Можно. А как? Как вообще измерить инерцию? Поставлен вопрос, который имеет в физике исключительную важность. Перед ответом — еще одно замечание. Оно хоть и не ново для внимательных читателей, но должно их немножко запутать, сбить с толку и вместе с тем дать верное направление мысли. Вот какое замечание. Инерция действует всюду, в любых условиях, в любых состояниях. Она неотделима от тела — будь то сосулька, дождевая капля или целая планета. Она — не то, что вес, который может быть, а может и не быть. Потому что невесомое тело тоже обладает инерцией — недаром мы уничтожали Землю вместе с ее тяготением, когда швыряли в космос копье, полетевшее затем по инерции, или устраивали поединок невесомых боксеров, в котором победил инерционнейший. Это замечание и должно вас запутать. И вот почему. В кажущемся противоречии с тем, что сейчас было сказано, инерцию тела проще всего определить с помощью взвешивания. Что нужно охотникуВ магазин приходит охотник и просит отвесить ему пять килограммов дроби. Какое физическое свойство он покупает? Инерцию. Инерционный полет выстреленных дробинок — вот что ему требуется. Ведь благодаря инерции, стремлению сохранить равномерное прямолинейное движение летящие дробинки погубят утку, которая на них неосторожно наткнется. Заметьте: охотнику совсем не нужен вес дробинок. Охотник рад купить невесомую, но достаточно инерционную дробь — легче было бы шагать по лесу. Если бы можно было охотиться в далеком космосе (на каких-нибудь живых комет, придуманных фантастами), перед выходом на охоту космонавты запасались бы именно невесомыми дробинками или пулями. Но дробь продается на вес. Ибо вот непреложное правило: если уж тело имеет тяжесть, то в одинаковых условиях взвешивания она тем больше, чем больше инерционность, присущая телу. Поэтому исход боя наших невесомых боксеров был предрешен заранее: тяжеловес на Земле инерционнее легковеса и остается таким же в ванне невесомости. На случай, если вам придется судить боксерские встречи в межпланетных полетах, запомните: весовые категории спортсменов следует сохранить, но лучше переименовать их в категории инерционности. Да и на Земле их вернее называть именно так. Все сказанное, однако, не значит, что единицами веса можно измерять инерцию. Килограммы веса не годятся на эту должность по той же старой причине: они «прогульщики». Пока дробинки в магазине или в охотничьем патронташе — они весят, а после выстрела — невесомы. Как же быть? Кого взять на вакантную должность? Что нужно домашним хозяйкамИнерцию покупают не часто. Редко приобретают в чистом виде и вес — это делают, например, спортсмены-тяжелоатлеты, когда обзаводятся гирями, гантелями и штангами. Количество вещества в физике называют массой. Лучше сказать: чем больше в теле вещества, тем больше его масса. И по тысячелетнему опыту тружеников прилавка, подтвержденному физиками, массу можно измерять по «бесплатному приложению» — весу. Потому-то во всех продуктовых магазинах стоят весы. Причем тут, как и при взвешивании инерционности, прямая пропорциональность: во сколько раз больше масса тела, во столько раз больше и его вес (разумеется, опять-таки при равных условиях взвешивания). Но, в отличие от веса, масса не «прогульщица». Она всегда при теле: и на Земле, и в космосе, при любом движении. В том числе и во время свободного падения, когда тело невесомо. Так же, как инерция. Отсюда вывод: именно количество вещества, массу, можно принять на вакантную должность меры инерции. И в единицах массы измерять инерционную способность тел. Лебедь и щукаНе будем спешить. Позволим себе воспоминания и повторения. Отыскана мера для измерения инерции — количество вещества, масса. Количество вещества, значит, замедляет разгон и торможение тела. Но обратите внимание: то же самое количество вещества, та же самая масса, весит. Будучи неподвижной и находясь вблизи Земли, давит на опору. А когда опору убирают, начинает падать. Вот только сейчас, после подготовки, содержащейся на предыдущих страницах, я рискну наконец назвать вес «по-школьному» — силой тяготения. А в связи с этим пришла пора разъяснить, что именно Ньютон понимал под термином сила. В физике сила есть всегда результат взаимодействия тел, их влияние друг на друга, то, что нарушает покой или равномерное прямолинейное движение взаимодействующих тел, сообщает им ускорение. Сила тяготения — влияние Земли на камень. Таинственное влияние, которое Ньютон назвал дальнодействием, потому что оно происходит без контакта, «через пустоту». Даже если камня вблизи Земли нет, там есть нечто, что подействовало бы на камень, будь он там. Это нечто, посредством которого Земля «через пустоту» влияет на камень, именуют гравитационным полем или полем тяготения. По какому закону дальнодействующая сила тяготения действует на тело — об этом пойдет речь в следующей главе. А сейчас отметим лишь то, что эта сила приложена к веществу тела, к его массе. Именно за массу «хватает» Земля «через пустоту» камень или копье и заставляет их падать, тянет к себе, ускоряет. Такова точка зрения Ньютона. Еще раз. Действуя на сосульку, сорвавшуюся с карниза, земное притяжение ее разгоняет. Массе присуще ускорение в поле тяжести. Но, кроме того, она же, эта же самая масса, благодаря своей инерционности, противится ускорению, замедляет разгон сосульки. Вот вам замечательное противоречие, заложенное не в человеческих рассуждениях, а в самой сути природы! Прочувствуйте его хорошенько. Можно условиться в следующем (физики так и делают): в одном и том же теле уживаются две разные массы, наделенные противоположными свойствами. Та, что «слушается» силу тяготения, ускоряется к Земле, называется тяжелой массой. Или гравитационной. А та, что «не желает» поддаваться силе, «старается» сохранить покой или равномерное прямолинейное движение, уменьшает поэтому разгон, — инертной, инерционной. Сосулька падает — и в ней непрерывно конкурируют противоположные стремления: ускоряться и не ускоряться. В одном возу из старой крыловской басни спрятались невидимый лебедь и невидимая щука — вот, если хотите, сравнение (не очень верное, правда, — это скоро выяснится). Во всяком случае, теперь ясно, что делать дальше. Надо разгадать «спор» двух масс. Тогда, надо надеяться, будет понятней и само явление падения сосульки. Сила побеждаетВ басне о раке, лебеде и щуке «воз и ныне там». Он неподвижен, потому что к нему приложены силы, уравновешивающие друг друга. У нас — иное. Отличие не только в том, что отсутствует «рак», это не так уж важно. Наш «воз» не неподвижен, несмотря на старания «лебедя» (инерции), он падает вниз — туда, куда его тянет «щука» (сила тяготения). Значит ли это, что тяжелая масса больше инертной? Нет. Инерция — не сила (хоть и существуют так называемые силы инерции — о них будет сказано немного позже). Сравнивать инерцию с лебедем, строго говоря, нельзя, ибо настоящий лебедь, который «рвется в облака», прикладывает к настоящему возу именно силу — то, что изменяет скорость воза, придает ему ускорение. Инерция же — это пассивное «непослушание» силе. Дабы не запутаться в словах, применим математические символы. a=F/mi Из нее, в частности, следует, что лишь в предельном случае — при бесконечно большой инертной массе — ускорение равно нулю. А когда инертная масса хоть и велика, но конечна, то даже под ничтожным напором тело пусть очень медленно, но разгоняется. Сила побеждает любую инерцию. Активное начало держит верх над пассивностью. И поэтому все, что имеет массу, должно падать. Внимание! Мы, кажется, близки к ньютоновской (классической) разгадке одного из чудес падения. В сосульках и пылинках, песчинках и жерновах непрерывно «спорят» две массы: тяжелая и инертная. И хоть самому факту падения этот спор не мешает (сила тяготения всегда побеждает и сдвигает тело с места), но именно тяжелая и инертная массы определяют исход гонки падающих тел. Как же они соотносятся, эти две массы, какая из них все-таки больше? Теперь сообразить нетрудно. Пусть больше тяжелая масса. Тогда она «переспорила» бы соседку и тяжелые тела лучше «слушались» бы силу, чем «упрямились», — падали бы быстрее легких. Падающий жернов обогнал, бы падающую песчинку. Но с первых страниц этой книжки мы отлично помним, что это не так. Пусть больше инертная масса. Тогда, наоборот, легкие тела падали бы быстрее тяжелых. Песчинка обогнала бы жернов. Однако и этого не наблюдается в природе. Гонка падающих тел не имеет победителя. Единственно возможный вывод: массы-соседки не могут друг друга «переспорить», а потому тяжелая масса равна инертной. Всегда равна, в любых условиях. Чтобы до конца соблюсти точность, надо сказать, что во всяком случае обе массы пропорциональны: во сколько раз возрастает одна, во столько увеличивается и другая, а при соответствующем выборе единиц измерения пропорциональность становится равенством. Вот она, как будто, причина чуда, которую мы так долго искали! Равенство тяжелой и инертной масс! Можно поставить множество тонких опытов для проверки этого заключения. Тут не только свободное падение тел. Всевозможные маятники, балансы, крутильные весы, вариометры позволяют скрупулезнейшим образом экспериментально измерить обе массы. В начале нашего века многочисленные опыты такого рода исполнил венгерский физик Роланд Этвеш. В тончайшем приборе, который изобрел Этвеш, и в других, более поздних, равенство тяжелой и инертной масс было подтверждено вплоть до одиннадцатого знака после запятой. Даже в стомиллионных долях процента оно оказалось безупречным! Вне всякой зависимости от химического состава, плотности, состояния тел. Именно поэтому жернов и пушинка падают в пустоте одинаково быстро. Именно поэтому они в падении ничего не весят. Хочется свободно вздохнуть и сделать перерыв в бегстве от нашего удивления. В самом деле, почему? Что это за странное равенство? Тут ньютоновская механика молчит. Ответа не знает. Ответ лежит за ее пределами, куда мы в свое время заглянем. И в конце концов окажется, что существует совсем иной, гораздо более простой (с точки зрения «устройства природы», хоть и гораздо более сложный для понимания) способ объяснения загадки падения. Способ, обходящийся без разговоров о делении массы на тяжелую и инертную, даже без истолкования веса как дальнодействующей, мгновенно проникающей «через пустоту» силы тяготения… Поскольку сразу постичь все это невозможно, примиритесь с постепенностью познания. Еще долго мы не покинем ньютоновских владений, где нас ждет немало поучительного и многозначительного. |
3.1: Инерция – Физика LibreTexts
На обыденном языке мы говорим о чем-то или о ком-то, «обладающих большой инерцией», что, по сути, означает, что их очень трудно привести в движение. Такое использование слова «инерция» согласуется с «законом инерции», который мы ввели в предыдущей главе (который, среди прочего, гласит, что покоящийся объект, если его предоставить самому себе, просто останется в покое), но он выходит за рамки этого, пытаясь количественно оценить, насколько сложно заставить объект двигаться.
Такое использование слова «инерция» согласуется с «законом инерции», который мы ввели в предыдущей главе (который, среди прочего, гласит, что покоящийся объект, если его предоставить самому себе, просто останется в покое), но он выходит за рамки этого, пытаясь количественно оценить, насколько сложно заставить объект двигаться.
По опыту мы знаем, что более легкие объекты легче привести в движение, чем более тяжелые, но у большинства из нас, вероятно, есть интуиция, что гравитация (сила, которая притягивает объект к земле и, следовательно, определяет его вес) не задействована. существенно здесь. Представьте себе, например, разницу между ударами по волейболу и мячу для боулинга. Нетрудно поверить, что последнему было бы так же больно, если бы мы сделали это, плавая в свободном падении на космической станции (в состоянии эффективной «невесомости»), как если бы мы сделали это прямо здесь, на поверхности Земли.Другими словами, дело не в том (обязательно), насколько тяжело что-то на ощупь, а в том, насколько массивный .
Но что это за качество «массивности», которое мы интуитивно ассоциируем с большой инерцией? Есть ли способ (кроме повторного использования веса) присвоить ему числовое значение?
Относительная инерция и столкновения
Один из возможных способов определения относительных инерций двух объектов, по крайней мере концептуально, – это попытаться использовать один из них для приведения в движение другого.Большинство из нас знакомо с тем, что происходит, когда два идентичных объекта (предположительно, имеющих одинаковую инерцию) сталкиваются: если столкновение происходит в лоб (то есть движение до и после ограничивается прямой линией), они в основном обменные скорости. Например, бильярдный шар, ударившись по другому, остановится, а второй полетит с той же скоростью, что и первый. Игрушка, которую иногда называют «шары Ньютона» или «колыбель Ньютона», также демонстрирует этот эффект. Интуитивно мы понимаем, что то, что нужно, чтобы остановить первый шар, точно такое же, как и для того, чтобы привести второй в движение с той же скоростью.
А что, если сталкивающиеся объекты имеют разную инерцию? Мы ожидаем, что изменение их скоростей в результате столкновения будет другим: скорость объекта с наибольшей инерцией изменится не очень сильно, и, наоборот, изменение скорости объекта с наименьшей инерцией будет сравнительно больше. График зависимости скорости от времени для двух объектов может выглядеть примерно так, как показано на рисунке \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {1} \): пример зависимости скорости отграфик времени для столкновения двух объектов с разной инерцией. На этом рисунке объект 1, первоначально движущийся со скоростью \ (v_ {1i} \) = 1 м / с, сталкивается с объектом 2, первоначально находящимся в состоянии покоя. После столкновения, которое здесь, как предполагается, занимает миллисекунду или около того, объект 1 фактически отскакивает назад, поэтому его конечная скорость равна \ (v_ {1f} \) = −1/3 м / с, тогда как объект 2 движется в вправо со скоростью \ (v_ {2f} \) = 2/3 м / с. Таким образом, изменение скорости объекта 1 равно \ (\ Delta v_1 = v_ {1f} −v_ {1i} \) = −4/3 м / с, тогда как для объекта 2 мы имеем \ (\ Delta v_2 = v_ { 2f} – v_ {2i} \) = 2/3 м / с.
Таким образом, изменение скорости объекта 1 равно \ (\ Delta v_1 = v_ {1f} −v_ {1i} \) = −4/3 м / с, тогда как для объекта 2 мы имеем \ (\ Delta v_2 = v_ { 2f} – v_ {2i} \) = 2/3 м / с.
Заманчиво использовать это соотношение \ (\ Delta v_1 / \ Delta v_2 \) как меру относительной инерции двух объектов, только мы бы хотели использовать его в перевернутом виде и с противоположным знаком. : то есть, так как \ (\ Delta v_2 / \ Delta v_1 \) = −1/2, мы бы сказали, что объект 2 имеет дважды инерции объекта 1. Но тогда мы должны спросить: является ли это надежным, повторяемым мера? Будет ли это работать при любом столкновении (в разумных пределах, конечно: нам явно нужно оставаться в одном измерении и исключать внешние воздействия, такие как трение), и при любой начальной скорости?
Начнем с того, что у нас есть основания ожидать, что не имеет значения, стреляем ли мы из объекта 1 в объект 2 или из объекта 2 в сторону объекта 1, потому что в предыдущей главе мы узнали, что только относительное движение обнаруживается , а относительное движение то же самое в обоих случаях. Рассмотрим, например, как выглядит столкновение на рисунке \ (\ PageIndex {1} \) для гипотетического наблюдателя, движущегося вместе с объектом 1 со скоростью 1 м / с. Ему кажется, что объект 1 находится в состоянии покоя, и именно объект 2 приближается к нему со скоростью -1 м / с. Чтобы увидеть, как ему кажется результат столкновения, просто добавьте те же −1 м / с к конечным скоростям, которые мы получили ранее: объект 1 будет двигаться со скоростью \ (v_ {1f} \) = −4/3 м / с, и объект 2 будет двигаться со скоростью \ (v_ {2f} \) = −1/3 м / с, и мы получим ситуацию, подобную показанной на рисунке \ (\ PageIndex {2} \), где обе кривые просто сдвинуты вниз на 1 м / с:
Рассмотрим, например, как выглядит столкновение на рисунке \ (\ PageIndex {1} \) для гипотетического наблюдателя, движущегося вместе с объектом 1 со скоростью 1 м / с. Ему кажется, что объект 1 находится в состоянии покоя, и именно объект 2 приближается к нему со скоростью -1 м / с. Чтобы увидеть, как ему кажется результат столкновения, просто добавьте те же −1 м / с к конечным скоростям, которые мы получили ранее: объект 1 будет двигаться со скоростью \ (v_ {1f} \) = −4/3 м / с, и объект 2 будет двигаться со скоростью \ (v_ {2f} \) = −1/3 м / с, и мы получим ситуацию, подобную показанной на рисунке \ (\ PageIndex {2} \), где обе кривые просто сдвинуты вниз на 1 м / с:
Рисунок \ (\ PageIndex {2} \): Другой пример (на самом деле такое же столкновение, как на рисунке \ (\ PageIndex {1} \), только для наблюдателя, первоначально движущегося вправо со скоростью 1 м / с).
Но тогда это именно то, что мы должны ожидать найти и в нашей лаборатории, если бы мы действительно послали второй объект со скоростью 1 м / с к первому, находящемуся в покое. Все отдельные скорости изменились относительно рисунка \ (\ PageIndex {1} \), но скорость изменилась. , \ (\ Delta v_1 \) и \ (\ Delta v_2 \) явно остались прежними, и поэтому такова наша (предварительная) мера относительной инерции объектов.
Все отдельные скорости изменились относительно рисунка \ (\ PageIndex {1} \), но скорость изменилась. , \ (\ Delta v_1 \) и \ (\ Delta v_2 \) явно остались прежними, и поэтому такова наша (предварительная) мера относительной инерции объектов.
Очевидно, тот же аргумент может быть использован для вывода, что тот же результат будет получен, когда оба объекта изначально движутся навстречу друг другу, если их относительная скорость такая же, как в этих примерах, а именно 1 м / с .Однако, если мы не проведем эксперименты, мы не сможем точно предсказать, что произойдет, если мы увеличим (или уменьшим) их относительную скорость. Фактически, мы могли представить, как два объекта разбиваются на очень высокой скорости, так что они могут даже серьезно повредиться в процессе. Тем не менее, экспериментально (и это отнюдь не очевидный результат!) Мы все равно найдем то же значение −1/2 для отношения \ (\ Delta v_2 / \ Delta v_1 \), по крайней мере, до тех пор, пока коллизия не настолько жесток, чтобы предметы действительно распадались на части.
Возможно, самым удивительным результатом наших экспериментов было бы следующее: представьте, что объекты имеют «липкую» сторону (например, маленькие черные прямоугольники, показанные на рисунках, могут быть полосками липучки), и мы развернем их так, чтобы когда они сталкиваются, они в конечном итоге прилипают друг к другу. В этом случае (который, как мы увидим позже, называется полностью неупругим столкновением ), график \ (v \) – vs – \ (t \) может выглядеть как на рисунке \ (\ PageIndex {3} \) ниже.
Теперь два объекта движутся вместе вправо, довольно медленно: \ (v_ {1f} = v_ {2f} \) = 1/3 м / с.Изменения скорости равны \ (\ Delta v_1 \) = −2/3 м / с и \ (\ Delta v_2 \) = 1/3 м / с, оба из которых отличаются от того, что было раньше на рис. \ (\ PageIndex {1} \) и \ (\ PageIndex {2} \): тем не менее, соотношение \ (\ Delta v_2 / \ Delta v_1 \) по-прежнему равно -1/2, как и во всех предыдущих случаи.
Рисунок \ (\ PageIndex {1} \) склеился при столкновении.
Инерционная масса: определение и свойства
На этом этапе было бы разумно предположить, что это соотношение \ (\ Delta v_2 / \ Delta v_1 \), на самом деле, говорит нам что-то о внутреннем свойстве двух объектов, которое мы назвали выше их «относительной инерции».Таким образом, легко увидеть, как можно присвоить значение инерции любого объекта (по крайней мере, концептуально): выбрать «стандартный» объект и произвольно решить, что его инерция будет иметь числовое значение 1 , в зависимости от того, какие единицы вы выберете для него (эти единицы фактически окажутся килограммами, как вы увидите через минуту). Затем, чтобы определить инерцию другого объекта, который мы обозначим индексом 1, просто организуйте одномерное столкновение между объектом 1 и эталоном, при правильных условиях (в основном, без чистых внешних сил), измерьте изменения скорости \ (\ Delta v_1 \) и \ (\ Delta v_s \), и возьмите величину \ (- \ Delta v_s / \ Delta v_1 \) в качестве числового значения отношения инерции объекта 1 к инерции стандартный объект. В символах используется буква \ (m \) для обозначения инерции объекта,
В символах используется буква \ (m \) для обозначения инерции объекта,
\ [\ frac {m_ {1}} {m_ {s}} = – \ frac {\ Delta v_ {s}} {\ Delta v_ {1}} \ label {eq: 3.1} \]
Но, поскольку \ (m_s \) = 1 по определению, это дает нам непосредственно числовое значение \ (m_1 \).
Причина, по которой мы используем букву \ (m \), как вы, должно быть, догадались, состоит в том, что на самом деле определяемая таким образом инерция оказывается идентичной тому, что мы традиционно называем «массой». Точнее, величина, определенная таким образом, равна инертной массе объекта .Упомянутый ранее замечательный факт, что сила тяжести между двумя объектами оказывается пропорциональной их инерционным массам, позволяет нам определять инерционную массу объекта с помощью более традиционной процедуры, просто взвешивая его, а не тщательно продумывая. столкновение между ним и стандартным килограммом на хоккейной площадке. Но, в принципе, мы могли представить себе существование двух разных величин, которые следует называть «инертной массой» и «гравитационной массой», и идентичность (или, точнее, – насколько нам известно – точная пропорциональность) два – довольно загадочный экспериментальный факт 1 .
В любом случае, судя по тому способу, которым мы ее построили, инерционная масса, определенная как в уравнении (\ ref {eq: 3.1}), действительно отражает в количественном отношении концепцию, которую мы пытались выразить в начале. главы: а именно, насколько сложно может быть привести объект в движение. В принципе, однако, необходимо провести другие эксперименты, чтобы убедиться, что он действительно обладает свойствами, которые мы традиционно связываем с понятием массы. Например, предположим, что мы соединяем вместе два объекта массы \ (m \).Масса полученного объекта \ (2m \)? Эксперименты со столкновениями действительно показали бы, что это имеет место с большой точностью в макроскопическом мире (которым мы занимаемся в этом семестре), но это хороший пример того, как нельзя ничего принимать как должное: на микроскопическом уровне это Это снова факт, что инертная масса атомного ядра на меньше , чем сумма масс всех составляющих его протонов и нейтронов 2 .
Вероятно, последнее, что нужно будет проверить, это то, что коэффициент инерции не зависит от стандартного .Предположим, что у нас есть два объекта, которым мы присвоили массы \ (m_1 \) и \ (m_2 \), устроив так, чтобы каждый из них независимо сталкивался со «стандартным объектом». Если мы теперь организуем столкновение между объектами 1 и 2 напрямую, обнаружим ли мы, что соотношение изменений их скорости определяется соотношением отдельно определенных масс \ (m_1 \) и \ (m_2 \)? Нам определенно нужно, чтобы это было так, чтобы концепция инерции была действительно полезной; но опять же, мы не должны ничего предполагать, пока не проверим это! К счастью, тесты действительно показали, что в каждом случае ожидаемая взаимосвязь имеет место 3
.\ [- \ frac {\ Delta v_ {2}} {\ Delta v_ {1}} = \ frac {m_ {1}} {m_ {2}} \ label {eq: 3.2}. \]
На данный момент у нас есть не только полезное определение инерции, но и настоящий закон природы , как я объясню далее.
1 Этот факт, возведенный Эйнштейном в категорию принципа (принцип эквивалентности ), является отправной точкой общей теории относительности.
2 И это не просто мелочь: вся ядерная энергетика зависит от этой маленькой разницы.
3 Уравнение \ ref {eq: 3.2} на самом деле оказывается справедливым также на микроскопическом (или квантовом ) уровне, хотя там мы предпочитаем формулировать результат, говоря, что сохраняется сохранение импульса (см. Следующий раздел) .
Инерция: сила, удерживающая Вселенную
Инерция – это сила, скрепляющая Вселенную. В прямом смысле. Без него все развалилось бы. Это также то, что держит нас взаперти деструктивными привычками и удерживает их от изменений.
*
«Если бы можно было щелкнуть выключателем и выключить инерцию, Вселенная мгновенно схлопнулась бы в сгусток материи», – пишут Питер и Нил Гарно в книге В тисках далекой Вселенной: Наука об инерции .
… смерть – это наша общая цель. Никто не избежал этого. Так и должно быть, потому что смерть, скорее всего, является лучшим изобретением жизни. Это агент изменения жизни; он очищает старое, чтобы освободить место для нового … Ваше время ограничено, поэтому не тратьте его зря на чужую жизнь.
Стив Джобс
Инерция – это сила, скрепляющая Вселенную. В прямом смысле. Без него материи не хватало бы электрических сил, необходимых для формирования ее текущего устройства. Инерции противодействуют тепловая и кинетическая энергия, производимая движущимися частицами. Вычтите его, и все остынет до -459,67 градусов по Фаренгейту (абсолютный ноль). Однако мы так мало знаем об инерции и о том, как использовать ее в повседневной жизни.
Основы
Немецкий астроном Иоганн Кеплер (1571–1630) ввел слово «инерция».Об этом говорит этимология термина. Кеплер получил это слово от латинского «неумелость, невежество; бездействие или праздность ». Верная своему происхождению, инерция удерживает нас в постели ленивым воскресным утром (нам нужно применить энергию активации, чтобы преодолеть это состояние).
Верная своему происхождению, инерция удерживает нас в постели ленивым воскресным утром (нам нужно применить энергию активации, чтобы преодолеть это состояние).
Инерция означает сопротивление изменениям, в частности сопротивление изменениям в движении. Инерция может проявляться в физических объектах или в сознании людей.
Мы рано познаем принцип инерции.Все мы знаем, что для того, чтобы что-то двигаться, изменить направление или остановить, требуется сила.
Наше интуитивное ощущение того, как работает инерция, позволяет нам в определенной степени контролировать мир вокруг нас. Изучение вождения предлагает дополнительные уроки. Без внешних физических сил машина продолжала бы двигаться по прямой в том же направлении. Требуется сила (энергия), чтобы заставить автомобиль двигаться и преодолеть инерцию, которая удерживала его на парковочном месте. Изменение направления на поворот или разворот требует дополнительной энергии.Инерция – вот почему автомобиль не останавливается в момент торможения.
Чем тяжелее транспортное средство, тем сложнее преодолеть инерцию и заставить его остановиться. Легкий велосипед останавливается с легкостью, а пассажирскому поезду с восемью вагонами требуется хорошая миля, чтобы остановиться. Точно так же, чем быстрее мы бежим, тем больше времени нужно, чтобы остановиться. Бежать по прямой намного проще, чем петлять по людному тротуару, меняя направление, чтобы уворачиваться от людей.
Любой объект, который можно вращать, например колесо, обладает инерцией вращения.Это говорит нам о том, насколько сложно изменить скорость объекта вокруг оси. Инерция вращения зависит от массы объекта и его распределения относительно оси.
Инерция – это первый закон движения Ньютона, фундаментальный принцип физики . Ньютон резюмировал это следующим образом: «vis insita, или врожденная сила материи, – это сила сопротивления, с помощью которой каждое тело, в той мере, в какой оно находится, стремится сохранить свое нынешнее состояние, будь то покой или равномерное движение. вперед по прямой.”
вперед по прямой.”
При разработке своего первого закона Ньютон опирался на работы Галилео Галилея. В письме 1624 г. к Франческо Инголи Галилей изложил принцип инерции:
Я говорю вам, что если естественные тела имеют от Природы возможность перемещаться каким-либо движением, это может быть только круговое движение, и при этом невозможно, чтобы Природа наделила какое-либо из своих целостных тел склонностью двигаться прямым движением. . У меня есть много подтверждений этого предположения, но пока достаточно одного, а именно этого.
Я полагаю, что части вселенной находятся в наилучшем расположении, так что ни одна из них не находится не на своем месте, то есть Природа и Бог идеально устроили свою структуру … Следовательно, если части мира хорошо упорядочены, прямое движение излишне и неестественно, и они могут иметь его только тогда, когда какое-то тело принудительно удаляется с его естественного места, в которое оно затем возвращается к прямой линии.
В 1786 году Иммануил Кант уточнил: «Любое изменение материи имеет внешнюю причину.(Каждое тело остается в состоянии покоя или движения в том же направлении и с той же скоростью, если внешняя причина не заставляет его покинуть это состояние.)… Этот механический закон можно назвать только законом инерции (lex inertiæ) …. »
Теперь, когда мы понимаем принцип, давайте посмотрим, как мы можем лучше понять его и применить в наших интересах.
Принятие решений и когнитивная инерция
Все мы испытываем когнитивную инерцию: тенденцию придерживаться существующих идей, убеждений и привычек, даже если они больше не служат нам.Мало кто действительно способен пересмотреть свое мнение в свете опровергающей информации. Вместо этого мы поддаемся предвзятости подтверждения и ищем подтверждения существующих убеждений. Намного легче продолжать думать о том, о чем мы всегда думали, чем размышлять о возможности того, что мы можем ошибаться, и обновлять свои взгляды. Чтобы преодолеть когнитивный диссонанс, нужно потрудиться, точно так же, как нужно приложить усилия, чтобы остановить машину или изменить направление движения.
Чтобы преодолеть когнитивный диссонанс, нужно потрудиться, точно так же, как нужно приложить усилия, чтобы остановить машину или изменить направление движения.
Когда окружающая среда меняется, привязанность к старым убеждениям может быть вредной или даже фатальной.Неважно, не воспринимаем ли мы изменения или не реагируем на них, результат один и тот же. Даже когда другим очевидно, что мы должны измениться, для нас это не очевидно. Намного легче увидеть что-то, когда вы не вовлечены напрямую. Если я спрошу вас, с какой скоростью вы сейчас двигаетесь, вы, скорее всего, ответите ноль, но вы движетесь вокруг Солнца со скоростью 18 000 миль в час. Перспектива – это все, а точка зрения, которая имеет значение, наиболее точно соответствует реальности.
Иногда вы принимаете решение о чем-то, не зная почему, и ваше решение сохраняется по инерции.С каждым годом меняться становится все труднее.
Милан Кундера, Невыносимая легкость бытия
Когнитивная инерция – причина того, что изменение наших привычек может быть трудным . По умолчанию всегда используется путь наименьшего сопротивления, который легко принять и сложнее подвергнуть сомнению. Возьмем, к примеру, свой банк. Возможно, вы знаете, что в других банках есть варианты получше. Или у вас возникли проблемы с вашим банком, на рассмотрение которых ушло много времени. Тем не менее, очень немногие люди действительно меняют свой банк, и многие из нас остаются со счетом, который мы впервые открыли.В конце концов, отход от статус-кво потребует много усилий: исследование альтернатив, перенос балансов, закрытие счетов и т. Д. А что, если что-то пойдет не так? Звучит рискованно. Затраты на переключение высоки, поэтому мы придерживаемся статус-кво.
По умолчанию всегда используется путь наименьшего сопротивления, который легко принять и сложнее подвергнуть сомнению. Возьмем, к примеру, свой банк. Возможно, вы знаете, что в других банках есть варианты получше. Или у вас возникли проблемы с вашим банком, на рассмотрение которых ушло много времени. Тем не менее, очень немногие люди действительно меняют свой банк, и многие из нас остаются со счетом, который мы впервые открыли.В конце концов, отход от статус-кво потребует много усилий: исследование альтернатив, перенос балансов, закрытие счетов и т. Д. А что, если что-то пойдет не так? Звучит рискованно. Затраты на переключение высоки, поэтому мы придерживаемся статус-кво.
Иногда нам помогает инерция. В конце концов, все расспрашивать было бы утомительно. Но во многих случаях стоит преодолеть инерцию и привести что-то в движение, или изменить направление, или остановить его.
С инерцией важно то, что труден только начальный толчок.После этого прогресс становится более плавным. Эрнест Хемингуэй умел преодолевать инерцию в своих произведениях. Зная, что начало работы всегда было самым сложным, он решил заканчивать работу каждый день в момент, когда у него был импульс (а не когда у него заканчивались идеи). На следующий день он сможет забрать оттуда. Хемингуэй объясняет в «Празднике подвижности»:
Эрнест Хемингуэй умел преодолевать инерцию в своих произведениях. Зная, что начало работы всегда было самым сложным, он решил заканчивать работу каждый день в момент, когда у него был импульс (а не когда у него заканчивались идеи). На следующий день он сможет забрать оттуда. Хемингуэй объясняет в «Празднике подвижности»:
Я всегда работал, пока что-то не делал, и всегда останавливался, когда знал, что будет дальше. Так я мог быть уверен, что продолжу путь на следующий день.
Позже в книге он описывает другой метод, заключающийся в написании всего одного предложения:
Не волнуйтесь. Вы всегда писали раньше и будете писать сейчас. Все, что вам нужно сделать, это написать одно верное предложение. Напишите самое верное предложение, которое вы знаете. Итак, наконец, я написал одно верное предложение и продолжил. Тогда это было легко, потому что всегда было одно верное предложение, которое я знал, видел или слышал, как кто-то сказал.
Если я начинал писать подробно или как кто-то представлял или представлял что-то, я обнаруживал, что могу вырезать этот завиток или орнамент, выбросить его и начать с первого действительно простого декларативного предложения, которое я написал.
Мы можем многому научиться из подхода Хемингуэя к борьбе с инерцией и применить его не только в письменной форме, но и в других областях. Как и в случае с физикой, импульс с самого начала может унести нас далеко. Нам просто нужно собрать необходимую энергию активации и приступить к работе.
Смещение статус-кво: «Когда сомневаешься, ничего не делай»
Когнитивная инерция также проявляется в форме предвзятости статус-кво. Принимая решения, мы редко бываем рациональными. Столкнувшись с конкурирующими вариантами и информацией, мы часто выбираем вариант по умолчанию, потому что это просто.Чтобы делать что-то иное, чем то, что мы уже делаем, требуется умственная энергия, которую мы предпочли бы сохранить. Во многих областях это помогает нам избежать усталости от решений.
Во многих областях это помогает нам избежать усталости от решений.
Многие из нас большую часть времени едят одно и то же, носят одинаковую одежду и следуют распорядку дня. Эта тенденция обычно нам хорошо служит. Но статус-кво не обязательно является оптимальным решением. В самом деле, это может быть совершенно вредно или, по крайней мере, бесполезно, если что-то изменилось в окружающей среде или если мы хотим оптимизировать использование времени.
Инерция – главный враг любой попытки изменить мужские привычки. Цивилизация ограничена по инерции.
Эдвард Л. Бернейс, Propaganda
В статье под названием «Если вам это нравится, имеет ли значение, правда ли это?» Фелипе де Бригар [1] является убедительной иллюстрацией предвзятости статус-кво. Один из самых известных мысленных экспериментов касается «машины опыта» Роберта Нозика. Нозик попросил нас представить, что ученые создали машину виртуальной реальности, способную имитировать любые приятные переживания. Нам предлагается возможность подключиться к сети и прожить остаток жизни в постоянном, но фальшивом удовольствии. Позже машина впечатлений послужила вдохновением для создания серии фильмов «Матрица». Представленный мысленным экспериментом, большинство людей отказываются и заявляют, что предпочли бы реальность. Но что, если мы перевернем повествование? Де Бригар считал, что мы против машины опыта, потому что она противоречит статус-кво, жизни, к которой мы привыкли.
Нам предлагается возможность подключиться к сети и прожить остаток жизни в постоянном, но фальшивом удовольствии. Позже машина впечатлений послужила вдохновением для создания серии фильмов «Матрица». Представленный мысленным экспериментом, большинство людей отказываются и заявляют, что предпочли бы реальность. Но что, если мы перевернем повествование? Де Бригар считал, что мы против машины опыта, потому что она противоречит статус-кво, жизни, к которой мы привыкли.
В ходе эксперимента он попросил участников представить, как их разбудил звонок в дверь субботним утром.Человек в черном, представившийся мистером Смитом, стоит у двери. Он утверждает, что обладает важной информацией. Г-н Смит объясняет, что произошла ошибка, и вы действительно подключены к машине впечатлений. Все, через что вы прошли до сих пор, было симуляцией. Он предлагает выбор: оставаться включенным или вернуться в неизвестную реальную жизнь. Неудивительно, что во втором случае гораздо меньше людей желало вернуться к реальности, чем оставаться в ней в первой. Элемент отвращения – это не сама машина переживаний, а отход от статус-кво, который она представляет.
Элемент отвращения – это не сама машина переживаний, а отход от статус-кво, который она представляет.
Заключение
Инерция – всепроникающая, проблематичная сила. Это тяга, которая заставляет нас цепляться за старые пути и мешает пробовать новое. Но, как мы видели, это тоже необходимо. Без него Вселенная рухнула бы. Инерция – это то, что позволяет нам поддерживать модели функционирования, поддерживать отношения и проживать день, не подвергая сомнению все. Мы можем преодолеть инерцию во многом так же, как это сделал Хемингуэй, – признав ее влияние и предприняв необходимые шаги для создания этого крайне важного начального импульса.
***
Конечные ноты
[1] https://www.tandfonline.com/doi/abs/10.1080/09515080
2290
Inertia Demo | Демонстрационный зал физики UCSC
Рисунок 1
Материалы:
- Инерционный демонстрационный блок, показанный на Рисунке 2 [Шкаф A2]
- 2 шт.
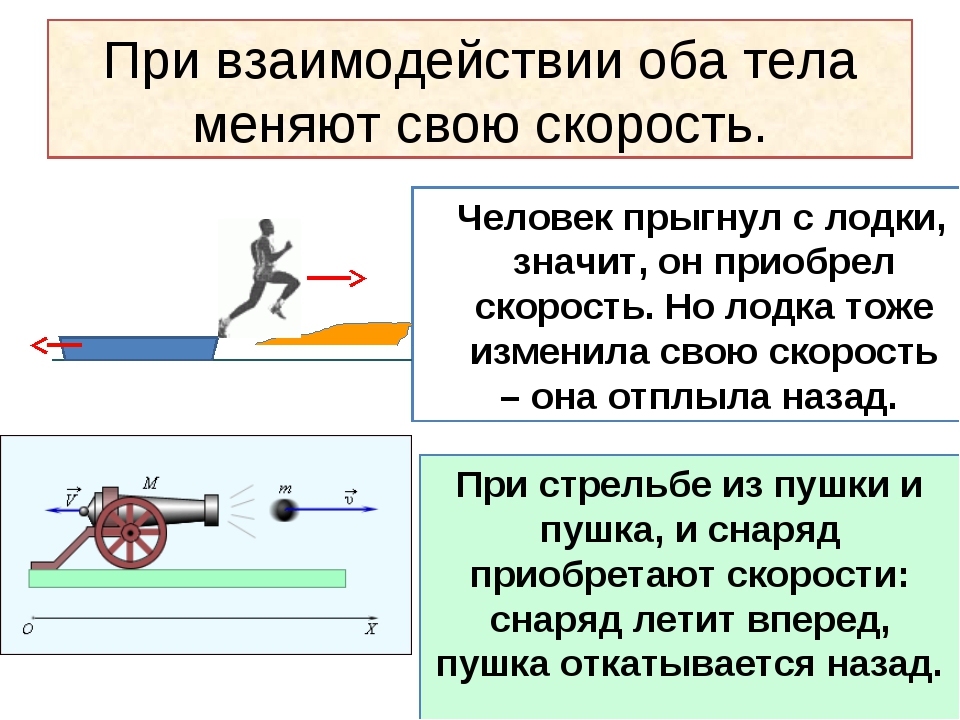 По 1 кг
По 1 кг - 2 удлиненных стержня для ручек
- Толстая (но легко бьющаяся) хлопковая нить
- 2 шт.
- 2x цоколя
- 3 штанги
- 2 зажима 90 °
- Толстые перчатки [Шкаф B3]
- Мешки с песком для набивки стола и крепления основания стоек [Шкаф A3]
Рисунок 2: Инерционная демонстрационная коробка
Демо:
Два одинаковых груза подвешены на веревке, а еще две веревки подвешены под ними с длинными стержнями вместо ручек.Когда рукоятку рывком тянут вниз, рвется нижняя струна, но когда ее тянут с равной силой, рвется верхняя струна.
Пояснение:
Эта демонстрация демонстрирует Первый закон Ньютона (покоящийся объект будет оставаться в покое, если на него не действует сила) и Второй закон (F = Ma) движения, и его можно объяснить, используя любой из них. Использование Второго закона Ньютона требует больше математики, чем простое объяснение его по инерции, но может дать интересное понимание реальной физики в действии.
- T T = натяжение верхней струны
- F P или F ’ P = сила, с которой человек натягивает нижнюю струну
- Mg = масса массы M (предположим, что струна без массы)
Натяжение верхней струны происходит из-за веса массы (изначально никто не тянул): T T = Mg
Натяжение нижней струны изначально равно 0 (никто не тянет – мы предполагаем, что маленький стержень безмассовый): T B = 0
Существует критическая сила натяжения T C , при которой струна разрывается.
КОРПУС 1
Человек медленно тянет за ручку с усилием F P
Есть много времени, чтобы почувствовать вес F P
Напряжение :
В точке F P + Mg = T C верхняя струна порвется (T T > T B всегда в этом случае)
Общая сила, которую должен приложить человек, составляет P = T C – Mg
ДЕЛО 2
Человек быстро тянет за ручку с силой F ’ P (вниз)
Не хватает времени, чтобы вес почувствовал F’ P
Напряжение:
В точке F ’ P = T C разорвется нижняя колонна . Требуемая величина T C такая же, как в случае 1, где T C = F P + Mg. Общая сила, которую человек должен сейчас приложить, составляет F ’ P = F P + Mg (вес груза больше не« помогает »ему достичь критической силы натяжения)
Требуемая величина T C такая же, как в случае 1, где T C = F P + Mg. Общая сила, которую человек должен сейчас приложить, составляет F ’ P = F P + Mg (вес груза больше не« помогает »ему достичь критической силы натяжения)
Верхняя струна никогда не ощущает силы F ’ P и, следовательно, никогда не достигает критического натяжения.
Инерция массы относительно велика, поэтому она будет сопротивляться любому движению.
Струна здесь несколько эластична, и ее можно рассматривать как пружину. Представьте себе, как привязать пружину к слону на катке. Если вы потянете за другой конец пружины, потребуется время, чтобы пружина растянулась и в конечном итоге сдвинула слона; мы говорим, что у слона много инерции. Если вместо слона подключить мышку и потянуть за пружину, то мышь практически сразу начнет двигаться (пружина не так сильно растягивается). Мышь имеет гораздо меньшую инерцию и значительно меньше сопротивляется движению, чем слон.
————————————————————————–
СЛЕДУЮЩЕЕ ОБЪЯСНЕНИЕ НЕПРАВИЛЬНО , но обычно его можно найти в Интернете. Может быть полезно понять, почему это неверно, если есть вопросы, относящиеся к этому «объяснению».
————————————————————————–
Использование второго закона движения Ньютона:
F NET = Ma
Для F NET (чистая сила в направлении y) мы учитываем силы, действующие на вес, M.Это дает нам
T B + Mg – T T = Ma
Где a – ускорение, с которым груз опускается вниз человеком, а g – ускорение свободного падения. Ускорение определяется как положительное в направлении вниз.
Переставляя, получаем:
T B – T T = Ma – Mg
T B – T T = M (a-g)
КОРПУС 1
Когда груз опускается медленно, с ускорением, намного меньшим, чем у гравитации:
а <г
M (а-г) <0
T B – T T <0
T B
Если вы ускоряетесь вниз намного меньше, чем ускорение свободного падения, натяжение нижней струны намного меньше, чем натяжение верхней струны *. Поскольку натяжение вверху больше, эта струна порвется первой.
Поскольку натяжение вверху больше, эта струна порвется первой.
* При a → 0, T T = T B + Mg
ДЕЛО 2
При быстром опускании груза с ускорением, намного превышающим ускорение свободного падения:
а> г
M (а-г)> 0
T B – T T > 0
T B > T T
Это означает, что натяжение нижней струны больше, чем натяжение верхней, поэтому нижняя струна будет ломаться первой.
————————————————————————–
Опять же, приведенное выше объяснение – это НЕ , почему верхняя струна рвется с медленной, равномерной силой и почему нижняя струна рвется при быстром натяжении. Хотя это кажется ясным объяснением того, что происходит, есть две основные проблемы.
Первая проблема заключается в том, что он изолирует ускорение нижней струны и рукоятки (а) от общего ускорения, ощущаемого системой (g). Мы знаем, что эти два ускорения связаны и не могут быть разделены так легко.
Вторая проблема с этим решением (и ее легче всего определить с помощью контрольного эксперимента) заключается в том, что математика не зависит от массы и ее расположения вдоль струны. Это уравнение отделяет натяжение нижней струны от натяжения верхней струны, но не объясняет, почему разница натяжения могла бы возникнуть только при наличии массы, разделяющей струну. Теоретически это означает, что уравнение должно оставаться верным, если бы не было массы (была только одна струна с ручкой), где натяжение верхней струны эквивалентно натяжению в верхней части струны и натяжению в верхней части струны. нижняя струна эквивалентна натяжению нижней части той же струны.Это означает, что если вы повторите эксперимент с одной веревкой и без веса, быстрое натягивание приведет к разрыву струны около низа, а медленное натяжение приведет к разрыву струны наверху.
Когда этот контрольный эксперимент был проведен, мы обнаружили, что этого не произошло. В большинстве случаев струна рвалась около дна *, независимо от того, как быстро мы натягивали струну.
Поскольку мы не смогли показать, что натяжение напрямую связано с расстоянием от места приложения силы, мы должны полностью исключить это решение.Мы считаем, что лучшее объяснение можно дать, если предположить, что струна имеет измеримый (но очень маленький) коэффициент упругости, который становится очевидным при большой массе. Наиболее просто это объясняется примером слона и катка в верхней части страницы.
* несколько раз струна порывалась около вершины, но мы считаем, что это больше связано с внутренними слабыми местами струны, а не с какими-либо существенными различиями в натяжении как функции от x (расстояние от точки приложения силы) Более того, мы не смогли достоверно воспроизвести разрыв струны около вершины, что наводит нас на мысль, что это аномальное событие.
Примечания:
- Возьмитесь за ручки двумя руками по обе стороны от штанги, чтобы пальцы не оказались ниже траектории падения груза.
- Смотри пальцами !!!
- Поместите мешки с песком ниже того места, где будет падать груз (ниже веса равномерного усилия), чтобы не повредить стол.

- Завяжите узлы для двух дополнительных отрезков струны на случай, если при одном натяжении порвется неправильный участок струны
Автор Софья Шольц
Луна и инерция – Законы Ньютона – WJEC – GCSE Physics (Single Science) Revision – WJEC
Масса Луны меньше массы Земли.У него меньше напряженность гравитационного поля. Меньшая масса Луны не привлечет массу в 1 кг с такой силой, как на Земле.
На Луне г = 1,6 Н / кг.
Другими словами, масса 1 кг на Луне имеет вес 1,6 Н, а масса 5 кг будет весить 8 Н.
- Вопрос
а) Какова масса человека, который весит 120 Н.
 Луна? (г = 1,6 Н / кг)
Луна? (г = 1,6 Н / кг)б) Каковы были бы масса и вес того же человека на Земле, где г = 10 Н / кг?
- Показать ответ
a) m = W ÷ g
= 120 N ÷ 1.6 Н / кг
= 75 кг
б) Это вопрос с подвохом. Масса на Земле будет такой же, как вы рассчитали на Луне = 75 кг.
Вес становится W = m × g
= 75 кг × 10 Н / кг
= 750 Н
$0.$2.$0″> Инерция
Инерция – это сопротивление изменению движения.
Посмотрите на следующую схему. Если карту потянуть быстро, монета останется на том же месте – она не двинется вместе с картой. Затем он упадет в чашку.
Инерция объекта зависит от его массы. Больше массы – больше инерции. Для изменения движения объекта с большой инерцией потребуется большая равнодействующая сила. Например, ведро с песком толкнуть сложнее, чем пустое ведро.
Физика – Инерция – Мартин Бейкер
На предыдущей странице обсуждалась динамика и то, как она сохраняется в закрытой системе. Эта страница посвящена обмену импульсом между телами с помощью сил.
Не все силы передают импульс, в некоторых случаях силы могут быть уравновешены и, следовательно, не влияют на динамику.(см. страницы статики). Если силы не сбалансированы, то будет передан импульс, который создаст силу (инерцию), которая равна и противоположна сумме сил, действующих на объект.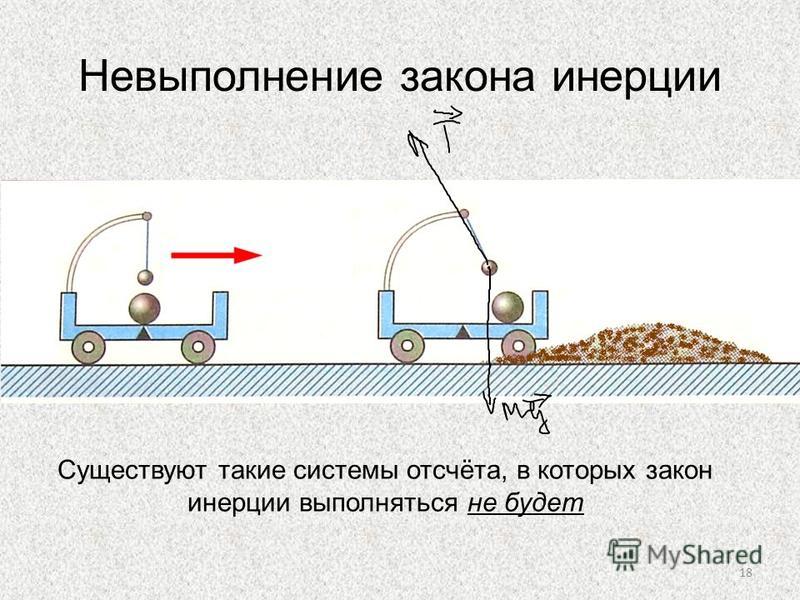
При столкновении двух объектов происходит обмен импульсом очень быстро (очень большая сила за очень короткое время), в этом случае мы называем это импульсом, как описано здесь.
Ньютон Второй закон
Свойством массы является ее сопротивление изменению скорости. Это количественно по второму закону Ньютона, который гласит, что ускорение составляет:
- Пропорционально чистой внешней силе.
- обратно пропорциональна его массе.
- По направлению силы.
Другими словами:
F = m a
| где: | |||
символ | описание | тип | шт. |
Ф. | полезная сила | вектор | кг м / с 2 |
| м | масса | скаляр | кг |
| ускорение | вектор | м / с 2 | |
Также есть аналог для вращения:
| τ a = [I a ] α или | в инерциальной фиксированной системе координат (меняется со временем) |
| τ r = [I r ] α + ω × [I r ] ω | в координатах тела (тензор инерции фиксирован) |
| где: | |||
символ | описание | тип | шт. |
| τ a | крутящий момент в абсолютных координатах (тело перемещается относительно земли) | бивектор | Н · м |
| τ r | крутящий момент в относительных координатах (рули или жиклеры на кузове) | бивектор | Н · м |
| [I a ] | тензор инерции в абсолютных координатах (это будет меняться в зависимости от ориентации, и поскольку тело вращается, элементы тензора будут меняться со временем) | тензор | кг м 2 |
| [I r ] | тензор инерции в относительных координатах (поскольку он относительно тела будет постоянным) | тензор | кг м 2 |
| α | угловое ускорение | бивектор | с -2 |
Первая форма уравнения выглядит простейшей, но значения меняются со временем, поэтому вторую форму проще использовать. Поскольку, как правило, очень сложно постоянно пересчитывать изменяющуюся матрицу инерции, если смотреть из инерциальной фиксированной системы отсчета, сохранение углового момента чаще всего записывается в системе координат, закрепленной во вращающемся твердом теле.
Поскольку, как правило, очень сложно постоянно пересчитывать изменяющуюся матрицу инерции, если смотреть из инерциальной фиксированной системы отсчета, сохранение углового момента чаще всего записывается в системе координат, закрепленной во вращающемся твердом теле.
Если вектор вращения совмещен с главной осью вращающегося тела, то член: ω × [I r ] ω становится нулевым, член: ω × [I r ] ω описывает поведение, известное как гироскопическое или процессуальное движение.
| Тензор – Набор компонентов, подчиняющийся некоторому закону преобразования в n-мерном пространстве. космос. более |
При работе в 3-х измерениях, затем F, a, T и могут быть представлены в виде векторов, а m и I – в виде матриц.
Например, тогда уравнения становятся:
| F = m a | ||||||||||||||
| τ = [I] α |
|
где x, y, z – взаимно перпендикулярные направления координат. Обратите внимание, что
масса, м одинакова во всех направлениях, тогда как координаты инерции
матрица зависит от ориентации объекта, а отдельные элементы представляют
объемные интегралы следующим образом:
Обратите внимание, что
масса, м одинакова во всех направлениях, тогда как координаты инерции
матрица зависит от ориентации объекта, а отдельные элементы представляют
объемные интегралы следующим образом:
i xx = ∫ ∫ ∫ (y 2 + z 2 ) p дв
i xy = – ∫ ∫ ∫ (x y) p дв
i xz = – ∫ ∫ ∫ (x z) p дв
i yx = – ∫ ∫ ∫ (y x) p дв
i yy = ∫ ∫ ∫ (x 2 + z 2 ) p дв
i yz = – ∫ ∫ ∫ (y z) p дв
я zx = – ∫ ∫ ∫ (z x) p дв
i zy = – ∫ ∫ ∫ (z y) p дв
i zz = ∫ ∫ ∫ (x 2 + y 2 ) p дв
6d векторов
До сих пор линейная и угловая составляющие рассматривались отдельно, однако
они связаны, поэтому их полезно комбинировать.Показанный здесь метод использует
обозначение пространственного вектора Featherstone (см. http://www.syseng.anu.edu.au/~roy/technical. html)
Спасибо Майклу Шанцу, рассказавшему мне об этом (см. Файл hybridgdc.pdf на
http://michaelshantz.com).
html)
Спасибо Майклу Шанцу, рассказавшему мне об этом (см. Файл hybridgdc.pdf на
http://michaelshantz.com).
В этих обозначениях приведенные выше уравнения объединены следующим образом:
Таким образом, при работе в трехмерном пространстве это может быть расширено, чтобы стать Уравнения движения Ньютона-Эйлера (поскольку Ньютон создал линейные и эйлеровы уравнения) угловой).
| где: | |||
символ | описание | тип | шт. |
| ч | м * с = масса умноженная на расстояние | вектор | кг * м |
| τ | крутящий момент | бивектор | кг · м 2 / с 2 |
| f | сила | вектор | кг м / с 2 |
| α | угловой разгон | бивектор | м -2 |
| линейное ускорение | вектор | м / с 2 | |
| i | инерция | кг · м2 | |
Эти термины h объясняются тем, что при вращении твердого объекта
и связывается с другим объектом в точке, смещенной от его оси вращения, затем
Линейные силы могут быть преобразованы в крутящие моменты и наоборот.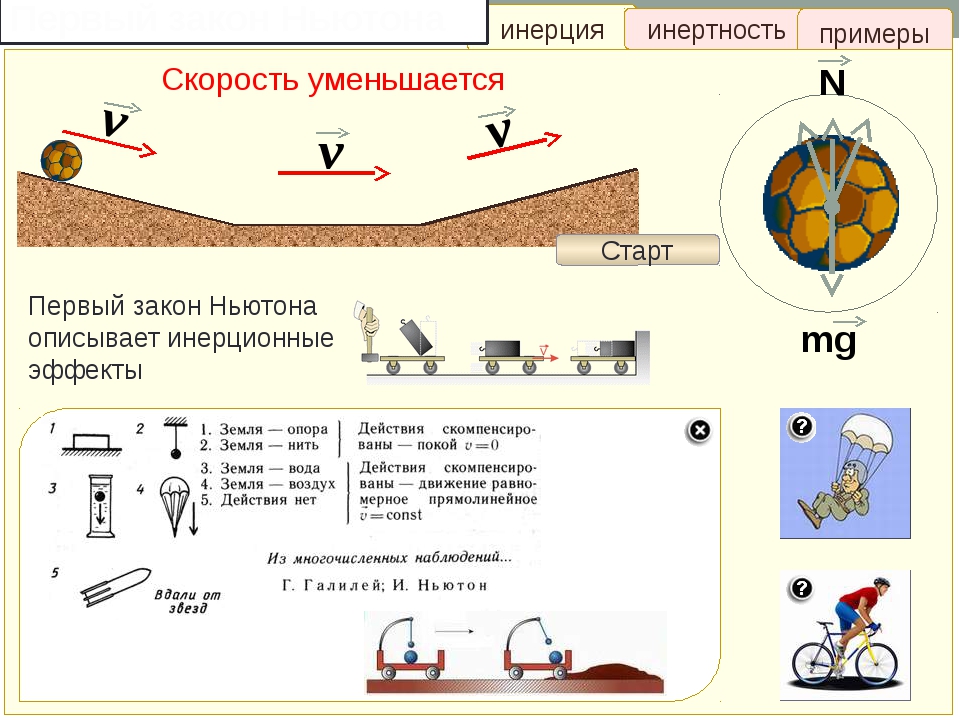
Когда сила приложена к свободно плавающему твердому объекту, то равное и противоположное сила создается за счет инерции. Поскольку две силы компенсируются расстоянием ‘s’, тогда это создаст поворотный момент.
Этот крутящий момент равен силе, умноженной на ее перпендикулярное расстояние от центр вращения.
τ = r × F
| где: | |||
символ | описание | тип | шт. |
| τ | крутящий момент | бивектор | Н · м |
| r | расстояние от центра вращения | вектор | м |
Ф. | сила | вектор | N |
| × | оператор вектора векторного произведения | ||
заменяем F = m a (при условии м постоянна) дает,
τ = r × m a
, следовательно, определяя h = m * дает
τ = h × a
В трехмерном случае T, h и a – векторы, а × – векторное произведение:
| = |
|
Это дает h-члены в полной матрице
Сила инерции.
 Основополагающий принцип физики… | Марк Малви
Основополагающий принцип физики… | Марк МалвиИдея о том, что «движущийся объект имеет тенденцию оставаться в движении, если на него не действует внешняя сила» – это то, что большинство людей смутно помнят как вещь, которую они узнали на уроках естествознания, которые они терпели, но никогда не использовали и не заботились поскольку. Я здесь, чтобы предположить, что эта концепция – инерция – не только первый закон движения Ньютона, но и самая мощная сила, действующая на вашу жизнь, и что наблюдение за ее действием позволяет вам использовать ее силу для своей выгоды.Не в каком-то туманном мистическом смысле с оттенком шарлатанства самопомощи, а в прямом и практическом смысле.
Мое первоначальное признание инерции как социальной концепции было связано с занятостью. Люди, которых я знал, которые раньше начали работать в том, что в конечном итоге стало их выбранной профессией, занимали более высокие должности и зарабатывали больше, чем те, кому требовалось больше времени, чтобы найти и потратить время на свое истинное призвание.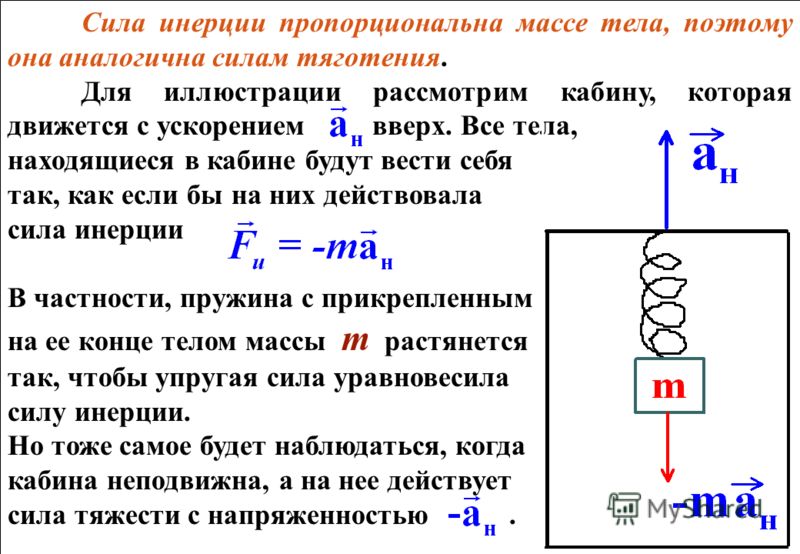 Это может показаться вам очевидным наблюдением. То есть: Чем раньше вы начнете, тем дальше вы будете двигаться. Но только когда я начал замечать, что та же концепция действует и в других сферах жизни, я понял, что может работать более глубокий принцип.
Это может показаться вам очевидным наблюдением. То есть: Чем раньше вы начнете, тем дальше вы будете двигаться. Но только когда я начал замечать, что та же концепция действует и в других сферах жизни, я понял, что может работать более глубокий принцип.
Например, родственное понятие связано с формированием привычек. Привычки – это техника для более частого выполнения чего-либо (сродни бороздкам, образованным в результате многократного использования, которые, в свою очередь, образуют путь, от которого труднее отклониться), но преимущества, получаемые от этой частоты (например, знакомство, понимание или опыт) имеют отношение к силе инерции. Чем чаще вы что-то делаете, тем чаще вы будете продолжать это делать. Или, как выразилась Энни Диллард: «То, как мы проводим наши дни, – это, конечно, то, как мы проводим нашу жизнь».
Соединение этих аспектов непрерывного движения – времени начала и частоты – естественным образом приводит вас к финансовой сфере и идее сложных процентов. Это относится к процентам, начисленным на первоначальную сумму , а также к накопленным процентам за предыдущие периоды . Это проценты по процентам, что означает, что по мере того, как вы вкладываете больше денег, вы одновременно увеличиваете и сумму заработанных процентов.Совокупный эффект сложных процентов является причиной того, почему родители и другие советники умоляют нас как можно раньше начать откладывать на пенсию и хранить наши деньги на пенсионном счете, полном индексных фондов, а не под матрасом или в новой машине. Чем раньше вы начнете, тем больше вы получите , часто даже больше, чем если бы вы начали позже, но внесли большие суммы. Эта идея позволяет вам сосредоточиться на долгосрочных выплатах – будь то деньгами, отношениями, здоровьем, занятиями, привычками – а не на краткосрочной выгоде.Способность времени накапливать эффекты часто недооценивается, поэтому идею инерции важно помнить.
Это относится к процентам, начисленным на первоначальную сумму , а также к накопленным процентам за предыдущие периоды . Это проценты по процентам, что означает, что по мере того, как вы вкладываете больше денег, вы одновременно увеличиваете и сумму заработанных процентов.Совокупный эффект сложных процентов является причиной того, почему родители и другие советники умоляют нас как можно раньше начать откладывать на пенсию и хранить наши деньги на пенсионном счете, полном индексных фондов, а не под матрасом или в новой машине. Чем раньше вы начнете, тем больше вы получите , часто даже больше, чем если бы вы начали позже, но внесли большие суммы. Эта идея позволяет вам сосредоточиться на долгосрочных выплатах – будь то деньгами, отношениями, здоровьем, занятиями, привычками – а не на краткосрочной выгоде.Способность времени накапливать эффекты часто недооценивается, поэтому идею инерции важно помнить.
Физики хорошо знакомы с неожиданно большими совокупными эффектами непрерывного движения не только из-за характера их работы, но и из-за их инструмента: математики. Земля вращается вокруг Солнца в результате своей тенденции оставаться в движении, находясь под действием искривления пространства-времени, и мы ощущаем это движение как гравитацию. (Известно, что Эйнштейн показал, что гравитация – это ускорение). Гравитация – это причина, по которой игрушечная машинка катится по деревянному склону в течение нескольких секунд и приземляется на дно.Если вы хотите узнать скорость автомобиля в любой момент, вы используете исчисление, чтобы найти ее производную в данный момент времени. Вы можете нанести все эти моменты на график и соединить их в линию или кривую, а наклон («подъем / пробег») этой линии графика в заданной точке – это скорость игрушечной машины («миль / час») в в тот самый момент. Достаточно просто. Но что, если вы хотите узнать совокупный эффект всех этих крошечных изменений скорости? Как выглядит совокупность всех этих небольших мгновенных изменений? Это интеграл, а интеграл равен – вся площадь под той единственной линией графика, которую вы нарисовали .
Земля вращается вокруг Солнца в результате своей тенденции оставаться в движении, находясь под действием искривления пространства-времени, и мы ощущаем это движение как гравитацию. (Известно, что Эйнштейн показал, что гравитация – это ускорение). Гравитация – это причина, по которой игрушечная машинка катится по деревянному склону в течение нескольких секунд и приземляется на дно.Если вы хотите узнать скорость автомобиля в любой момент, вы используете исчисление, чтобы найти ее производную в данный момент времени. Вы можете нанести все эти моменты на график и соединить их в линию или кривую, а наклон («подъем / пробег») этой линии графика в заданной точке – это скорость игрушечной машины («миль / час») в в тот самый момент. Достаточно просто. Но что, если вы хотите узнать совокупный эффект всех этих крошечных изменений скорости? Как выглядит совокупность всех этих небольших мгновенных изменений? Это интеграл, а интеграл равен – вся площадь под той единственной линией графика, которую вы нарисовали . Это огромная сумма по сравнению с маленькой линией, которая просто образует его верхнюю границу. Вот почему ученые и математики скорее интуитивно чувствуют силу накопления, чем нефизики вроде меня. Мне нужно было позаимствовать их инструменты, чтобы поделиться их интуицией.
Это огромная сумма по сравнению с маленькой линией, которая просто образует его верхнюю границу. Вот почему ученые и математики скорее интуитивно чувствуют силу накопления, чем нефизики вроде меня. Мне нужно было позаимствовать их инструменты, чтобы поделиться их интуицией.
Этот пример с гравитацией подводит меня к другому вопросу о силе инерции, которая связана с тем, насколько легко что-то остановить. Чтобы заставить что-то двигаться из положения покоя, требуется больше усилий, чем удерживать его в движении, когда оно уже движется.Это физический факт объектов реального мира. Вы, вероятно, интуитивно чувствуете эту концепцию, потому что вам пришлось толкать тяжелую дверь или шар для боулинга и обнаруживать, что для этого требуется гораздо меньше усилий, когда он немного набирает скорость. Вы также поймете, что медленно движущийся шар для боулинга легче остановить, чем шар, движущийся на полной скорости на полпути. Величина инерции чего-либо зависит от его массы. Чем больше у чего-то инерции, тем больше у него массы. Более массивный объект имеет большую тенденцию сопротивляться изменениям, когда он приводится в движение.Я использую этот факт, чтобы напомнить себе, что от вредных привычек, нежелательных отношений или ужасной работы легче отказаться раньше, чем позже. Они тем тяжелее, чем больше в них накапливается инерция. Этот инерционный инструмент принятия решений на самом деле противоположен другим: Чем раньше вы попытаетесь остановить, тем легче это будет. И, наоборот, чем дольше что-то тяжелое остается в движении, тем труднее его остановиться.
Более массивный объект имеет большую тенденцию сопротивляться изменениям, когда он приводится в движение.Я использую этот факт, чтобы напомнить себе, что от вредных привычек, нежелательных отношений или ужасной работы легче отказаться раньше, чем позже. Они тем тяжелее, чем больше в них накапливается инерция. Этот инерционный инструмент принятия решений на самом деле противоположен другим: Чем раньше вы попытаетесь остановить, тем легче это будет. И, наоборот, чем дольше что-то тяжелое остается в движении, тем труднее его остановиться.
Тогда есть обратное самому первому закону Ньютона: не только движущийся объект стремится оставаться в движении, но и неподвижный объект стремится оставаться в покое. То, чем вы обычно занимаетесь, вообще ничего не включает. Инерция обычно объясняет, почему люди остаются на работе или в отношениях, которые им не нравятся.
После идентификации этой эвристики я начал везде видеть инерцию. Это важно, потому что метафоры не только в умении замечать сходства, они на самом деле полезны. Они позволяют думать об абстрактных вещах более просто и интуитивно. Не только это, , но как только вы прикрепите слово или понятие к чему-то, вы будете склонны замечать это .Слова помогают нам в буквальном смысле видеть.
Они позволяют думать об абстрактных вещах более просто и интуитивно. Не только это, , но как только вы прикрепите слово или понятие к чему-то, вы будете склонны замечать это .Слова помогают нам в буквальном смысле видеть.
Вот еще несколько способов, которыми я применил идею инерции как инструмента – или то, что философ Дэниел Деннетт называет «насосом интуиции» – когда дело доходит до принятия решений:
- Когда я думал об инвестировании в криптовалюты, я решил инвестировать раньше, когда цена низкого и потенциального повышения курса чрезвычайно перевешивает обратную сторону потери моих инвестиций, а не ждать, чтобы увидеть, окажется ли сначала законным и жизнеспособным и потеряет ли способность накапливать эффекты.
- Я подписался на Pinterest сразу после его запуска в 2010 году и начал яростно прикреплять цитаты и изображения, чтобы наполнить мой профиль и распространять информацию, и я все еще получаю уведомления о людях, прикрепляющих их к своим доскам и подписывающихся на меня, несмотря на то, что почти нет дополнительные усилия с моей стороны с тех пор.
 Я видел аналогичный «успех» у первых, кто начал использовать другие социальные платформы, у которых количество подписчиков продолжает расти намного легче, чем у тех, кто опоздал. С тех пор я подписываюсь на новые продукты или услуги и использую их, когда они запускаются, вместо того, чтобы ждать, пока они сначала добьются успеха.
Я видел аналогичный «успех» у первых, кто начал использовать другие социальные платформы, у которых количество подписчиков продолжает расти намного легче, чем у тех, кто опоздал. С тех пор я подписываюсь на новые продукты или услуги и использую их, когда они запускаются, вместо того, чтобы ждать, пока они сначала добьются успеха. - Когда я делаю предварительный заказ на книги или читаю новые книги сразу после выпуска, я более склонен оставлять отзыв, потому что вероятность того, что он получит более высокую оценку (и, следовательно, увидит больше людей), выше, чем если бы я оставил обзор через несколько месяцев позже на дне уже установленный авторитетный сборник.
- Я прекращаю читать книгу на первых 50–100 страницах, если она не оказывается интересной, приятной или сложной. То же самое и с сообщениями в блогах, альбомами, телешоу. Это потому, что я знаю, что чем дальше я буду углубляться в них, тем труднее будет их вложить в них, независимо от того, насколько отвратительными или утомительными я могу их найти.
 («Ну, я зашел так далеко…»)
(«Ну, я зашел так далеко…») - Употребление большого количества зеленых овощей, пить больше воды, сокращение нежелательной пищи и начало физических упражнений в возрасте 20 лет – это не просто раннее привлечение хороших привычек в движение, что я теперь считаю легче выдерживать, но накопленные эффекты и инерция физического здоровья неисчислимы. Трудно оценить хорошее здоровье – когда все в порядке, не на что смотреть. Но чем больше времени вы уделяете здоровому образу жизни, тем больше положительных эффектов вы накапливаете с течением времени (микропитание для клеток и органов, клетчатка для потребления кишечной флоры, мышечная активность и рост, прочность костей за счет нагрузки, сердечно-сосудистая система, гибкость и т. Д.), и тем больше негативных эффектов вы будете стараться избегать вообще. (высокое кровяное давление, воспаление, растяжения, разрывы и т. д.). Чем дольше вы сможете вести себя здоровым образом, тем более здоровым вы будете, как правило, быть.
- Когда я видел, как друзья увольняются с работы или берут отпуск перед тем, как вернуться на работу, я понял, насколько сложно и затратно по времени может быть возобновление работы, особенно по сравнению с теми, кто оставался в движении в течение этого времени и продолжал продвигаться вперед.
 относительная простота.Это не означает, что вы никогда не должны бросать работу, и такие вещи, как творческий отпуск или отпуск по уходу за ребенком, жизненно важны и ценны, но я также был свидетелем того, насколько полезным может быть выбор другого вида движения, а не остановки, прерывания или полной паузы. . Начать с отдыха тяжело. Это не новое откровение, но то, что я ценю более глубоко, поскольку оно связано с идеей инерции, а не просто с фактом жизни.
относительная простота.Это не означает, что вы никогда не должны бросать работу, и такие вещи, как творческий отпуск или отпуск по уходу за ребенком, жизненно важны и ценны, но я также был свидетелем того, насколько полезным может быть выбор другого вида движения, а не остановки, прерывания или полной паузы. . Начать с отдыха тяжело. Это не новое откровение, но то, что я ценю более глубоко, поскольку оно связано с идеей инерции, а не просто с фактом жизни.
Хорошо, вы можете сказать, но почему вначале вы утверждали, что инерция – это «самая мощная сила», действующая на нашу жизнь? Конечно, есть другие силы или идеи, которые более важны, например, тяжелая работа, или внимательность, или здоровье, или любовь, верно? Да, все это чрезвычайно важно, но все они связаны с исследуемой здесь идеей инерции.
Чем раньше вы начнете, тем дальше вы будете двигаться и тем больше пользы вы получите.
Чем чаще вы что-то делаете, тем чаще вы будете продолжать это делать.
Чем раньше вы попытаетесь остановиться, тем легче это будет.
То, чем вы обычно занимаетесь, не включает в себя вообще ничего.
Цицерон однажды заявил, что благодарность – это не только величайшая добродетель, но и родитель для всех остальных. Я бы сказал то же самое об инерции: это не только величайший из всех моих принципов принятия решений, но и родительский для всех остальных.
Простой физический проект, который покажет вам, как работает инерция
Всем нужны демонстрационные версии. Лично мне нравится этот. Его не так уж сложно построить, и им легко пользоваться.
Возьмите большой деревянный брусок (он должен иметь хорошую массу). Я использовал оставшуюся часть 4 × 4.
Возьмите деревянный дюбель – может быть, длиной около 1 метра (может быть и короче) – диаметр должен быть достаточно толстым, чтобы можно было ударить одним концом молотком, и он не сломался.
Просверлите отверстие в блоке, чтобы дюбель вошел, но с трудом.
 Он должен быть достаточно тугим, чтобы блок не скользил, но достаточно свободным, чтобы вы могли его сдвинуть.
Он должен быть достаточно тугим, чтобы блок не скользил, но достаточно свободным, чтобы вы могли его сдвинуть.
Вот как выглядит моя версия.
Теперь о демо. Держите дюбель вертикально и ударьте по нему молотком. По мере того, как вы несколько раз ударяете по вершине палки, блок начинает двигаться вверх по штифту. Это круто. Попробуй. Вот как это выглядит.
Не бейте себя молотком.Это было бы плохо. А как насчет версии с замедленной съемкой? Ну вот.
А как же физика? Это просто волшебство или есть еще объяснение.
Все дело в массе
Один из лучших способов описать природу силы и движения – использовать следующее уравнение (в одном измерении).
Если одна и та же сила действует на два разных объекта (с разной массой), более массивный будет иметь меньшее ускорение. Большой блок имеет довольно большую массу (по сравнению с дюбелем).Это означает, что когда между рукоятью и блоком действует сила трения, блок имеет небольшое ускорение и в основном остается на месте. Часто мы называем это свойство «инерцией». Это тенденция объекта НЕ менять свое движение.
Часто мы называем это свойство «инерцией». Это тенденция объекта НЕ менять свое движение.
Но почему блок движется вверх по стержню? Это не совсем так. На самом деле, когда молоток ударяет по палке, палка опускается. Он оказывает на блок силу трения, так что блок также перемещается вниз, но не так сильно. После удара молотка моя рука тянет палку обратно туда, где она началась.Поскольку это движение руки намного медленнее, блок поднимается вместе с палкой. В результате блок оказывается выше, чем он был начат. Влезла на палку.
Видеоанализ
Ради удовольствия, позвольте мне изобразить вертикальное положение палки и блока при ударе молотка.
Вы можете легко увидеть, что и блок, и палка перемещаются вниз во время ударов (на этом графике показаны два удара). Однако не так просто увидеть, что блок движется вниз по сравнению с движением палки.Вот график, который просто показывает расстояние между точкой на палке и точкой на блоке.
Я добавил две линейные посадки к частям, в которые попал молоток.


 Любой ребенок способен на такое, если только он предварительно уберет с дороги помехи движению копья. Главных помех немного — всего две. Первая — Земля. Она влечет к себе брошенное копье (так сказал бы Кеплер) и заставляет его в конце концов упасть. Вторая помеха — воздух, который тормозит копье. Вот и все. Уничтожьте Землю и воздух — и от малейшего толчка ваше копье улетит куда угодно.
Любой ребенок способен на такое, если только он предварительно уберет с дороги помехи движению копья. Главных помех немного — всего две. Первая — Земля. Она влечет к себе брошенное копье (так сказал бы Кеплер) и заставляет его в конце концов упасть. Вторая помеха — воздух, который тормозит копье. Вот и все. Уничтожьте Землю и воздух — и от малейшего толчка ваше копье улетит куда угодно.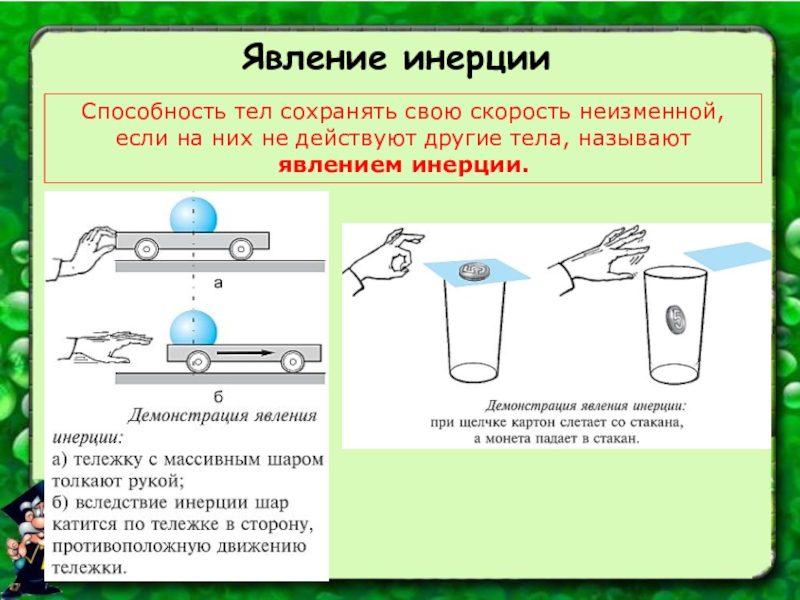
 О нем догадывались многие мыслители — и гениально многогранный Леонардо да Винчи, и Галилей, и французский философ Рене Декарт. Но только великий английский ученый Исаак Ньютон до конца понял его значение, назвал его первым законом механики и поставил в основу этой области физического знания. В конце главы мы к этому закону еще вернемся. А потом и в конце книжки.
О нем догадывались многие мыслители — и гениально многогранный Леонардо да Винчи, и Галилей, и французский философ Рене Декарт. Но только великий английский ученый Исаак Ньютон до конца понял его значение, назвал его первым законом механики и поставил в основу этой области физического знания. В конце главы мы к этому закону еще вернемся. А потом и в конце книжки. А на самом деле — нет.
А на самом деле — нет. Удивились? Очень хорошо.
Удивились? Очень хорошо.
 Значит, исчезнет тяжесть. Только на этот раз искривится путь.
Значит, исчезнет тяжесть. Только на этот раз искривится путь. Это почти в десять раз дольше орбитального полета корабля «Восток».
Это почти в десять раз дольше орбитального полета корабля «Восток». Объясните сами, почему это неверно.
Объясните сами, почему это неверно.

 Достаточно одного раунда.
Достаточно одного раунда. ..»).
..»).

 Здесь прямая пропорциональность. Давным-давно об этом знают и охотники, и артиллеристы, и продавцы в охотничьих магазинах. И, конечно, физики.
Здесь прямая пропорциональность. Давным-давно об этом знают и охотники, и артиллеристы, и продавцы в охотничьих магазинах. И, конечно, физики. Толпы людей, снующих ежедневно по магазинам, не интересуются ни весом, ни инерцией. Ну зачем вам, скажем, инерционность яблока? Чтобы швырнуть его и разбить чье-то окно? Никчемное занятие! Домашние хозяйки, как и охотники, страдающие от тяжести дроби, с удовольствием лишили бы веса свои сумки, набитые снедью. В булках и колбасах, пачках сахара и пакетах крупы нас интересует не тяжесть, а количество вещества. Ибо десятком невесомых сосисок можно отлично позавтракать в кабине космического корабля.
Толпы людей, снующих ежедневно по магазинам, не интересуются ни весом, ни инерцией. Ну зачем вам, скажем, инерционность яблока? Чтобы швырнуть его и разбить чье-то окно? Никчемное занятие! Домашние хозяйки, как и охотники, страдающие от тяжести дроби, с удовольствием лишили бы веса свои сумки, набитые снедью. В булках и колбасах, пачках сахара и пакетах крупы нас интересует не тяжесть, а количество вещества. Ибо десятком невесомых сосисок можно отлично позавтракать в кабине космического корабля. Тело тем больше давит на опору, чем больше в нем вещества, чем больше его масса.
Тело тем больше давит на опору, чем больше в нем вещества, чем больше его масса. Так, как вслед за Кеплером учил Ньютон.
Так, как вслед за Кеплером учил Ньютон.

 С их помощью все сказанное записывается коротко и наглядно во втором законе механики: ускорение тела (а) прямо пропорционально приложенной силе (F) и обратно пропорционально инерции, то есть инертной массе тела. Вот формула:
С их помощью все сказанное записывается коротко и наглядно во втором законе механики: ускорение тела (а) прямо пропорционально приложенной силе (F) и обратно пропорционально инерции, то есть инертной массе тела. Вот формула:
 И в результате падающие тела падают так, как увидел Галилей: с постоянным ускорением, не зависящим от массы.
И в результате падающие тела падают так, как увидел Галилей: с постоянным ускорением, не зависящим от массы. С тем, однако, чтобы после перерыва выставить еще одно «почему»: почему же тяжелая масса равна инертной?
С тем, однако, чтобы после перерыва выставить еще одно «почему»: почему же тяжелая масса равна инертной?
