Масса и плотность вещества, теория и онлайн калькуляторы
Масса и плотность вещества, теория и онлайн калькуляторыКоэффициенты пропорциональности между ускорением и силой, постоянные для конкретного тела, отличаются для разных тел. Этот коэффициент связан с таким свойством тела как инертность. Чем больше инертность, тем меньше ускорение тела, которое сообщает телу действующая на него сила.
Физическая величина, которая численно характеризует свойство инертности тела – это масса (инертная масса). Обозначается масс буквой $m$. Применяя понятие массы связь между ускорением и силой можно выразить как:
\[\overline{a}=\frac{\overline{F}}{m}\left(1\right).\]
Масса – мера инертности
Масса, которая входит в формулу (1) является мерой инертности. Данный параметр не зависит от силы, оказывающей воздействие на тело и других условий, в которых находится тело, например, температуры, гравитации и т.д.
Свойства массы
Эмпирически получены такие свойства массы, как:
- Масса – аддитивная скалярная величина, которая не зависит от места положения тела в пространстве.
 Аддитивность означает, что масса тела равна сумме масс частей тела. Это свойство в точности выполняется для макроскопических тел и нарушается, если энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в ядро атома. То, что масса является скалярной величиной, значит, что инертные свойства тел одинаковы во всех направлениях.
Аддитивность означает, что масса тела равна сумме масс частей тела. Это свойство в точности выполняется для макроскопических тел и нарушается, если энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в ядро атома. То, что масса является скалярной величиной, значит, что инертные свойства тел одинаковы во всех направлениях. - Масса тела не зависит от скорости, если она много меньше скорости света.
Массу можно определять при помощи взвешивания или используя динамический способ. Динамический способ нахождения массы заключается в следующем. Если один раз для рассматриваемого тела измерить ускорение и действующую на тело силу одновременно, то можно применяя формулу (1) вычислить массу. Зная массу тела можно рассчитывать ускорение тела по известной силе и по известному ускорению находить силу.
Гравитационная масса
\[F=\gamma \frac{m_1m_2}{r^2}\left(2\right). \]
\]
Измерение гравитационной массы проводят при помощи взвешивания. Тела располагают неподвижно относительно Земли и сравнивают действующие на них силы тяготения. Определенная таким способом масса называется гравитационной.
Эмпирически показывают, что гравитационные массы инертные массы совпадают. В механике Ньютона совпадение инертной и гравитационной масс не имеет физической основы. Это просто экспериментальный факт, который установлен с высокой точностью, если это было бы не так, то классическая динамика не пострадала бы. В релятивистской теории тяготения равенство инертной и гравитационной массы имеет принципиальное значение и положено в основу теории.
И так, масса тела – это количественная мера инертных и гравитационных свойств тела.
Единицей измерения массы в Международной системе единиц является килограмм:
\[\left[m\right]=кг.\]
Плотность вещества
Если из одного и того же вещества изготовить тела разных объемов ($V$), то их массы будут разными. Но экспериментально установлено, что отношение масс этих тел к их объемам буде постоянной величиной:
Но экспериментально установлено, что отношение масс этих тел к их объемам буде постоянной величиной:
\[\frac{m_1}{V_1}=\frac{m_2}{V_2}=const\ \left(3\right).\]
Отношение массы тела к его объему служит характеристикой вещества и называется плотностью. Обозначают плотность буквой $\rho $.
\[\rho =\frac{m}{V}\left(4\right).\]
Плотность вещества зависит от температуры, внешнего давления, агрегатного состояния. Плотность можно еще определить как массу единицы объема вещества. Плотность является скалярной физической величиной. Для однородного тела плотность является постоянной величиной для всей массы тела.
Для неоднородных тел, используется понятие средней плотности ($\left\langle \rho \right\rangle $):
\[\left\langle \rho \right\rangle =\frac{m}{V}\left(5\right).\]
Иногда применяют понятие плотность тела в точке, которая равна:
\[\rho ={\mathop{\lim }_{\Delta V\to 0} \frac{\Delta m}{\Delta V}\left(6\right),\ }\]
где $\Delta m$ – элементарная масса тела (малая часть массы тела), содержащая исследуемую точку тела; $\Delta V$ – объем данного элемента тела. 3}$.
3}$.
Плотность смеси веществ нельзя вычислить как сумму плотностей отдельных составляющих смеси.
Примеры задач с решением
Пример 1
Задание. Какова плотности смеси газов, если температура равна T, давление $p$, масса первой компоненты $m_1$ (ее молярная масса ${\mu }_1$), масса второй компоненты $m_2$ (ее молярная масса ${\mu }_2$)? Считайте газы в смеси идеальными.
Решение. Плотность смеси ($\rho $) равна:
\[\rho =\frac{m}{V}\left(1.1\right),\]
где массу смеси ($m$) найдем как:
\[m=m_1+m_2\left(1.2\right).\]
Так как газы можно считать идеальными, то объем смеси будем искать, используя уравнение Менделеева – Клапейрона:
\[pV=\nu RT\ \left(1.3\right),\]
где $\nu ={\nu }_1+{\nu }_2=\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2}-\ $число молей вещества; $R$ – универсальная газовая постоянная.
\[V=\frac{\nu RT}{p}=\frac{(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2})RT}{p}\left(1.4\right).\]
Подставим правую часть (1.4) вместо объема и правую часть (1.2) вместо массы в формулу (1.1):
\[\rho =\frac{\left(m_1+m_2\right)p}{(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2})RT}.\]
Ответ. $\rho =\frac{\left(m_1+m_2\right)p}{(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2})RT}$
Пример 2
Задание. Под действием силы $F$ тело движется прямолинейно так, что его скорость изменяется в соответствии с графиком рис.1. Какова масса тела?
Решение. Основой для решения задачи служит второй закон Ньютона, который запишем, учитывая, что движение тела в нашей задаче прямолинейное:
\[F=ma=m\frac{dv}{dt}\left(2.1\right).\]
Уравнение изменения скорости ($v(t)$), исходя из графика имеет вид:
\[v\left(t\right)=Ct-B\ \left(2. 2\right).\]
2\right).\]
Вычислим:
\[\frac{dv}{dt}=C\ \left(2.3\right).\]
Используя формулы (2.1) и (2.3) выразим массу тела:
Ответ. $m=\frac{F}{C}$
Читать дальше: начальная фаза колебаний.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Инертное компрессорное масло | ANDEROL C-NRT 68
Заказать
Anderol C-NRT 68 – уникальное высокоустойчивое синтетическое компрессорное масло.
Специально разработанная формула масла обеспечивает инертность и долговременную смазывающую способность на различных промышленных предприятиях, где невозможно избежать контакта с химическими реагентами.
В случаях, когда какие-либо другие химические вещества перестают работать, данный продукт будет устойчив ко всем агрессивным газам и быстрому разрушению, что неизбежно с любым другим продуктом на основе минералов / эфиров / ПАО.
Дополнительная термическая и окислительная стабильность базовой жидкости в сочетании с ингибиторами окисления продлевает срок службы масла при повышенных температурах.
Благодаря отличным детергентным свойствам предотвращается образование осадка / лаковых отложений.
ПреимуществаСинтетические масла Anderol® – единственные синтетические смазочные материалы с длительным сроком службы и имеют более чем 70-летнюю историю успешной эксплуатации.
- Химически инертен к химическим газам кислотного характера
- Отсутствие металлических присадок, препятствующих каталитическим процессам
- Увеличивает интервалы технического обслуживания
- Значительно снижает опасность возгорания и взрыва
- Очень хорошее отделение воды
- Снижает расход масла
- Полностью устраняет лаковые отложения и осадки
- Снижает потребление энергии
Рекомендуется использовать для смазки цилиндра и картера в поршневых и лопастных компрессорах и вакуумных насосах в присутствии следующих газов:
- Воздух
- Бутадиен
- Монооксид углерода
- Печные газы
- Двуокись углерода (сухая)
- Гелий
- Водород
- Газы фтора
- Сульфид водорода (сухой)
- Природный газ
- Метан
- Азот
- Пропан
- Синтез-газ
- Гексафторид серы
- Биогаз
Номинальный диапазон рабочих температур: от -40°C до 170°C.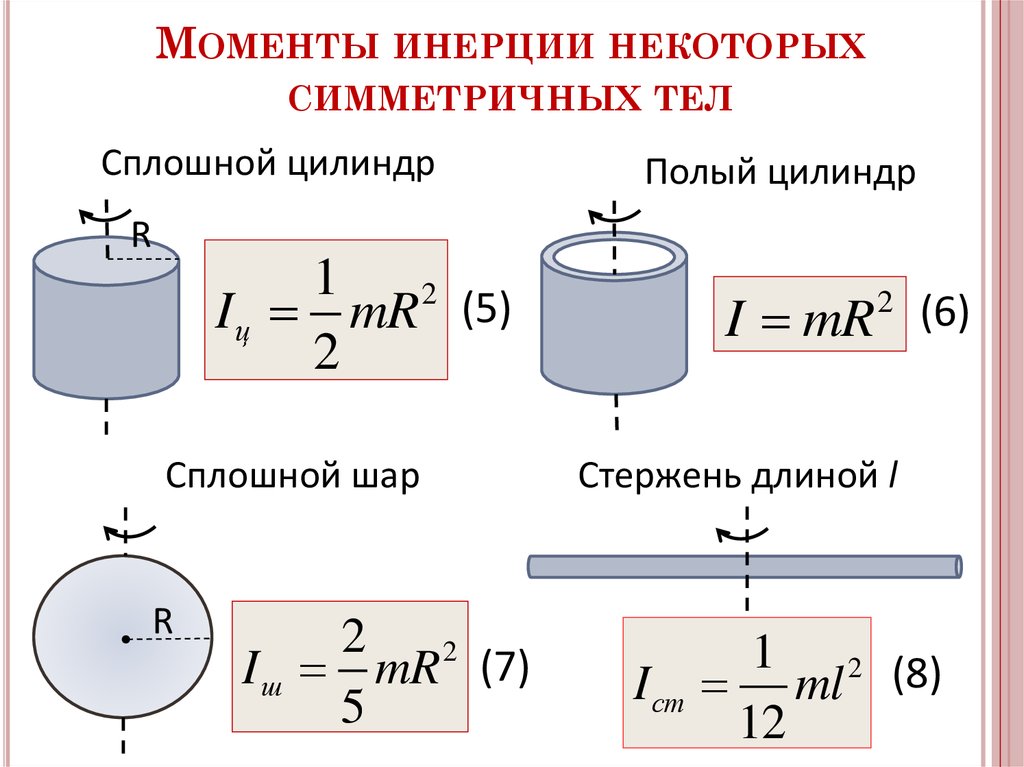
Свойства |
Метод испытания |
ANDEROL C-NRT 68 |
| ISO VG | ASTM D-2422 | 68 |
| Внешний вид при 20°C | Визуально | Прозрачная желтая жидкость |
| Вязкость при 40°C, сСт | ASTM D-445 | 64.5 |
| Вязкость при 100°C, сСт | ASTM D-445 | 9.7 |
| Индекс вязкости | 133 | |
| Плотность при 15°C, кг/л | ASTM D-1298 | 0.856 |
| Общее кислотное число, мг КОН/г | ASTM D-664 | 0. 03 03 |
| Температура вспышки, °C | ASTM D-92 | 234 |
| Температуры застывания, °C | ASTM D-97 | <-56 |
| Деэмульгируемость при 54°C, мин | ASTM D-1401 |
20 л
208 л
Документы и файлыANDEROL C-NRT 68
Ищете подходящее решение для своей компании?Спросите у нас
Россия, 196602, г. Санкт-Петербург, г. Пушкин, ул. Гусарская, д. 4, лит Ц
Режим работы: пн-пт 9:00 – 17:30 (по Московскому времени)
8 (812) 244-48-14
8 (812) 292-00-75
Вращательная динамика – Выведите формулу для момента инерции массы
спросил
Изменено 2 года, 4 месяца назад
Просмотрено 1к раз
$\begingroup$
Мне всегда интересно, как на самом деле выводится формула для момента инерции. 2$, но некоторые выводят его, говоря, что момент инерции прямо пропорционален массе и квадрату расстояния, но мне нужно убийственное объяснение, почему он пропорционален квадрату расстояния от оси вращения. ?
2$, но некоторые выводят его, говоря, что момент инерции прямо пропорционален массе и квадрату расстояния, но мне нужно убийственное объяснение, почему он пропорционален квадрату расстояния от оси вращения. ?
- динамика вращения
- момент инерции
$\endgroup$
3
$\begingroup$
Массовый момент инерции определяется угловым моментом системы слипшихся частиц, вращающихся вместе. Каждая частица вносит небольшую часть углового момента, и при суммировании вращательное движение можно исключить из выражения, оставив между ними момент инерции массы. 92 } _ {\ rm mmoi} \; \омега = I \,\омега$$
Полное развитие этой идеи в 3D дано в этом ответе. Также прочитайте этот аналогичный ответ здесь.
$\endgroup$
$\begingroup$
Рассмотрим небольшую массу m, прикрепленную к концу тонкого безмассового стержня длиной r. 2\omega$$
2\omega$$
Обратите внимание, что здесь речь идет о моменте количества движения относительно оси , в общем случае, когда мы берем его относительно точки, импульс инерции оказывается тензором 3-го ранга. Подробнее об этом здесь.
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
10.
 3 Динамика вращательного движения: инерция вращения
3 Динамика вращательного движения: инерция вращенияЦели обучения Вращательная инерция и момент инерции
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Понимать взаимосвязь между силой, массой и ускорением
- Изучение поворотного эффекта силы
- Изучить аналогию между силой и крутящим моментом, массой и моментом инерции, а также линейным ускорением и угловым ускорением
Информация, представленная в этом разделе, поддерживает следующие цели обучения AP® и научные практики:
- 4.D.1.1 Учащийся может описать представление и использовать его для анализа ситуации, в которой несколько сил действуют на вращающаяся система жестко связанных тел изменяет угловую скорость и момент импульса системы. (СП 1.2, 1.4)
- 4.
 D.1.2 Учащийся может планировать стратегии сбора данных, предназначенные для установления того, что крутящий момент, угловая скорость, угловое ускорение и угловой момент могут быть точно предсказаны, когда переменные обрабатываются как по часовой стрелке или против часовой стрелки по отношению к четко определенную ось вращения и уточнить вопрос исследования на основе изучения данных. (СП 3.2, 4.1, 5.1, 5.3)
D.1.2 Учащийся может планировать стратегии сбора данных, предназначенные для установления того, что крутящий момент, угловая скорость, угловое ускорение и угловой момент могут быть точно предсказаны, когда переменные обрабатываются как по часовой стрелке или против часовой стрелки по отношению к четко определенную ось вращения и уточнить вопрос исследования на основе изучения данных. (СП 3.2, 4.1, 5.1, 5.3) - 5.E.2.1 Учащийся способен описать или рассчитать угловой момент и инерцию вращения системы в терминах местоположения и скорости объектов, составляющих систему. Ожидается, что учащиеся будут делать качественные рассуждения с составными объектами. Ожидается, что учащиеся будут выполнять вычисления с фиксированным набором протяженных объектов и точечных масс. (СП 2.2)
Если вам когда-либо приходилось крутить велосипедное колесо или толкать карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 10.10. На самом деле, ваша интуиция надежно предсказывает многие из задействованных факторов. Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
10.10. На самом деле, ваша интуиция надежно предсказывает многие из задействованных факторов. Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Рисунок 10.10 Для вращения колеса велосипеда требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу FF размером 12{F} {} к точке массой мм размером 12{m} {}, которая находится на расстояние rr size 12{r} {} от точки вращения, как показано на рисунке 10. 11. Поскольку сила перпендикулярна rr размером 12{r} {}, ускорение a=Fma=Fm размера 12{a= {{F} над {m} } } {} получается в направлении FF размера 12{F } {}. Мы можем изменить это уравнение так, что F=maF=ma size 12{F= ital “ma”} {}, а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что a=rαa=rα size 12{a=rα} {}, и подставим это выражение в F=maF=ma size 12{F= ital “ma”} {}, что даст
11. Поскольку сила перпендикулярна rr размером 12{r} {}, ускорение a=Fma=Fm размера 12{a= {{F} над {m} } } {} получается в направлении FF размера 12{F } {}. Мы можем изменить это уравнение так, что F=maF=ma size 12{F= ital “ma”} {}, а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что a=rαa=rα size 12{a=rα} {}, и подставим это выражение в F=maF=ma size 12{F= ital “ma”} {}, что даст
10,40 F=mrα.F=mrα. size 12{F= ital “mr”α”.”} {}
Вспомним, что крутящий момент – это вращательная эффективность силы. В этом случае, поскольку размер FF 12{“F”} {} перпендикулярен размеру RR 12{r} {}, крутящий момент просто τ=Frτ=Fr размер 12{τ=rα} {}. Итак, если мы умножим обе части приведенного выше уравнения на размер rr 12{r} {}, мы получим крутящий момент в левой части. То есть,
10,41 rF=mr2αrF=mr2α размер 12{ ital “rF”= ital “mr” rSup { размер 8{2} } α} {}
или
10,42 τ=mr2α.τ=mr2α. size 12{τ= ital “mr” rSup { size 8{2} } α. } {}
} {}
Последнее уравнение является вращательным аналогом второго закона Ньютона (F=maF=ma size 12{F= ital “ma”} {}), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2mr2 size 12{ ital “mr” rSup { size 8{2} } } {} аналогичен массе или инерции. Величина mr2mr2 размером 12{ ital “mr” rSup { size 8{2} } } {} называется инерцией вращения или моментом инерции точки массой mm размером 12{m} {} расстоянием rr размером 12{r} {} от центра вращения.
Рис. 10.11 Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила FF размером 12{F} {} приложена к объекту перпендикулярно радиусу rr размером 12{r} {}, заставляя его ускоряться относительно точки поворота. Сила удерживается перпендикулярно размеру rr 12{r} {}.
Создание соединений: динамика вращательного движения
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.
Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.
Инерция вращения и момент инерции
Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 10.11, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем момент инерции
II размер 12{I} {} объекта должен быть суммой
mr2mr2 size 12{ ital “mr” rSup { size 8{2} } } {} для всех точечных масс, из которых он состоит. То есть,
I=∑mr2I=∑mr2 size 12{I= Sum {} ital “mr” rSup { size 8{2} } } {}. Здесь
II размер 12{I} {} аналогичен
мм размером 12{м}{} в поступательном движении. Из-за расстояния
rr size 12{r} {}, момент инерции любого объекта зависит от выбранной оси. Собственно, расчет
Размер II 12{I} {} выходит за рамки этого текста, за исключением одного простого случая – обруча, вся масса которого находится на одном и том же расстоянии от его оси. Таким образом, момент инерции кольца вокруг своей оси равен
MR2MR2 размер 12{ ital “MR” rSup { размер 8{2} } } {}, где
Размер MM 12{M} {} – это его полная масса, а размер RR 12{R} {} – его радиус. Мы используем размер MM 12{M} {} и размер RR 12{R} {} для всего объекта, чтобы отличить их от размера 12{m} {} мм и размера rr 12{r} {} для точечных масс. Во всех других случаях мы должны обращаться к рисунку 10.12 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для размера II 12{I} {}, которые были получены путем интегрирования по непрерывному телу. Обратите внимание, что размер II 12{I} {} имеет единицы массы, умноженные на квадрат расстояния (кг⋅м2кг⋅м2 размер 12{“кг” cdot “м” rSup { размер 8{2} } } {}), как мы могли бы ожидать от его определения.
Таким образом, момент инерции кольца вокруг своей оси равен
MR2MR2 размер 12{ ital “MR” rSup { размер 8{2} } } {}, где
Размер MM 12{M} {} – это его полная масса, а размер RR 12{R} {} – его радиус. Мы используем размер MM 12{M} {} и размер RR 12{R} {} для всего объекта, чтобы отличить их от размера 12{m} {} мм и размера rr 12{r} {} для точечных масс. Во всех других случаях мы должны обращаться к рисунку 10.12 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для размера II 12{I} {}, которые были получены путем интегрирования по непрерывному телу. Обратите внимание, что размер II 12{I} {} имеет единицы массы, умноженные на квадрат расстояния (кг⋅м2кг⋅м2 размер 12{“кг” cdot “м” rSup { размер 8{2} } } {}), как мы могли бы ожидать от его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением:
10,43 net τ=Iαnet τ=Iα размер 12{τ=Iα} {}
или
10,44 α=net τI,α=net τI, размер 12{α= { { ital “net”τ} над {I } } “,”} {}
где чистый размер ττ 12{τ} {} — это суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в τ=Iα, α=net τIτ=Iα, α=net τI size 12{τ=Iα,““`α= { { ital “net”τ} over {I} } } {} является вращательный аналог второго закона Ньютона и очень широко применим. Это уравнение действительно справедливо для любой крутящий момент, приложенный к любому объекту относительно любой оси .
Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в τ=Iα, α=net τIτ=Iα, α=net τI size 12{τ=Iα,““`α= { { ital “net”τ} over {I} } } {} является вращательный аналог второго закона Ньютона и очень широко применим. Это уравнение действительно справедливо для любой крутящий момент, приложенный к любому объекту относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса в обоих случаях одинакова, но момент инерции намного больше, когда дети находятся на краю.
Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса в обоих случаях одинакова, но момент инерции намного больше, когда дети находятся на краю.
Эксперимент на вынос
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от одного до двенадцати, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. Вы можете свободно прибить круг к стене. Держите круг неподвижно и с цифрой 12, расположенной вверху, прикрепите кусок синей замазки, липкого материала, используемого для крепления постеров к стенам, к цифре три. Насколько большим должен быть комок, чтобы просто повернуть круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое для числа три, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте вращать круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
Как это изменение повлияет на количество синей замазки, необходимое для числа три, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте вращать круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
В каком направлении вращался круг, когда вы добавляли замазку в номер три, по часовой или против часовой стрелки? В каком из этих направлений была результирующая угловая скорость? Была ли угловая скорость постоянной? Что мы можем сказать о направлении по часовой стрелке или против часовой стрелки углового ускорения? Как можно изменить положение замазки, чтобы создать угловую скорость в противоположном направлении?
Стратегия решения задач по динамике вращения
- Изучите ситуацию, чтобы определить, участвуют ли крутящий момент и масса во вращении . Нарисуйте тщательный набросок ситуации.
- Определить интересующую систему .

- Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить сеть τ=Iα, α=net τI net τ=Iα, α=net τI size 12{τ=Iα,“`α= { { ital “net”τ} over {I} } } {}, вращательный эквивалент второго закона Ньютона, чтобы решить проблему . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
- Как всегда, проверьте правильность решения .
Выполнение соединений
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.
Рисунок 10.12 Некоторые инерции вращения.
Пример 10.7 Расчет влияния распределения массы на карусель
Рассмотрим отца, толкающего карусель на детской площадке на рис. 10.13. Он прикладывает силу 250 Н к краю 50-килограммовой карусели, имеющей радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Рис. 10.13. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.
Стратегия
Угловое ускорение задается непосредственно выражением .
10,45 α=τIα=τI размер 12{α= {{τ} над {I} } } {}
Чтобы определить αα размера 12{α} {}, мы должны сначала вычислить крутящий момент ττ размера 12{τ } {}, который в обоих случаях одинаков, и момент инерции II величиной 12{I} {}, который во втором случае больше. Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что
10,46 τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. размер 12{τ=”rFsinθ”= \( 1 “.” “50м” \) \( “250Н” \) =”375Н” “.” “m.”} {}
τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. размер 12{τ=”rFsinθ”= \( 1 “.” “50м” \) \( “250Н” \) =”375Н” “.” “m.”} {}
Решение для (a)
Момент инерции твердого диска относительно этой оси на рисунке 10.12 равен
10.47 12MR2,12MR2, размер 12{ { {1} свыше {2} } итал. “MR” rSup {размер 8{2} } “,”} {}
, где M=50 кгM=50 кг размер 12{M=”50″ “.” 0 итал. “кг”} {} и R=1,50 мR=1,50 м размер 12{R=1 “.” “50”м} {}, так что
10,48 I=(0,500)(50 кг)(1,50 м)2=56,25 кг⋅м2.I=(0,500)(50 кг)(1,50 м)2=56,25 кг⋅м2. размер 12{I=0 “.” 5 \( “50” “.” “0kg” \) \( 1 “.” “50m” \) rSup { size 8{2} } =”56″ “.” “25кг” “.” “m” rSup { size 8{2} } “.”} {}
Теперь, после подстановки известных значений, находим угловое ускорение равным
10,49 α=τI=375 Н⋅м56,25 кг⋅ m2=6,67рад2.α=τI=375 Н⋅м56,25 кг⋅м2=6,67рад2. размер 12{α= {{τ} над {I} } = {{“375″`”N” “.” “м”} более {“56” “.” “25”`”кг” “.” “m” rSup {размер 8{2} } } } =6 “.” “67”` {{“rad”} over {s rSup {size 8{2} } } } “. “} {}
“} {}
Решение для (b)
Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели. Чтобы найти общий момент инерции II размера 12{I} {}, мы сначала найдем момент инерции ребенка IcIc размера 12{I rSub { размер 8{c} } } {}, считая ребенка эквивалентным точке массы на расстоянии 1,25 м от оси. Тогда
10,50 Ic=MR2=(18 кг)(1,25 м)2=28,13 кг⋅м2. Ic=MR2=(18 кг)(1,25 м)2=28,13 кг⋅м2. размер 12{I rSub { размер 8{c} } =”MR” rSup { размер 8{2} } = \(“18” “.” 0`”кг” \) \( 1 “.””25″` м \) rSup {размер 8{2}} =”28” “.” “13”`”кг” “.” m rSup {размер 8{2} } “.”} {}
Суммарный момент инерции равен сумме моментов инерции карусели и ребенка относительно одной оси. Чтобы оправдать для себя эту сумму, изучите определение II размера 12{I}{}.
10,51 I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2 размер 12{I=”28″ “.” “13”`”кг” “.” m rSup {размер 8{2}} +”56″ “. ” “25”`”кг” “.” m rSup { размер 8{2} } =”84″ “.” “38”`”кг” “.” m rSup { размер 8{2} } } {}
” “25”`”кг” “.” m rSup { размер 8{2} } =”84″ “.” “38”`”кг” “.” m rSup { размер 8{2} } } {}
Подстановка известных значений в уравнение для размера αα 12{α} {} дает
10,52 α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2.α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2. размер 12{α= {{τ} над {I} } = {{“375N” “.” м} более {“84” “.” “38кг” “.” m rSup {размер 8{2} } } } =4 “.” “44” { {“rad”} over {s rSup { size 8{2} } } } “.”} {}
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели. круглый, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если бы, например, отец продолжал толкать перпендикулярно в течение 2 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, а только 8,89.рад/с, когда на нем находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
Создание соединений: воздействие нескольких сил на одну систему
Большой гончарный круг диаметром 60 см и массой 8 кг. Он приводится в действие двигателем мощностью 20 Н, воздействующим на внешний край. Также имеется тормоз, способный оказывать усилие 15 Н в радиусе 12 см от оси вращения, на нижней стороне.
Каково угловое ускорение при работе двигателя?
Крутящий момент находится по формуле τ = rF sin θ = (0,300 м)(20 Н) = 6 Н·мτ = rF sin θ = (0,300 м)(20 Н) = 6 Н·м.
Момент инерции рассчитывается как I = 12 MR2 = 12(8 кг)(0,300 м)2 = 0,36 кг⋅м2I = 12 MR2 = 12(8 кг)(0,300 м)2 = 0,36 кг⋅м2.
Таким образом, угловое ускорение будет α = τI = 6 Н⋅м0,36 кг⋅м2 = 17 рад/с2α = τI = 6 Н⋅м0,36 кг⋅м2 = 17 рад/с2.
Обратите внимание, что трение всегда действует в направлении, противоположном вращению, происходящему в данный момент в этой системе. Если гончар ошибается и включает одновременно и тормоз, и двигатель, сила трения тормоза создаст крутящий момент, противоположный крутящему моменту двигателя.
Если гончар ошибается и включает одновременно и тормоз, и двигатель, сила трения тормоза создаст крутящий момент, противоположный крутящему моменту двигателя.
Крутящий момент от тормоза τ = rF sin θ = (0,120 м)(15 Н) = 1,80 Н⋅мτ = rF sin θ = (0,120 м)(15 Н) = 1,80 Н.
Таким образом, чистый крутящий момент равен 6 Н·м – 1,80 Н·м = 4,20 Н·м. 6 Н·м – 1,80 Н·м = 4,20 Н·м..
А угловое ускорение равно α = τI = 4,20 Н⋅м0,36 кг⋅м2 = 12 рад/с2α = τI = 4,20 Н⋅м0,36 кг⋅м2 = 12 рад/с2.
Проверьте свое понимание
Крутящий момент является аналогом силы, а момент инерции является аналогом массы. Сила и масса — физические величины, зависящие только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Являются ли крутящий момент и момент инерции такими же простыми?
Решение
Нет. Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения.

 Аддитивность означает, что масса тела равна сумме масс частей тела. Это свойство в точности выполняется для макроскопических тел и нарушается, если энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в ядро атома. То, что масса является скалярной величиной, значит, что инертные свойства тел одинаковы во всех направлениях.
Аддитивность означает, что масса тела равна сумме масс частей тела. Это свойство в точности выполняется для макроскопических тел и нарушается, если энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в ядро атома. То, что масса является скалярной величиной, значит, что инертные свойства тел одинаковы во всех направлениях. D.1.2 Учащийся может планировать стратегии сбора данных, предназначенные для установления того, что крутящий момент, угловая скорость, угловое ускорение и угловой момент могут быть точно предсказаны, когда переменные обрабатываются как по часовой стрелке или против часовой стрелки по отношению к четко определенную ось вращения и уточнить вопрос исследования на основе изучения данных. (СП 3.2, 4.1, 5.1, 5.3)
D.1.2 Учащийся может планировать стратегии сбора данных, предназначенные для установления того, что крутящий момент, угловая скорость, угловое ускорение и угловой момент могут быть точно предсказаны, когда переменные обрабатываются как по часовой стрелке или против часовой стрелки по отношению к четко определенную ось вращения и уточнить вопрос исследования на основе изучения данных. (СП 3.2, 4.1, 5.1, 5.3) 