Матрицы
Вопросы:
· Что такое матрицы?
· Реализация матриц в языке Python.
· Операции обработки матриц.
Часто
в программировании бывает полезным использование прямоугольных таблиц. Пример
такой таблицы – таблица Пифагора или таблица для игры в крестики-нолики.
Очевидно, ячейку такой таблицы можно идентифицировать по номерам её строки и
столбца. Такие таблицы называются матрицами. Матрица – это прямоугольная
таблица, состоящая из элементов одного типа. Каждый элемент матрицы имеет два
индекса: номер строки и номер столбца. Обычно при программировании матрицы
реализуются через двухмерные массивы. Но так как в языке Python нет массивов,
то при реализации матриц к нам на помощь снова приходят списки. Однако мы
знаем, что у каждого элемента списка всего один индекс, а у каждого элемента
матрицы их должно быть два. Это можно исправить, если в качестве элементов
списка будут выступать другие списки.
Рассмотрим наиболее распространённые операции над матрицами. Самый простой способ задать матрицу – это в квадратных скобках, обозначающих внешний список, перечислить значения его элементов, то есть внутренние списки. Таким образом, в других, внутренних квадратных скобках мы будем задавать значения элементов внутренних списков.
a = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
Эту же запись можно сделать и в одну строку. На несколько строк она была разделена лишь для наглядности.
Попробуем вывести на экран заданную матрицу. Сначала попробуем вывести её как одну переменную, задав в качестве аргумента функции
 В этом
модуле опишем функцию, которую назовём PrintMatrix.
Аргументом этой функции будет список списков. Назовём его a.
В теле функции запишем цикл для перебора индексов элементов внешнего списка. Это
будет цикл с параметром
В этом
модуле опишем функцию, которую назовём PrintMatrix.
Аргументом этой функции будет список списков. Назовём его a.
В теле функции запишем цикл для перебора индексов элементов внешнего списка. Это
будет цикл с параметром 
def PrintMatrix (a):
for i in range (len (a)):
for j in range (len (a[i])):
print (‘{:4d}’.format (a[i][j]))
print ()
Сохраним описанный модуль, но не будем запускать его на выполнение. Для того, чтобы протестировать описанную функцию, загрузим её из описанного модуля. В интерактивном режиме среды разработки функции можно загружать из модулей, которые находятся в корневом каталоге интерпретатора. Загрузив функцию, вызовем её для вывода заданной матрицы
Однако,
код описанной функции вывода можно сократить. Для этого во внешнем цикле, в
параметре row, будем перебирать
элементы внешнего списка, а не их индексы, а во внутреннем цикле, в параметре
«Икс», будем перебирать элементы списка «Роу».
def PrintMatrix (a):
for row in a:
for x in row:
print (‘{:4d}’.format (x))
print ()
Сохраним модуль и снова загрузим из него описанную функцию. Вызовем загруженную функцию для матрицы. Как видим, результат совпадает с изначальным.
Как же можно создать новую матрицу, заполненную некоторыми значениями, например, нулями? Кому-то придёт в голову мысль о том, чтобы сначала создать список из одного элемента, после чего с помощью умножения этого списка на количество столбцов матрицы создать его строку. А затем с помощью умножения на количество строк матрицы получить необходимое количество таких строк в списке.
a = [0] * 3
a = [a] * 3
Теперь
попробуем изменить значение одного из элементов матрицы. Для этого обратимся к
нему по его индексам, и выведем на экран изменённую матрицу.
a[0][1] = 0
PrintMatrix (a)
0 1 0
0 1 0
0 1 0
Оказывается, в ней изменился не только указанный элемент, но и весь столбец. Почему так случилось? Вспомним о том, что мы узнали ранее о копировании списков. Если попытаться передать имя списка в любую инструкцию, то в неё будет передана не копия исходного списка, а ссылка на область памяти, в которой хранится исходный список. То есть при выполнении второго оператора мы заполнили внешний список не копиями внутреннего, а лишь ссылками на область памяти, в которой он хранится, и при обращении к любой строке внешнего списка мы изменяем именно эту область оперативной памяти.
Для
того, чтобы создать полноценный список списков, создадим сперва пустой список,
после чего запишем цикл, который будет повторяться столько раз, сколько строк
должно быть в матрице. В этом цикле будем в конец созданного списка добавлять
список, состоящий из элементов, равных нулю, в количестве, равном количеству
столбцов матрицы.
a = []
for i in range (3):
a = a + [[0] * 3]
Снова попробуем изменить один из элементов матрицы и просмотреть её. На этот раз изменился только тот элемент, который мы указали. Также такую матрицу можно создать с помощью выражения-генератора, в котором в качестве элементов создаваемого списка укажем списки, созданные с помощью повторения одного элемента, равного нулю. Попробуем изменить один из элементов созданной матрицы и просмотрим её. Действительно, изменился лишь указанный элемент.
Рассмотрим
несколько алгоритмов обработки матриц. В созданный модуль «Матрикс» добавим
функцию расчёта суммы элементов матрицы. Назовём её sumMatrix.
У неё будет один параметр – матрица, сумму элементов которой нужно вычислить. В
теле функции объявим переменную s
= 0,
в которой будем вычислять сумму элементов матрицы. Теперь для перебора
элементов матрицы мы можем воспользоваться вложенным циклом. Просто скопируем
такой цикл из функции
Просто скопируем
такой цикл из функции
def SumMatrix (a):
s = 0
for row in a:
for x in row:
s = s + x
return s
Сохраним модуль и в интерактивном режиме среды разработки подключим функцию SumMatrix. Создадим матрицу из 2 строк и 4 столбцов, заполненную тройками. Теперь применим для этой матрицы описанную функцию SumMatrix. В этой матрице каждый элемент равен трём, и всего в ней две строки и четыре столбца. Значит сумма элементов матрицы равна 24. Функция вернула именно это значение. Она работает правильно, но её код можно сократить. Мы можем убрать внутренний цикл, а на его месте записать инструкцию, увеличивающую

def SumMatrix (a):
s = 0
for row in a:
s = s + sum (row)
return s
Сохраним модуль. Снова подключим из него тестируемую функцию и используем её для вычисления суммы элементов той же матрицы. Результат не изменился. Функция работает правильно.
Рассмотрим несколько определений. Квадратной матрицей называется матрица, в которой количество строк равно количеству столбцов. Элементы квадратной матрицы, у которых номер строки равен номеру столбца, называются её главной диагональю. Противоположная главной диагонали линия элементов называется побочной диагональю. В ней номер строки элемента равен разности размерности матрицы, уменьшенной на единицу, и номера столбца элемента.
Есть
целый ряд задач, связанных с этими определениями. Рассмотрим пример. Очевидно,
что главная и побочная диагонали квадратной матрицы делят её на сектора.
Создать квадратную матрицу размерностью n
строк на n столбцов, заполненную
нулями, и заполнить в ней верхний сектор единицами, левый – двойками, правый –
тройками и нижний – четвёрками.
Рассмотрим,
как делит матрицу главная диагональ. Она делит матрицу на 3 части. Элементы,
которые находятся на диагонали, нас не интересуют. В элементах, которые выше
главной диагонали, то есть в верхнем и правом секторах, номер строки меньше
номера столбца, в элементах ниже её, то есть в левом и нижнем секторах, наоборот,
номер строки больше номера столбца. Также матрицу делит побочная диагональ. В
элементах, которые выше побочной диагонали, номер строки всегда меньше, чем
разность размерности матрицы, уменьшенной на единицу, и номера столбца. Ниже
побочной диагонали, наоборот, номер строки больше разности размерности матрицы,
уменьшенной на единицу, и номера столбца. Зная, что верхний сектор квадратной
матрицы находится выше и главной, и побочной диагоналей, мы можем соединить два
соответствующих условия союзом И, получив таким образом условие
принадлежности элемента матрицы к верхнему сектору. Аналогично выводятся
условия принадлежности элемента матрицы и к остальным секторам.
Напишем программу для решения задачи. Организуем ввод размерности матрицы. Для этого запишем бесконечный цикл, а в нём – инструкцию для вывода на экран запроса на ввод n без перехода на следующую строку. Дальше запишем инструкцию для считывания значения n. Запишем выражение–генератор для создания матрицы a из n строк и n столбцов, заполненной нулями.
Теперь
будем перебирать элементы матрицы и проверять, к какому сектору они принадлежат.
Так как мы будем анализировать индексы элементов матрицы, то в циклах будем
перебирать именно индексы, а не сами элементы. Номер строки будет в параметре i,
а номер столбца – в j.
В цикле запишем ветвление с условием принадлежности текущего элемента списка к
верхнему сектору, то есть то, что i
< j and
i < n
– 1 – j. Если это условие
выполняется, присвоим текущему элементу матрицы значение 1. Если элемент списка
не принадлежит к верхнему сектору – проверим его принадлежность к левому
сектору. Если он принадлежит к левому сектору – присвоим ему значение 2. Точно
так же будем проверять принадлежность элементов к правому и нижнему секторам. И
в случае принадлежности к одному из них будем присваивать элементу
соответствующее значение. После цикла выведем элементы матрицы на экран. Для
этого загрузим из описанного ранее модуля Matrix
функцию PrintMatrix
и вызовем её для матрицы a.
Если элемент списка
не принадлежит к верхнему сектору – проверим его принадлежность к левому
сектору. Если он принадлежит к левому сектору – присвоим ему значение 2. Точно
так же будем проверять принадлежность элементов к правому и нижнему секторам. И
в случае принадлежности к одному из них будем присваивать элементу
соответствующее значение. После цикла выведем элементы матрицы на экран. Для
этого загрузим из описанного ранее модуля Matrix
функцию PrintMatrix
и вызовем её для матрицы a.
print (‘n =’)
n = int (input ())
a = []
for i in range (n):
a = a + [[0] * n]
for i in range (n):
for j in range (n):
if i < j and i < n – 1 – j:
a[i] = 1
elif i < j and i > n – 1 – j:
a[i] = 2
elif i > j and i > n – 1 – j:
a[i] = 3
elif i > j and i < n – 1 – j:
a[i] = 4
from Matrix import PrintMatrix
PrintMatrix (a)
Сохраним
описанный модуль в одном каталоге с модулем Matrix
и запустим его на выполнение. Введём размерность, равную 10. Матрица с
пронумерованными секторами была выведена на экран. Программа работает
правильно. Задача решена.
Введём размерность, равную 10. Матрица с
пронумерованными секторами была выведена на экран. Программа работает
правильно. Задача решена.
Для работы с многомерными массивами и проведения сложных математических расчётов есть расширение для языка Python, которое называется NumPy. Его вы можете рассмотреть самостоятельно, если захотите.
Мы узнали:
· Матрицей называется прямоугольная таблица из элементов одного типа. Каждый элемент матрицы имеет 2 индекса – номер строки и номер столбца матрицы, в которых он располагается.
· Для реализации матриц в языке Python используются списки, элементами которых являются списки.
Графы
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§17. Графы.
Что такое граф?
Ключевые слова:• граф • вершина • ребро • матрица смежности • степень вершины • связный граф • взвешенный граф • весовая матрица • ориентированный граф • оптимальный путь • количество путей
Давайте подумаем, как можно наглядно представить такую информацию:
От пос.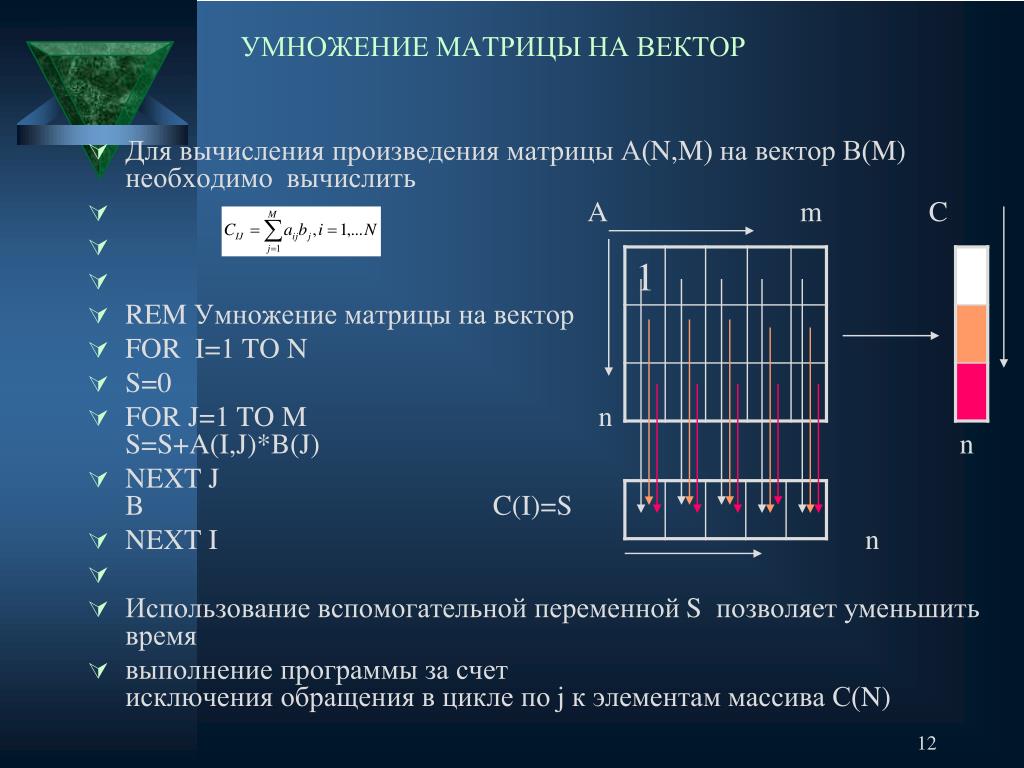 Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.
Можно, например, нарисовать такую схему (рис. 3.17, а).
Рис. 3.17
В информатике для исследования таких схем используют графы.
Граф — это набор вершин (узлов) и связей между ними — рёбер.
Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.
Матрица смежности графа
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).
Рис. 3.18
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).
Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).
Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?
В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).
Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).
Рис. 3.19
Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.
3.20) два разных изображения графа.
Рис. 3.20
Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?
Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?
Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?
Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?
Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?
Связный граф
В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).
3.21).
Рис. 3.21
Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Постройте матрицу смежности графа, изображённого на рис. 3.21.
Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.
Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.
Найдите все циклы в графе на рис. 3.17.
Дерево — это связный граф, в котором нет циклов.
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).
3.22).
Рис. 3.22
Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.
Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например, число -1 или очень большое число. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит так (рис. 3.23).
Рис. 3.23
Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.
Что означают пустые ячейки в весовой матрице?
Как по весовой матрице сразу определить, сколько рёбер в графе?
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?
3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?
Рис. 3.24
Оптимальный путь в графе
Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.
Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?
Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).
Рис. 3.25
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.
Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую
Рис. 3.26
Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).
Рис. 3.27
Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.
Почему нельзя на этом остановиться, ведь путь из А в В найден?
Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)
Рис. 3.28
Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.
Аналогично строим вторую часть схемы (рис. 3.29).
Рис. 3.29
3.29
Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.
Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.
Ориентированный граф
Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.
Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.
Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.
На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.
Рис. 3.30
Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.
Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.
Рис. 3.31
Количество путей
Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.
Рис. 3.32
Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.
В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.
По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?
Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).
Рис. 3.33
Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).
Рис. 3.34
В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4.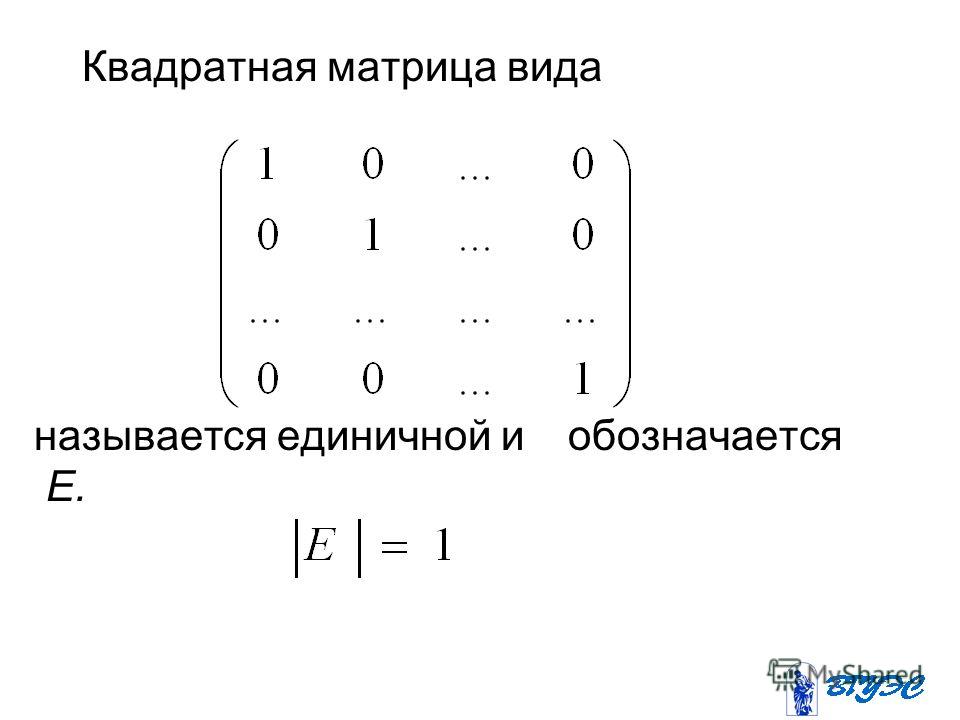 Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).
Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).
Рис. 3.35
Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).
Рис. 3.36
Выводы
• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»
Оглавление
§16. Списки и деревья.
§17. Графы.
§18. Игровые стратегии.
Задание №19. Работа с массивами
Автор материалов – Лада Борисовна Есакова.
Массив – это тип или структура данных в виде набора компонентов (элементов массива), расположенных в памяти непосредственно друг за другом. При этом доступ к отдельным элементам массива осуществляется с помощью индексации, то есть ссылки на массив с указанием номера (индекса) нужного элемента. Размерность массива — это количество индексов, необходимое для однозначного доступа к элементу массива
Одномерный массив представляет собой пронумерованную последовательность элементов одного и того же типа, имеющих общее имя. Для обращения к элементу массива используют имя и порядковый номер элемента в квадратных скобках: A[i].
Двумерный массив представляет собой матрицу элементов одного и того же типа в которой элемент, расположенный на пересечении i-й строки и j-го столбца, обозначается A[i,j].
Одномерные массивы
Пример 1.
В программе описан одномерный целочисленный массив A с индексами от 0 до 10. Ниже представлен фрагмент этой программы, записанный на разных языках программирования, в котором значения элементов массива сначала задаются, а затем меняются.
Ниже представлен фрагмент этой программы, записанный на разных языках программирования, в котором значения элементов массива сначала задаются, а затем меняются.
Бейсик | Паскаль |
| FOR i=0 TO 10 A(i)=i-1 NEXT i FOR i=1 TO 10 A(i-1)=A(i) NEXT i A(10)=10 | for i:=0 to 10 do A[i]:=i-1; for i:=1 to 10 do A[i-1]:=A[i]; A[10]:=10; |
Си | Алгоритмический язык |
| for (i = 0; i <= 10; i++) A[i]=i-1; for (i = 1; i <= 10; i++) A[i-1]=A[i]; A[10]=10; | нц для i от 0 до 10 A[i]:=i-1 кц нц для i от 1 до 10 A[i-1]:=A[i] кц A[10]:=10 |
Как изменятся элементы этого массива после выполнения фрагмента программы?
1) все элементы, кроме последнего, окажутся равны между собой
2) все элементы окажутся равны своим индексам
3) все элементы, кроме последнего, будут сдвинуты на один элемент вправо
4) все элементы, кроме последнего, уменьшатся на единицу
Решение:
Выполним последовательно все действия, описанные в программе. После первого цикла массив примет вид:
После первого цикла массив примет вид:
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значение | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Второй цикл сдвигает элементы массива на один влево:
i=1, A[0]:=A[1] = 0
i=2, A[1]:=A[2] = 1,
…
i=10, A[9]:=A[10] = 9.
А затем десятому элементу присваивается значение 10: A[10]:=10:
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значение | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный ответ указан под номером 2.
Ответ: 2
Пример 2.
В программе используется одномерный целочисленный массив A с индексами от 0 до 9. Значения элементов равны 4, 7, 3, 8, 5, 0, 1, 2, 9, 6
соответственно, т.е. A[0] = 4, A[1] = 7 и т.д.
Определите значение переменной c после выполнения следующего фрагмента этой программы (записанного ниже на пяти языках программирования).
Решение:
Если i-й элемент массива меньше нулевого, то программа меняет их местами и увеличивает значение переменной c на 1.
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Значение | 4 | 7 | 3 | 8 | 5 | 0 | 1 | 2 | 9 | 6 |
Первый раз условие «i-й элемент массива меньше нулевого» выполнится при i=2. Массив примет вид:
Массив примет вид:
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Значение | 3 | 7 | 4 | 8 | 5 | 0 | 1 | 2 | 9 | 6 |
А переменная с примет значение 1.
Второй раз условие «i-й элемент массива меньше нулевого» выполнится при i=5. Массив примет вид:
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Значение | 0 | 7 | 4 | 8 | 5 | 3 | 1 | 2 | 9 | 6 |
А переменная с примет значение 2.
Больше условие «i-й элемент массива меньше нулевого» не выполнится ни разу. Значит, с = 2.
Ответ: 2
Пример 3.
В программе описаны одномерный целочисленный массив А с индексами от 0 до 10 и целочисленные переменные i и t. Ниже представлен фрагмент этой программы, записанный на разных языках программирования.
Бейсик | Паскаль |
| FOR i = 0 TO 10 A(i) = i NEXT i t = A(10) FOR i = 9 TO 0 STEP -1 A(i+1) = A(i) NEXT i A(0) = t | for i := 0 to 10 do A[i] := i; t := A[10] for i := 9 downto 0 do A[i+1] := A[i]; A[0] := t; |
Си | Алгоритмический язык |
| for (i = 0; i <= 10; i++) A[i] = i; t = A[10]; for (i = 9; i >= 0; i–) A[i+1] = A[i]; A[0] = t; | нц для i от 0 до 10 A[i] := i кц t := A[10] нц для i от 9 до 0 шаг -1 A[i+1] := A[i] кц A[0] := t |
Чему окажутся равны элементы этого массива после выполнения фрагмента программы?
1) 10 0 0 0 0 0 0 0 0 0 0
2) 10 2 3 4 5 6 7 8 9 10 10
3) 10 10 10 10 10 10 10 10 10 10 10
4) 10 0 1 2 3 4 5 6 7 8 9
Решение:
Выполним последовательно все действия, описанные в программе. После первого цикла массив примет вид:
После первого цикла массив примет вид:
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значение | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Второй цикл работает в обратном порядке, от 9 до 0:
i = 9: A[10] := A[9] = 9,
i = 8: A[9] := A[8] = 8,
…
i = 1: A[2] := A[1] = 1
i = 0: A[1] := A[0] = 0,
А затем нулевому элементу присваивается значение 10 (A[0] := 10):
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значение | 10 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Правильный ответ указан под номером 4.
Ответ: 4
Двумерные массивы
Пример 4.
Значения элементов двумерного массива A размером 5×5 задаются с помощью вложенного цикла в представленном фрагменте программы:
for i:=1 tо 5 do
for j:=1 tо 5 do begin
A[i,j] := i*j;
end;
Сколько элементов массива будут иметь значения больше 10?
Решение:
Выполним последовательно все действия, описанные в программе:
i=1 (Заполняем первую строку матрицы)
j=1, A[1,1]:= 1*1 =1
j=2, A[1,2]:= 1*2 =2
j=3, A[1,3]:= 1*3 =3
j=4, A[1,4]:= 1*4 =4
j=5, A[1,5]:= 1*5 =5
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 |
i=2 (Заполняем вторую строку матрицы)
j=1, A[2,1]:= 2*1 =2
j=2, A[2,2]:= 2*2 =4
j=3, A[2,3]:= 2*3 =6
j=4, A[2,4]:= 2*4 =8
j=5, A[2,5]:= 2*5 =10
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 5 | 8 | 10 |
| 3 | |||||
| 4 | |||||
| 5 |
…. .
.
i=5 (Заполняем пятую строку матрицы)
j=1, A[5,1]:= 5*1 =5
j=2, A[5,2]:= 5*2 =10
j=3, A[5,3]:= 5*3 =15
j=4, A[5,4]:= 5*4 =20
j=5, A[5,5]:= 5*5 =25
Значение элементов матрицы равно произведению номеров его строки и столбца
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 5 | 8 | 10 |
| 3 | 3 | 6 | 9 | 12 | 15 |
| 4 | 4 | 8 | 12 | 16 | 20 |
| 5 | 5 | 10 | 15 | 20 | 25 |
Значение больше 10 имеют 8 элементов матрицы.
Ответ:8
Презентация Матрица в Maxima доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация Матрица в Maxima, предмет презентации: Информатика. Этот материал в формате pptx (PowerPoint) содержит 30 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 30 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Определение, виды, операции
Матрицы
В деятельности каждого инженера существенное значение имеют упрощенные методы расчета. Большинство инженерных задач можно упростить, используя математический аппарат. С этой целью в электротехнике применяют матричные методы расчёта сложных электрических цепей.
Существует несколько матричных методов расчёта, один из них метод контурных токов в матричной форме, который применяется на практике. Для этого необходимо знать, что представляет собой матрица.
Матрица
Матрицей размера m × n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Матрица
Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются заглавными буквами латинского алфавита, элементы – малыми буквами; i – номер строки, j – номер столбца
Виды матриц
Матрица, состоящая из одной строки, называется матрицей – строкой, а из одного столбца – матрицей – столбцом
Матрица называется квадратной , если число ее строк равно числу столбцов.
матрица – строка
Матрица
столбец
Элементы матрицы, у которых номер столбца равен номеру строки, называются диагональными и образуют главную диагональ матрицы
Диагональная матрица
Виды матриц
Если у диагональной матрицы все диагональные элементы равны единице, то матрица называется единичной – Е
Если все элементы равны нулю – это нулевая матрица
Виды матриц
матрица противоположная матрице А
Виды матриц
верхняя треугольная матрица
нижняя треугольная матрица
Виды матриц
Транспонирование матриц
Транспонирование матрицы – это операция над матрицей, при которой ее строки и столбцы меняются местами:
Определение
3)
2)
4)
Свойства транспонирования:
1)
Произведением матрицы А = (аij) на число k называется матрица С = (сij) тех же размеров, у которой сij = k·aij для любых i,j. C = k A
C = k A
Произведение матрицы на число:
Операции над матрицами
Свойства умножения матрицы на число:
2)
3)
4)
для любых А, В одинаковых размеров, любых α, β
R
1)
Операции над матрицами
Умножение матрицы на число
Произведением матрицы А на число k называется матрица C =kА
Суммой матриц А = (аij) и В = (bij) одинаковых размеров называется матрица С = (сij) тех же размеров, у которой сij = аij + bij, для любых i, j.
C = A + B
Операции над матрицами
Суммой матриц А = (аij) и В = (bij) одинаковых размеров называется матрица С = (сij) тех же размеров, у которой сij = аij + bij, для любых i, j.
C = A + B
Операции над матрицами
Операции над матрицами
Даны матрицы А и В одинакового размера;
Найти: матрицу С = А + В
Сложение матриц
Разность двух матриц одинакового размера определяется через предыдущие операции:
А – В = А + (-1)В.
Вычитание матриц
Операции над матрицами
Самостоятельная работа
1. Транспонировать данную матрицу
Найти матрицу 2Мт и 3М
3Nт и 2N
Вариант 1 Матрица M
Вариант 2 Матрица N
3. Найти А+В, А – В, 3А +2В, 2А-3В
Операции над матрицами в компьютерной системе Максима
Операции над матрицами в компьютерной системе Максима
Операции над матрицами в компьютерной системе Максима
Операции над матрицами в компьютерной системе Максима
Операции над матрицами в компьютерной системе Максима
Сложение матриц
Операции над матрицами в компьютерной системе Максима
Произведением матрицы
А = (аik) размеров mn
на матрицу
В = (bkj) размеров np
называется матрица С = (сij)
размеров mp, у которой
cij = ai1b1j + ai2b2j + … + ainbnj.
C = AB
Операции над матрицами
Умножение матриц
Произведением матриц А · В называется такая матрица С, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В
Операции над матрицами.
Умножение матриц
Свойства умножения матриц:
1) AE = EA = A
2) A0 = 0A = 0
3) (AB)D = A(BD)
5) A + B)D = AD + BD
D(A + B) = DA + DB
(при условии, что все указанные операции имеют смысл).
Для квадратных матриц АВ≠ВА
Свойства умножения матриц:
.
Найти:
Дано:
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Обратная матрица в Excel. Как найти обратную матрицу в Эксель в 2 этапа — Информатика ► Информатика в школе и дома
Практические работы в MS Excel – задания, советы, решения и ответы
Информатика и ИКТОставить комментарийна Обратная матрица в Excel. Как найти обратную матрицу в Эксель в 2 этапа — Информатика
Оглавление:
- 1 Обратная матрица в Excel. Как найти обратную матрицу в Эксель в 2 этапа — Разбираем подробно
- 2 Находим значение определителя
- 3 Определяем значение обратной матрицы
- 4 Сферы использования расчетов с обратной матрицей
- 5 Заключение
Want create site? Find Free WordPress Themes and plugins.
Обратная матрица в Excel. Как найти обратную матрицу в Эксель в 2 этапа — Разбираем подробно
Обратная матрица – это сложное математическое понятие, для нахождения которой необходимо выполнить множество непростых действий на бумаге. Однако программа Excel решает данную задачу в более короткие сроки и без особых усилий со стороны исполнителя. Давайте разберемся, каким образом можно найти обратную матрицу в несколько этапов на одном из примеров.
Однако программа Excel решает данную задачу в более короткие сроки и без особых усилий со стороны исполнителя. Давайте разберемся, каким образом можно найти обратную матрицу в несколько этапов на одном из примеров.
Замечание эксперта! Обязательным условием для нахождения обратной матрицы, является соответствие исходных данных квадратной матрице, а определителя нулю.
Находим значение определителя
Чтобы выполнить это действие, необходимо воспользоваться функцией МОПРЕД. Как именно это делается, рассмотрим на примере:
- Записываем квадратную матрицу в любом свободном месте.
- Выбираем свободную ячейку, после чего находим напротив строки формул кнопку «fx» («Вставить функцию») и кликаем по ней ЛКМ.
1
- Должно открыться окно, где в строке «Категория:» останавливаемся на «Математические», а ниже выбираем функцию МОПРЕД. Соглашаемся с выполненными действиями кликнув по кнопке «ОК».

- Далее в открывшемся окне заполняем координаты массива.
Совет! Заполнить адресацию можно одним из двух способов: вручную или кликнув кнопкой мыши в месте ввода информации о массиве и, определив выделением зоны место расположения квадратной матрицы, получить адрес массива автоматически.
- После проверки введенных ручным или автоматическим образом данных жмите «ОК».
2
- После всех проведенных манипуляций свободная ячейка должна отобразить определитель матрицы, значение которого понадобится для нахождения обратной матрицы. Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.
3
Определяем значение обратной матрицы
Как только вычисление определителя закончено, можно переходить к определению обратной матрицы:
- Выбираем место расположения верхнего элемента обратной матрицы, открываем окно «Вставка функции».

- Выбираем категорию «Математические».
- В расположившихся снизу функциях пролистываем список и останавливаем выбор на МОБР. Кликаем по кнопке «ОК».
4
- Аналогично ранее выполняемым действиям при нахождении значений определителя вписываем координаты массива с квадратной матрицей.
- Убеждаемся в правильности выполненных действий и жмем «ОК».
- В выбранной верхней левой ячейке будущей обратной матрицы появится результат.
- Для копирования формулы для нахождения значений в других ячейках используем свободное выделение. Для этого, зажав ЛКМ, растягиваем на всю область будущей обратной матрицы.
5
- Жмем на клавиатуре кнопку F2 и переходим к набору комбинации «Ctrl+Shift+Enter». Готово!
6
Рекомендация эксперта! Для удобства выполнения действий по нахождению обратной матрицы в таблице Excel расположение массива с квадратной матрицей и выбранная область для ячеек с обратной матрицей должны располагаться на одном уровне по отношению к столбцам.
Таким образом будет проще определить границы адресации второго массива. Пример указан на иллюстрации ниже.
7
Сферы использования расчетов с обратной матрицей
Экономика – это область, которая требует проведения постоянных и очень сложных расчетов. Для облегчения используется матричная система расчетов. Нахождение обратной матрицы – это быстрый способ обработки большого объема информации за максимально короткие сроки, конечный результат которого будет представлен в наиболее удобном для восприятия виде.
Другая область применения – это 3D моделирование изображений. Всевозможные программы имеют встроенные инструменты для проведения подобного рода расчетов, что в значительной степени облегчает работу конструкторам при производстве расчетов. Наиболее популярной программой среди 3D моделистов считается Компас-3D.
Существуют и другие сферы деятельности, где можно применить систему расчетов обратной матрицы, но все же основной программой для проведения матричных расчетов можно считать Excel.
Заключение
Нахождение обратной матрицы нельзя назвать такой же распространенной математической задачей, как вычитание, сложение или деление, но если появилась необходимость в ее решении, то все действия могут произведены в табличном процессоре Excel. Если человеческий фактор склонен допускать ошибки, то компьютерная программа выдаст 100% точный результат.
Did you find apk for android? You can find new Free Android Games and apps.
Найти:Рубрики
РубрикиВыберите рубрикуIT Новости — технологии, софт, гаджеты со всего мира и России (347)Все статьи (1 778)ЕГЭ учебные пособия – Подготовка по информатике к экзамену скачать читать бесплатно (3)Информатика — учебники 1-11 класс онлайн читать (214) Учебники Информатики 1 класс онлайн, скачать, читать (5) Учебники Информатики 10 класс онлайн, скачать, читать (22) Учебники Информатики 11 класс онлайн, скачать, читать (18) Учебники Информатики 2 класс онлайн, скачать, читать (17) Учебники Информатики 3 класс онлайн, скачать, читать (28) Учебники Информатики 4 класс онлайн, скачать, читать (31) Учебники Информатики 5 класс онлайн, скачать, читать (19) Учебники Информатики 6 класс онлайн, скачать, читать (20) Учебники Информатики 7 класс онлайн, скачать, читать (35) Учебники Информатики 8 класс онлайн, скачать, читать (35) Учебники Информатики 9 класс онлайн, скачать, читать (37)КИМ Информатика 8 класс Масленикова (15)Методическая копилка — Дошкольная Информатика (3)Методическая копилка по информатике: уроки, конспекты, занимательные задачи (47) Методическая копилка по информатике — 5 класс — уроки, конспекты, занимательные задачи (3) Методическая копилка по информатике — 6 класс — уроки, конспекты, занимательные задачи (18)НОВОСТИ об ИГРАХ — новинки, обновления, свежие игровые новости (377)ОГЭ учебные пособия — Подготовка по информатике к экзамену скачать читать бесплатно (6)Решебник ГДЗ Информатика учебник 9 класс Угринович (22)Решебник ГДЗ Семакин Информатика 8 класс Учебник (27)Решебник ГДЗ Учебника Информатика 9 КЛАСС Босова Вопросы и задания (22)Решебник Информатика 2 класс Горячев, Горина, Суворова (128)Решебник Информатика 2 класс Матвеева, Челак (102)Решебник Информатика 3 класс Горячев, Горина, Суворова (72)Решебник Информатика 3 класс Матвеева, Челак (129)Решебник Информатика 4 класс Горячев, Горина, Суворова (105)Решебник Информатика 4 класс Матвеева, Челак (189)Решебник Информатика Рабочая тетрадь 9 класс Семакин (14)Решебник к Рабочей тетраде Информатика 5 класс Босова (131)Решебник к Рабочей тетраде Информатика 6 класс Босова (202)Решебник к Рабочей тетраде Информатика 7 класс Босова (147)Решебник к Рабочей тетраде Информатика 8 класс Босова (202)Решебник к учебнику Информатика 5 класс Босова (36)Решебник к учебнику Информатика 6 класс Босова (18)Решебник к учебнику Информатика 7 класс Босова (27)Решебник к учебнику Информатика 8 класс Босова (11)Решебник к учебнику Информатика 9 класс Семакин (27)Решебник учебника Информатика 8 класс Угринович (5)Решение задач по информатике для школьников (2 174) Задачи и советы по работе в MS Office — практика и теория (1 892) Практические работы в MS Access — задания, советы, решения и ответы (165) Практические работы в MS Excel — задания, советы, решения и ответы (1 285) Практические работы в MS Power Point — задания, советы, решения и ответы (145) Практические работы в MS Word — задания, советы, решения и ответы (297) Задачи по программированию с решением для школьников (267) Занимательные задачи по информатике для школьников (15)Сайтостроение — создать с нуля, уроки, новости, полезное (355)Онлайн-калькулятор
Онлайн-калькулятор Math можно использовать для проверки своего решения по многим математическим и экономическим дисциплинам. Результат решения – это отчет в формате Word (и Excel при необходимости), содержащий ход решения с комментариями, исходные формулы и выводы.
Результат решения – это отчет в формате Word (и Excel при необходимости), содержащий ход решения с комментариями, исходные формулы и выводы.
Теория вероятностей и математическая статистика
Математическое ожидание дискретной случайной величины: нахождение дисперсии и среднеквадратического отклонения
Корреляционная таблица: ковариация и уравнения регрессии
Системы случайных величин: X и Y
Выборочный метод: оценка среднего значения, дисперсия, доверительные интервалы.
Другие калькуляторы
Информатика
Перевод чисел из одной системы счисления в другую
Формат чисел с плавающей точкой
Сложение двоичных чисел
Таблица истинности: построение СКНФ и СДНФ с картами Карно (Вейча), минимизация булевой функции
Построение логической схемы (графически)
Другие калькуляторы
Линейная алгебра
Ранг матрицы
Обратная матрица через алгебраические дополнения . Определение миноров матрицы, алгебраических дополнений, транспонированной матрицы
Определение миноров матрицы, алгебраических дополнений, транспонированной матрицы
Обратная матрица методом Жордано-Гаусса
Методы нахождения определителей: разложением по строкам и столбцам, методом треугольников, методом Гаусса (метод приведения к треугольному виду), методом декомпозиции
Умножение матриц
Преобразование матрицы до треугольной
LU разложение матрицы
Другие калькуляторы
Методы решения СЛАУ
Исследование системы линейных уравнений (на совместность и определенность)
Решения СЛАУ методом Гаусса (а также Жордано-Гаусса)
Решения СЛАУ методом Крамера
Решения СЛАУ методом обратной матрицы
Решения СЛАУ методом простой итерации
Решения СЛАУ методом Зейделя
Другие калькуляторы
Методы оптимизации
Метод Ньютона (метод дихотомии, модифицированный метод Ньютона, метод хорд, комбинированный метод, метод золотого сечения, метод итераций).
Метод множителей Лагранжа.
Все сервисы
Аналитическая геометрия
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
По координатам вершин пирамиды найти: угол между векторами, объем пирамиды, уравнение плоскости, расстояния от точки до плоскости, площадь треугольника.
Все сервисы
Математический сервис
Формула дискриминанта. Корни квадратичной функции.
Найти корни уравнения
Решить дифференциальные уравнения
Вычислить интеграл
Найти производную
Разложить на множители
Найти предел
Построить график функции
Градиент
Построить график функции методами дифференциального исчисления
Комплексные числа
Другие калькуляторы
Линейное программирование
Графический метод решения задач линейного программирования. Геометрический способ решения.
Геометрический способ решения.
Решение симплексным методом (М-метод, двухэтапный метод, двухфазный метод)
Двойственный симплекс-метод (P-метод)
Двойственная задача линейного программирования
Транспортная задача
Задача коммивояжера
Задача о назначениях
Другие калькуляторы
Целочисленное программирование
Метод Гомори. Метод отсечений.
Графический метод.
Метод ветвей и границ.
Все сервисы
Динамическое программирование
Задача оптимального распределения инвестиций
Задача замены оборудования
Метод прямой и обратной прогонки
Все сервисы
Сетевое планирование
Сетевая модель. Параметры сетевой модели (ранний срок свершения событий, поздний срок свершения события, резерв времени)
Разрез сети. Минимальный разрез сети. Максимальный поток сети.
Модели теории игр
Оптимальная стратегия. Цена игры, седловая точка.
Игры с природой. Критерии Максимакса, Байеса, Лапласа, Вальда, Сэвиджа и Гурвица.
Биматричные игры.
Другие калькуляторы
Системы и модели массового обслуживания
Одноканальные модели систем массового обслуживания: Одноканальная СМО с отказами в обслуживании, Одноканальная СМО с ограниченной длиной очереди, Одноканальная СМО с неограниченной очередью.
Многоканальные модели систем массового обслуживания: Многоканальная СМО с отказами в обслуживании, Многоканальная СМО с ограниченной длиной очереди, Многоканальная СМО с неограниченной очередью.
Другие калькуляторы
Статистика
Выявление тренда методом аналитического выравнивания: по прямой, по параболе, по экспоненте, степенной функции, по гиперболе.
Группировка статистических данных.
Аналитическая группировка статистических данных.
Показатели вариации: средняя арифметическая, медиана, мода, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Доверительный интервал: для математического ожидания, для дисперсии, для генеральной доли.
Проверка гипотез о виде распределения: критерий согласия Пирсона.
Однофакторный дисперсионный анализ
Коэффициент ранговой корреляции Спирмена
Коэффициент Фехнера
Другие калькуляторы
Эконометрика
Уравнение парной линейной регрессии. Коэффициент корреляции. Статическая надежность регрессионного моделирования с помощью F- критерия Фишера и с помощью t-критерия Стьюдента.
Уравнение нелинейной регрессии. Экспоненциальная, степенная, показательная, равносторонняя гипербола.
Уравнение множественной регрессии. Матричный метод. Матрица парных коэффициентов корреляции
Матричный метод. Матрица парных коэффициентов корреляции
Уравнение множественной регрессии для двух переменных с помощью формул Крамера. Система уравнений.
Другие калькуляторы
Полезные советы при пользовании сервисом
Кодирование матрицы
Кодирование матрицыО курсе
Курс преподается в Университете Брауна с 2008 г.,
и преподается осенью
2017. Слайды из прошлых выпусков курса Университета Брауна доступны здесь.
Укороченная версия преподавалась на Coursera.
Цель данного курса состоит в том, чтобы предоставить студентам, заинтересованным в
информатика введение в векторы и матрицы и
их использование в приложениях CS.
Курс основан на приложениях из областей, выбранных из
среди: компьютерное зрение, криптография, теория игр, графика,
поиск информации и веб-поиск, а также машинное обучение.
Ресурсы курса
Данные и код поддержки, необходимые для проведения здесь представлены задания.
Автоматическая сортировка доступен для некоторых задач.
Вот первая и вторая лаборатория из первого издания. Эти ничего не имеют делать с линейной алгеброй. Они предусмотрены для приведения читатель в курсе той части Python, которую мы используем в книге. Вот документ, предназначенный для помощи людям в осуществлении перехода от петель к пониманиям.
Присоединяйтесь к списку рассылки для получения обновлений о добавлении ресурсов.
Слайды
Слайды из курса, преподававшегося в Университете Брауна осенью 2013 г.:
- Функция
- Поле
- Вектор
- Векторное пространство
- Матрица
- Основа
- Размер
- Гауссова
Ликвидация
- Внутренний продукт
- Ортогонализация
- Специальные базы
- Единственное значение Разложение
- Собственный вектор
- Линейная программа
Подпишитесь на обновления
О книге
Примеры приложений
Вот примеры приложений, рассматриваемых в Кодирование
Матрица .
-
кроссфейд
Отрезок между точками задается выпуклой комбинации этих точек; если “точки” являются изображениями, то сегмент линии — это простой переход между изображениями.
Исправление перспективы
Имея фотографию доски, сделанную под углом, синтезируйте бесперспективный вид доски.
То же преобразование можно использовать при использовании Wiimote для создания недорогая интерактивная доска или световое перо (благодаря Джонни Чанг Ли).
Коды исправления ошибок
Коды исправления ошибок используются, например, мобильными телефонами для сохранять данные, передаваемые по зашумленному каналу, в то время как поддержание высокой пропускной способности.
Целочисленная факторизация
522253825433285668885771662040104167 = 891428822186035241∙5858614983443
Разложение целого числа на множители — сложная вычислительная задача (и криптосистема RSA зависит от ее жесткости).
 В
ядро самых сложных алгоритмов целочисленного факторинга
— простая задача линейной алгебры.
В
ядро самых сложных алгоритмов целочисленного факторинга
— простая задача линейной алгебры.Размытие изображения
Размытие изображения — это простое линейное преобразование.
Поиск в аудиоклипе
Можно сформулировать поиск одного аудиоклипа в другом как свертка. Свертку можно вычислить очень быстро с помощью быстрого преобразования Фурье.
Поиск по изображению
Свертку также можно выполнять в двух измерениях, что позволяет для быстрого поиска субизображения в изображении.
Сжатие аудио и изображений
Сжатие аудио и изображений способствует эффективному хранению и коробка передач. Методы сжатия с потерями, такие как те, которые используются в MP3 (аудио) и JPEG (изображения), основаны на часть по линейной алгебре,
например. вейвлет-преобразование и преобразование Фурье.
вейвлет-преобразование и преобразование Фурье. 100% оригинал размер
40% оригинал размер
10% оригинал размер
Распознавание лиц
«Классический» подход к распознаванию лиц — собственные лица, метод, связанный с анализом главных компонентов.
Преобразование 2D-графики
Простые преобразования, возникающие в графике, такие как вращение, перемещение и масштабирование могут быть выражены с помощью матрицы.
Отбой
Lights Out — это головоломка, в которой вы должны выбрать правильные кнопки нажимать, чтобы загорелись все огни вне. Поиск решения может быть выражен как проблема в линейная алгебра.
Лесной пролет минимального веса
Поиск остовного дерева минимального веса графа может быть интерпретируется как задача нахождения базиса минимального веса для векторного пространства
, полученного из графика.
График
Хороший рисунок графа может быть получен из собственных векторов родственная матрица.
Для чего используется матрица в информатике
В информатике и математике матрица (во множественном числе «матрицы») — это набор чисел, расположенных в строках и столбцах. Числа в матрице могут представлять данные или математические уравнения. Они используются как способ быстрого приближения к более сложным вычислениям.
Содержание
Полезны ли матрицы в программировании?
Матрица полезна во многих вычислениях. Обычно большинство из нас думает, что компьютерная инженерия — это программирование, алгоритмы, сети и структуры данных. Но есть так много междисциплинарных областей, которые требуют математики и вычислений.
Как матрицы используются в робототехнике и автоматизации?
Матрицы преобразования можно использовать для описания того, под каким углом должны находиться сервоприводы, чтобы достичь желаемого положения в пространстве, или может быть, что подводному автономному транспортному средству необходимо достичь или выровняться с несколькими различными препятствиями внутри воды.
Каково основное использование матрицы?
1. Каковы применения матриц? Они используются для построения графиков, статистики, а также для проведения научных исследований и исследований практически в разных областях. Матрицы также можно использовать для представления реальных данных, таких как численность населения, уровень детской смертности и т. д.
Что такое матрица с примером?
Матрица представляет собой прямоугольный массив чисел или символов, которые обычно расположены в строках и столбцах. Например, у нас есть матрица 3×2, потому что количество строк здесь равно 3, а количество столбцов равно 2.
youtube.com/embed/ptAES23_R28″>Что такое матрица?
В математике матрица (множественное число матриц) представляет собой прямоугольный массив чисел, символов или выражений, расположенных в строках и столбцах. Матрицы обычно записываются в квадратных скобках. Размер матрицы определяется количеством содержащихся в ней строк и столбцов.
Какова роль матриц и измерений в программной инженерии?
Метрики используются для поддержания контроля над процессом разработки программного обеспечения. Метрики можно использовать для измерения размера, стоимости, усилий, качества продукта проекта, а также для оценки качества выполняемого процесса и личной продуктивности.
Что такое матрица решений в инженерии?
Методы матрицы решений используются для определения атрибутов, их взвешивания и надлежащего суммирования взвешенных атрибутов, чтобы дать относительное ранжирование среди альтернатив дизайна. Матрица решений состоит из строк и столбцов, которые позволяют оценивать альтернативы по различным критериям принятия решений.
Что называют матрицей?
матрица, набор чисел, расположенных в строках и столбцах так, чтобы образовать прямоугольный массив. Числа называются элементами или элементами матрицы. Матрицы имеют широкое применение в технике, физике, экономике и статистике, а также в различных разделах математики.
Можем ли мы возвести матрицу в квадрат?
Квадратная матрица — это тип матрицы. Но когда мы говорим о возведении матрицы в квадрат, мы на самом деле выполняем операцию умножения матрицы на саму себя. Если бы нам нужно было возвести Matrix в квадрат, мы бы умножили Matrix саму на себя. Он будет следовать процессу умножения матриц.
Почему матрица важна в информатике?
Умножение матриц можно рассматривать как решение линейных уравнений для конкретных переменных. Но это указывает на одну из причин, по которой матрицы так распространены в компьютерных науках: они позволяют компьютерам, по сути, выполнять большую вычислительную тяжелую работу заранее. 4 A4, умножаем само на себя 4 раза и так далее. Степени матриц подчиняются тем же правилам, что и степени чисел.
4 A4, умножаем само на себя 4 раза и так далее. Степени матриц подчиняются тем же правилам, что и степени чисел.
Каковы преимущества Matrix в разработке программного обеспечения?
Преимущества Software Metrics Повышение рентабельности инвестиций (ROI) Определение областей, требующих улучшения. Управляйте рабочими нагрузками. Сократите сверхурочную работу. Сократите расходы.
В каких работах используются матрицы?
Электронные сети, самолеты и космические корабли, а также химическая инженерия требуют идеально выверенных вычислений, которые получаются путем матричных преобразований. В больницах медицинские визуализации, компьютерная томография и МРТ используют матрицы для работы.
Почему используются метрики?
Метрики помогают преобразовать расплывчатые требования, которые предъявляет клиент, в ряд цифр, которые можно использовать для точного отображения эффективности процесса. Метрики говорят нам, достаточно ли хорош процесс, чтобы удовлетворить требования клиента, или его нужно улучшить.
Чем полезно использование матрицы решений при исследовании финансовых счетов или продуктов?
Матричный анализ решений помогает выбрать один из нескольких вариантов, при этом необходимо учитывать множество различных факторов. Чтобы использовать этот инструмент, разложите варианты в виде строк в таблице. Настройте столбцы, чтобы показать факторы, которые необходимо учитывать.
Какова мощность матрицы?
Определение: мощность матрицы, если ???? это квадратная матрица и ???? является положительным целым числом, ???? ч сила ???? дан кем-то ???? знак равно × ???? × ⋯ × ???? , где есть ???? копии матрицы???? .
Чем матрица полезна для решения бизнес-задач?
Матрица решений может помочь вам не только принимать сложные решения, но и расставлять приоритеты в задачах, решать проблемы и создавать аргументы для защиты уже принятого решения. Это идеальный инструмент для принятия решений, если вы выбираете среди нескольких сопоставимых решений с несколькими количественными критериями.
Это идеальный инструмент для принятия решений, если вы выбираете среди нескольких сопоставимых решений с несколькими количественными критериями.
Как матрицы используются в компьютерной графике?
Использование матриц в компьютерной графике широко распространено. Примеры матричных операций включают переводы, повороты и масштабирование. Другие концепции преобразования матрицы, такие как поле зрения, рендеринг, преобразование цвета и проекция. Понимание матриц является основной необходимостью для программирования 3D видеоигр.
Используются ли матрицы в программной инженерии?
Матрица графа — это структура данных, которая может помочь в разработке инструмента для автоматизации тестирования пути. Свойства матриц графов имеют основополагающее значение для разработки инструмента тестирования, и, следовательно, матрицы графов очень полезны для понимания концепций и теории тестирования программного обеспечения.
Зачем нужны метрики качества программного обеспечения?
Метрики тестирования программного обеспечения полезны для оценки работоспособности, качества и прогресса в тестировании программного обеспечения. Без метрик было бы практически невозможно дать количественную оценку, объяснить или продемонстрировать качество программного обеспечения.
Без метрик было бы практически невозможно дать количественную оценку, объяснить или продемонстрировать качество программного обеспечения.
Применение матрицы в компьютерных науках и технологиях
Заголовки статей
Исследование сжатых матриц в трилинейной модели сжатого зондирования
стр.3380
Исследование комбинированной оптимизации параметров и выбора символов для SVM на основе имитации отжига и улучшенного QPSO
стр.3384
Интеллектуальный анализ метеорологических данных, основанный на сокращении грубых наборов атрибутов и дереве решений
стр.3388
Применение линейной алгебры в реальной жизни
стр. 3392
3392
Применение матрицы в компьютерных науках и технологиях
стр.3396
Оптимальный параллельный алгоритм сортировки слиянием на основе OpenMP
стр.3400
Исследование организации очередей трафика на основе компьютерного моделирования и теории массового обслуживания
стр.3404
Применение технологии улучшения речи в системе имитации полета
стр.3408
Извлечение признаков радужки на основе алгоритма оценки нечеткой кластеризации
стр.3412
Главная Прикладная механика и материалы Прикладная механика и материалы Vols. 556-562 Применение матрицы в информатике и…
556-562 Применение матрицы в информатике и…
Предварительный просмотр статьи
Аннотация:
Применение матрицы в области компьютера слишком много. Это простой инструмент расчета, может быть представлен в простой форме и в сложной форме. В этой статье приводится несколько примеров из компьютерных наук и технологий, на которые можно ответить с помощью матричного метода. Для того, чтобы помочь студентам узнать применение матрицы в информатике и технологии, чтобы стимулировать интерес к обучению.
Доступ через ваше учреждение
* – Автор, ответственный за переписку
использованная литература
[1]
Ян Вэй, Гао Шупин расчет линейной алгебры и применение руководства, Си, пресса Университета электроники и науки.
[2] Чен Хуайчен Ян Вэй, редактор инженерной линейной алгебры, издательство электронной промышленности.
[3] Чжан Сяосян Кафедра математики линейной алгебры Юго-восточного университета, моделирование корпуса сборки.
[4]
Исследовательская лабораторная группа факультета математики, геометрии и алгебры Пекинского университета по высшей алгебре, издательство Higher Education Press.
[5] Математический факультет инженерной математики Университета Тунцзи – линейная алгебра, четвертое издание, издательство высшего образования.
[6] Т.Б. Мэйплс и Г.А. Спанос. Исследование производительности селективной схемы шифрования для защиты сетевого видео в реальном времени. В материалах 4-й Международной конференции по компьютерным коммуникациям и сетям, сентябрь (2008 г.).
DOI: 10.1109/icccn.1995.540095
Цитируется
Гипотеза моделирования: мы живем в видеоигре?
Мы живем в компьютерной симуляции?
Вопрос кажется абсурдным.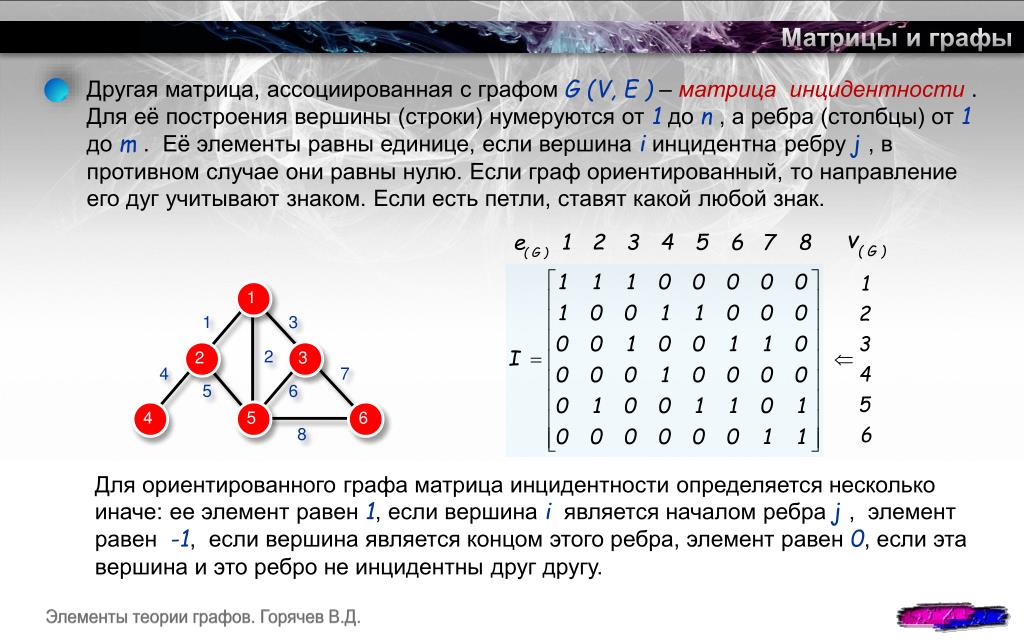 Тем не менее, есть много умных людей, которые убеждены, что это не только возможно, но и вероятно.
Тем не менее, есть много умных людей, которые убеждены, что это не только возможно, но и вероятно.
В влиятельной статье, в которой изложена теория, оксфордский философ Ник Бостром показал, что по крайней мере одна из трех возможностей верна: 1) Все человекоподобные цивилизации во Вселенной вымирают, прежде чем они разовьют технологические возможности для создания симулированных реальностей. ; 2) если какая-либо цивилизация действительно достигнет этой фазы технологической зрелости, ни одна из них не удосужится запустить симуляции; или 3) развитые цивилизации будут иметь возможность создавать множество симуляций, а это означает, что смоделированных миров гораздо больше, чем не смоделированных.
Мы не можем знать наверняка, что из этого верно, заключает Бостром, но все они возможны, и третий вариант может быть даже наиболее вероятным исходом. Это трудный аргумент, чтобы обернуть голову, но он имеет определенный смысл.
Ризван Вирк, ученый-компьютерщик и дизайнер видеоигр, опубликовал в 2019 году книгу The Simulation Hypothesis , , в которой более подробно исследуется аргумент Бострома и прослеживается путь от сегодняшних технологий к тому, что он называет «точкой моделирования, момент, когда мы могли реально построить Матрица – подобная симуляция.
Я ничего не смыслю в компьютерных науках, но идея о том, что мы все персонажи в видеоигре развитой цивилизации, просто потрясающая. Так что я связался с Вирком и попросил его разобрать его для меня.
Далее следует слегка отредактированная стенограмма нашего разговора.
Шон Иллинг
Притворись, что я абсолютно ничего не знаю о «гипотезе моделирования». Какая к черту гипотеза симуляции?
Ризван Вирк
Гипотеза симуляции — это современный эквивалент идеи, существовавшей некоторое время, и это идея о том, что физический мир, в котором мы живем, включая Землю и остальную часть физической вселенной, на самом деле является частью компьютера. моделирование.
Вы можете думать об этом как о видеоигре с высоким разрешением или высокой точностью, в которой мы все являемся персонажами, и лучший способ понять это в рамках западной культуры — это фильм «Матрица », который многие видели, или даже если они не видели [его], то теперь это стало культурным явлением, выходящим за рамки киноиндустрии.
В этом фильме Киану Ривз играет персонажа Нео, который встречает парня по имени Морфеус, метко названного в честь греческого бога снов, и Морфеус дает ему выбор: принять красную или синюю таблетку. И если он примет красную таблетку, то проснется и осознает, что вся его жизнь, включая его работу, здание, в котором он жил, и все остальное было частью этой сложной видеоигры, и он просыпается в мире за пределами игра.
Это базовая версия гипотезы моделирования.
Шон Иллинг
Мы сейчас живем в смоделированной вселенной?
Ризван Вирк
В физике есть множество загадок, которые лучше объясняются с помощью гипотезы моделирования, чем с помощью материальной гипотезы.
Правда в том, что мы многого просто не понимаем в нашей реальности, и я думаю, скорее всего, мы находимся в какой-то смоделированной вселенной. Теперь это гораздо более сложная видеоигра, чем игры, которые мы производим, точно так же, как сегодня World of Warcraft и Fortnite намного сложнее, чем Pac-Man или Space Invaders. Им потребовалось несколько десятков лет, чтобы понять, как моделировать физические объекты с помощью 3D-моделей, а затем как визуализировать их с ограниченной вычислительной мощностью, что в конечном итоге привело к этому потоку общих онлайн-видеоигр.
Им потребовалось несколько десятков лет, чтобы понять, как моделировать физические объекты с помощью 3D-моделей, а затем как визуализировать их с ограниченной вычислительной мощностью, что в конечном итоге привело к этому потоку общих онлайн-видеоигр.
Я думаю, что есть большая вероятность, что мы на самом деле живем в симуляции, хотя мы не можем сказать это со стопроцентной уверенностью. Но есть много свидетельств, указывающих в этом направлении.
Шон Иллинг
Когда вы говорите, что есть аспекты нашего мира, которые имели бы больше смысла, если бы они были частью симуляции, что именно вы имеете в виду?
Ризван Вирк
Ну, есть несколько разных аспектов, один из которых — это та тайна, которую они называют квантовой неопределенностью, то есть идея о том, что частица находится в одном из нескольких состояний, и вы не знаете, что это, пока вы не наблюдаете за частица.
Вероятно, лучше всего понять это можно с помощью ныне печально известного примера кота Шредингера, кота, который, по теории физика Эрвина Шредингера, должен был находиться в коробке с каким-то радиоактивным материалом, и существовал 50-процентный шанс, что кот мертв и 50-процентный шанс, что кошка жива.
Здравый смысл подсказывает нам, что кот уже либо жив, либо мертв. Мы просто не знаем, потому что не заглядывали в коробку. Мы открываем коробку, и нам становится ясно, жив кот или мертв. Но квантовая физика говорит нам, что кошка и жива, и мертва одновременно, пока кто-нибудь не откроет коробку и не понаблюдает за ней. Основное правило заключается в том, что вселенная отображает только то, что необходимо наблюдать.
Шон Иллинг
Какое отношение кот Шрёдингера имеет к видеоигре или компьютерному симулятору?
Ризван Вирк
Вся история разработки видеоигр связана с оптимизацией ограниченных ресурсов. Если бы вы спросили кого-нибудь в 1980-х годах, можете ли вы отрендерить такую игру, как World of Warcraft, которая представляет собой полностью трехмерную или виртуальную игру, они бы ответили: «Нет, на это уйдут все вычислительные мощности мира. Мы не могли визуализировать все эти пиксели в режиме реального времени».
Но со временем появились методы оптимизации. Суть всех этих оптимизаций заключается в том, чтобы «рендерить только то, что наблюдается».
Суть всех этих оптимизаций заключается в том, чтобы «рендерить только то, что наблюдается».
Первой крупной игрой, в которой это удалось, называлась Doom, которая была очень популярна в 1990-х годах. Это был шутер от первого лица, и он мог отображать только световые лучи и объекты, которые хорошо видны с точки зрения виртуальной камеры. Это метод оптимизации, и это одна из вещей, которая напоминает мне видеоигру в физическом мире.
Шон Иллинг
Я собираюсь сделать то, что всегда делают люди, не являющиеся учеными, когда хотят звучать научно и ссылаются на бритву Оккама. Не является ли гипотеза о том, что мы живем в физическом мире из плоти и крови, более простым — и, следовательно, более вероятным — объяснением?
Ризван Вирк
Я назову очень известного физика Джона Уилера. Он был одним из последних физиков, работавших с Альбертом Эйнштейном и многими великими физиками 20-го века. Он сказал, что изначально считалось, что физика занимается изучением физических объектов, что все сводится к частицам. Это то, что часто называют ньютоновской моделью. Но потом мы открыли квантовую физику и поняли, что все вокруг — поле вероятностей, а не физические объекты. Это была вторая волна в карьере Уиллера.
Это то, что часто называют ньютоновской моделью. Но потом мы открыли квантовую физику и поняли, что все вокруг — поле вероятностей, а не физические объекты. Это была вторая волна в карьере Уиллера.
Третьей волной в его карьере было открытие того, что на уровне ядра все является информацией, все основано на битах. Поэтому Уилер придумал известную фразу под названием «это из битов», которая заключается в том, что все, что мы воспринимаем как физическое, на самом деле является результатом битов информации. Он не дожил до появления квантовых компьютеров, но это больше похоже на это.
Итак, я бы сказал, что если мир на самом деле не физический, если он основан на информации, то более простым объяснением может быть то, что мы находимся в симуляции, созданной на основе компьютерных наук и информации.
«Правда в том, что мы многого просто не понимаем в нашей реальности»
Шон Иллинг
Есть ли в принципе способ окончательно доказать, что мы живем в симуляции?
Ризван Вирк
Что ж, есть аргумент оксфордского философа Ника Бострома, который стоит повторить. Он говорит, что если хотя бы одна цивилизация достигла точки создания одной из этих высокоточных симуляций, то они могут создать буквально миллиарды смоделированных цивилизаций, каждая из которых состоит из триллионов существ, потому что все, что вам нужно, — это больше вычислительной мощности.
Он говорит, что если хотя бы одна цивилизация достигла точки создания одной из этих высокоточных симуляций, то они могут создать буквально миллиарды смоделированных цивилизаций, каждая из которых состоит из триллионов существ, потому что все, что вам нужно, — это больше вычислительной мощности.
Итак, он приводит статистический аргумент, что смоделированных существ больше, чем биологических, просто потому, что их так быстро и легко создать. Следовательно, если мы сознательные существа, мы, скорее всего, будем смоделированными существами, а не биологическими. Это больше философский аргумент.
Шон Иллинг
Если бы мы жили в компьютерной программе, я предполагаю, что эта программа состояла бы из правил, и что эти правила могли бы нарушаться или приостанавливаться людьми или существами, запрограммировавшими симуляцию. Но законы нашего физического мира кажутся довольно постоянными, так что не является ли это признаком того, что это может быть не симуляция?
Ризван Вирк
Компьютеры следуют правилам, но тот факт, что правила применяются всегда, не исключает и не исключает того, что мы можем быть частью компьютерной симуляции. Одной из связанных с этим концепций является концепция, называемая вычислительной несводимостью, и это идея о том, что для того, чтобы что-то вычислить, вы не можете просто вычислить это в уравнении; Вы должны фактически пройти через шаги, чтобы выяснить, каким будет конечный результат.
Одной из связанных с этим концепций является концепция, называемая вычислительной несводимостью, и это идея о том, что для того, чтобы что-то вычислить, вы не можете просто вычислить это в уравнении; Вы должны фактически пройти через шаги, чтобы выяснить, каким будет конечный результат.
И это часть раздела математики, называемого теорией хаоса. Есть старая идея, что бабочка машет крыльями в Китае, и это приводит к урагану где-то еще в мире. Чтобы понять это, вы должны пройти и смоделировать каждый шаг пути. Тот факт, что правила кажутся применимыми, не означает, что мы не находимся в симуляции.
На самом деле, это может быть еще одним доказательством того, что мы находимся в симуляции.
Шон Иллинг
Если бы мы жили в такой же убедительной симуляции, как Матрица , была бы какая-то заметная разница между симуляцией и реальностью? Почему в конечном счете имеет значение, был ли наш мир реальным или иллюзорным?
Ризван Вирк
На эту тему ведется много споров. Некоторые из нас не хотели бы знать и предпочли бы принять метафорическую «синюю таблетку», как в 9.0411 Матрица .
Некоторые из нас не хотели бы знать и предпочли бы принять метафорическую «синюю таблетку», как в 9.0411 Матрица .
Вероятно, самый важный вопрос, связанный с этим, заключается в том, являемся ли мы NPC (неигровые персонажи) или PC (игровые персонажи) в видеоигре. Если мы ПК, то это означает, что мы просто играем персонажа в видеоигре жизни, которую я называю Великой Симуляцией. Думаю, многие из нас хотели бы это знать. Мы хотели бы знать параметры игры, в которую мы играем, чтобы мы могли лучше понять ее, лучше ориентироваться в ней.
Если мы NPC или смоделированные персонажи, то я думаю, что это более сложный ответ и более пугающий. Вопрос в том, все ли мы NPC в симуляции, и какова цель этой симуляции? Знание того, что мы находимся в симуляции, а цели симуляции и цели нашего персонажа, я думаю, все равно были бы интересны многим — а теперь мы вернулись к случаю с персонажем-голодеком. от Звездный путь , который обнаруживает, что существует мир «там» (за пределами голодека), в который он не может попасть, и, возможно, некоторые из нас в таком случае предпочли бы не знать.
Шон Иллинг
Насколько мы близки к технологическим возможностям для создания искусственного мира, столь же реалистичного и правдоподобного, как Матрица ?
Ризван Вирк
Я выделяю 10 стадий технологического развития, через которые должна пройти цивилизация, чтобы достичь того, что я называю точкой симуляции, то есть точки, в которой мы можем создать такую гиперреалистичную симуляцию. Мы находимся примерно на пятом этапе, связанном с виртуальной реальностью и дополненной реальностью. Шестой этап посвящен тому, чтобы научиться визуализировать эти вещи без необходимости надевать очки, и тот факт, что 3D-принтеры теперь могут печатать 3D-пиксели объектов, показывает нам, что большинство объектов можно разложить на части как информацию.
Но действительно трудная часть — и об этом мало кто из технологов говорил — находится в Матрице , причина, по которой они думали, что они полностью погружены, заключалась в том, что этот шнур входил в кору головного мозга, и вот где сигнал прозвучал. Этот интерфейс мозг-компьютер — это та область, в которой мы еще не достигли большого прогресса, но мы делаем успехи в этом. Это на ранних стадиях.
Этот интерфейс мозг-компьютер — это та область, в которой мы еще не достигли большого прогресса, но мы делаем успехи в этом. Это на ранних стадиях.
Итак, я предполагаю, что через несколько десятилетий или 100 лет мы достигнем точки симуляции.
Эта статья была впервые опубликована 18 апреля 2019 г.
Подпишитесь на рассылку новостей Future Perfect. Дважды в неделю вы будете получать сводку идей и решений для решения наших самых больших проблем: улучшения здоровья населения, уменьшения страданий людей и животных, уменьшения катастрофических рисков и, проще говоря, улучшения делать добро.
Наша цель в этом месяце
Сейчас не время для платного доступа. Настало время указать на то, что скрыто у всех на виду (например, сотни отрицателей выборов в бюллетенях по всей стране), четко объяснить ответы на вопросы избирателей и дать людям инструменты, необходимые им для активного участия в американской политике. демократия. Подарки читателям помогают сделать наши журналистские статьи, основанные на исследованиях, бесплатными для всех. К концу сентября мы планируем добавить 5000 новых финансовых спонсоров в наше сообщество сторонников Vox. Поможете ли вы нам достичь нашей цели, сделав подарок сегодня?
демократия. Подарки читателям помогают сделать наши журналистские статьи, основанные на исследованиях, бесплатными для всех. К концу сентября мы планируем добавить 5000 новых финансовых спонсоров в наше сообщество сторонников Vox. Поможете ли вы нам достичь нашей цели, сделав подарок сегодня?
| assignments/python_lab1.pdf | 460.87kB | ||
| assignments/python_lab2.pdf | 127.41kB | ||
| assignments/python_lab3.pdf | 136,48 КБ | ||
| задания/python_lab4.pdf | 142,70 КБ | ||
| задания/python_lab5.pdf | 198,5720571 | assignments/python_lab6.pdf | 165.62kB |
| assignments/python_lab7.pdf | 166.02kB | ||
assignments/python_lab8. pdf pdf | 4.82MB | ||
| assignments/python_lab9.pdf | 193.57kB | ||
| задания/README.txt | 0.27kB | ||
| лекции/уроки/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 8.0 Как отправлять задания.mp4 | 9,20 МБ | ||
| лекций в неделю0-функция-и-поле/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 0.0 Введение в курс, часть 1 (953).mp4 | 130,04 МБ | 1 лекций /week0-the-function-and-the-field/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 0.1 Введение в курс, часть 2 (849).mp4 | 90.84MB |
| лекций/week0-the-function-and- the-field/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 0.2 Функция Функция и другие предварительные сведения (2055).mp4 | 148. 30MB 30MB | ||
| лекций/неделя0-функция-и-поле/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 0.3 Поле Введение в комплексные числа (552).mp4 | 36.54MB | ||
| лекций/неделя0-функция-и-поле/Кодирование матричной линейной алгебры с помощью компьютерных приложений 0.4 The Field Playing with C (1519).mp4 | 92.15MB | ||
| лекций/неделя0-the-function -и-поле/Кодирование матричной линейной алгебры с помощью компьютерных приложений 0.5 Поле, играющее с GF(2) (1028).mp4 | 71.38MB | ||
| лекций/неделя1-the-vector/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 1.0 Вектор -vector/Кодирование матричной линейной алгебры с помощью компьютерных приложений 1.1 Вектор Сложение векторов и умножение скалярных векторов (1016).mp4 | 63.58MB | ||
лекций/неделя1-the-vector/Кодирование матричной линейной алгебры с помощью компьютера Научные приложения 1.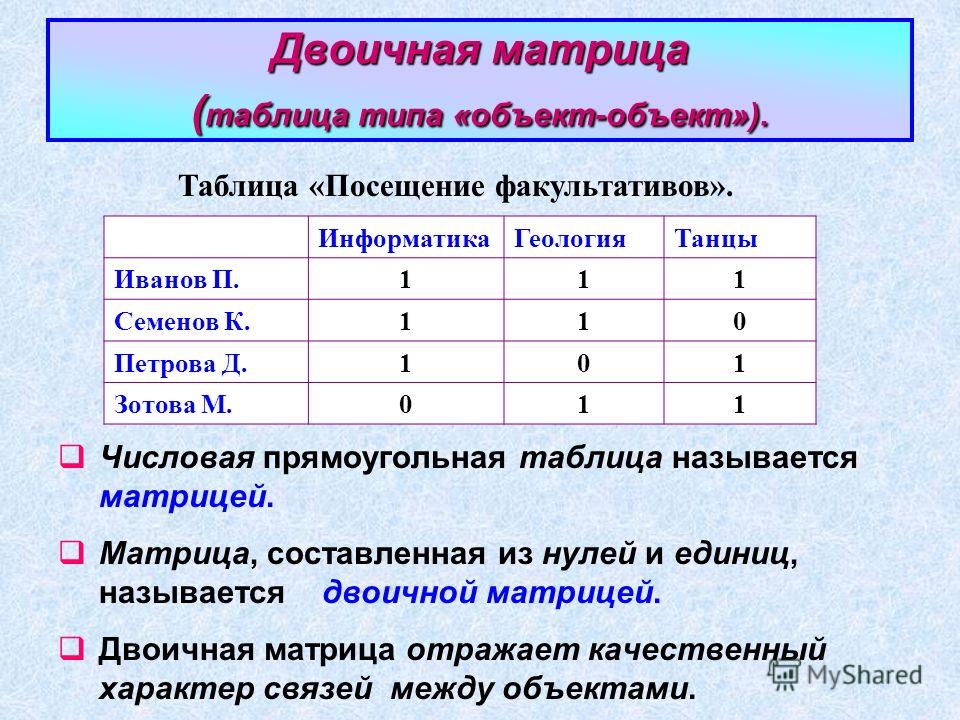 2 Представления векторов на основе векторного словаря (910) 2 Представления векторов на основе векторного словаря (910) | лекций/неделя1-the-vector/Кодирование матричной линейной алгебры с помощью компьютерных приложений 1.4 The Vector Dot-product (849).mp4 | 54.09MB | |
| лекций/неделя1-the-vector/Кодирование матричной линейной алгебры через приложения компьютерных наук 1.5 Векторное скалярное произведение векторов над GF(2) (444).mp4 | 13,55 МБ | ||
| лекций/неделя1-the-vector/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 1.6 Вектор Решение треугольной системы линейных уравнений (400).mp4 | 10,02 МБ | лекций/ | |
| 29.36MB | |||
лекций/week2-the-vector-space/Кодирование матричной линейной алгебры с помощью компьютера Научные приложения 2. 1 The Vector Space Span.mp4 1 The Vector Space Span.mp4 | 22.53MB | ||
| лекций/неделя2-the-vector-space/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 2.2 Геометрия векторного пространства наборов векторов.mp4 | 80.21MB | 1 лекций the-vector-space/Кодирование матричной линейной алгебры с помощью приложений информатики 2.3 Векторное пространство 2.4 Функция контрольной суммы векторного пространства.mp4 | 10.35MB |
| лекций/неделя3-the-matrix/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 3.0 Матрица Кодирование матричной линейной алгебры с помощью приложений информатики 3.1 Матрица Матрица-вектор и умножение вектор-матрицы.mp4 | 33.58MB | ||
лекций/неделя3-the-matrix/Кодирование матричной линейной алгебры с помощью приложений информатики 3.2 Матрица Умножение матрицы на вектор в терминах скалярных произведений. mp4 mp4 | 32,95 МБ | ||
| лекций/неделя3-the-matrix/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 3.3 Матрица Null space.mp4 | 11,17 МБ | ||
| 14.43MB | |||
| лекций/неделя3-the-matrix/Кодирование матричной линейной алгебры с помощью приложений информатики 3.5 Матрица Матрицы и их функции.mp4 | 59.52 МБ | ||
| лекций/неделя3-the-matrix/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 3.6 Матричные линейные функции.mp4 | 89.87MB | ||
| 70.58MB | |||
лекций/неделя3-the-matrix/Кодирование матричной линейной алгебры с помощью компьютерных приложений 3. 8 Матрица Матричное умножение матриц и функция композиция.mp4 8 Матрица Матричное умножение матриц и функция композиция.mp4 | 19.35MB | ||
| лекций/неделя3-the-matrix/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 3.9 The Matrix Matrix inverse.mp4 | 77.70MB | ||
| 10.91MB | |||
| лекций/неделя4-the-basis/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 4.1 Основа Сжатие с потерями.mp4 | 11.46MB | ||
| лекций/неделя4-the-basis/Кодирование матричной линейной алгебры с помощью компьютерных приложений 4.10 The Basis The Exchange Lemma.mp4 | 28.07MB | 1 | |
75. 45MB 45MB | |||
| лекций/неделя4-the-basis/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 4.4 Базисная линейная зависимость.mp4 | 107.27MB | ||
| -техкурс лекций Матричная линейная алгебра с помощью приложений компьютерных наук 4.5 The Basis Basis.mp4 | 24.20MB | ||
| лекций/неделя4-the-basis/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 4.6 The Basis Уникальное представление.mp4 | 7,18 МБ | ||
| лекций/неделя4-the-basis/Кодирование матричной линейной алгебры с помощью приложений компьютерных наук 4.7 Изменение основы.mp4 | 14,49 МБ | ||
| 32.91MB | |||
 | |||
КС 6210
CS 6210: Матричные вычисления
Корнельский университет, осень 2020 г.
Режим обучения: онлайн, синхронные лекции.
Лекции: 10:20–11:10 MWF, виртуальные в увеличении.
Преподаватель: Остин Бенсон, доцент компьютерных наук ([email protected]).
Часы работы: с 16:00 до 17:00 по средам или по предварительной записи, виртуально в Zoom.
TA: Джон Пол Райан, аспирант компьютерных наук ([email protected]).
Часы работы: с 12:00 до 13:00 по четвергам, виртуально в Zoom.
CLASS ZOOM ССЫЛКИ ЗДЕСЬ
Темы курса: прямые и итерационные алгоритмы для вычисления решений квадратичных линейных систем, наименьших квадратов и задач на собственные значения; матричные факторизации, такие как QR, LU и SVD; анализ стабильности и ошибок; методы подпространств Крылова; специальные соображения для разреженных матриц.
Ресурсы
Администрация курса:
- CMS для управления курсовой работой.

- Piazza для вопросов и ответов.
- Записные книжки Jupyter и данные для демонстраций занятий.
Рекомендуемый материал для чтения:
- [GVL] Матричные вычисления. Г. Х. Голуб и К. Ф. Ван Лоан.
- [ТБ] Численная линейная алгебра. Л. Н. Трефетен и Д. Бау III. Доступно онлайн на портале навыков Корнелла (прямой ссылки нет, нужно искать).
- [D] Прикладная числовая линейная алгебра. Дж. В. Деммель. Доступно в Интернете по подписке Cornell SIAM.
- [B] Осенний курс 6210 профессора Дэвида Биндела 2019 года.
Другой полезный материал:
- Точность и устойчивость численных алгоритмов. Н. Дж. Хайэм. Доступно в Интернете по подписке Cornell SIAM.
- Заметки по курсу профессора Майкла Сондера (Лекция 1 для справочной информации; Лекции 4+5 для итерационных методов).
- Итерационные методы решения линейных систем. А. Гринбаум. Доступно в Интернете по подписке Cornell SIAM.

- Итерационные методы для линейных систем. Ю. Саад. Доступно в Интернете на веб-сайте профессора Саада.
- Предложение Prof. Anil Damle Fall 2018 из 6210 штук.
- Документация по языку Julia для линейная алгебра, разреженные массивы и итерационные решатели.
Расписание домашних заданий
- Домашнее задание 1 до пятницы, 18 сентября, в 10:19 по восточному времени (до занятий) [источник]
- Домашнее задание 2 до пт 2 окт в 10:19утра по восточному времени (перед уроком) [источник]
- Домашнее задание 3 до пятницы, 16 октября, в 10:19 по восточному времени (до занятий) [источник]
- Домашнее задание 4 до пятницы, 30 октября, в 10:19 по восточному времени (до занятий) [источник]
- Домашнее задание 5 до пятницы, 13 ноября, в 10:19 по восточному времени (до занятий) [источник]
- Домашнее задание 6 до пятницы, 4 декабря, в 10:19 по восточному времени (до занятий) [источник]
- Домашнее задание 7 до ср 16 дек в 10:19утра по восточному времени (перед уроком) [источник]
Расписание лекций
Примечание: данное расписание является предварительным и может быть изменено.
Лекция 1 (W 9/2): введение, умножение матриц
Материалы для чтения: TB 1; Д 1.1–1.3.
[заметки]
[видео]
Лекция 2 (F 9/4): умножение матриц на ЭВМ, ранг, структурированные матрицы
Чтение: ТБ 1; Б 30 августа, 04 сентября.
[заметки]
[видео]
[демо]
Лекция 3 (М 9/7): нормы
Чтение: ТБ 2–3; ГВЛ 2.
[заметки]
[видео]
Лекция 4 (З 9/9): СВД
Литература: ТБ 4–5; ГВЛ 2.4.
[заметки]
[видео]
[демо]
Лекция 5 (F 9/11): чувствительность и кондиционирование
Показания: TB 12; Д 1.3.
[заметки]
[видео]
[демо]
Лекция 6 (M 9/14): с плавающей запятой
Показания: D 1,5; Б 13 сент.
[заметки]
[видео]
[демо]
Лекция 7 (W 9/16): стабильность
Литература: ТБ 14–15.
[заметки]
[видео]
Лекция 8 (F 9/18): начать исключение Гаусса и LU
Показания: TB 20. [заметки]
[видео]
[заметки]
[видео]
Лекция 9 (М 9/21): поворот и блокировка
Показания: ТБ 21; Д 2.4.
[заметки]
[видео]
Лекция 10 (W 9/23): анализ ошибок
Показания: TB 22; Д 2.4.
[заметки]
[видео]
Лекция 11 (F 9/25): разреженный прямой
Чтение: D 2.7.4; Б 30 сент.
[заметки]
[видео]
[демо]
Лекция 12 (М 9/28): структурированные системы и Холецкий
Литература: ТБ 23; Б 27 сент.
[заметки]
Лекция 13 (W 9/30): наименьшие квадраты
Чтение: ТБ 11.
[заметки]
[видео]
Лекция 14 (Ф 10/2): проекторы и Грам-Шмидт
Литература: ТБ 6–8.
[заметки]
[видео]
Лекция 15 (M 10/5): Домохозяин и Гивенс
Чтение: TB 10; Д 3.4.
[заметки]
[видео]
Лекция 16 (W 10/7): чувствительность методом наименьших квадратов и формирование условий
Показания: D 3.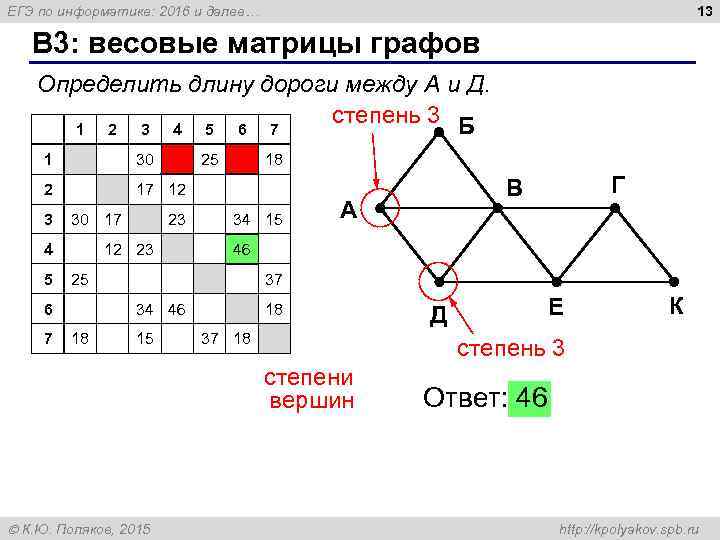 3–3.4; Б 9 окт.
[заметки]
[видео]
3–3.4; Б 9 окт.
[заметки]
[видео]
Лекция 17 (F 10/9): стабильность Хаусхолдера; управление плохим состоянием
Показания: Д 3,4–3,5; Б 16 окт.
[заметки]
[видео]
Лекция 18 (M 10/12): статистические интерпретации
Чтение: B 16 окт.
[заметки]
[видео]
[демо]
Осенний перерыв (W 10/14): без лекций
Лекция 19 (F 10/16): стартовые задачи на собственные значения
Чтение: TB 24–25; ГВЛ 7.
[заметки]
[видео]
Лекция 20 (М 10/19): степенной метод и обратная итерация, форма Хессенберга
Литература: ТБ 26–27; ГВЛ 7.
[заметки]
[видео]
Лекция 21 (W 10/21): подпространственная/ортогональная итерация и итерация QR
Чтение: TB 28; ГВЛ 7.
[заметки]
[видео]
Лекция 22 (F 10/23): смещенная итерация QR
Чтения: TB 28–29; ГВЛ 7.
[заметки]
[видео]
Лекция 23 (M 10/26): смещенная итерация QR, начало симметричных задач на собственные значения
Показания: ТБ 29; ГВЛ 7. [заметки]
[видео]
[заметки]
[видео]
Лекция 24 (W 10/28): повторение старых решателей, а также некоторых новых
Литература: TB 25–30.
[заметки]
[видео]
Лекция 25 (Ф 10/30): вычисление СВД, теория возмущений собственных значений
Чтение: ТБ 31; Д 5.2.
[заметки]
[видео]
[демо]
Лекция 26 (М 11/2): больше теории возмущений
Чтение: D 4.3, 5.2.
[заметки]
[видео]
Лекция 27 (W 11/4): запуск итерационных методов
Материалы для чтения: D 6.1, 6.4.
[заметки]
[видео]
[демо]
Лекция 28 (Ф 11/6): стационарные итерационные методы
Литература: Д 6.5.
[заметки]
[видео]
Нет класса М 11/9 (путешествия)
Лекция 29 (W 11/11): Крыловские подпространства введение, Арнольди, Ланцош 3 ТБ, 2 с 3 ТБ, Чтение 9:3 05 [заметки] [видео]
Лекция 30 (F 11/13): CG через Lanczos
Литература: TB 36, 38. [заметки]
[видео]
[заметки]
[видео]
Без занятий (полуфинальные учебные дни).
Неделя 13Без занятий (полуфиналы + перерыв на День Благодарения).
Неделя 14 Лекция 31 (М 11/30): Анализ ошибок КГ
Показания: ТБ 38.
[заметки]
[видео]
Лекция 32 (W 12/2): CG как градиентный метод
Показания: ТБ 38; ГВЛ 11.3.
[заметки]
[видео]
Лекция 33 (Ф 12/4): МИНРЕС
Чтение: ГВЛ 11.4; Заметки Майкла Сондера.
[заметки]
[видео]
Лекция 34 (М 12/7): GMRES и предварительное кондиционирование
Чтение: ТБ 35, 40.
[заметки]
[видео]
[демо]
Лекция 35 (W 12/9): LSQR и LSMR
Чтение: TB 39; Заметки Майкла Сондера.
[заметки]
[видео]
Лекция 36 (F 12/11): Итерационные решатели для собственных задач
Литература: ТБ 34. [заметки]
[видео]
[заметки]
[видео]
Лекция 37 (М 12/14): Тензорные разложения низкого ранга
Чтение: ГВЛ 12.5.
[заметки]
[видео]
[демо]
Лекция 38 (W 12/16): обзор/подведение итогов/будущее
Чтение: ГВЛ; ТБ; Д; Б.
[заметки]
[видео]
Курсовая работа
Курсовая работа будет управляться через CMS, а задания отправляться на нее. Обязательная курсовая работа состоит из трех компонентов:
- Домашние задания (70%).
Будет семь домашних заданий с теоретической и/или компоненты кодирования. Каждый оценивается в 10% от вашей оценки. - Итоговый экзамен (25%).
Будет проведен выпускной экзамен на дом, формат которого аналогичен предыдущим предложениям 6210. Это составляет 25% вашей оценки. Промежуточных и полуфинальных матчей нет. - Участие (5%).
Приходить на занятия, задавать вопросы, приходить в рабочее время, предоставление отзывов, участие в Piazza и другие мероприятия вместе с курсом будет засчитываться для участия.



 Таким образом будет проще определить границы адресации второго массива. Пример указан на иллюстрации ниже.
Таким образом будет проще определить границы адресации второго массива. Пример указан на иллюстрации ниже. В
ядро самых сложных алгоритмов целочисленного факторинга
— простая задача линейной алгебры.
В
ядро самых сложных алгоритмов целочисленного факторинга
— простая задача линейной алгебры. вейвлет-преобразование и преобразование Фурье.
вейвлет-преобразование и преобразование Фурье. 


