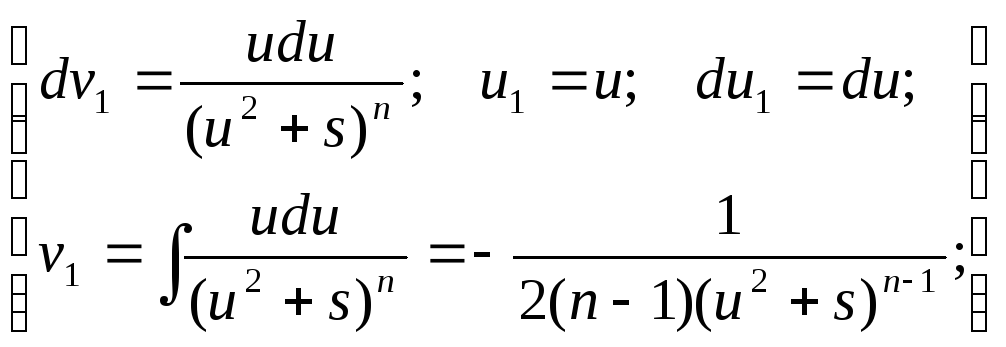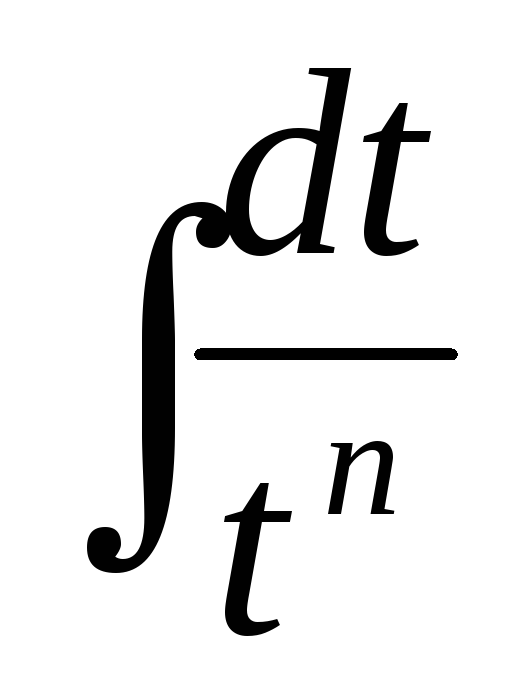Интеграл для чайников: Как решать неопределенные интегралы. Гайд для чайников — Офтоп на DTF

Как решать неопределенные интегралы. Гайд для чайников — Офтоп на DTF

Матан — самое сильное колдунство на сегодняшний день.

Лурк

3182 просмотров

Мы остались с ним в пустом классе и он медленно начал объяснять мне, как правильно брать разные интегралы разными способами. И вот уже в конце нашего первого занятия он предложил мне взять мой первый в жизни интеграл. Но как только я его увидела, я жутко испугалась и убежала.

Сайт МИФИ

Два математика в ресторане поспорили, насколько хорошо знают математику большинство людей. Один (пессимист) утверждал, что большинство ее вообще не знает, а другой (оптимист) — что хоть и не много, но знают. Когда пессимист отошел в туалет, оптимист подозвал симпатичную официантку-блондинку и говорит:

— Когда мой коллега вернется, я задам вам вопрос. Суть не важна.

Все, что вы должны сделать — это сказать “Треть икс куб”.

2 по dх?

— Треть икс куб… – отвечает официантка.

Пессимист сильно удивляется, на что официантка добавляет:

— А хули ты удивляешься, блять? Училась по гайдам с ДТФ.

Все очень просто. Глядим на эту картинку:

Да, это скриншот с Word. Криворукие программисты сайта дтф за десять лет так и не прикрутили поддержку формул в постах.

Слева от знака равно находится то, что тебе дано изначально. Функция1 – это функция, зависящая от х. Функция2 – это то, что тебе нужно получить из функции1 путем математических манипуляций. Получил? Молодец, даже инспектор Гаджет не справился бы лучше. Теперь прибавь к этому буковку “С” и ответ готов. Тебе не нужно знать, что такое dx, что такое С и вообще теорию интегралов, тебе достаточно знать правила преобразования функции1 в функцию2, чтобы получить 2 на контрольной. И в этом посте я дам тебе такие правила.

Теперь смотрим на эту картинку:

Хочешь стать самым крутым? Придется выучить эту срань. 2 по dх?

— Треть икс куб… – отвечает официантка.

Пессимист сильно удивлен, оптимист довольно улыбается.

Когда официантка приносит счёт, вмешивается пессимист:

— Дамочка, а чему равно число пи?

Официантка подумала немного и выдала:

— Дор?

Готов к потере интегральной девственности? Вот первый пример:

Такое даже Буратино может решить в уме.

Запоминаем:

• Интеграл от суммы (разности) равен сумме (разности) интегралов.
• Если перед подынтегральной функцией стоит константа, то ее можно вынести за знак интеграла.

Применяя оба правила на практике получаем:

Распад исходного интеграла на более мелкие является крупнейшей геоматематической катастрофой этого блога.

Для решения первых двух интегралов используем пункт 3 из таблицы. Вместо n нужно подставить соответствующие значения (n=2 для первого случая, n=1 для второго).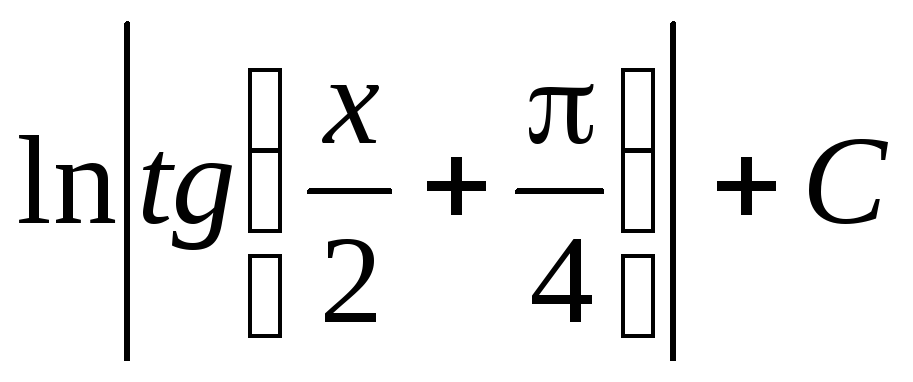

Для третьего интеграла – пункт 2 из таблицы. И получается вот что:

Кто-то может сказать, что у нас сумма 3 разных интегралов, а, соответственно, сумма трех разных С. Но С – это любое число, а сумма трех любых чисел дает любое число.

Содержание скрыто

Показать

Два дагестанских математика в ресторане поспорили, насколько хорошо знают математику большинство людей. Далее события развивались с утомительной неизбежностью.

Как привлечь внимание дурака? Читай дальше.

Сейчас мы этот интеграл почленно делить будем. Вот:

По статистике, 85% аудитории Доты 2 не поняло, что произошло.

Ну первый интеграл ты знаешь как решать, если не анимешник. Второй интеграл – табличный, пункт 4. А теперь самостоятельная работа. Закончи пример и дай ответ.

Молодец, что не забыл С. Идем дальше.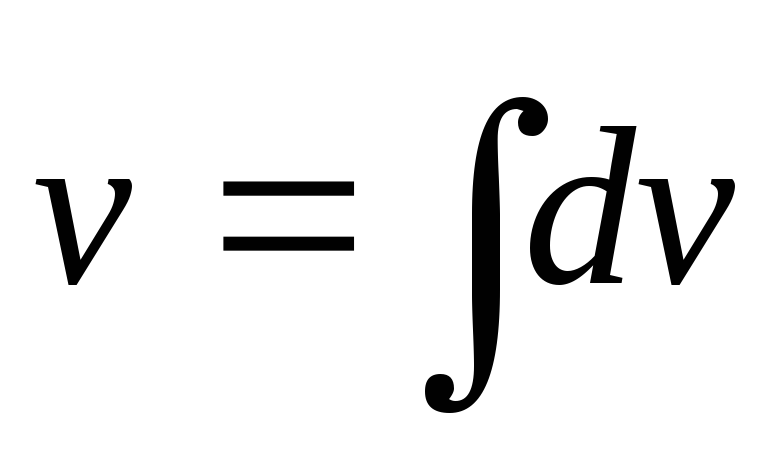 2 по dх?

— Не знаю, не разбираюсь в этом, да и оно мне, собственно, до пизды, — отвечает официантка.

Изучим решение интегралов по частям (по-Питерски).

Нижняя строчка означает, что u и v – это какие-то функции от х.

Применять данный метод надо, когда у нас произведение двух разных функций под интегралом. Пример:

U это х, а dv это sin(x)dx. Теперь нужно найти du и v, чтобы у нас были все элементы формулы. Раз u=x, то du=dx. Если dv=sin(x)dx, то v=-cos(x) (это я небольшой интегральчик взял). Подставляем в формулу выше:

Ну интеграл от косинуса ты знаешь где искать. Окончательный ответ:

Готов к полному пиздецу?

Полный пиздец как он есть.

Применим метод, который в нашей семье передается из поколения в поколение – метод неопределенных коэффициентов. Бачим сюда:

Ловко, да? Все, что нам нужно – это найти эти а, б и с. Дальше интеграл распадется на три табличных.

Это мы коммунистическим путем привели левую часть к общему знаменателю.

Теперь можно и сократить знаменатели.

Надо раскрыть скобки.

Ну тут даже камню понятно, что: а+б+с=1; 5а+2б+с=-19; 6а-3б-2с=6. Решается оно так:

Ну а теперь:

Глядим на пункт 4 в таблице и получаем (если что dx и d(x+3) это одно и тоже):

Модуль ставить обязательно. Ты же помнишь, что функция под логарифмом всегда должна быть больше нуля?

Вот и все. Полученных знаний тебе хватит, чтобы не обосраться на первой контрольной и слегка обосраться на второй.

как решать, правила вычисления, объяснение. Основные свойства определенного интеграла

Словари. Энциклопедии. История. Литература. Русский язык » Литература » Определенные и неопределенные интегралы сообщение. Интегралы для чайников: как решать, правила вычисления, объяснение. Основные свойства определенного интеграла

Решение интегралов – задача легкая, но только для избранных.

Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Изучаем понятие « интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились

Ньютон и Лейбниц , но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных , необходимые и для понимания интегралов, уже есть у нас в блоге.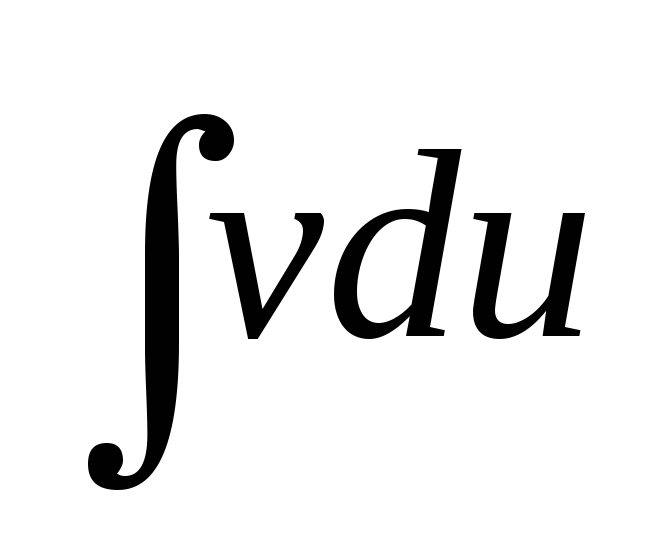

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции

f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами.

Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

« Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

В этой статье мы перечислим основные свойства определенного интеграла. Большинство этих свойств доказываются на основе понятий определенного интеграла Римана и Дарбу .

Вычисление определенного интеграла очень часто проводится с использованием первых пяти свойств, так что мы будем при надобности на них ссылаться. Остальные свойства определенного интеграла, в основном, применяются для оценки различных выражений.

Прежде чем перейти к основным свойствам определенного интеграла , условимся, что a не превосходит b .

Для функции y = f(x) , определенной при x = a , справедливо равенство .

То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма для любого разбиения промежутка и любого выбора точек равна нулю, так как , следовательно, пределом интегральных сумм является ноль.

Для интегрируемой на отрезке функции выполняется .

Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b .

для интегрируемых на отрезке функций y = f(x) и y = g(x) .

Доказательство.

Запишем интегральную сумму функции для данного разбиения отрезка и данного выбора точек :

где и – интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.

Переходя к пределу при получим , что по определению интеграла Римана равносильно утверждению доказываемого свойства.

Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке функции y = f(x) и произвольного числа k справедливо равенство .

Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:


Пусть функция y = f(x) интегрируема на интервале X , причем и , тогда .

Это свойство справедливо как для , так и для или .

Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.

Если функция интегрируема на отрезке , то она интегрируема и на любом внутреннем отрезке .

Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.

Если функция y = f(x) интегрируема на отрезке и для любого значения аргумента , то .

Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек при будет неотрицательной (не положительной).

Следствие.

Для интегрируемых на отрезке функций y = f(x) и y = g(x) справедливы неравенства:


Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.

Пусть функция y = f(x) интегрируема на отрезке , тогда справедливо неравенство .

Доказательство.

Очевидно, что . В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо . Это двойное неравенство можно записать как .

Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке и для любого значения аргумента , тогда , где и .

Доказательство проводится аналогично. Так как m и M – наименьшее и наибольшее значение функции y = f(x) на отрезке , то .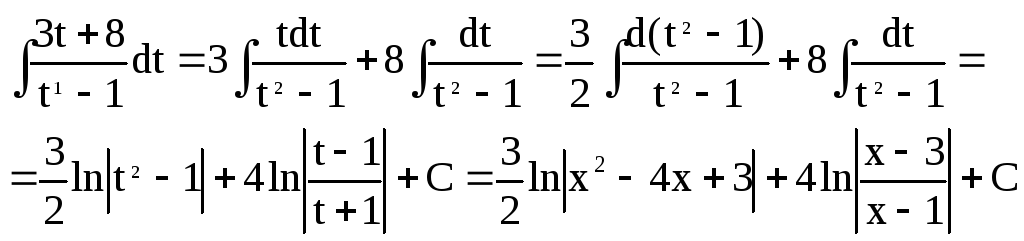 Домножение двойного неравенства на неотрицательную функцию y = g(x) приводит нас к следующему двойному неравенству . Интегрируя его на отрезке , придем к доказываемому утверждению.

Следствие.

Если взять g(x) = 1 , то неравенство примет вид .

Первая формула среднего значения.

Пусть функция y = f(x) интегрируема на отрезке , и , тогда существует такое число , что .

Следствие.

Если функция y = f(x) непрерывна на отрезке , то найдется такое число , что .

Первая формула среднего значения в обобщенной форме.

Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке , и , а g(x) > 0 для любого значения аргумента . Тогда существует такое число , что .

Вторая формула среднего значения.

Если на отрезке функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число , что справедливо равенство .

Данные свойства используются для осуществления преобразований интеграла с целью его приведения к одному из элементарных интегралов и дальнейшему вычислению.

1. Производная неопределенного интеграла равна подынтегральной функции:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

4. Постоянный множитель можно выносить за знак интеграла:

Причем a ≠ 0

5. Интеграл суммы (разности) равен сумме (разности) интегралов:

6. Свойство является комбинацией свойств 4 и 5:

Причем a ≠ 0 ˄ b ≠ 0

7. Свойство инвариантности неопределенного интеграла:

Если , то

8. Свойство:

Если , то

Фактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной , который более подробно рассмотрен в следующем разделе.

Рассмотрим пример:

Сначала мы применили свойство 5, затем свойство 4, затем воспользовались таблицей первообразных и получили результат.

Алгоритм нашего онлайн калькулятора интегралов поддерживает все перечисленные выше свойства и без труда найдет подробное решение для вашего интеграла.

Данные свойства используются для осуществления преобразований интеграла с целью его приведения к одному из элементарных интегралов и дальнейшему вычислению.

1. Производная неопределенного интеграла равна подынтегральной функции:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

4. Постоянный множитель можно выносить за знак интеграла:

Причем a ≠ 0

5. Интеграл суммы (разности) равен сумме (разности) интегралов:

6. Свойство является комбинацией свойств 4 и 5:

Причем a ≠ 0 ˄ b ≠ 0

7. Свойство инвариантности неопределенного интеграла:

Если , то

8. Свойство:

Если , то

Фактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной , который более подробно рассмотрен в следующем разделе.

Рассмотрим пример:

Сначала мы применили свойство 5, затем свойство 4, затем воспользовались таблицей первообразных и получили результат.

Алгоритм нашего онлайн калькулятора интегралов поддерживает все перечисленные выше свойства и без труда найдет подробное решение для вашего интеграла.

В дифференциальном исчислении решается задача:под анной функции ƒ(х) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F ” (x)=ƒ(х) (или дифференциал). Искомую функцию F(x) называют первообразной функции ƒ(х) .

Функция F(x) называетсяпервообразной функции ƒ(х) на интервале (а; b), если для любого х є (а;b) выполняется равенство

F ” (x)=ƒ(x) (или dF(x)=ƒ(x)dx).

Например , первообразной функции у=х 2 , х є R, является функция, так как

Очевидно, что первообразными Будут также любые функции

где С – постоянная, поскольку

Tеоpeмa 29. 1. Если функция F(x) является первообразной функции ƒ(х) на (а;b), то множество всех первообразных для ƒ(х) задается формулой F(x)+С, где С – постоянное число.

▲ Функция F(x)+С является первообразной ƒ(х).

Действительно, (F(x)+C) ” =F ” (x)=ƒ(x).

Пусть Ф(х) – некоторая другая, отличная от F(x), первообразная функции ƒ(х) , т. е. Ф ” (x)=ƒ(х). Тогда для любого х є (а;b) имеем

А это означает (см. следствие 25. 1), что

где С – постоянное число. Следовательно, Ф(х)=F(x)+С.▼

Множество всех пepвoобpaзныx функций F(x)+С для ƒ(х) называетсянеопределенным интегралом от функции ƒ(х) и обозначается символом∫ ƒ(х) dx.

Таким образом, по определению

∫ ƒ(x)dx= F(x)+C.

Здесь ƒ(х) называетсяподынтегральнoй функцией , ƒ(x)dx — подынтегральным выражением, х –переменной интегрирования , ∫ –знаком неопределенного интеграла .

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у=F(x)+C (каждому числовому значению С соответствует определенная кривая семейства) (см.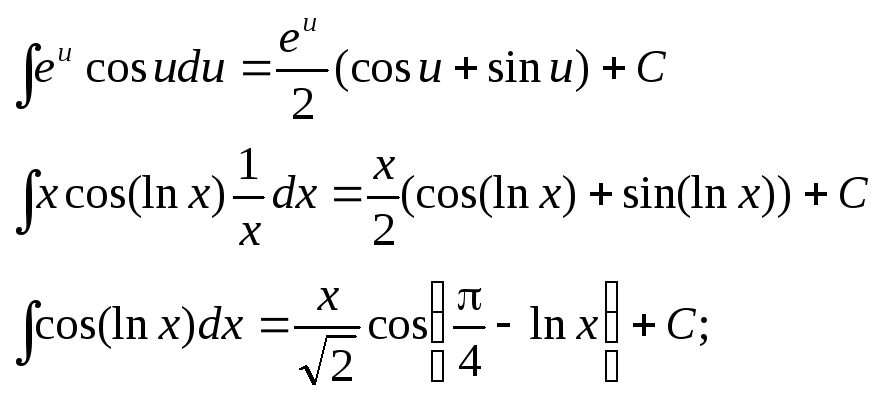 рис. 166). График каждой первообразной (кривой) называетсяинтегральной кривой .

Для всякой ли функции существует неопределенный интеграл?

Имеет место теорема, утверждающая, что «всякая непрерывная на (а;b) функция имеет на этом промежутке первообразную», а следoвaтельно, и неопределенный интеграл.

Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:

d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) ” =ƒ(х).

Дeйcтвительнo, d(∫ ƒ(х) dx)=d(F(x)+С)=dF(x)+d(C)=F ” (x) dx =ƒ(х) dx

(∫ ƒ (x) dx) ” =(F(x)+C)”=F”(x)+0 =ƒ (x).

Блaгoдapя этому свойству правильность интегрирования проверяется дифференцированием. Например, равенство

∫(3x 2 + 4) dx=х з +4х+С

верно, так как (х 3 +4х+С)”=3x 2 +4.

2. Hеопpедeлeнный интеграл от диффepeнциaла некоторой функции равен сумме этой функции и произвольной постоянной:

∫dF(x)= F(x)+C.

Действительно,

3. Постоянный множитель можно выносить за знак интеграла:

α ≠ 0 – постоянная.

Действительно,

(положили С 1 /а=С.)

4. Неопределенный интеграл от aлгeбpaическoй суммы конечного числа непрерывных функций равен aлгебpaичecкoй сумме интегралов от слагаемых функций:

Пусть F”(x)=ƒ(х) и G”(x)=g(x). Тогда

где С 1 ±С 2 =С.

5. (Инвариантность формулы интегрирования).

Если, где u=φ(х) – произвольная функция, имеющая непрерывную производную.

▲ Пусть х – независимая переменная, ƒ(х) – непрерывная функция и F(x) – ее пepвoобpaзнaя. Тогда

Положим теперь u=ф(х), где ф(х) – непрерывно-дифференцируемая функция. Рассмотрим сложную функцию F(u)=F(φ(x)). В силу инвараинтности формы первого дифференциала функции (см. с. 160) имеем

Отсюда▼

Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.

Так, из формулыпутем замены х на u (u=φ(х))получаем

В частности,

Пример 29.1. Найти интеграл

где С=C1+С 2 +С 3 +С 4 .

Пример 29.2. Найти интеграл Решение:

• 29.3. Таблица основных неопределенных интегралов

Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул диффepeнциaльнoгo исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла.

Например , так как

d(sin u)=cos u . du,

Вывод ряда формул таблицы будет дан при рассмотрении основных методов интегрирования.

Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения пepвoобpaзных (т. е. интегрирования функции) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать.

Отметим, что в таблице основных интегралов переменная интегрирования и может обозначать как независимую переменную, так и функцию от независимой переменной (coгласнo свойству инвариантности формулы интeгpиpoвания).

В справедливости приведенных ниже формул можно убедиться, взяв диффepeнциaл правой части, который будет равен подынтегральному выражению в левой части формулы.

Докажем, например, справедливость формулы 2. Функция 1/u определена и непрерывна для всех значений и, отличных от нуля.

Если u > 0, то ln|u|=lnu, тогда Поэтому

Eсли u Значит

Итак, формула 2 верна. Aнaлoгичнo, провepим формулу 15:

Таблица оснoвныx интегралов

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Определение определенного интеграла и принцип его работы

Вы можете аппроксимировать площадь под кривой, складывая правый, левый прямоугольники или прямоугольники со средней точкой. Чтобы найти точную площадь, нужно использовать определенный интеграл.

Когда вы аппроксимируете площадь под кривой, вершины прямоугольников образуют форму зуба пилы, которая не идеально подходит для функции плавного изгиба. Итак, чтобы найти точных площадей под кривой с использованием прямоугольников, вам нужно найти площадь бесконечного числа бесконечно тонких прямоугольников, чьи «вершины» идеально соответствуют кривой. На самом деле вы не можете использовать бесконечное количество прямоугольников, но с фантастическим изобретением пределов примерно так и происходит.

Вот «простое» определение определенного интеграла, которое используется для вычисления точных площадей. Он основан на пределе суммы Римана правильных прямоугольников. Точная площадь под кривой между a и b определяется определенным интегралом , который определяется следующим образом:

При вычислении приблизительной или точной площади под кривой все три суммы — левая, правая и середина — называются суммами Римана в честь великого немецкого математика Г. Ф. Б. Римана (1826–1866). По сути, любая сумма, составленная из прямоугольников, является суммой Римана, включая странные суммы, состоящие из прямоугольников неравной ширины.

Используя эту формулу, вот точная площадь под x ² + 1 между 0 и 3:

Этот результат довольно удивителен, если подумать. Используя предельный процесс, вы получаете точный ответ из 12 — что вроде как 12,00000000… с точностью до бесконечного числа знаков после запятой — для области под гладкой кривой функцией, x ² + 1, на основе областей прямоугольников с плоской вершиной, которые проходят вдоль кривой неровным пилообразным образом.

Нахождение точной площади числа 12 с помощью предела суммы Римана требует большой работы. Этот сложный метод интегрирования сравним с трудным определением производной с использованием формального определения, основанного на разностном коэффициенте. И подобно тому, как вы используете разностное частное для нахождения производной, вы не будете использовать предел суммы Римана для вычисления площади, как только вы изучите более быстрый метод нахождения площади.

Вы только что отработали область под x ² + 1, используя формулу суммы правильных прямоугольников. (Кстати, если вы собираетесь вычислять площадь сложным способом, используя предел суммы Римана, вы также можете всегда использовать правильные прямоугольники; это, вероятно, самый простой способ). Однако оказывается, что вы могли бы использовать левые прямоугольники или прямоугольники со средней точкой. На самом деле, вы могли бы использовать сочетание разных типов прямоугольников (не пытайтесь повторить это дома). Независимо от того, какой тип прямоугольников вы используете, предел всегда будет одинаковым.

Это подводит вас к следующей совершенно экстремальной, грязной интеграции, которая принимает во внимание все эти возможности. Вы, вероятно, никогда не будете использовать следующее определение определенного интеграла. Так почему вы должны этому учиться? Хороший вопрос. Как насчет красоты чистой математики? Или, если вы не купитесь на это и вас интересует только практическая причина, едва ли не единственная практическая мотивация для изучения этого определения заключается в том, что оно может быть на экзамене.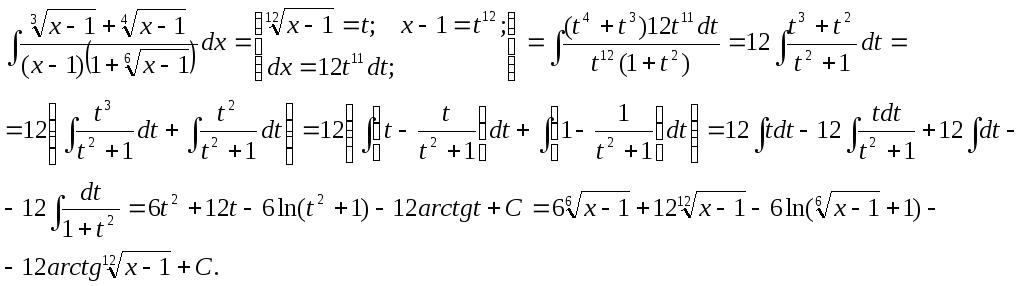

Определенный интеграл (реальное определение Маккоя):

Эту статью можно найти в категории:

• Исчисление,

Интеграция данных для чайников

Перейти к основному содержанию

Авторское право © 2000-2015 принадлежит John Wiley & Sons, Inc. или связанным с ней компаниям.

Киран Кодитхала

Киран Кодитхала

Генеральный директор и предприниматель стремится трансформировать технологические вертикали, органично интегрируя их

Опубликовано 16 февраля 2016 г.

+ Подписаться

…ссылка для “99% из нас”, которые борются с интеграцией данных…

Нужна ли интеграция SaaS?

 

Итак, в чем проблема?

Интеграция данных — сложный бизнес

Существует несколько платформ интеграции данных, промежуточных платформ и других методологий интеграции. Однако интеграция данных — сложный бизнес, потому что это проблема «n-squared»: когда вы подключаете больше узлов, результирующая сетка соединений растет экспоненциально. Эффективная платформа интеграции данных должна быть спроектирована таким образом, чтобы она учитывала сложность общих исходных и целевых систем и сводила к минимуму сложность… но как этого добиться?

Вот как бы мы хотели, чтобы это работало в «земле обетованной»

1. Создать API (интерфейс прикладного программирования)
2. Поделитесь этим API с партнером, используя интерактивную модель, которую можно использовать для проверки соединений
3. Партнеры настраивают свои приложения в соответствии с вашими API (или вы можете просто сопоставить и замаскировать, если это необходимо)
4. Мы можем жить долго и счастливо

Однако вот этапы интеграции в современном мире.

..

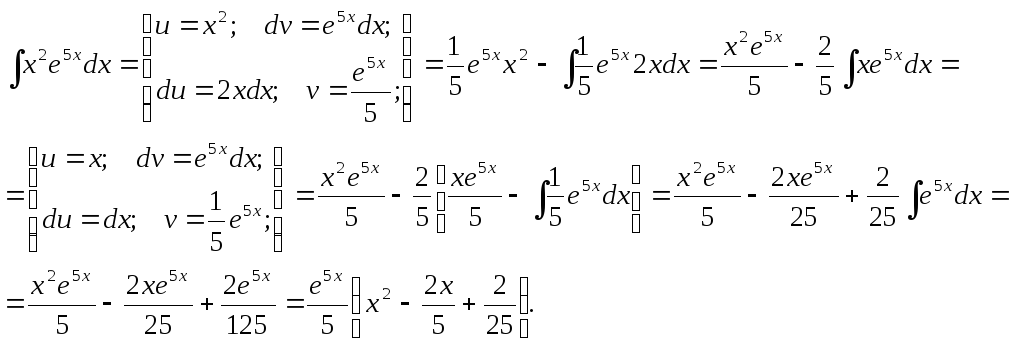1. Понимание корпоративных данных для вашего предприятия
2. Создать API
3. Настройте каждый API для настройки политик безопасности для каждого партнера
4. Настройка правил сопоставления полей (преобразования) для каждого партнера
5. Настройка Поиск правил сопоставления значений (перевода) для каждого партнера
6. API публикации
7. Партнёры поезда
8. Настройка API в соответствии с потребностями каждого партнера
9. Обучить ИТ-команду разработке хороших API-интерфейсов
10. Обучение партнеров использованию API в том виде, в каком они поставляются
11. Отслеживание использования API партнером
12. Отслеживание политик безопасности данных и нарушений

Интеграция данных на базе Illuminate

 

 

 

Давайте разработаем функции для платформы интеграции данных для высшего образования

Платформа интеграции данных для высшего образования должна поддерживать функции, упрощающие эти “реальные” задачи. Он должен:

• Иметь стандартную модель данных
• Наличие уровня безопасности
• Поддержка Развертывание под ключ
• Поддержка Взаимодействие и взаимодействие ко многим распространенным приложениям высшего образования
• Поддержите масштабируемое предприятие и развивайтесь вместе с вами

Интеграция для ИТ-директоров и технических директоров

 

Резюме

Интеграция данных в высшем образовании исторически была проблемой, но она больше не должна вызывать разочарования. Платформа Illuminate от N2N предоставляет надежный веб-сервис для управления вашими потребностями в интеграции данных. У вас может быть простая в использовании информационная панель для управления партнерами по обмену данными, для управления API, для управления доступом к данным (и безопасностью на уровне поля) и для управления преобразованиями данных, и все это в сочетании с ведением журнала транзакционных обменов, чтобы вы знали, с кем ваши данные были переданы. Если вы один из «99%”, которые борются с интеграцией данных, свяжитесь с N2N, и мы покажем вам путь вперед.

• Как 2020 навсегда изменил мой способ ставить цели

  4 янв. 2021 г.

• Рождественское желание натуралиста

  25 декабря 2020 г.

• Corona Times: работа из дома — взгляд генерального директора стартапа

  15 мая 2020 г.

• Corona times: Приключения папы с дефицитом внимания

  11 мая 2020 г.

  

• Поколение Короны

  26 апр. 2020 г.

• Видение 2020 — Восстание машин спасет высшее образование

  26 января 2020 г.

• Философия фэнтези: Макиавелли против Канта?

  24 января 2020 г.

• Стать Übermensch (Сверхчеловеком)

  24 декабря 2019 г.