Интеграл от деления: Интегрирование дробей - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Интегрирование дробей

Рациональной дробью называется дробь P(x)/Q(x), числитель P(x) и знаменатель Q(x) которой – многочлены. Рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе.

У любой неправильной дроби можно выделить её целую часть. Для этого следует по правилу деления многочленов разделить числитель на знаменатель. Поэтому любую неправильную дробь можно представить в виде суммы её целой части и некоторой правильной дроби.

Например, неправильную дробь

можно представить в виде

Таким образом, если необходимо проинтегрировать неправильную дробь, то, представив её в виде суммы многочлена и правильной дроби, с помощью метода разложения сведём решение к интегрированию правильной дроби.

Подготовиться к интегрированию дробей самостоятельно, а затем посмотреть ответ.

Пример 0. Представить в виде суммы многочлена и правильной дроби следующие дроби:

1) ;

2) .

Посмотреть ответ.

Ограничимся интегрированием лишь правильных рациональных дробей, знаменателями которых являются многочлены первой и второй степени. В общем виде интегралы от таких дробей записываются следующим образом:

(1)

(2)

При интегрировании дробей можно использовать следующую формулу, получаемую с помощью метода замены переменной:

(3)

Кроме того, на нашем сайте есть материал Интегрирование рациональных функций и метод неопределённых коэффициентов.

Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн

Пример 1. Найти интеграл дроби

Подынтегральная функция является неправильной рациональной дробью. Используя приведённое выше её представление в виде суммы многочлена и правильной дроби, а также формулу (3), последовательно получим

Любой интеграл вида (2) сводится к нахождению одного или двух следующих интегралов:

(4)

Поэтому рассмотрим эти интегралы. Первый из них находится по формуле (3) при a = 1.

А теперь формулы для вычисления остальных приведённых интегралов.

(5)

(6)

(7)

(8)

(9)

Формулы (5)-(9) можно условно считать табличными интегралами. С их помощью можно найти любой интеграл вида (2). Предварительно такой интеграл приводят к интегралам группы (4). Для этого в знаменателе подынтегральной функции выделяют полный квадрат (это делается при помощи формул сокращённого умножения и ) и представляют его в одном из следующих видов:

или

где m > 0 и n > 0.

В первых двух случаях замена переменной

в третьем непосредственное применение метода разложения приведёт к одному или двум интегралам группы (4).

Пример 2. Найти интеграл дроби

Решение. Результат применения формулы (5) при a = 8:

Пример 3. Найти интеграл дроби

Решение. Выделим в знаменателе подынтегральной функции полный квадрат:

а затем произведём замену переменной t = x + 3 (тогда dt = dx). В результате этого:

то есть получили табличный интеграл. Применяем формулу 5):

откуда, возвращаясь к старой переменной, окончательно получим

Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн

Нет времени вникать в решение? Можно заказать работу!

Пример 4. Найти интеграл дроби

Решение. Выделяя в знаменателе подынтегральной функции полный квадрат, получаем

Произведём теперь замену переменной t = x – 3 (или x = t + 3; тогда dx = dt). Поэтому

Результат применения формул (8) и (5) при a = 1:

Возвращаясь к “старой” переменной, окончательно получим

Пример 5. Найти интеграл дроби

Решение. Знаменатель представляет собой полный квадрат разности:

Поэтому

Применяя далее формулы (7) и (6), найдём

Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.

Пример 6. Найти интеграл дроби

Решение. Выделим в знаменателе подынтегральной функции полный квадрат:

Произведём замену переменной t = x – 4 (или x = t + 4; тогда dx = dt):

Результат применения форумул (8) и (9):

Возвращаясь к “старой” переменной, окончательно получим

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Интеграл

Начало темы “Интеграл”

Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов

Найти неопределённый интеграл: начала начал, примеры решений

Метод замены переменной в неопределённом интеграле

Интегрирование подведением под знак дифференциала

Метод интегрирования по частям

Продолжение темы “Интеграл”

Интегрирование рациональных функций и метод неопределённых коэффициентов

Интегрирование некоторых иррациональных функций

Интегрирование тригонометрических функций

Определённый интеграл

Несобственные интегралы

Площадь плоской фигуры с помощью интеграла

Объём тела вращения с помощью интеграла

Вычисление двойных интегралов

Длина дуги кривой с помощью интеграла

Площадь поверхности вращения с помощью интеграла

Определение работы силы с помощью интеграла

Интегрирование рациональных дробей

Данный онлайн калькулятор служит для вычисления интегралов рациональных дробей вида .

Решение онлайн
Видеоинструкция

Инструкция. Введите числитель и знаменатель дроби. Нажмите кнопку Решить.

Пусть подынтегральное выражение есть рациональная дробь , где и – полиномы (многочлены) степеней

k и n соответственно. Не умаляя общности, можем считать, что k < n, так как в противном случае всегда можно представить числитель в виде P(x) = Q(x)R(x) + S(x), где R(x) и S(x) – полиномы, называемые обычно, как и в случае действительных чисел, частным и остатком, причем степень полинома S(x) меньше n. Тогда
, (1.1)
а интеграл от полинома R(x) мы вычислять умеем. Покажем на примере, как можно получить разложение (1.1). Пусть P(x)=x⁷+3x⁶+3x⁵–3x₃+4x₂+x-2, Q(x)=x³+3x²+x-2.

Разделим полином P(x) на полином Q(x) так же, как мы делим вещественные числа (решение получаем через калькулятор деления столбиком). Имеем

Таким образом, мы получили целую часть дроби (частное от деления полинома P на полином Q) R(x) = x⁴+2x²–4x+7 и остаток S(x) = 9x²–14x+12 от этого деления.
По основной теореме алгебры любой полином может быть разложен на простейшие множители, то есть представлен в виде , где x_l

– корни полинома Q(x) повторенные столько раз, какова их кратность.
Пусть полином Q(x) имеет n различных корней x₁, x₂,…, x_n. Тогда правильная рациональная дробь может быть представлена в виде , где A₁, A₂,…,A_n – числа подлежащие определению. Если x_i – корень кратности α, то ему в разложении на простейшие дроби соответствует α слагаемых .

Если x_j – комплексный корень кратности α полинома с действительными коэффициентами, то комплексно сопряженное число x_j – тоже корень кратности α этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида , если x_j, x_j – корни кратности один. Если x_j, x_j – корни кратности α, то им соответствует α слагаемых и соответствующее разложение имеет вид
Таким образом, интегрирование правильных рациональных дробей свелось к интегрированию простейших дробей, из которых , , являются табличными, может быть найден по рекуррентной формуле, которая получается интегрированием по частям. Интегралы , в случае, когда знаменатель имеет комплексные корни (дискриминант D=p²-4q<0), сводятся, с помощью выделения полного квадрата, к интегралам , заменой .

Одним из способов нахождения коэффициентов A_j, M_j, N_j в разложении правильной рациональной дроби является следующий. Правую часть полученного разложения с неопределенными коэффициентами A_j, M_j, N_j приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами. Приравнивая коэффициенты при одинаковых степенях x (так как полиномы равны, если равны коэффициенты при одинаковых степенях x), получаем систему линейных уравнений для определения этих коэффициентов.

Примеры
1. Найти .
Корни знаменателя – x₁ = -2 кратности 1 и x₂=1 кратности 2. Поэтому x³ – 3x + 2 = (x+2)(x-1)² и подынтегральная функция может быть представлена в виде
Приводя к общему знаменателю, получаем

Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей последнего соотношения, получаем

Решая эту систему, находим A₁=7/9, A₂=2/9, A₃=1/3.

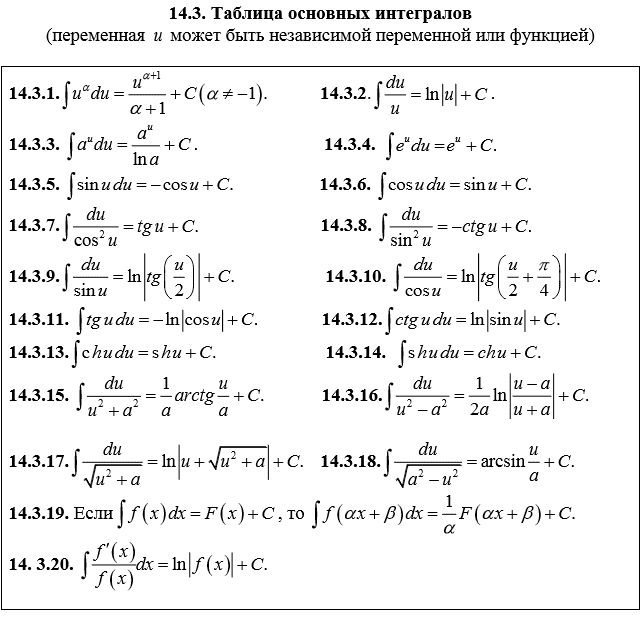
Таким образом,

2. Найти .
Корни знаменателя – x₁=2 кратности 1 и два комплексных корня x_2,3, = -1±i. Поэтому x³ – 2x – 4 = (x-2)(x² + 2x+2) и подынтегральная функция может быть представлена в виде
Приводя к общему знаменателю, получаем Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей последнего соотношения, получаем

Решая эту систему, находим A=1, M=1, N=2.
Таким образом, =ln|x-2|+¹/₂ln(x²+2x+2)+arctg(x+1)+C

Также рекомендуется ознакомиться с возможностью решения интегралов онлайн.

Пример. Найти .
Решение. Используем метод разложения на простейшие. Знаменатель имеет действительные корни, причем корень –1 имеет кратность два. Разложим подынтегральную функцию на простейшие слагаемые

Приравняем числители и учтем, что коэффициенты при одинаковых степенях х, стоящие слева и справа должны совпадать
2x+1 = A(x-1)²+Bx(x-1) + Dx = (A+B)x²+(-2A-B+D)x+A
→ A=1, B=-1, D=3

Следовательно

Непосредственное интегрирование

Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.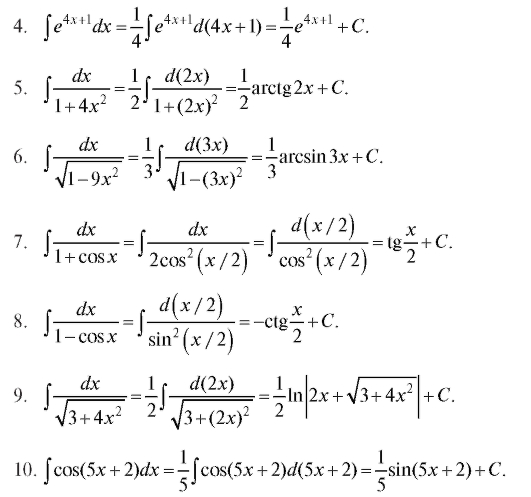 См. Таблица интегралов.

[Править] Подведение под знак дифференциала

Данный метод эквивалентен методу замены переменной (см. далее):

[Править] Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл Сделаем подстановку где — функция, имеющая непрерывную производную.

Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

[править] Интегрирование выражений вида

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.

Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.

Если n и m чётные, то удобнее сделать подстановку tg x = t.

[править] Примеры

Вычислить:

Пусть тогда и

[править] Интегрирование по частям

Основная статья: Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:

В частности, с помощью n-кратного применения этой формулы находится интеграл

где P_n_{+ 1}(x) — многочлен (n + 1)-ой степени.

[править] Интегрирование рациональных дробей

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь , знаменатель которой разложен на множители

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

где A_ij,α_lt,β_lt — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

[Править] Примеры

Вычислить:

Разложим подынтегральное выражение на простейшие дроби:

Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:

α(x + 3) + β(x − 3) = 2x + 3

(α + β)x + 3α − 3β = 2x + 3

Следовательно

Тогда

Теперь легко вычислить исходный интеграл

Интегрирование простейших рациональных дробей.

Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:

У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:

где Затем применяются следующие формулы:

Интеграл может быть вычислен за k шагов с помощью формулы редукции

Пример 1

Вычислить интеграл .

Решение.

Разложим подынтегральное выражение на простейшие дроби:

Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:

Следовательно,

Тогда

Теперь легко вычислить исходный интеграл

Пример 2

Вычислить интеграл .

Решение.

Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель.

Получаем

Пример 3

Вычислить интеграл .

Решение.

Пример 4

Вычислить интеграл .

Решение.

Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов:

Определим ы:

Следовательно,

Получаем

Интеграл, соответственно, равен

Пример 5

Найти интеграл .

Решение.

Разложим подынтегральное выражение на сумму двух дробей.

Найдем неизвестные коэффициенты.

Отсюда получаем

Подынтегральное выражение представляется в виде

Исходный интеграл равен

Пример 6

Найти интеграл .

Решение.

Разложим знаменатель в подынтегральном выражении на множители:

Далее представим подынтегральное выражение в виде суммы простейших дробей

Определим коэффициенты:

Следовательно,

Отсюда находим

Теперь вычислим исходный интеграл

Пример 7

Вычислить интеграл .

Решение.

Перепишем знаменатель рациональной дроби в следующем виде:

Поскольку полученные множители являются несократимыми квадратичными функциями, то подынтегральное выражение представляется в виде

Определим неизвестные коэффициенты.

Получаем

Следовательно,

Интегрируем каждое слагаемое и находим ответ.

Пример 8

Вычислить интеграл .

Решение.

Разложим знаменатель на множители:

Запишем подынтегральную дробь в виде суммы простейших дробей.

Сгруппируем члены с одинаковыми степенями чтобы определить неизвестные коэффициенты из системы линейных уравнений.

Следовательно,

Таким образом, подынтегральное выражение представляется в виде

Окончательно находим

Пример 9

Вычислить интеграл .

Решение.

Разложим подынтегральное выражение на сумму простейших дробей, учитывая что знаменатель имеет кратный корень 3-го порядка:

Определим неизвестные коэффициенты.

Получаем систему уравнений

Следовательно,

Исходный интеграл равен

Пример 10

Вычислить интеграл .

Решение.

Поскольку – несократимый квадратный трехчлен, выделим в знаменателе полный квадрат:

Найдем полученный интеграл с помощью формулы редукции

Получаем ответ:

Пример.

Т.к. ( , то

Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

Итого:

Пример.

Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:

6x⁵ – 8x⁴ – 25x³ + 20x² – 76x – 7 3x³ – 4x² – 17x + 6

6x⁵ – 8x⁴ – 34x³ + 12x² 2x² + 3

9x³ + 8x² – 76x – 7

9x³ – 12x² – 51x +18

20x² – 25x – 25

Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:

3x³ – 4x² – 17x + 6 x – 3

3x³ – 9x² 3x² + 5x – 2

5x² – 17x

5x² – 15x

– 2x + 6

-2x + 6

Таким образом 3x³ – 4x² – 17x + 6 = (x – 3)(3x² + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:

Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

Окончательно получаем:

Пример.

Найдем неопределенные коэффициенты:

Тогда значение заданного интеграла:

Пример 1

Найти неопределенный интеграл.

Шаг 1. Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно, и сейчас я объясню как:

Сначала смотрим на числитель и выясняем старшую степень многочлена: Старшая степень числителя равна двум.

Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждой скобке находим старшую степень и мысленно умножаем: – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.

Вывод: Старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной.

Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной.

Сейчас мы будем рассматривать только правильные дробно-рациональные функции. Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока.

Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель: Вообще говоря, здесь уже произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще? Объектом пыток, несомненно, выступит квадратный трехчлен. Решаем квадратное уравнение:

Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители:

Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители.

Начинаем оформлять решение:

Шаг 3. Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых (элементарных) дробей. Сейчас будет понятнее.

Смотрим на нашу подынтегральную функцию:

И, знаете, как-то проскакивает интуитивная мысль, что неплохо бы нашу большую дробь превратить в несколько маленьких. Например, вот так:

Возникает вопрос, а можно ли вообще так сделать? Вздохнем с облегчением, соответствующая теорема математического анализа утверждает – МОЖНО. Такое разложение существует и единственно.

Только есть одна загвоздочка, коэффициенты мы пока не знаем, отсюда и название – метод неопределенных коэффициентов.

Как вы догадались, последующие телодвижения так, не гоготать! будут направлены на то, чтобы как раз их УЗНАТЬ – выяснить, чему же равны .

Будьте внимательны, подробно объясняю один раз!

Итак, начинаем плясать от:

В левой части приводим выражение к общему знаменателю:

Теперь благополучно избавляемся от знаменателей (т.к. они одинаковы):

В левой части раскрываем скобки, неизвестные коэффициенты при этом пока не трогаем:

Заодно повторяем школьное правило умножение многочленов. В свою бытность учителем, я научился выговаривать это правило с каменным лицом: Для того чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

С точки зрения понятного объяснения коэффициенты лучше внести в скобки (хотя лично я никогда этого не делаю в целях экономии времени):

Составляем систему линейных уравнений. Сначала разыскиваем старшие степени: И записываем соответствующие коэффициенты в первое уравнение системы:

Хорошо запомните следующий нюанс. Что было бы, если б в правой части вообще не было ? Скажем, красовалось бы просто без всякого квадрата? В этом случае в уравнении системы нужно было бы поставить справа ноль: . Почему ноль? А потому-что в правой части всегда можно приписать этот самый квадрат с нулём: . Если в правой части отсутствует какие-нибудь переменные или (и) свободный член, то в правых частях соответствующих уравнений системы ставим нули.

Далее процесс идет по снижающейся траектории, от водки к пиву, отмечаем все «иксы»:

Записываем соответствующие коэффициенты во второе уравнение системы:

И, наконец, минералка, подбираем свободные члены.

Эх,…что-то я расшутился. Шутки прочь – математика наука серьезная. У нас в институтской группе никто не смеялся, когда доцент на лекции сказала, что разбросает члены по координатной прямой и выберет из них самые большие. Настраиваемся на серьезный лад. Хотя… кто доживет до конца этого урока, все равно будет тихо улыбаться.

Система готова:

Решаем систему:

(1) Из первого уравнения выражаем и подставляем его во 2-ое и 3-е уравнения системы. На самом деле можно было выразить (или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты.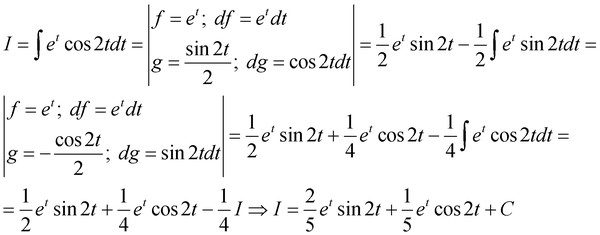 (2) Приводим подобные слагаемые во 2-ом и 3-м уравнениях.

(3) Почленно складываем 2-ое и 3-е уравнение, при этом, получая равенство , из которого следует, что

(4) Подставляем во второе (или третье) уравнение, откуда находим, что

(5) Подставляем и в первое уравнение, получая .

Если возникли трудности с методами решения системы отработайте их на уроке Как решить систему линейных уравнений?

После решения системы всегда полезно сделать проверку – подставить найденные значения в каждое уравнение системы, в результате всё должно «сойтись».

Почти приехали. Коэффициенты найдены, при этом:

Чистовое оформление задание должно выглядеть примерно так:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Как видите, основная трудность задания состояла в том, чтобы составить (правильно!) и решить (правильно!) систему линейных уравнений. А на завершающем этапе всё не так сложно: используем свойства линейности неопределенного интеграла и интегрируем. Обращаю внимание, что под каждым из трёх интегралов у нас «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле.

Проверка: Дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найдем правильно. В ходе проверки пришлось приводить выражение к общему знаменателю, и это не случайно. Метод неопределенных коэффициентов и приведение выражения к общему знаменателю – это взаимно обратные действия.

Пример 2

Найти неопределенный интеграл.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Вернемся к дроби из первого примера: . Нетрудно заметить, что в знаменателе все множители РАЗНЫЕ. Возникает вопрос, а что делать, если дана, например, такая дробь: ? Здесь в знаменателе у нас степени, или, по-математически кратные множители. Кроме того, есть неразложимый на множители квадратный трехчлен (легко убедиться, что дискриминант уравнения отрицателен, поэтому на множители трехчлен никак не разложить).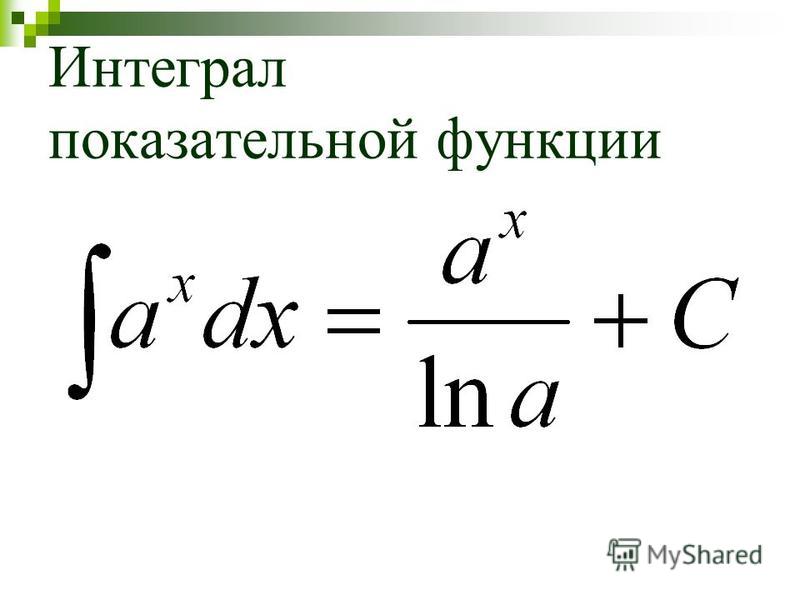 Что делать? Разложение в сумму элементарных дробей будет выглядеть наподобие с неизвестными коэффициентами вверху или как-то по-другому?

Пример 3

Представить функцию в виде суммы элементарных дробей с неизвестными коэффициентами.

Шаг 1. Проверяем, правильная ли у нас дробь Старшая степень числителя: 2 Старшая степень знаменателя: 8 , значит, дробь является правильной.

Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Очевидно, что нет, всё уже разложено. Квадратный трехчлен не раскладывается в произведение по указанным выше причинам. Гуд. Работы меньше.

Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей. В данном случае, разложение имеет следующий вид:

Смотрим на наш знаменатель: При разложении дробно-рациональной функции в сумму элементарных дробей можно выделить три принципиальных момента:

1) Если в знаменателе находится «одинокий» множитель в первой степени (в нашем случае ), то вверху ставим неопределенный коэффициент (в нашем случае ). Примеры №1,2 состояли только из таких «одиноких» множителей.

2) Если в знаменателе есть кратный множитель , то раскладывать нужно так: – то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя: и , еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу.

3) Если в знаменателе находится неразложимый многочлен второй степени (в нашем случае ), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае с неопределенными коэффициентами и ).

На самом деле, есть еще 4-ый случай, но о нём я умолчу, поскольку на практике он встречается крайне редко.

Пример 4

Представить функцию в виде суммы элементарных дробей с неизвестными коэффициентами.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Строго следуйте алгоритму!

Если Вы разобрались, по каким принципам нужно раскладывать дробно-рациональную функцию в сумму, то сможете разгрызть практически любой интеграл рассматриваемого типа.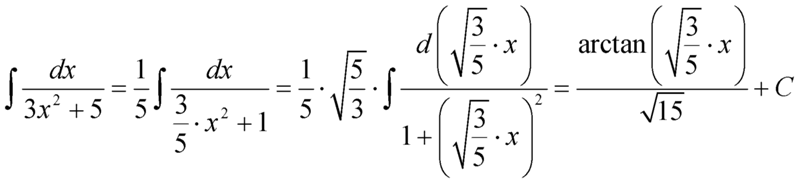

Пример 5

Найти неопределенный интеграл.

Шаг 1. Очевидно, что дробь является правильной:

Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Можно. Здесь сумма кубов . Раскладываем знаменатель на множители, используя формулу сокращенного умножения

Шаг 3. Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Обратите внимание, что многочлен неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию с неизвестными коэффициентами, а не просто одну буковку.

Приводим дробь к общему знаменателю:

Составим и решим систему:

(1) Из первого уравнения выражаем и подставляем во второе уравнение системы (это наиболее рациональный способ).

(2) Приводим подобные слагаемые во втором уравнении.

(3) Почленно складываем второе и третье уравнения системы.

Все дальнейшие расчеты, в принципе, устные, так как система несложная.

(1) Записываем сумму дробей в соответствии с найденными коэффициентами .

(2) Используем свойства линейности неопределенного интеграла. Что произошло во втором интеграле? С этим методом Вы можете ознакомиться в последнем параграфе урока Интегрирование некоторых дробей.

(3) Еще раз используем свойства линейности. В третьем интеграле начинаем выделять полный квадрат (предпоследний параграф урока Интегрирование некоторых дробей).

(4) Берём второй интеграл, в третьем – выделяем полный квадрат.

(5) Берём третий интеграл. Готово.

А вот вам еще пара примеров для самостоятельного решения, один похожий, другой – труднее.

Пример 6

Найти неопределенный интеграл.

Пример 7

Найти неопределенный интеграл.

Интегрирование неправильной дробно-рациональной функции

Перейдем к рассмотрению случая, когда старшая степень числителя больше либо равна старшей степени знаменателя.

Пример 8

Найти неопределенный интеграл.

Совершенно очевидно, что данная дробь является неправильной:

Основной метод решения интеграла с неправильной дробно-рациональной функций – это деление числителя на знаменатель. Да-да, делить будем столбиком, как самые обычные числа в школе.

Напоминаю алгоритм. Сначала рисуем «заготовку» для деления:

ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами.

Теперь маленькая задачка, на какой множитель нужно умножить , чтобы получить ? Очевидно, что на :

Далее умножаем сначала на , потом – на , потом – на , потом – на 0 и записываем результаты слева:

Проводим черточку и производим вычитание (из верха вычитаем низ): Старшая степень остатка равна двум, старшая степень делителя – больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то то алгоритм деления увеличился бы на один шаг.

Итак, наше решение принимает следующий вид:

Делим числитель на знаменатель:

(1) Что дало деление? Много хорошего: теперь у нас два слагаемых, первое – интегрируется совсем просто, а второе – правильная дробь, которую мы решать уже умеем.

После деления всегда желательно выполнять проверку. В рассматриваемом примере можно привести к общему знаменателю , и в результате получится в точности исходная неправильная дробь

(2) От первого слагаемого сразу берем интеграл. Знаменатель дроби раскладываем на множители

Дальше всё идет по накатанной схеме:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Готово.

И, наконец, заключительный пример для самостоятельного решения. Он очень интересен, рекомендую всем!

Пример 9

Найти неопределенный интеграл.

Только что обратил внимание, что во всех примерах урока в ходе решения систем у нас получались «хорошие» целые коэффициенты . По той причине, что почти все интегралы я взял из сборника Рябушко. На практике же, когда автор методички придумает какой-нибудь корявый интеграл, часто будут появляться разные нехорошести. Таким образом, если в ходе решения интеграла от дробно-рациональной функции у Вас получаются дробные значения коэффициентов , то в этом нет ничего страшного, ситуация даже обыденна.

Желаю успехов!

Решения и ответы:

Пример 2: Решение:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Комментарий: в правой части у нас нет слагаемого с , поэтому в первом уравнении системы ставим справа ноль.

Пример 4: Решение:

Шаг 1. Проверяем, правильная ли у нас дробь Старшая степень числителя: 6 Старшая степень знаменателя: 8 , значит, дробь является правильной.

Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители. Множитель разложить нельзя, а вот – можно:

Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей. В данном случае, разложение имеет следующий вид:

Пример 6: Решение:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Пример 7: Решение:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Пример 9: Решение:

(1) Здесь неправильная дробь, поскольку старшие степени числителя и знаменателя равны: 3 = 3. Для того чтобы разделить числитель на знаменатель придётся временно раскрыть скобки в знаменателе.

(2)-(3) Теперь можно разделить на знаменатель , но делать этого… я не буду. Можно поступить хитрее. Используем прием, который рассмотрен в первом параграфе урока Интегрирование некоторых дробей.

(4) От первого слагаемого сразу берем интеграл. Знаменатель оставшейся, уже правильной, дроби снова записываем в виде произведения множителей. Тут я немного подсократил разложение, надеюсь, всем понятно, что

Далее накатанная колея…

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Иррациональные функции

Пример 1

Найти неопределенный интеграл

Анализируя подынтегральную функцию, приходишь к печальному выводу, что она совсем не напоминает табличные интегралы. Вот если бы всё это добро находилось в числителе – было бы просто. Или бы корня внизу не было. Или многочлена. Никакие методы интегрирования дробей тоже не помогают. Что делать?

Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции.

Отмечу, что эта замена немного своеобразная, ее техническая реализация отличается от «классического» способа замены, который рассмотрен на уроке Метод замены в неопределенном интеграле.

В данном примере нужно провести замену , то есть, вместо «икса» под корнем у нас окажется . Почему замена именно такая? Потому-что , и в результате замены корень пропадёт.

Если бы в подынтегральной функции вместо квадратного корня у нас находился , то мы бы провели замену . Если бы там был – то и так далее.

Хорошо, у нас превратится в . Что произойдет с многочленом ? Сложностей нет: если , то .

Осталось выяснить, во что превратится дифференциал . Делается это так:

Берем нашу замену и навешиваем дифференциалы на обе части:

(я распишу максимально подробно)

Оформление решения должно выглядеть примерно так:

Проведем замену:

(1) Проводим подстановку после замены (как, что и куда, уже рассмотрено).

(2) Выносим константу за пределы интеграла. Числитель и знаменатель сокращаем на .

(3) Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат

(4) Интегрируем по таблице, используя формулу .

(5) Проводим обратную замену. Как это делается? Вспоминаем, от чего плясали: если , то .

Внимание! Для изучения дальнейших примеров необходимо хорошо проработать первый параграф урока Интегрирование некоторых дробей.

Пример 2

Найти неопределенный интеграл

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Как-то так получилось, что в примерах 1, 2 «голый» числитель с одиноким дифференциалом . Что же. Исправим ситуацию.

Пример 3

Найти неопределенный интеграл

Предварительный анализ подынтегральной функции опять показывает, что лёгкого пути нет. А поэтому нужно избавляться от корня.

Проведем замену: За обозначаем ВСЁ выражение под корнем. Замена из предыдущих примеров здесь не годится (точнее, сделать-то её можно, но это не избавит нас от корня). Навешиваем дифференциалы на обе части:

С числителем разобрались. Что делать с в знаменателе? Берем нашу замену и выражаем из неё: Если , то

(1) Проводим подстановку в соответствии с выполненной заменой. (2) Причесываем числитель. Константу здесь я предпочел не выносить за знак интеграла (можно делать и так, ошибкой не будет)

(3) Раскладываем числитель в сумму. Еще раз настоятельно рекомендую ознакомиться с первым параграфом урока Интегрирование некоторых дробей. Канители с разложением числителя в сумму в иррациональных интегралах будет предостаточно, очень важно отработать это прием.

(4) Почленно делим числитель на знаменатель.

(5) Используем свойства линейности неопределенного интеграла. Во втором интеграле выделяем квадрат для последующего интегрирования по таблице.

(6) Интегрируем по таблице. Первый интеграл совсем простой, во втором используем табличную формулу высокого логарифма

(7) Проводим обратную замену. Если мы проводили замену , то, обратно:

Пример 4

Найти неопределенный интеграл

Это пример для самостоятельного решения, если вы невнимательно проработали предыдущие примеры, то допустите ошибку! Полное решение и ответ в конце урока.

Принципиально так же решаются интегралы с несколькими одинаковыми корнями, например , и т.д. А что делать, если в подынтегральной функции корни разные?

Пример 5

Найти неопределенный интеграл

Вот и пришла расплата за голые числители. Когда встречается такой интеграл, обычно становится страшно. Но страхи напрасны, после проведения подходящей замены подынтегральная функция упрощается. Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.

Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в виде : . Нас будут интересовать знаменатели степеней: Записываем эти знаменатели: 2, 3, 3. Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше.

Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать.

Как многие уже догадались, замена в рассматриваемом интеграле будет следующей:

Оформляем решение:

Проведем замену:

(1) Производим подстановку.

(2) Избавляемся от корней. Выносим константу за знак интеграла. Сокращаем числитель и знаменатель на .

(3) Сокращаем числитель и знаменатель еще на .

(4) Раскладываем числитель в сумму (как это сделать, уже неоднократно упоминалось).

(5) Почленно делим числитель на знаменатель.

(6) Интегрируем по таблице. При этом константу я снова «прилепил» к каждому из трех слагаемых (можно этого и не делать, момент несущественный).

(7) Проводим обратную замену. Если , то, обратно: . В ходе обратной замены некоторые корни лучше сразу сократить (обычно это делается устно). В рассмотренном примере сокращение корней встретилось в первом слагаемом:

Как видите, особых сложностей нет, несмотря на то, что сначала интеграл показался трудным и страшным.

Пример 6

Найти неопределенный интеграл

Это пример для самостоятельного решения.

Интегрирование биномиальных интегралов

Так называемый биномиальный интеграл имеет следующий вид: . Такой интеграл берётся в трёх случаях.

1) Случай первый. Самый лёгкий. Если степень – целое число.

Например:

Представим интеграл в стандартном виде (это лучше делать на черновике): Мы видим, что степень – целая, а, значит, действительно имеет место первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в примерах 5, 6, поэтому приводить почти такие же решения особого смысла нет – я просто покажу, какую замену здесь нужно провести. Смотрим на знаменатели дробей: Записываем знаменатели: 2, 5. Находим наименьшее общее кратное этих чисел. Очевидно, это 10: оно делится и на 2 и на 5, кроме того – десятка самая маленькая в этом смысле. После замены все корни гарантировано пропадут. Повторюсь, примеров для первого случая не будет, так как они очень похожи на недавно разобранные интегралы.

Иллюстрирующие программы, реализующие алгоритмы интегрирования рациональных дробей Текст научной статьи по специальности «Математика»

Список использованных источников

1. Демидович Б. П., Моденов В. П. Дифференциальные уравнения. — СПб.: Лань, 2006. — 288 c.

2. НоутонП., Шилдт Г. Java 2: пер. с англ. — СПб.: БХВ-Петербург, 2003. — 1073 с.

3. Попов А. А. Тренажер по аналитическому решению линейных дифференциальных уравнений методом Лагранжа // Новые информационные технологии в образовании: материалы междунар. науч.-практ. конф. — Екатеринбург, 2011. — Ч. 1. — С. 199-202.

А. А. Попов, С. Н. Царегородцев

Марийский государственный университет, г. Йошкар-Ола

Иллюстрирующие программы, реализующие алгоритмы

ИНТЕГРИРОВАНИЯ РАЦИОНАЛЬНЫХ ДРОБЕЙ

Приведено описание интерактивных компьютерных программ на языке Java, реализующих задачи интегрирования дробно-рациональных выражений. Запрограммированы процессы выделения целой части неправильной дроби, разложения правильной дроби на простые дроби с использованием метода неопределенных коэффициентов и интегрирования простых дробей.

Интегрирование дробно-рациональных выражений построено на элементарных преобразованиях, позволяющих свести исходный интеграл к сумме интегралов от простых дробей. Студентам необходимо освоить такие вопросы, как выделение целой части дроби, разложение правильной дроби на простые множители с помощью метода неопределенных коэффициентов, нахождение коэффициентов разложения из системы линейных алгебраических уравнений, выделение полного квадрата в квадратном трехчлене [1]. Представить весь процесс решения на аудиторной доске, как правило, требует значительных усилий преподавателя. С другой стороны, подобные решения легко алгоритмизируются и могут быть представлены в виде компьютерных иллюстрирующих программ.

Выделение целой части дроби, и выделение полного квадрата в знаменателе дроби рассмотрены отдельно от метода неопределенных коэффициентов. В исходном интеграле степень многочлена в числителе больше степени многочлена в знаменателе. Все коэффициенты выбраны так, чтобы в процессе деления многочлена на многочлен не образовывались дробные числа, а знаменатель не имел действительных корней. В итоге получается интеграл от суммы степенных функций и правильной дроби. При делении запоминаются коэффициенты многочленов, которые образуются в промежуточных действиях. Рассмотрены варианты интегрирования простой дроби с квадратным трехчленом путем выделения полного квадрата в знаменателе и сведения интеграла к двум табличным интегралам при различных комбинациях знаков коэффициентов в знаменателе.

Метод неопределенных коэффициентов иллюстрируется на интеграле вида

г A3 x + A2 x + A1 x + A0

I—-3—–2—-—1—–0-—- dx .

(x – a)(x-b)(x + px + q)

Подынтегральная функция является правильной дробью, в знаменателе которой, кроме квадратного трехчлена, имеются еще два линейных сомножителя. Коэффициенты выбираются так, что в разложении подынтегральной функции на простые дроби

A3 x3 + A2 x2 + A1 x + A0 F3 + F2 + F1 x + F0

(x- a)(x -b)(x2 + px + q) x- a x -b x2 + px + q

неопределенные коэффициенты F после их нахождения оказались бы целыми числами. После приведения правой части к общему знаменателю, отбрасывания одинаковых знаменателей и приравнивания коэффициентов при одинаковых степенях x получается система линейных алгебраических уравнений для неизвестных коэффициентов, после нахождения которых исходный интеграл можно представить в виде суммы интегралов от простых дробей. Случай разложения, когда a = b, выделен отдельно.

В качестве языка программирования был выбран язык Java [2]. Рассмотренным трем вариантам разложения соответствуют три класса, в каждом из которых записано специально закодированное решение в виде массива строк. В качестве специальной разметки строк здесь выбраны последовательности символов «<…>{…}» и «[…]». В угловые скобки помещается числитель дроби, в фигурные скобки — знаменатель дроби, в квадратные скобки — показатель степени. В разложениях на простые дроби неизвестными являются только коэффициенты F. Индексы специально не кодируются, т. к. заранее известно, что каждый из них следует после символа F. x- \) (x- 2) (x-1) (x1+2x+2)

2xa-13x–Sx+fr-

=FJ(xi+2x‘+b-j<i-2n’2)+F:,(x’+2*J+2x-2*”-4x-4)+

+F, (*!-2л:-х’+ 2*)+Fj<x2-2x’x+ 2)

Рис. 2. Окно с текущим содержимым для задачи, использующей метод неопределенных коэффициентов

На рисунке 2 приведено начало решения задачи, когда подынтегральная функция разлагается на простые дроби. Далее на месте третьей и четвертой строк, которые делаются невидимыми, производится перегруппировка слагаемых, а затем на месте пятой и шестой строк записывается система линейных алгебраических уравнений.

Задачи интегрирования рациональных дробей включают большой объем аналитических преобразований, и именно для таких задач удобно использовать интерактивные иллюстрации с посимвольным выводом информации, моделирующей процесс написания формул на аудиторной доске.

Список использованных источников

1. Кудрявцев Л. Д. Краткий курс математического анализа: учеб. для вузов. — М.: Наука, 1989. — 736 с.

2. НоутонП., Шилдт Г. Java 2: пер. с англ. — СПб.: БХВ-Петербург, 2003. — 1073 с.

Интегрирование рациональных функций

Дробной – рациональной функцией называется функция, равная частному от деления двух многочленов:

R(x) = .

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, в противном случае – неправильной. Отметим, что всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби:

где r(x) – многочлен, степени меньше степени знаменателя Q(x). Таким образом, интегрирование рациональной функции сводится к интегрированию правильной рациональной дроби. А интегрирование правильной рациональной дроби сводится к интегрированию простейших дробей типа:

1. ; 2. ;

3. ; 4. .

(x² +рх + q – не имеет действительных корней.)

Интегрирование простейших рациональных дробей:

1. .

2. .

3. Основной способ нахождения интеграла состоит в предварительном выделении полного квадратного трехчлена:

Рассмотрим этот способ на примере.

Пример 53. Вычислить интеграл

Решение. Выделим полный квадрат в знаменателе и преобразуем дробь:

х²+2х -1 = х²+2х +1-1-1 = (х+1)² -2.

Тогда = = – =

= – +С.

4. Если введем новую переменную t, положив t = х + и

х² + рх + q = t² + a², где a² = q – , то интеграл =I_n можно вычислить с помощью реккурентной формулы

I_n = .

9.5. Интегрирование рациональных дробей с помощью разложения на простейшие дроби

Случай 1. Знаменатель имеет только действительные различные корни, т.е. разлагается на неповторяющиеся множители первой степени.

Пример 54. Найти интеграл

Решение. Так как каждый из двухчленов входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде

Освобождаясь от знаменателей, получим

При х = 1 6 = 3А, А = 2;

при х = 2 11 = -2В, В= – ;

при х = 4 27 = 6С, С = .

Итак, разложение рациональной дроби на простейшие имеет вид

Таким образом,

Случай 2. Знаменатель имеет лишь действительные корни, причем некоторые из них кратные, т.е. знаменатель разлагается на множители первой степени и некоторые из них повторяются.

Пример 55. Найти интеграл

Решение. Множителю соответствует сумма трех простейших дробей , а множителю – простейшая дробь Итак,

Освободимся от знаменателя:

х = 1	2 = 4А; A =
x = -3	10 = -64D; D = –
x = 0	1= -3B + 3C +
x = -1	2 = 1- 4B + 8C +

Откуда В = , С = .

Окончательное разложение данной дроби на простейшие имеет вид

Таким образом, получим

Случай 3. Среди корней знаменателя имеются простые комплексные корни, т.е. разложение знаменателя содержит квадратичные неповторяющиеся множители.

Пример 56. Найти интеграл

Решение. Разлагаем дробь на простейшие дроби

Освобождаемся от знаменателя:

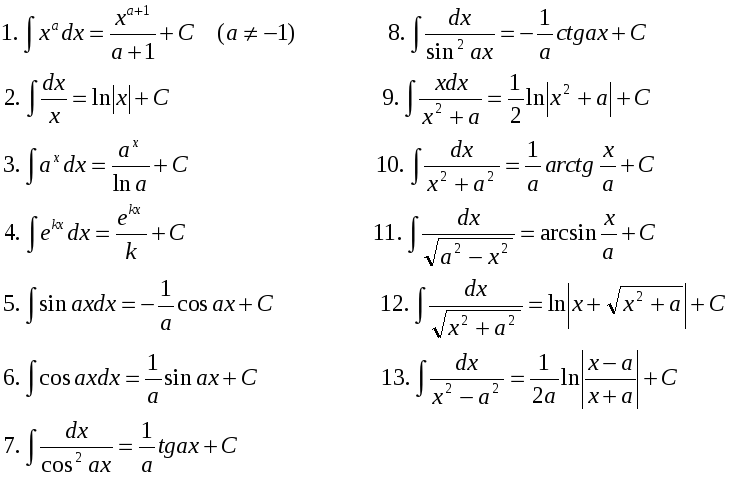. Выпишем коэффициенты при одинаковых степенях:

при х²:	0 = А+В
x:	0 = A+C
x⁰:	1 = A

Откуда найдем А = 1, В = -1, С = -1.

Итак,

Следовательно,

= ln|x|-

– – = ln|x| – –

– +C.

Случай 4. Среди корней знаменателя имеются кратные комплексные корни, т.е. разложение знаменателя содержит повторяющиеся квадратичные множители.

Пример 57. Найти интеграл

Решение. Так как есть двукратный множитель, то

Освобождаясь от знаменателей, получим

Приравняем коэффициенты при одинаковых степенях :

Следовательно,

9.5. Интегрирование иррациональных функций

Неопределенный интеграл вида интегрируется

путем введения новой переменной .

Интегралы вида интегрируются путем выделения полного квадрата из квадратного трехчлена.

Пример 58. Вычислить интеграл .

Решение:

= , где

Пример 59. Вычислить интеграл .

Решение:

Интеграл вида , где n Î Z, интегрируются путем введения новой переменной t ⁿ = ax + b.

Пример 60. Вычислить интеграл .

Решение:

= -2t-2 = -2 +С.

Интегралы вида , где P_n (x) – многочлен степени n, вычисляются с помощью реккурентной формулы

= , (21)

где Q _n_–₁(x) – многочлен степени (n – 1) с неопределенными коэффициентами и l – число. Коэффициенты многочлена и число l находятся при помощи дифференцирования тождества (21).

Пример 61. Вычислить интеграл .

Решение. Применяем формулу (21):

= (Ах+В) . Дифференцируем это тождество: . Откуда

х² = А(х² + 4) + х(Ах+В) + l.

Выпишем коэффициенты при одинаковых степенях:

х²: 1 = А +А

х: 0 = Вх

х⁰: 0 = 4A + l.

Итак, А = , В = 0, l = -2. Следовательно,

= = +С.

Интеграл от дифференциального бинома , где m, n, p – рациональные числа:

1) если р – целое число, то делаем замену х = t ^s, где s – общий знаменатель дробей m и n;

2) если – целое число, то делаем замену а+bх ⁿ = t ^s, где s – знаменатель дроби р;

3) если +р – целое число, то делаем замену ах ^–ⁿ+b = t ^s, где s – знаменатель дроби р.

Пример 62. Вычислить интеграл

Решение:

= =

9.7. Интегрирование тригонометрических функций

1.Интегралы вида где R – рациональная функция, приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки В результате этой подстановки имеем:

;

Пример 63. Найти интеграл

Решение. Введем новую переменную tg . Тогда = =

= = = arctg +

+C = +C.

Универсальная подстановка во многих случаях приводит к сложным вычислениям, так как при ее применении и выражаются через в виде рациональных дробей, содержащих .

В некоторых частных случаях нахождение интеграла вида может быть упрощено:

1. Если – нечетная функция относительно , т.е., если , то интеграл рационализируется подстановкой

2. Если – нечетная функция относительно , т.е., если , то интеграл рационализируется с помощью подстановки

3. Если – четная функция и относительно и относительно , т.е., если , то к цели приводит подстановка

Пример 64. Найти интеграл

Решение. Так как подынтегральная функция нечетна относительно синуса, то полагаем

2. Интегралы вида

Выделим здесь два случая, имеющие особенно важное значение.

Случай 1. По крайней мере один из показателей m или n – нечетное положительное число.

Если n – нечетное положительное число, то применяется подстановка Если же m – нечетное положительное число, подстановка

Пример 65. Найти интеграл

Решение. Полагая получим

Случай 2. Оба показателя степени m и n – четные положительные числа. Здесь следует преобразовать подынтегральную функцию с помощью следующих формул:

(22)

(23)

(24)

Пример 66. Найти интеграл

Решение. Из формулы (22) следует, что

Применив теперь формулу (23), получаем

Итак,

3. Интегралы вида

Тригонометрические формулы

дают возможность произведение тригонометрических функций представить в виде суммы.

Дата добавления: 2020-07-18; просмотров: 260; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

08. Интегрирование рациональных дробей

Рациональной дробью или рациональной функцией называется отношение двух полиномов (многочленов), то есть выражение вида , где

–

Полиномы (многочлены) степеней K и N соответственно. Если степень полинома (многочлена) в числителе меньше степени полинома в знаменателе, то есть то такую рациональную дробь называют правильной.

В дальнейшем будем считать, что , так как в противном случае всегда можно представить числитель в виде где И -полиномы, называемые обычно, как и в случае действительных чисел, частным и остатком, причем степень полинома меньше N. Тогда

, (1.2)

А интеграл от полинома Мы вычислять умеем.

Покажем на примере, как можно получить разложение (1.2). Пусть

Разделим полином На полином Так же, как мы делим вещественные числа. Имеем

Таким образом, мы получили целую часть дроби (частное от деления полинома На полином ) и остаток от этого деления. Поэтому можем записать .

Простейшими рациональными дробями назовём дроби , , , , , ,, .

Рассмотрим интегрирование этих дробей. Интегралы , , являются табличными, а интеграл может быть найден или по рекуррентной формуле (1. 1) полученной выше интегрированием по частям, или с помощью таблиц . Интегралы , в случае, когда знаменатель имеет комплексные корни (дискриминант ), сводятся, с помощью выделения полного квадрата, к интегралам , заменой . Наконец, как это указывалось ранее, интегралы , выделением в числителе дифференциала выражения Сводятся к интегралам , .

Таким образом, осталось научиться раскладывать правильные рациональные дроби на сумму простейших.

По основной теореме алгебры [6] любой полином может быть разложен на простейшие множители, то есть представлен в виде , где –действительные или комплексные корни полинома , повторенные столько раз, какова их кратность.

Пусть полином имеет различных корней . Тогда правильная рациональная дробь может быть представлена в виде , где – числа, подлежащие определению. Если – корень кратности α, то ему в разложении на простейшие дроби соответствует α слагаемых . Если – комплексный корень кратности Полинома с действительными коэффициентами, то комплексно сопряженное число – тоже корень кратности этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида если – корни кратности один. Если – корни кратности , то им соответствует Слагаемых и соответствующее разложение имеет вид

Таким образом, интегрирование правильных рациональных дробей свелось к интегрированию простейших дробей рассмотренных в начале пункта.

Одним из способов нахождения коэффициентов в разложении правильной рациональной дроби является следующий. Правую часть полученного разложения с неопределенными коэффициентами приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами. Приравнивая коэффициенты при одинаковых степенях (так как полиномы равны, если равны коэффициенты при одинаковых степенях ), получаем систему линейных уравнений для определения этих коэффициентов. Продемонстрируем изложенное на примерах.

Примеры

1. Найти .

Корни знаменателя – кратности 1 и кратности 2. Поэтому и подынтегральная функция может быть представлена в виде

Приводя к общему знаменателю, получаем

Приравнивая коэффициенты при одинаковых степенях в числителях правой и левой частей последнего сотношения, получаем

Решая эту систему, находим .

Таким образом,

2. Найти .

Корни знаменателя – кратности 1 и два комплексных корня. Поэтому и подынтегральная функция может быть представлена в виде

Приводя к общему знаменателю, получаем

Решая эту систему, находим

Таким образом,

3. Найти .

Корни знаменателя кратности 2 и пара комплексно сопряжённых корней кратности 1. Поэтому подынтегральная функция может быть представлена в виде

Приводя к общему знаменателю и подобные, получаем

Решая эту систему, находим .

Таким образом,

4. Найти .

Корни знаменателя – кратности 1 и два комплексных корня кратности 2. Поэтому подынтегральная функция может быть представлена в виде

Дальнейшие вычисления предлагается проделать самостоятельно.

Задание 1.4

Вычислить интегралы:

1.; 2..

Написать разложение рациональной дроби на элементарные (не находя коэффициентов).

3.; 4..

Ответы:

1. ;

2. .

3.;

4..

< Предыдущая		Следующая >

Формула интегрального частного правила с примерами |Правило интеграционного подразделения u/v |

Главная > Правило интегрирования по частям

Что такое правило интегрирования и его формулы?

Правило интегрального частного — это способ интегрирования двух функций, заданных в форме числителя и знаменателя. Это правило также называют антипроизводным частным или правилом деления.

Формула правила интегрального деления выводится из формулы интегрирования по частям u/v. 9{ 2 } } dx

Эта формула имеет собственное ограничение, поэтому не следует полностью полагаться на интегрирование дробных функций.

Точка, которую необходимо запомнить для интегрального частного/правила деления

Это аналогичный результат интегрирования по частям с использованием частного правила.
Правило деления лучше всего подходит для дифференцирования, а правило произведения лучше всего подходит для интегрирования
Правило частного требует дополнительного интегрирования для решения интегральной задачи, чем правило интегрирования по частям.
Правило первообразных частных является еще одной формой интегрирования по частям и имеет очень ограниченное применение.

Как интегрировать дробь или функцию деления, используя правило частного?

Чтобы решить функцию дробного интеграла, вы можете использовать цепное правило, которое дает вам подстановку, и правило произведения, которое дает вам интегрирование по частям.

Используя эти оба правила, вы можете решить или показать свое окончательное решение в соответствии с этим результатом-

Из этой формулы вы можете получить представление о том, что вам нужно для дальнейшего интегрирования делимой функции.

Или вы можете использовать правило интегрирования по частям для решения интегральных функций деления, взяв одну функцию за u, а другую за v в соответствии с правилом ILATE.

I = обратная тригонометрическая функция

L = логарифмическая функция

A = алгебраическая функция

T = тригонометрическая функция 9{ } v.du

Примечание. Не существует прямого правила, которое решает задачу дроби или интеграла деления так, как это делает правило произведения.

Мы используем различные методы, чтобы справиться с такими проблемами, как интегрирование частичной дроби для повторяющегося или неповторяющегося линейного фактора, метод интегрирования подстановки, интегрирование по частям и т. { 2 } + 10z } dz 9{ } \ frac { \ frac { 1 } { 2 } du } { u } = 1/2 ln | u | + C

= 1/2 ln (z² + 4) + C Ответ

Также проверьте –

Интегрирование по частям для определенного интеграла
Интегрирование по частям табличным методом
Примеры уравнения полуокружности
39

Часто задаваемые вопросы

Для чего используется правило интегрального частного?

Правило интегрального частного в основном используется для определения того, что вам нужно для интегрирования функций двух делений. Правило частного возникло из дифференцирования, а формула целочисленной делимости — это просто еще одна форма интегрирования по частям для дальнейшей проверки того, как интегрировать делимые функции

Антипродуктовое разделение — это другое название интегрального делимого правила, и оно лучше всего работает для дифференциации, а не для интеграции.

Как быстро решить интеграцию дроби или деления?

Нет короткого пути для быстрого решения интегральной делимой функции. Но вы можете взять идею из правила первообразного частного или использовать другие методы, такие как подстановка интеграла, частичное дробное интегрирование или интегрирование по частям.

Калькулятор длинного деления – Решите многочленное длинное деление онлайн

Знакомство с калькулятором деления на длинные числа

Калькулятор деления на длинные полиномы представляет собой онлайн-инструмент, который используется для вычисления или деления многозначных чисел. Калькулятор полиномиального деления помогает делить многозначные числа и дает ответ в несколько шагов.

Это также поможет в решении уравнений и даст результат делителя, который дает частное. Определенные интегралы или неопределенные интегралы можно вычислить с помощью Калькулятор полиномов от деления .

Инструмент экономит ваше время, потраченное на решение деления в большую сторону вручную. Этот калькулятор облегчит вам решение неправильных интегралов или уравнений, и все это бесплатно.

Как найти онлайн-калькулятор деления многочленов?

Калькулятор длинного деления с шагом известен как самый продвинутый онлайн-калькулятор, который можно легко найти в Интернете. Этот расширенный калькулятор многочленов с делением на длинное деление можно искать или находить простыми шагами. Эти простые шаги:

В интернете гугл поможет найти калькулятор полиномиального деления . По сути, вы можете ввести основное ключевое слово этого калькулятора Интегральный калькулятор длинного деления с шагами в строке поиска Google. Google немедленно направит вас к этому инструменту. Все зависит от вас, чтобы выбрать правильный вариант и выбрать основной калькулятор.
Связанный: Google также помогает найти другие современные интегральные приложения, такие как интегральный калькулятор Римана или интегральный калькулятор трапеций.
Google покажет вам различные результаты после ввода ключевых слов. Главное для выбора этого инструмента — понять инструкции и рекомендации по использованию этого калькулятора. Выберите инструмент после внимательного прочтения инструкций и использования полиномов калькулятора деления на длинные.
Другой способ найти это напрямую — написать название веб-сайта «Integral Calculator». На сайте разработано много 9Калькуляторы интеграции 0006 , из которых вы можете легко найти калькулятор полиномов деления.

Используйте наш лучший калькулятор площади между кривыми, чтобы найти точную площадь под кривой.

Преимущества использования калькулятора полиномиального деления на длинное деление

Мы уже знаем, что деление на длинное деление — длительная процедура, которую приходится решать вручную. Таким образом, использование этого калькулятора дает множество преимуществ, которые могут заключаться в следующем:

Калькулятор интеграла деления помогает вычислить задачи всего за несколько секунд и шаг за шагом решить функции деления на 1.
Помогает сэкономить время и избавляет от ручных расчетов
Он помогает практиковать понятия деления в длину онлайн, и вы также можете узнать о делении в длину с помощью этого калькулятора.
Этот калькулятор предоставляет график и возможные промежуточные шаги длинного деления и его возможное количество шагов.
Он также предоставляет действительную часть, мнимую часть и альтернативную форму определенных интегралов или неопределенных интегралов в результате.
Этот бесплатный калькулятор помогает вычислять точные результаты.

Связанный: Чтобы получить точные результаты метода подстановки, вы должны попробовать наш бесплатный калькулятор тригонометрического интеграла, а также калькулятор интеграции u-подстановки.

Результаты, полученные с помощью калькулятора интегрирования в длинное деление

Результаты, полученные с помощью калькулятора интегрирования в длинное деление с шагом , очень точны. Он шаг за шагом даст ответы на каждую функцию, которые легко понять.

Результаты, полученные с помощью этого калькулятора, являются окончательными и содержат простые шаги для правильного понимания деления в большую сторону. Это поможет найти действительную часть, мнимую часть, промежуточные шаги, альтернативную форму интегралов и разложение интегралов в ряды в результатах.

Надежен ли калькулятор интегралов с длинным делением?

Результаты, полученные с помощью калькулятора интегрирования деления в длину, можно считать надежными. Этот калькулятор поможет быстрее рассчитать функции и шаг за шагом предоставит точные результаты.

Помогает сэкономить время и решить проблемы всего за несколько секунд. Этот калькулятор даст возможность учиться во время практики во время выполнения.

Связанный: Использование этого интегрирования с использованием калькулятора неполных дробей поможет вам легко решать и изучать интегрирование неполными дробями.

Как использовать интегральный калькулятор длинного деления?

Использование этого инструмента облегчит вам решение функций или уравнений. Он имеет простые инструкции и рекомендации, которые легко понять. Вот некоторые из основных шагов для использования этой интеграции с помощью калькулятора деления в большую сторону:

Первым шагом является выбор функции или ввод функции из калькулятора.
Выберите, хотите ли вы оценивать функции деления в длинном ряду как определенный интеграл или неопределенный интеграл.
Если вы хотите выбрать определенный интеграл, то выберите верхнюю и нижнюю границы для процесса интегрирования, а если вы хотите выбрать неопределенные интегралы, то нет необходимости выбирать верхнюю или нижнюю границу. Он автоматически исчезает после выбора неопределенного интеграла.
Выберите переменные относительно x, y, z в соответствии с вашей функцией.
Затем нажмите кнопку «Рассчитать», чтобы обработать функцию. Калькулятор полиномиального длинного деления выдаст результаты за несколько секунд и даст вам решение шаг за шагом.

Зачем использовать Калькулятор интеграции длинного деления?

Калькулятор интегрального деления известен как лучший источник для вычисления деления на длинное, интегрирования, функций, выражений и определенных интегралов или неопределенных интегралов. Это поможет в оценке длительного процесса деления.

Целью использования этого калькулятора является достижение наилучших результатов за короткое время. Он также используется для пошагового получения результата деления. Это помогает в выборе переменных и определенных интегралов, а также неопределенных интегралов в соответствии с вашим выбором расчета. Это поможет в расчете всех делений бесплатно и предоставит простые инструкции, которым легко следовать.

Так что продолжайте использовать современные и продвинутые инструменты интеграции, такие как интегрирование по частям и многие другие, которые этот интегральный калькулятор предоставляет для точного решения интеграла с шагами.

Часто задаваемые вопросы

Каковы четыре этапа интеграции длинного подразделения?

Четыре шага интегрирования делением:

Проверьте интеграл, чтобы увидеть, больше ли степень полинома в числителе.
Алгебраически разделить числитель на знаменатель.
Перепишите интеграл после деления.
Проинтегрируйте оставшийся интеграл, чтобы найти решение.

Но вам не нужно запоминать эти шаги, если вы делаете свои расчеты по этому интегрированию с помощью калькулятора деления.

Когда использовать интеграцию длинных разделов?

Если интеграл имеет дробную форму (P(x)) / (Q(x)) и P(x) больше, чем Q(x), то для его вычисления необходимо использовать метод деления в длинную сторону. Он преобразует дробную форму функции в простую форму, а затем легко интегрирует.

Метод длинного деления аналогичен методу частичной дроби. Вы можете использовать калькулятор деления многочленов для нахождения интеграла от неправильных дробей онлайн.

При использовании интегрирования неполными дробями обязательно ли использовать длинное деление?

При интегрировании функции неполной дробью необходимо следить, чтобы степень полинома числителя была меньше знаменателя. Если степень многочлена числителя больше знаменателя, то необходимо использовать метод деления в длинную сторону.

Что такое метод длинного деления в интегрировании?

Метод длинного деления в интегрировании — это способ решения дробных интегралов. В этом методе дробь преобразуется в простую форму делением в большую сторону. Это помогает решить интеграл, уменьшая степень многочлена в числителе.

Таким образом, длинное деление является одним из важных методов решения интеграла дробей. Вы можете использовать полиномы калькулятора деления для решения этого типа интегралов.0001

. 1995 ноябрь; 121(11):3687-702.

дои: 10.1242/dev.121.11.3687.

Х Накато ¹ , Т. А. Фатч, С. Б. Селлек

принадлежность

¹ ARL Отделение нейробиологии, Аризонский университет, Тусон 85721, США.

PMID: 8582281
DOI: 10. 1242/dev.121.11.3687

H Накато и др. Разработка. 1995 ноябрь

. 1995 ноябрь; 121(11):3687-702.

дои: 10.1242/dev.121.11.3687.

Авторы

H Накато ¹ , Т. А. Фатч, С. Б. Селлек

принадлежность

¹ ARL Отделение нейробиологии, Аризонский университет, Тусон 85721, США.

PMID: 8582281
DOI: 10.1242/dev.121.11.3687

Абстрактный

Мы разработали генетический скрининг для получения мутантов, влияющих на формирование паттерна клеточного деления в развивающейся центральной нервной системе дрозофилы. Локус с аномальной задержкой деления (dally) идентифицировали с использованием комбинации методов «усилительной ловушки» и поведенческого скрининга. Упорядоченная прогрессия клеточного цикла клеток-предшественников пластинки, которые генерируют синаптические нейроны-мишени для фоторецепторов, нарушена у мутантов dally. Первое из двух делений клеток-предшественников пластинки показывает отсроченное вступление в митоз. Второе деление, запускаемое межклеточным сигналом от аксонов фоторецепторов, не происходит. Подобно предшественникам пластинок, клетки, которые генерируют омматидии взрослого глаза, демонстрируют два синхронизированных деления, обнаруженных вдоль морфогенетической борозды в глазном диске, а первый цикл деления у мутантов dally демонстрирует отсроченное продвижение в фазу М, подобное тому, что наблюдается у предшественника первой пластинки. деление клеток. dally мутации также влияют на жизнеспособность и вызывают морфологические дефекты в некоторых тканях взрослых особей, включая глаза, антенны, крылья и гениталии. Секвенирование кДНК dally выявило потенциальную открытую рамку считывания из 626 аминокислот, гомологичную семейству интегральных мембранных протеогликанов, родственных глипикану. Эти белки, содержащие гепарансульфат, присоединены к внешнему листку плазматической мембраны посредством гликозилфосфатидилинозитоловой связи. Протеогликаны гепарансульфата могут служить корецепторами для множества секретируемых белков, включая фактор роста фибробластов, фактор роста эндотелия сосудов, фактор роста гепатоцитов и членов семейств Wnt, TGF-бета и Hedgehog. Дефекты клеточного деления, обнаруженные у мутантов dally, указывают на то, что Glypican группа интегральных мембранных протеогликанов участвует в контроле клеточного деления во время развития.

Цитируется

Сложные белковые взаимодействия опосредуют функцию Lar дрозофилы в мышечной ткани.
Каваками Дж., Брукс Д., Залмай Р., Хартсон С.Д., Буяин С., Гейсбрехт Э.Р. Каваками Дж. и др. ПЛОС Один. 2022 27 мая; 17 (5): e0269037. doi: 10.1371/journal.pone.0269037. Электронная коллекция 2022. ПЛОС Один. 2022. PMID: 35622884 Бесплатная статья ЧВК.
Модуляция пути ежа с помощью глипикан-3-конъюгированного гепарансульфата.
Лю Ю.С., Вербовски Б.М., Салич А. Лю Ю.С. и соавт. Дж. Клеточные науки. 2022 15 марта; 135 (6): jcs259297. doi: 10.1242/jcs.259297. Epub 2022 17 марта. Дж. Клеточные науки. 2022. PMID: 35142364
Молекулярно-генетические методы определения функций протеогликанов у дрозофилы.
Боуден Н., Такемура М., Накато Х. Боуден Н. и др. Методы Мол Биол. 2022;2303:405-414. дои: 10.1007/978-1-0716-1398-6_32. Методы Мол Биол. 2022. PMID: 34626396 Бесплатная статья ЧВК.
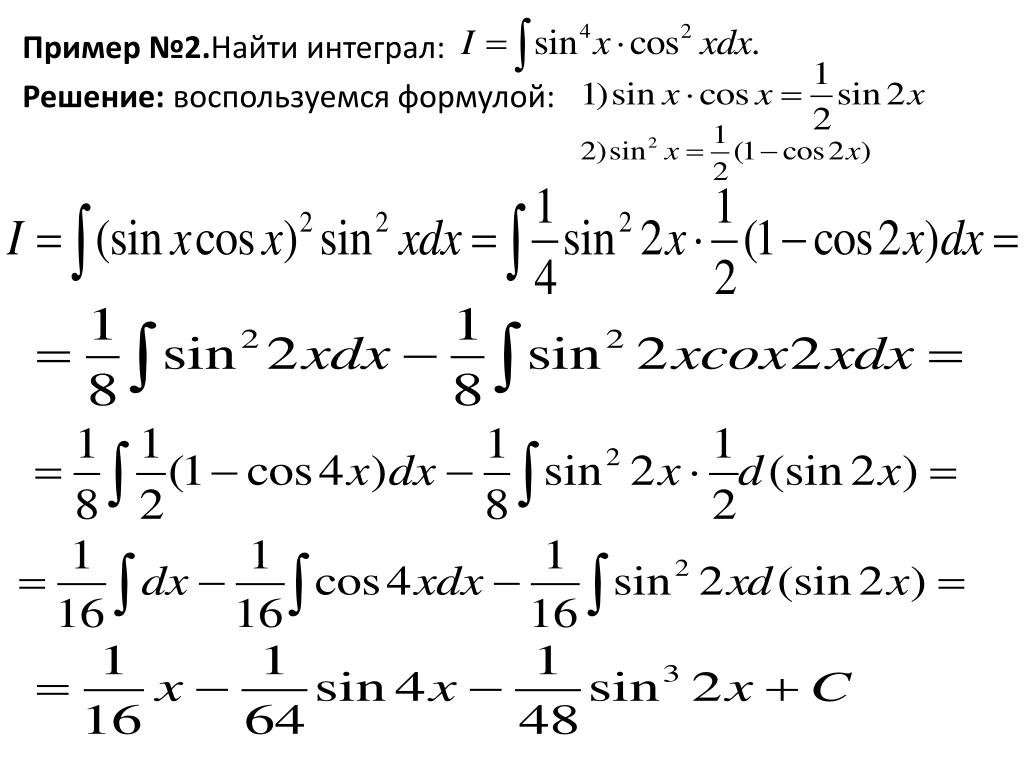
Glypicans определяют уникальные роли корецепторов Hedgehog boi и ihog в опосредованном цитонемами формировании градиента.
Саймон Э., Хименес-Хименес С., Сейхо-Барандиаран И., Агилар Г., Санчес-Эрнандес Д., Агирре-Тамарал А., Гонсалес-Мендес Л., Риполл П., Герреро И. Саймон Э. и др. Элиф. 2021 6 августа; 10: e64581. doi: 10.7554/eLife.64581. Элиф. 2021. PMID: 34355694 Бесплатная статья ЧВК.
Глипиканы и гепарансульфат в развитии синапсов, пластичности нейронов и неврологических расстройствах.
Камимура К., Маэда Н. Камимура К. и др. Передние нейронные цепи. 2021 10 фев; 15:595596. doi: 10.3389/fncir.2021.595596. Электронная коллекция 2021. Передние нейронные цепи. 2021. PMID: 33679334 Бесплатная статья ЧВК. Обзор.

Просмотреть все статьи “Цитируется по”

Типы публикаций

термины MeSH

вещества

Грантовая поддержка

NS 07292/NS/NINDS NIH HHS/США

детективов по борьбе с болезнями Уганды: неотъемлемая часть остановки распространения COVID-19 | Отдел глобальной охраны здоровья | Global Health

Быстрый рост числа случаев COVID-19 во время первой волны в Уганде в 2020 году создал огромную нагрузку на медицинские учреждения и службы страны. Многие вспышки произошли в местах высокого риска, где распространена переполненность, например, в больницах и тюрьмах. Поскольку первая волна продолжалась по всей Уганде, меры общественного здравоохранения, направленные на прекращение распространения COVID-19,стал еще более критическим.

Важной программой, направленной на борьбу с угрозами общественному здравоохранению, такими как COVID-19, является Программа стипендий в области общественного здравоохранения Уганды (PHFP), двухгодичная программа обучения эпидемиологии в полевых условиях, поддерживаемая Центрами США по контролю и профилактике заболеваний (CDC). На протяжении всей пандемии стипендиаты PHFP из Уганды участвовали во многих расследованиях вспышек COVID-19, два из которых указаны ниже.

Стипендиаты PHFP помогают разработать национальные рекомендации по уходу на дому при COVID-19

В начале пандемии обычной практикой в Уганде была госпитализация всех, у кого был положительный результат на COVID-19. Эта практика была очень эффективной для сдерживания вспышки, но она была дорогостоящей и ограничивала количество больничных коек. Поскольку учреждения быстро заполнялись, Уганда была вынуждена перейти к уходу на дому (HBC), когда уход обычно обеспечивали члены семьи. Однако не существовало национальных руководств по передовому опыту HBC, что затрудняло внедрение этого подхода.

Только в ноябре 2020 года в округе Касесе и прилегающем округе Кабароле, которые находятся на западе Уганды, было зарегистрировано более 750 случаев заболевания COVID-19. Без четких и унифицированных руководств по передовым методам стало трудно замедлить распространение COVID-19 среди сообществ с пациентами с HBC. Таким образом, многие из этих случаев произошли среди членов семьи пациентов в условиях HBC.

Ведение расследования COVID-19 в двух округах

Ведущий следователь Джеффри Амания беседует с человеком, который ранее вылечился от COVID-19. Фото: д-р Ричард Мигиша/Программа стипендий в области общественного здравоохранения Уганды

Два стипендиата-эпидемиолога из PHFP Уганды провели расследование передачи COVID-19 в домашнем хозяйстве в округах Касесе и Кабароле при поддержке районных медицинских работников и CDC. Ученые обнаружили, что наличие более одного человека в комнате (т. е. «переполненный дом»), наличие инфицированного члена семьи с кашлем и тесный контакт с инфицированным человеком повышают риск заражения других членов семьи. вирус, вызывающий COVID-19. Кроме того, члены домохозяйства с высоким кровяным давлением имели повышенный риск заражения.

Г-н Джеффри Амания, выпускник программы PHFP в Уганде в 2022 году и ведущий исследователь, заявил: «Было легко проверить первоначальные случаи и поместить их в домашнюю изоляцию, но отсутствие обучения тому, как осуществлять уход на дому, плохая или отсутствие мониторинга симптомов и отсутствие знаний о группах риска увеличили количество и тяжесть случаев заболевания в этих домах».

Представление результатов исследования для разработки национальных рекомендаций

Г-н Аманья представил результаты исследования в офис HBC Министерства здравоохранения Уганды. Офис HBC использовал эти данные для разработки рекомендаций HBC для Уганды. В руководящих принципах говорится, что члены домохозяйства с COVID-19 должны проявлять особую осторожность, чтобы изолировать себя от людей с высоким риском серьезного заболевания COVID-19, в том числе от людей пожилого возраста, с ослабленным иммунитетом, с определенной инвалидностью или сопутствующими заболеваниями. . В руководящих принципах также говорится, что для того, чтобы дом считался подходящим для HBC, необходима отдельная комната с адекватной вентиляцией.

Работа стипендиатов программы PHFP из Уганды при поддержке районных сотрудников здравоохранения и CDC предоставила Министерству здравоохранения Уганды данные, необходимые для устранения недостатков в практических рекомендациях HBC.

Почему это важно: Уганда пережила разрушительную вторую и третью волны COVID-19 в 2021 и начале 2022 года, что вынудило страну снова вернуться к HBC. Недавно разработанные руководящие принципы содержат четкие инструкции, которые помогают гражданам Уганды оставаться здоровыми, заботясь о членах своей семьи.

Профилактика COVID-19 в тюрьмах Уганды: работа простых вмешательств

Стипендиаты программы общественного здравоохранения Уганды д-р Ричард Мигиша и Джоб Морукиленг и супервайзер Клэр Бирибава проводят интервью с работниками здравоохранения в тюрьме Морото, Уганда, для выработки гипотез, октябрь 2020 г. Фото: Служба тюрем Уганды.

Вспышки COVID-19 также представляют серьезную угрозу в тюрьмах. Из-за скопления людей профилактические меры, такие как физическое дистанцирование, не всегда осуществимы.

3 сентября 2020 г. заключенный, находившийся на карантине в тюрьме Морото, расположенной на северо-востоке Уганды, дал положительный результат на SARS-CoV-2, вирус, вызывающий COVID-19. Затем были протестированы сотрудники учреждения и все его население из 692 заключенных. В общей сложности 202 заключенных и 8 сотрудников дали положительный результат. Под руководством CDC два научных сотрудника-эпидемиолога из PHFP Уганды исследовали вспышку в тюрьме Морото, чтобы определить, как был занесен и распространен COVID-19, и предложили рекомендации по предотвращению дальнейшего распространения болезни.

Понимание хода вспышки

Стипендиаты PHFP провели расследование и узнали, что COVID-19 был занесен в тюрьму Морото от заключенного, который заразился во время недавнего пребывания в ближайшей региональной специализированной больнице. Он прошел тестирование перед выпиской из больницы, но вернулся в тюремную карантинную камеру до того, как стали известны результаты теста. Карантинная камера была переполнена 65 другими заключенными, что затрудняло физическое дистанцирование. К тому времени, когда результат теста оказался положительным, COVID-19уже распространился на остальную часть объекта, вероятно, через сотрудников общепита.

Важность профилактических мер

«Эта вспышка произошла одновременно с другой вспышкой в тюрьмах Уганды и имела почти идентичные результаты», — сказала д-р Джули Харрис, постоянный советник CDC для стипендиатов PHFP в Уганде. «Оба исследования показали, что доступ к маскам и мытью рук снижает риск заражения на 70–80%. Мы поделились этими выводами с пенитенциарной системой Уганды, чтобы порекомендовать им сделать маски и приспособления для мытья рук доступными для заключенных во всех тюрьмах».

Благодаря рекомендациям группы пенитенциарная система Уганды лучше защищает граждан страны и помогает предотвратить новые вспышки.

Программы развития кадров, такие как PHFP в Уганде, повышают ценность местных и национальных систем здравоохранения. Вместе стипендиаты PHFP из Уганды и CDC подчеркнули важность своевременного выявления заболеваний, реагирования на вспышки, а также доступности и реализации простых профилактических мер. Работа выпускников PHFP помогает повысить глобальную безопасность в области здравоохранения, лучше защищая здоровье населения во время COVID-19.пандемия.

Как ПДОДИ может помочь исцелить социальное разделение – Интегральная жизнь

Меню

Выбор редакции Эпоха трансформации

Робб Смит

19 ноября 2020 г.

Главные темы): образ жизни Политика События в мире

Акцент на интеллекте(ах): познавательный Этический Ценности Волевой

Робб Смит 19 ноября 2020 г. Познавательный, Выбор редакции, Этический, Стиль жизни, Перспективы, Политика, Эпоха трансформации, Ценности, Воля, Какое более обнадеживающее будущее для цивилизации?, Мировые отношения

Т
Серия Эпохи Трансформации — это серия письменных статей и сопутствующих веб-трансляций, которые Робб Смит будет вести для сообщества Интегральной Жизни в режиме реального времени по мере того, как разворачивается Великое Освобождение (ВГР), дающее начало Эпохе Трансформации.
В этой подборке лучших моментов из Разделенные умы, разделенные общества: как ILP может помочь исцелить социальное разделение , Сессия генерального директора Integral Life Робба Смита на нашем недавнем онлайн-ретрите Exhale Робб утверждает, что отчасти наша ответственность заключается в том, чтобы помочь другим уменьшить их страхи в мире, который становится все более сложным. и кажется более угрожающим десяткам миллионов людей, особенно тем, кто находится на более ранних стадиях развития, образования и открытости. Это не призыв к умиротворению, и соперничество ярко выражено, а скорее призыв начать понимать нашу глобальную политическую ситуацию с точки зрения развития: постконвенциональные способности Интеграла/Бирюзового должны прийти на помощь нашим Оранжевым институтам и Зеленой культуре, чтобы встречайте красные и янтарные политические ценности там, где они есть. Если мы этого не сделаем, то переход к Эпохе Трансформации и Великому Освобождению, в котором мы находимся, поскольку наши экономические, культурные и политические разногласия растут, будет более трудным и бурным, чем это должно быть.
Робб считает, что ILP может помочь нам в этом. Помогая нам проснуться, повзрослеть, привести себя в порядок и проявить себя, ПИЖ является мощной основой для устранения разрыва внутри каждого из нас, который держит нас в ловушке наших собственных страхов и мешает нам предлагать действительно целостные решения наших нынешних проблем и проблем. разногласия. В самом деле, только создавая трансформирующие контейнеры, которые смягчают постоянное ощущение угрозы внутри нашего разделенного политического тела, например, посредством политики, которая помогает удовлетворить потребности в безопасности, или политики, которая больше фокусируется на общих ценностях, а не на культурной войне, — мы можем смягчить дисфункцию, подпитывающую сверхбдительность, и выиграть войну за просвещенную любовь, которая потребуется, чтобы предотвратить продолжающийся регресс к дооранжевому, допросветительскому насилию, что Робб считает метастазирующим раком (в самом сердце Запада), что весьма вероятно. станет еще хуже, если бодрствующие сообщества не помогут переломить ситуацию.
Примечание. Эти основные моменты отредактированы для сохранения конфиденциальности участников, которые задавали вопросы во время обсуждения Робба.
Темы включают:
0:00 — Политические оппоненты: возлюби достоинство, смягчи страх
2:45 — Пробужденные сообщества могут быть трансформирующими
4:45 — Вступая в эпоху трансформации
9:56 — Сохраняя свою власть Во время Великого Освобождения
15:45 — Дооранжевая война за власть
18:20 — Преодолевая этапы
19:18 — Помогите людям преодолеть страх
21:15 — ПИЖ поможет вам развить свои навыки и силу
Предыдущие эпизоды из
Эпоха трансформации
Статья Когнитивное Этическое Свободное Лидерство Перспективы Преобразования Возрастные Ценности Видео Какое будущее более обнадеживающее для цивилизации? Мировые отношения Мировоззрения
Робб Смит 2 марта 2022 г. 80 Ответов
Вторжение России в Украину — это не просто нарушение суверенитета Украины, это скоординированное нападение при содействии Китая. ..
Смотреть сейчас
Великое освобождение, эпоха трансформации
+Просмотреть все
Станьте участником сегодня, чтобы посмотреть эту видео-презентацию и поддержать глобальное появление Интегрального сознания
Преимущества членства включают: Получите полный доступ к еженедельным беседам ведущих мыслителей
Библиотека журналов
Получите полный доступ к растущей библиотеке Journal of Integral Theory & Practice
Live Experience
Оставайтесь на связи, участвуя в живых мероприятиях и дискуссиях Integral Life
Курсы и продукты
Получите неограниченную скидку 20% на все продукты и курсы от наших друзей и партнеров
Бесплатные бонусные подарки
Скачать The Integral Электронная книга Vision Кена Уилбера (стоимостью 19 долларов на Amazon) и серия биографий Кена Уилбера
Поддержка движения
Поддержите нашу миссию по обучению и распространению интегрального сознания, которое важнее, чем когда-либо в его истории
Узнайте больше о планах членства →
О Роббе Смите
Робб Смит — ведущий мыслитель эпохи трансформации и глобального интегрального движения. Он является соучредителем и генеральным директором Integral Life.
ILP
О Integral Life
Integral Life — это цифровое медиа-сообщество, управляемое членами, которое поддерживает рост, образование и применение интегральной философии и интегративной метатеории к сложным проблемам 21 века. Интегральная жизнь предлагает перспективы, практики, анализ и сообщество, чтобы помочь людям развить все способности интегрального сознания, чтобы процветать в быстро развивающемся мире.
Другие полезные вещи
Помощь и поддержка
Новости и объявления
Присоединяйтесь к Integral Life
Что такое интегральный подход?
Моя учетная запись
Избранные гости
Условия обслуживания
Подпишитесь на обновления по электронной почте
Получайте уведомления о новых средствах массовой информации и методах, которые могут расширить ваш кругозор и изменить вашу жизнь.
Произвольно маршрутизируемые мультиплексированные фотонные схемы с разделением по модам для плотной интеграции
Abstract
Встроенное интегрированное мультиплексирование с разделением по модам (MDM) — новый метод для передачи данных большой емкости. За последние несколько лет, хотя было разработано несколько конфигураций для реализации встроенных схем MDM, их практическое применение значительно затруднено из-за большой занимаемой площади и межмодовых перекрестных помех. Самое главное, по-прежнему отсутствует высокоскоростная передача сигнала МДМ в произвольно маршрутизируемом контуре. Здесь мы демонстрируем схемы MDM, основанные на оцифрованных метаструктурах, которые имеют чрезвычайно компактные размеры. Сигналы со скоростью 112 Гбит/с, закодированные в каждом режиме, произвольно маршрутизируются по цепям, состоящим из множества резких изгибов и компактных пересечений с коэффициентом битовых ошибок ниже предела прямой коррекции ошибок. Это значительно улучшит плотность интеграции и принесет пользу различным встроенным многомодовым оптическим системам.
Введение
Ортогональные направляющие моды в интегрированных оптических волноводах считаются важной степенью свободы, обеспечивающей гибкость и масштабируемость для широкого спектра внутрикристальных приложений, таких как оптические межсоединения ^1,2,3,4 , квантовые информатика ^5,6 , нелинейная оптика ^7,8 и так далее. В последнее время мультиплексирование с разделением режимов (MDM) становится мощной технологией для увеличения пропускной способности фотонного чипа. По сравнению с мультиплексированием с разделением по длине волны, для MDM требуется только монохроматический источник света, и точный контроль длины волны не требуется ⁹ . Типичная оптическая система требует различных многомодовых устройств, таких как (дем)мультиплексор ^10,11,12, ответвитель ¹³, переключатель ^14,15,16, модовый фильтр ¹⁷, разветвитель ^18,19 и многие другие строительные блоки ^20,21,22 . Взаимосвязи между этими элементами должны основываться на многомодовых волноводах с несколькими ортогональными и попутно распространяющимися модами. Это довольно сложно, поскольку передача сигнала в таких многомодовых фотонных схемах уязвима для резких изгибов и перекрестных соединений из-за утечки излучения и межмодовой связи. Для достижения адиабатического распространения волны в изогнутом волноводе необходима слишком большая занимаемая площадь ²³ . Независимое от режима пересечение также сложно для мод более высокого порядка, поскольку сигналы MDM необходимо демультиплексировать в одиночные моды перед пересечением волновода ²⁴ . В обоих случаях сигнал MDM маршрутизируется за счет большой площади чипа, что в конечном итоге ограничивает плотность интеграции.
Для произвольной трассировки многомодового волновода изгиб и пересечение являются двумя ключевыми элементами. Недавно были предложены различные волноводные структуры для обеспечения волновода с малыми потерями и низкими межмодовыми перекрестными помехами (CT) для сценария изгиба и перекрестного соединения ^{25,26,27,28,29,30,31} . Однако в большинстве демонстраций достигается только двухрежимный изгиб и пересечение. Недавно Габриэлли и соавт. продемонстрировали трехмодовое изгибание с низкой межмодовой связью, но радиус изгиба большой и необходима литография в оттенках серого ²⁹ . Также сообщалось о пересечении трех режимов на основе структуры линзы Maxwell «рыбий глаз» с площадью основания 11,6 × 11,6 мкм ², где требуется точно спроектированная конусность фокусировки ³¹ .
В этой статье мы демонстрируем сверхкомпактные и произвольно разведенные схемы для трех мод посредством беспрецедентно малого изгиба (радиус 3,9 мкм) и пересечения (8 × 8 мкм ² ). Резкий изгиб и прямая поперечная связь для мод TE ₀ , TE ₁ и TE ₂ достигаются за счет сложного волновода, который реализуется дискретной метаструктурой с рядом наноотверстий. Алгоритм оптимизации используется для разработки сложной структуры распределения наноотверстий. Специализированный профиль преломления обеспечивает согласование мод между многомодовым волноводом и областью изгиба/пересечения. Кроме того, предлагаемые нами устройства могут быть совместимы со стандартным процессом производства кремниевой фотоники (см. Дополнительное примечание 5). Мы добились трехмодового изгиба с 0,71‒0,9Потери 5 дБ и пересечение с потерями 0,28–0,82 дБ в полосе пропускания 80 нм. Наконец, сигналы со скоростью 112 Гбит/с, закодированные в каждом режиме, успешно маршрутизируются по произвольно спроектированным цепям с частотой ошибок по битам (BER) при упреждающем исправлении ошибок (FEC).
Результаты
Трехрежимный изгиб
Микроизгиб с цифровой метаструктурой (DMS) разработан и показан на рис. 1a. Область изгиба разделена на дискретные пиксели с минимальным размером элемента 130 нм. Платформа устройства представляет собой кремний на изоляторе (КНИ) с 220-нм верхним кремнием и 2-мкм скрытым оксидом. Мы определяем бинарное состояние материала для каждого пикселя, т. е. это может быть либо кремний, либо воздух (путем вытравливания кремния). Это позволяет получить локальный контраст преломления Δ n = 2,48 для управления распространением волны. Ширина волновода выбрана равной 2,3 мкм, что позволяет использовать достаточное количество пикселей. Распределение наноотверстий (воздушных пикселей) можно определить с помощью различных алгоритмов оптимизации ^{32,33,34,35,36,37} . Здесь мы используем алгоритм прямого бинарного поиска (DBS) для оптимизации структуры (см. «Методы»). Во-первых, мы разработали чрезвычайно компактный изгиб с внутренним радиусом кривизны всего 2,75 мкм (эффективный радиус: 3,9 мкм) для трехмодовой мультиплексной системы с разделением каналов. Изгиб может поддерживать передачу TE ₀ , TE ₁ и TE ₂ с ТТ с малыми потерями и низкими межмодовыми потерями. Распределения оптического поля для различных мод моделируются трехмерным методом конечных разностей во временной области (FDTD) и показаны на рис. 1b–d. Видно, что оптические волны для всех мод сжимаются и фокусируются в угловую область изгиба несколькими наноотверстиями вблизи внутренней боковой стенки изогнутого волновода. Внешняя граница практически отражает пучок в выходной волновод с сохраненным профилем моды. Хотя это не абсолютно адиабатический процесс, межмодовые помехи могут быть хорошо подавлены до незначительного уровня. Мы также количественно изучаем, как эти наноотверстия влияют на производительность устройства, заполняя некоторые из отверстий кремнием и повторно моделируя спектры пропускания. Мы обнаружили, что три изолированных отверстия вблизи внешней кривизны почти не влияют на передачу всех мод. Эффективность падает <2% без этих отверстий для воздуха. Однако другие наноотверстия имеют решающее значение для производительности устройства. Смоделированные спектры прибора от 1500 до 1580 нм показаны на рис. 1e–g. Смоделированные вносимые потери (IL) составляют 0,4, 0,7 и 0,84 дБ для TE 9.0777 0 , TE ₁ и TE ₂ соответственно. КТ составляют <-20 дБ для всех мод в диапазоне длин волн 80 нм, что достаточно для незначительных штрафов за отношение сигнал/шум (SNR) ^2,4 .
Рис. 1
Результаты проектирования и моделирования изгиба на основе цифровой метаструктуры (DMS). a Принципиальная схема спроектированного трехрежимного изгиба с DMS. б ‒ г Смоделированные распределения оптического поля для микроизгиба с тремя модами (ТЭ ₀ ‒ТЭ ₂ ). e ‒ g Моделируемые спектры пропускания для микроизгиба с тремя модами (TE ₀ ‒TE ₂ )
Изображение в натуральную величину
Процесс изготовления устройства можно найти в разделе «Методы». Чтобы продемонстрировать резкий изгиб волновода с несколькими модами, мы изготовили схему MDM, состоящую из мультиплексора мод (MUX), двух каскадных изгибов и демультиплексора мод (DEMUX), как показано на рис. 2a. MUX также представляет собой компактную DMS с площадью основания всего 3,4 × 3,9 дюйма.мкм ² , что подробно описано в дополнительном примечании 1. Как показано на рис. 2a, схема имеет три входных порта, помеченных как I1 (режим TE ₀), I2 (режим TE ₁) и l3. (режим TE ₂) и три выходных порта, обозначенных как O1–O3 (режимы TE ₀ – TE ₂), соответственно. Тем временем, как показано на рис. 2b, изготавливается дополнительная эталонная схема с режимом MUX с режимом «встречно-параллельно», чтобы нормализовать передачу устройства и извлечь потери на изгибе. Решетчатый ответвитель с поперечной электрической (TE) поляризацией используется для сопряжения волокна и волновода. Потери связи составляют ~6 дБ на грань. Изогнутый волновод на основе DMS хорошо изготовлен в соответствии с нашей разработкой, что видно из изображения, полученного с помощью сканирующего электронного микроскопа (СЭМ) с увеличением, показанного на рис. 2c. Установка для измерения спектров пропускания устройства описана в разделе «Методы». Нормализованные спектры пропускания, измеренные на портах O1–O3, представлены на рис. 2d–f при запуске непрерывной волны с входных портов I1–I3 соответственно. Измеренные потери на изгибе составляют 0,71, 0,74 и 0,9.5 дБ для мод TE ₀ , TE ₁ и TE ₂ соответственно. Измеренные ТТ составляют <-20 дБ для всех ведущих мод от 1500 до 1580 нм, что вполне согласуется с результатами моделирования.
Рис. 2
Изготовление и экспериментальные результаты изгиба на основе цифровой метаструктуры (DMS). a Вид сверху под микроскопом схемы мультиплексирования с разделением мод (MDM), состоящей из мультиплексора (MUX), изгибающего и демультиплексора (DEMUX). b Микроскопическое изображение эталонной схемы: мультиплексоры (DE)MUX вплотную друг к другу. c Изображение изготовленного изгиба, полученное с помощью сканирующего электронного микроскопа. d ‒ f Измеренные спектры пропускания схемы МДМ для оптической волны, запущенной из I1 (мода TE ₀), I2 (мода TE ₁) и l3 (мода TE ₂) соответственно
Полноразмерное изображение
Трехмодовое пересечение
Маршрутизация на кристалле неизбежно требует решения проблемы перекрестного соединения волновода. Здесь мы разрабатываем трехмодовое пересечение со следом всего 8 × 8 мкм ² . Структурная принципиальная схема устройства представлена на рис. 3а. Устройство имеет квадратурную симметрию с минимальным размером элемента 130 нм. Ширина входного/выходного волновода пересечения установлена равной 1,4 мкм для поддержки режимов TE ₀, TE ₁ и TE ₂. Каждая квадратурная область является осесимметричной и занимает площадь чипа всего 4 × 4 мкм ² . Эта проектная область разделена на 25 × 25 дискретных пикселей. Процесс оптимизации аналогичен проектированию изгиба. На рисунках 3b–d показаны смоделированные профили оптического поля в плоскости наноструктурного пересечения, когда входные волны TE ₀ , TE ₁ и TE ₂ соответственно. В угловой области пересечения расположено несколько наноотверстий, что обеспечивает запрещенную зону с низким индексом, чтобы избежать расширения мод. Следовательно, профиль каждой моды может хорошо сохраняться при распространении через область пересечения. Существует небольшая утечка мод в ортогональный волновод. Это можно дополнительно уменьшить, установив дополнительную цель оптимизации для уменьшения такой утечки мощности. Чтобы количественно исследовать характеристики пересечения, мы вычисляем эффективность передачи и моду CT, принимая во внимание интеграл перекрытия мод. На рис. 3e–g показаны рассчитанные спектры IL и CT. Смоделированные ИЖ для ТЭ ₀ , TE ₁ и TE ₂ составляют 0,2, 0,55 и 0,59 дБ соответственно. Смоделированные ТТ составляют <−30 дБ для всех мод в диапазоне длин волн от 1500 до 1580 нм.
Рис. 3
Результаты проектирования и моделирования трехмодового пересечения. a Принципиальная схема проектируемого трехрежимного перехода с цифровой метаструктурой. б ‒ г Моделируемые распределения оптического поля для трехмодового пересечения с ТЕ ₀ ‒ ТЕ ₂ . e ‒ g Смоделированные спектры пропускания для трехмодового пересечения с TE ₀ ‒TE ₂
Изображение в натуральную величину . Микроскопическое изображение схемы показано на рис. 4а. Устройства были изготовлены с использованием того же процесса, что и гибка. Из-за сверхнизких потерь при отдельном пересечении мы каскадируем различные количества пересечений для точного извлечения IL устройства. На рис. 4b показано изображение под микроскопом четырехступенчатой каскадной схемы пересечения, которая более поддается измерению, чем одиночное пересечение. На рис. 4c увеличенное СЭМ-изображение наноструктурного пересечения подтверждает, что желаемый рисунок был успешно перенесен на уровень устройства. Спектры пропускания каскадного пересечения измеряются и нормируются. Измеренные IL и CT для TE ₀ ‒TE ₂ мод одиночного пересечения показаны на рис. 4г–е соответственно. IL составляют 0,28, 0,68 и 0,82 дБ для мод TE ₀ , TE ₁ и TE ₂ соответственно. ТТ для всех режимов характеризуются измерением оптической мощности на других выходных портах. Спектры показывают, что ТТ составляют <-20 дБ для всех трех ведущих мод.
Рис. 4
Изготовление и экспериментальные результаты трехмодового пересечения. а Вид сверху под микроскопом на схему мультиплексирования с разделением мод (MDM), состоящую из мультиплексора, кросса и демультиплексора. b Микроскоп четырехкаскадного пересечения. c Снимок сфабрикованного перекрестка, сделанный с помощью сканирующего электронного микроскопа. d ‒ f Измеренные спектры передачи для схемы МДМ
Изображение в полный размер
Схемы маршрутизации МДМ
Большинство предыдущих демонстраций по схеме МДМ с трудом разводили многомодовые волноводы из-за ограниченных возможностей резкого поворота и компактности перекрестное соединение. Здесь мы демонстрируем возможность произвольной и компактной внутрикристальной маршрутизации высокоскоростных сигналов (112 Гбит/с) в схемах MDM. В принципе, сигнал MDM может быть доставлен в любое место расположения чипа по любому пути маршрутизации при условии, что доступны изгиб и пересечение с низкими потерями. Для демонстрации концепции мы произвольно проектируем две схемы MDM с предлагаемым изгибом и пересечением. Цепь MDM 1 состоит из MUX, четырех ответвлений, пересечения и DEMUX. Микроскопическое изображение трехрежимной мультиплексной схемы с разделением каналов показано на рис. 5а. Такая схема допускает как резкое изгибание, так и перекрестное соединение, которое можно масштабировать для сценариев каскадной структуры или массива волноводов. Определим входные порты I1–I3 и выходные порты O1–O3 для ТЭ ₀ ‒TE ₂ мод соответственно. На рис. 5b, c показаны измеренные спектры IL и CT для всех мод после прохождения по цепи. Потери возникают из-за MUX, DEMUX, двухкратного перекрестного соединения и четырехкратного изгиба. Средний IL составляет ~8 дБ, а ТТ <−20 дБ в диапазоне длин волн 1500‒1580 нм.
Рис. 5
Изготовление и экспериментальные результаты схемы 1 мультиплексирования с разделением мод (MDM). демультиплексор. b Измеренные вносимые потери для различных портов ввода/вывода. c Измеренные характеристики перекрестных помех для различных портов ввода/вывода
Изображение с полным размером
Цепь MDM 2 состоит из MUX, десяти отводов и DEMUX. Волновод имеет спиральную конфигурацию и может быть дополнительно масштабирован до плотного спирального волновода. Эта схема используется для подтверждения возможности непрерывного изменения направления маршрутизации. Микроскопическое изображение схемы 2 МДМ показано на рис. 6а. Измеренные спектры IL и CT контура 2 показаны на рис. 6b, c. Средний IL для всех модовых каналов составляет 12 дБ от 1500 до 1580 нм. Измерено, что CT цепи MDM 2 составляет <-20 дБ в том же диапазоне длин волн.
Рис. 6
Изготовление и экспериментальная демонстрация схемы 2 мультиплексирования с разделением мод (MDM). b Измеренные вносимые потери для различных портов ввода/вывода. c Измеренные характеристики перекрестных помех для различных портов ввода/вывода
Изображение с полным размером
Помимо простого измерения потерь в цепи и трансформатора тока, мы проверили возможность высокоскоростной маршрутизации сигналов через предложенные схемы MDM. Каждый поток дискретных многотональных (DMT) сигналов со скоростью 112 Гбит/с с одинаковым распределением битов передается по каждому каналу цепей MDM один за другим. Хотя мы измеряем каждый модовый канал передачи сигнала отдельно, мы ожидаем возможности одновременной передачи мультиплексированных по модам сигналов. Это связано с тем, что дополнительные потери сигнала в основном возникают из-за межрежимного трансформатора тока цепей MDM. Согласно теоретическим предсказаниям ^2,4 , дополнительные штрафы, вызванные ТТ, незначительны для продемонстрированных схем маршрутизации. Подробную экспериментальную установку и метод цифровой обработки сигналов можно найти в дополнительном примечании 4. Измеренные отклики SNR при параллельном (B2B) случае и передаче MDM представлены на рис. 7a. Отклики SNR практически не изменились после передачи по схеме MDM с очень небольшой разницей по сравнению со случаем B2B, и различия подразумевают различные характеристики передачи среди трех каналов из-за IL, CT и даже нестабильности обстоятельств. Отклик SNR, измеренный в случае B2B, используется для генерации сигнала DMT с помощью алгоритма распределения битов, показанного на рис. 7b. Максимальное распределение битов равно 5, что соответствует 32-QAM. Затем одни и те же сигналы DMT один за другим направляются в каналы разных режимов. Спектрально эффективный метод DMT позволяет нам достичь скорости 112 Гбит / с по одной полосе в условиях ограниченной полосы пропускания. Созвездия с битовым индексом 5 (32-QAM) и 4 (16-QAM) в разных диапазонах поднесущих показаны на вставке к рис. 7b, что указывает на хорошее качество сигнала для форматов модуляции высокого порядка. Выполняется измерение BER, и результаты показаны на рис. 7b. Измеренные кривые BER для DMT со скоростью 112 Гбит/с представлены на рис. 7c, которые в основном ниже предела 20% FEC 9.0378 38 . Таким образом, достигается сверхкомпактная маршрутизация высокоскоростных сигналов. Кроме того, характеристика также была выполнена на более низкой скорости 80-Гбит / с с 4-уровневой амплитудно-импульсной модуляцией (PAM-4) (см. Дополнительное примечание 4).
Рис. 7
Экспериментальные результаты высокоскоростной маршрутизации сигналов в схемах мультиплексирования с разделением по модам (MDM). a Отклик отношения сигнал-шум для двухсторонней передачи (B2B) и MDM-каналов. б Распределение битов для разных поднесущих. Врезка: созвездия разных поднесущих. c Измеренные кривые коэффициента битовых ошибок для B2B и MDM-передачи 100 и 112 Гбит/с дискретного многотонального сигнала
Полноразмерное изображение
Обсуждение
пересечение. Характеристики устройств обобщены в дополнительном примечании 2. Управление оптической волной в такой крошечной структуре зависит от проектирования индекса в глубоком субволновом масштабе. Оптимизированный профиль индекса является ключом к согласованию мод, что помогает нам избежать утечки мод и межмодовой связи. Показатель контрастности наноотверстий с воздушной оболочкой равен 9.0789 н = 2,48. Однако обычно на слой кремния наносится толстая оксидная оболочка, снижающая контраст показателя на 20 %. Здесь мы подтвердили при моделировании, что оксидная оболочка не влияет на конструкцию такого компактного устройства МДМ. Цифровая метаструктура для изгиба и пересечения с оксидной оболочкой разработана в соответствии с правилом проектирования IMEC (см. Дополнительное примечание 5).
Важно проверить вклад этих дискретизированных наноотверстий. Мы численно исследовали работу изгибающейся и пересекающейся структуры, если все вытравленные пиксели снова заполнены кремнием. Для такого крутого изгиба и компактного пересекающегося волновода IL и CT значительно увеличиваются, как мы и ожидали (см. Дополнительное примечание 6). Это, в свою очередь, доказывает эффективность разработки индексов с помощью обратного проектирования.
Методы
Конструкция устройства
Сначала применяется дискретизация к расчетной области устройства. Геометрия каждого пикселя может быть круговой, квадратной или другой сложной формы. Минимальный размер элемента может быть определен в соответствии с возможностями изготовления. Здесь каждый пиксель может быть либо диэлектриком с высоким показателем преломления, либо оболочкой с низким показателем преломления. Метод DBS используется для нахождения правильного распределения двоичных пикселей, которое соответствует целям проектирования. Для исходного шаблона устройства все состояния пикселей выбраны кремниевыми. Затем материальное состояние каждого пикселя изменяется один за другим, и проверяются показатели качества (FOM). Здесь ФОМы – это ИЖ и ТТ для ТЭ 96 \ влево [ {\ влево | {\ frac {{\ beta _ {k, i}}} {{\ beta _ {1, i}}} – 1} \ right | \le \rho _{k,i}} \right]$$
(2)
где η _{j , i} – эффективность передачи j -й моды от j -й до 1500-й моды 1580 нм в I -й итерации ( J = 1 для TE ₀, J = 2 для TE ₁ и J = 3 для TE _{7 2}
), и . _{7897899777777770 и J = 3 для TE _{7 2 9078), и}970770 = 3 для TE _{7 2 9078), и}9. и _{778), и}90 = 3 _{8), и}9. к , и} – K -й CT с 1500 до 1580 нм в I -й итерации ( K = 1 для TE ₀ – TE ₁, K = 2 для TE _{7777777777777777777777777777777777777777777777777 гг.}, K = 3 для TE ₁ – TE ₀, K = 4 для TE ₁ – TE ₂, K = 5 для TE ₂, K = 5 для TE ₂, K = 5 для TE ₂, K = 5 для TE ₂, K = 5 для TE ₂, K _{. и k = 6 для TE ₂ ‒TE ₁ ). σ _j,i – радиус сходимости для эффективности j -я мода в -й -й итерации, а ρ _{j , i} – радиус сходимости для k -й КТ, который является монотонным в -й итерации, убывающая функция.}
Одна итерация завершается после проверки всех состояний пикселей. Затем этот процесс повторяется снова для дальнейшего улучшения FOM в соответствии с проектными задачами. Требуется несколько итераций, чтобы выполнить условие сходимости, где σ и ρ сходятся к нулю: ³⁹
}}}{{\eta _{j,{\mathrm{цель}}}}}} \right)$$
(3)
и
$$\rho _{k,i} = {\ mathrm{\delta}} \times\left( {\frac{{\beta _{k,i}}}{{\beta _{k,{\mathrm{цель}}}}} – 1}\right) $$
(4)
где ε и δ коэффициент сходимости, η _{j ,цель} — это цель передачи j -го режима, а β _{k , цель} — это задача передачи k -го CT.
Выполняем проектирование и оптимизацию устройства с использованием восьмиядерного десктопа. Для гибочного устройства в среднем требуется ~ 50 часов, чтобы получить конвергентные результаты после 4 итераций. Для устройства пересечения требуется ~40 ч после 3 итераций.
Процесс изготовления устройства
Устройства изготавливаются на пластине КНИ с верхним слоем кремния толщиной 220 нм на скрытом оксиде толщиной 2 мкм. В качестве мягкой маски на КНИ используется позитивный фоторезист ZEP 520A. Устройства моделируются с помощью электронно-лучевой литографии (Raith eLINE), работающей при напряжении 30 кВ, после чего верхний слой кремния полностью протравливается на глубину 220 нм с помощью одноступенчатого сухого травления с индуктивно-связанной плазмой.
Измерительная установка и методы
Для определения характеристик устройства установка состоит из свип-лазера (Yenista T100S-HP/SCL), каскада связи оптоволокна с микросхемой и настольного измерителя мощности. Непрерывный выходной сигнал лазера поляризован TE с помощью контроллера поляризации. Решетчатые ответвители используются для сопряжения одномодовых волокон и кремниевых волноводов. Угол наклона в 10 градусов по отношению к нормали к поверхности предназначен для подавления обратного отражения. Измеренные потери связи каждого решетчатого ответвителя составляют ~ 6 дБ. Спектры передачи получаются путем измерения выходной мощности чипа с помощью настольного измерителя мощности. Для высокоскоростных экспериментов установка описана в дополнительном примечании 4.
Доступность данных
Данные, подтверждающие результаты этого исследования, можно получить у соответствующих авторов по обоснованному запросу.
Каталожные номера
Dai, D., Wang, J. & Shi, Y. Кремниевый (де)мультиплексор, обеспечивающий высокую пропускную способность фотонных сетей на кристалле с одноволновой несущей. Опц. лат. 38 , 1422–1424 (2013).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Wu, X. et al. 3 × 104 Гбит / с одиночное межсоединение λ мультиплексной сети с разделением режимов с многожильным волокном. Дж. Лайт. Технол. 36 , 318–324 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Луо, Л. и др. Мультиплексирование с разделением режимов на кремниевой микросхеме, совместимое с WDM. Нац. коммун. 5 , 3069 (2014).
ОБЪЯВЛЕНИЕ Статья Google ученый
Хсу, Ю. и др. Встроенное оптическое межсоединение 2,6 Тбит/с, поддерживающее мультиплексирование с разделением по режимам и сигнал PAM-4. Фотон. Технол. лат. 30 , 1052–1055 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
“>
Фэн, Л. и др. Встроенный источник запутанных пар фотонов поперечной моды. Квантовая информация NPJ. 5 , 2 (2019).
ОБЪЯВЛЕНИЕ Статья Google ученый
Фэн, Л. и др. Встроенное когерентное преобразование фотонной квантовой запутанности между различными степенями свободы. Нац. коммун. 7 , 11985 (2016).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Киттлаус Э., Оттерстром Н. и Ракич П. Интермодальное рассеяние Бриллюэна на кристалле. Нац. коммун. 8 , 15819 (2017).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Киттлаус Э., Оттерстром Н., Харел П., Гертлер С. и Ракич П. Невзаимная межполосная бриллюэновская модуляция. Нац. Фотон 12 , 613–619 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
“>
Донг, П. Кремниевые фотонные интегральные схемы для мультиплексирования с разделением по длине волны. Дж. Сел. Верхний. Квантовый электрон. 22 , 6100609 (2016).
Google ученый
Дин, Ю. и др. Встроенное двухрежимное мультиплексирование с разделением каналов с использованием мультиплексора и демультиплексора режимов на основе конического направленного ответвителя. Опц. Экспресс 21 , 10376–10382 (2013).
ОБЪЯВЛЕНИЕ Статья Google ученый
Дрисколл, Дж. и др. Асимметричные Y-переходы в кремниевых волноводах для встроенного мультиплексирования с разделением мод. Опц. лат. 11 , 1854–1856 (2013).
ОБЪЯВЛЕНИЕ Статья Google ученый
Ван Дж., Чен П., Чен С., Ши Ю. и Дай Д. Улучшенный 8-канальный демультиплексор полупроводникового режима. Опц. Экспресс 22 , 12799–12807 (2014).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Lai, Y. et al. Компактный решетчатый ответвитель с двумя частями для связи мод высшего порядка. Опц. лат. 43 , 3172–3175 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Стерн, Б. и др. Переключатель мультиплексирования с разделением режимов на кристалле. Optica 2 , 530–535 (2015).
КАС Статья Google ученый
Jia, H. et al. Оптический коммутатор, совместимый с мультиплексированием с разделением по длинам волн и мультиплексированием с разделением по модам для фотонных сетей на кристалле. Опц. Экспресс 25 , 20698–20707 (2017).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
“>
Xiong, Y., Priti, R. & Ladouceur, O. Высокоскоростной двухрежимный коммутатор для мультиплексирования оптических сетей с разделением режимов. Optica 4 , 1098–1102 (2017).
Артикул Google ученый
Guan, X., Ding, Y. & Frandsen, L. Сверхкомпактный широкополосный фильтр пропускания мод более высокого порядка, изготовленный в кремниевом волноводе для многомодовой фотоники. Опц. лат. 40 , 3893–3896 (2015).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Chang, W. et al. Инверсный дизайн и демонстрация сверхкомпактного широкополосного двухрежимного делителя мощности на 3 дБ. Опц. Экспресс 26 , 24135–24144 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Xu, H. & Shi, Y. Сверхширокополосный двухрежимный делитель мощности на 3 дБ на основе Y-образного соединения с преобразователями мод. Опц. лат. 41 , 5047–5050 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
Frandsen, L. et al. Преобразование мод с оптимизированной топологией в фотонно-кристаллическом волноводе, изготовленном из материала кремний-на-изоляторе. Опц. Экспресс 22 , 8525–8532 (2014).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Jia, H., Zhou, T., Fu, X., Ding, J. & Yang, L. Обратный дизайн и демонстрация ультракомпактного кремниевого устройства обмена модами метаструктуры. АСУ Фотон 5 , 1833–1838 (2018).
КАС Статья Google ученый
Дорин Б. и Йе В. Двухрежимное мультиплексирование с разделением в кольцевом резонаторе кремний-на-изоляторе. Опц. Экспресс 22 , 4547–4558 (2014).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Jiang, X., Wu, H. & Dai, D. Изгиб многомодового волновода с низкими потерями и низкими перекрестными помехами на кремнии. Опц. Экспресс 26 , 17680–17689 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Чанг В. и др. Ультракомпактный многомодовый волноводный переход на субволновом асимметричном Y-переходе. Фотон. J. 10 , 1–8 (2018).
Google ученый
Sun, C., Yu, Y. & Zhang, X. Ультракомпактный волноводный переход для оптической сети мультиплексирования с разделением мод. Опц. лат. 42 , 4913–4916 (2017).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Sun, C. , Yu, Y., Chen, G. & Zhang, X. Сверхкомпактный изогнутый многомодовый кремниевый волновод со сверхнизкими межмодовыми перекрестными помехами. Опц. лат. 42 , 3004–3007 (2017).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Чанг В. и др. Сверхкомпактный двухмодовый волноводный переход на субволновых многомодовых интерференционных ответвителях. Фотон. Рез. 6 , 660–665 (2018).
КАС Статья Google ученый
Лю, Ю. и др. Очень острые адиабатические изгибы, основанные на обратном плане. Опц. лат. 42 , 2482–2485 (2018).
ОБЪЯВЛЕНИЕ Статья Google ученый
Габриелли, Л., Лю, Д., Джонсон, С. и Липсон, М. Встроенная трансформирующая оптика для изгибов многомодовых волноводов. Нац. коммун. 3 , 1217 (2012).
ОБЪЯВЛЕНИЕ Статья Google ученый
Xu, H. & Shi, Y. Сверхчеткий изгиб многомодового волновода с помощью преобразователей мод на основе метаматериалов. Лазер Фотон. Ред. 12 , 1700240 (2018 г.).
ОБЪЯВЛЕНИЕ Статья Google ученый
Xu, H. & Shi, Y. Линза типа «рыбий глаз» Максвелла на основе метаматериала для пересечения многомодового волновода. Лазер Фотон. Ред. 12 , 1800094 (2018 г.).
ОБЪЯВЛЕНИЕ Статья Google ученый
Шен Б., Полсон Р. и Менон Р. Увеличение плотности пассивных фотони-интегральных схем с помощью нанофотонной маскировки. Нац. коммун. 7 , 13126 (2016).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
“>
Piggott, A. et al. Инверсное проектирование и демонстрация компактного и широкополосного встроенного демультиплексора длин волн. Нац. Фотон 9 , 374–378 (2015).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Лу, Дж. и Вукович, Дж. Обратное проектирование нанофотонных структур с использованием дополнительной выпуклой оптимизации. Опц. Экспресс 18 , 3793–3804 (2010 г.).
ОБЪЯВЛЕНИЕ Статья Google ученый
Covey, J. & Chen, R. T. Эффективный идеально вертикальный решетчатый ответвитель волокно-чип для кремниевых горизонтальных многощелевых волноводов. Опц. Экспресс 21 , 10886–10896 (2013).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Michaels, A. & Yablonovitch, E. Обратная конструкция идеально вертикальных решетчатых ответвителей с почти единичной эффективностью. Опц. Экспресс 26 , 4766–4779 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Ма, В., Ченг, Ф. и Лю, Ю. Проектирование хиральных метаматериалов по запросу с поддержкой глубокого обучения. ACS Nano 12 , 6326–6334 (2018).
КАС Статья Google ученый
Онохара, К. и др. Упреждающая коррекция ошибок на основе мягкого решения для транспортных систем со скоростью 100 Гбит/с. Дж. Сел. Верхний. Квантовый электрон. 16 , 1258–1267 (2010).
КАС Статья Google ученый
Сюй, К. и др. Встроенный фотонный делитель мощности с произвольным соотношением мощностей. Опц. лат. 42 , 855–858 (2017).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
СПРАВЕДЕНИЯ СПИСОК ЛИТЕРАТУРА
Благодарности
Эта работа поддерживается Национальным фондом естественных наук (NSFC) (грант № 61875049, 61675128 и 61875124) и Комиссия по инновациям в области науки и технологии Shenzhen (грант NOS. и KQJSCX20180328165451777).
Информация об авторе
Авторы и организации
Государственная ключевая лаборатория перестраиваемых лазерных технологий, Министерство промышленности и информационных технологий Ключевая лаборатория микро-нано оптоэлектронной информационной системы, Харбинский технологический институт (Шэньчжэнь), 518055, Шэньчжэнь, П.Р. Китай
Инцзе Лю, Ке Сюй, Шуай Ван, Хучэн Се, Юцзе Ван, Шуминь Сяо, Юн Яо и Цинхай Сун
Государственная ключевая лаборатория передовых систем и сетей оптической связи, Шанхайский университет Цзяо Тонг, 200240, Шанхай, КНР Китай
Weihong Shen, Jiangbing Du & Zuyuan He
Центр совместной инновации Extreme Optics, Университет Shanxi, 030006, Taiyuan, P. R. China
Shumin xiao & Qinghai Song
73737373373373373373373373373373337333733373337373uors и Qinghai Song
737373733733733733733733733733733373373373333733373. публикации
Вы также можете искать этого автора в PubMed Google Scholar
Ke Xu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
Shuai Wang
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Weihong Shen
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Hucheng Xie
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Юцзе Ван
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Shumin Xiao
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Yong Yao
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Jiangbing Du
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Zuyuan He
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Qinghai Song
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
K. X. задумал проект. Ю.Л. и Х.Х. провел численное моделирование. С.В., Ю.В. и Ю.Л. изготовил устройства МДМ. Ю.Л. охарактеризованы компоненты и схемы МДМ. В.С. и JD выполнили высокоскоростные эксперименты. Y.L., K.X., J.D., S.X., Y.Y., Q.S. и Z.H. обсуждали и анализировали измеренные данные. Ю.Л. и К.Х. написал первый черновик рукописи. Все авторы обсудили результаты и внесли свой вклад в написание статьи.
Авторы переписки
Переписка с Кэ Сюй, Юн Яо, Цзянбин Ду или Цинхай Сун.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Информация для рецензирования: Nature Communications благодарит Майкла Галили и других анонимных рецензентов за их вклад в рецензирование этой работы. Доступны отчеты рецензентов.
Примечание издателя: Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Дополнительная информация
Дополнительная информация
Файл рецензирования
Права и разрешения
Открытый доступ Использование, распространение, распространение, лицензия Creative Commons и воспроизведение на любом носителе или в любом формате, при условии, что вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Перепечатка и разрешения
Об этой статье
Дополнительная литература
Расширяемые манипуляции с режимами на кристалле на основе метаматериалов
Сюаньру Чжан
Галстук Джун Цуй
Свет: наука и приложения (2022)
Произвольное манипулирование пространственным режимом на кристалле с поддержкой метаматериалов
Цзиньлун Сян
Чжиюань Тао
Йикай Су
Свет: наука и приложения (2022)
Сверхкомпактное оптическое межсоединение с высокой эффективностью и низкими перекрестными помехами обратной конструкции на основе пересечения волноводов и демультиплексора длин волн
Яньхун Сюй
Цзе Хуан
Женжун Чжан
Научные отчеты (2021)
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества.

Интегрирование дробей

Подготовиться к интегрированию дробей самостоятельно, а затем посмотреть ответ.

Интегрирование рациональных дробей

Непосредственное интегрирование

[Править] Подведение под знак дифференциала

[Править] Метод замены переменной (метод подстановки)

[Править] Примеры

Иллюстрирующие программы, реализующие алгоритмы интегрирования рациональных дробей Текст научной статьи по специальности «Математика»

Интегрирование рациональных функций

08. Интегрирование рациональных дробей

Формула интегрального частного правила с примерами |Правило интеграционного подразделения u/v |

Калькулятор длинного деления – Решите многочленное длинное деление онлайн

Знакомство с калькулятором деления на длинные числа

Как найти онлайн-калькулятор деления многочленов?

Преимущества использования калькулятора полиномиального деления на длинное деление

Результаты, полученные с помощью калькулятора интегрирования в длинное деление

Надежен ли калькулятор интегралов с длинным делением?

Как использовать интегральный калькулятор длинного деления?

Зачем использовать Калькулятор интеграции длинного деления?

Часто задаваемые вопросы

Каковы четыре этапа интеграции длинного подразделения?

Когда использовать интеграцию длинных разделов?

При использовании интегрирования неполными дробями обязательно ли использовать длинное деление?

Что такое метод длинного деления в интегрировании?

принадлежность

Авторы

принадлежность

Абстрактный

Похожие статьи

Цитируется

Типы публикаций

термины MeSH

вещества

Грантовая поддержка

детективов по борьбе с болезнями Уганды: неотъемлемая часть остановки распространения COVID-19 | Отдел глобальной охраны здоровья | Global Health

Стипендиаты PHFP помогают разработать национальные рекомендации по уходу на дому при COVID-19

Ведение расследования COVID-19 в двух округах

Представление результатов исследования для разработки национальных рекомендаций

Профилактика COVID-19 в тюрьмах Уганды: работа простых вмешательств

Понимание хода вспышки

Важность профилактических мер

Как ПДОДИ может помочь исцелить социальное разделение – Интегральная жизнь

Предыдущие эпизоды из

Станьте участником сегодня, чтобы посмотреть эту видео-презентацию и поддержать глобальное появление Интегрального сознания

Преимущества членства включают: Получите полный доступ к еженедельным беседам ведущих мыслителей

Библиотека журналов

Live Experience

Курсы и продукты

Бесплатные бонусные подарки

Поддержка движения

О Роббе Смите

О Integral Life

Другие полезные вещи

Подпишитесь на обновления по электронной почте

Произвольно маршрутизируемые мультиплексированные фотонные схемы с разделением по модам для плотной интеграции

Abstract

Введение

Результаты

Трехрежимный изгиб

Трехмодовое пересечение

Схемы маршрутизации МДМ

Обсуждение

Методы

Конструкция устройства

Процесс изготовления устройства

Измерительная установка и методы

Доступность данных

Каталожные номера

Благодарности

Информация об авторе

Авторы и организации

Contributions

Авторы переписки

Заявление об этике

Конкурирующие интересы

Дополнительная информация

Дополнительная информация

Дополнительная информация

Файл рецензирования

Права и разрешения