Интеграл синуса
Согласно формулам интегрирования интеграл от синуса sin (x) равен косинусу, причем со знаком минус. Многие часто допускает ошибки потому что не может запомнить, что производная от синуса равна минус косинусу, а от косинуса – синусу со знаком плюс.
Те кто изучает первоначальную должны помнить что к правой стороне следует добавить постоянную
Ету постоянную определяют с дополнительной условия.
График синуса имеет вид
Синус нечетная, а косинус – четная функция, поэтому при интегрировании появляется знак минус. В начале всем кажется все простым и понятным. Но рано или поздно наступает время усложнять интеграл, то есть интегрировать синус двойного угла, тройного аргумента и т.д. И во многих возникают трудности с интегрированием. Для вывода формулы интеграла для sin (k*x) проведем все выкладки сначала. Для того чтобы свести интеграл к табличной формулы надо внести коэффициент под дифференциал, но это изменит сам интеграл. Поэтому одновременно делим на коэффициент
Зная эту формулу, интеграл от синуса двойного угла записываем одной строкой
Далее можем проинтегрировать синус тройного угла
и т.
д.
int(sin(k*x)=-1/k*cos(k*x).
По такой же формуле выводят интеграл от синуса половины угла, который равен минус 2 косинус половины угла.
Интеграл от синуса одной третьей х равен
Пример 1. Найти интеграл от sin(4*x).
Решение: По формуле интегрирования находим
Пример 2. Вычислить интеграл от sin(5*x).
Решение: Выполняем интегрирования
Пример 3. Проинтегрировать выражение sin(7*x).
Решение: Находим неопределенный интеграл
Пример 4. Найти интеграл функции y=sin(x/5).
Решение: Находим неопределенный интеграл
Как только Вы научитесь вычислять простые интегралы от синуса можете переходить к определенному интегралу
Пример 5. Найти первоначальную от sin(x) которая в нуле равна 2.
Решение: Вычисляем первоначальную
Из условия на первоначальную находим постоянную
-cos(0)+C=2;
C=2+cos(0)=3.
Возвращаемся к первоначальной и подставляем найденную постоянную
Это и есть ответ к задаче.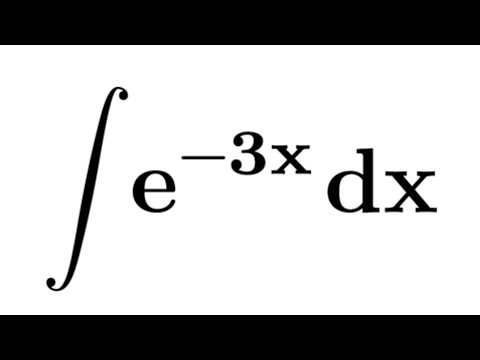
Пример 7. Проинтегрировать синус двойного угла y=sin(2*x) от 0 до 45 градусов.
Решение: Записываем интеграл от синуса и подставляем пределы интегрирования
По физическому содержанию определенный интеграл равен площади фигуры ограниченной функцией sin (x) и осью абсцисс.
Но определенный интеграл и площадь, это не одно и то же. Интеграл может быть отрицательным, а площадь нет. Если функция большую площадь имеет под осью абсцисс, то ее определенный интеграл отрицательный.
Площадь криволинейной трапеции равна интегралу от разницы уравнения верхней кривой и нижней.
В данном случае верхняя кривая это ось абсцисс или y = 0. Нижняя – это график синуса. Поэтому формула площади синус функции равна 1, или определенному интегралу по модулю.
Если функция антисимметрична относительно оси абсцисс то ее интеграл равен нулю, а площадь равна двойному интегралу графика над осью абсцисс. Например, интеграл синуса двойного угла от -45 до 45 градусов равен нулю
В то же время площадь заштрихованной фигуры равна единице.
На графике это будет выглядеть.
Из следующих материалов Вы узнаете, как найти интеграл от функции вида
какие формулы свертки и замены переменных при этом следует использовать. Также Вы овладеете методикой вычисления интегралов вида полином умноженый на синус функцию
где – полином от переменной. В таких случаях применяют интегрирования по частям, но об этом пойдет речь позже.
На этом знакомство с интегрированием синуса завершается. Интегралы от других тригонометрических и обратных к ним функций Вы найдете на страницах категории “Интегрирование функций”.
| 1 | Trovare la Derivata – d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata – d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata – d/dx | 1/x | |
| 6 | Trovare la Derivata – d/dx | x^2 | |
| 7 | Trovare la Derivata – d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata – d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata – d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata – d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata – d/dx | x^3 | |
| 17 | Trovare la Derivata – d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata – d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata – d/dx | sin(2x) | |
| 23 | Trovare la Derivata – d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata – d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata – d/dx | cos(2x) | |
| 28 | Trovare la Derivata – d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata – d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata – d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata – d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata – d/dx | 2e^x | |
| 35 | Trovare la Derivata – d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata – d/dx | -sin(x) | |
| 37 | Trovare la Derivata – d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata – d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata – d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata – d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata – d/dx | x/2 | |
| 46 | Trovare la Derivata – d/dx | -cos(x) | |
| 47 | Trovare la Derivata – d/dx | sin(3x) | |
| 48 | Trovare la Derivata – d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata – d/dx | x^x | |
| 52 | Trovare la Derivata – d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata – d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata – d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata – d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata – d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata – d/dx | y=x^2 | |
| 62 | Trovare la Derivata – d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata – d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata – d/dx | e^2 | |
| 67 | Trovare la Derivata – d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata – d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata – d/dx | x^5 | |
| 73 | Trovare la Derivata – d/dx | 2/x | |
| 74 | Trovare la Derivata – d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata – d/dx | x^(1/2) | |
| 76 | Trovare la Derivata – d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata – d/dx | cos(x^2) | |
| 78 | Trovare la Derivata – d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata – d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata – d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata – d/dx | логарифм x | |
| 86 | Trovare la Derivata – d/dx | arctan(x) | |
| 87 | Trovare la Derivata – d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata – d/dx | 5e^x | |
| 89 | Trovare la Derivata – d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata – d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata – d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata – d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata – d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata – d/dx | натуральный логарифм x^2 |
Интеграл от Sin(x): Геометрическая интуиция – BetterExplained
Вы занимаетесь своими делами, когда какой-то сопляк спрашивает, что означает интеграл от $\sin(x)$.
Ваши варианты:
- Притвориться спящим (только не в инженерной библиотеке снова)
- Стандартный ответ: «Как и для любой функции, интеграл от синуса — это площадь под его кривой».
- Геометрическая интуиция: «Интеграл синуса равен горизонтальному расстоянию по окружности».
Вариант 1 заманчив, но давайте взглянем на остальные.
Почему “площадь под кривой” неудовлетворительна
Описывать интеграл как “площадь под кривой” все равно, что описывать книгу как список слов. Технически правильно, но сообщение пропущено, и я подозреваю, что вы не прочли предписанное.
Если вы не попали в Леголенд, интегралы означают не только прямоугольники.
Расшифровка интеграла
Моя загадка в исчислении заключалась в том, что у меня не было интуиции для всей механики.
Когда мы видим:
$\int \sin(x) dx$
Мы можем обратиться к нескольким идеям:
Интеграл — это просто причудливое умножение.
Умножение накапливает числа, которые не изменяются (3 + 3 + 3 + 3). Интегралы складывают числа, которые могут измениться на , на основе шаблона (1 + 2 + 3 + 4). Но если мы прищурим глаза и притворимся, что предметы идентичны, мы получим умножение.$\sin(x)$ просто процент. Да, это также причудливая кривая с хорошими свойствами. Но в любой момент (например, 45 градусов) это одна процент от -100% до +100%. Просто обычные цифры.
$dx$ — крошечная, бесконечно малая часть пути, по которому мы идем. От 0 до $x$ — это полный путь, поэтому $dx$ (интуитивно) имеет ширину в нанометр.
Умножение накапливает числа, которые не изменяются (3 + 3 + 3 + 3). Интегралы складывают числа, которые могут измениться на , на основе шаблона (1 + 2 + 3 + 4). Но если мы прищурим глаза и притворимся, что предметы идентичны, мы получим умножение.Хорошо. С этими тремя интуициями наше грубое (грубое!) преобразование в простой английский:
Интеграл sin(x) умножает предполагаемую длину пути (от 0 до x) на процент
Мы намереваемся пройти простой путь от 0 до x, но вместо этого получаем меньший процент. (Почему? Потому что $\sin(x)$ обычно меньше 100%).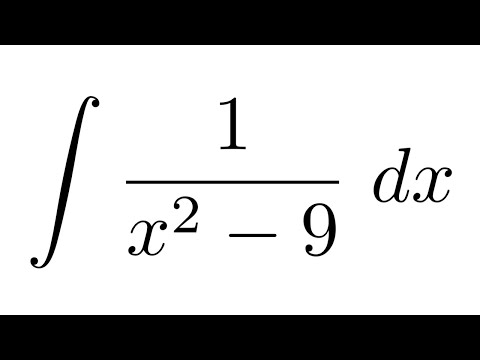
Таким образом, мы ожидаем что-то вроде 0,75x.
На самом деле, если бы $\sin(x)$ имело фиксированное значение 0,75, наш интеграл был бы:
$\int \text{fixedsin}(x) \ dx = \int 0,75 \ dx = 0,75 \ int dx = 0.75x$
Но настоящий $\sin(x)$, этот негодяй, меняется по ходу дела. Посмотрим, какую часть нашего пути мы реально пройдём.
Визуализируйте изменение Sin(x)
Теперь давайте визуализируем $\sin(x)$ и его изменения:
Вот ключ декодера:
$x$ – наш текущий угол в радианах. На единичной окружности (радиус = 1) угол равен расстоянию по окружности.
$dx$ — это крошечное изменение нашего угла, которое становится таким же изменением по окружности (перемещение на 0,01 единицы по нашему углу приводит к перемещению на 0,01 по окружности).
В нашем крошечном масштабе круг представляет собой многоугольник со многими сторонами, поэтому мы движемся по отрезку длины $dx$. Это ставит нас в новое положение.
Со мной? С помощью тригонометрии мы можем найти точное изменение высоты/ширины при скольжении по окружности на $dx$.
Подобные треугольники, наши изменения только нашего исходного треугольника, повернутого и масштабированного.
- Исходный треугольник (гипотенуза = 1): высота = $\sin(x)$, ширина = $\cos(x)$
- Изменить треугольник (гипотенуза = dx): высота = $\sin(x) dx$, ширина = $\cos(x) dx$
Теперь помните, что синус и косинус — это функции, возвращающие проценты. (Число вроде 0,75 не имеет своей ориентации. Оно появляется и делает вещи на 75 % их размеров в любом направлении, в котором они смотрят.)
Таким образом, учитывая, как мы нарисовали наш Треугольник Изменений, $\sin(x) dx$ является нашим горизонтальным изменением. Наша простая английская интуиция:
Интеграл sin(x) суммирует горизонтальное изменение вдоль нашего пути
Визуализация интегральной интуиции
Хорошо.
Давайте нарисуем график этого плохого мальчика, чтобы увидеть, что происходит. С нашей интуицией «$\sin(x) dx$ = крошечное горизонтальное изменение» мы имеем:
По мере того, как мы вращаемся, у нас есть набор сегментов линии $dx$ (красный). Когда синус мал (около х=0), мы почти не видим никакого горизонтального движения. По мере того как синус становится больше (верхняя часть круга), мы приближаемся к 100% по горизонтали. 9\pi = -\cos(\pi) – -\cos(0) = -(-1) -(-1) = 1 + 1 = 2$
Йоуза. Видишь, как неловко эти двойные отрицания? Почему визуальная интуиция была намного проще?
Наш путь по окружности (от $x=0$ до $x=\pi$) движется справа налево. Но ось x идет положительной слева направо. Когда мы преобразуем расстояние вдоль нашего пути в Стандартную площадь™, нам приходится переворачивать наши оси:
Наше желание представить вещи в официальном формате затопило интуицию происходящего.
Фундаментальная теорема исчисления
Мы больше не говорим об Фундаментальной теореме исчисления.
(Это что-то, что я сделал?)
Вместо того, чтобы складывать все крошечные сегменты, просто сделайте: конечная точка – начальная точка.
Интуиция смотрела нам прямо в лицо: $\cos(x)$ является антипроизводной и отслеживает горизонтальное положение, так что мы просто берем разницу между горизонтальными положениями! (С неудобными минусами, чтобы поменять местами оси.)
Это 93$ без калькулятора. Если вы утверждаете, что понимаете экспоненты, это должно быть возможно, верно?
Мы не всегда можем визуализировать вещи. Но для наиболее распространенных функций мы обязаны визуальной интуиции. Я, конечно, не могу увидеть 2 единицы площади от 0 до $\pi$ под синусоидой.
Счастливая математика.
Приложение: Средняя эффективность
Любопытно, что “средняя” эффективность движения вокруг вершины круга (от 0 до $\pi$) составляет: $ \frac{2}{\pi} = 0,6366 $ 9x$ — это ребенок, который ест конфеты, растет и поэтому может есть больше конфет.
$\sin(x) $ – это ребенок, который ест конфеты, заболевает, ждет аппетита и съедает еще конфет.
Приложение: Площадь не является буквальной
«Площадь» в нашем интеграле не является буквальной площадью, это процент нашей длины. Мы визуализировали умножение в виде двумерного прямоугольника в нашем общем интеграле, но это может сбивать с толку. Если вы зарабатываете деньги и облагаетесь налогом, представляете ли вы себе 2d область (доход * (1 – налог))? Или просто беспомощно уменьшающееся количество?
Площадь в первую очередь указывает на то, что произошло умножение. Не позволяйте команде «Интегралы — это литеральная площадь» побеждать в каждой битве!
Другие сообщения из этой серии
- Нежное введение в изучение исчисления
- Понимание исчисления с помощью метафоры банковского счета
- Доисторическое исчисление: открытие Пи
- Аналогия исчисления: интегралы как умножение
- Исчисление: построение интуиции для производной
- Как понимать деривативы: произведение, мощность и правила цепочки
- Как понимать производные: правило частных, показатели степени и логарифмы
- Интуитивно понятное знакомство с ограничениями
- Интуиция для ряда Тейлора (аналогия ДНК)
- Зачем нужны пределы и бесконечно малые числа?
- Обучение исчислению: преодоление нашей искусственной потребности в точности
- Дружеский разговор о том, 0,999. .. = 1
- Аналогия: камера исчисления
- Практика абстракции: графы исчисления
- Quick Insight: более простая арифметика с исчислением
- Как прибавить от 1 до 100 с помощью исчисления
- Интеграл Sin(x): Геометрическая интуиция
.. = 1Интегрирование и взятие интеграла
Интегрирование — это алгебраический метод нахождения интеграла функции в любой точке графика.
Нахождение интеграла
функции по х означает нахождение площади по оси х по кривой.
Интеграл обычно называют антипроизводной
, потому что интегрирование — это процесс, обратный дифференцированию.
Основная теорема исчисления показывает, что антидифференцирование — это то же самое, что и интегрирование.
Физическое понятие интеграла аналогично производной.
при заданном положении объекта. Если мы знаем скорость объекта в определенное время, интеграл даст нам положение объекта в это время.
Точно так же, как производная дает мгновенную скорость изменения, 9Интеграл 0231 даст общее расстояние в любой момент времени.
Интеграл получается не только при попытке найти процесс, обратный взятию производной
, но и при попытке решить задачу о площади
. Точно так же, как процесс
дифференцирования используется для нахождения наклона в любой точке графика, процесс
Интеграция Римана
До того, как была разработана интеграция, мы могли только аппроксимировать площадь функций
, разделив пространство на прямоугольники и добавив области.
Мы можем приблизить площадь к оси x, увеличив количество прямоугольников 90 231 под кривой. Площадь этих прямоугольников была рассчитана путем умножения длины на 90 231 ширины или 90 265 на 90 266 на изменение 90 265 х 90 266. После вычисления площади сумма 90 231 прямоугольников будет аппроксимировать площадь.
, тем лучше будет приближение. Это формула для суммы Римана,
, где i — любое начальное значение x, а n — количество прямоугольников:
Это был утомительный процесс и никогда не давал точной площади кривой. К счастью,
Ньютон и Лейбниц разработали метод интегрирования, который позволил им найти
точную площадь кривой в любой точке.
Подобно тому, как процесс дифференцирования находит функцию наклона
, поскольку расстояние между двумя точками становится бесконечно малым, процесс интегрирования
становится бесконечно большим.
Определение интеграла от f(x) из [a,b]
Интеграл функции x от a до b представляет собой сумму прямоугольников кривой
на каждом интервале изменения x по мере того, как количество прямоугольников стремится к бесконечности.
Обозначения в левой части обозначают определенный интеграл от f(x)
интегральную функцию и вычитаем его из b в интегральной функции:
где F обозначает интегрированную функцию. Это точно вычисляет площадь под
любой непрерывной функцией.
Общее правило мощности для интеграции
Для проведения интегрирования важно знать общее правило мощности. Это полная противоположность степенному правилу дифференцирования.
Давайте посмотрим на общую функцию
Когда мы берем интеграл от функции, мы сначала прибавляем 1 к показателю степени, а затем
После того, как мы сделали это с каждым термином, мы добавляем константу в конце.
Напомним, что
, взяв производную от константы, уберет ее, поэтому взятие интеграла от
функции даст нам константу. Мы помечаем его C, потому что константа
неизвестна — это может быть любое число! Поскольку у нас может быть бесконечно много возможных функций
для интеграла, мы называем его неопределенным интегралом.
Сделаем пример.
Найдите интеграл от
Начнем с первого термина. Мы смотрим на показатель степени 2 и увеличиваем его на 1,
, затем делим член на полученный показатель степени 3.
Затем мы смотрим на следующий член и делаем то же самое. Поскольку его показатель степени равен
1, результирующий показатель степени будет равен 2, поэтому мы делим весь член на 2.
Последний член имеет значение x, но мы его просто не видим. Мы можем представить себе последний срок
как -3x 0 .