Примеры решения типовых задач по интегральному исчислению функции одной переменной
Задача 25. Вычислить неопределенный интеграл
Решение. Если интеграл не может быть вычислен непосредственно по формулам интегрирования элементарных функций, то во многих случаях введение новой переменной T позволяет преобразовать подынтегральное выражение f(X) DX к такому виду, интегрирование которого можно провести либо по таблице, либо известным приемом.
Независимую переменную X заменим по формуле
Где – дифференцируемая функция.
Затем определим
,
И .
Полученная формула носит название формулы замены переменной в неопределенном интеграле.
В данном примере, согласно методу замены переменной (подстановки) получаем
Задача 26. Вычислить интеграл
Решение. Вычислим данный интеграл методом интегрирования по частям.
Формула интегрирования по частям
Предполагает, что в правой части может быть вычислен легче, чем исходный интеграл.
Приведем следующие рекомендации для применения метода интегрирования по частям.
1. Понижение степени многочлена PN(X) в интеграле типа:
Обозначение многочлена PN(X) через U приводит к понижению степени многочлена в .
2. Избавление от трансцендентных функций в интегралах типа:
В результате обозначения трансцендентных функций через U в эти функции будут отсутствовать.
В данном примере через U целесообразно обозначить трансцендентную функцию . В итоге получим:
Задача 27. Вычислить интеграл
Решение. В данном примере интегрирование по частям применяют несколько раз:
Задача 28. Вычислить определенный интеграл
Решение. Сделаем подстановку. Пусть . Тогда 2х+5=Z3; 2Dx=3Z3Dz; Dx=3/2Z2Dz. Определим пределы интегрирования для переменной Z.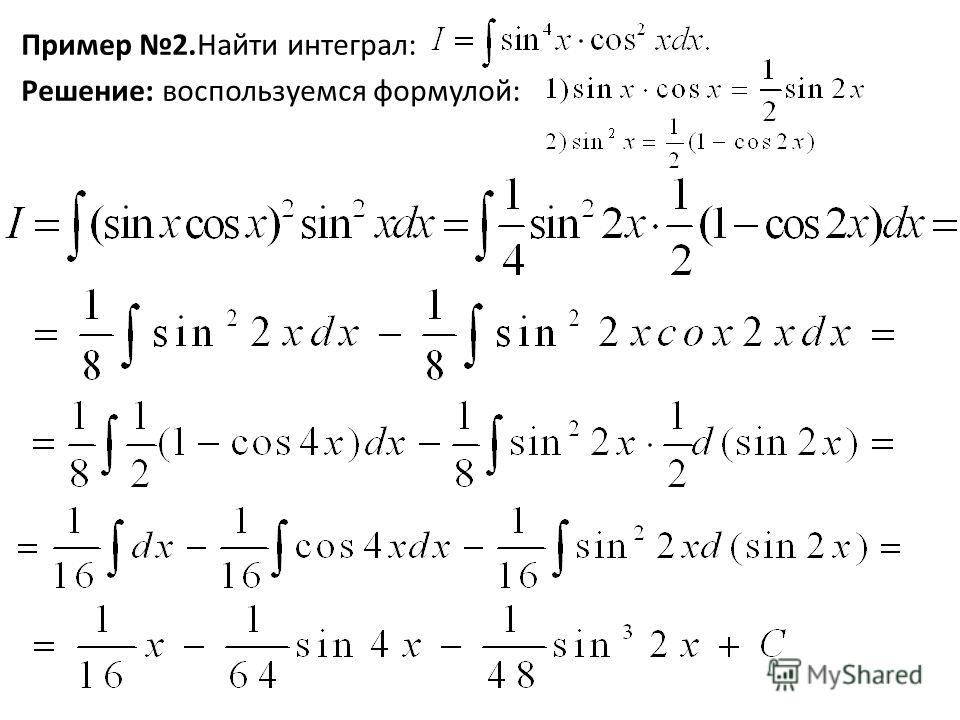
При Х=-2 получаем Z=1, при Х=11 получаем Z=3.
Выразив подынтегральное выражение через Z и переходя к новым пределам получим
Так как разность кубов , то, сократив на знаменатель, получим
Задача 29. Вычислить площадь поверхности эллипсоида, полученного вращением вокруг оси
(1)
Решение. Площадь поверхности, образованной вращением вокруг оси Ох дуги кривой Y=F(X) между точками с абсциссами Х=а и Х=B, вычисляется по формуле
(2)
Из уравнения эллипса (1) находим . Производная . Используя формулу (2), получим
Чтобы вычислить последний интеграл, положим . Тогда Z=0 при Х=0 и Z=p/4 при Х=2. Имеем
Задача 30. Вычислить несобственный интеграл или установить его расходимость.
Решение. Подынтегральная функция имеет бесконечный разрыв при
е. в точке, принадлежащей интервалу интегрирования. Данный интеграл является несобственным. Если подынтегральная функция F(X) интеграла имеет бесконечный разрыв при Х=с, где А<С<B, а во всех других точках отрезка [A,B] непрерывна, то по определению полагают:(*)
Если оба предела в правой части(*) существуют, то интеграл называется сходящимся. Если хотя бы один из указанных пределов не существует, то интеграл называется расходящимся.
Следовательно, данный интеграл – сходящийся.
Замечание. Равенство (*) можно использовать для каждой отдельной точки разрыва, принадлежащей интервалу (A,B).
| < Предыдущая | Следующая > |
|---|
Как правильно решить интегралы
Практическое применение интегралов в жизни
Реальный мир не идеален и не прямолинеен.
В нем нет геометрических форм без изъяна, нет движения без ускорения. И зависимости между величинами редко представлены прямой линией. Поэтому вычисления не обходятся без интегралов.
Определение
Интеграл — важнейшее понятие математики. Связано с необходимостью отыскивать функции по их производным и измерять объемы и площади, работу сил за какой-либо промежуток времени.
Множество частных случаев из жизни делают интегрирование не просто полезным, а необходимым действием. Интеграл поможет:
- рассчитать стоимость, изучив зависимость потребности от предложений;
- вычислить время выполнения работы, с учетом усталости людей;
- узнать, как изменяется долг по кредиту в течение времени;
- определить прирост жителей города
Место интегралам нашлось не только в физико-математических науках, но и в астрономии, экономике, медицине, биологии и архитектуре.
Понимая практическую значимость интегралов, легче усвоить базовые понятия и применять их в решении задач.
Из истории интегрирования
Интегрирование рассматривается, как сложение бесконечно малых частей бесконечное количество раз.
Интегральный расчет получен при определении площадей и объемов. Правила измерения квадратуры были известны древним ученым. В Египте и Вавилоне вычисляли площади круга и объем усеченной пирамиды.
Значительный вклад внесли древнегреческие ученые. Первый метод интегрирования назвали «исчерпание» по аналогии с водой, которую черпают кружкой из ведра. В Древней Греции Архимед объяснил задачу вычисления площади круга без знаний о числе «Пи».
Описание метода
Для нахождения площади круга в него вписываются геометрические фигуры. Высчитывается предел последовательности площадей этих фигур, который и принимается за площадь круга.
Данный способ вычисления площади рассматривает идею интегрирования. То есть нахождения предела безграничной суммы. Метод нашел применение в решении прикладных задач в разных научных областях.
Ньютон и Лейбниц сформулировали теорию интегрирования опираясь на законы дифференциального исчисления. Чтобы разобраться в классической теории нужно получить базовые знания.
Смысл интегрирования заключается в двух видах задач: геометрических и аналитико-алгебраических. В первом случае находят площади фигур, во втором подсчитывают суммарное значение переменной величины, принимающей различные значение единиц времени, длины и других измерений.
Понятие «Интеграл» в простом изложении
Термин «интеграл» произошел от латинского integer, то есть «целостный». Данный термин предложил математик Лейбниц еще в 17 веке.
Определение
Интеграл – это сложение маленьких частей и даже обозначение ∫ представляет собой вытянутую s, что означает сумму.
Интеграл – первообразная функции. Интегрирование – определение первообразной.
В математике интеграл вычисляет площадь, ограниченную кривой линией. Неопределенный интеграл – это вся фигура. Определенный интеграл – площадь некоторой части.
Запись интеграла функции:
х – аргумент, его можно заменить любой другой переменной, в отношении которой будет осуществляться интегрирование. d – бесконечно малое число. Сочетание «dx» называют приращением и рассматривают, как бесконечно малый «икс».
На рисунке криволинейная трапеция разбита на столбцы шириной х, число столбцов – d.
Неопределённый интеграл
Определение
Неопределенный интеграл – это сумма всех первообразных данной функции, которая не имеет границ интегрирования.
Сумма F(x)+C всех первоначальных функций f(x) на интервале а< x<b является неопределенным интегралом от функции f(x) на этом интервале и обозначается ∫f(x)dx .
Если функция F(x) является первообразной для f(x) , то по определению
∫ — знак интеграла, f(x)dx — подынтегральное выражение, f(x) — подынтегральная функция, х — переменная интегрирования, С — произвольная постоянная.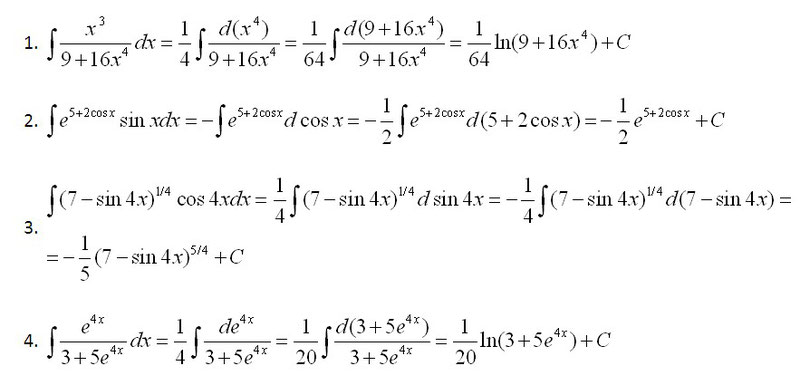
{b} f(x) d x
\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры вычисления интегралов
Найти неопределенный интеграл.
Часто при решении используют тригонометрические формулы.
Решение определенного интеграла.
Давайте рассмотрим несколько примеров вычисления интегралов:
Пример 1.
Пример 2.
Словарь базовых понятий.
Для понимания сути интеграла необходимо разбираться в базовых понятиях: функция, производная, приращение, предел.
Функция – отношение между элементами, где изменение одного элемента, повлечёт изменение другого.
Производная – функция, которая описывает скорость трансформации второй функции в каждой данной точке. Вторая функция называется первообразной. По сути — это предел отношения приращения функции к приращению аргумента.
Высчитывание проводят, используя таблицу производных со стандартными функциями.
Приращение – количественная степень изменения функции при вероятном изменении аргумента.
Предел – величина, к которой стремится значение функции, при стремлении аргумента к определённому значению.
Решение задач с интегралами могут показаться сложными. Выполнение практических заданий поможет преодолеть трудности.
Решение интегралов сводится к простым видоизменениям подынтегральной функции и поиску её в таблице интегралов.
Мы также можем отметить, что интегралы играют не последнюю роль в нашей жизни. В Биологических науках, к примеру, при их помощи узнают прирост популяции видов, в медицине используют в различных исследованиях, например, в томографии, в астрономии рассчитывают передвижение космических объектов и многое другое. Да и вообще трудно найти область, в которой не применяются данные методы вычисления.
Алгоритм– Нахождение интегрального решения уравнения
спросил
Изменено 8 лет, 9 месяцев назад
Просмотрено 2к раз
Это часть большого вопроса.
На самом деле это математическая задача. Так что было бы очень здорово, если бы кто-нибудь мог указать мне какой-либо алгоритм для получения решения этой проблемы, или псевдокод мне поможет.
Вопрос. Для заданного уравнения проверьте, имеет ли оно интегральное решение. Например:
(26а+5)/32=б
Здесь a — целое число. Есть ли алгоритм, чтобы предсказать или найти, может ли b быть целым числом. Мне нужно общее решение, не относящееся к этому вопросу. Уравнение может варьироваться. Спасибо
- алгоритм
- математика
- линейная алгебра
- уравнение
- алгебра
3
Ваша задача является примером линейного диофантова уравнения. Об этом в Википедии сказано:
Это диофантово уравнение [т. е. a x + b y = c ] имеет решение (где x и y — целые числа) тогда и только тогда, когда c кратно наибольшему общему делителю a и b.
Более того, если (x, y) — решение, то остальные решения имеют вид (x + k v, y — k u), где k — произвольное целое число, а u и v — частные a и b (соответственно) на наибольший общий делитель а и b.
В этом случае (26 а + 5)/32 = b эквивалентно 26 а – 32 b = -5. НОД коэффициентов неизвестных равен НОД (26, -32) = 2. Поскольку -5 не кратно 2, решения нет.
Общее диофантово уравнение является полиномом от неизвестных и может быть решено (если вообще возможно) только более сложными методами. Веб-поиск может найти специализированное программное обеспечение для решения этой проблемы.
Линейные диофантовы уравнения имеют вид ax + by = c
с является наибольшим общим делителем a и b это означает a=z'c и b=z''c тогда это тождество Безу вида с a=z' и b=z'' и уравнение имеет бесконечное число решений. Таким образом, вместо метода пробного поиска вы можете проверить , если c является наибольшим общим делителем (GCD) a и b
Если действительно a и b кратны c , тогда x и y можно вычислить с помощью расширенного алгоритма Евклида, который находит целые числа x и y
(в качестве примечания: это справедливо и для любой другой евклидовой области, т. е. полиномиального кольца, и каждая евклидова область является уникальной областью факторизации). Вы можете использовать Итеративный метод , чтобы найти эти решения:
Интегральное решение уравнения `a + bx = c + dy`
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
страница не найдена – Колледж Уильямс
| ’62 Центр театра и танца, ’62 Центр | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий/помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр изучения карьеры, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Приемная, Уэстон Холл | 597-2211 | 597-4052 факс |
| Позитивные действия, Хопкинс-холл | 597-4376 | |
| Африканские исследования, Голландия | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art/Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Студия фотографии, Spencer Studio Art | 597-2030 | |
| Студия гравюры, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Студия видео/фото, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Голландия | 597-2391 | 597-3028 факс |
| Астрономия/астрофизика, Физика Томпсона | 597-2482 | 597-3200 факс |
| Отделение легкой атлетики, физического воспитания, отдыха, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочная пристань, озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Хоккейный каток Ice Line, Lansing Chapman | 597-2433 | |
| Очные занятия, Спортивный центр Чандлера | 597-3321 | |
| Физкультура | 597-2141 | |
| Мокрая линия бассейна, Спортивный центр Чендлера | 597-2419 | |
| Информация о спорте, Хопкинс-холл | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Корты для сквоша | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Биология Томпсона | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Томпсон Биология | 597-2126 | 597-3495 факс |
| Безопасность и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа/Системы сигнализации | 597-4970/4033 | |
| Служба сопровождения, Хопкинс-холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Распределительный щит | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
Центр Экономики Развития, ул. |