Интеграл – это… Что такое Интеграл?
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.
Процесс нахождения интеграла называется интегрированием.
Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения.
Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является интеграл Римана.
Типы интегралов
По области интегрирования
Интегралы, зависящие от параметров
Дифференцирование по параметру
Пусть задан интеграл вида
В таком случае, производная по параметру t будет равна[1]
История
Интеграл в древности
Интегрирование прослеживается ещё в древнем Египте,
 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н. э. Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод впоследствии использовали Цзу Чунчжи и Цзу Гэн для нахождения объёма шара.
до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н. э. Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод впоследствии использовали Цзу Чунчжи и Цзу Гэн для нахождения объёма шара.Следующий крупный шаг в исчисление интегралов был сделан в Ираке, в XI веке, математиком Ибн ал-Хайсамом (известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвёртой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определённого интеграла, чтобы найти объём параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвёртой степени. Таким образом, он был близок к поиску общей формулы для интегралов от полиномов, но он не касается любых многочленов выше четвёртой степени.
Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвёртой степени. Таким образом, он был близок к поиску общей формулы для интегралов от полиномов, но он не касается любых многочленов выше четвёртой степени.
Следующий значительный прогресс в исчислении интегралов появится лишь в XVI веке. В работах Кавальери с его методом неделимых, а также в работах Ферма, были заложены основы современного интегрального исчисления. Дальнейшие шаги были сделаны в начале XVII века Барроу и Торричелли, которые представили первые намеки на связь между интегрированием и дифференцированием.
Обозначение
Ньютон использовал (не везде) в качестве символа интегрирования значок квадрата (перед обозначением функции или вокруг него), но эти обозначения не получили широкого распространения. Современное обозначение неопределённого интеграла было введено Лейбницем в 1675 году. Он образовал интегральный символ из буквы
 summa (тогда ſumma, сумма).[2] Современное обозначение определённого интеграла, с указанием пределов интегрирования, были впервые предложены Жаном Батистом Жозефом Фурье в 1819-20 годах.
summa (тогда ſumma, сумма).[2] Современное обозначение определённого интеграла, с указанием пределов интегрирования, были впервые предложены Жаном Батистом Жозефом Фурье в 1819-20 годах.См. также
Примечания
- ↑ Будылин А. М. Вариационное исчисление (рус.). Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета. — Цифровое издание. Часть 3.3.1. Дифференцирование интеграла по параметру..
- ↑ Florian Cajori A history of mathematical notations. — Courier Dover Publications, 1993. — P. 203. — 818 p. — (Dover books on mathematics). — ISBN 9780486677668
Литература
- Никольский С. М. Глава 9. Определенный интеграл Римана // Курс математического анализа. — 1990. — Т. 1.
- Ильин В. А., Позняк, Э.
 Г. Глава 6. Неопределенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики).
Г. Глава 6. Неопределенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики). - Ильин В. А., Позняк, Э. Г. Глава 10. Определенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики).
- Демидович Б.П. Отдел 3. Неопределенный интеграл // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).
- Демидович Б.П. Отдел 4. Определенный интеграл // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).
Ссылки
Красивейший интеграл Эрмита, который переворачивает школьную математику | Математика не для всех
Приветствую Вас, уважаемые Читатели! Сегодня достаточно сложный материал, особенно для тех, кто давненько не сталкивался с интегралами. Впрочем, я постараюсь настолько, насколько это возможно, показать Вам совершенно удивительную дорожку к натуральным числам, проявляющуюся в хитросплетениях бесконечности, интеграла и числа Эйлера. Позвольте представить, интеграл Эрмита:
Позвольте представить, интеграл Эрмита:
В данном интеграле k – это некое число, и что-то подсказывает, что результат вычисления этого интеграла будет с ним связан (да еще как!!!). Чтобы вычислить такой интеграл необходимо применить формулу интегрирования по частям:
Очень важным моментом будет выбор переменных. Сделаем его таким образом, чтобы при взятии производной показатель степени k уменьшился. Смотрите:
Забыл дописать dx в первой строчкеЗабыл дописать dx в первой строчке
Таким образом наш интеграл разбивается на два слагаемых. Давайте разберемся с первым: для этого нам понадобится просто подставить вместо x пределы интегрирования:
Мы применили k раз правило Лопиталя для раскрытия неопределенности бесконечность/бесконечностьМы применили k раз правило Лопиталя для раскрытия неопределенности бесконечность/бесконечность
Первое слагаемое, как стало понятно, равно 0. Что делать со вторым? Ключевая идея в том, чтобы продолжать интегрирование по частям. (-x)) и пределов интегрирования (от 0 до бесконечности).
(-x)) и пределов интегрирования (от 0 до бесконечности).
Так что же нам мешает взять k не целым числом, а, например, рациональным??? А ничего, ведь площадь под графиком – она и в Африке площадь, а, значит, мы только что получили расширение понятия факториала на все числа, в т.ч. комплексные и подобрались к одному из ключевых понятий математического анализа – гамма-функции.
Шарль Эрмит – крупнейший французский математик второй половины 19 века. Источник: https://famous-mathematicians.com/images/charles-hermite.jpgШарль Эрмит – крупнейший французский математик второй половины 19 века. Источник: https://famous-mathematicians.com/images/charles-hermite.jpg
Кроме того, этот интеграл используется в крайне красивом доказательстве трансцендентности числа Эйлера, о котором я расскажу позже, если Вам нравятся такие материалы. Спасибо за внимание!
Читайте также:
- Что такое трансцендентные числа ?
- Самый важный из интегралов
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.

Математика для блондинок: Таблица интегралов
Не научный бред с элементами реализма на тему неопределенного интеграла.Не просите маня в комментариях найти какой-нибудь интеграл. Я не умею находить интегралы, я могу только над ними по прикалываться. Прежде, чем здесь появится таблица неопределенных интегралов, нужно представить определение неопределенного интеграла. Прямо каламбур получился. Неопределенным интеграл называется так не потому, что определение для него никто не придумал, а потому, что с ним нельзя точно определиться. Математики меня заклюют за такое разъяснение.
| Неопределенный интеграл и его свойства |
| Таблица основных неопределенных интегралов |
Если вы любите по вечерам вместо семечек щелкать неопределенные интегралы, тогда большая таблица интегралов для вас.
 Если вы где-то учитесь, настоятельно рекомендую пользоваться большой таблицей интегралов в качестве ответов, которые обычно размещают в конце учебника. Помните, что вы не в детском садике и задачку без действий вам никто не задаст. Даже в задаче на одно действие между условием и ответом записывают это действие.
Если вы где-то учитесь, настоятельно рекомендую пользоваться большой таблицей интегралов в качестве ответов, которые обычно размещают в конце учебника. Помните, что вы не в детском садике и задачку без действий вам никто не задаст. Даже в задаче на одно действие между условием и ответом записывают это действие.
Это для тех, кто не любит читать всё то, что я пишу. Столь солидную таблицу интегралов я самым бесстыдным образом позаимствовал с сайта Интегралы.ру (здесь же есть решение интегралов онлайн). Таблица интегралов разбита на 12 групп, все их мы рассмотрим более подробно на отдельных страницах.
Все эти формулы можно увидеть на отдельных страницах этого сайта.
Таблица интегралов 1 – приведены формулы с переменной в первой и второй степени из 1 и 2 разделов.
Таблица интегралов 2 – приведены формулы с квадратными корнями из разделов 3, 4, 5, 6 и 7.
Таблица интегралов 3 – приведены формулы интегрирования из разделов 8, 9 и 10.
Таблица интегралов 4 – приведены формулы интегрирования показательных, тригонометрических и логарифмических функций из разделов 11 и 12.
Как найти неопределенный интеграл? Очень просто. Тупо берете формулу, тупо подставляете в пример. Лично я так делал. Иногда можно чего-то там перегруппировать, упростить, вынести за знак интеграла. .. На звание самого лучшего в мире искателя интегралов я не претендовал, о чем нисколько не жалею. Вообще, живых интегралов я за свою жизнь так и не встретил. Все они для меня вымерли, как динозавры, сразу же после окончания учебы. Да, я ещё кое-что о них помню. Только и всего.
.. На звание самого лучшего в мире искателя интегралов я не претендовал, о чем нисколько не жалею. Вообще, живых интегралов я за свою жизнь так и не встретил. Все они для меня вымерли, как динозавры, сразу же после окончания учебы. Да, я ещё кое-что о них помню. Только и всего.
Теперь немного бла-бла-бла на тему неопределенных интегралов. Чистый бред. Прошу не путать с заявлением о приеме меня в математики.
Очень интересен каламбур, написанный буковками под таблицей основных неопределенных интегралов. На первый взгляд получается, что первообразная на первообразной сидит и первообразной погоняет. Ясно, что записанное выражение и дураку понятно. Но бывают ещё и особо одаренные представители рода человеческого, типа меня. У меня просто мозги отключаются, когда я вижу или читаю подобные фразы. Наверное, инстинкт самосохранения срабатывает – мозг боится собственного вывиха. Долго вспоминал, где у меня лево, где право.
Через пару дней напряженной умственной работы, я пришел к выводу, что в левой части описывается ситуация, когда мы точно знаем, от какой первообразной функции мы получили производную.
Теперь эта же мысль, но языком математических формул. Используем определение и свойства неопределенных интегралов. Возьмем первообразную функцию с константой и посмотрим, что происходит.
| Первообразная функция |
 Если мы сперва дифференцируем первообразную функцию, то константа теряется. После интегрирования её нужно восстанавливать для сохранения равенства. Если применить свойства неопределенного интеграла и взаимно сократить интегрирование и дифференцирование, то первообразная останется в своем первоначальном виде, с константой.
Если мы сперва дифференцируем первообразную функцию, то константа теряется. После интегрирования её нужно восстанавливать для сохранения равенства. Если применить свойства неопределенного интеграла и взаимно сократить интегрирование и дифференцирование, то первообразная останется в своем первоначальном виде, с константой.Здесь получается фокус с тузом в рукаве. В определении неопределенного интеграла константа является частью первообразной функции F(x) и отдельно не выделяется – туз спрятан в рукаве. После интегрирования мы добавляем константу, потерявшуюся при дифференцировании – туз достаем из рукава на всеобщее обозрение. В этом случае главным является не сам фокус, а факт присутствия туза у фокусника как до, так и после демонстрации трюка.
Что такое константа? Это число. Геометрически при помощи изменения константы можно сместить график функции F(x) вдоль оси игреков вниз или вверх. В определении неопределенного интеграла указано, что совокупность всех этих первообразных и представляет из себя этот злополучный интеграл. Но это только одна сторона медали.
Но это только одна сторона медали.
В определении не указывается, что вся совокупность первообразных рассматривается в одной, кем-то когда-то выбранной, системе координат. А если мы выберем одну первообразную, тогда изменение константы будет смещать систему координат. С точки зрения выбранной первообразной, неопределенный интеграл – это совокупность всех систем координат, в которых может рассматриваться данная первообразная функция.
Чудеса относительности. Если мы сидим попой на поверхности Земли, то мы видим, как Солнце бегает по небу. Если мы сидим попой на Солнце (не бойтесь поджариться, ведь математика – абстрактная наука и позволяет сидеть на чем угодно), то мы видим, как Земля вращается вокруг собственной оси. Всё зависит от выбранной нами точки зрения, что в математике соответствует выбору системы координат.
С учетом относительности влияния константы на сладкую парочку “функция – система координат”, первое предложение в определении неопределенного интеграла можно записать так:
Неопределенный интеграл для функции f(x) – это совокупность всех первообразных данной функции или совокупность всех систем координат данной первообразной функции.
Не знаю, как посмотрят на такое развитие сюжета математики, но получилось слишком заумно. Всё это дело можно упростить, если отказаться от пыток восстановить константу в первообразной функции. Ещё раз проконтролируем свои действия. Если у нас есть первообразная функция с константой или без, мы можем точно сказать, как выглядит её производная. Если у нас есть производная, мы не можем точно сказать, от какой именно первообразной она получена.
Всё дело заключается в том, что при взятии производной происходит изменение системы координат. Если мы рассматриваем производную f(x) в измененной системе координат, то восстановить первоначальную систему координат первообразной функции F(x) невозможно. Нельзя воскресить мертвое. Вместо математической точности у нас получается гадание на кофейной гуще. И это гадание выражается в прибавлении константы к скелету первообразной функции.
Задачу эту можно решить на уровне задних парт третьего класса. Почему задних парт? Они находятся дальше всех от испепеляющего светоча знаний, льющегося с классной доски. Почему третьего класса? У них ещё не выработан благоговейный трепет перед учебниками. Просто начинаем фантазировать. Придумываем какое-нибудь новое определение и при помощи него разруливаем ситуацию.
Почему третьего класса? У них ещё не выработан благоговейный трепет перед учебниками. Просто начинаем фантазировать. Придумываем какое-нибудь новое определение и при помощи него разруливаем ситуацию.
Функция в собственной системе координат Fo(x) – это функция, у которой константа приравнивается к нулю. Так сказать, функция в собственном соку. Классическим примером функций в собственной системе координат можно считать тригонометрические функции. При изучении они рассматриваются без константы.
Поскольку определение неопределенного интеграла уже написано и правила хорошего тона настоятельно не рекомендуют его рихтовать, придумаем еще одно определение какой-нибудь промежуточной фигни. Пусть эта фигня будет называться “определенная первообразная“. Теперь берем определение неопределенного интеграла и на его основе пишем свое определение определенной первообразной.
Определенная первообразная для функции f(x) – это первообразная данной функции в собственной системе координат Fo(x). Если функция f(x) определена и непрерывна на промежутке (a, b) и F(x) – её первообразная, то есть F'(x)=f(x) при a меньше x меньше b
Если функция f(x) определена и непрерывна на промежутке (a, b) и F(x) – её первообразная, то есть F'(x)=f(x) при a меньше x меньше b
| Определенная первообразная |
| Свойства определенной первообразной |
Дальше ещё несколько слов о константе в неопределенном интеграле. При дифференцировании функции константа превращается в ноль. В математике существует первая, вторая, третья и так далее, производные. Можно предположить, что столько же существует и неопределенных интегралов. Берем результат интегрирования и снова интегрируем. Вот что может получиться…
При дифференцировании функции константа превращается в ноль. В математике существует первая, вторая, третья и так далее, производные. Можно предположить, что столько же существует и неопределенных интегралов. Берем результат интегрирования и снова интегрируем. Вот что может получиться…
Ветхий Завет от Матана.
Вначале ничего не было. Потом было слово. Точнее, два слова – Неопределенный Интеграл. И создал Неопределенный Интеграл константу. А потом Он создал переменную. И стала переменная плюс константа. А потом Неопределенный Интеграл создал…
| Первообразная константы |
Если вас не устраивает такая история сотворения мира, эти же формулы можно трактовать как историю Большого Взрыва. Ведь ученые уверяют, что началось всё с точки, то есть с нуля.
Сергей Манулов, давний друг этого сайта, предлагал мне опубликовать в одной таблице интегралы рядом с производными. Так действительно будет нагляднее и понятней. Но здесь есть два момента. Во-первых, таблица получится такой широкой, что в этот сайт явно не влезет. Во-вторых, насколько я помню, таблица производных несколько меньше, чем таблица интегралов. Ну не любят математики играть в производные. Кого интересует исследование всяких каракуль, пусть даже и обличенных в математические формулы? А вот игры в интегралы среди математиков очень даже популярны. По своей популярности они могут уступать разве что играм в комплексные числа. Наверное, так получается потому, что при помощи определенных интегралов можно находить площади криволинейных трапеций или что-то там ещё. Математики играют в свои любимые игрушки и вроде как полезным делом заняты.
Так действительно будет нагляднее и понятней. Но здесь есть два момента. Во-первых, таблица получится такой широкой, что в этот сайт явно не влезет. Во-вторых, насколько я помню, таблица производных несколько меньше, чем таблица интегралов. Ну не любят математики играть в производные. Кого интересует исследование всяких каракуль, пусть даже и обличенных в математические формулы? А вот игры в интегралы среди математиков очень даже популярны. По своей популярности они могут уступать разве что играм в комплексные числа. Наверное, так получается потому, что при помощи определенных интегралов можно находить площади криволинейных трапеций или что-то там ещё. Математики играют в свои любимые игрушки и вроде как полезным делом заняты.
Что нужно помнить о неопределенных интегралах? Как молитва заканчивается словом “Аминь”, так любой неопределенный интеграл заканчивается словами “плюс константа”.
Справочник репетитора по математике. Список табличных интегралов
Табличные интегралы для занятий по математическому анализу. В помощь студентам первых курсов технических, экономических и математических ВУЗов, преподавателям и репетиторам по математике.
В помощь студентам первых курсов технических, экономических и математических ВУЗов, преподавателям и репетиторам по математике.
Неопределенных интегралы от основных функций.
1. Интеграл от степенной функции
2. Интеграл от константы
3. Интеграл от синуса
4. Интеграл от косинуса
5. Интеграл от экспоненты
6. Интеграл от показательной функции
7. Интеграл от обратной пропорциональности
8.Интеграл, равный тангенсу
9. Интеграл, равный котангенсу
10. Интеграл от тангенса
11. Интеграл от котангенса
12. Интеграл, равный арксинусу
13. Интеграл, равный минус арккосинусу
14. Интеграл от секонса
Интеграл от секонса
15. Интеграл от косеконса
16. Интеграл, от обратной величины к разности квадратов
17. Полезный интеграл, сводящийся к арксинусу
18. Полезный интеграл, сводящийся к арктангенсу
19. Интеграл, сводящийся к натуральному логарифму
Комментарий репетитора по математике: к табличным обычно относят простейшие интегралы, в записи которых участвуют элементарные (основные) функции математического анализа. Табличные интегралы можно использовать для вычисления любых других интегралов (типовых или сложных) на любом этапе реализации алгоритма их нахождения. Техника интегрирования допускает следующий план: как только вам встетился табличный интеграл — применяйте его без каких-либо доказательств или вывода.
Интегралы расположены в порядке роста уровня сложности их вывода и частоте использования в решении задач. Удачи в совершенствовании умения вычислять интегралы.
Удачи в совершенствовании умения вычислять интегралы.
Колпаков А.Н., профессиональный репетитор по математике в Москве.Строгино, м. Щукинская.
Интеграл и его практическое применение
МБПОУ «Псковский агротехнический колледж»Сближение теории с практикой дает
самые благоприятные результаты, и не
одна только практика от этого
выигрывает, сами науки развиваются под
влиянием ее.
П. Л. Чебышев
Тема: «Интеграл и его
практическое применение»
Преподаватель математики
Чернопийская Е.Н.
Цель работы:
Расширить область математических знаний.
Развивать логическое мышление.
Вывести общие формулы, позволяющие решать
задачи интегрирования.
Исследовать, что интеграл широко применяется в
различных сферах жизнедеятельности.
Объект исследования:
область математики – интегрирование.
Задачи исследования:
– собрать, изучить и систематизировать
материал об интеграле;
– рассмотреть, как интеграл используется при
решении различных жизненных ситуаций;
– использование интеграла в различных сферах
жизнедеятельности.

4. Что такое интеграл и что значит интеграция и интегрирование?
Выполнил студент группы 61 -11Петров Данил
5. Значение слов в толковом словаре
ИНТЕГРАЛпо Ефремовой:
Интеграл – целая величина, рассматриваемая как сумма своих бесконечно малых частей.
по Ожегову:
Интеграл – величина, получающаяся в результате действия, обратного дифференцированию
в Энциклопедическом словаре:
Интеграл – (от лат. integer – целый) – см. Интегральное исчисление.
по словарю Ушакова:
ИНТЕГРАЛ, интеграла, (от латинского integer – целый) (математическое понятие). Конечная
измеримая величина в отношении к бесконечно малой части ее – к дифференциалу.
по словарю Даля:
Математическое латинское понятие. конечная, измеримая величина, в отношении к бесконечно
малой части ее, к дифференциалу. Интегральное вычисление, искусство отыскивать интеграл по
дифференциалу. Интегрировать, вычислять, находить интеграл;
ИНТЕГРИРОВАНИЕ
Интегрирование – операция отыскания неопределенного интеграла (см.
 Интегральное
Интегральноеисчисление) или решения дифференциального уравнения. Значение слова
Интегрировать по Ефремовой:
Интегрировать – Объединять части в единое целое.
Находить интеграл данной функции.
по Ожегову:
Интегрировать – Найти (находить) интеграл данной функции
Интегрировать Объединить (-нять) в одно целое
по словарю Ушакова:
интегрирую, интегрируешь. Найти (находить) интеграл данной функции. Значение
слова Интегральный по словарю Ушакова:
ИНТЕГРАЛЬНЫЙ
интегральная, интегральное. 2. Неразрывно-связанный, составляющий неотъемлемую
часть целого (науч.).
7. Выполнили студенты группы 61 -11 Ефимов Дмитрий Короткевич Евгений Андрейчук Сергей
Немного историиВЫПОЛНИЛИ СТУДЕНТЫ ГРУППЫ 61 -11
ЕФИМОВ ДМИТРИЙ
КОРОТКЕВИЧ ЕВГЕНИЙ
АНДРЕЙЧУК СЕРГЕЙ
8. Определение
Интеграл функции — аналогсуммы последовательности.
Неформально говоря,
(определённый) интеграл
является площадью части графика
функции (в пределах
интегрирования), то есть
площадью криволинейной трапеции.

Процесс нахождения интеграла
называется интегрированием.
Символ введен Лейбницем (1675 г.).
Этот знак является изменением латинской
буквы S (первой буквы слова сумма). Само
слово интеграл придумал Я. Бернулли
(1690 г.). Вероятно, оно происходит от
латинского integero, которое переводится,
как приводить в прежнее состояние,
восстанавливать.
10. Интеграл в древности
Возникновение задач интегральногоисчисления связано с нахождением
площадей и объемов. Ряд задач такого
рода был решен математиками древней
Греции. Античная математика
предвосхитила идеи интегрального
исчисления в значительно большей
степени, чем дифференциального
исчисления. Большую роль при решении
таких задач играл исчерпывающий метод,
созданный Евдоксом Книдским (ок. 408 ок. 355 до н. э.) и широко применявшийся
Архимедом (ок. 287 – 212 до н. э.).
11. Интеграл в древности
Однако Архимед не выделил общего содержанияинтеграционных приемов и понятий об интеграле, а
тем более не создал алгоритма интегрального
исчисления.
 Ученые Среднего и Ближнего Востока в
Ученые Среднего и Ближнего Востока вIX – XV веках изучали и переводили труды Архимеда
на общедоступный в их среде арабский язык, но
существенно новых результатов в интегральном
исчислении они не получили.
Деятельность европейских ученых в это время
была еще более скромной. Лишь в XVI и XVII веках
развитие естественных наук поставило перед
математикой Европы ряд новых задач, в частности
задачи на нахождение квадратур (задачи на
вычисление площадей фигур), кубатур (задачи на
вычисление объемов тел) и определение центров
тяжести .
12. История возникновения интеграла
Труды Архимеда, впервые изданные в 1544 (налатинском и греческом языках), стали привлекать
широкое внимание, и их изучение явилось одним из
важнейших отправных пунктов развития
интегрального исчисления. Архимед предвосхитил
многие идеи интегрального исчисления. Но
потребовалось более полутора тысяч лет, прежде
чем эти идеи нашли четкое выражение и были
доведены до уровня исчисления.

Математики XVII столетия, получившие многие
новые результаты, учились на трудах Архимеда.
Активно применялся и другой метод – метод
неделимых, который также зародился в Древней
Греции.
13. История возникновения интеграла
На такой кажущейся теперь поменьшей мере сомнительной основе И.
Кеплер (1571 – 1630 гг.) в своих
сочинениях “Новая астрономия” (1609 г.) и
“Стереометрия винных бочек” (1615 г.)
правильно вычислил ряд площадей
(например площадь фигуры, ограниченной
эллипсом) и объемов (тело резалось на
бесконечно тонкие пластинки).
Эти исследования были продолжены
итальянскими математиками Б. Кавальери
(1598 – 1647 годы) и Э. Торричелли (1608 1647 годы).
14. История возникновения интеграла
В XVII веке были сделаны многиеоткрытия, относящиеся к интегральному
исчислению.
Однако при всей значимости
результатов, полученных математиками
XVII столетия, исчисления еще не было.

Необходимо было выделить общие идеи,
лежащие в основе решения многих
частных задач, а также установить связь
операций дифференцирования и
интегрирования, дающую достаточно
точный алгоритм.
15. История возникновения интеграла
Это сделалиНьютон и Лейбниц,
открывшие
независимо друг от
друга факт,
известный вам под
названием формулы
Ньютона – Лейбница.
Тем самым
окончательно
оформился общий
метод.
16. История возникновения интеграла
Предстояло еще научитьсянаходить первообразные многих
функций, дать логические основы
нового исчисления и т. п. Но главное
уже было сделано:
дифференциальное и интегральное
исчисление создано.
17. История возникновения интеграла
Методы математического анализаактивно развивались в следующем
столетии (в первую очередь следует
назвать имена Л. Эйлера, завершившего
систематическое исследование
интегрирования элементарных функций, и
И.
 Бернулли). В развитии интегрального
Бернулли). В развитии интегральногоисчисления приняли участие русские
математики М. В. Остроградский (1801 1862 гг.), В. Я. Буняковский (1804 – 1889
гг.), П. Л. Чебышев (1821 – 1894 гг.).
18. История возникновения интеграла
Строгое изложениетеории интеграла появилось
только в прошлом веке,
Решение этой задачи связано
с именами О. Коши, одного
из крупнейших математиков
немецкого ученого Б. Римана
(1826 – 1866 гг.),
французского математика Г.
Дарбу (1842 – 1917).
19. История возникновения интеграла
Ответы на многиевопросы, связанные с
существованием
площадей и объемов
фигур, были получены
с созданием К.
Жорданом (1826 – 1922
гг.) теории меры.
20. История возникновения интеграла
Различные обобщенияпонятия интеграла уже в
начале нашего столетия
были предложены
французскими
математиками А. Лебегом
(1875 – 1941 гг.) и А.
Данжуа (1884 – 1974)
советским математиком А.

Я. Хинчиным (1894 -1959
гг.)
Повторение вопросов теории:
•Как называется функция F(x) для функции f(x)
в записи формулы Ньютона – Лейбница?
•Неопределенный интеграл – это…
•Каким действием нужно проверять результат
интегрирования?
•Назовите основные методы интегрирования.
•В чем заключается геометрический смысл
определенного интеграла?
•Как вычислить площадь
фигуры, ограниченной
линиями на рисунке?
22. Найти площадь заштрихованной фигуры
25. Какой метод интегрирования надо применить при вычисления интеграла ?
26. Решение – 5 минут
На оценку 5 можно решитьНепосредственное интегрирование –
решить 4 примера или
Метод замены переменной – 2
примера или
Метод интегрирования по частям – 1
пример ( выбор за вами)
Может ли современная наука
обойтись без применения
интегралов.
В каких сферах современной науки
применяется интеграл и в каких
случаях?
28.
 Применение определенного интеграла в физике Команда:
Применение определенного интеграла в физике Команда:Кодесников Владислав
Гримович Никита
Игнатьев Иван
Воробьева Александра
Андрейчук Сергей
ФИЗИКА
Работа электрического заряда
Работа переменной силы
Масса
Перемещение
Давление
Количество теплоты
t2
x2
A F ( x)dx
x1
S-перемещение
v-скорость
а- ускорение
A – работа,
F – сила,
N – мощность
a(t )dt
t1
t2
s (t )dt
t2
A N (t )dt
t1
t1
Физика
t2
q J (t )dt
x2
m ( x)dx
t1
q – электрический
заряд,
I –сила тока
m – масса тонкого
стержня,
ρ – линейная
плотность
t2
Q c(t )dt
t1
x1
Q – количество теплоты
с – теплоемкость
39. Задачи для самостоятельного решения
Вычислите количество электричества,протекшего по проводнику за промежуток
времени [ 2;3 ], если сила тока задается
формулой I 3t 2 2t 5
Ответ: 9
Найти путь, пройденный телом за 4
секунды от начала движения,
если скорость тела v(t) = 10t + 2 (м/с).

Ответ: 88 м
40. Применение определенного интеграла в биологии
КомандаГуляева Евгения
Голубева Валерия
Ефимов Дмитрий
Елина Дарина
Иванов Даниил
БИОЛОГИЯ
Длина перелета перелетных птиц
Биомасса популяции
Скорость размножения членов
популяции
Численность популяции
Длина перелета
перелетных птиц
S-перемещение
v-скорость
а- ускорение
Биология
Вычисление
биомассы
популяции
Скорость размножения
членов популяции
43. Примеры решения
задача 1 Количество зараженных вначальный момент времени 7 ч закон
скорости заражения от 1 человека в
зависимости от времени у = 6х +1 за один
день. Сколько ожидается зараженных
через три дня ?
Решение:
1 человек заразит
От 7 человек заражение: 7*30 = 210
Ответ: 210 ч
44. Задачи для самостоятельного решения
Из эксперимента известно, что скоростьразмножения бактерий М = 5м +4 за одну
минуту.
 Какое количество бактерий будет
Какое количество бактерий будетчерез 10 минут ?
Ответ: 290 б
45. Применение определенного интеграла в экономике
КомандаРейникова Алена
Короткевич Евгений
Бондарева Ольга
Леонова Анастасия
Артемьева Виктория
ЭКОНОМИКА
Количество товара
Производительность
Объем продукции
q – количество товара,
p – цена единицы товара
(p*;. q*) – точка равновесия
СS – потребительский излишек
PS – излишек производителя
G – коэффициент Джини
Экономика
T
П=
pt
I
(
t
)
e
dt
0
f – производительность,
t- время,
V- объём продукции
П – дисконтированная стоимость
денежного потока ,
I- скорость денежного потока,
р – годовая процентная ставка,
t – время
48. Пример №1
Экспериментально установлено,что продуктивность
труда работника приближенно выражается
формулой:
f (t) = -0,0033t²- 0,089t + 20,96
t-рабочее время в часах.

Вычислить объем выпуска продукции за
квартал, считая рабочий
день 8- часовым,
кол-во рабочих дней в квартале – 62.
Решение.
Объем выпуска продукции в течение смены является первообразной для
функции, выражающей продуктивность труда следовательно
8
V
f t dt
0
В течение квартала
8
V = 62∫ f (t )dt =
0
8
= 62∫ (0.0033t
0
2
0.089t + 20.92)dt = 62
t
0.0033 0.089t + 20.96t
3
8
∫ = 62(
≈ 10185(ед)
Ответ: объем выпуска продукции за квартал
равен 10185 единицам.
0
0,001 512 2,848 +167,68) ≈
50. Пример №2
Экспериментально установлено,что зависимость расхода бензина автомобилем от скорости на 100 км,
пути выражается формулой:
Q = 18-0,3υ + 0,003υ2, где 30
Определить средний расход бензина, если скорость движения 50-60 км/ч
Решение:
60
V =
∫
f (t )dt
50
V=∫
(18 – 0,3 , 2 )d
60 50
(18 0,3 0,003 ) 60
2
3
=
10
50
=
= 1/10(18·60 – 0, 3·1800 + 0,003·72000 – 18·50 + 0, 31250 – 0,
00341667) =
= 10.
 6 л
6 лОтвет: на 100км пути при скорости 50-60 км/ч, расходует
в среднем 10.6 л
51. Задачи для самостоятельного решения
1. Определить объем продукции,произведенный рабочим за третий час
рабочего дня, если производительность
труда характеризуется функцией: у = 3/
(3х + 1) + 4
Ответ:
2. Определить запас товаров в магазине,
образуемый за три дня, если поступление товаров
характеризуется функцией f(t) = 2t + 5.
Ответ: 24
53. Применение определенного интеграла в математике
КомандаТрофимов Анатолий
Петров Даниил
Калинкин Игорь
Семенова Дарья
Яковлева Диана
Савельев Андрей
ГЕОМЕТРИЯ
Площадь фигуры
Объем тела вращения
Вычисление площади
плоской фигуры в
полярных
координатах
Вычисление площади плоской
фигуры в прямоугольных
координатах
Математика
Вычисление площади
поверхности тела
вращения
Вычисление
интеграла
Автор
Трофимов Анатолий
студент 1 курса г
Вычисление длины дуги
кривой
56.
 Определение криволинейной трапеции Фигуру,
Определение криволинейной трапеции Фигуру,ограниченн
ую
графиком
функции,
отрезком
[a;b]
и прямыми
x = a, x = b
называют
криволине
йной
трапецией
57. Задача №1
Вычислить площадь фигуры,ограниченной линиями
y x3 , x 1, x 3, y 0
у
3
4
4
4
3
x
3
1
81 1 80
3
S x dx
20
41 4 4 4 4 4
1
0 1
3
х
2. Вычисление
объёмов тел
b
Формула V S x dx
– основная формула для
вычисления объемов
тел.
a
Пусть вокруг оси OX вращается
криволинейная трапеция, ограниченная
непрерывной линией y = f(x) > 0,
отрезком [a; b] и прямыми x = a, x = b.
.
Полученная при
вращении фигура
называется телом
вращения. Объем полученного
y
тела вычисляется по
формуле:
0
а
b
x
b
Vx y dx
2
a
y
0
x
Если криволинейная трапеция,
ограниченная графиком
функции
x = q(y) > 0, прямыми y = c, y =
d и осью OY, то объем тела,
образованного вращением
этой фигуры вокруг оси OY
d
равен:
Vy x dy
2
c
Вычисление объема тела вращения
Вычислить объем тела, образованного
вращением фигуры, ограниченной
линиями:
вокруг
y x 2; x 0; y 4
оси OY.

4
Vy
0
8
4
2 4
16 0
y
y dy ydy
2
2
20
0
2
63. Задача №2
Вычислить объем тела, образованноговращением одной арки синусоида 0,
(график функции y=sin x на промежутке
) вокруг оси Ох.
у
0
π
х
64. Решение задачи №2
1cos
2
x
1
2
V = sin xdx
dx x sin 2 x
2
2
2
2
0
0
1
1
sin 2 0 sin 0
2 2
2
2
2
2
65. Применяя определенный интеграл можно вывести ряд формул объемов стереометрических фигур Объем шара:
3R
x
2
2
2
2
2
V R x dx R x dx R x
3 R
R
R
R
R
3
3
3
3
3 R3
R
2
R
6
R
2
R
4 3
3
3
R R 2 R
R
3
3
3
3
3
Объем конуса
H
R2 2
R2
V
x dx
2
2
H
H
0
R 2
h3
H
x
2
dx
0
H 3 R 2 0 1
2
R
H
2
3
H
3 3
R 2
h3
x3 H
3 0
67.
 Задачи для самостоятельного решения Найти объём усечённого конуса, образованного
Задачи для самостоятельного решения Найти объём усечённого конуса, образованноговращением прямой y = x + 1 вокруг оси OX и
ограниченной линиями x = 0 и x = 3 .
Ответ: 21
Вычислить объем тела, полученного вращением
фигуры, ограниченной линиями у 2 х х у=0
вокруг оси ОХ.
Ответ: 16π\15
2
68. Практическая работа.
Вычислить объем тела образованноговращением вокруг оси Ох,
ограниченного указанными линиями
у = х2-9 и у = 0.
Из пластилина вылепить фигуру,
которая получится при решении
данной задачи, без учета масштаба.
Уже Архимед успешно находил площади фигур, несмотря на то, что в
математике его времени не было понятия интеграла
Но лишь интегральное исчисление дает общий метод решения
задач из различных областей наук.
Недаром даже поэты воспевали интеграл.
Смысл- там, где змеи интеграла
Меж цифр и букв , меж d и f.
Там – власть, там творческие горны!
Пред волей чисел все – рабы.

И солнца путь вершат, покорны
Немым речам и ворожбы.
В.Брюсов.
Мини- тест.
Задания для студентов на оценку «3»
№1. С помощью формулы Ньютона- Лейбница
вычисляют:
а) первообразную функция
б) площадь криволинейной трапеции
в) интеграл
г) производную
№2. Вычислите
Ответы: а) 13,5;
б) 10,5;
;
г) 18
№3. Найдите площадь фигуры, ограниченной осью
Ох и параболой у = 9 – x2
Ответы: а) 18; б) 36; в) 72; г) нельзя вычислить
71. Задания для студентов на оценку «4» и «5»
№1.ВычислитеОтветы: а)
; б)
;
в)
; г) 9
№2.Вычислите площадь фигуры, ограниченной
линиями у =
Ответы: а) ;
б)
; в)
Заключение
Применение физических моделей при введении понятия
интеграла, рассмотрении его свойств, отработке
техники интегрирования и изучении приложений
способствует осознанному качественному усвоению
материала, развитию правильного представления об
изучаемом понятии, его огромной значимости в
различных науках, формированию мировоззрения, таких
специальных качеств, как умение строить
математические модели реальных процессов и явлений,
исследовать и изучать их, а, следовательно,
способствует развитию мышления, памяти, внимания и
речи.

Спасибо за внимание
74. Литература:
Основная:1.В.П. Омельченко «Математика», Ростов н/Д, 2005г.
2. Н.В.Богомолов «Практические задания по математике»- М.: Высш.шк.,2002г
3. Г.Н. Яковлев «Алгебра и начала анализа» – М.: Наука, 1987г., ч.1.
4. А.Н. Колмогоров «Алгебра и начала анализа»
Дополнительная:
М.И. Башмаков «Алгебра и начала анализа». -М.: Дрофа, 2003г.
В.Т. Лисичкин «Математика»- М.: Высш.шк., 1991г.
М.И.Башмаков «Дидактические материалы»- М.: Дрофа, 2003г.
Интернет – ресурсы:
1. www.mathprofi.ru/integraly_primery_reshenij.html
2. xreferat.ru/54/842-1-primenenie-integralov-k-resheniyu-prikladnyh-zadach.html
3. http://www.myshared.ru/slide/615344/
4. www.bibliofond.ru/view.aspx?id=35224
Первообразная. Интеграл. Формула Ньютона-Лейбница | Подготовка к ЕГЭ по математике
Математики любят всякому действию сопоставить противодействие.
Сложению противодействует вычитание, умножению – деление, возведению в степень – извлечение корня и т. п.
п.
И противодействие дифференцированию (то есть взятию производной) есть! Это интегрирование.
Но давайте по порядку.
Первообразная
Первообразной функцией (также называют антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть .
Вычисление первообразной называется интегрированием.
Пример:
+ показать
Множество первообразных функций для называют неопределенным интегралом функции y = f(x) и обозначают :
Определенный интеграл
Определенный интеграл записывается так:
То есть у нас появляются границы интегрирования. – нижняя граница интегрирования, – верхняя.
Так вот формула Ньютона-Лейбница позволяет вычислять определенный интеграл следующим образом:
При вычислении первообразных вы можете пользоваться таблицей первообразных.
Пример:
+ показать
Вычислить интегралРешение:
Ответ: 0,25.
Геометрический смысл определенного интеграла
Сначала нам придется познакомиться с понятием «криволинейная трапеция».
Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой неотрицательной непрерывной функции , осью и прямыми :
Так вот, с геометрической точки зрения площадь криволинейной трапеции, ограниченной графиком функции , осью и прямыми есть интеграл от на отрезке :
Примеры:
+ показать
1. Найти площадь фигуры, ограниченной графиком функции , осью и прямымиРешение:
В общем-то, перед нами – прямоугольная трапеция с основаниями 3 и 7 и высотой 2.
Мы легко можем посчитать площадь трапеции по формуле :
.
Но, все же, мы посчитаем площадь через интеграл, а затем сверим результаты.
Итак,
Ну вот, все сошлось.
Ответ: 10.
Никто не спорит, здесь можно обойтись и без интеграла, но без него не обойтись в случаях, когда представляет из себя кривую, отличную от прямой линии.
2. Найти площадь фигуры, ограниченной графиком функции , осью и прямыми
Решение:
Ответ:
Статья “Методика преподавания интеграла в школе”
Методика преподавания интеграла в школе
И.И. Иванова – Группа, курс, факультет и т.д.
Аннотация: в данной статье анализируются вопросы теоретического и практического изучения темы «интеграл» в школьном курсе математики. Определяются основные направления преподавания данной темы. Выявляется последовательность изучения материала.
Ключевые слова: методика,
интеграл, проблемы преподавания, прикладные задачи, математический анализ,
последовательность рассмотрения материала.
Как известно, современный этап развития мирового сообщества характеризуется прогрессом в разных областях науки, высокой актуальностью новых технических и технологических идей, широчайшим распространением математических методов в большинстве видов практической деятельности человека. В целом же, математика представляет на практике общие и достаточно точные методы для изучения окружающих человека природных, социальных, экономических и иных явлений. В этой связи, с учетом достаточно быстрого развития возможностей компьютерной обработки данных, повышается и роль математического моделирования, изучаемого в школах.
Одной из самых сложных
тем в курсе математики старшей школы является «Интеграл». Вопросы
теоретического и практического применения интеграла, методики преподавания данной
темы всегда являлись объектом достаточно широкого исследования многих ученых. По
сути, изучение первичных понятий и методов математического анализа имеет
огромное значение для развития всех учащихся школы, но, при этом,
педагогическая практика показывает, что те проблемы, которые возникают при
преподавании «интеграла» в школе, не уменьшаются. Знания большого числа школьников
по данной теме носят только формальный характер, механический. У них отсутствует
структура знаний, не формируется полное представление о понятии «интеграла», не
выработаны навыки решения задач. Причинами всех сложившихся проблем и
трудностей являются высокая степень «отдаленности» понятий, даваемых в
учебниках, от истинны, сложная логическая структура их определений и
последовательности, недостаточное время для понимания, и другие факторы. Именно
поэтому полноценное успешное изучение раздела «интеграл» в старшей школе зависит
от решения всех проблем, которые связаны с правильной постановкой целей
изучения курса, тщательным отбором содержания теоретического и дидактического
материалов, и методическими приемами, и особенностями данной темы. [1]
Знания большого числа школьников
по данной теме носят только формальный характер, механический. У них отсутствует
структура знаний, не формируется полное представление о понятии «интеграла», не
выработаны навыки решения задач. Причинами всех сложившихся проблем и
трудностей являются высокая степень «отдаленности» понятий, даваемых в
учебниках, от истинны, сложная логическая структура их определений и
последовательности, недостаточное время для понимания, и другие факторы. Именно
поэтому полноценное успешное изучение раздела «интеграл» в старшей школе зависит
от решения всех проблем, которые связаны с правильной постановкой целей
изучения курса, тщательным отбором содержания теоретического и дидактического
материалов, и методическими приемами, и особенностями данной темы. [1]
По сути, можно сказать,
что интеграл принадлежит к числу тех математических понятий, происхождение и
развитие которых напрямую связано с решением всех прикладных задач. Данное
понятие и построенные на его основе методы применяются в наши дни в самых разных
областях деятельности человека, в том числе в таких науках, как: физика, химия,
биология, экономика, и так далее. [2]
Интеграл – это, безусловно, важнейшее понятие в математическом
анализе. Его применяют в тех случаях, когда пытаются найти площадь, которая
находится под кривой, когда необходимо найти пройденный путь при неравномерном
движении или узнать, какая масса у неоднородного тела, и так далее.
Именно поэтому, для наиболее успешного усвоения основных понятий, связанных с
разделом «интеграл», необходимо:
[2]
Интеграл – это, безусловно, важнейшее понятие в математическом
анализе. Его применяют в тех случаях, когда пытаются найти площадь, которая
находится под кривой, когда необходимо найти пройденный путь при неравномерном
движении или узнать, какая масса у неоднородного тела, и так далее.
Именно поэтому, для наиболее успешного усвоения основных понятий, связанных с
разделом «интеграл», необходимо:
1. Вводить все существующие понятия и определения наиболее естественным путем.
2. Как можно чаще привлекать учащихся к самостоятельному изучению и определению рассматриваемого понятия.
3. В процессе изучения выявлять связи интеграла с уже известными понятиями.
4. Стараться мотивировать вводимые понятия, термины, определения, увеличивать их значимость.
5. Как можно чаще повторять учащимися известные математические понятия, которые связаны с изучением интеграла.
6. Постоянно следить за
речью учащихся, требовать четкости, краткости, строгости в определении понятий. [3]
[3]
7. Перед самым введением понятия интеграла и первообразной целесообразно повторить с учащимися взаимообратные операции. [4] По сути, интеграл является одним из ключевых понятий математического анализа. Чтобы задать понятие интеграла нужно дать определение производной функции. Первообразной функция F(x) для функции y=f(x) называется тогда, когда на некотором промежутке (a,b) для любого x∈(a,b) выполняется равенство F′(x)=f(x). [5]
8. Далее важно выдать ученикам рассмотреть таблицу нахождения производных функции.
9. Весьма целесообразно обратить внимание учащихся на то, что интеграл зависит только от вида подынтегральной функции и пределов интегрирования и не зависит от переменного интегрирования.
10. Для активизации познавательной деятельности учащихся важно предложить самостоятельно доказать некоторые свойства интеграла, а, также, рассмотреть задачи из учебников геометрии и физики, в решении которых используется интеграл. [6]
11. Важно объяснить
ученикам, что любые навыки нахождения интегралов могут пригодиться не только в
математике, но и в других точных дисциплинах. Таблица является основой
интегрального исчисления. Для того чтобы использовать ее достаточно лишь найти
необходимые значения. [7]
Таблица является основой
интегрального исчисления. Для того чтобы использовать ее достаточно лишь найти
необходимые значения. [7]
12. Необходимо продемонстрировать как можно больше примеров решения интегралов, не требовать от учеников скорого понимания и идеального решения, лишь в процессе изучения и решения задач указывая на ошибки.
Необходимо отметить, что
интеграл в общеобразовательной школе изучается только в 11 классе. По ФГОС СОШ
на базовом уровне на изучение темы отводится 8 часов, рассматриваются темы:
«Первообразная», «Определенный интеграл» и проводится контрольная работа. В
учебниках базового уровня сначала вводится понятие первообразной, указываются
правила отыскания первообразных, составляется их таблица, затем определяется
площадь криволинейной трапеции. Далее вводится понятие определенного интеграла,
рассматриваются физические задачи на приложение интеграла. В профильных классах
так же, как и в классах базового уровня, сначала вводится понятие
первообразной, правила отыскания первообразной, составляется таблица
первообразных. Так же, определяется понятие неопределенного интеграла, его
свойства, рассматриваются методы интегрирования. После определяется площадь
криволинейной трапеции через площадь ступенчатой фигуры, понятие определенного
интеграла через приращение первообразной и по формуле Ньютона – Лейбница.
Обобщается понятие определенного интеграла для неограниченных функций и с
бесконечными пределами, вводится интеграл с переменным верхним пределом,
указываются свойства определенного интеграла, выражаемыми равенствами и
неравенствами, и так далее. [8]
Так же, определяется понятие неопределенного интеграла, его
свойства, рассматриваются методы интегрирования. После определяется площадь
криволинейной трапеции через площадь ступенчатой фигуры, понятие определенного
интеграла через приращение первообразной и по формуле Ньютона – Лейбница.
Обобщается понятие определенного интеграла для неограниченных функций и с
бесконечными пределами, вводится интеграл с переменным верхним пределом,
указываются свойства определенного интеграла, выражаемыми равенствами и
неравенствами, и так далее. [8]
В основном, с самого
начала изучения раздела «интеграл», операция интегрирования определяется
учителем как операция, обратная дифференцированию, далее вводится понятие
первообразной, при этом, не вводится ни определение неопределенного интеграла,
ни его обозначение. Таблица правил интегрирования в этом случае естественно
получается из таблицы производных. Формулируется утверждение, что все
первообразные для функции F(x) имеют вид F(x)+С, где F(x) – первообразная,
найденная в таблице. Связь между первообразной и площадью криволинейной
трапеции устанавливается формулой Ньютона – Лейбница. Далее возникает
определенный интеграл как предел интегральной суммы, однако, при этом, формула
Ньютона – Лейбница также оказывается справедливой. [9]
Связь между первообразной и площадью криволинейной
трапеции устанавливается формулой Ньютона – Лейбница. Далее возникает
определенный интеграл как предел интегральной суммы, однако, при этом, формула
Ньютона – Лейбница также оказывается справедливой. [9]
Подводя итоги, можно
сказать, что интеграл – это одно из те понятий в
школьном курсе математике, которое позволяет найти площадь под кривой, которое
помогает вникнуть в изучение математического анализа. Данная тема рассматривается
только 11 классе школы, и в разных учебниках по математике прописана
своя последовательность, но, при этом, все они структурированы так, чтобы
максимально понятно и логично преподать информацию ученикам. В остальном уже
дело за самими учителями и учениками. В целом, весьма полезно решать задачи,
так как они способствуют лучшему развитию мышления. Например, решение задач с
применением определенного интеграла способствуют развитию абстрактного
мышления, но, при этом, для решения таких задач необходима база теоретических
обобщенных знаний по математике.
Список использованной литературы
1. Афанасьева Е.В. Формирование основных понятий на уроках математики, как разновидность логических познавательных УУД, 2020. [Электронный ресурс]: https://nsportal.ru/shkola/matematika/library/2020/01/08/formirovanie-osnovnyh-ponyatiy-na-urokah-matematiki-kak (Дата обращения: 20.06.2020)
2. Лукьянова Т.И., Мансурова Е.Р. Интеграл в школьном курсе математики // Физико-математические образование: проблемы и перспективы: сб. статей. – Елабуга: Изд-во Казан. Ун-та, 2017. – С. 51-55.
3. Марчук Н.А., Гульманов Н.К., Асетов А.А. Методические особенности преподавания темы «Интеграл» // International scientific review, 2016. – №3. – С. 197-201.
4. Справочник. Интегралы. Внесение под знак дифференциала. [Электронный ресурс]: https://spravochnick.ru/matematika/integraly_vnesenie_pod_znak_differenciala/ (Дата обращения: 20.06.2020)
5. Справочник.
Примеры на решение интегралов. [Электронный ресурс]:
https://spravochnick.ru/matematika/primery_na_reshenie_integralov/ (Дата
обращения: 19.06.2020)
Справочник.
Примеры на решение интегралов. [Электронный ресурс]:
https://spravochnick.ru/matematika/primery_na_reshenie_integralov/ (Дата
обращения: 19.06.2020)
6. Толоконцев А.А. Проект изучения темы «Интеграл» (11 класс). Урок решения ключевых задач по теме «Вычисление площадей с помощью интегралов». [Электронный ресурс]: https://gigabaza.ru/doc/156046-pall.html (Дата обращения: 19.06.2020)
7. Улендеева Н.И. Изучение темы «Первообразная и интеграл» с учащимися 11 класса в курсе алгебры и начала математического анализа профильной школы // Самарский научный вестник, 2013. – №2(3) – С.56-58.
8. Скачано с www.znanio.ru
5: Интеграция – математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2510
\ (\ newcommand {\ vecs} [1] {\ overset {\ scriptstyle \ rightharpoonup} {\ mathbf {# 1}}} \) \ (\ newcommand {\ vecd} [1] {\ overset {- \! – \! \ rightharpoonup} {\ vphantom {a} \ smash {# 1}}} \) \ (\ newcommand {\ id} {\ mathrm {id}} \) \ (\ newcommand {\ Span} {\ mathrm {span}} \) \ (\ newcommand {\ kernel} {\ mathrm {null} \,} \) \ (\ newcommand {\ range} {\ mathrm {range} \,} \) \ (\ newcommand {\ RealPart} {\ mathrm {Re}} \) \ (\ newcommand {\ ImaginaryPart} {\ mathrm {Im}} \) \ (\ newcommand {\ Argument} {\ mathrm {Arg}} \) \ (\ newcommand { \ norm} [1] {\ | # 1 \ |} \) \ (\ newcommand {\ inner} [2] {\ langle # 1, # 2 \ rangle} \) \ (\ newcommand {\ Span} {\ mathrm {span}} \) \ (\ newcommand {\ id} {\ mathrm {id}} \) \ (\ newcommand {\ Span} {\ mathrm {span}} \) \ (\ newcommand {\ kernel} { \ mathrm {null} \,} \) \ (\ newcommand {\ range} {\ mathrm {range} \,} \) \ (\ newcommand {\ RealPart} {\ mathrm {Re}} \) \ (\ newcommand {\ ImaginaryPart} {\ mathrm {Im}} \) \ (\ newcommand {\ Argument} {\ mathrm {Arg}} \) \ (\ newcommand {\ norm} [1] {\ | # 1 \ |} \ ) \ (\ newcommand {\ inner} [2] {\ langle # 1, # 2 \ rangle} \) \ (\ newcommand {\ Span} {\ mathrm {s pan}} \)
- Авторы и авторство
- 5.
 1: Приближение областей
1: Приближение областей - В этом разделе мы разрабатываем методы аппроксимации области между кривой, определяемой функцией f (x), и осью x на отрезке [a, b]. Как и Архимед, мы сначала аппроксимируем площадь под кривой, используя формы известной площади (а именно, прямоугольники). Используя все меньшие и меньшие прямоугольники, мы приближаемся к площади все ближе и ближе. Ограничение позволяет нам точно рассчитать площадь под кривой.
- 5.
- 5.∗ _i) ∆x, \], если существует предел. Если этот предел существует, функция f (x) называется интегрируемой на [a, b] или интегрируемой функцией. Числа a и b называются пределами интегрирования; в частности, a – это нижний предел, а b – верхний предел. Функция f (x) – это подынтегральное выражение, а x – переменная интегрирования.
- 5.3: Основная теорема исчисления
- Фундаментальная теорема исчисления дала нам метод вычисления интегралов без использования сумм Римана.
 Однако недостатком этого метода является то, что мы должны иметь возможность найти первообразное, а это не всегда легко.
Однако недостатком этого метода является то, что мы должны иметь возможность найти первообразное, а это не всегда легко.
- 5.4: Формулы интеграции и теорема чистого изменения
- Теорема чистого изменения утверждает, что при изменении количества конечное значение равно начальному значению плюс интеграл скорости изменения. Чистое изменение может быть положительным, отрицательным или нулевым. Площадь под четной функцией в симметричном интервале может быть вычислена путем удвоения площади по положительной оси абсцисс.Для нечетной функции интеграл по симметричному интервалу равен нулю, поскольку половина площади отрицательна.
- 5.5: Замена
- В этом разделе мы исследуем метод, называемый интегрированием заменой, чтобы помочь нам найти первообразные. В частности, этот метод помогает нам находить первообразные, когда подынтегральное выражение является результатом производной цепного правила.

- 5.6: Интегралы, включающие экспоненциальные и логарифмические функции
- Экспоненциальные и логарифмические функции возникают во многих реальных приложениях, особенно связанных с ростом и спадом.Подстановка часто используется для вычисления интегралов, включающих экспоненциальные функции или логарифмы.
- 5.7: Интегралы, приводящие к обратным тригонометрическим функциям
- Напомним, что тригонометрические функции не взаимно однозначны, если области не ограничены. При работе с обратными тригонометрическими функциями мы всегда должны внимательно учитывать эти ограничения. Также в разделе «Производные» мы разработали формулы для производных обратных тригонометрических функций.Разработанные там формулы непосредственно приводят к формулам интегрирования, включающим обратные тригонометрические функции.
- 5R: Упражнения по обзору главы 5
Авторы и авторство
Гилберт Стрэнг (Массачусетский технологический институт) и Эдвин «Джед» Херман (Харви Мадд) со многими авторами.
 Этот контент OpenStax находится под лицензией CC-BY-SA-NC 4.0. Загрузите бесплатно с http://cnx.org.
Этот контент OpenStax находится под лицензией CC-BY-SA-NC 4.0. Загрузите бесплатно с http://cnx.org.
- Наверх
- 4R: Упражнения на повторение главы 4
- 5.1: Приближенные районы
- Была ли эта статья полезной?
- Да
- Нет
- Вид товара Глава
- .
- Автор
- Гилберт Стрэнг и Эдвин «Джед» Герман
- Лицензия
- CC BY-NC-SA
- Программа OER или издатель
- OpenStax
- Показать страницу TOC
- №
- Теги
 2 + С,
\ end {align} ∫ye2ydy = ∫udv = uv − ∫vdu = 21 ye2y − 21 ∫e2ydy = 21 ye2y − 21 ⋅21 e2y + C = 21 x2lnx − 41 x2 + C,
2 + С,
\ end {align} ∫ye2ydy = ∫udv = uv − ∫vdu = 21 ye2y − 21 ∫e2ydy = 21 ye2y − 21 ⋅21 e2y + C = 21 x2lnx − 41 x2 + C,где CCC – постоянная интегрирования. □ _ \ квадрат □
Интеграл по путям: математические аспекты – Scholarpedia
Интегралы по пространствам траекторий или, в более общем смысле, полей были введены в качестве эвристических инструментов в нескольких областях физики и математики. Математически они должны быть задуманы как расширения конечномерных интегралов, подходящие для охвата приложений, для которых изначально задумывались эвристические интегралы по путям .
Одноименные соглашения об именах: функциональные интегралы, бесконечномерные интегралы, полевые интегралы. Интегралы по путям (или функционалы) Фейнмана и интегралы по путям Винера (или интегралы по мерам Винера) являются частными случаями. Вероятно также встречается понятие плоского интеграла . Конкретная реализация гауссовских интегралов по траекториям дается «функционалами белого шума».

В данной статье будет представлена математическая теория интегралов Фейнмана по траекториям , а теория и приложения интегралов по траекториям вероятностного типа, таких как интегралы Винера, будут представлены в разделе Вероятностные интегралы: математические аспекты.
Интегралы по траекториям Фейнмана не следует путать с «интегралами Фейнмана», возникающими при изучении членов, возникающих в разложениях возмущений в квантовой теории поля, которые связаны с диаграммами Фейнмана. Последние являются конечномерными комплексными интегралами и обсуждаются, в частности, в связи с перенормировкой.
Интегралы по траекториям Фейнмана: Истоки
В 1948 г., следуя предложению Дирака, Р.П. Фейнман предложил новое наводящее на размышления описание временной эволюции состояния нерелятивистской квантовой частицы, движущейся в \ (d \) -мерном пространстве под действием силового поля с потенциалом \ (V \.tV (\ gamma (s)) ds. \] Подход Фейнмана особенно многозначителен, поскольку он создает мост между классическим лагранжевым описанием физического мира и квантовым, вновь вводя в квантовую механику классическое понятие траектории, которое было запрещено традиционной формулировкой теории.
 Это позволяет, по крайней мере эвристически, связать квантовую эволюцию с каждым классическим лагранжианом. Более того, это делает очень интуитивным изучение «полуклассического предела» квантовой механики, т.е.{\ frac {i} {\ hbar} S_t (\ gamma)} \) ведет себя как сильно осциллирующая функция, и, согласно эвристической экстраполяции метода стационарной фазы на случай интеграла по путям, основной вклад в интеграл должен давать от тех путей, которые делают фазовый функционал \ (S _t \. \) стационарным. Они, согласно принципу наименьшего действия Гамильтона, являются в точности классическими орбитами системы.
Фейнман распространил эту эвристическую формулировку на описание динамики более общих квантовых систем, включая релятивистские квантовые поля, и использовал ее для вывода процедур (правила Фейнмана, диаграммы Фейнмана), которые позволяют выполнять вычисления, дающие числа, даже когда строгие аргументы не работают.С тех пор эвристические интегралы по траекториям Фейнмана стали основой большей части современной физики (включая квантовые поля, в частности калибровочные поля) и стимулировали развитие многих областей математики.
Это позволяет, по крайней мере эвристически, связать квантовую эволюцию с каждым классическим лагранжианом. Более того, это делает очень интуитивным изучение «полуклассического предела» квантовой механики, т.е.{\ frac {i} {\ hbar} S_t (\ gamma)} \) ведет себя как сильно осциллирующая функция, и, согласно эвристической экстраполяции метода стационарной фазы на случай интеграла по путям, основной вклад в интеграл должен давать от тех путей, которые делают фазовый функционал \ (S _t \. \) стационарным. Они, согласно принципу наименьшего действия Гамильтона, являются в точности классическими орбитами системы.
Фейнман распространил эту эвристическую формулировку на описание динамики более общих квантовых систем, включая релятивистские квантовые поля, и использовал ее для вывода процедур (правила Фейнмана, диаграммы Фейнмана), которые позволяют выполнять вычисления, дающие числа, даже когда строгие аргументы не работают.С тех пор эвристические интегралы по траекториям Фейнмана стали основой большей части современной физики (включая квантовые поля, в частности калибровочные поля) и стимулировали развитие многих областей математики.
Математические задачи
Несмотря на успешную предсказательную силу концепции интеграла по путям Фейнмана, ей не хватает математической строгости. Во-первых, плоская мера \ (D \ gamma \) типа Лебега на пространстве путей не определена с математической точки зрения и не может использоваться в качестве эталонной меры , т.е.2ds} D \ gamma} \] в терминах интеграла по \ (\ sigma \) – аддитивной (комплекснозначной) мере можно попытаться определить \ (I (f) \) как линейный непрерывный функционал на подходящем линейном пространстве функций \ (е \. \)
Разные подходы
Последовательный подход
Этот подход наиболее близок к первоначальному выводу формулы Фейнмана, и он в значительной степени реализован в физической литературе, а также в качестве практического инструмента для выполнения вычислений в точно решаемых моделях, см. E.{это (A + B)} \] (где сумма \ (A + B \) должна интерпретироваться соответствующим образом). Нельсон (1964) применил последнее уравнение к строгому математическому определению интегралов по траекториям Фейнмана в предположении, что потенциал \ (V \) принадлежит классу, рассмотренному Като (подробное обсуждение см.
 В книге Джонсона и Лапидуса). Некоторое время спустя Фридман (1971/72) изучил (3) в связи с описанием непрерывных квантовых наблюдений (см. Также A.D. Sloan (1981) и ссылки в книге С.Альбеверио, Р. Хёг-Крон и С. Маццукки (2008).
В книге Джонсона и Лапидуса). Некоторое время спустя Фридман (1971/72) изучил (3) в связи с описанием непрерывных квантовых наблюдений (см. Также A.D. Sloan (1981) и ссылки в книге С.Альбеверио, Р. Хёг-Крон и С. Маццукки (2008).Другая версия последовательного подхода, также известная как аппроксимация квантования времени , состоит в определении интеграла Фейнмана как предела конечномерных приближений, данного в (2), путем аппроксимации путей \ (\ gamma \) с помощью кусочно-линейные пути или кусочно-классические пути (т.е. пути, которые кусочно решают классическое уравнение движения Ньютона). Приближение квантования времени, в частности с кусочно-многоугольными путями, широко используется в физической литературе не только как инструмент для определения интеграла по путям Фейнмана, но и как практический метод вычисления для конкретных решаемых моделей, см.+ \, \) и подходящего функционала \ (f \) на пространстве \ (C_t \) непрерывных путей на интервале \ ([0, t] \, \) имеет место формула: \ [ \ int_ {C_t} f (\ omega) dW_ \ lambda (\ omega) = \ int_ {C_t} f (\ sqrt \ lambda \ omega) dW (\ omega).
 \]
Если \ (\ lambda \) комплексный, левая часть не определена должным образом, но правая часть может иметь смысл при условии, что функционал \ (f \) имеет подходящие свойства аналитичности и измеримости. В частности, для \ (\ lambda = i \, \) он является естественным кандидатом на аналитически продолженный интеграл Винера .tV (\ omega (s) + x)) ds} u (0, \ omega (t) + x) dW (\ omega).
\]
Эта формула верна. например, если \ (V \) ограничено и непрерывно, но также когда \ (V \) достаточно произвольно и ограничено снизу, см., например, Johnson and Lapidus.
\]
Если \ (\ lambda \) комплексный, левая часть не определена должным образом, но правая часть может иметь смысл при условии, что функционал \ (f \) имеет подходящие свойства аналитичности и измеримости. В частности, для \ (\ lambda = i \, \) он является естественным кандидатом на аналитически продолженный интеграл Винера .tV (\ omega (s) + x)) ds} u (0, \ omega (t) + x) dW (\ omega).
\]
Эта формула верна. например, если \ (V \) ограничено и непрерывно, но также когда \ (V \) достаточно произвольно и ограничено снизу, см., например, Johnson and Lapidus.Путем введения в уравнение теплопроводности и в соответствующую формулу Фейнмана-Каца действительный положительный параметр \ (\ lambda \, \), связанный с физическим временем, или с массой, или с постоянной Планка, и позволяя ему Принимая комплексные значения, можно получить, по крайней мере эвристически, для \ (\ lambda = i \) уравнение Шредингера и функциональное интегральное представление его решения.Эта процедура может быть строго реализована в условиях аналитичности и медленного роста потенциала и исходных данных.
 В частности, можно рассматривать потенциалы, которые являются суммой квадратичной части плюс ограниченный потенциал с особенностями (Нельсон (1964), Досс (1980)), потенциалы с определенным полиномиальным ростом (Досс (1980), Альбеверио и Маццукки (2009) , Albeverio, Khrennikov and Smolyanov (1999), Grothaus, Streit and Vogel (2009)) и потенциалы с экспоненциальным ростом, которые являются преобразованиями Лапласа мер (Albeverio, Brzeźniak and Haba (1998), Kuna, Streit and Westerkamp (1998)).2 (\ му) \ подмножество (S_d) ‘.
\]
Элементы \ ((S_d) ‘\) называются распределениями белого шума (или Hida) , а элементы в \ ((S_d) \) являются соответствующими тестовыми функциями (обе относительно бесконечномерных реальных пространств.
Подробное рассмотрение этой темы см., Например, в книгах Т. Хида, Х. Х. Куо, Дж. Поттхоффа, Л. Стрейта (1993), Н. Обаты (1994) и Х. Х. Куо (1996).
В частности, можно рассматривать потенциалы, которые являются суммой квадратичной части плюс ограниченный потенциал с особенностями (Нельсон (1964), Досс (1980)), потенциалы с определенным полиномиальным ростом (Досс (1980), Альбеверио и Маццукки (2009) , Albeverio, Khrennikov and Smolyanov (1999), Grothaus, Streit and Vogel (2009)) и потенциалы с экспоненциальным ростом, которые являются преобразованиями Лапласа мер (Albeverio, Brzeźniak and Haba (1998), Kuna, Streit and Westerkamp (1998)).2 (\ му) \ подмножество (S_d) ‘.
\]
Элементы \ ((S_d) ‘\) называются распределениями белого шума (или Hida) , а элементы в \ ((S_d) \) являются соответствующими тестовыми функциями (обе относительно бесконечномерных реальных пространств.
Подробное рассмотрение этой темы см., Например, в книгах Т. Хида, Х. Х. Куо, Дж. Поттхоффа, Л. Стрейта (1993), Н. Обаты (1994) и Х. Х. Куо (1996).Распределение Хида \ (\ Phi \ in (S_d) ‘\) может быть однозначно охарактеризовано его T-преобразованием, бесконечномерным аналогом преобразования Фурье, то есть функционалом \ (T \ Phi: S_d \ to { \ mathbb C} \) определяется как \ [ \ xi \ in S_d \ mapsto T \ Phi (\ xi): = \ langle \ langle e ^ {i \ langle \ xi, \, \ cdot \, \ rangle}, \ Phi \ rangle \ rangle, \] где \ (\ langle \ langle e ^ {i \ langle \ xi, \, \ cdot \, \ rangle}, \ Phi \ rangle \ rangle \) обозначает распределение между \ (e ^ {i \ langle \ xi, \, \ cdot \, \ rangle} \ in (S_d) \) и \ (\ Phi \ in (S’_d) \.
 \)
\)Основная теорема характеризации позволяет идентифицировать функционалы, которые являются Т-преобразованиями распределений Хида. Действительно, в 1991 г. Дж. Поттхофф и Л. Стрейт доказали, что функционал \ (F: S_d \ to {\ mathbb C} \) является T-преобразованием единственного распределения Хида тогда и только тогда, когда он обладает следующими свойствами:
- Для всех \ (\ xi, \ eta \ in S_d \) отображение
\ [ z \ in {\ mathbb R} \ mapsto F (\ xi + z \ eta) \ in {\ mathbb C} \] имеет аналитическое продолжение в \ ({\ mathbb C} \) как целая функция.t \ omega (\ sigma) d \ sigma \, \) \ (N \) обозначает нормализацию, а \ (\ delta (\ gamma (0) -y) \) фиксирует начальную точку пути.
Эти методы построения позволяют обрабатывать более общие потенциалы, такие как (зависящий от времени) гармонический осциллятор, преобразования Фурье и Лапласа ограниченных мер и некоторые потенциалы с полиномиальным ростом, см., Например, работу М. де Фариа, J.
 Potthoff, L. Streit (1991), DC Khandekar и L. Streit (1992), A. Lascheck, P. Leukert, L.Streit, W. Westerkamp (1993), M. Grothaus, D.C. Khandekar, J.L. da Silva, L. Streit (1997), T. Kuna, L. Streit, W. Westerkamp (1998),
М. Гротхаус, Л. Штрайт, А. Фогель (2009).
Potthoff, L. Streit (1991), DC Khandekar и L. Streit (1992), A. Lascheck, P. Leukert, L.Streit, W. Westerkamp (1993), M. Grothaus, D.C. Khandekar, J.L. da Silva, L. Streit (1997), T. Kuna, L. Streit, W. Westerkamp (1998),
М. Гротхаус, Л. Штрайт, А. Фогель (2009).Важные приложения подхода белого шума включают математические модели Черна-Саймонса топологических квантовых полей, следующие базовым идеям Атьи-Виттена.
Двойственность Парсеваля
Этот подход был предложен К. Ито в 1961 году и в дальнейшем систематически и широко развивался Альбеверио и Хёг-Кроном в 70-х годах.2} d \ mu_f (\ gamma). \]
Можно доказать, что функции \ (f \), как в (7), образуют банахову алгебру \ ({\ mathcal F} ({\ mathcal H}) \, \), где норма функции \ ( f \) – это полная вариация соответствующей меры \ (\ mu_f \, \), а интеграл Френеля – линейный непрерывный функционал на \ ({\ mathcal F} ({\ mathcal H}) \. \)
Основные приложения этого подхода включают разработку детального метода стационарной фазы в бесконечных измерениях с приложениями к изучению связи между квантовой и классической механикой на \ (\ R ^ d \) (с потенциалами являются преобразования Фурье ограниченного комплексные меры по теории рассеяния \ (\ R ^ d \, \) и построение абелевой модели Черна-Саймонса, см.
 {\ frac {i} { \ hbar} \ Phi (P_nx)} dP_nx},
\]
где интегралы в правой части понимаются как конечномерные осциллирующие интегралы.В случае, когда фазовая функция \ (\ Phi \) является квадратичной формой, интеграл также называется бесконечномерным интегралом Френеля.
Полная характеризация самого большого класса функций, интегрируемых по Френелю, все еще остается открытой проблемой, даже в конечных размерностях, но можно найти интересные подмножества таких функций, как алгебра Френеля. Действительно, для любой функции \ (f: {\ mathcal H} \ to {\ mathbb C} \), проверяющей (7) для некоторого \ (\ mu_f \, \), можно доказать, что она интегрируема по Френелю и ее бесконечная размерный интеграл Френеля дается равенством Парсеваля, т.е.е. (8) (что в данном случае это теорема, а не определение, как в подходе, описанном в предыдущем разделе).
{\ frac {i} { \ hbar} \ Phi (P_nx)} dP_nx},
\]
где интегралы в правой части понимаются как конечномерные осциллирующие интегралы.В случае, когда фазовая функция \ (\ Phi \) является квадратичной формой, интеграл также называется бесконечномерным интегралом Френеля.
Полная характеризация самого большого класса функций, интегрируемых по Френелю, все еще остается открытой проблемой, даже в конечных размерностях, но можно найти интересные подмножества таких функций, как алгебра Френеля. Действительно, для любой функции \ (f: {\ mathcal H} \ to {\ mathbb C} \), проверяющей (7) для некоторого \ (\ mu_f \, \), можно доказать, что она интегрируема по Френелю и ее бесконечная размерный интеграл Френеля дается равенством Парсеваля, т.е.е. (8) (что в данном случае это теорема, а не определение, как в подходе, описанном в предыдущем разделе).Доказательство равенств типа Парсеваля для бесконечномерных осциллирующих интегралов было расширено Альбеверио и Маццукки в 2005 году, чтобы охватить случай, когда фазовая функция является многочленом, старший член которого имеет степень 4 (этот случай особенно важен для физики, полиномиальное взаимодействие 4-го порядка, характерное для лагранжевой квантовой теории поля).
 tV (\ gamma (\ tau) + x) d \ tau} \ psi_0 (\ gamma (0) + x) d \ gamma
\]
корректно определено и является представлением решения \ (\ psi (t, x) \) уравнения Шредингера. Аналогичные результаты были получены Альбеверио и Маццукки в 2005 году для потенциалов полиномиального типа с ростом четвертой степени, включая также случай, когда потенциал может явно зависеть и от времени.
tV (\ gamma (\ tau) + x) d \ tau} \ psi_0 (\ gamma (0) + x) d \ gamma
\]
корректно определено и является представлением решения \ (\ psi (t, x) \) уравнения Шредингера. Аналогичные результаты были получены Альбеверио и Маццукки в 2005 году для потенциалов полиномиального типа с ростом четвертой степени, включая также случай, когда потенциал может явно зависеть и от времени.Нестандартный анализ
Альтернативный подход к строгому математическому определению интегралов по траекториям Фейнмана использует нестандартный анализ и описан в книге Альбеверио и др.* {\ mathbb N} \. \) Результатом будет просто внутренняя величина . Для подходящего класса потенциалов можно показать, что его стандартная часть существует и решает уравнение Шредингера. Даже если этот подход обеспечивает очень убедительную реализацию интегралов по траекториям Фейнмана, он еще не получил систематического развития, некоторые вклады были внесены Т. Накамурой (1991) и К. Лоо (2000). Недавно Ф.С.
 2 \ tilde \ psi (p) -i V (-i \ nabla_p) \ tilde \ фунт / кв. дюйм (p) \\
\ тильда \ psi (0, p) = \ тильда \ phi (p), \\
\ end {array} \ right.d \, \) существуют положительная конечная мера \ (\ nu \) и комплекснозначная измеримая функция \ (f \) такие, что \ (\ mu (dk) = f (k) \ nu (dk) \. \) Без ограничения общности можно считать, что
\ (\ nu (\ {0 \}) = 0 \, \), так как в противном случае условие может быть выполнено переносом потенциала. Тогда мера \ (\ nu \) является конечной мерой Леви, и можно рассматривать процесс Пуассона, имеющий меру Леви \ (\ nu \) (см., Например, книгу П. Проттера (1990) для этих понятий). Этот процесс почти наверняка имеет кусочно-постоянные пути.n (-если (\ delta_j))} \ tilde \ phi (P (t))],
\]
где математическое ожидание берется относительно меры, связанной с пуассоновским процессом, а примерный путь \ (P (\ cdot) \) задается выражением
\ [
P (\ tau) = \ left \ {\ begin {array} {l}
P_0 = p, \ quad 0 \ leq \ tau <\ tau_1 \\
P_1 = p + \ delta_1, \ quad \ tau_1 \ leq \ tau <\ tau_2 \\
.
2 \ tilde \ psi (p) -i V (-i \ nabla_p) \ tilde \ фунт / кв. дюйм (p) \\
\ тильда \ psi (0, p) = \ тильда \ phi (p), \\
\ end {array} \ right.d \, \) существуют положительная конечная мера \ (\ nu \) и комплекснозначная измеримая функция \ (f \) такие, что \ (\ mu (dk) = f (k) \ nu (dk) \. \) Без ограничения общности можно считать, что
\ (\ nu (\ {0 \}) = 0 \, \), так как в противном случае условие может быть выполнено переносом потенциала. Тогда мера \ (\ nu \) является конечной мерой Леви, и можно рассматривать процесс Пуассона, имеющий меру Леви \ (\ nu \) (см., Например, книгу П. Проттера (1990) для этих понятий). Этот процесс почти наверняка имеет кусочно-постоянные пути.n (-если (\ delta_j))} \ tilde \ phi (P (t))],
\]
где математическое ожидание берется относительно меры, связанной с пуассоновским процессом, а примерный путь \ (P (\ cdot) \) задается выражением
\ [
P (\ tau) = \ left \ {\ begin {array} {l}
P_0 = p, \ quad 0 \ leq \ tau <\ tau_1 \\
P_1 = p + \ delta_1, \ quad \ tau_1 \ leq \ tau <\ tau_2 \\
. .. \\
P_n = p + \ delta_1 + \ delta_2 + … + \ delta_n, \ quad \ tau_n \ leq \ tau \ leq t. \\
\ end {array} \ right.
\]
.. \\
P_n = p + \ delta_1 + \ delta_2 + … + \ delta_n, \ quad \ tau_n \ leq \ tau \ leq t. \\
\ end {array} \ right.
\]Этот подход также успешно применялся к другим квантовым системам, таким как ферми-системы, релятивистские квантовые системы, описываемые уравнением Клейна-Гордона и уравнением Дирака, а также некоторые модели квантовой теории поля, см. E.грамм. статьи Ф. Комба, Р. Хёг-Крона, Р. Родригеса, М. Сиругу и М. Сиругу-Коллина (1980, 1981, 1982).
p-adics
P-адическая квантовая теория – это подход к квантовой теории, в котором основное поле действительных чисел (соответственно комплексных чисел) заменяется неархимедовым полем \ ({\ mathbb Q} _p \) p-адических чисел (относительных к простому числу p) или, соответственно, к некоторым его комплексным расширениям. Неархимедов символ \ ({\ mathbb Q} _p \, \), который, кстати, такой же, как \ (\ mathbb R \), является замыканием рационального \ (\ mathbb Q \) относительно норма (а именно p-адическая норма вместо обычной евклидовой нормы) заставляет анализ, основанный на ней, а именно «p-адический анализ», представляет несколько новых функций, которые упрощают, например, e.
 g., обсуждение сходимости рядов или, в более общем смысле, представляет некоторые выгодные особенности дискретности, которых нет в вещественных числах. С этой точки зрения расширение квантовой механики (и, в более общем смысле, физики) от обычных условий до p-адических, имеет хорошую мотивацию. Изначально это было ясно показано в работах Воловича и Владимирова в связи с возможной микроскопической структурой пространства-времени, а затем сначала было применено ко многим областям физики, см., например, работы Воловича и Владимирова (1989–1994), а затем и по другим наукам, см., e.г., произведения А.Ю. Хренников, например книга, опубликованная в 2004 году, по динамике информации в когнитивных, психологических, социальных и аномальных явлениях.
g., обсуждение сходимости рядов или, в более общем смысле, представляет некоторые выгодные особенности дискретности, которых нет в вещественных числах. С этой точки зрения расширение квантовой механики (и, в более общем смысле, физики) от обычных условий до p-адических, имеет хорошую мотивацию. Изначально это было ясно показано в работах Воловича и Владимирова в связи с возможной микроскопической структурой пространства-времени, а затем сначала было применено ко многим областям физики, см., например, работы Воловича и Владимирова (1989–1994), а затем и по другим наукам, см., e.г., произведения А.Ю. Хренников, например книга, опубликованная в 2004 году, по динамике информации в когнитивных, психологических, социальных и аномальных явлениях.Интегралы по траекториям Фейнмана (и связанные с ними вероятностные интегралы) обсуждались как в отношении квантовой механики, так и над p-адическим пространством, соответственно. p-адическое пространство-время с \ (\ mathbb C \) -значной волновой функцией, а также с \ (\ mathbb Q \) -значными волновыми функциями.
 Для первых отметим, что аналог меры Винера на некоторых банаховых пространствах с неархимедовыми локальными полями был построен Сато (1994).Марковские процессы над неархимедовыми полями изучались С.Н. Эванс (1989), С. Альбеверио и В. Карвовски (1990), Х. Канеко (2004), А. Кочубей (2001), Т. Ясуда (2000), В.С. Владимиров, И. Волович, Е.И. Зеленов (1994), Хренников (2004).
Для первых отметим, что аналог меры Винера на некоторых банаховых пространствах с неархимедовыми локальными полями был построен Сато (1994).Марковские процессы над неархимедовыми полями изучались С.Н. Эванс (1989), С. Альбеверио и В. Карвовски (1990), Х. Канеко (2004), А. Кочубей (2001), Т. Ясуда (2000), В.С. Владимиров, И. Волович, Е.И. Зеленов (1994), Хренников (2004).А.Н. Кочубей и М.Р.Сайт-Аметов (2004) распространили методы евклидовой квантовой теории поля на p-адический случай и построили негауссовские меры, соответствующие подходящим полиномиальным взаимодействиям. Обсуждается аналог формулы Фейнмана-Каца, например.г., в работах Т. Дигернеса, В.С. Варадараджан и Д. Э. Вейшарт (2008). Расширения адельных пространств (таким образом, объединяющие случаи с базовым полем \ (\ mathbb R \) и те, что с базовым пространством \ ({\ mathbb Q} _p \, \) для любого p) обсуждались А. Блэром. (1994) и Б. Драгович и соавторы (2009) (также в связи с проблемами эвристических подходов в таких областях, как космология, теория струн и квантовая гравитация).
 Дальнейшие расширения касались аналогии мер и процессов Пуассона-Маслова в работе О.Смолянов, Н.Н. Шанарова (2008).
В то время как все эти подходы предназначены для интегралов вероятностного типа, работа А. Хренникова посвящена определению интегралов Фейнмана по траекториям для \ (\ mathbb C \) – значных соответственно. \ ({\ mathbb Q} _p \) – значная квантовая механика над p-адическими пространствами соответственно. суперпространства, во многом в духе подхода двойственности, основанного на формуле Парсеваля (обобщенные функции над коммутативным числовым полем).
Еще неизвестно, насколько полезной может быть разработка этих подходов в связи с приложениями к физике.
Дальнейшие расширения касались аналогии мер и процессов Пуассона-Маслова в работе О.Смолянов, Н.Н. Шанарова (2008).
В то время как все эти подходы предназначены для интегралов вероятностного типа, работа А. Хренникова посвящена определению интегралов Фейнмана по траекториям для \ (\ mathbb C \) – значных соответственно. \ ({\ mathbb Q} _p \) – значная квантовая механика над p-адическими пространствами соответственно. суперпространства, во многом в духе подхода двойственности, основанного на формуле Парсеваля (обобщенные функции над коммутативным числовым полем).
Еще неизвестно, насколько полезной может быть разработка этих подходов в связи с приложениями к физике.Приложения
Квантовая механика
Основная цель любого подхода к математическому определению интегралов по путям Фейнмана – реализация представления () решения уравнения Шредингера () в терминах хорошо определенного функционального интеграла. Аналогично, существует также представление Фейнмана через интеграл по путям для фундаментального решения уравнения Шредингера, полученное формально заменой в задаче Коши () начальных данных \ (\ psi_0 \) распределением \ (\ delta \).
 d \) довольно легко может быть обработано с помощью всех подходов.К сожалению, этот класс потенциалов исключает некоторые потенциалы, представляющие физический интерес. Случай неограниченных возмущений, являющихся преобразованиями Лапласа мер, включая потенциал Морса, изучен с помощью анализа белого шума и аналитически продолженных интегралов Винера.
Примечательно, что рассмотрение этих потенциалов является пертурбативным в строгом смысле, поскольку соответствующий ряд Дайсона сходится.
Строгая трактовка «непертурбативных потенциалов» представляет дополнительные трудности, и были изучены лишь некоторые частные случаи.Существующие результаты включают потенциалы с особенностями, такие как кулоновский потенциал (Nelson (1964), Doss (1980)) и полиномиальные потенциалы с определенной степенью (Albeverio and Mazzucchi (2005), Doss (2010), Grothaus, Streit and Vogel (2009). ).
Примечательно, что, как впервые указал Нельсон, формулировка интеграла по путям Фейнмана может обеспечить однозначную конструкцию квантовой динамики даже в тех случаях, когда она не определяется однозначно традиционными методами, поскольку квантовый гамильтонов оператор по существу не является самодостаточным.
d \) довольно легко может быть обработано с помощью всех подходов.К сожалению, этот класс потенциалов исключает некоторые потенциалы, представляющие физический интерес. Случай неограниченных возмущений, являющихся преобразованиями Лапласа мер, включая потенциал Морса, изучен с помощью анализа белого шума и аналитически продолженных интегралов Винера.
Примечательно, что рассмотрение этих потенциалов является пертурбативным в строгом смысле, поскольку соответствующий ряд Дайсона сходится.
Строгая трактовка «непертурбативных потенциалов» представляет дополнительные трудности, и были изучены лишь некоторые частные случаи.Существующие результаты включают потенциалы с особенностями, такие как кулоновский потенциал (Nelson (1964), Doss (1980)) и полиномиальные потенциалы с определенной степенью (Albeverio and Mazzucchi (2005), Doss (2010), Grothaus, Streit and Vogel (2009). ).
Примечательно, что, как впервые указал Нельсон, формулировка интеграла по путям Фейнмана может обеспечить однозначную конструкцию квантовой динамики даже в тех случаях, когда она не определяется однозначно традиционными методами, поскольку квантовый гамильтонов оператор по существу не является самодостаточным. прилегающий.Это было подробно проиллюстрировано на примере кварцевого осциллятора с «неправильным» знаком Маццукки (2008).
прилегающий.Это было подробно проиллюстрировано на примере кварцевого осциллятора с «неправильным» знаком Маццукки (2008).Стохастическое уравнение Шредингера, теория измерений
Интегралы по траекториям Фейнмана являются гибким инструментом и могут предоставить функциональное интегральное описание временной эволюции большого класса квантовых систем. Интересные примеры можно найти в теории непрерывного квантового измерения.
Действительно, были предложены некоторые эвристические формулы интегралов по путям Фейнмана для описания динамики квантовой частицы, подвергающейся непрерывному измерению ее положения.d, \ end {массив} \Правильно. \] где \ (H \) – квантово-механический гамильтонов оператор, \ (B \) – \ (d – \) размерный Броуновское движение, \ (dB (t) \) – это Дифференциал Ито и \ (\ lambda> 0 \) – константа связи, которая пропорциональна точности измерения.
Строгие интегральные представления Фейнмана по путям для решения уравнения Белавкина и, следовательно, строгие реализации формулы Менского, в случае, когда потенциал, появляющийся в гамильтониане \ (H \), является преобразованием Фурье комплексной меры на \ ({\ mathbb R} ^ d \, \) были получены в терминах бесконечномерных осциллирующих интегралов Альбеверио, Колокольцовым и Смоляновым (1996/97) и Альбеверио, Гуаттери и Маццукки (2003).
 Соответствующие результаты описаны в книге Колокольцова и в книге Экснера.
Соответствующие результаты описаны в книге Колокольцова и в книге Экснера.Квантовая теория поля
Эвристические интегралы по траекториям Фейнмана обычно используются физиками в качестве инструмента для формулирования современных теорий квантовых полей, калибровочных полей, квантовой гравитации и различных подходов к квантовой гравитации (петлевая квантовая гравитация, теория струн). Разрыв, который существует между эвристикой и строгостью в отношении евклидовых интегралов по траекториям в отношении этих областей, не является неожиданным, возможно, присутствует также между эвристикой и строгостью в отношении интегралов по траекториям Фейнмана в этих областях.Есть некоторые области, такие как квантовые поля на искривленных многообразиях или квантовая гравитация, где прямой релятивистский подход Фейнмана с интегралами по траекториям может быть в принципе ближе к несуществующей «реальной теории», чем к евклидову подходу, поскольку, за исключением специального пространства – Иногда нет естественного способа выполнить аналитическое продолжение от евклидова к релятивистскому подходу.
 До сих пор строгие подходы к интегралам по траекториям Фейнмана для релятивистских квантовых полей ограничивались моделями с отсечкой по пространству и ультрафиолету (т.е. с взаимодействием, ограниченным ограниченной областью пространства, и с регуляризацией, чтобы избежать расхождений из-за сингулярной природы полей, как уже ожидалось для случая свободного поля). См. Книгу Альбеверио. Høegh-Krohn и Mazzucchi (2008), где рассматривается случай ограниченных непрерывных регуляризованных взаимодействий с ограничением пространства. устранение обрезаний было достигнуто для таких моделей в рамках евклидовой системы, но только в пространственно-временном измерении 2, см. работы Альбеверио и Хёг-Крона (1973) и Фрёлиха и Зайлера (1976).{я \ Phi (\ gamma)} f (\ gamma) d \ gamma
\]
но в этом случае интегрирование производится на пространстве \ (\ Gamma \) геометрических объектов, т.е. на пространстве связных 1-форм на главном расслоении над трехмерным многообразием \ (M \, \) с компактным структурная группа Ли \ (G \) («калибровочная группа»).
До сих пор строгие подходы к интегралам по траекториям Фейнмана для релятивистских квантовых полей ограничивались моделями с отсечкой по пространству и ультрафиолету (т.е. с взаимодействием, ограниченным ограниченной областью пространства, и с регуляризацией, чтобы избежать расхождений из-за сингулярной природы полей, как уже ожидалось для случая свободного поля). См. Книгу Альбеверио. Høegh-Krohn и Mazzucchi (2008), где рассматривается случай ограниченных непрерывных регуляризованных взаимодействий с ограничением пространства. устранение обрезаний было достигнуто для таких моделей в рамках евклидовой системы, но только в пространственно-временном измерении 2, см. работы Альбеверио и Хёг-Крона (1973) и Фрёлиха и Зайлера (1976).{я \ Phi (\ gamma)} f (\ gamma) d \ gamma
\]
но в этом случае интегрирование производится на пространстве \ (\ Gamma \) геометрических объектов, т.е. на пространстве связных 1-форм на главном расслоении над трехмерным многообразием \ (M \, \) с компактным структурная группа Ли \ (G \) («калибровочная группа»). 1 \ times \ Sigma \, \ ) \ (\ Sigma \) является двумерным многообразием) являются особенно техническими, и мы ссылаемся на оригинальную работу А.Хан (2004, 2008).
Первые шаги в большом \ (k \) (т.е. «полуклассическом») расширении, имеющем большое значение в топологии из-за эвристической связи с инвариантами узлов Васильева, были предприняты Альбеверио и Митома (2009).
1 \ times \ Sigma \, \ ) \ (\ Sigma \) является двумерным многообразием) являются особенно техническими, и мы ссылаемся на оригинальную работу А.Хан (2004, 2008).
Первые шаги в большом \ (k \) (т.е. «полуклассическом») расширении, имеющем большое значение в топологии из-за эвристической связи с инвариантами узлов Васильева, были предприняты Альбеверио и Митома (2009).Статистическая механика (классико-квантовая). Функционал Фейнмана-Вернона.
Интегралы по траекториям Фейнмана для математического ожидания относительно температурных состояний гармонического осциллятора были впервые обсуждены в книге Albeverio, Høegh-Krohn and Mazzucchi (2008).Обсуждение проводилось в рамках евклидовой структуры квантовой и классической статистической механики с взаимодействием в недавней книге Альбеверио, Кондратьева, Козицкого и Рёкнера (2009). Обсуждение полуклассического предела было начато Альбеверио и Хёг-Кроном и продолжено в Альбеверио, Кондратьев, Козицкий и Рёкнер (2009).
Описание интегралов по путям Фейнмана квантовых открытых систем, то есть систем, взаимодействующих с внешней средой, было впервые введено Фейнманом и Верноном.
 d \, \) i.Т (\ гамма (г) + х- \ гамма ‘(г) -у) d
rd s}.
\]
Этот эвристический формализм широко применялся для описания нескольких физических систем, например, в модели квантового броуновского движения Калдейры-Леггетта.
d \, \) i.Т (\ гамма (г) + х- \ гамма ‘(г) -у) d
rd s}.
\]
Этот эвристический формализм широко применялся для описания нескольких физических систем, например, в модели квантового броуновского движения Калдейры-Леггетта.Формулы () и () были строго математически реализованы в терминах бесконечномерных осциллирующих интегралов, см. Albeverio, Cattaneo, Di Persio and Mazzucchi (2007).
Квантовые вычисления
Строгое изучение проблем квантовых вычислений очень сложно.Большинство методов, разработанных к настоящему времени, относятся к случаю систем с конечномерным пространством состояний, см., Например, Fei, albeverio, cabello, Jing, Goswami (2010). Интегралы Фейнмана по траекториям для таких систем обсуждались (без приложений к квантовым вычислениям) в работе Э.К. Томаса (2000). Одна из проблем построения квантовых компьютеров касается лучшего понимания явлений декогеренции, связанных с взаимодействием интересующей системы с окружающей зашумленной средой. В работе Альбеверио, Каттанео, Ди Персио и Маццукки (2007) эта проблема обсуждается с помощью интегралов по траекториям Фейнмана.
 Квантовые вычисления, с их проблемой построения подходящих запутанных состояний, также несколько естественно соприкоснулись с топологическими проблемами запутанности, и модель Черна-Саймонса топологических квантовых полей была приведена для обсуждения таких проблем в работе Л. Х. Кауфмана. и JJ Ломонако (2010), Э. Деннис, А. Китаев и Дж. Прескилл (2002) и К. Наяк, С. Саймон, А. Стерн, М. Фридман, С. Дас Сарма (2008).
Квантовые вычисления, с их проблемой построения подходящих запутанных состояний, также несколько естественно соприкоснулись с топологическими проблемами запутанности, и модель Черна-Саймонса топологических квантовых полей была приведена для обсуждения таких проблем в работе Л. Х. Кауфмана. и JJ Ломонако (2010), Э. Деннис, А. Китаев и Дж. Прескилл (2002) и К. Наяк, С. Саймон, А. Стерн, М. Фридман, С. Дас Сарма (2008).Поскольку модель Черна-Саймонса была построена строго с помощью интегралов по траекториям Фейнмана, естественно попытаться связать эту конструкцию с упомянутым подходом к запутанности с помощью моделей топологической квантовой теории поля.
Диссипативные системы
Квантовая механика со комплексным потенциалом обсуждалась как модель для простых диссипативных систем, а систематическое обсуждение в терминах строгих интегралов по траекториям Фейнмана (и связанных с ними методов) было представлено в книге П. Экснера. Дальнейшие разработки в этом направлении обсуждались в работах С.
 Черемчанцева (1983), А. де Бивар-Вайнхольца и М.Л. Лапидус (1990), С. Альбеверио и З. Бжежняк (1995), Г.В. Джонсон и М.n} \ to {\ mathbb C} \, \) особый интерес представляет изучение их асимптотического поведения в пределе, когда \ (\ epsilon \ to 0 \. \). Этот интерес связан с тем, что такие асимптотики дает, с одной стороны, возможность приблизительно вычислить интеграл, с другой – связывает интеграл с математическими и физическими проблемами, которые представляют интерес сами по себе.
Основным инструментом для исследования асимптотики интеграла () является метод стационарной фазы , первоначально введенный Стоксом и Кельвином при описании волновых явлений.n \), дающие ненулевой вклад в значение интеграла, являются окрестности стационарных точек фазовой функции \ (\ Phi \, \), т.е. точки \ (x_c \), удовлетворяющие уравнению
\ [
\ Phi ‘(x) = 0,
\]
где \ (\ Phi ‘\) обозначает градиент \ (\ Phi \. \)
В случае, когда гессиан \ (\ Phi ” (x_c) \) имеет нетривиальное ядро (т.е. \ (\ det \ Phi ” (x_c) \ neq 0 \)), а критические точки изолированы, легко получает разложение \ (I (\ epsilon) \) по степеням \ (\ epsilon \) как сумму вкладов, поступающих от одиночных критических точек, причем основной вклад дают комплексные гауссовские интегралы (с фазовой функцией \ (\ гидроразрыв {1} {2} (x, \ Phi ” (x_c) x) \)).
Черемчанцева (1983), А. де Бивар-Вайнхольца и М.Л. Лапидус (1990), С. Альбеверио и З. Бжежняк (1995), Г.В. Джонсон и М.n} \ to {\ mathbb C} \, \) особый интерес представляет изучение их асимптотического поведения в пределе, когда \ (\ epsilon \ to 0 \. \). Этот интерес связан с тем, что такие асимптотики дает, с одной стороны, возможность приблизительно вычислить интеграл, с другой – связывает интеграл с математическими и физическими проблемами, которые представляют интерес сами по себе.
Основным инструментом для исследования асимптотики интеграла () является метод стационарной фазы , первоначально введенный Стоксом и Кельвином при описании волновых явлений.n \), дающие ненулевой вклад в значение интеграла, являются окрестности стационарных точек фазовой функции \ (\ Phi \, \), т.е. точки \ (x_c \), удовлетворяющие уравнению
\ [
\ Phi ‘(x) = 0,
\]
где \ (\ Phi ‘\) обозначает градиент \ (\ Phi \. \)
В случае, когда гессиан \ (\ Phi ” (x_c) \) имеет нетривиальное ядро (т.е. \ (\ det \ Phi ” (x_c) \ neq 0 \)), а критические точки изолированы, легко получает разложение \ (I (\ epsilon) \) по степеням \ (\ epsilon \) как сумму вкладов, поступающих от одиночных критических точек, причем основной вклад дают комплексные гауссовские интегралы (с фазовой функцией \ (\ гидроразрыв {1} {2} (x, \ Phi ” (x_c) x) \)). {\ frac {i} {\ hbar} S_t (\ gamma)} \ psi_0 (\ gamma) d \ gamma,
\]
в полуклассическом пределе , т.е.е. когда постоянная Планка \ (\ hbar \) может считаться незначительной и играет роль малого параметра \ (\ epsilon \. \)
Роль фазовой функции \ (\ Phi \) играет функционал действия \ (S_t \, \) и, согласно принципу наименьшего действия Гамильтона, его стационарные точки являются в точности классическими орбитами системы.
{\ frac {i} {\ hbar} S_t (\ gamma)} \ psi_0 (\ gamma) d \ gamma,
\]
в полуклассическом пределе , т.е.е. когда постоянная Планка \ (\ hbar \) может считаться незначительной и играет роль малого параметра \ (\ epsilon \. \)
Роль фазовой функции \ (\ Phi \) играет функционал действия \ (S_t \, \) и, согласно принципу наименьшего действия Гамильтона, его стационарные точки являются в точности классическими орбитами системы.Строгая математическая формулировка этих идей, то есть реализация бесконечномерной версии метода стационарной фазы для исследования асимптотики функционального интеграла фейнмановского типа, является довольно сложной задачей.После того как интеграл Фейнмана () математически реализован в терминах хорошо определенного функционала, становится даже трудно проверить, допускает ли он вообще асимптотическое разложение. Некоторые довольно технические результаты были получены в основном в случае невырожденных фазовых функций в рамках Френеля или бесконечномерных осциллирующих интегралов Альбеверио и Хё-Крона, Альбеверио, Буте де Монвель-Бертье и Бжезняк (1995) и Резенде ( 1985).
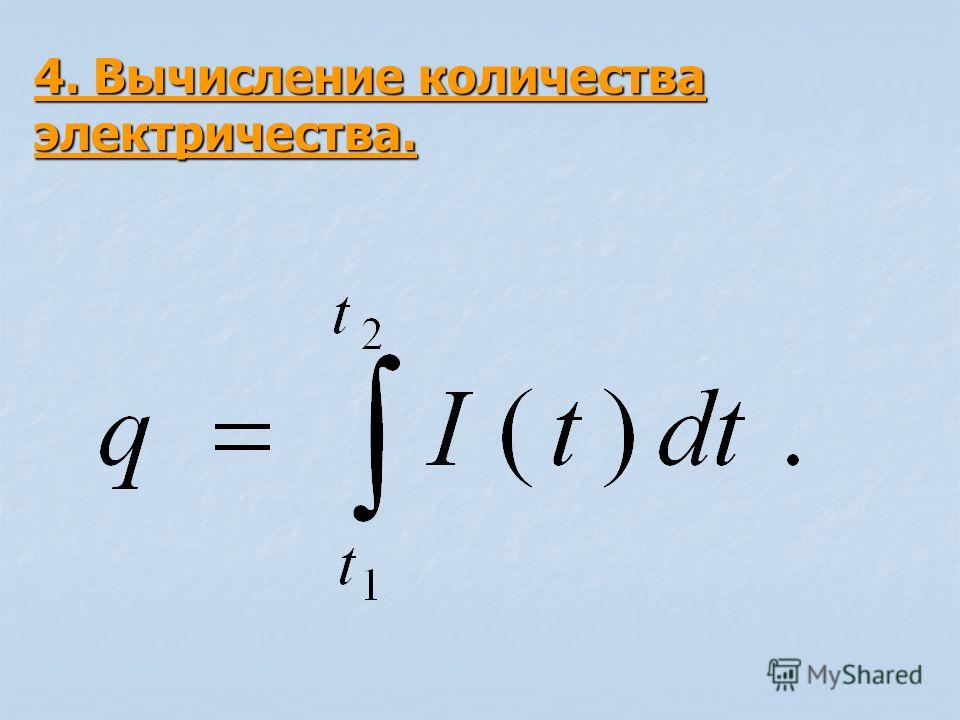 {(j) }) \) находится в \ (x \) в момент \ (t \.{- \ frac {i} {\ hbar} Ht}) \) к классическим периодическим орбитам системы. Это можно рассматривать как квантовый аналог формулы следа Сельберга, связывающего след теплового ядра на многообразиях постоянной отрицательной кривизны с суммой вкладов, связанных с периодическими геодезическими.
Интерес к такого рода отношениям возобновился в последние годы, поскольку, согласно теории квантового хаоса, тип распределения собственных значений энергии данной квантово-механической системы должен отражать тип распределения лежащей в основе классической системы, а именно: интегрируема, соотв.хаотичный.
Формула следа также имеет интересные связи с некоторыми проблемами теории чисел (фактически, например, для лапласиана на торе она выражается тета-функциями, которые через преобразование Меллина связаны с дзета-функцией, см., Например, Альбеверио, Бланшар и Хёг-Крон (1982)).
{(j) }) \) находится в \ (x \) в момент \ (t \.{- \ frac {i} {\ hbar} Ht}) \) к классическим периодическим орбитам системы. Это можно рассматривать как квантовый аналог формулы следа Сельберга, связывающего след теплового ядра на многообразиях постоянной отрицательной кривизны с суммой вкладов, связанных с периодическими геодезическими.
Интерес к такого рода отношениям возобновился в последние годы, поскольку, согласно теории квантового хаоса, тип распределения собственных значений энергии данной квантово-механической системы должен отражать тип распределения лежащей в основе классической системы, а именно: интегрируема, соотв.хаотичный.
Формула следа также имеет интересные связи с некоторыми проблемами теории чисел (фактически, например, для лапласиана на торе она выражается тета-функциями, которые через преобразование Меллина связаны с дзета-функцией, см., Например, Альбеверио, Бланшар и Хёг-Крон (1982)).Недавно в статье Альбеверио и Митома (2009) асимптотические методы были применены к регуляризованной версии [[# Топологическая квантовая теория поля | топологическая теория поля Черна-Саймона}} и дали интересные результаты об инвариантах Васильева.
 , в направлении строгого установления эвристических результатов, полученных из «пертурбативной версии» моделей Черна-Саймона.
, в направлении строгого установления эвристических результатов, полученных из «пертурбативной версии» моделей Черна-Саймона.Фермионные некоммутативные суперсимметричные интегралы по путям
В связи с квантовой физикой с участием ферми-частиц был разработан формализм «некоммутативных» фейнмановских интегралов по траекториям. Он носит более алгебраический характер, чем тот из «коммутативных» интегралов по путям Фейнмана, который мы обсуждали, однако отчасти он использует обсуждаемые нами интегралы по путям, расширяя их в «некоммутативный мир». Это также случай интегралов по траекториям, обсуждаемых в связи с суперсимметричными теориями (уравнивание бозонов и ферми-частиц).Мы не вдаваемся в подробности этих расширений, которые заслуживают отдельного рассмотрения, и ограничиваемся приведением нескольких ссылок, например работы А. Роджерса (1987), О. Смолянов, Э. Шавгулидзе (1989), А. Иномата и Дж. Юнкер (1994), Р. Леандр и А. Роджерс (2006).
Список литературы
- Альбеверио, S; Blanchard, Ph и Høegh-Krohn, R (1982).
 Интегралы Фейнмана по путям и формула следов для операторов Шредингера. Comm. Математика. Phys. 83 (1): 49-76.DOI: 10.1007 / bf01947071.
Интегралы Фейнмана по путям и формула следов для операторов Шредингера. Comm. Математика. Phys. 83 (1): 49-76.DOI: 10.1007 / bf01947071. - Альбеверио, С. и Бжежняк, З. (1993). Конечномерный приближенный подход к осциллирующим интегралам и стационарной фазе в бесконечных измерениях. J. Funct. Анальный. 113 (1): 177-244. DOI: 10.1006 / jfan.1993.1051.
- Альбеверио, S; Хан, А. и Сенгупта, А. Н. (2004). Строгие интегралы по траекториям Фейнмана с приложениями к квантовой теории, калибровочным полям и топологическим инвариантам. Стохастический анализ и математическая физика (SAMP / ANESTOC 2002).Мировая наука. Издательство River Edge, NJ: 1-60.
- Albeverio, S. и Høegh-Krohn, R (1967). Осциллирующие интегралы и метод стационарной фазы в бесконечно многих измерениях с приложениями к классическому пределу квантовой механики. Инвент. Математика. 40 (1): 59-106. DOI: 10.1007 / bf01389861.
- Альбеверио, С. и Маццукки, С.
 (2005). Обобщенные интегралы Френеля. Бык. Sci. Математика. 129 (1): 1-23. DOI: 10.1016 / j.bulsci.2004.05.005.
(2005). Обобщенные интегралы Френеля. Бык. Sci. Математика. 129 (1): 1-23. DOI: 10.1016 / j.bulsci.2004.05.005. - Альбеверио, С. и Маццукки, С. (2005).Интегралы Фейнмана по траекториям для полиномиально растущих потенциалов. J. Funct. Анальный. 221 (1): 83-121. DOI: 10.1016 / j.jfa.2004.07.014.
- Альбеверио, S; Høegh-Krohn, R и Mazzucchi, S (2008). Математическая теория интегралов Фейнмана по путям. Введение. 2-е и дополненное издание. Конспект лекций по математике 523. Springer-Verlag, Berlin.
- Кэмерон, Р. Х (1960). Семейство интегралов, соединяющих интегралы Винера и Фейнмана. J. Math. и Phys. 39: 126-140.
- Дирак, П.А. М (1933). Лагранжиан в квантовой механике. Physik. Z. Sowjetunion 3: 64. Перепечатано в избранных статьях по квантовой электродинамике, изд. Schwinger J, Dover (Нью-Йорк, 1958).
- Досс, Х (1980). Для стохастического решения уравнения Шредингера и аналитических коэффициентов. Comm.
 Математика. Phys. 73 (3): 247-264. DOI: 10.1007 / bf01197701.
Математика. Phys. 73 (3): 247-264. DOI: 10.1007 / bf01197701. - Элворти, Д. и Трумэн, А. (1984). Карты Фейнмана, формулы Камерона-Мартина и ангармонические осцилляторы. Ann. Inst. H. Poincaré Phys. Теор. 41 (2): 115-142.
- Кумано-го, Н. и Фудзивара, Д. (2008). Интегралы Фейнмана по траекториям и квазиклассическое приближение. RIMS Kokyuroku Bessatsu B5: 241–263.
- Фейнман, Р. П. (1948). Пространственно-временной подход к нерелятивистской квантовой механике. Обзор современной физики 20 (2): 367-387. DOI: 10.1103 / revmodphys.20.367.
- Фридман, С. Н. (1971/72). Формулы полугруппового произведения, сжатия и непрерывные наблюдения в квантовой механике. Indiana Univ. Математика. J. 21: 1001-1011.
- Хида, Т; Куо, H H; Поттхофф Дж. И Страйт Л. (1993). Белый шум. Бесконечномерное исчисление. Математика и ее приложения, 253. Kluwer Academic Publishers Group, Дордрехт.
- Ито, К. (1961). Интеграл Винера и интеграл Фейнмана.
 Proc. Четвертый симпозиум по математической статистике и теории вероятностей в Беркли. California Univ. Press, Berkeley 2: 227-238.
Proc. Четвертый симпозиум по математической статистике и теории вероятностей в Беркли. California Univ. Press, Berkeley 2: 227-238. - Ито, К. (1967). Обобщенные равномерные комплексные меры в гильбертовом метрическом пространстве с их приложениями к интегралу по путям Фейнмана. Proc. Пятый симпозиум по математической статистике и теории вероятностей в Беркли. California Univ. Press, Berkeley 2 (1): 145-161.
- Джонсон, Г. В. и Лапидус, М. Л. (2000). Интеграл Фейнмана и операционное исчисление Фейнмана. Издательство Оксфордского университета, Нью-Йорк.
- Mazzucchi, S (2009). Математические интегралы Фейнмана по траекториям и приложения. World Scientific Publishing, Сингапур.
- Нельсон, Э. (1964). Интегралы Фейнмана и уравнение Шредингера. J. Math. и Phys. 5: 332-343. DOI: 10,1063 / 1,1704124.
Дополнительная литература
- DeWitt-Morette C (редактор) и др. (1995). Спецвыпуск по функциональной интеграции.
 J. Math. и Phys. 36 (5): 2135-2564.
J. Math. и Phys. 36 (5): 2135-2564. - Альбеверио, S; Høegh-Krohn, R; Фенстад, Дж. Э. и Линдстрём, Т. (1986). Нестандартные методы стохастического анализа и математической физики. Academic Press, Inc., Орландо, Флорида.
- Альбеверио, S; Кондратьев Ю. Козицкий, Ю. и Рокнер, М. (2009).Статистическая механика квантовых решетчатых систем. Интегральный подход. Европейское математическое общество (EMS), Цюрих.
- Атья, М. Ф. (1979). Геометрия полей Янга-Миллса. Lezioni Fermiane. Scuola normale superiore, Пиза.
- Березин Ф.А., Шубин М.А. (1991). Уравнение Шредингера. Kluwer Academic Publishers Group, Дордрехт.
- Быценко, А А; Коньола, G; Elizalde, E; Моретти, В. и Зербини, С. (2003). Аналитические аспекты квантовых полей.World Scientific Publishing Co., Ривер Эдж, Нью-Джерси.
- Картье, П. и ДеВитт-Моретт, К. (2006). Функциональная интеграция: действие и симметрии. Издательство Кембриджского университета, Кембридж.
- Экснер, П.
 (2000). Открытые квантовые системы и интегралы Фейнмана. D. Reidel Publishing Co., Дордрехт.
(2000). Открытые квантовые системы и интегралы Фейнмана. D. Reidel Publishing Co., Дордрехт. - Фаддеев, Л.Д., Славнов, А.А. (1991). Калибровочные поля. Введение в квантовую теорию. (2-е издание). Эддисон-Уэсли Паблишинг Компани, Т.
- Фейнман, Р. П. и Хиббс, А. Р. (1965).Квантовая механика и интегралы по траекториям. McGraw-Hill Companies, Нью-Йорк.
- Grosche, C. и Steiner, F (1998). Справочник интегралов Фейнмана по траекториям. Шпрингер, Берлин, Гейдельберг.
- Hörmander, L (2003). Анализ линейных дифференциальных операторов в частных производных. I. Теория распределения и анализ Фурье. Springer-Verlag, Берлин.
- Хуанг, К. (1998). Квантовая теория поля. От операторов к интегралам по путям. ohn Wiley & Sons, Inc., Нью-Йорк.
- Клаудер, Дж. Р. (2000).Помимо обычного квантования. Издательство Кембриджского университета, Кембридж.
- Kleinert, H (1995). Интегралы по траекториям в квантовой механике, статистике и физике полимеров.
 World Scientific, Сингапур.
World Scientific, Сингапур. - Колокольцов В Н (2000). Полуклассический анализ диффузий и случайных процессов. Springer-Verlag, Берлин.
- Lapidus, M L (2008). В поисках нулей Римана. Струны, фрактальные мембраны и некоммутативные пространства-времени. Американское математическое общество, Провиденс, Род-Айленд.
- Леандр Р. (2006). Интегралы по траекториям в некоммутативной геометрии. Энциклопедия математической физики. Elsevier: 8-12.
- Маслов В.П., Федорюк М.В. (1981). Квазиклассическое приближение в квантовой механике. D. Reidel Publishing Co., Дордрехт-Бостон, Массачусетс.
- Менский М.В. (2000). Квантовые измерения и декогеренция. Модели и феноменология. Kluwer Academic Publishers, Дордрехт.
- Паризи, Г. (1988). Статистическая теория поля.Бенджамин / Каммингс Паблишинг Ко., Рединг, Массачусетс.
- Попов В Н (1983). Функциональные интегралы в квантовой теории поля и статистической физике. D. Reidel Publishing Co.
 , Дордрехт-Бостон, Массачусетс.
, Дордрехт-Бостон, Массачусетс. - Риверс, Р. Дж. (1990). Методы интегралов по путям в квантовой теории поля. Издательство Кембриджского университета, Кембридж.
- Roepstorff, G (1994). Интеграл по путям в квантовой физике. Введение. Springer-Verlag, Берлин.
- Ровелли, С. (2004). Квантовая гравитация.Издательство Кембриджского университета, Кембридж.
- Шульман, Л. С. (2005). Методы и приложения интеграции путей. Dover Publications, США.
- Разные, авторы (). Интегралы по путям от мэВ до МэВ: Материалы международных конференций. World Scientific Publishing Co., Ривер Эдж, Нью-Джерси.
См. Также
Интеграл по траектории, принцип наименьшего действия
Неотъемлемых фактов для детей
Интеграция предназначена для поиска поверхности s , учитывая a , b и y = f (x) .Формула для интеграла от a до b , изображенная на графике выше:
Формула: Что такое интеграл (анимация)В математике интеграл – это пространство под графиком уравнения (иногда называемое «площадью под кривой»).
 Интеграл является обратной производной, а интегральное исчисление противоположно дифференциальному исчислению. Производная – это крутизна (или “наклон”) как скорость изменения кривой. Слово «интегральный» также может использоваться как прилагательное, означающее «относящийся к целым числам».
Интеграл является обратной производной, а интегральное исчисление противоположно дифференциальному исчислению. Производная – это крутизна (или “наклон”) как скорость изменения кривой. Слово «интегральный» также может использоваться как прилагательное, означающее «относящийся к целым числам».Обозначение интегрирования в исчислении: высокая буква «S». Этот символ был впервые использован Готфридом Вильгельмом Лейбницем, который использовал его как стилизованную букву «» (для summa , латинское слово «сумма») для обозначения суммы площади, охватываемой уравнением, например, y = f ( х) .
Интегралы и производные являются частью раздела математики, называемого исчислением. Связь между ними очень важна и называется фундаментальной теоремой исчисления.Теорема гласит, что интеграл можно обратить производной, аналогично тому, как сложение может быть обращено вычитанием.
Интеграция помогает при попытке умножить единицы в проблему. Например, если проблема со скоростью требует ответа только с расстоянием, одним из решений является интегрирование по времени.
 Это означает умножение времени, чтобы отменить время в. Это делается путем сложения вместе небольших кусочков графика скорости. Срезы близки к нулю по ширине, но бесконечное сложение их вместе приводит к получению целого.Это называется суммой Римана.
Это означает умножение времени, чтобы отменить время в. Это делается путем сложения вместе небольших кусочков графика скорости. Срезы близки к нулю по ширине, но бесконечное сложение их вместе приводит к получению целого.Это называется суммой Римана.Сложение этих срезов дает уравнение, производной от которого является первое уравнение. Интегралы похожи на способ сложить вручную множество мелких вещей. Это похоже на суммирование, которое складывается. Разница с интегрированием состоит в том, что мы также должны складывать все десятичные дроби и дроби между ними.
Другой случай, когда интеграция полезна, – это определение объема твердого тела. Он может складывать двухмерные (без ширины) срезы твердого тела вместе до бесконечности – до тех пор, пока не будет получена ширина.Это означает, что объект теперь имеет три измерения: два исходных и ширину. Это дает объем описываемого трехмерного объекта.
Методы интеграции
Первоначальное
Согласно основной теореме исчисления, интеграл является первообразной.
Если мы возьмем функцию, например, и антидифференцируем ее, мы можем сказать, что интеграл от есть. Мы говорим как интеграл , а не как интеграл , потому что первообразная функции не уникальна.Например, также отличает. По этой причине при взятии первообразной необходимо добавить константу C. Это называется неопределенным интегралом. Это потому, что при нахождении производной функции константы равны 0, как в функции
- .
- . Обратите внимание на 0: мы не можем найти его, если у нас есть только производная, поэтому интеграл равен .
- .
Простые уравнения
Простое уравнение, например, можно проинтегрировать относительно x, используя следующую технику.Чтобы интегрировать, вы добавляете 1 к степени, равной x , а затем делите x на значение этой новой степени. Следовательно, интегрирование нормального уравнения следует этому правилу:
В конце показано, что мы интегрируем относительно x , то есть при изменении x . Можно увидеть, что это обратное дифференциации. Однако при интегрировании добавляется константа C. Это называется постоянной интегрирования. Это необходимо, потому что дифференцирование целого числа приводит к нулю, поэтому интегрирование нуля (которое может быть помещено в конец любого подынтегрального выражения) дает целое число C.Значение этого целого числа может быть найдено с использованием заданных условий.
Уравнения, содержащие более одного члена, просто интегрируются путем интегрирования каждого отдельного члена:
Интеграция с использованием e и ln
Существуют определенные правила интегрирования с использованием е и натурального логарифма. Самое главное, что это интеграл самого себя (с добавлением постоянной интегрирования):
Натуральный логарифм ln полезен при интегрировании уравнений с.Они не могут быть интегрированы с использованием приведенной выше формулы (прибавить единицу к степени, разделить на степень), потому что прибавление единицы к степени дает 0, а деление на 0 невозможно. Вместо этого интеграл равен:
В более общем виде:
Две вертикальные полосы указывают абсолютное значение; знак (положительный или отрицательный) игнорируется. Это потому, что натуральный логарифм отрицательных чисел не имеет значения.
Недвижимость
Сумма функций
Интеграл от суммы функций – это сумма интеграла каждой функции.то есть
- .
Доказательство этого несложно: определение интеграла – это предел сумм. Таким образом,
Обратите внимание, что оба интеграла имеют одинаковые пределы.
Константы в интеграции
Когда константа находится в интеграле с функцией, константу можно вычесть. Кроме того, когда константа c не сопровождается функцией, ее значение составляет c * x .То есть
- и
Это можно сделать только с константой.
Доказательство опять же по определению интеграла.
Другое
Если a, b и c расположены по порядку (т. Е. Друг за другом по оси x), интеграл от f (x) от точки a до точки b плюс интеграл от f (x) от точки b до c равен интеграл от точки а до с. То есть
- , если они в порядке. (Это также верно, когда a, b, c не в порядке, если мы определим
- .)
- Это следует фундаментальной теореме исчисления (FTC):.
- Опять же, следуя FTC:.
Связанные страницы
Изображения для детей
Двойной интеграл вычисляет объем под поверхностью z = f (x, y)
Линейный интеграл суммирует элементы вдоль кривой.
Численные квадратурные методы: метод прямоугольников, трапецеидальная линейка, метод Ромберга, квадратура Гаусса
Интеграция против интегральной – в чем разница?
интеграция | интеграл | Связанные термины | Интеграл является родственным термином для интеграции . Как существительные, разница между интегралом
и интегралом состоит в том, что интеграция – это акт или процесс создания целого или целого, в то время как интеграл – это (математика) число, предел сумм, вычисляемых в процесс, в котором область определения функции делится на небольшие подмножества, и, возможно, номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, а затем все эти продукты суммируются.Прилагательное
интеграл – это , составляющий целое вместе с другими частями или факторами; не опускается и не снимается.Другие сравнения: в чем разница?
Английский
Существительное
( en имя существительное )- Акт или процесс создания целиком или целиком.
- (общество) Процесс приспособления к сообществу, особенно применительно к «видимым» (этническим, иммигрантам …) меньшинствам
- (исчисление) Операция нахождения функции.
- (биология). В эволюции – процесс уплотнения многообразия в относительно простое и постоянное; Предполагается, что они чередуются с дифференциацией в качестве агента в развитии видов.
Производные термины
* интеграционист * интеграция корпоративных приложений * горизонтальная интеграция * неопределенная интеграция * интегральное исчисление * положение об интеграции * расовая интеграция * вертикальная интеграция * прямая интеграция * Обратная интеграцияСвязанные термины
* целое число * интегрируемый * интеграл * интегрировать * интеграторАнаграммы
* —-Английский
Прилагательное
( прилагательное )- Составляющие вместе с другими частями или факторами единое целое; не опускается и не снимается
- * Юг,
- Прекращение зла и доброе дело – две великие неотъемлемые части , которые выполняют эту обязанность.
- (математика) Имеет отношение или является целым числом.
- (математика) Относительно интегрирования.
- (устаревшее) целиком; неповрежденный
- * Фрэнсис Бэкон
- Местное движение удерживает тела за одно целое .
Синонимы
* (, составляющие ) имманентный, неотъемлемый, необходимыйПроизводные термины
* цельный кирпич * цельное закрытие * интегральная космология * цельный кубоид * интегральный ток * интегральная кривизна * интегральная кривая * целостная область * интегральный чертеж * интегральная экология * составной элемент * интегральная энергия * интегральное расширение * интегральный быстрый реактор * интегральный полевой блок * интегральная функция * интегральная геометрия * интегральный график * интегральная группа гомологий * интегральное ядро * интегральный мембранный белок * интегральная политика * цельный полигедрон * целочисленный полином * интегральная постметафизика * интегральная психология * интегральная преобразующая практика * интегральная йога * честностьСвязанные термины
* целое числоСуществительное
( интеграл википедии ) ( en имя существительное )- (математика) Число, предел сумм, вычисляемых в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, все эти затем суммируются продукты.3} {3} плюс константа.
Синонимы
* ( предел сумм ) определенный интеграл * ( первообразная ) первообразная, неопределенный интеграл,Антонимы
* ( первообразное ) производноеПроизводные термины
* определенный интеграл * полуцелой * неправильный интеграл * неопределенный интеграл * интегральное исчисление * интегральное уравнение * интегральная теория * интегральное преобразование * интеграция * Интеграл Римана * Интеграл Римана-Стилтьеса * Интеграл ЛебегаСвязанные термины
* целое числоинтеграл – Викисловарь
Английский [править]
Этимология [править]
Заимствовано из среднефранцузского целого , из средневекового латинского integrālis , из латинского целого («целое»); см. целое число.
Произношение [править]
- Существительное
- (Великобритания) enPR: ĭnʹtĭ-grəl, IPA (ключ) : / ˈɪntɪɡɹəl /
- (США) enPR: ĭnʹtə-grəl, IPA (ключ) : / ˈɪntəɡɹəl /
- Прилагательное
- Словари дают такое же произношение, как и существительное, но прилагательное часто произносится с ударением на втором слоге:
Прилагательное [править]
целое ( сравнительное больше целое , превосходное самое целое )
- Составление целого вместе с другими частями или факторами; не опускаемый или съемный
- 1692–1717 , Роберт Саут, Двенадцать проповедей, проповеданных по разным случаям , том (просьба указать | volume = от I до VI), 6-е издание, Лондон: […] Дж [Эймс] Беттенхэм, для Джоны Бойера, […], Опубликовано 1727, OCLC 21766567 :
- Прекращение зла и доброе дело – две великие неотъемлемые части , которые выполняют эту обязанность.
- Синонимы: имманентный, неотъемлемый, необходимый; см. Также Тезаурус: внутренний
- 1692–1717 , Роберт Саут, Двенадцать проповедей, проповеданных по разным случаям , том (просьба указать | volume = от I до VI), 6-е издание, Лондон: […] Дж [Эймс] Беттенхэм, для Джоны Бойера, […], Опубликовано 1727, OCLC 21766567 :
- (математика) Of, относящееся к целому числу или являющееся целым числом.
- (математика) Относительно интегрирования.
- (устаревшее) Целое; неповрежденный.
- 1631 , Фрэнсис [Бэкон], «(пожалуйста, укажите | век = от I до X)», в Sylua Syluarum: Or A Naturall Historie. За десять веков. […] , 3-е издание, Лондон: […] VVilliam Rawley; Написано Джоном Х [авилендом] для Уильяма Ли […], OCLC 1044372886 :
Локальное движение сохраняет тела интегральными .
- 1631 , Фрэнсис [Бэкон], «(пожалуйста, укажите | век = от I до X)», в Sylua Syluarum: Or A Naturall Historie. За десять веков. […] , 3-е издание, Лондон: […] VVilliam Rawley; Написано Джоном Х [авилендом] для Уильяма Ли […], OCLC 1044372886 :
Производные термины [править]
Связанные термины [править]
Переводы [править]
, составляющие единое целое вместе с другими частями или факторами; не опускается или снимается
математическое значение: целое число, относящееся к целому числу или являющееся целым числом
математика: относящаяся к интеграции
- Приведенные ниже переводы необходимо проверить и вставить выше в соответствующие таблицы переводов, удалив все цифры.Числа не обязательно совпадают с числами в определениях. См. Инструкции в Викисловаре: макет статьи § Переводы.
Проверяемые переводы
Существительное [править]
интеграл ( множественное число интеграл )
- (математика) Число, предел сумм, вычисляемых в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, все затем эти продукты суммируются.{3}} {3}}} плюс константа.
- Синонимы: первообразная, неопределенный интеграл, ∫
- Антоним: производный
Производные термины [править]
Связанные термины [править]
Переводы [править]
Анаграммы [править]
Каталонский [править]
Этимология [править]
Заимствовано из средневековой латыни integrālis , из латинского целое число .
Прилагательное [править]
интеграл ( мужской и женский род множественного числа интегралы )
- интегральный
Среднефранцузский [править]
Этимология [править]
Заимствовано из средневековой латыни integrālis , из латинского целое число .
Прилагательное [править]
интегральный м ( женский род единственного числа интегралы , мужской род множественного числа интегрированный , женский род множественного числа интегралы )
- интеграл, необходимый для функционирования всего
- целиком; весь
Потомки [править]
Источники [править]
- интеграл на Dictionnaire du Moyen Français (1330–1500) (на французском языке)
на португальском [править]
Этимология [править]
Заимствовано из средневековой латыни integrālis , из латыни целое число («целиком; нетронутый»).
Произношение [править]
- IPA (ключ) : (Бразилия) /ĩ.teˈɡɾaw/, [ĩ.teˈɡɾaʊ̯]
- IPA (ключ) : (Португалия) /ĩ.tɨˈɡɾal/, [ĩ.tɨˈɣɾaɫ]
- Расстановка переносов: встроенный
- Рифмы: -al, -aw
Прилагательное [править]
интегральный м или f ( множественное число интегрированное , сопоставимое )
- интегральный; весь; весь
- (еды) целиком (из которого не был удален ни один из его компонентов)
Цитаты [править]
Цитаты с использованием этого термина см. В разделе Цитирование: интеграл.
Синонимы [править]
Производные термины [править]
Существительное [править]
интегральный f или м (в варианте) ( во множественном числе интегрально )
- (математика) интеграл (пределы сумм)
- (математика) первообразная
- Синоним: antiderivada
Котировки [править]
Цитаты с использованием этого термина см. В разделе Цитирование: интеграл.
Связанные термины [править]
Дополнительная литература [править]
- «интегральный» в Dicionário Priberam da Língua Portuguesa .
Румынский [править]
Этимология [править]
Заимствовано из французского intégral , средневековой латыни integrālis .
Произношение [править]
Прилагательное [править]
интегральный м или n ( женский род единственного числа интегралă , мужской род множественного числа интеграл , женский и средний множественное число интеграл )
- интегральный
- Синонимы: întreg, complete
Cклонение [править]
Связанные термины [править]
испанский [править]
Этимология [править]
Заимствовано из средневековой латыни integrālis , из латинского целое число («целое»).
Произношение [править]
- IPA (ключ) : / inteˈɡɾal /, [ĩn̪.t̪eˈɣ̞ɾal]
Прилагательное [править]
интеграл ( множественное число интеграл )
- интегральный
- целиком
- коричневый (рис)
- цельнозерновой
Производные термины [править]
Связанные термины [править]
Существительное [править]
интеграл f ( множественное число интеграл ) | интеграл
- (математика) интеграл
Дополнительная литература [править]
Шведский [править]
Этимология [править]
(Эта этимология отсутствует или неполна.Пожалуйста, дополните его или обсудите в скриптории этимологии.)
Произношение [править]
Существительное [править]
интегральный c
- (математика) интеграл
Cклонение [править]
Анаграммы [править]
Турецкий [править]
Этимология [править]
Заимствовано у французского intégral . {b} \! F (x) \, dx \,}
Cклонение [править]
Интуиция за интеграцией.Введение в интегральное исчисление… | by Kaushik Chatterjee
Введение в интегральное исчисление с акцентом на основные концепции и прекрасную интуицию, которая лежит в основе алгебры.
Интегральное исчисление и дифференциальное исчисление – две стороны одной медали. Однако интеграция может показаться более сложной, чем дифференциация, поскольку она включает введение иностранных обозначений и абстрактных идей. Однако сами по себе идеи прекрасно интуитивно понятны и позволяют переводить сложные идеи в простые алгебраические манипуляции.Эта статья стремится предоставить интуитивно понятный взгляд на интегральное исчисление, показывая, как математика логически вытекает из идей, и подробно описывает использование интеграции.
Классическая интеграция – это не более чем вычисление площадей под кривыми. В средней школе мы все научились вычислять площади различных правильных и неправильных многоугольников. Мы также узнали формулы для определения площади круга и эллипса. Но как бы вы рассчитали площадь других изогнутых форм? А как насчет того, чтобы найти область под изогнутой функцией, такой как показанная ниже?
Как бы вы нашли площадь между кривой и осью x между точками a и b? Предоставлено: Wikipedia. Вы обнаружите, что ни один из методов, которые вы изучили до сих пор, не позволяет вам этого сделать.Именно здесь вступает в игру мастерство интегрального исчисления. Однако оказывается, что вычислить эту площадь не так сложно, как может показаться, и процедура основана на более привычных методах.
Итак, как же нам найти этот район? Что, если мы разделим область на более стандартные формы – например, прямоугольник. Мы знаем, как найти площадь прямоугольника – это просто длина x ширина. Давайте разделим область на прямоугольники одинаковой ширины, которые находятся под кривой.Это выглядит так:
Эти прямоугольники аппроксимируют площадь под кривой – они дают нам представление о фундаментальной концепции интегрирования и исчисления в целом.Это наша оценка с 4 прямоугольниками. Мы можем вычислить площадь каждого из этих прямоугольников, поскольку знаем ширину (расстояние между конечными точками a и b , деленное на 4) и высоту (функция, вычисляемая в правой конечной точке). Это явно не очень хорошая оценка – посмотрите на все это пространство.Но что будет, если вместо 4 прямоугольников использовать 10? Или 1000? Или 100 000? Что произойдет, если мы позволим ширине каждого прямоугольника приблизиться к 0, а количество прямоугольников станет все ближе и ближе к бесконечности?
Ну, тогда у нас будет точная площадь . Это интуитивно понятно: по мере того, как ширина прямоугольников становится все меньше и меньше, отдельные прямоугольники лучше и лучше подходят к кривой; суммы их площадей сходятся к истинной площади между кривой и осью абсцисс.Вот красивая анимация, иллюстрирующая этот момент:
Шаг представляет ширину области. Мы можем видеть сходимость, когда ширина приближается к 0.Эту идею можно сделать точной, описав ее математически:
Поначалу эта формула может показаться довольно устрашающей, но все, что я сделал, это переписал свои точные слова в математические обозначения. . Давайте рассмотрим это по частям, работая изнутри. Внутри суммирования мы просто вычисляем площадь прямоугольника, умножая значение функции в правой конечной точке на ширину прямоугольника, как описано ранее.Эта ширина определяется разницей конечных точек, деленной на количество делений (это гарантирует, что каждая ширина эквивалентна). Фактический интеграл затем может быть вычислен путем суммирования площадей всех прямоугольников по мере того, как количество прямоугольников приближается к бесконечности.
Однако здесь описывается только один вид интеграла. Оказывается, вам не нужен , чтобы гарантировать, что прямоугольники имеют одинаковую ширину, и не обязательно иметь высоту, эквивалентную правой конечной точке.Более общее представление этой формулы выглядит следующим образом (это то, что вы, скорее всего, увидите), используя стандартную нотацию исчисления:
Это известно как сумма Римана , в честь Бернхарда Римана, одного из отцов-основателей комплексный анализ. Теперь это выглядит еще страшнее, но мы просто добавили еще несколько деталей. Эта формула совершенно ясно заявляет, что вы можете вычислить площадь между функцией и осью x как сумму прямоугольников. Площадь каждого прямоугольника задается произвольной шириной Δx, а высота задается значением функции x, где x выбирается по некоторым критериям (левая конечная точка, средняя точка, наибольшее значение и т. Д.).
Приведенное выше уравнение кажется сложным, но все, что оно делает, это математически количественно оценивает то, что было ранее заявлено. По мере того, как ширина прямоугольников становится бесконечно малой (все ближе и ближе к 0), наши приближения для площади с использованием прямоугольников становятся все более и более точными. Уравнение обобщает интеграл благодаря тому факту, что ширина не обязательно должна быть согласованной и что высоту прямоугольника можно определить с помощью различных критериев; однако конечный интеграл всегда будет одним и тем же.
Обозначение интеграла, ∫, представляет собой просто удлиненную букву S (обозначающую сумму ), и мы вычисляем интеграл функции f (x) между двумя точками: a и b. dx просто обозначает бесконечно малое значение ширины каждого раздела (это эквивалент Δx в нашем интеграле, поскольку Δx стремится к 0).
Интеграл, вычисляемый между двумя точками, известен как определенный интеграл . Определенный интеграл позволяет нам фактически вычислить площадь между функцией и осью x (или осью y, или даже другой функцией, но это немного сложнее).
Как на самом деле вычисляется этот интеграл? К счастью, вам не нужно проделывать долгий процесс суммирования множества прямоугольников. Первая часть фундаментальной теоремы исчисления утверждает, что:
F (x) – это стандартная запись для первообразной из f (x) . Это означает, что производная F (x) равна f (x) , то есть F ’(x) = f (x) . Антидифференциация – это процесс, с помощью которого, учитывая производную функции, вы устанавливаете исходную функцию: если f ’(x) = 2x, то какую исходную функцию мы дифференцировали? Результатом является неопределенный интеграл, возвращающий функцию; определенный интеграл возвращает значение.Это вторичная цель интеграла: это функция, обратная производной. Математически это показано во второй части фундаментальной теоремы исчисления,
Вышеупомянутый интеграл является неопределенным интегралом , так как у него нет конечных точек. Все, что делает этот интеграл, – это находит первообразную функции. Чтобы оценить это, вы должны быть знакомы с дифференциальным исчислением и правилами производных. Есть множество правил, которые вы можете использовать для ее решения, и они основаны на том, как вычисляются производные.
Вот основные правила. Если вас смущает эта диаграмма или вы не понимаете, откуда взялись эти правила, я рекомендую вам дополнительно изучить производные (которые так же интуитивно понятны, как интегралы, если не больше).
Итак, чтобы найти область между функцией и осью x, вы сначала выполняете антидифференциацию для функции, а затем оцениваете ее на обеих конечных точках (помните, что первообразная по-прежнему является функцией). Наконец, вычтите первый результат из второго, как указано в основной теореме.
Пока все это было очень абстрактным и техническим, поэтому давайте применим эти концепции на примере. Мы хотим найти площадь функции f (x) = 3x² между конечными точками 0 и 6. Первый шаг – найти первообразную этой функции. Антидифференцируя его, получаем F (x) = x³ (используя Правило №4 из диаграммы). Если вы хотите перепроверить, просто возьмите производную F (x) : если она равна f (x) , то есть исходная функция, она верна.
Мы знаем, что значения для наших конечных точек вставляются в F (x) . F (0) = 0³ = 0 и F (6) = 6³ = 216. Теперь вычтем F (0) из F (6) : 216 – 0 = 216. ∴ Область между График функции f (x) и ось x составляет 216 единиц ² . Теперь это было не так уж сложно, правда? Проблемы интеграции могут усложняться и становятся все более сложными, но основной принцип нахождения некоторой ценности путем суммирования меньших и меньших участков остается прежним.
