Учебные материалы по математике | Первообразная функция и неопределенный интеграл
СОДЕРЖАНИЕ
1. Первообразная функция и неопределенный интеграл
2. Таблица простейших интегралов
3. Интегрирование методом замены переменной
4. Метод интегрирования по частям
5. Понятие о неберущихся в конечном виде интегралах
6. Интегрирование рациональных функций
7. Интегрирование тригонометрических рациональных выражений
8. Интегрирование простейших иррациональных выражений
Н Е О П Р Е Д Е Л Ё Н Н Ы Й И Н Т Е Г Р А Л
1. Первообразная функция и неопределенный интеграл
Восстановление функции F(x) по известной производной этой функции F’(x)=f (x) (или по известному ее дифференциалу dF(x)=f(x)dx) называется интегрированием, а искомая функция F(x) называется первообразной функцией.
Всякая функция f(x) имеет бесчисленноемножество различных первообразных функций, отличающихся друг от друга на постоянное слагаемое, т.
[F(x)+C]’=F‘(x)=f(x). Cовокупность всех первообразных F(x)+C одной и той же функции f(x) называется неопределенным интегралом этой функции и обозначается символом
, (1)
где x — переменная интегрирования, f(x) — подынтегральная функция, f(x)dx — подынтегральное выражение.
Геометрически, графики всех первообразных функций для f(x) представляют в системе координат XOY семейство кривых, которые получаются одна из другой путем параллельного переноса вдоль оси Y на величину С.
Как следует из понятия неопределенного интеграла, интегрирование и нахождение дифференциала являются обратными действиями.
Действительно, если первообразная, а значит и неопределенный интеграл для функции f(x) существует, то подынтегральное выражение представляет собой дифференциал любой из этих первообразных
f(x)dx=F'(x)d(x)=dF(x),
тогда
d∫f(x)dx=d[F(x)+C]=F'(x)dx=f(x)dx, (2)
∫dF(x)=∫ f(x)dx=F(x)+C, (3)
т. е. знаки d и ∫ взаимно сокращаются.
Укажем основные свойства неопределенного интеграла, правильность которых можно проверять дифференцированием.
І. Постоянный множитель выносится за знак интеграла.
∫Af(x)dx=A∫ f(x)dx (4)
2. Интеграл от алгебраической суммы (разности) функций равен сумме (разности) интегралов.
∫[f(x)± φ(x)]dx
3. Неопределенный интеграл не зависит от выбора переменной интегрирования.
∫f(u)du= F(u)+C, (6)
где u — независимая переменная или функция x, u=u(x). Этот результат следует непосредственно из правила дифференцирования сложной функции
; , ,
тогда
.
4. Интеграл ∫udv
Из формулы дифференцирования произведения двух функций d(uv)=udv+vdu
интегрированием получается следующее равенство
∫udv = uv – ∫vdu, (7)
которое называется формулой интегрирования по частям.
2. Таблица простейших интегралов
Пользуясь тем, что интегрирование – операция обратная вычислению дифференциала можно записать основные формулы интегрирования
1. α ≠ -1
2.
3.
4.
5.
6.
7.
8.
9.
Для полноты таблицы добавим еще две формулы.
10.
11.
В этих формулах u — независимая переменная или функция от независимой переменной, a – постоянная (в формуле 7 а ).
Приведем простейшие примеры вычисления интегралов:
Пример 1.
Пример 2.
Пример 3.
1.Разлагая интеграл 1 по свойству 2 на три интеграла и вынося постоянный множитель за знак интеграла (свойство 1), приведем интеграл к следующему виду:
далее первый и второй интегралы вычисляются по формуле 1 таблицы, а
в третьем — знаки ∫ и d взаимно сокращаются (интегрирование и взятие дифференциала – обратные действия).
.
2.Интеграл табличный, формула 3.
3.Подынтегральная функция (пр.3) может быть преобразована и сведена к разности двух функций, а значит к двум интегралам, интегрируемых по формуле 1 таблицы.
Для вычисления различных интегралов дополним таблицу определенными приёмами и методами интегрирования.
3. Интегрирование методом замены переменной.
Метод замены переменной или подстановки является одним из самых эффективных приемов интегрирования и вытекает из свойства 3.
Пусть требуется вычислить , во многих случаях удается в качестве новой переменной выбрать такую функцию
,
тогда достаточно найти интеграл
чтобы из него подстановкой u=u(x) получить искомый интеграл, т. е.
(9)
Рассмотрим частный случай замены переменной, если ∫ f(x)dx=F(x)+C, то
(8)
Действительно, , тогда
т. е. и функция оказывается первообразной
для f(ax+b).
Пример 4.
Пример 5. .
Пример 7.
так как , то полагая , получим
При выборе подстановки , упрощающей подынтегральное выражение, нужно помнить, что в его составе должен найтись множитель , дающий дифференциал новой переменной.
В примере 7- это множитель
Приведем ряд примеров на вычисление интегралов, которые заменой переменной сводятся к табличным.
Пример 8.
полагаем тогда и
Пример 9.
Замена подставляя новую переменную в исходный интеграл, получим
Пример 10.
В состав подынтегрального выражения входит множитель , являющийся
дифференциалом функции lnx , отсюда подстановка u=lnx, du=d(lnx) т. е.
Пример 11.
Подстановка x3 = u, du=3x2dx сводит искомый интеграл к другому интегралу, который является табличным.
ΩΩΩ
Интегрирование дробей, содержащих квадратный трехчлен
(10)
при условии, что квадратный трехчлен x2 +px+q не имеет действительных корней .
Для вычисления интеграла из квадратного трехчлена выделяется полный квадрат двучлена т.
Искомый интеграл принимает следующий вид:
Первый интеграл аналогичен интегралу из примера 8, второй табличный
/формула 6/.
Пример 12.
Выделяем полный квадрат x2 +4x+10=(x2+4x+4)+(10-4), делаем замену x+2=u, тогда 3x-1=3u-7, du=dx, подставляем в интеграл
4. Метод интегрирования по частям
Согласно свойству 4 вычисление интеграла может быть сведено к отысканию другого интеграла . Применение формулы целесообразно, если будет проще, чем или подобен ему. Для применения формулы интегрирования по частям к интегралу следует подынтегральное выражение представить в виде произведения двух множителей
д.Пример 13.
Примем за , тогда , подставляя в формулу (7), получим
Второй интеграл вычисляется подстановкой , окончательный результат
Принимаем за , находим подставляем в (7)
«Где в практической жизни используется интеграл?» — Яндекс Кью
Математика и математики
Популярное
Сообщества
Не, скрою, слово интеграл запомнилось не только из уроков математики, но и любимому фильму “Электроник”. Поэтому этот интеграл-интригал вспоминается иногда.
Вопрос – где он используется в повседневной жизни, какое практическое применение, кроме вычислений, у него есть. Как говорится, где увидеть, как пощупать?)
Спасибо!
МатематикаИнтегралы
Плотонова Ольга
Математика и математики
402Z”>16 сентября 2021 ·
27,2 K
ОтветитьУточнитьAndrei Novikov
Математика
2,3 K
кандидат физико-математических наук, математик, исследователь, data scientist, предпринима… · 16 сент 2021
На интегралах по вероятности держится половина статистического вывода. Отказываетесь от интегралов – отказываетесь от умений в области анализа данных.
1 эксперт согласен
Комментарий был удалён за нарушение правил
Комментировать ответ…Комментировать…
Владимир Горбацевич
Математика
1,7 K
математика нестандартный психоанализ · 27 сент 2021
В практической (обыденной) жизни используются не сами интегралы, а результаты их применения. Любой сложный прибор (от микросхемы до самолета и ракеты) разрабатывается с использованием интегралов.
А вот объем реального физического тела интегралом вовсе не вычисляется – для этого нужно этот предмет задать уравнениями, а это очень сложно. Но можно этот объем вычислить… Читать далее
1 эксперт согласен
Комментировать ответ…Комментировать…
Maxim Vyalkov
Математика
1,3 K
Интересующие темы: история математики, история христианства, библеистика. · 28 сент 2021
1. При вычислении площадей и объёмов вообще. 2. Везде, где в принципе нужно посчитать площадь криволинейной трапеции на графике (интеграл Римана) 3. Везде, где в принципе нужно определить “меру” чего-либо (интеграл Лебега). Пункты 2-3 имеют самое широкое применение от агропорма до финансовой аналитики. 4. Оценка рыночного равновесия и исследование функций спроса и… Читать далее
1 эксперт согласен
Георгий Степико
4 октября 2021
А в повседневной то жизни где?
Комментировать ответ…Комментировать…
Владимир Горбацевич
Математика
1,7 K
математика нестандартный психоанализ · 10 июн 2022
Ответ зависит от того, что понимать под “повседневной жизнью”.
Если понимать это как жизнь ученого или инженера, то интеграл там нужен очень часто (даже иногда повседневно!) при проведении множества теоретических расчетов, которые затем могут быть использованы на практике. Но для некоторых людей (например, для меня) интеграл используется просто как средство для… Читать далее
Комментировать ответ…Комментировать…
Архип
Математика
23
студент Физфака МГУ, интересуюсь (на уровне научпоп статей) биологией, химией… · 30 сент 2021
Зависит от того, что вы называете “повседневной жизнью”. У кого-то, кто работает инженером, статистическим аналитиком, физиком, интегралы встречаются чаще, чем математики на мехмате. Если же человек работает грузчиком – интеграл ему вряд ли нужен, даже если он знает, что это такое и с чем его едят. Вывод: интеграл используется везде, где есть слово “образование”, кроме… Читать далее
Если есть какие-либо вопросы/замечания, пишите
Перейти на vk.
com/bpem9l_0t4ucjlehu9lКомментировать ответ…Комментировать…
Достоверно
Ильяс Вербинский
19
Студент университета, участник различных интеллектуальных, творческих конкурсов, межрегио… · 6 июн 2022
1) При расчетах площади, объема фигур, ограниченных одной или несколькими кривыми. 2) При решении различных физических задач, где применяется интегральная сумма для нахождения величин, состоящей из множества маленьких величин. 3) При проверки правильности нахождения производных тех или иных функций. Читать далее
2 эксперта согласны
Леонид Коганов
10 июня 2022
“При проверкЕ…”. Предложный падеж русского языка, госп. Вербинский. При ком, при чём. На ус намотать и по… Читать дальше
Комментировать ответ…Комментировать…
Дмитрий Заварзин
5
Структурирую хаос · 19 мая 2022
У всех жизнь разная.
Я в своей повседневной жизни не использую сварочные аппараты, а вот сварщик – каждый рабочий день. Так и тут. Можно, конечно, ту же сумму дать как интеграл по соответствующему пространству – тогда вот – при суммировании. А если вы инженер, ученый (физик, экономист…) и далее – то это ваш рабочий инструмент, как сварочный аппарат для сварщика. Вот там… Читать далее
1 эксперт согласен
Леонид Коганов
20 мая 2022
Простите, уважаемый Коллега, вопрос в строну: просто мне (по близорукости? не могу знать! – Л.К.) показалось,что… Читать дальше
Комментировать ответ…Комментировать…
Dmitry Maslov
4,9 K
Инженер путей сообщения – строитель · 16 сент 2021
Если хочется именно пощупать, возьмите в руки абсолютно любой предмет. Его объём можно вычислить через интеграл ∫∫∫dxdydz. Если мы сможем этот предмет разрезать, то его площадь сечения опять будет интегралом ∫∫dydz.
А если не щупать, то в инженерно-технических расчётах без интеграла вообще никак, он практически везде.
1 эксперт согласен
Михаил Мулюков
подтверждает
17 сентября 2021
Остроумный и достойный ответ, вызывающий массу аналогий: вес предметов, длина пути, электрический заряд – всё это… Читать дальше
Комментировать ответ…Комментировать…
Константин Астахов
17
Инженер (тот самый, с лысой головой на бубликовом спейсшаттле в “Прометее” 🙂 · 14 июн 2022
Типичный случай повседневного неосознанного использования операции интегрирования – усреднение, т.е. получение среднего значения:
1. Среднеквадратичное значение напряжения в домашней сети 230 В (где-то еще бывает 220, но это не катастрофа, техника держит). Это значит, что если проинтегрировать по времени квадрат мгновенного значения напряжения между фазой и нулем за.
.. Читать далее
Комментировать ответ…Комментировать…
Леонид Коганов
189
Член ММО – Московского математического Общества. Кстати, старейшего в мире. Л.М. Коганов. · 20 мая 2022
Везде, где используются понятия величины и меры, где мы вынуждены суммировать плотность / удельную меру вдоль чего-то, будь то отрезок / кусок линии, площадка или ограниченный как правило замкнутой поверхностью об’ём, мы обязаны представить указанную “результирующую” величину в виде интеграла. Того или иного вида. Взятие интеграла есть некоторое отдельное “искусство”… Читать далее
Alexey Buldakov
24 мая 2022
Интегралы используются в различных расчëтах. Часто применяю интегралы Фурье. Один раз при расчёта помех от блока… Читать дальше
Комментировать ответ…Комментировать…
О сообществе
Математика и математики
Сообщество практикующих математиков разного уровня.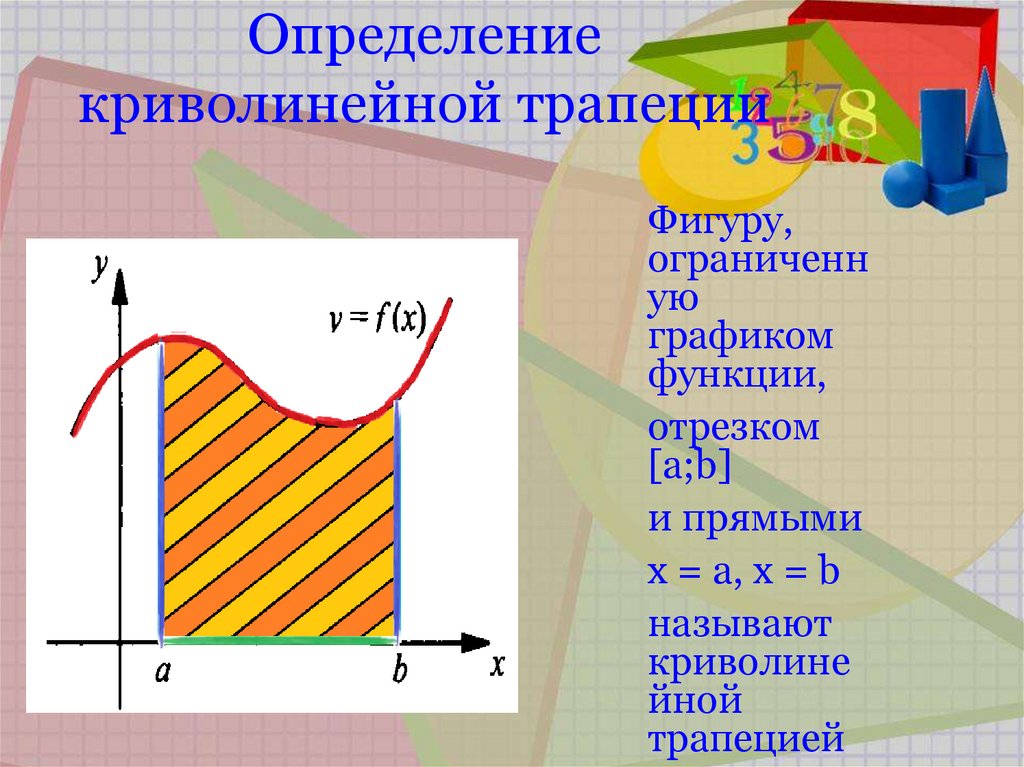
Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!
Интегралы: математический смысл — Nexus Wiki
Основная идея исчисления заключается в том, как связаны изменения. Когда мы смотрим на производные, мы обращаем внимание на то, как были связаны изменения двух переменных, когда изменения были небольшими. Но мы хотим иметь возможность пойти дальше этого. Допустим, изменения большие? Если мы знаем производную, мы можем построить большие изменения, складывая маленькие изменения. Мы делаем это с концепцией интеграла . В самом прямом смысле производная и интеграл обратны друг другу. На этой странице мы рассмотрим математику построения интеграла и его математический смысл.
Приближение интеграла прямоугольниками —сумма Римана. Нажмите на изображение
, чтобы увидеть его вживую. (Википедия)
Если вы помните из занятий по математическому анализу, как интеграл строится из сумм (как в интеграле Римана), вы, вероятно, можете пропустить эту страницу и сразу перейти к следующей странице: Как я могу на самом деле использовать интегралы? , где мы обсуждаем различные способы его использования, чтобы иметь смысл в этом классе.
Если вы не помните, как построить интеграл таким образом, чтобы вы могли подумать о том, что это значит, следите за нашим обсуждением на этой странице. Делайте это осторожно, шаг за шагом.
Производная как отношение малых изменений
Начнем с абстрактной математической версии. У нас есть функция $f$, зависящая от независимой переменной (значение которой мы можем выбирать свободно) $x$. Идея производной состоит в том, чтобы определить функцию, которая представляет отношение того, насколько изменится $f$, когда $x$ изменится (немного). Итак,
$$g(x) = f'(x) = \frac{df}{dx}$$
Обозначение содержит некоторое внутреннее противоречие. Выражение слева, $g(x)$, говорит о том, что мы рассматриваем эту производную как функцию $x$, поэтому мы знаем ее в любой отдельной точке. Выражение справа говорит, что производная – это изменение $f$, деленное на изменение $x$. Чтобы получить сдачу, вы должны рассмотреть два разных x.
Способ, которым мы избегаем этого, заключается в том, что мы рассматриваем “изменение” как “значение $x$, чуть меньшее, чем $x$, до значения $x$, лишь чуть большего”.
Так что это все равно, что смотреть фильм и говорить: «Скорость в 96-м кадре — это изменение положения от 95-го до 97-го кадра, деленное на временной интервал от 95-го до 97-го кадра». Это довольно громоздко, но важно для размышлений о том, что на самом деле означает скорость — или любая производная. Люди в математике тратят много усилий, чтобы избавиться от этого; но для нас лучше думать об этом таким образом.
Суммирование небольших изменений: интеграл
Если вы знаете $f$, вы дифференцируете его, чтобы получить $g$. Но что нам делать, если мы знаем функцию $g$ и хотим пойти другим путем и найти $f$? Сначала это может показаться странным. Как бы мы узнали производную функции, если бы не знали функцию? Но на самом деле это происходит постоянно. Один из ключевых принципов этого термина будет заключаться в том, чтобы показать, что ускорение объекта определяется совокупностью сил, которые он испытывает. Таким образом, мы можем узнать ускорение объекта, вычислив силы. Но ускорение есть производная от скорости! Итак, $a = dv/dt$, и мы знаем $a$ как функцию времени, но хотим найти $v$.
И тогда мы можем знать $v=dx/dt$ как функцию времени, но хотим вычислить $x$.
Давайте попробуем это, используя $g$ и $f$ , чтобы мы могли сосредоточиться на общей структуре математики, не отвлекаясь на конкретное “что это такое”.
Если серьезно отнестись к производной как отношению, мы можем умножить обе части нашего уравнения на небольшое изменение “$dx$”, чтобы получить следующее:
$$df = g(x)dx$$
Читать это как: “изменение $f$ равно $g$ (производная от $f$), умноженное на изменение $x$”. Было бы яснее, что это означает, если бы мы использовали дельты вместо d и обратили внимание на концы интервала дх. Это выглядит следующим образом:
$$\Delta x = x_1 – x_0$$
$$\Delta f = g(x)dx \; \правая стрелка \; f(x_1) – f(x_0) = g(x_0) \Delta x$$
Поскольку мы рассматриваем изменение, у нас есть два значения $x$, но $g$ является функцией $x$ только один раз . Мы выбираем начальное значение, хотя, вероятно, было бы более эстетично выбрать оценку $g$ в середине интервала, $\frac{x_0 + x_1}{2}$.
Но тогда все выглядело бы намного грязнее, и оказалось, что это не имело бы никакого значения.
Теперь давайте сделаем много шагов размера \Delta x:
$$x_1 – x_0 = \Delta x$$
$$x_2 – x_1 = \Delta x$$
$$x_3 – x_2 = \Delta x \\ …$$
… означает “представьте, что этот процесс продолжается”. Мы напишем «N» для верхнего значения нашего последнего шага.
Если мы теперь запишем, как изменяется $f$ на каждом шаге, мы получим
$$f(x_1) – f(x_0) = g(x_0) \Delta x$$
$$f(x_2) – f (x_1) = g(x_1) \Delta x$$
$$f(x_3) – f(x_2) = g(x_2) \Delta x \\ …$$
, где снова три точки означают «продолжать».
Теперь нужно сложить все уравнения в строке выше. Это дает нам
$$[f(x_N) – f(x_{N-1})] + [f(x_{N-1}) – f(x_{N-2})] +… + [f(x_2) – f(x_1)] + [f(x_1) – f(x_0)] \\
= g(x_{N-1}) \Delta x + g(x_{N-2}) \ Delta x+ … + g(x_1) \Delta x + g(x_0) \Delta x$$
Хотя это выглядит беспорядочно, происходит кое-что интересное.
Все условия слева отменяются, кроме первого и последнего! (Конечная точка одного интервала и начальная точка следующего одинаковы, но один раз он входит со знаком +, а один раз со знаком -.) Но термины справа (с символами $g$) просто добавляют — отмены нет. В результате изменение $f$ от первого к последнему определяется суммой множества членов $g\Delta x$. Мы записываем эту сумму терминов, используя обозначение суммирования с большой греческой буквой «S» (= сигма = Σ) для «суммы». Правая часть второй строки ниже означает именно то, что написано над ней. 9{x_f}{ g(x) dx}$$
изменение с “0” на “i” (начальное) и с “N” на “f” (финальное). Этот результат показывает, что наша сумма (или интеграл) производных может сказать нам, как изменяется f по мере удаления x от начального значения. Это означает, что наш интеграл может давать значения всей функции $f$ для любого значения x, если мы знаем начальную точку и производную от $f$.
Определенные и неопределенные интегралы: основная теорема исчисления
В зависимости от того, как мы используем этот последний результат, мы можем интерпретировать его по-разному.
{x}{ \frac{df}{dx’}dx’}$$ 9{x}{ \frac{df}{dx’}dx’} + C$$
Поскольку мы рассматриваем здесь $x$ как переменную, это называется неопределенным интегралом .
Выражения в этом разделе часто называют фундаментальной теоремой исчисления , поскольку они показывают, что производная и интеграл обратны друг другу.
Некоторые простые интегралы
Поскольку мы знаем производные некоторых простых алгебраических выражений, мы также можем легко получить интегралы этих выражений. Поскольку мы знаем 9{x} sin(x’) dx’ = -cos(x) + C$$
Хотя они полезны, мы будем чаще использовать описанные здесь формальные идеи для создания эвристик, которые помогут нам связать различные графики. См. следующее на стр. Как я могу использовать интегралы?
Джо Редиш 04.09.11
Интегральный день | Математическая программа
29 октября – День Интеграла! Почему? Современный знак интеграла был впервые написан 29 октября 1675 года великим немецким математиком Готфридом Лейбницем (1646–1716) в неопубликованной рукописи.
Учитывая важность исчисления (это одно из самых полезных изобретений во втором тысячелетии нашей эры) и важность интеграции (это одно из трех фундаментальных понятий исчисления), мы просто есть , чтобы отпраздновать.
Наши праздники проходят в Math Suite и рядом с ним и включают в себя “печенье с вычислениями” и “суммирующий сидр”, украшения для интегралов/суммирования и большой дисплей, заполненный “интегральными граффити”. Смелые ученики соревнуются в интегральном конкурсе: ученик, решивший наибольшее количество интегралов, получает кофейную кружку «Математика — неотъемлемая часть моей жизни» и восхищение сверстников. Многие составляющие нашего празднования имеют тему Хэллоуина из-за близости Дня Интеграла к 31 октября.
Весной 14 марта факультет математики отмечает День числа Пи.
Пейдж Миллер демонстрирует свою кофейную кружку «Математика — неотъемлемая часть моей жизни» после победы в интегральном конкурсе на Integral Day 2018.
Крис О’Салливан, Сэм Терхаар и Рэйчел Пелсанг отдыхают после создания нашего дисплея Integral Day в канун Дня Integral 2015. Доска объявлений сначала была покрыта меловой карточкой, чтобы превратить ее в классную доску, а затем команда добавила «интегральное граффити».
Механические интеграторы
Некоторые из наших торжеств включали демонстрацию механических интеграторов Филом Уингером, бывшим заместителем вице-президента по объектам в Сент-Бонавентуре. Механический интегратор — это устройство, которое механически решает задачу, которую решают определенные интегралы.
Г-н Уингер представил пузырьковый секстант и полярный планиметр.
Пузырьковый секстант
Пузырьковый секстант использовался штурманом патрульного бомбардировщика военно-морского флота для наблюдения за углом от вертикали небесных тел, таких как солнце. Он использует пузырек в качестве вертикального ориентира, накладывая изображение пузыря на изображение солнца, видимого через регулируемую призму.
Мистер Уингер владеет моделью начала 19 века.40с.
Проблема с использованием пузырьковой ссылки заключается в том, что она подвержена ускорению, отличному от силы тяжести, например раскачиванию самолета в турбулентности. Решением этой проблемы является усреднение показаний за период времени, значительно превышающий период возмущений. Устройство Вингера усредняет показания прибора за двухминутный период.
Усреднение функции по интервалу — это применение интегрирования, превращающее секстант с пузырьками в механический интегратор.
Студент использует секстант с пузырьками, поскольку Фил Уингер обеспечивает «турбулентность».
Полярный планиметр
Планиметр — это инструмент, который позволяет человеку измерить площадь области, отслеживая ее границы. Планиметры бывают разных типов; Мистер Уингер владеет полярным планиметром.
Вычисление площади региона является классическим применением интегрирования, превращая планиметр в механический интегратор.