Интегралы какие бывают: Виды интегралов

{6}(x+y+z) d x d y d z \)

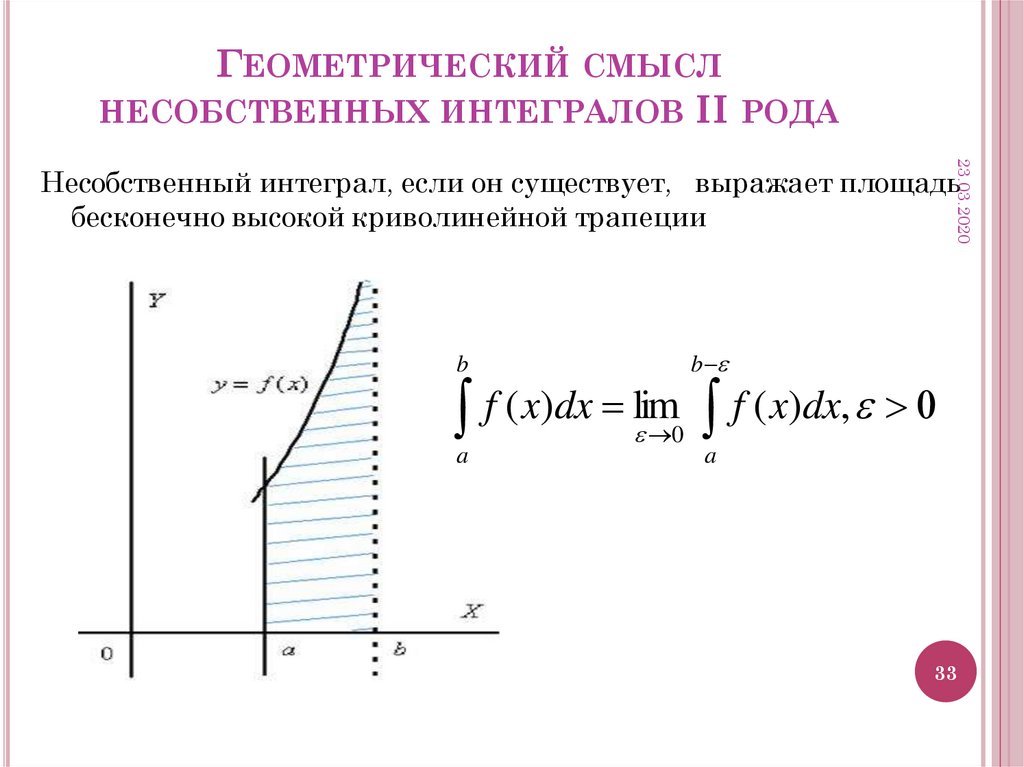
Криволинейные и поверхностные интегралы

ОПРЕДЕЛЕНИЕ

Криволинейный интеграл является интегралом, который вычисляется вдоль кривой в плоскости или в пространстве. Пусть задана кривая \(\ c \) и функция \(\ f(x ; y) \) непрерывна на этой кривой. Тогда криволинейный интеграл первого вида функции \(\ f(x ; y) \) вдоль кривой \(\ \mathrm{C} \) называется интегралом \(\ \int_{C} f(x ; y) d s \) .

Например. \(\ \int_{C}(x+y) d s \) где \(\ P(x ; y) \)

ОПРЕДЕЛЕНИЕ

Если функции \(\ Q(x ; y) \) и \(\ \int_{C} P(x ; y) d x+Q(x ; y) d y \) определены на кривой \(\ \mathrm{C} \), то криволинейный интеграл второго рода называется интегралом вида \(\ \int_{C}(x+y) d x+(x-y) d y \) .

Например: \(\ f(x ; y 😉 \)

Подробнее о криволинейных интегралах по ссылке.

ОПРЕДЕЛЕНИЕ

Поверхностный интеграл первого вида функции \(\ \iint_{S} f(x ; y ; z) d S \) над некоторой поверхностью \(\ s \) называется интегралом \(\ \iint_{S}(x+y+z) d S \)

Например: \(\ \iint_{S}(x+y+z) d S \) , где \(\ \mathrm{S} \) – часть плоскости \(\ x+2 y+3 z=0 \), которая лежит в первом октанте. {-x} d x \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Сходимость несобственных интегралов Интегрирование по частям Интегрирование заменой переменной Внесение под знак дифференциала

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно – исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Определенный интеграл

Мы начинаем новую тему — интегрирование. Задача интегрирования формулируется как задача отыскания площади — казалось бы, ничего общего с теми вещами, которые мы обсуждали до сих пор — производными, скоростями роста и т.д. Однако, очень быстро обнаружится, что связь есть, причём самая непосредственная.

24.1Интеграл Римана

24.1.1Интеграл и площадь

Рассмотрим некоторую функцию f, определенную на отрезке [a,b]. Пусть во всех точках отрезка значение функции неотрицательно. Мы хотим найти площадь фигуры, ограниченной графиком y=f(x), горизонтальной осью и вертикальными прямыми x=a и x=b. Как это сделать?

Чтобы начать отвечать на этот вопрос, нужно подумать о том, что вообще такое «площадь». Мы знаем, что площадь прямоугольника — это произведение его длины и ширины. Мы также знаем (считаем это аксиомой или частью определения), что если у нас есть две фигуры, и мы складываем из них третью «без нахлёста», то площадь новой фигуры равна сумме площадей исходных фигур. И ещё, что если у нас есть две равные фигуры (то есть такие, которые можно положить друг на друга так, чтобы они совпали), то их площади равны. Из этих трёх правил можно вывести много других. Например, прямоугольник разбивается своей диагональю на два равных прямоугольных треугольника, и значит площадь каждого из них вдвое меньше площади прямоугольника, и равна половине произведения катетов. Произвольные треугольник разбивается высотой на два прямоугольных, откуда легко вывести, что его площадь равна половине произведения высоты на основания. Более сложные многоугольники можно разбивать на треугольники и находить их площади таким образом. Так мы определяем площади довольно широкого класса фигур — но далеко не всех. Что делать, если мы имеем дело не с многоугольником, а фигурой, ограниченной какой-то «кривой» линией, не состоящей из прямолинейных отрезков? Такую фигуру нельзя разбить на прямоугольники или треугольники. Однако, её можно

приблизить более простыми фигурами с известными площадами, добиться того, чтобы эти приближения становились всё лучше и лучше, и перейти к пределу. Именно таким образом определяется интеграл Римана.

24.1.2Разбиения и интегральные суммы

Наша идея следующая. Давайте разобьем фигуру, площадь которой мы хотим найти, на тонкие вертикальные полоски. Они выглядят почти как прямоугольники, только верхняя сторона не совсем прямая. Их можно приблизить прямоугольниками, найти их площадь и сложить. Получится приближение к искомой площади. Затем количество прямоугольников можно увеличивать и делать их всё более тонкими. Куда при этом устремится их совокупная площадь — то и будет (по определению) площадью нашей фигуры.

Чтобы это сформулировать аккуратно, придётся ввести несколько новых понятий.

Определение 1. Набор точек (x0,x1,…,xn) называется разбиением отрезка [a,b], если

a=x0<x1<…<xn−1<xn=b,

то есть все точки xk, k=0,…,n лежат на отрезке [a,b], следующая точка правее предыдущей, нулевая совпадает с левым концом, а последняя — с правым.

Для данного разбиения P=(x0,…,xn) введём также обозначения:

Ik=[xk−1,xk],Δxk=xk−xk−1,k=1,…,n,

Ik=[xk−1,xk],Δxk=xk−xk−1,k=1,…,n,

то есть Ik — это k-й отрезок разбиения, Δxk — его длина.

Определение 2. Диаметром разбиения P называется максимум длин отрезков этого разбиения:

d(P)=max{Δxk∣k=1,…,n}.

Определение 3. Выберем теперь в каждом из отрезков Ik по точке x∗k произвольным образом (она может совпадать с правым или левым концом отрезка, тут нет запретов). Тогда разбиение P вместе с набором точек (x∗1,…,x∗n) называется размеченным разбиением отрезка [a,b].

Определение 4. Для данной функции f и данного размеченного разбиения P определим интегральную сумму:

S(P,f):=f(x∗1)Δx1+…+f(x∗n)Δxn=n∑k=1f(x∗k)Δxk.(24.1)

S(P,f):=f(x∗1)Δx1+…++f(x∗n)Δxn=n∑k=1f(x∗k)Δxk.(24.1)

Интегральная сумма имеет следующую интерпретацию. Над каждым из отрезков Ik построим прямоугольник, у которого ширина совпадает с этим отрезком, а высота равна значению f(x∗k). Интегральная сумма — это сумма площадей таких прямоугольников. Если порезать интересующую нас фигуру на вертикальные полоски прямыми x=xk, то площади этих полосок будут близки к площадям соответствующухи прямоугольников, и можно ожидать, что чем тоньше будут полоски (то есть чем меньше диаметр разбиения), тем точнее будет приближение.

24.1.3Определенный интеграл как предел

Тут очень хочется записать какой-то предел при d(P)→0, однако проблема в том, что S(P,f) не является функцией от диаметра разбиения d(P) — для разных разбиений даже с одинаковым диаметром могут получаться разные значения интегральных сумм. Поэтому использовать обычное определение предела нельзя. Но ничто не помешает нам изготовить новое определение, специально для этого случая. Оно будет очень похожим на обычное.

Определение 5. Число I∈R называется интегралом Римана от функции f по отрезку [a,b], если для всякого ε>0 найдётся такое δ>0 что для всех размеченных разбиений P верно утверджение: если d(P)<δ, то

|S(P,f)−I|<ε.

Можно записать, что

limd(P)→0S(P,f)=I,

понимая здесь под пределом ровно то, что сказано в определении 5.

Обозначается интеграл таким образом:

I=:∫baf(x)dx.

Здесь ∫ — знак интеграла, a и b — пределы интегрирования (нижний и верхний соответственно), f — подынтегральная функция. Кто такой dx, объяснить сложнее, но если посмотреть на определение интегральной суммы (см. (24.1)), видно, что там было f(x∗k)Δxk. При переходе к пределу, сумма превращается в знак интеграла, f(x∗k) превращается просто в f(x), а Δxk превращается в dx. В порядке шутки можно сказать, что при переходе к пределу угловатая фигура, составленная из прямоугольников, превращается в нашу нашу настоящую фигуру с плавной криволинейной границей, а угловатые значки ∑ и Δ превращаются в плавные значки ∫ и d. Почему полезно «таскать с собой» воспоминание про Δxk, станет ясно чуть позже, когда мы обсудим формулы замены переменной в интеграле.

Пример 1. Пусть для всех x∈R, f(x)=2. Тогда

∫baf(x)dx=∫ba2dx=2(b−a),

поскольку искомая площадь — это площадь прямоугольника с шириной (b−a) и высотой 2.

24.2Свойства определённого интеграла

24.2.1Интегрируемые и неинтегрируемые функции

Для начала нужно сказать, что, как и любой предел, интеграл может существовать, а может и не существовать. Если интеграл существует, функция f называется интегрируемой (по Риману) на отрезке [a,b]. Тот факт, что значение интеграла определяется однозначно (то есть не бывает двух разных чисел I1 и I2, удовлетворяющих определению 5), доказывается точно так же, как доказывается аналогичное утверждение для пределов последовательностей или функций — сделайте это самостоятельно.

Не все функции интегрируемы. Например, функция Дирихле

D(x)={1,x∈Q,0,x∉Q.

не является интегрируемой ни на каком отрезке [a,b]. Действительно, для любого, сколь угодно мелкого разбиения, на любом отрезке разбиения найдутся как рациональные, так и иррациональные точки. Выбирая x∗k иррациональными, можно сделать интегральную сумму нулевой. А выбирая x∗k рациональными, можно сделать интегральную сумму равной b−a>0. Значит, никакого одного предела, к которому стремились бы интегральные суммы с уменьшением диаметра разбиения, не существует.

Трудно описать множество всех интегрируемых функций, однако для наших целей важно сказать, что функции из некоторых важных для нас классов таким свойством обладают.

Теорема 1. Пусть функция f непрерывна на отрезке [a,b]. Тогда она интегрируема на этом отрезке.

Я не буду доказывать эту теорему — это требует некоторых усилий, носящих скорее технический характер. (Ключевые слова для тех, кому интересно: верхняя и нижняя суммы Дарбу. ) Скажу лишь пару слов про основной механизм. Как показывает пример с функцией Дирихле, препятствием к интегрируемости оказывается ситуация, при которой свобода в выборе x∗k∈Ik даёт нам возможность сильно менять значение функции — и следовательно интегральной суммы. Если функция непрерывна, её значения в близких точках близки, и значит меняя x∗k в пределах маленького отрезка Ik, мы не поменяем значение функции слишком сильно, чтобы это существенно повлияло на интегральную сумму.

Непрерывность является достаточным условием интегрируемости, но не является необходимым — например, кусочно-непрерывные функции, чьи разрывы являются скачками, тоже интегрируемы. Чуть позже мы обсудим это подробнее.

24.2.2Интеграл как площадь с учётом знака

Когда мы определяли интеграл, мы начинали с задачи нахождения площади под графиком неотрицательной функции. Однако, определение, которое в результате получилось, не содержит ограничений на знак функции: f(x) может принимать как положительные, так и отрицательные значения. Если для какого-то из отрезков разбиения Ik значение f(x∗k) отрицательное, соответствующее слагаемое в интегральной сумме f(x∗k)Δxk также отрицательно, а его абсолютное значение равно площади прямоугольника шириной Δxk и высотой |f(x∗k)|; на картинке логично изображать такой прямоугольник растущим «вниз» от горизонтальной оси. Таким образом, те участки, на которых подынтегральная функция отрицательна, вносят отрицательный вклад в интеграл. Если отрезок [a,b] разбивается на несколько отрезков, на каждом из которых функция f знакопостоянна, интеграл имеет следующую интерпретацию. Нужно посчитать площадь между кривой и горизонтальной осью на тех участках, где функция положительна, и вычесть из неё площадь между кривой и горазонтальной осью на участках, где функция отрицательна. Таким образом, можно сказать, что интеграл — это площадь с учётом знака.

24.2.3Линейность и интегрирование неравенств

Сформулируем несколько очень естественно выглядящих свойств интегралов.

Утверждение 1. Пусть функции f и g интегрируемы на отрезке [a,b]. Тогда функция h(x)=f(x)+g(x) также интегрируема на отрезке [a,b] и сумма интегралов равна интегралу суммы:

∫ba(f(x)+g(x))dx=∫baf(x)dx+∫bag(x)dx

∫ba(f(x)+g(x))dx==∫baf(x)dx+∫bag(x)dx

Утверждение 2. Пусть функция f интегрируема на отрезке [a,b] и c — некоторая константа. Тогда интеграл от функции h(x)=cf(x) определён и

∫bacf(x)dx=c∫baf(x)dx,

иными словами, константу можно выносить за знак интегрирования.

Эти свойства похожи на аналогичные свойства дифференцирования. В совокупности они называются линейностью интеграла — а почему так, вы узнаете на курсе линейной алгебры. Утверждение 2 имеет геометрическую интерпретацию: если функция умножается на c, график вытягивается в c раз по вертикали, поэтому площадь мод ним умножается на c. Геометрическая интерпретация утверждения 1 несколько менее очевидна (см. статью про метод Кавальери).

Утверждение 3. Пусть функции f и g интегрируемы на отрезке [a,b] и пусть для всех x∈[a,b], f(x)≤g(x). Тогда

∫baf(x)dx≤∫bag(x)dx.

А у этого утверждения есть простая геометрическая интерпретация: если f и g неотрицательны, интегралы равны площадям под соответсвующими графиками, и фигура под графиком f находится нестрого внутри фигуры под графиком g, а значит имеет не большую площадь.

Утверждения 1, 2 и 3 доказываются с помощью одного и того же заклинания: это верно для интегральных сумм, значит, это верно и для интегралов. Аккуратные доказательства полностью аналогичны доказательствам соответствующих утверждений для пределов — арифметики пределов и предельного перехода в неравенствах. Записать эти доказательства — хорошее упражнение.

24.2.4Интегрируемость и ограниченность

Утверждение 4. Если функция f интегрируема на отрезке [a,b], то она ограничена на этом отрезке.

Доказательство.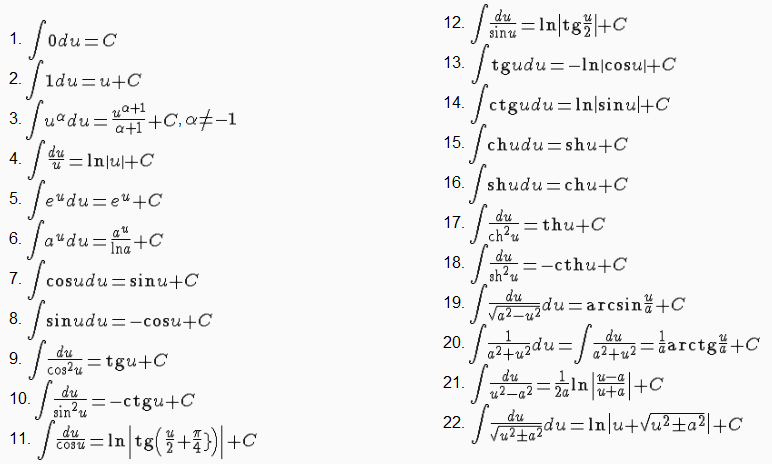 От противного. Пусть f не является ограниченной на [a,b]. Мы докажем, что для любого, сколь угодно мелкого разбиения, можно подобрать такую разметку, что интегральную сумма будет сколь угодно большой. Действительно, если функция не является ограниченной на [a,b], она не является ограниченной на каком-то из отрезков разбиения Im. Пусть у нас есть какая-то разметка x∗k. Можно сдвинуть точку x∗m таким образом, чтобы площадь Δxmf(x∗m) было сколь угодно большой по модулю. Если остальные точки разметки при этом не менять, соответствующие им слагаемые интегральной суммы также не будут меняться. А если у нас есть сумма, в которой одной слагаемое можно сделать сколь угодно большим по модулю, а остальные не меняются, то и всю сумму можно сделать сколь угодно большой по модулю. И значит никакого конечного предела нет.

Более формальное доказательство выглядит следующим образом. Пусть

∫baf(x)dx=I.

Это означает, что для всякого ε>0 найдётся такая δ=δ(ε)>0, что для всякого размеченного разбиения P, если d(P)<δ, то |I−S(P,f)|<ε. Положим ε=1 и возьмём δ1:=δ(1). Из свойств модуля следует, что в этом случае для всех разбиений, у которых d(P)<δ1,

|S(P,f)|<|I|+1(24.4)

Рассмотрим теперь произвольное размеченное разбиение P, у которого d(P)<δ1. Пусть оно состоит из n отрезков

Ik=[xk−1,xk],x∗k∈Ik,k=1,…,n.

Если функция f не является ограниченной на [a,b], найдётся по крайней мере один из отрезков разбиения Im, на котором она не является ограниченной. (Действительно, если бы она была ограниченной на каждом из отрезков разбиения, для каждого k∈{1,…,n} существовало бы такое число Ck, что для всех x∈Ik, |f(x)|≤Ck. Но тогда число C=max{C1,…,Cn} ограничивало бы f(x) для любого x∈[a,b], и значит функция была бы ограниченной на этом отрезке.) Докажем, что модифицируя разметку отрезка Im, то есть меняя x∗m на какой-то z∗m∈Im, мы можем получить сколь угодно большую по модулю интегральную сумму, и значит (24.4) выполняться не может.

Действительно, поскольку f не является ограниченной на отрезке Im, для всякого C найдётся такое x=x(C)∈Im, что |f(x)|>C. Возьмём

C=1Δxm⎛⎜ ⎜⎝n∑k=1k≠m|f(x∗k)Δxk|+|I|+1⎞⎟ ⎟⎠.

В правой части стоит сумма модулей всех слагаемых в интегральной сумме, кроме m-го. Нам пришлось также поделить её на Δxm — буквально через секунду станет понятно, почему.

Пусть z∗m=x(C). В этом случае

|f(z∗m)Δxm|>n∑k=1k≠m|f(x∗k)Δxk|+|I|+1,

то есть слагаемое, отвечающее отрезку Im, имеет модуль, с запасом превосходящий сумму модулей всех остальных слагаемых. Поскольку |a+b|≥|a|−|b| (проверьте, что это всегда правда), отсюда следует, что модуль интегральной суммы

∣∣ ∣ ∣∣f(z∗m)Δxm+n∑k=1k≠mf(x∗k)Δxk∣∣ ∣ ∣∣>|I|+1,

что противоречит (24.4).∎

24.2.5Аддитивность интеграла

Утверждение 5. Пусть функция f интегрируема на отрезках [a,b] и [b,c]. Тогда она интегрируема на отрезке [a,c] и

∫caf(x)dx=∫baf(x)dx+∫cbf(x)dx.(24.5)

∫caf(x)dx=∫baf(x)dx++∫cbf(x)dx.(24.5)

Это свойство называется аддитивностью интеграла Римана.

Набросок доказательства. Будем называть интеграл ∫caf(x) интегралом I, ∫baf(x)dx — интегралом I1 и ∫cbf(x)dx — интегралом I2.

Геометрически наше свойство выглядит очевидным: фигура, соответствующая интегралу I, составлена из фигур, соответствующих интегралам I1 и I2, и её площадь очевидно должна быть равна сумме площадей этих фигур.

Если поверить в интегрируемость функции f на отрезке [a,c], доказать, что интегралы равны, довольно просто. Действительно, возьмём произвольное размеченное разбиение отрезка [a,b] и произвольное размеченное разбиение отрезка [b,c]. Объединим эти разбиения: получим размеченное разбиение отрезка [a,c]. Интегральная сумма для интеграла I, соответствующая этому разбиению, будет суммой двух интегральных сумм, соответствующих интегралам I1 и I2. Выбирая достаточно мелкие разбиения, можно сделать эти две интегральные суммы сколь угодно близкими к соответствующим интегралам I1 и I2. А значит интегральную сумму для интеграла I можно сделать сколь угодно близкой к сумме интегралов I1 и I2. Таким образом, именно эта сумма и является пределом интегральных сумм, то есть интегралом I.

Для совсем аккуратного доказательства нам нужно показать, что если какое-нибудь разбиение отрезка [a,c] (не обязательно составленное как объединение разбиений по каждому из отрезков [a,b] и [b,c]) является достаточно мелким, то соответствующая интегральная сумма близка к сумме двух интегралов. Чтобы это сделать, дополнительно разобьем отрезок разбиения, содержащий точку b, на два отрезочка поменьше — ровно по точке b. Разметку на новых отрезочках выберем произвольным образом. В результате этой операции мы попали в предыдущий случай: опять интегральная сумма, соответствующая I, является суммой интегральных сумм, соответствующих I1 и I2. Однако, в результате дополнительного разбиения интегральная сумма, соответствующая I, изменилась. Легко показать, что изменилась она не сильно: изменения затронули лишь один отрезок исходного разбиения, и максимально возможное изменение соответствующей площади не превосходит ширины этого отрезка (маленькой, поскольку диаметр разбиения можно выбрать маленьким), умноженной на максимально возможное изменение значения функции f, ограниченное константой: если модуль функции f ограничен какой-то константой C, то модель разности её значений в двух разных точках не больше 2C. А функция f ограничена в силу интегрируемости. Значит, погрешность, которая возникает из-за дополнительного разбиения отрезка, стремится к нулю вместе с диаметром разбиения, и следовательно не влияет на предел.∎

24.3Заключение

Дифференцирование и интегрирование — два столпа математического анализа. В этой лекции, основываясь на геометрической задаче отыскания площади, мы начали строить теорию интеграла Римана — дали определение и обсудили несколько важных свойств. Однако, у нас пока нет ни малейших представлений о том, как считать интегралы, кроме как пользуясь определением — что не только муторно, но и редко когда приводит к успеху. На следующей лекции мы познакомимся к формулой Ньютона — Лейбница, связывающей интегрирование с дифференцированием — и с её помощью научимся вычислять некоторые (хотя и далеко не все) определенные интегралы.

---

← Предыдущая глава Следующая глава →

Основные формулы интеграции – Math Insight версия суммирования

. Но, как это ни парадоксально, часто интегралы вычисляются , рассматривая интегрирование как операцию, обратную по отношению к дифференцированию . (Этот факт представляет собой так называемую Фундаментальную теорему исчисления .)

Обозначение, на котором мы остановились по историческим причинам, столь же своеобразна, как и обозначение производных: интеграл от функция $f(x)$ относительно $x$ записывается как $$\int f(x)\;dx$$

Замечание о том, что интегрирование является (почти) обратной операцией дифференциация означает, что если $${d\over dx}f(x)=g(x)$$ тогда $$\int g(x)\;dx=f(x)+C$$ Дополнительный $C$, называемый константой интегрирования , на самом деле необходимо, так как после всякого дифференцирования уничтожаются константы, которые вот почему интеграция и дифференциация не 92} \; dx&=\arctan x+C \end{align*}

А поскольку производная суммы есть сумма производных, то интеграл от суммы есть сумма интегралов: $$ \int f(x)+g(x)\;dx=\int f(x)\;dx+\int g(x)\;dx$$ И точно так же константы «проходят» знак интеграла: $$\int c\cdot f(x)\;dx=c\cdot \int f(x)\;dx$$

Например, многочлены легко интегрировать даже включая такие термины, как $\sqrt{x}$ и более общие степенные функции.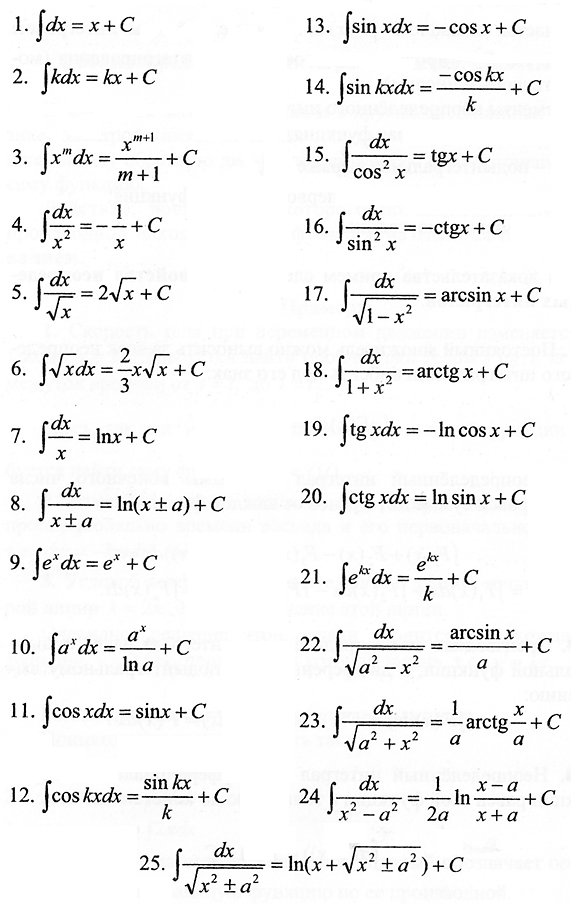 {3/2} \более 3/2}+3\ln x+C$$ Обратите внимание, что нам нужно включить только одну «константу интегрирования». 92 }}\; дх=?$

6: Приложения интеграции – Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2518

• Гилберт Странг и Эдвин «Джед» Герман
• OpenStax

В этой главе мы используем определенные интегралы для расчета силы, действующей на плотину, когда водохранилище заполнено, и исследуем, как изменение уровня воды влияет на эту силу. Гидростатическая сила — лишь одно из многих применений определенных интегралов, которые мы исследуем в этой главе. От геометрических приложений, таких как площадь поверхности и объем, до физических приложений, таких как масса и работа, до моделей роста и распада, определенные интегралы являются мощным инструментом, помогающим нам понять и смоделировать мир вокруг нас.

• 6.0: Прелюдия к приложениям интеграции

  Плотина Гувера — чудо инженерной мысли. Когда озеро Мид, водохранилище за плотиной, заполнено, плотина выдерживает большую нагрузку. Однако уровень воды в озере значительно колеблется в результате засух и различных потребностей в воде.

• 6.1: Площади между кривыми

  Точно так же, как определенные интегралы можно использовать для нахождения площади под кривой, их также можно использовать для нахождения площади между двумя кривыми. Чтобы найти площадь между двумя кривыми, заданными функциями, проинтегрируйте разность функций. Если графики функций пересекаются или область сложная, используйте абсолютное значение разности функций. В этом случае может потребоваться вычисление двух или более интегралов.

  • 6.1E: Упражнения к разделу 6.1

• 6.2: Определение объемов путем разрезания

  В этом разделе мы используем определенные интегралы для нахождения объемов трехмерных твердых тел. Мы рассматриваем три подхода — срезы, диски и шайбы — для нахождения этих объемов в зависимости от характеристик твердого тела.

  • 6.2E: Упражнения к разделу 6.2

• 6.3: Объемы вращения — цилиндрические оболочки

  В этом разделе мы рассмотрим метод цилиндрических оболочек, последний метод нахождения объема тела вращения. Мы можем использовать этот метод для тех же типов твердых тел, что и метод диска или метод шайбы; однако при использовании метода диска и шайбы мы интегрируем по оси координат, параллельной оси вращения. При методе цилиндрических оболочек интегрируем по оси координат, перпендикулярной оси вращения.

  • 6.3E: Упражнения к разделу 6.3

• 6.4: Длина дуги кривой и площадь поверхности

  Длину дуги кривой можно рассчитать с помощью определенного интеграла. Длина дуги сначала аппроксимируется с использованием отрезков прямой, что приводит к сумме Римана. Принятие предела дает нам формулу определенного интеграла. Тот же процесс можно применить к функциям от y. Понятия, используемые для расчета длины дуги, можно обобщить, чтобы найти площадь поверхности вращения. Интегралы, полученные по формулам длины дуги и площади поверхности, часто трудно оценить.

  • 6.4E: Упражнения к разделу 6.4

• 6.5: Физические приложения интеграции

  В этом разделе мы рассмотрим некоторые физические приложения интеграции. Несколько физических приложений определенного интеграла распространены в технике и физике. Определенные интегралы можно использовать для определения массы объекта, если известна его функция плотности. Работу также можно рассчитать путем интегрирования силовой функции или при противодействии силе тяжести, как в задаче о насосе. Определенные интегралы также можно использовать для расчета силы, действующей на объект, погруженный в жидкость.

  • 6. 5E: Упражнения к разделу 6.5

• 6.6: Моменты и центры масс

  В этом разделе мы рассматриваем центры масс (также называемые центроидами) и центроиды при определенных условиях. Основная идея центра масс — это понятие точки баланса. Многие из нас видели исполнителей, которые крутят тарелки на концах палочек. Артисты стараются, чтобы несколько из них вращались, не позволяя ни одному из них упасть. Математически эта точка наилучшего восприятия называется центром масс тарелки. 96.6E: Упражнения к разделу 6.6 Тем не менее, мы упустили некоторые ключевые детали в предыдущих обсуждениях. Например, мы не изучали, как обращаться с экспоненциальными функциями с иррациональными показателями. Определение числа e — еще одна область, в которой предыдущее развитие было несколько неполным. Теперь у нас есть инструменты для работы с этими понятиями более математически строгим способом, и мы делаем это в этом разделе.

  • 6. 7E: Упражнения к разделу 6.7

• 6.8: Экспоненциальный рост и спад

  Одно из наиболее распространенных применений экспоненциальных функций связано с моделями роста и убывания. Экспоненциальный рост и затухание проявляются во множестве естественных приложений. От роста населения и постоянного начисления процентов до радиоактивного распада и закона охлаждения Ньютона — экспоненциальные функции встречаются в природе повсеместно. В этом разделе мы исследуем экспоненциальный рост и затухание в контексте некоторых из этих приложений.

  • 6.8E: Упражнения к разделу 6.8

• 6.9: Вычисление гиперболических функций

  Мы познакомились с некоторыми их основными свойствами гиперболических функций в разделе Введение в функции и графики. В этом разделе мы рассмотрим формулы дифференцирования и интегрирования для гиперболических функций и их обратных функций.

  • 6.9E: Упражнения к разделу 6.9

• 6.10: Обзорные упражнения главы 6

Миниатюра: Область между двумя функциями.

---

Эта страница под названием 6: Applications of Integration распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Глава

   Автор

   ОпенСтакс

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

2. Метки

   1. автор @ Эдвин «Джед» Герман
   2. автор@Гилберт Странг
   3. источник@https://openstax.