Интегралы неопределенные и определенные: Неопределённые и определённые интегралы. Методы интегрирования — методическая рекомендация. Алгебра, 11 класс.

Чем отличается определенный интеграл от неопределенного

Сегодня слово «Интеграл» можно услышать довольно часто, причем, зачастую, в самых неожиданных местах, например на биржевом канале по телевизору, или по новостям. Нередко мы слышим словосочетание «интегральные показатели» , слово «интегрированный», «интегративный» и тому подобное. Ну, по большому счету, чиновники и телеведущие, вообще, очень любят разные умные слова, правда вряд ли они понимают их истинное значение. А мы сегодня поговорим о том, что же такое интеграл, какие виды интеграла существуют и в чем их отличия.

Что такое интеграл

Интеграл- это латинское слово, которое пришло к нам из античности, и означает оно «Целый», или «Полный». То есть, ясно, что если про некий объект, например, сосуд молока говорили «интегер», это означало, что он полный, и молока в нем сколько было, столько и осталось.

Со временем это слово стали употреблять в совершенно разных дисциплинах- в философии, политике, экономике, в алгебре и геометрии. Но наиболее простую интерпретацию интегралу дает математика.

Определенный интеграл

Итак, интеграл -это некая сумма отдельных частей.  Вот наиболее простые примеры для, более четкого понимания сути этого термина:

1. Предмет — это интеграл(сумма) молекул.
2. Лист в клетку — это интеграл(сумма) клеток.
3. Солнечная система — это интеграл(сумма) солнца и планет.
4. Общество — это интеграл людей.
5. Отрезок- это интеграл (сумма) метров. Если маленький отрезок, то сантиметров, миллиметров или микроскопических отрезков.
6. Площадь какой-либо поверхности — это интеграл квадратных метров, квадратных сантиметров или миллиметров, а также микроскопических площадей.
7. Объем- это интеграл кубических метров или, как их еще называют — литров.

Что такое определенный и неопределенный интегралы?

Начнем с определенного, так как его смысл поддается пониманию легче.

Геометрия изучает площади. Например, если вы хотите поклеить дома обои, вам надо знать площадь стен, чтобы узнать, сколько обоев вы должны купить. Тогда вы просто умножаете длину стены на высоту и получаете ее площадь. В данном случае, эта площадь является интегралом квадратных метров или сантиметров, в зависимости от того, в каких единицах вы ее измеряли. Но поверхности, площадь которых нам требуется вычислить далеко не всегда имеют форму прямоугольника, квадрата, или даже круга. В большинстве случаев — это сложные фигуры с волнистыми сторонами. Наиболее распространенный пример —  площадь фигуры под кривой, имеющей уравнение y=1/x . Дело в том, что найти ее площадь при помощи обычных формул, которыми мы находим площадь квадрата, круга или даже сферы — невозможно. Для этой цели был разработан определенный интеграл.

Суть метода в том, что нашу сложную фигуру нужно разбить на очень узкие прямоугольники, настолько узкие, что высота каждых двух соседних практически равна. Ясно, что по сути, можно уменьшать толщину этих прямоугольников бесконечно, поэтому для обозначения их толщины используется размер dx. X — это координата, а приставка d — это обозначение бесконечно уменьшаемой величины.

Поэтому, когда мы пишем dx — это значит, что мы берем отрезок по оси x , длина которого очень мала, практически равна нулю.

Итак, мы уже условились, что площадь любой фигуры- это интеграл квадратных метров или любых других фигур с более мелкими площадями. Тогда наша фигура, площадь которой мы ищем, представляет собой интеграл или сумму тех бесконечно тонких прямоугольников, на которые мы ее разбили. А ее площадь- это сумма их площадей. То есть вся наша задача сводится к тому, чтобы найти площадь каждого из этих прямоугольников, а затем их все сложить- это и есть определенный интеграл.

Теперь поговорим о неопределенном интеграле. Только, для того, чтобы понять, что это такое, сначала нужно узнать о производной. Итак, начнем.

Производная — это угол наклона касательной к какому-либо графику в какой-нибудь ее точке. Иными словами — производная — это то, насколько график наклонен в данном его месте. К примеру, прямая линия в любой точке имеет один и тот же наклон, а кривая- разный, но он может повторяться. Для вычисления производной существуют специальные формулы, а процесс ее вычисления называют дифференцированием. Т.е. дифференцирование — это определение угла наклона графика в данной точке.

Таблица основных неопределенных интегралов

А для того, чтобы сделать наоборот — узнать формулу графика по углу ее наклона, прибегают к операции интегрирования, или суммирования данных обо всех точках. Интегрирование и дифференцирование- два взаимообратных процесса. Только здесь уже пользуются не тем интегралом, который был в первом пункте ( для определения площади ), а другим — неопределенным, то есть, не имеющим пределов.

Предположим, что нам известно, что производная некоей функции равна 5. 5 — это угол наклона графика  к оси х в данной точке. Тогда, проинтегрировав производную, мы узнаем, что функция этой производной, которую еще называют первообразной —  у=5х+с , где с- любое число. Для интегрирования, так же как и для дифференцирования есть специальные формулы, которые можно найти в таблицах.

Заключение

В заключение прорезюмируем, что основное отличие определенного интеграла от неопределенного — в их назначениях. Определенные интегралы используются для вычисления ограниченных параметров, таких как площадь, длина или объем, а неопределенный — при вычислении параметров, не имеющих границ, то есть функций.

Интересное видео на эту тему:

НаукаКомментировать

Интеграл – Умскул Учебник

На этой странице вы узнаете:

• Как связаны Ньютон и Лейбниц?
• Почему площадь криволинейной трапеции считается через интеграл?

Интеграл

В топ-5 страшилок по математике неизменно входит интеграл. Так ли он ужасен на самом деле? 

Если объяснять простыми словами, интеграл — это площадь фигуры под графиком функции. b f(x)dx = F(b) — F(a)\)

Для данного интеграла пределом является отрезок от a до b

Как связаны Ньютон и Лейбниц? И Ньютон, и Лейбниц, бесспорно, являются великими учеными. Как и у обычных людей, у них бывают споры. Именно такой спор и послужил названию одной из формул в математике в честь этих двух замечательных ученых. Формула Ньютона-Лейбница используется для вычисления определенного интеграла. Она была выведена Ньютоном и Лейбницем независимо друг от друга. Есть мнение, что Ньютон свою версию создал раньше Лейбница, но опубликовал позже, из-за этого и случился спор, который завершился только после смерти обоих ученых.

Формула Ньютона-Лейбница

Если функция f(x) непрерывна на промежутке [a; b], то 

где F(x) – первообразная для функции f(x),
a – нижний предел интегрирования, 
b – верхний предел интегрирования

Данная формула применяется для вычисления определенного интеграла

Пример вычисления определенного интеграла по формуле Ньютона – Лейбница:

Интеграл для нахождения площади фигуры

Представим, что нам нужно посчитать расстояние, пройденное автомобилем с непостоянной скоростью в промежуток времени [a; b]. b f(x)dx\)

Почему площадь криволинейной трапеции считается через интеграл? Чтобы понять это, разобьем фигуру на конечное число узких прямоугольных столбцов.  Найдем общую площадь, умножив высоту каждого столбика на его ширину и сложив все полученные значения, такая площадь будет приблизительной.  Если разделить данную фигуру на большее количество столбиков, только уже меньших по ширине, получим более точное значение. Повторять такое действие можно до бесконечности, следовательно, ширина будет стремиться к нулю, а количество прямоугольников — к бесконечности.  Сумму такого количества прямоугольников запишем в виде предела при количестве прямоугольников, стремящемся к бесконечности. При таких условиях рассматриваемая сумма площадей сходится к пределу, описываемому следующим образом , и равна какому-то числу.

А если фигура расположена под осью абсцисс, для вычисления площади фигуры нужно добавить минус к изначальной формуле. 5 3dx\)

1. 3
2. 5
3. 12
4. 14

Задание 2.
Вычислите площадь фигуры ограниченной \(y = \sin x, x = 0,  x = \frac{\pi}{2}\)

1. 1
2. 0
3. 1,5
4. 2

Задание 3.
Вычислите площадь фигуры ограниченной y = 2x² — 5, x = -1,  x = 1

1. 9
2. \(8\frac{2}{3}\)
3. \(\frac{20}{3}\)
4. 8

Задание 4.
Вычислите площадь фигуры ограниченной y = x² — 3 и y = -2x² + 9

1. 32
2. 18
3. 24
4. 2

Ответы:  1. – 3; 2. – 1; 3. – 2; 4. – 1

Неопределенные интегралы

Дифференцирование в математическом анализе неразрывно связано с интегрированием. Эти обратные друг другу действия — две стороны одной медали. Задача вычисления неопределенного интеграла обратна задаче нахождения производной функции. Неопределенный интеграл имеет также название первообразной, которое по ряду причин используется реже. Для вычисления неопределенных интегралов в среде MathCAD используется оператор, который можно легко найти на панели Calculus. Под знаком интеграла пользователь должен ввести функцию, для которой он хочет найти первообразную, а после знака дифференциала — переменную, по которой будет производиться интегрирование. Как видите, и здесь MathCAD верен себе, то есть дает пользователю возможность использовать, опять-таки, знакомые по математическому анализу обозначения неопределенных интегралов. Нужно отметить также, что для неопределенных интегралов необходимо применять символьное вычисление выражений, то есть знак “стрелочки”, а не знак равенства.

Следует, впрочем, помнить, что многие интегралы просто принципиально не выражаются в элементарных функциях. В том случае, если вы подсунули MathCAD’у один из таких весьма распространенных интегралов, ситуация может иметь два различных финала: либо MathCAD успешно проинтегрирует выражение и выдаст результат с использованием каких-либо специальных функций, либо же честно признается, что его такое интегрировать не учили.

Во втором случае вы увидите после “стрелочки”, стоящей за интегралом, запись вида indef_int(f(x), x). Естественно, вместо f(x) и x будут соответственно стоять подынтегральная функция и та переменная, по которой вы хотели провести интегрирование. Оба возможных варианта продемонстрированы на иллюстрации ниже.

Со специальными функциями тоже все не так просто. Синтаксис, используемый для их записи в MathCAD’е, все же несколько отличается от принятого в математике, а потому, вполне вероятно, для того, чтобы разобраться в том, что за специальные функции скрываются за той или иной записью, придется воспользоваться справочной системой среды MathCAD. Для этого нажмите F1, в появившемся окне выберите вкладку Search, в поле рядом с кнопкой Go введите имя функции, информацию по которой вам нужно найти, а затем нажмите эту самую кнопку. Среди результатов поиска может оказаться и несколько разделов, и имеет смысл просмотреть их все.

В общем-то, даже в том случае, если MathCAD поднимает белый флаг при виде неопределенного интеграла, это не значит, что его вовсе невозможно вычислить в элементарных или специальных функциях. Вполне возможно, что с помощью каких-либо преобразований вам удастся привести его к виду, пригодному для решения в MathCAD. Также имеет смысл поискать решение в старых печатных справочниках или “погуглить” в интернете. Вполне возможно, что у MathCAD’а просто не хватило творческого воображения на то, чтобы до конца “раскрутить” ваш сложный интеграл.

Неопределенные интегралы — это, конечно же, хорошо, но все же на практике куда как чаще используются интегралы определенные. И, думаю, для вас не окажется неожиданностью тот факт, что MathCAD прекрасно умеет справляться и с этим видом интегралов. Определенный интеграл, как вы понимаете, отличается от неопределенного наличием пределов интегрирования. Фактически неопределенный интеграл — это функция (первообразная подынтегральной функции), в то время как определенный интеграл — это просто какое-то число. То есть его мы можем вычислить не только аналитически, но и численно, что позволяет нам рассчитывать значения определенных интегралов даже тогда, когда первообразная рассчитана быть не может.

Оператор для расчета определенных интегралов в MathCAD’е находится на панели Calculus недалеко от оператора расчета неопределенных интегралов и отличается от него, как я уже совсем недавно говорил, наличием пределов сверху и снизу от символа интеграла. После того, как вы запишете подынтегральное выражение, переменную интегрирования и собственно пределы, можно ставить знак равенства или стрелочку для вычисления определенного интеграла. В первом случае интеграл будет вычислен численно, во втором — аналитически.

Вопрос о том, какой способ вычисления интегралов использовать: численный или аналитический, — не такой надуманный и праздный, как может сначала показаться. Дело в том, что аналитически определенные интегралы вычисляются, во-первых, точнее, а во-вторых, быстрее, нежели численно. Правда, может возникнуть ситуация, аналогичная той, которую вы можете увидеть на иллюстрации выше — то есть символьный процессор не доведет процесс вычислений до конца, а оставит интеграл в виде смеси численных значений и функций.

В применении системы MathCAD для расчета определенных интегралов есть немало тонких моментов, которые не возникали при расчете интегралов неопределенных. Особенно это касается численных методов расчета интегралов. Эти методы позволяют рассчитать даже такие интегралы, которые не поддаются аналитическому вычислению. Однако за все надо платить, а потому использование численных методов интегрирования способно приводить к значительным погрешностям в результате, что, сами понимаете, при решении весьма значительного по своей распространенности класса задач не просто нежелательно, а часто даже совершенно недопустимо.

Сообщество Экспонента

• вопрос
• 22.09.2022

Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое

Коллеги, добрый день.   Необходимо использовать corrcoef, а массивы разной длины.   Как сделать кол-во элементов одинаково?

Коллеги, добрый день.   Необходимо использовать corrcoef, а массивы разной длины.   Как сделать кол-во элементов одинаково?

8 Ответов

• вопрос
• 20.09.2022

Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…

• MATLAB

20.09.2022

• Публикация
• 15.09.2022

Системы управления, Другое

Видел видос на канале экспоненты по созданию топливной системы.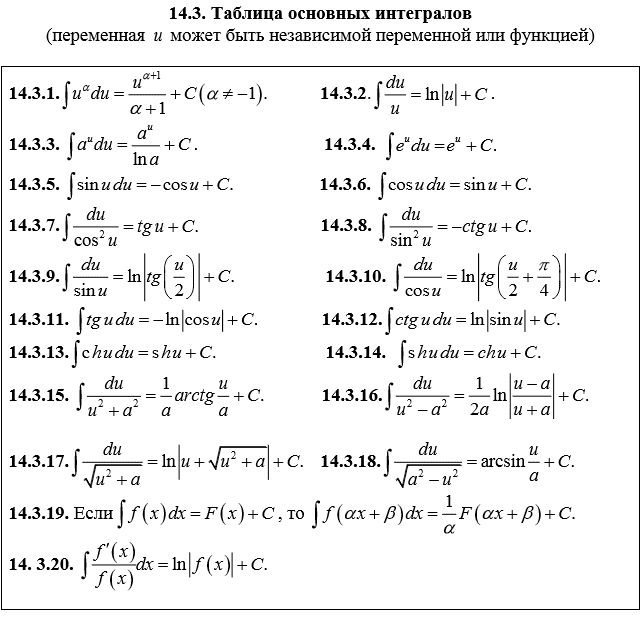 Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…

Моделирование гидравлических систем в simulink

• Публикация
• 10.09.2022

Системы управления, Электропривод и силовая электроника, Другое

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.

• Публикация
• 24.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                                                          &. ..

Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.

• вопрос
• 23.08.2022

Математика и статистика, Радиолокация, Цифровая обработка сигналов

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

4 Ответа

• ЦОС
• цифровая обработка сигналов

23.08.2022

• Публикация
• 23.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                                                          &…

Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.

• Публикация
• 16.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                      

Здесь собрана литература по методам множественного доступа с пространственным разделением.

• вопрос
• 22.07.2022

Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1. txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

2 Ответа

• чтение

22.07.2022

• вопрос
• 17.07.2022

Математика и статистика, Цифровая обработка сигналов

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

• MATLAB
• Signal Processing

17.07.2022

Неопределенный и определенный интеграл — презентация на Slide-Share.ru 🎓

1

Первый слайд презентации: Неопределенный и определенный интеграл

Разработано преподавателем математики Проскуряковой И. С.

Изображение слайда

2

Слайд 2: Цели и задачи урока:

Дать понятие неопределенного интеграла И зучить основные свойства неопределенного интеграла Научить находить неопределенный интеграл Дать понятие определенного интеграла Ф ормула Ньютона-Лейбница Изучить основные свойства определенного интеграла Геометрический смысл определённого интеграла

Изображение слайда

3

Слайд 3

Определение: Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если для всех x из этого промежутка

Изображение слайда

4

Слайд 4: Основное свойство первообразных

Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также является первообразной функции f(x).

Изображение слайда

5

Слайд 5: Неопределенный интеграл

Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается где C – произвольная постоянная Символ  – знак неопределенного интеграла, означает операцию интегрирования заданной функции, которая называется подынтегральной функцией – подынтегральное выражение x – переменная интегрирования

Изображение слайда

6

Слайд 6: Немного истории

«Интеграл» – латинское слово integro «восстанавливать» или integer – «целый». Одно из основных понятий математического анализа, возникшее в связи потребностью измерять площади, объемы, отыскивать функции по их производным. Впервые это слово употребил в печати шведский ученый Якоб Бернулли (1690 г.).

Изображение слайда

7

Слайд 7

Символ был введен Лейбницем (1675г.). Этот знак является изменением латинской буквы S – первой буквы слова summa.

Изображение слайда

8

Слайд 8: В развитии интегрального исчисления приняли участие русские математики:

В.Я. Буняковский (1804 – 1889) М.В. Остроградский (1801 – 1862) П.Л. Чебышев (1821 – 1894)

Изображение слайда

9

Слайд 9

Операции интегрирования и дифференцирования взаимно обратны и последовательное выполнение над некоторой функцией интегрирования и дифференцирования восстанавливает исходную функцию.

Изображение слайда

10

Слайд 10: Свойства неопределенного интеграла

Изображение слайда

11

Слайд 11: Таблица неопределенных интегралов

Изображение слайда

12

Слайд 12: Примеры:

Изображение слайда

13

Слайд 13: Определенный интеграл

1. Давайте разобьем наш отрезок на n равных частей, отметим внутри отрезка [а; b ] точки и через каждую точку проведем прямую параллельную оси ординат. Тогда наша фигура разобьется на n столбиков. Площадь трапеции будет равна сумме площадей столбиков.

Изображение слайда

14

Слайд 14

a b x y 0 В результате получим промежутки: 2. На каждом выберем произвольную точку 3. Найдем … = = формула интегральной суммы

Изображение слайда

15

Слайд 15

Опр : Если при любом разбиении отрезка [a, b] на части и при любом выборе точек на каждой части интегральная сумма стремится к одному и тому же пределу, то его называют определенным интегралом и обозначают:

Изображение слайда

16

Слайд 16: Определенный интеграл

Такой предел на самом деле существует, и для него было введено специальное обозначение и название – определенный интеграл. Важно! Определенный интеграл существует только в случае непрерывной или кусочно-непрерывной функции. Определенный интеграл от непрерывной функции y = f ( x ) на отрезке [ a ; b ] обозначается как Читается как определенный интеграл от a до бэ эф от икс дэ икс. Числа a и b – пределы интегрирования. (Нижний и верхний пределы).

Изображение слайда

17

Слайд 17

Теорема : Если функция непрерывна на отрезке [a, b], а функция является первообразной для на этом отрезке, то справедлива формула: формула Ньютона-Лейбница

Изображение слайда

18

Слайд 18

Изображение слайда

19

Слайд 19: Основные свойства определенного интеграла

Изображение слайда

20

Слайд 20: Основные свойства определенного интеграла

а b с

Изображение слайда

21

Слайд 21: Определенный интеграл

Пример. Вычислить определенный интеграл Решение. Первообразной для служит Воспользуемся формулой Ньютона – Лейбница Ответ: 31/5 ,

Изображение слайда

22

Слайд 22

Пример:

Изображение слайда

23

Слайд 23: Геометрический смысл определенного интеграла

Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:

Изображение слайда

24

Слайд 24: Вычисление площадей

0 у х 1 3 2 6 Пример. Вычислить площадь фигуры, ограниченной линиями y = 2x, x=1, x=3. Решение. Ответ: 8 кв.ед.

Изображение слайда

25

Слайд 25: Пример. Вычислить площадь фигуры, ограниченной графиком функции y = cos ( x ) на отрезке [0;π/2]

Решение. Давайте построим график косинуса на нашем отрезке Площадь полученной фигуры вычисляется с помощью определенного интеграла, гда a =0, b = π/2, f ( x )= cos ( x ) Ответ: 1

Изображение слайда

26

Слайд 26

0 x π – π 1 -1 y Ответ: 2 кв.ед

Изображение слайда

27

Слайд 27

Домашнее задание: 1. 7. 2. 8. 3. 4. 9. 5. 6.

Изображение слайда

28

Последний слайд презентации: Неопределенный и определенный интеграл

10.Вычислить определенный интеграл 11. Вычислить площадь фигуры, ограниченной функцией y = sin ( x ) на отрезке [2 π;3π]. 12. Вычислить площадь фигуры, ограниченной линиями

Изображение слайда

Конспект занятия “Неопределенный и определенный интегралы, их свойства” | План-конспект по алгебре на тему:

(Лекция) Тема  Неопределенный и определенный интегралы и  их свойства.

Цель:

Обучающая:

 Студент должен знать:

• Определение первообразной  функции
• Определение неопределенного интеграла
• Свойства неопределенного интеграла
• Таблицу неопределенных интегралов
• Формулу Ньютона – Лейбница

 Студент должен уметь:

• Применять формулу Ньютона – Лейбница

Воспитательная: прививать познавательность, заинтересованность изучаемым материалом, воспитывать ответственность и исполнительность.

 Развивающая: развитие логического мышления, памяти, речи, познавательного интереса.

  Оснащение занятия: мел, доска.

Технологическая карта занятия.

№	Содержание этапов занятия	время
1.	Организационный момент	2’
2.	Тема, цели, актуализация, план лекции	3’
3.	Изучение нового материала: Первообразная функции и неопределенный интеграл Основные свойства неопределенного интеграла Таблица основных интегралов Простейшие способы интегрирования Понятие определенного интеграла Свойства определенного интеграла Формула Ньютона – Лейбница Применение определённого интеграла для вычисления площадей плоских фигур	70′
4.	Закрепление по ходу лекции	10’
5.	Подведение итогов, обобщение	3’
6.	Домашнее задание	2’

1. Первообразная функция и неопределенный интеграл.

 Существует действие, обратное дифференцированию – интегрирование, т.е. нахождение функции F(x) по известной ее производной  или дифференциалу f(x)dx.

 F(x) – первообразная функции f(x)

Совокупность первообразных F(x)+c для данной функции f(x) или данного дифференциала f(x)dx называют неопределенным интегралом от функции f(x) и обозначают

-подынтегральное выражение

 – подынтегральная функция

С – постоянная интегрирования.

 Пример:    так как  

2. Основные свойства неопределённого интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции 

 2.Дифференциал от неопределенного интеграла равен подынтегральному выражению

 3. Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому C:    

 4. Постоянный множитель  С  можно выносить за знак неопределенного интеграла:

 5. Интеграл от алгебраической суммы конечного числа функций  равен алгебраической сумме интегралов от слагаемых.

Интегралы в приводимой ниже таблице называются табличными. Их надо знать наизусть и уметь их узнавать.

3. Таблица основных интегралов.

1.                                 2.                      3.         

4.                        5.                                 6. 

  7.               8.                               9.  

   Подведение итогов, обобщение    

Домашнее задание            

Практическое занятие

Тема Неопределенный и определенный интегралы и их свойства.

Цели:

обучающая:

студент должен знать:

• определение первообразной функции;
• определение неопределённого интеграла;
• определение определённого интеграла.

студент должен уметь:

• находить неопределённый интеграл методом непосредственного интегрирования, методом замены переменной;
• вычислять определённый интеграл, применяя формулу Ньютона – Лейбница

Развивающая: развитие речи, памяти, логического мышления, внимания, познавательного интереса.

Воспитательная: воспитание самоуважения, аккуратности, трудолюбия, ответственности, дисциплинированности.

Технологическая карта практического занятия.

№	Содержание этапов занятия	время
1	Организационный момент.	2′
2	Тема, цели, актуализация, план практического занятия.	3′
3	Решение заданий	60′
4	Самостоятельная работа «Вычисление интегралов»	20′
5	Итоги практического занятия.	3′
6	Домашнее задание	2′

Найти интегралы:

1)  

2)  

     

3

4)

5)

вычислить площадь фигуры, ограниченной линиями:

     

 «Неопределенные и определенные интегралы»

Вариант 1

1) Найти неопределённый интеграл: 

2) Вычислить определённый интеграл: 

3) Найти площадь фигуры, ограниченной линиями: 

Вариант 2

1) Найти неопределённый интеграл: 

2) Вычислить определённый интеграл:

3) Найти площадь фигуры, ограниченной линиями:   

Вариант 3

1) Найти неопределённый интеграл:   

2) Вычислить определённый интеграл:

3) Найти площадь фигуры, ограниченной линиями:   

Вариант 4

1) Найти неопределённый интеграл: 

2) Вычислить определённый интеграл:

3) Найти площадь фигуры, ограниченной линиями:   

Вариант 5

1) Найти неопределённый интеграл:   

2) Вычислить определённый интеграл:

3) Найти площадь фигуры, ограниченной линиями:     

Ответы

	1	2	3
1
2
3
4
5

Разница между определенными и неопределенными интегралами [обновлено в 2022 г.

]

Последнее обновление: 20 сентября 2022 г. / Факт проверен / 3 минуты

Одна из самых важных областей математики включает исчисление. Исчисление – это способ систематического решения задач, который обычно связан с нахождением свойств или значений функций с помощью интегралов и производных.

Определенные и неопределенные интегралы

Основное различие между определенным и неопределен к нему применяются ограничения, и он дает общее решение проблемы.

Определенный интеграл функции неизвестной переменной — это представление числа, имеющего верхний и нижний пределы. Неопределенный интеграл — это представление семейства функций без ограничений.

Таблица сравнения между определенными и неопределенными интегралами

Параметр сравнения

Depanite Integrals

Indefinite Integrals

IT -ITERTALLALS

ANTERGAL

A. нижний и верхний пределы и при решении дает постоянный результат.

Неопределенный интеграл — это интеграл, в котором не применяются ограничения и к интегралу добавляется обязательная произвольная константа.

Что он представляет

Определенный интеграл представляет собой число, когда его верхний и нижний пределы постоянны.

Неопределенный интеграл — это общее представление семейства различных функций с производными f.

Применяемые пределы

Верхний и нижний пределы, применяемые в определенном интеграле, всегда постоянны.

В неопределенном интеграле нет ограничений, так как это общее представление.

Полученное решение

Значения или решения, полученные из определенных интегралов, являются постоянными, однако они могут быть как положительными, так и отрицательными.

Решение неопределенного интеграла является общим решением, и к нему добавляется постоянное значение, которое обычно обозначается C.

Используется для

Определенный интеграл широко используется в физике и технике. Некоторые из областей использования определенного интеграла включают вычисление значений силы, массы, работы, площадей между кривыми, объемов, длины актов кривых, площадей поверхностей, моментов и центра масс, экспоненциального роста и затухания и т. д.

Неопределенные интегралы используются в таких областях, как бизнес, науки, включая инженерию, экономику и т. д. Они используются в тех областях, где требуется общее решение проблемы.

Что такое определенный интеграл?

Определенный интеграл определяется как представление числа, которое дает постоянный результат. Определенный интеграл всегда имеет верхний предел и нижний предел.

Решение может быть как положительным, так и отрицательным. Решение, полученное из определенного интеграла, всегда лежит в определенной области.

Некоторые области, где используются определенные интегралы, включают расчет работы, силы, массы, площадей, площадей поверхности, площади между кривыми, длины дуг, моментов, центра масс, экспоненциального роста и затухания и т. д.

Что неопределенный интеграл?

Неопределенный интеграл определяется как интеграл без ограничений. Неопределенный интеграл — это представление семейства различных функций, имеющих производную f.

Решение, полученное при решении неизвестной функции неопределенного интеграла, является обобщенным решением и, следовательно, в нем также есть переменные. Площадь решения неопределенного интеграла не указывается.

Неопределенные интегралы используются там, где требуется общее решение задачи. Неопределенные интегралы используются в бизнесе, науке, технике, экономике и т. д.

Основные различия между определенным и неопределенным интегралом

1. Определенный интеграл можно определить как интеграл, который имеет пределы, с другой стороны, неопределенный интеграл можно определить как интеграл без ограничений.
2. Определенный интеграл — это представление числа, когда оно имеет постоянные верхний и нижний пределы, тогда как неопределенный интеграл — это представление общего решения для семейства функций, имеющих производную f.

Заключение

Два типа интегралов имеют свои свойства и функции, которые играют важную роль при решении задач. Если сначала решить определенный интеграл, используя неопределенные интегралы, а затем применяя ограничения, то он может иметь некоторые разрывы.

Ссылки

1. https://www.tandfonline.com/doi/abs/10.1080/10652469.2014.1001385
2. https://www.koreascience.or.kr/article/JAKO2500931
   1.page

Найдите «Спроси любую разницу» в Google. Оцените этот пост!

[Всего: 0]

Один запрос?

Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы он был вам полезен. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/семьей. SHARING IS ♥️

Содержание

сообщить об этом объявлении

5.5: Неопределенные интегралы и правило подстановки

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5481

Цели обучения

• Применение основных формул интегрирования.
• Объясните значение теоремы о чистом изменении.
• Используйте теорему о чистых изменениях для решения прикладных задач.
• Применить интегралы от нечетных и четных функций.

В этом разделе мы используем некоторые основные формулы интегрирования, изученные ранее, для решения некоторых ключевых прикладных задач. Важно отметить, что эти формулы представлены в терминах неопределенных интегралов. Хотя определенные и неопределенные интегралы тесно связаны между собой, следует помнить о некоторых ключевых различиях. Определенный интеграл — это либо число (когда пределы интегрирования — константы), либо отдельная функция (когда один или оба предела интегрирования — переменные). Неопределенный интеграл представляет собой семейство функций, каждая из которых отличается на константу. По мере того, как вы будете лучше знакомиться с интегрированием, вы почувствуете, когда использовать определенные интегралы и когда использовать неопределенные интегралы. Вы, естественно, выберете правильный подход к данной проблеме, не слишком задумываясь об этом. Однако до тех пор, пока эти концепции не закрепятся в вашем сознании, тщательно подумайте, нужен ли вам определенный интеграл или неопределенный интеграл, и убедитесь, что вы используете правильную запись, основанную на вашем выборе. 92 – 3x\справа) \, dx = −\frac{10}{3} \nonumber \]

Теорема о чистом изменении

Теорема о чистом изменении рассматривает интеграл скорости изменения . В нем говорится, что при изменении количества новое значение равно первоначальному значению плюс интеграл скорости изменения этого количества. Формула может быть выражена двумя способами. Второй более знаком; это просто определенный интеграл.

Теорема о чистом изменении

Новое значение изменяющейся величины равно первоначальному значению плюс интеграл скорости изменения: 9b_aF'(x)dx=F(b)−F(a). \label{Net2} \]

Вычитание \(F(a)\) из обеих частей уравнения \ref{Net1} дает уравнение \ref{Net2}. Поскольку это эквивалентные формулы, какую из них мы используем, зависит от приложения.

Значение теоремы о чистом изменении заключается в результатах. Чистое изменение может быть применено к площади, расстоянию и объему, и это лишь некоторые из приложений. Чистое изменение учитывает отрицательные величины автоматически, без необходимости писать более одного интеграла. Чтобы проиллюстрировать это, давайте применим теорему о чистом изменении к скорость функция, результатом которой является смещение.

Мы рассмотрели простой пример этого в разделе «Определенный интеграл». Предположим, что автомобиль движется прямо на север (в положительном направлении) со скоростью 40 миль в час между 14:00 и 14:00. и 16:00, затем машина движется на юг со скоростью 30 миль в час между 16:00 и 16:00. и 17:00 Мы можем изобразить это движение, как показано на рисунке \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\): График показывает зависимость скорости от времени для заданного движения автомобиля.

Как и раньше, мы можем использовать определенные интегралы для расчета чистого перемещения, а также общего пройденного расстояния. 95_430\,дт=80+30=110. \nonumber \]

Таким образом, между 14:00 и 17:00 машина проехала в общей сложности 110 миль.

Подводя итог, чистый водоизмещение может включать как положительные, так и отрицательные значения. Другими словами, функция скорости учитывает как расстояние вперед, так и расстояние назад. Чтобы найти чистое смещение, проинтегрируйте функцию скорости по интервалу. С другой стороны, общее пройденное расстояние всегда положительно. Чтобы найти общее расстояние, пройденное объектом независимо от направления, нам нужно проинтегрировать абсолютное значение функции скорости. 92}{2}−5(3)\right]−0=\frac{27}{2}−15=\frac{27}{2}−\frac{30}{2}=−\frac{3 {2}. \nonumber \]

Чистое водоизмещение равно \( −\frac{3}{2}\) м (рис. \(\PageIndex{2}\)).

Рисунок \(\PageIndex{2}\): График показывает зависимость скорости от времени для частицы, движущейся с линейной функцией скорости.

Пример \(\PageIndex{3}\): определение общего пройденного расстояния

Используйте пример \(\PageIndex{2}\) для нахождения общего расстояния, пройденного частицей, в соответствии с функцией скорости \(v(t) =3t−5\) м/с за интервал времени \([0,3].\)

Решение

Общее пройденное расстояние включает как положительные, так и отрицательные значения. Следовательно, мы должны проинтегрировать абсолютное значение функции скорости, чтобы найти общее пройденное расстояние.

Чтобы продолжить пример, используйте два интеграла, чтобы найти общее расстояние. Сначала найдите \(t\)-пересечение функции, так как именно там происходит деление интервала. Приравняйте уравнение к нулю и решите относительно \(t\). Таким образом,

\[ \begin{align*} 3t−5 &=0 \\[4pt] 3t &=5 \\[4pt] t &=\frac{5}{3}. \end{выравнивание*}\] 94}{4}\right]−0 \\[4pt] &=10−\frac{16}{4} \\[4pt] &=6. \end{align*} \nonumber \]

Таким образом, моторная лодка использует \(6\) галлонов бензина за \(2\) часа.

Пример \(\PageIndex{5}\): Начало главы: Iceboats

Как мы видели в начале главы, лучших гонщика на ледяных лодках могут развивать скорость, в пять раз превышающую скорость ветра. Однако Эндрю – средний ледоход, поэтому он развивает скорость, равную только удвоенной скорости ветра.

Рисунок \(\PageIndex{3}\): (кредит: модификация работы Картера Брауна, Flickr)

Предположим, что однажды утром Эндрю выводит свой ледоход, когда все утро дует легкий бриз со скоростью \(5\) в час. Однако, когда Эндрю настраивает свою ледяную лодку, ветер начинает усиливаться. В течение первых получаса его катания на льдине скорость ветра увеличивается в соответствии с функцией \(v(t)=20t+5.\). Во вторые полчаса прогулки Эндрю остается стабильным на скорости \(15\) миль в час. Другими словами, скорость ветра определяется как

\[ v(t)=\begin{cases}20t+5, & \text{for } 0≤t≤\frac{1}{2}\\15, & \text{for} \frac{1}{2}≤t≤1\end{cases} \nonumber \] 91_{1/2} \\[4pt]
&=\left(\frac{20}{4}+5\right)−0+(30−15) \\[4pt]
&=25. \end{align*}\]

Эндрю находится в 25 милях от начальной точки через 1 час.

Упражнение \(\PageIndex{3}\)

Предположим, что вместо того, чтобы оставаться устойчивым в течение вторых получасов прогулки Эндрю, ветер начинает стихать в соответствии с функцией \(v(t)=−10t+ 15.\) Другими словами, скорость ветра определяется как

\[ v(t)=\begin{cases}20t+5, & \text{for } 0≤t≤\frac{1}{2} \\−10t+15, &\text{для } \frac{1}{2}≤t≤1\end{случаев}. \номер\]

В этих условиях, как далеко от исходной точки находится Андрей через 1 час?

Подсказка

Не забывайте, что ледяная лодка Эндрю движется в два раза быстрее ветра.

Ответить

\(17,5\) миль

Интегрирование четных и нечетных функций

Мы видели в разделе «Функции и графики», что четная функция — это функция, в которой \(f(−x)=f(x)\) для всех \(x\) в области — то есть график кривой не изменится при замене \(x\) на \(−x\). Графики четных функций симметричны относительно оси \(y\). нечетная функция – это функция, в которой \(f(-x)=-f(x)\) для всех \(x\) в области, а график функции симметричен относительно начала координат.

Интегралы четных функций, когда пределы интегрирования от \(−a\) до \(a\), включают две равные площади, потому что они симметричны относительно оси \(y\). Интегралы нечетных функций, когда пределы интегрирования равны \([−a,a],\), оцениваются как нуль, потому что площади выше и ниже оси \(x\) равны.

Интегралы четных и нечетных функций 98−2)\,dx\) и убедиться в справедливости формулы интегрирования четных функций.

Решение

Симметрия показана на графиках на рисунке \(\PageIndex{4}\). На графике (а) показана область под кривой и над осью \(x\). Нам нужно сильно увеличить этот график, чтобы увидеть регион. На графике (b) показана область над кривой и под осью \(x\). Знаковая область этой области отрицательна. Оба представления иллюстрируют симметрию относительно оси \(y\) четной функции. У нас есть 92_{0}=\frac{512}{3}−4=\frac{500}{3} \nonumber \]

Так как \( 2⋅\frac{500}{3}=\frac{1000}{ 3},\) мы проверили формулу для четных функций на данном конкретном примере.

Рисунок \(\PageIndex{4}\): На графике (a) показана положительная площадь между кривой и осью \(x\), тогда как на графике (b) показана отрицательная площадь между кривой и \(x\) \)-ось. Оба вида показывают симметрию относительно оси \(y\).

Пример \(\PageIndex{7}\): интегрирование нечетной функции

Вычисление определенного интеграла от нечетной функции \(−5 \sin x\) на интервале \([−π,π].\) 94\,дх.\)

Подсказка

Интегрировать четную функцию.

Ответить

\(\dfrac{64}{5}\)

Основные понятия

• Теорема о чистом изменении утверждает, что при изменении количества конечное значение равно первоначальному значению плюс интеграл скорости изменения. Чистое изменение может быть положительным числом, отрицательным числом или нулем.
9b_aF'(x)\,dx=F(b)−F(a) \nonumber \]

Глоссарий

Теорема о чистом изменении

если мы знаем скорость изменения количества, теорема о чистом изменении говорит, что будущее количество равно первоначальному количеству плюс интеграл скорости изменения количества

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Показать страницу TOC

   нет

2. Метки

   На этой странице нет тегов.

Обзор исчисления AP: неопределенные интегралы – Блог Magoosh

Шон Олт, , 27 января 2017 г., , AP

Неопределенные интегралы составляют значительную часть экзаменов AP Calculus AB и BC. В этой обзорной статье мы выделяем несколько концепций и методов, с которыми вам необходимо ознакомиться.

Что такое неопределенные интегралы?

Есть два вида интегралов, определенные и неопределенные интегралы. В этой статье обсуждаются только неопределенные интегралы. Более общий обзор, включая информацию об определенных интегралах, можно найти в этом обзоре интегралов.

Неопределенный интеграл функции f является наиболее общей первообразной функции f .

Здесь функция F является любой частной первообразной для f . То есть F  ^‘ ( x ) = f ( x ). Например, F ( x ) = x ² является производной для f ( x ) = 2 х , так как ( х ² )’ = 2 х .

C – это константа интегрирования . Он обозначает любую константу и должен быть частью вашего ответа на неопределенный интеграл.

Например,

Что делать с ” + 

C  ” В любом случае?

Причина, по которой нам нужно добавить это «+  C  », заключается в том, что мы можем описать абсолютно каждую первообразную для f . Помните правило производной для постоянных функций:

Следовательно, если существует конкретная функция F ( x ) такая, что F  ‘( x ) = f ( x ), то для любой константы C

, 0

Таким образом, наиболее общая производная от f ( x ) будет F ( x ) + C .

Неопределенные интегральные методы

Почти все знают, что нельзя забивать гвоздь отверткой. И молотки не помогают при забивании шурупов. Точно так же вы должны знать, что каждая неопределенная интегральная задача требует своего набора инструментов.

Мы обсудим несколько инструментов интегрирования, в том числе основные правила первообразных, подстановку, интегрирование по частям и неполные дроби. Другие более продвинутые инструменты могут быть рассмотрены в будущих статьях Magoosh.

Кроме того, важно понимать, что каждая техника требует некоторой практики, прежде чем вы действительно сможете овладеть ею. Не рассчитывайте стать экспертом в первый же день.

Основные антипроизводные правила

Эти правила на самом деле просто производные правила в обратном порядке. Вот список основных первообразных правил.

Замена

Правило замены , или, как его чаще называют, u -подстановка, является правилом, которое «обращает» правило цепочки.

Это правило помогает, когда подынтегральная функция является композицией двух функций. То есть, если есть функция внутри другая функция. Например, мы определили бы (5 x + 1) ⁸ как композицию функций u = 5 x + 1 и f ( u ) = u 8 90 Итак, если бы нам нужно было узнать неопределенный интеграл от (5 x + 1) ⁸ , мы могли бы использовать подстановку.

шагов для замены

Замена может быть затруднена, поскольку формула требует специальной настройки. Однако, если вы будете следовать шагам, описанным ниже, то вы обязательно будете делать это правильно каждый раз.

1. Определите часть функции, которую вы пытаетесь заменить, и запишите ее: u = g ( x ). Может быть неочевидно, что выбрать, поэтому сначала не бойтесь проб и ошибок.
2. Возьмите дифференциал вашей замены. То есть найдите производную от g и запишите ее в виде du = g  ‘( x ) dx .
3. Замените оба u и du в исходный интеграл. Это может включать решение дифференциала для dx , а затем замену dx в интеграле.
4. Если новый интеграл включает только u и du , то упрощаем и интегрируем стандартными методами.
5. Наконец, подставьте u = g ( x ) обратно, чтобы ваш ответ был выражен исходной переменной x .

Использование правила подстановки

Сначала мы должны решить, что заменить. Опыт подсказывает нам искать выражения в скобках.

Не забудьте взять дифференциал. Я считаю полезным решить для dx .

Теперь можно заменить 5 x + 1 на u и dx на (1/5) du . Затем интегрируйте и, наконец, снова подключите u = 5 x + 1 .

Интеграция по частям

Интегрирование по частям (IBP) — это мощный метод, который можно использовать, когда в подынтегральном выражении присутствуют определенные виды продуктов. На самом деле, вы можете думать о IBP как о способе «обратить» правило продукта.

Предположим, что u и v являются дифференцируемыми функциями от x . Тогда формула IBP утверждает, что:

Пример использования IBP

Обычно мы используем IBP, когда в подынтегральном выражении есть произведения степеней x , экспоненциальные функции и/или тригонометрические функции.

Здесь мы выберем u = 3 x , и dv = cos x dx . Опять же, наш выбор определяется опытом. Если бы вы выбрали функции наоборот, то интеграл усложнился бы.

Теперь найдите du , взяв производную, и v , проинтегрировав.

Далее мы используем формулу IBP, чтобы переписать исходный интеграл другим способом. Попробуйте отследить, где u , v , du и dv появляются в задаче. ( Подсказка: Они имеют цветовую маркировку. )

Частичные дроби

Наконец, что не менее важно, давайте поговорим о методе частичных дробей (PF). Мы можем использовать PF всякий раз, когда подынтегральное выражение представляет собой рациональную функцию , знаменатель которой имеет степень не менее 2. Основная идея состоит в том, чтобы разбить дробь на сумму более простых дробей.

В этом коротком обзоре не хватит времени, чтобы объяснить все детали. Так что, если вам интересно узнать больше, ознакомьтесь с этой статьей.

Вместо этого давайте посмотрим на краткий пример техники в действии.

Ключ в том, чтобы использовать свои навыки алгебры, чтобы разложить знаменатель на множители и разделить на две дроби, находя неизвестные константы в каждом числителе.

Можно определить, что A = -2 и B = 3 в этом примере. Опять же, поскольку эта статья является всего лишь обзором, мы оставляем вам некоторые детали.

Теперь мы можем полностью решить задачу.

Резюме

На экзаменах AP по математическому анализу встречаются задачи на неопределенные интегралы самых разных типов. Помните, что неопределенный интеграл — это наиболее общая первообразная функции.

Среди широкого спектра доступных методов большинство проблем можно решить одним или несколькими из следующих методов.

• Основные формулы первообразных, включая правило степени и правила для специальных видов функций (таких как тригонометрические и экспоненциальные).
• Замена
• Интеграция по частям
• Частичные дроби

После длительной практики вы сможете выбрать наилучший метод для каждой интегральной задачи. Как и у хорошего плотника, использование правильного инструмента облегчает работу. Возможно, вы даже получите удовольствие от решения неопределенных интегралов!

Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!

Автор

Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!

Расчет AP

← Предыдущий

Следующий →

Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно!

Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели управления Magoosh. Спасибо!

Интегралы, определенные и неопределенные, а также пределы

Путь:   физические идеи > основы > Исчисление >

Интегрировать . Переходный глагол.  Кому указать всю; дать сумму или общее количество; как, интегрирующий анемометр, который указывает или регистрирует все действие ветер в заданное время. [Из словаря Вебстера 1913 года]

Когда мы интегрируем функцию, находим площадь под ее кривой. Как обозначение подразумевает, что при обычном интегрировании по Риману мы выполняем операцию разрезая регион на множество частей и суммируя площади всех их.

A Little More Background: Definite versus Indefinite Integrals

Figure 1a: Definite integral

Figure 1b: Вычисление интеграла

В нашем определении интеграла мы мало говорили о конечных точках области, по которой мы находим площадь. Область интегрирования хорошо определена только для определенного интеграла , для которого определены границы (рис. 1а).

Как мы уже говорили ранее, нотация дает нам рецепт для вычисления значения. Как показано на рисунке 1b, мы делим область на панели , каждая dx единиц ширины, найдите площадь каждой, умножив f(x) для панели на dx , и сложите их.

Конечно значение f(x) обычно варьируется по ширине каждой панели; мы скажем больше о что позже на странице. Но для целей понимания процесса, мы можем просто представить, что dx настолько малы, что f не различаются на каждой панели — или различаются настолько незначительно, что мы можем игнорировать это.

Рисунок 2: Неопределенный интеграл

Если границы не указаны, то интеграл неопределенный , и он уже не соответствует конкретному числовому значению (рисунок 2). В этом случае, хотя мы и не можем преобразовать интеграл в действительное число, мы все же можем спросить, какую функцию представляет интеграл, если принять аргумент функции за конечное значение региона интеграции. Например, неопределенный интеграл от 1 представляет собой функцию x . Однако, поскольку мы никогда не говорили, с чего мы начали интегрирование, общая площадь “слева” не определена; Это показано на рисунке 2 «затуханием» области, область которой мы измерение.

Чтобы использовать неопределенные интегралы в уравнениях, необходимо допустить неопределенное расширение «влево», и это делается путем добавления неопределенного постоянная интегрирования к результату. Таким образом, если немного развить наш тривиальный пример выше,

       

, где “ k ” не определено. В физической задаче значение k обычно определяется ограничениями задачи.

Подробнее об интеграле как пределе

Для полноты мы должны уточнить, что подразумевается под формальным определением, которое мы дали для интеграла, определением (1b). Основное утверждение определения (надеюсь!) достаточно ясно; мы повторим это здесь:

(1)    

но условие на x _k заслуживает некоторого комментария. Я также нигде не определил лимиты, и хотя читатель, вероятно, знаком с этой концепцией, я должен по-прежнему говорить именно то, что я подразумеваю под этим. Я определю предел и подробнее о состоянии на x _k в этом разделе.

Сначала я определил x _k , сказав:

(2)    

, а не указав конкретную точку на каждой панели. Я мог бы, например, сказать:

(3)   

Это определило бы площадь одной панели как ее ширину, умноженную на значение f в середине панели. Но с утверждением, которое я фактически использовал, мы не знаем, как выбрать x _k на каждой панели – выбор точной точки остается неопределенным.

Причина использования (2) вместо (3) просто удобство . Из-за того, как сформулировано определение 1b, я могу сказать следующее:

Всякий раз, когда существует предел в определении 1b, интеграл Римана хорошо определен и является значением этого предела.

Если бы вместо этого я использовал выражение в (3) для установки значения x _k , мне пришлось бы сказать что-то вроде этого:

Всякий раз, когда существует предел, и интегрируемая функция ведет себя достаточно хорошо, то Интеграл Римана хорошо определен и является значением этого предела.

А тогда мне нужно будет определить, что я имею в виду под «хорошим поведением». Используя чуть менее очевидную формулировку определения, я избежать необходимости помещать дополнительные условия в определение, чтобы избежать нахождение «ложных интегралов»; для функций с плохим поведением предел просто не будет, и проблема не поднимается. мы дадим пример плохо работающей функции далее на этой странице. Но во-первых, давайте разберемся с лимитом.

Предел определен

Предел в (1)  имеет значения S ,

(4)    

тогда и только тогда, когда мы можем заставить значение суммы быть равным4 произвольно близким 4 к S просто выбрав n достаточно большой. В английском языке для любого ε>0 можно найти некоторое значение N такое, что для any n > N значение суммы будет в пределах ε от S . Символически

(5)    

Однако здесь есть одна загвоздка. Мы не сказали, как именно должно быть выбрано значение x _k ; все, что мы сказали, это то, что x _k должны лежать в пределах k-й панели. Итак, смысл — и предполагаемое значение – состоит в том, что (5) должно быть истинным независимо от того, как выбраны значения x _k  .

Верхняя и нижняя суммы

Если предел в (5) равен S для любой выбор из x значений внутри каждой панели, то, в частности, это должно быть верно для x значений, соответствующих как наименьшим , так и значениям для f внутри каждой панели. И наоборот, если верно, когда мы выбираем x так, чтобы f было максимальным в каждой панели, и это верно, когда мы выбираем x так, что f является минимумом внутри каждой панели, тогда кажется очевидным, что для должен быть верным любой выбор x x значений, для всех остальных сумм они должны лежать между этими двумя крайними значениями.

Когда мы выбираем x _k  так, чтобы f( x _k ) было максимально возможным в пределах каждой панели, мы называем результат верхней суммой .  Наоборот, если мы выберем x _k  так, что f( x _k ) как можно меньше внутри каждой панели, мы называем это нижней суммой .

Теперь мы указали, как должно быть выбрано x , и, следовательно, мы можем получить определенное значение как для верхней, так и для нижней суммы для заданного значения n . Если пределы как верхней, так и нижней суммы определены, и равны , то интеграл равен их (взаимному) пределу.

Когда пределов не существует:  Контрпример

Простым контрпримером является функция, которая равна 1 для каждого иррационального значения и нулю для каждого рационального значения:

   

Рассмотрим интеграл этой функции между нулем и 1. Как бы малы ни были панели, минимальное значение для f(x) на каждой панели равно 0, а максимальное значение равно 1 — таким образом, верхнее и меньшие суммы, как определено в предыдущем разделе, никогда не приближаются друг к другу. Другой.

На самом деле, если мы воспользуемся любым простым подходом к выбору значения f на каждой панели, мы получим значение 0 для суммы площадей панелей. Например, рассмотрим сумму:

   

Независимо от того, насколько большими мы делаем n , значение суммы остается равным нулю, поскольку точки, в которых мы оцениваем f , всегда рациональны, и поэтому каждый член сумма равна нулю. Однако нетрудно показать, что почти в каждой точке иррационально, и что на самом деле «длина», занимаемая всеми рациональные числа вместе равны нулю, так что мы каким-то образом упускаем из виду почти каждый момент, когда мы пытаемся интегрировать эту функцию.

рациональные числа счетны. (Запишите каждое рациональное значение между 0 и 1 в виде дроби, а/б. Теперь отсортируйте дроби по знаменателю . Легко видеть, что каждая дробь, которую мы можем назвать, находится на этом отсортированный список в некотором конечном месте; на самом деле произвольная дробь a/b должно появиться в списке не позднее позиции b ² .)

Итак, возьмите список всех рациональных чисел от 0 до 1.

Поместите интервал длины n /2 вокруг первого числа в списке.

Поместите интервал длиной n /4 вокруг секунды.

Продолжайте, помещая интервал длиной n /(2 ^k ) вокруг k ^-го -го члена списка.

общая длина всех интервалов равна

   

Следовательно, если выбрать n достаточно мала, мы можем сделать общую длину сколь угодно малой, но эти интервалы вместе взятые содержат все рациональные числа плюс какой-то “пух” вокруг каждого.

Таким образом, “правильный” результат интегрирования f от 0 до 1 будет единицей , а не нулем.

Страница впервые опубликована 04.11.2007

Определенные интегралы: что это такое и как их вычислить

В этой статье

1. Определение определенных интегралов

2. Определенные интегралы и неопределенные интегралы

3. Как вычислять определенные интегралы

4. Свойства определенных интегралов и ключевых уравнений

5. 3 практических упражнения и решения

Определение определенных интегралов

Что такое определенный интеграл? Определенные интегралы используются для вычисления площади между кривой и осью x на определенном интервале. (Если вам нужно повторить, см. наше руководство для начинающих по интегралам).

Если мы хотим вычислить определенный интеграл вещественнозначной функции fff по xxx на интервале [a, b], где aaa и bbb — действительные числа, а a≤ba \leq ba≤b, мы используем следующее обозначение: 9{b} f(x)dx = A∫ab​f(x)dx=A

В этих обозначениях изогнутый знак интеграла ∫\int∫ указывает на операцию взятия интеграла. Остальная часть этого обозначения состоит из трех частей:

• Подынтегральная функция f(x)f(x)f(x)

• Интегральные границы aaa и bbb, где aaa — нижняя граница, а bbb — верхняя граница. Их также называют лимитами.

• Дифференциал dxdxdx, который говорит нам, что мы интегрируем fff по переменной xxx. 9{b} f(x)dx∫ab​f(x)dx примерно так:

  Определенные интегралы и неопределенные интегралы

  Прежде чем мы узнаем, как именно решать определенные интегралы, важно понять разницу между определенными и неопределенными интегралами.

  Определенные интегралы находят площадь между кривой функции и осью x на определенном интервале, а неопределенные интегралы находят первообразную функции. Нахождение неопределенного интеграла и нахождение определенного интеграла — это операции, которые выводят разные вещи.

  Вычисление неопределенного интеграла принимает одну функцию и выводит другую функцию: первообразную функцию f (x) f (x) f (x), обозначаемую как F (x) F (x) F (x).

  Эта выходная функция сопровождается произвольной константой C и не включает нижние и верхние границы. Напротив, при вычислении определенного интеграла всегда выводится действительное число, представляющее площадь под кривой на определенном интервале. Вы можете увидеть разницу в их обозначениях ниже:

  Учитывая f(x)f(x)f(x), неопределенный интеграл отвечает на вопрос: «Какая функция при дифференцировании дает нам f(x)f(x)f(x)?» Неопределенный интеграл дает нам семейство функций FFF, так как бесконечные функции удовлетворяют этому вопросу. Таким образом, неопределенный интеграл дает нам «неопределенный» ответ. Определенный интеграл дает нам действительное число — уникальный «определенный» ответ.

  Вы можете узнать больше о разнице с этим образцом урока по неопределенным интегралам одного из наших преподавателей, доктора Ханны Фрай. 9b_a = F(b) – F(a)∫ab​f(x)dx=[F(x)]ab​=F(b)−F(a).

  Это означает, что для нахождения определенного интеграла функции на отрезке [a, b] мы просто берем разность между неопределенным интегралом функции, вычисленной при aaa, и неопределенным интегралом функции, вычисленной при bbb.

  Этот процесс можно разбить на четыре этапа:

  1. Найдите неопределенный интеграл F(x)F(x)F(x). Вы можете использовать правила интегрирования, которые вы изучили с неопределенными интегралами, чтобы помочь с этой частью.

  2. Найдите F(b)F(b)F(b). Это можно найти, подставив верхнюю границу bbb в неопределенный интеграл, найденный на шаге 1.

  3. Найдите F(а)F(а)F(а). 3-2xf(x)=4×3−2x на отрезке [1, 2]. 93-2x)dx = 12∫12​(4×3−2x)dx=12.

     Свойства определенных интегралов и ключевых уравнений

     Рассмотрим некоторые ключевые свойства определенных интегралов. Они будут полезны для решения более сложных интегральных задач. В следующих свойствах предположим, что fff и ggg — непрерывные функции, а kkk — константа.

     Правило интервала нулевой длины

     Когда a=b, длина интервала равна 0, поэтому определенный интеграл функции на [a, b] равен 0. 9{7} f(x)dx = 8∫37​f(x)dx=8

     Исследуйте отмеченные наградами курсы For-Credit от Outlier

     Outlier (от соучредителя MasterClass) собрал некоторые из лучшие в мире преподаватели, гейм-дизайнеры и режиссеры для создания будущего онлайн-колледжа.

     Ознакомьтесь с этими родственными курсами:

     Исчисление I

     Изучите курс

     Исчисление I

     Математика изменений.

     Изучить курс

     Введение в статистику

     Изучить курс

     Введение в статистику

     Как данные описывают наш мир.

     Изучить курс

     Введение в микроэкономику

     Изучить курс

     Введение в микроэкономику

     Почему маленькие решения имеют большое влияние.

     Изучение курса

     Интеграция – Определение определенного интеграла с использованием неопределенного интеграла

     Вопрос задан 9 лет, 7 месяцев назад

     Изменено 4 года, 6 месяцев назад 9b{f(t)dt}=F(b)-F(a)$$ где $F$ — любая непрерывная функция такая, что: $$(\forall t\in[a,b]\setminus C)(F'(t)\text{ существует и }F'(t)=f(t))$$ где $C$ — счетное множество. Тогда (если я правильно написал определение) можно доказать, что интеграл корректно определен.

     Некоторые неинтегрируемые по Лебегу функции интегрируемы с этим определением.

     1) Все ли интегрируемые по Лебегу функции интегрируемы по приведенному выше определению?

     2) Можно ли распространить это определение на измерения пространств? 9bf(x)=0$ (как интеграл Курцвейла–Хенстока или Лебега), поэтому единственным выбором будет постоянная $F$, но тогда $0=F'(x)=f(x)$ выполняется только вне $A$ . Таким образом, в общем случае набор исключений может быть произвольным нулевым набором. (Хуже быть не может: упомянутая Джеральдом Эдгаром теорема о дифференцировании Лебега справедлива и для интеграла Курцвейла–Хенстока.) В частности, ваш интеграл (в отличие от интеграла Курцвейла–Хенстока) не расширяет интеграл Лебега. Он даже не расширяет интеграл Римана, так как в качестве $A$ можно взять замкнутое множество. 9bf(x)\,dx=F(b)-F(a)$, если $F'(x)=f(x)$ для всех $x\in[a,b]$, кроме нулевого множества, и $ F$ — допустимая неопределенная интегральная функция. Таким образом можно получить характеристику интеграла Лебега, взяв $F$ абсолютно непрерывной. Для интеграла Курцвейла – Хенстока нужен более широкий класс функций, описание которых немного более тонкое, см., например, http://dx.doi.org/10.1007/s10587-008-0081-0.

     $\endgroup$

     $\begingroup$

     В случае, если исключительный набор $C$ пуст, я видел, что это называется 9х ф $$
     , и эта $F$, разумеется, непрерывна.