Интегрирование для чайников: Интегралы для чайников: как решать, правила вычисления, объяснение. Найти неопределённый интеграл: начала начал, примеры решений

высшая математика для чайников интегралы

Вы искали высшая математика для чайников интегралы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и высшая математика интегралы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «высшая математика для чайников интегралы».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как высшая математика для чайников интегралы,высшая математика интегралы,высшая математика интегралы для чайников,вычислить интеграл примеры решений,вычислить неопределенный интеграл примеры решений,задания интегралы,интеграл как брать,интеграл как находить,интеграл как решать,интеграл как решать примеры,интеграл матпрофи,интеграл пример,интеграл примеры,интеграл примеры решения,интегралы высшая математика,интегралы высшая математика для чайников,интегралы для чайников,интегралы для чайников как решать,интегралы для чайников примеры решения,интегралы задания,интегралы задачи,интегралы как находить,интегралы как решать,интегралы как решать примеры,интегралы неопределенные,интегралы неопределенные примеры решений,интегралы определенные примеры,интегралы примеры,интегралы примеры решения,интегралы примеры решения для чайников,интегралы примеры с решением,интегралы простые,интегралы с нуля,интегралы с нуля простым языком,интегрирование примеры,интегрирование сложной функции,интегрирование сложных функций,интегрирования примеры,как брать интеграл,как вычислить интеграл для чайников,как интегрировать,как найти неопределенный интеграл примеры,как находить интеграл,как находить интегралы,как решать интеграл примеры,как решать интегралы для чайников,как решать интегралы неопределенные,как решать интегралы определенные,как решать интегралы примеры,как решать интегралы примеры решения,как решать неопределенные интегралы,как решать неопределенные интегралы для чайников,как решать неопределенный интеграл,как решать определенные интегралы,как решать определенные интегралы примеры решения,как решать определенный интеграл,как решать первообразные,как решить интеграл определенный,как решить определенный интеграл,матпрофи интегралы,методы решения интегралов,неопределенные интегралы,неопределенные интегралы как решать,неопределенные интегралы примеры,неопределенные интегралы примеры с решением,неопределенные интегралы сложные,неопределенный интеграл для чайников,неопределенный интеграл как решать,неопределенный интеграл примеры,неопределенный интеграл примеры решений,неопределенный интеграл примеры решения,неопределенный интеграл примеры с решениями,неопределенный интеграл решения примеры,неопределенный интеграл формулы,определенные интегралы для чайников,определенные интегралы как решать,определенные интегралы примеры с решением,определенный интеграл для чайников,определенный интеграл как решать,определенных интегралов примеры с решением,первообразная примеры,первообразная примеры решения,первообразная примеры с решением,первообразные как решать,правила интегрирования неопределенного интеграла,пример интеграл,примеры интегралов,примеры интегралов неопределенных,примеры интегралов с решением,примеры интегралов с решением для студентов,примеры интегралы с решением,примеры интегрирования,примеры неопределенные интегралы,примеры неопределенных интегралов,примеры неопределенных интегралов с решением,примеры первообразных с решением,примеры решений интегралов,примеры решений неопределенный интеграл,примеры решений неопределенных интегралов,примеры решения интегралов,примеры решения интегралов неопределенных,примеры решения интегралов с ответами,примеры решения неопределенных интегралов,примеры с решением интегралов,примеры с решением неопределенных интегралов,примеры с решением определенных интегралов,примеры с решением первообразных,примеры с решениями определенный интеграл,простейшие интегралы,решение интегралов для чайников,решение интегралов определенных примеры,решение интегралов примеры,решение определенных интегралов примеры с решением,сложные неопределенные интегралы,способы решения интегралов,формулы неопределенный интеграл.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и высшая математика для чайников интегралы. Просто введите задачу в окошко и нажмите «решить» здесь (например, высшая математика интегралы для чайников).

Где можно решить любую задачу по математике, а так же высшая математика для чайников интегралы Онлайн?

Решить задачу высшая математика для чайников интегралы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

как решать, правила вычисления, объяснение. Основные свойства определенного интеграла

Словари. Энциклопедии. История. Литература. Русский язык » Литература » Определенные и неопределенные интегралы сообщение. Интегралы для чайников: как решать, правила вычисления, объяснение. Основные свойства определенного интеграла

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Изучаем понятие « интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились

Ньютон и Лейбниц , но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных , необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции

f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры.

Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

« Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

В этой статье мы перечислим основные свойства определенного интеграла. Большинство этих свойств доказываются на основе понятий определенного интеграла Римана и Дарбу .

Вычисление определенного интеграла очень часто проводится с использованием первых пяти свойств, так что мы будем при надобности на них ссылаться. Остальные свойства определенного интеграла, в основном, применяются для оценки различных выражений.

Прежде чем перейти к основным свойствам определенного интеграла , условимся, что a не превосходит b .

Для функции y = f(x) , определенной при x = a , справедливо равенство .

То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма для любого разбиения промежутка и любого выбора точек равна нулю, так как , следовательно, пределом интегральных сумм является ноль.

Для интегрируемой на отрезке функции выполняется .

Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b .

для интегрируемых на отрезке функций y = f(x) и y = g(x) .

Доказательство.

Запишем интегральную сумму функции для данного разбиения отрезка и данного выбора точек :

где и – интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.

Переходя к пределу при получим , что по определению интеграла Римана равносильно утверждению доказываемого свойства.

Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке функции y = f(x) и произвольного числа k справедливо равенство .

Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:


Пусть функция y = f(x) интегрируема на интервале X , причем и , тогда .

Это свойство справедливо как для , так и для или .

Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.

Если функция интегрируема на отрезке , то она интегрируема и на любом внутреннем отрезке .

Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.

Если функция y = f(x) интегрируема на отрезке и для любого значения аргумента , то .

Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек при будет неотрицательной (не положительной).

Следствие.

Для интегрируемых на отрезке функций y = f(x) и y = g(x) справедливы неравенства:


Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.

Пусть функция y = f(x) интегрируема на отрезке , тогда справедливо неравенство .

Доказательство.

Очевидно, что . В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо . Это двойное неравенство можно записать как .

Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке и для любого значения аргумента , тогда , где и .

Доказательство проводится аналогично.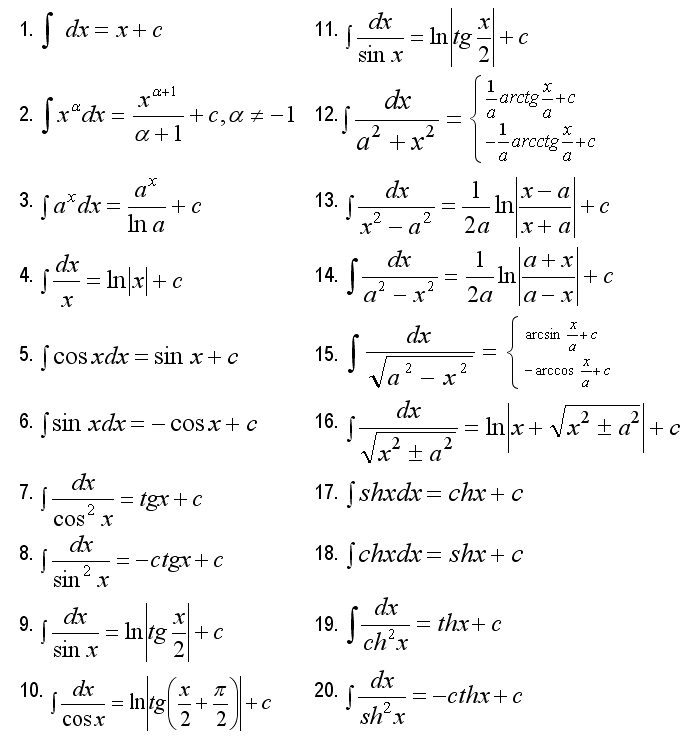 Так как m и M – наименьшее и наибольшее значение функции y = f(x) на отрезке , то . Домножение двойного неравенства на неотрицательную функцию y = g(x) приводит нас к следующему двойному неравенству . Интегрируя его на отрезке , придем к доказываемому утверждению.

Следствие.

Если взять g(x) = 1 , то неравенство примет вид .

Первая формула среднего значения.

Пусть функция y = f(x) интегрируема на отрезке , и , тогда существует такое число , что .

Следствие.

Если функция y = f(x) непрерывна на отрезке , то найдется такое число , что .

Первая формула среднего значения в обобщенной форме.

Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке , и , а g(x) > 0 для любого значения аргумента . Тогда существует такое число , что .

Вторая формула среднего значения.

Если на отрезке функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число , что справедливо равенство .

Данные свойства используются для осуществления преобразований интеграла с целью его приведения к одному из элементарных интегралов и дальнейшему вычислению.

1. Производная неопределенного интеграла равна подынтегральной функции:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

4. Постоянный множитель можно выносить за знак интеграла:

Причем a ≠ 0

5. Интеграл суммы (разности) равен сумме (разности) интегралов:

6. Свойство является комбинацией свойств 4 и 5:

Причем a ≠ 0 ˄ b ≠ 0

7. Свойство инвариантности неопределенного интеграла:

Если , то

8. Свойство:

Если , то

Фактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной , который более подробно рассмотрен в следующем разделе.

Рассмотрим пример:

Сначала мы применили свойство 5, затем свойство 4, затем воспользовались таблицей первообразных и получили результат.

Алгоритм нашего онлайн калькулятора интегралов поддерживает все перечисленные выше свойства и без труда найдет подробное решение для вашего интеграла.

Данные свойства используются для осуществления преобразований интеграла с целью его приведения к одному из элементарных интегралов и дальнейшему вычислению.

1. Производная неопределенного интеграла равна подынтегральной функции:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

4. Постоянный множитель можно выносить за знак интеграла:

Причем a ≠ 0

5. Интеграл суммы (разности) равен сумме (разности) интегралов:

6. Свойство является комбинацией свойств 4 и 5:

Причем a ≠ 0 ˄ b ≠ 0

7. Свойство инвариантности неопределенного интеграла:

Если , то

8. Свойство:

Если , то

Фактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной , который более подробно рассмотрен в следующем разделе.

Рассмотрим пример:

Сначала мы применили свойство 5, затем свойство 4, затем воспользовались таблицей первообразных и получили результат.

Алгоритм нашего онлайн калькулятора интегралов поддерживает все перечисленные выше свойства и без труда найдет подробное решение для вашего интеграла.

В дифференциальном исчислении решается задача:под анной функции ƒ(х) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F ” (x)=ƒ(х) (или дифференциал). Искомую функцию F(x) называют первообразной функции ƒ(х) .

Функция F(x) называетсяпервообразной функции ƒ(х) на интервале (а; b), если для любого х є (а;b) выполняется равенство

F ” (x)=ƒ(x) (или dF(x)=ƒ(x)dx).

Например , первообразной функции у=х 2 , х є R, является функция, так как

Очевидно, что первообразными Будут также любые функции

где С – постоянная, поскольку

Tеоpeмa 29. 1. Если функция F(x) является первообразной функции ƒ(х) на (а;b), то множество всех первообразных для ƒ(х) задается формулой F(x)+С, где С – постоянное число.

▲ Функция F(x)+С является первообразной ƒ(х).

Действительно, (F(x)+C) ” =F ” (x)=ƒ(x).

Пусть Ф(х) – некоторая другая, отличная от F(x), первообразная функции ƒ(х) , т. е. Ф ” (x)=ƒ(х). Тогда для любого х є (а;b) имеем

А это означает (см. следствие 25. 1), что

где С – постоянное число. Следовательно, Ф(х)=F(x)+С.▼

Множество всех пepвoобpaзныx функций F(x)+С для ƒ(х) называетсянеопределенным интегралом от функции ƒ(х) и обозначается символом∫ ƒ(х) dx.

Таким образом, по определению

∫ ƒ(x)dx= F(x)+C.

Здесь ƒ(х) называетсяподынтегральнoй функцией , ƒ(x)dx — подынтегральным выражением, х –переменной интегрирования , ∫ –знаком неопределенного интеграла .

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у=F(x)+C (каждому числовому значению С соответствует определенная кривая семейства) (см. рис. 166). График каждой первообразной (кривой) называетсяинтегральной кривой .

Для всякой ли функции существует неопределенный интеграл?

Имеет место теорема, утверждающая, что «всякая непрерывная на (а;b) функция имеет на этом промежутке первообразную», а следoвaтельно, и неопределенный интеграл.

Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:

d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) ” =ƒ(х).

Дeйcтвительнo, d(∫ ƒ(х) dx)=d(F(x)+С)=dF(x)+d(C)=F ” (x) dx =ƒ(х) dx

(∫ ƒ (x) dx) ” =(F(x)+C)”=F”(x)+0 =ƒ (x).

Блaгoдapя этому свойству правильность интегрирования проверяется дифференцированием. Например, равенство

∫(3x 2 + 4) dx=х з +4х+С

верно, так как (х 3 +4х+С)”=3x 2 +4.

2. Hеопpедeлeнный интеграл от диффepeнциaла некоторой функции равен сумме этой функции и произвольной постоянной:

∫dF(x)= F(x)+C.

Действительно,

3. Постоянный множитель можно выносить за знак интеграла:

α ≠ 0 – постоянная.

Действительно,

(положили С 1 /а=С.)

4. Неопределенный интеграл от aлгeбpaическoй суммы конечного числа непрерывных функций равен aлгебpaичecкoй сумме интегралов от слагаемых функций:

Пусть F”(x)=ƒ(х) и G”(x)=g(x). Тогда

где С 1 ±С 2 =С.

5. (Инвариантность формулы интегрирования).

Если, где u=φ(х) – произвольная функция, имеющая непрерывную производную.

▲ Пусть х – независимая переменная, ƒ(х) – непрерывная функция и F(x) – ее пepвoобpaзнaя. Тогда

Положим теперь u=ф(х), где ф(х) – непрерывно-дифференцируемая функция. Рассмотрим сложную функцию F(u)=F(φ(x)). В силу инвараинтности формы первого дифференциала функции (см. с. 160) имеем

Отсюда▼

Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.

Так, из формулыпутем замены х на u (u=φ(х))получаем

В частности,

Пример 29.1. Найти интеграл

где С=C1+С 2 +С 3 +С 4 .

Пример 29.2. Найти интеграл Решение:

• 29.3. Таблица основных неопределенных интегралов

Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул диффepeнциaльнoгo исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла.

Например , так как

d(sin u)=cos u . du,

Вывод ряда формул таблицы будет дан при рассмотрении основных методов интегрирования.

Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения пepвoобpaзных (т. е. интегрирования функции) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать.

Отметим, что в таблице основных интегралов переменная интегрирования и может обозначать как независимую переменную, так и функцию от независимой переменной (coгласнo свойству инвариантности формулы интeгpиpoвания).

В справедливости приведенных ниже формул можно убедиться, взяв диффepeнциaл правой части, который будет равен подынтегральному выражению в левой части формулы.

Докажем, например, справедливость формулы 2. Функция 1/u определена и непрерывна для всех значений и, отличных от нуля.

Если u > 0, то ln|u|=lnu, тогда Поэтому

Eсли u Значит

Итак, формула 2 верна. Aнaлoгичнo, провepим формулу 15:

Таблица оснoвныx интегралов

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Как работает интеграция: это просто причудливое дополнение

Самый фундаментальный смысл интеграции заключается в суммировании. И когда вы изображаете интеграцию на графике, вы можете видеть процесс суммирования как суммирование тонких прямоугольных полосок площади, чтобы получить общую площадь под этой кривой, как показано на этом рисунке.

Вы можете рассчитать заштрихованную область на приведенном выше рисунке, используя этот интеграл:

(Обратите внимание, что все здесь включает определенную интеграцию , а не неопределенная интеграция . Определенная интеграция – это когда удлиненный символ интеграции S имеет пределы интеграции: две маленькие константы или числа внизу и вверху символа. Вытянутое S без ограничений интегрирования указывает на неопределенный интеграл или первопроизводную .)

Посмотрите на тонкий прямоугольник на рисунке. Он имеет высоту f ( x ) и ширину dx (немного x ), поэтому его площадь ( длина умножить на ширина , конечно) равна f ( x ) · dx . Приведенный выше интеграл говорит вам сложить площади всех узких прямоугольных полос между a и b под кривой f ( x ). По мере того, как полосы становятся все уже и уже, вы все лучше и лучше оцениваете площадь. Сила интеграции заключается в том, что она дает вам точную площадь путем сложения бесконечного числа бесконечно тонких прямоугольников.

Независимо от того, какие крошечные биты вы суммируете — это могут быть небольшие биты расстояния, объема или энергии (или просто площади) — вы можете представить суммирование как сложение площадей тонких прямоугольных полос под изгиб. Если единицы измерения по обеим осям x и y являются единицами длины, скажем, футов , то каждый тонкий прямоугольник измеряет столько-то футов на такое-то количество футов, а его площадь — длина умножить на ширина — это некоторое число квадратных футов . В этом случае общая площадь всех прямоугольников между a и b дает вам ответ площади (хотя это не обязательно фактическая площадь под кривой, поскольку масштаб может быть другим; например, фактическая заштрихованная область на вышеприведенная цифра составляет несколько квадратных дюймов, но ваш ответ мог бы быть числом квадратных миль , если бы обе оси были размечены в милях). Дело в том, что в этом случае вы складываете площадей всех прямоугольников, и вы получите ответ площадей . Однако обычно, даже если вы суммируете площади прямоугольников, ваш ответ не будет ответом площади.

Скажем, единицы измерения по оси x – это часы ( t ), а по оси y – миль в час , тогда, поскольку скорость умножить на время равно расстояние , площадь каждого прямоугольника представляет собой расстояние, а общая площадь дает вам общее расстояние, пройденное за данный интервал времени. Или если 9Ось 0007 x обозначена в часах ( t ), а ось y – в киловаттах электроэнергии – в этом случае кривая f ( t ) дает использование энергии как функцию времени — тогда площадь каждой прямоугольной полосы ( киловатт умножить на часов ) представляет собой число киловатт-часов энергии. В этом случае общая площадь под кривой дает вам общее количество киловатт-часов потребления энергии между двумя моментами времени.

Другая возможность иллюстрируется приведенной выше лампой. Допустим, вы хотите рассчитать объем основания лампы. На рисунке ниже показано, как вы могли бы сделать это с помощью интеграции. На графике функция A ( x ) дает площадь поперечного сечения тонкого ломтика блина лампы как функцию его высоты, измеренной от нижней части лампы. Итак, на этот раз ось h помечена как дюймов (это h , как в высота от низа лампы), а y -ось помечена в квадратных дюймов , и, таким образом, каждый тонкий прямоугольник имеет ширину, измеренную в дюймах, и высоту, измеренную в квадратных дюймах. Следовательно, его площадь представляет собой дюймов , умноженных на квадратных дюймов , или кубических дюймов объема.

Эта заштрихованная область дает вам объем основания лампы.

Площадь тонкого прямоугольника на этом рисунке представляет собой объем тонкого ломтика блина лампы на высоте 5 дюймов от основания основания. Общая затененная площадь и, следовательно, объем цоколя лампы определяется следующим интегралом:

Объем = (площадь поперечного сечения) умножить на (толщину)

Это означает, что вы суммируете объемы всех тонких ломтиков блина от 0 до 15 дюймов (то есть от основания до верха основания лампы), каждый ломтик имеет объем, равный A ( ч ) (его площадь поперечного сечения) умножить на dh (его высоту или толщину).

Подводя итог — это каламбур! – математическое выражение справа от любого определенного символа интегрирования всегда означает немного чего-то, и интегрирование такого выражения означает сложение всех маленьких кусочков между некоторой начальной и некоторой конечной точками для определения суммы между двумя точками. .

Эту статью можно найти в категории:

• Исчисление ,

Как выполнить интеграцию по частям

Интеграция по частям — это интеграционная версия правила продукта для дифференцирования. Основная идея интегрирования по частям состоит в том, чтобы преобразовать интеграл, который вы не можете сделать , в простое произведение минус интеграл, который вы можете сделать . Вот формула:

Не пытайтесь пока это понять. Дождитесь следующих примеров.

Если вы помните это, вы легко можете вспомнить, что интеграл справа такой же, как интеграл слева, за исключением и и и поменялись местами.

Вот краткое описание метода.

Во-первых, вам нужно разделить подынтегральную функцию на u и dv , чтобы она соответствовала формуле. Для этой задачи выберите ln( x ) в качестве u. Затем все остальное — это dv, , а именно

Затем вы дифференцируете и , чтобы получить du , и интегрируете dv , чтобы получить и . Наконец, вы подключаете все к формуле, и вы дома.

Интеграция по частям.

Чтобы не усложнять задачу, организуйте задачи интеграции по частям с помощью рамки, подобной той, что показана на рисунке выше. Нарисуйте пустой прямоугольник 2 на 2, затем поместите u , ln( x ) в верхний левый угол и dv ,

в нижний правый угол, как показано на следующем рисунке.

Заполнение поля.

Стрелки на этом рисунке напоминают вам о дифференцировании слева и интегрировании справа. Думайте о дифференциации — более легкой вещи — как о движении вниз (как о движении под гору), а об интеграции — о более сложной вещи — как о подъеме (например, о движении в гору).

Теперь заполните поле:

Заполненное поле для

показано на следующем рисунке.

Хороший способ запомнить формулу интегрирования по частям — начать с верхнего левого квадрата и нарисовать воображаемое число 7 — поперек, а затем вниз влево, как показано на следующем рисунке. Это о-о-о-о-о-семерный мнемонический прием (понял? — «семерный» как «небесный» — ха, ха, ха, ха.)

Вспоминая, как вы рисуете семерку, вернитесь к фигуре с заполненной коробкой. . Формула интегрирования по частям говорит вам сделать верхнюю часть 7, а именно

минус интеграл от диагональной части 7,

(Кстати, этот метод гораздо проще сделать, чем объяснить.