Интересные приемы устного счета 5 класс: Приемы устного счета (5 класс) - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Некоторые приёмы устного счёта на уроках математики в 5-6 классах | Статья по математике (5, 6 класс) на тему:

Некоторые приёмы устного счёта на уроках математики в 5-6 классах.

Устные вычисления дают возможность не только быстро производить расчеты в уме, но и развивают память, культуру мысли, ее четкость, ясность и быстроту, сообразительность, умение отыскивать наиболее рациональные пути для решения поставленной цели, ясное понимание связи теории с практикой, уверенность в своих силах, помогает школьникам полноценно усваивать предметы физико-математического цикла.

Поэтому учителю математики надо обращать внимание на устный счет с того момента, когда учащиеся приходят к нему из начальной школы. Именно в среднем звене мы закладываем основы обучения математике наших воспитанников, раскрываем ее притягательные стороны. Хорошо развитые у учащихся навыки устного счета – одно из условий их успешного обучения в старших классах.

Умело поставленный и систематически проводимый устный счет развивает у учащихся способность быстро и безошибочно производить разнообразные устные вычисления. Нельзя не отметить, что отдельные приемы сокращенных вычислений, применяемые при устном счете, могут явиться дополнительным средством для закрепления математических знаний и алгебраических формул. Для того, чтобы учащиеся лучше осознали необходимость устных вычислений, их надо практиковать и при решении задач и примеров.

На уроках устный счет применяется следующих форм:

Беглый счет. При беглом счете преподаватель называет числа, говорит, какие действия надо над ними производить, а учащиеся говорят только ответ.

Беглый счет с последующей записью результата. Разница с предыдущим приемом заключается только в том, что если в первом случае учащиеся говорят ответ устно, то во втором они записывают его в тетрадях и показывают учителю.

Устный счет с предшествующей записью на классной доске чисел, даваемых для счета. Эта форма устных вычислений применяется как в том случае, когда числа, предложенные для счета, большие, так и в том случае, когда закрепляется какой-либо новый прием быстрых вычислений, при котором все внимание учащихся должно сосредоточиться не на числах, а на сущности самого приема.

Устный счет при решении задач. Учащиеся решают задачу либо устно, либо по написанным учителем на доске числовым данным задачи, либо для устного счета запоминают и содержание задачи, и числовые данные.

При устных вычислениях мысль учащихся все время работает над вопросом:

« Какой прием лучше применить в том или другом случае, чтобы как можно быстрее производить требуемые вычисления? »

Счет на пальцах

Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы – это очень наглядно и удобно.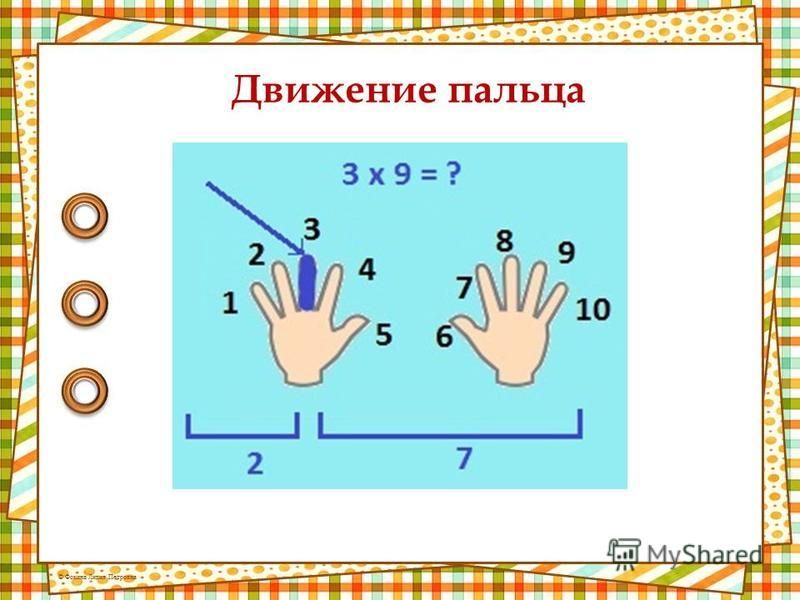 Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.

Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:

•Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.

•Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.

•Оставшееся количество пальцев слева будет соответствовать десяткам, справа – единицам. В нашем примере – 4 пальца слева и 5 справа. Ответ: 45.

Да, действительно, решение быстрое и наглядное! Но это – из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.

Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально, пока вы этим пользуетесь, и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.

Устный счет требует от учителя умелого подхода к индивидуальным особенностям каждого учащегося. Необходимо имеет в виду, что одни учащиеся при устном счете считают правильно и довольно быстро; другие быстро, но часто ошибаются; третьи хотя и верно, но довольно медленно считают; четвертые считают совсем плохо и требуют от учителя индивидуальной помощи.

Устный счет может практиковаться почти на каждом уроке математики. В зависимости от темы и материалам урока, они могут ставиться учителем в начале урока, середине или в конце.

В начале урока устный счет удобно применять тогда, когда нужно подготовить почву либо для изложения нового материала, либо для закрепления пройденных навыков.

В середине урока устный счет лучше всего проводить тогда, когда он может быть связан с проходимым или пройденным на уроке материалом.

В конце урока устный счет применяется обычно независимо от темы урока в специально оставленное для этой цели время (5-10 минут) как для упражнений в применении различных приемов быстрых вычислений, которыми учащиеся уже владеют, так и для объяснения учителем новых приемов.

Скорость вычисления как при беглом счете, так при устном решении задач всецело зависит от степени трудности примеров, от степени подготовленности детей, от их умения пользоваться приемами быстрых вычислений, от умения преподавателя вести эту работу.

Нельзя применять много различных видов упражнений на одном уроке, так как это утомляет учащихся и снижает их внимание. Практику устного счета надо развивать постоянно. Вообще надо сказать, что умело поставленный устный счет является для детей нередко чрезвычайно интересной работой, своего рода гимнастикой ума, игрой.

Для развития у учащихся умения быстро производить устные вычисления учитель должен тщательно рассматривать с детьми некоторые свойства чисел, их сочетания, способы разложения и т. д. Это обеспечит всю последующую технику быстрых вычислений.

1. Необходимо, чтобы таблицы сложения, вычитания, умножения и деления были усвоены с детьми в совершенстве.

2. Надо, чтобы дети легко и быстро находили дополнения чисел до любого большего круглого числа (т. е. кратные 10)

3. Надо научить учащихся быстро делить и умножать на 2.

4. Учащиеся должны уметь разложить любые числа по разрядам, т.е. представить их в виде суммы.

5. Ученики обязаны хорошо знать основные законы четырех арифметических действий, зависимость между компонентами и результатами действий.

6. Представить число в виде разности двух чисел.

7. Использовать при вычислениях возможность замены одних действий другими действиями.

8. Знать значение квадратов чисел до 30.

Приступая к устным вычислениям, учитель должен начинать с более легких примеров и приемов, которые по мере их усвоения усложняются.

Устный счет – очень нужный этап урока. Именно на этом этапе появляется настрой на весь урок. Устный опрос украшает урок, делает его логически стройным и интересным, способным лучшему усвоению программного материала.

Вычислять быстро, подчас на ходу – это требование времени. Числа окружают нас повсюду, а выполнение арифметических действий над ними приводит к результату, на основании которого мы принимаем то или иное решение. Понятно, что без вычислений не обойтись как в повседневной жизни, так и во время учебы в школе. Этим, кстати, объясняется столь стремительное развитие удобных калькуляторов. Тем не менее, калькулятор не может обеспечить ответ на все возникающие вопросы. Он не всегда имеется под рукой и бывает достаточно определить лишь примерный результат.

Многие навыки, сопутствующие вычислениям, неизбежно требуются и в быту, и в школьной практике. Так, нередко может потребоваться замена числа близким ему числом, например, 25% – это 0,25, т. е. четверть, сравнение чисел на основе качественных оценок.

Некоторые приемы устных вычислений по математике в 5 и 6 классах.

1. Умножение чисел, оканчивающихся нулями.

40•7 = (4•7)•10 8•60 = (8•6)•10

400•7 = (4•7)•100 4•600 = (4•6)•100

1200•50•=(12•5)•1000 120•70 = (12•7)•100

2. Умножение любого числа на двузначное путем разложения множителя на десятки и единицы.

46•12 = 46•10 + 46•2 243•31 = 234•30 + 243•1

3. Перестановка сомножителей.

2•93•5 = 2•5•93 = 10•93 4•17•25 = 17•4•25 = 17•100 125•201•8 = 201•125•8 = 201•1000

Особые приемы умножения.

Чтобы применять особые приемы умножения, необходимо уметь всякое целое число быстро устно умножить и делить на 2 и 3, а также уметь быстро устно складывать и вычитать числа в пределах сотни.

Умножение на 4 может быть сведено к двукратному последовательному умножению данного числа на 2.

48•4 = 48•2•2 157•4 = 157•2•2

Умножение на 5

42•5 = •10 = 21•10 = 210 93•5 = •10 = 465

Умножение на 6

При умножении на 6 можно применять два способа:

1) Последовательное умножение

52 • 6 = 52•2•3 = 104•3 = 312

2) Представление 6 в виде суммы 5 и 1

52 • 6 = 52 • (5+1) = 312

Умножение на 7

52 • 7 = 52 • (5+2) = 260 + 104 = 364

Умножение на 9

52 • 9 = 52 • (10-1) = 520 – 52 = 468

Умножение на 11

52 • 11 = 52 • (10+1) = 520 + 52 = 572

Умножение на 25 Умножение на 50

36 • 25 =36:4• 100 = 9 •100 = 900 52 • 50 =52:2 • 100 = 2600

Умножение двух одинаковых сомножителей, оканчивающихся на 5

Для этого достаточно число десятков помножить на число, единицей большей десятков и к произведению приписать 25.

45² = 2025 [ 4 • (4+1) = 20] 65² = 4225 [6 • 7 = 42 ]

55² = 3025 [5 • (5+1) = 30]

Можно применить умножение на 99 и 999.

Например: 52 • 99 = 52 • (100-1) = 5200 – 52 и т.д.

Устный счёт способствует развитию мыслительной деятельности учащихся. Выполнение устных упражнений развивает память, воображение, внимание, наблюдательность, умение сосредоточиться, способность воспринимать сказанное на слух, речь, точность, быстроту реакции учащихся.

Многие психологи отмечают, что устный счет способствует гармоничному развитию двух полушарий человека.

Использование устных упражнений на уроках математики в 5 – 6 классе преследует следующие цели, стоящие перед учителем при подготовке к уроку:

1.Повторение изученного материала; отработка умений и навыков применения знаний по определенной теме на практике.

2.Пропедевтика нового материала (т.е. система заданий и упражнений для подготовки к изучению нового материала).

3.Развитие вычислительных умений и навыков.

Понимая важность использования устных упражнений, учитель, работающий в 5 – 6 классе, должен не только грамотно спланировать содержание устной работы, но и форму ее проведения. Устная работа должна быть разнообразной, т.к. она направлена не только на активизацию мыслительной деятельности учащихся, на развитие интеллектуальных способностей учащихся, но и на развитие интереса к математике.

Существуют различные формы организации устной работы на уроках математики:

1.Математический диктант. 5 класс.

1.I слагаемое 28, II слагаемое 57. Найдите сумму этих чисел.

2.Уменьшаемое 64, вычитаемое 46. Найдите разность этих чисел.

3.Число 75 увеличьте на 17.

4.Найдите разность 51 и 38.

5.Найдите сумму 43 и 49.

6.Число 81 уменьшите на 24.

7.I слагаемое 25, а второе на 14 больше. Найдите сумму этих чисел.

2.Цепочка.

Учитель просит учащихся записать число. Учитель просит изменить данное число при помощи определенного математического действия, запомнить промежуточный результат и выполнить следующее действие, предлагаемое учителем, снова запомнить результат и т. д. На первых уроках можно разрешать учащимся писать промежуточные результаты, а в дальнейшем попробовать производить операции с промежуточными числами в уме и записать только конечный результат.

3.Круглые примеры.

Предлагается найти последний пример среди определенного числа примеров, записанных в разнобой. Учащиеся находят результат первого примера, далее им надо найти тот, который начинается с цифры, которая является результатом предыдущего примера и т.д. до тех пор, пока результат последнего примера не совпадет с начальной цифрой первого.

Данную работу можно организовать фронтально и индивидуально.

4.Ручеек.

На листочке даны примеры по количеству учащихся, сидящих на одном ряду. Решив первый пример, учащийся передает листочек сидящему за ним однокласснику. Тот должен найти ответ следующего по порядку примеру и передать листочек сидящему за ним однокласснику.

5.Лесенка.

На доске изображена лесенка примеров. Дается определенное время, за которое необходимо подняться на верхнюю ступеньку этой лесенки.

6.Расшифруй слово или фразу.

Таких заданий очень много в учебниках Л.Г. Петерсон и Г.В. Дорофеева.

Можно придумать и зашифровать тему урока или фамилию того или иного математика, ученого, которые внесли большой вклад в развитие математики.

7.Ромашка.

На доске изображены по кругу числа, а в середине или какое-то действие, или круг, разделенный на четыре или две части. В данных частях круга арифметические действия. Это задание направлено не только на отработку вычислительных навыков, но и на развитие внимания учащихся. Учитель поочередно связывает числа, расположенные по кругу, показывая на них указкой, определенными действиями из маленького круга.

8.Математический марафон.

На доске изображены примеры. Необходимо в уме быстро и правильно найти их результат и записать ответы в тетради.

Через определенное время проверить с классом данное задание и разобрать те задания, которые вызвали трудность.

9.Восстанови пример.

Учитель предлагает ученикам примеры, в которых пропущены или действия, или один из компонентов. Надо восстановить пропущенную запись.

10.Математическое лото.

Учащимся выдаются конверты с карточкой, на которой записаны примеры, расположенные в таблице, как в лото.Данные карточки можно предлагать или каждому ученику, или двум, сидящим на одной парте. Учащиеся решают примеры и закрывают ответы маленькими карточками, на которых изображены цифры, являющиеся ответами к примерам на карточке.

По команде учителя ученики прекращают работу и переворачивают маленькие карточки. На большой карточке должен получиться рисунок, или какая-нибудь геометрическая фигура.

11.Найди ошибку.

Эту форму устной работы чаще всего использую при работе над единицами измерения.

Предлагаю ученикам столбик равенств с метрическими величинами. Ученикам необходимо проверить правильно ли поставлены знаки равно и у себя в тетради отметить это в виде графической записи.

Если ученик согласен с поставленным знаком равно, то он в тетради изображает дугу, размером в две клеточки, если же не согласен, то отрезок длиной две клеточки.

Например:

Верно ли, что:

5 дм = 50 см 9 км 27 м = 927 м

6 мм = 60 см 65 см = 6 дм 5 см

8 км 78 м = 8780 м 369 мм = 3 см 69 мм

3 м 2 см = 302 см 973 см = 9 м 73 см

7 см 9 мм = 79 мм 5643 м = 5 км 643 м

1 дм 5 мм = 105 мм 730 дм = 73 м?

12.Оглянись назад.

Учитель предлагает ученикам определенное число и записывает его на доске, например 10,5.

Далее учитель называет какое-то число меньшее или большее, чем данное. Учащиеся устно должны назвать число, которое поможет вернуться к данному числу.

13.Качели.

Это задание способствует развитию памяти учащихся.

Учитель называет числа, например трехзначные. Учащиеся записывают данные числа наоборот, в обратном порядке, сначала пользуясь записями в тетради, а потом только по памяти.

14.«Числовые фокусы».

Можно в устные упражнения включать всевозможные числовые фокусы. Данные задания разнообразят урок и привнесут в него новизну.

Например:

«Проблема Гольдбаха».

Живший в 18 веке в России математик Гольдбах открыл удивительную вещь:

каждое четное число ему удавалось представить в виде суммы двух простых чисел

(включая число «1»).

Можно предложить 6-тиклассникам при изучении темы «Простые и составные числа» на одном уроке представить в виде суммы простых чисел первые 20 четных чисел; на втором уроке представить в виде суммы простых чисел числа от 20 до 50.

В России хорошо известна картина русского художника Николая Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского», написанная в 1895 году. Приведённая на доске задача, над которой размышляют ученики, требует достаточно высоких навыков устного счёта и смекалки. Вот её условие:

15.«Любопытные свойства натуральных чисел».

Возьмем любое число из 4-х цифр (например, 2365) и расставим их сначала в порядке возрастания (2356), затем убывания (6532). Из большего числа вычтем меньшее: 6532 – 2356 = 4176. С полученным числом проделаем то же самое: 7641 – 1467 = 6174. Интересно то, что к этому числу не более чем за 7 шагов мы приходим вышеуказанным способом от любого, взятого наугад четырехзначного числа.

3) 7641 – 1467 = 6174

Пример: 6598. Пример: 3582.

1.9865 – 5689 = 4176 1) 8532 – 2358 = 6174

2.7641 – 1467 = 6174.

Пример: 3198.

1.9831 – 1389 =8442

2.8442 – 2448 = 5994

3.9954 – 4599 = 5355

4.5553 – 3555 = 1998

5.9981 – 1899 = 8082

6.8820 – 288 = 8532

7.8532 – 2358 = 6174

Применение различных видов устной работы в основном зависит от творчества учителя. Какой бы вид работы не выбрал учитель на уроке, надо понимать, что устные упражнения способствуют не только развитию математических способностей учащихся, но и развитию вычислительных навыков. Как ни странно, учащиеся, которые хорошо считают, порой лучше и быстрее справляются с заданиями по математике, чем даже те ученики, которые по природе своей имеют лучшие математические способности.

Применяя в организации устной работы в 5-6 классе задания вычислительного характера, учитель тем самым экономит время на вычисления при решении задач, уравнений и неравенств.

Литература.

Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
Билл Хэндли «Считайте в уме как компьютер», Минск, Попурри, 2009г.
Минских Е. М. «От игры к знаниям», М., «Просвещение» 1982г.
Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. //Начальная школа. – 1990, №6.
Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
Перельман Я.И. Живая математика. – Екатеринбург, Тезис, 1994.
Перельман Я. И. Быстрый счет. Тридцать простых приемов устного счета.– Ленинград: Дом занимательной науки, 1941.

Интернет-источники

http://matsievsky.newmail.ru/sys-schi/file15.htm
http://sch69. narod.ru/mod/1/6506/hystory.html
www.school.edu.ru
www.ik.net/~stepanov/
http://www.junior.ru/students/chukhua/shestoe%20chyvstvo.htm

ГБОУ школа №471 Нетикова М.А.[Введите текст]Страница

2018_”Приемы устного счета в 5 классе” | Статья по математике (5 класс) по теме:

Государственное бюджетное образовательное учреждение дополнительного педагогического профессионального образования Центр повышения квалификации специалистов Красносельского района Санкт-Петербурга «Информационно-методический Центр»

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 247

«Приемы устного счета
на уроках математики»

учитель математики

Лушникова Людмила Константиновна

Санкт-Петербург

2017

Как проводить устный счет на уроках математики

Математика является одной из важнейших наук на земле и именно с ней человек встречается каждый день в своей жизни. Счет в уме является самым древним и простым способом вычисления. Знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов. Устные вычисления дают возможность не только быстро производить расчеты в уме, но и развивают память, культуру мысли, ее четкость, ясность и быстроту, сообразительность, умение отыскивать наиболее рациональные пути для решения поставленной цели, ясное понимание связи теории с практикой, уверенность в своих силах, помогает школьникам полноценно усваивать предметы физико-математического цикла.

Поэтому учителю математики надо обращать внимание на устный счет с того момента, когда учащиеся приходят к нему из начальной школы. Именно в среднем звене мы закладываем основы обучения математике наших учеников, раскрываем ее притягательные стороны. Хорошо развитые у учащихся навыки устного счета – одно из условий их успешного обучения в старших классах.

Формы устного счета.

На уроках устный счет применяется следующих форм

При устных вычислениях мысль учащихся все время работает над вопросом: «Какой прием лучше применить в том или другом случае, чтобы как можно быстрее производить требуемые вычисления? »

В конце урока устный счет применяется обычно независимо от темы урока в специально оставленное для этой цели время ( 5-10 минут ) как для упражнений в применении различных приемов быстрых вычислений, которыми учащиеся уже владеют, так и для объяснения учителем новых приемов.

Скорость вычисления как при беглом счете , так при устном решении задач всецело зависит от степени трудности примеров, от степени подготовленности детей, от их умения пользоваться приемами быстрых вычислений, от умения преподавателя вести эту работу.

Необходимо, чтобы таблицы сложения, вычитания, умножения и деления были усвоены с детьми в совершенстве.
Надо, чтобы дети легко и быстро находили дополнения чисел до любого большего круглого числа ( т. е. кратные 10)
Надо научить учащихся быстро делить и умножать на 2.
Учащиеся должны уметь разложить любые числа по разрядам, т.е. представить их в виде суммы.
Ученики обязаны хорошо знать основные законы четырех арифметических действий, зависимость между компонентами и результатами действий.
Представить число в виде разности двух чисел.
Использовать при вычислениях возможность замены одних действий другими действиями.
Знать значение квадратов чисел до 30.

Некоторые приемы устных вычислений
по математике в 5 и 6 классах.

1. Умножение чисел, оканчивающихся нулями.

40·7 = (4·7)·10=280; 8·60 = (8·6)·10=48·10=480;

400·7 = (4·7)·100=2800; 4·600 = (4·6)·100=24·100=2400;

1200·50·=(6·2·5)·1000=60000; 120·70 = (12·7)·100=8400.

2. Умножение любого числа на двузначное путем разложения множителя на десятки и единицы.

46·12 = 46·10 + 46·2=460+92=552;

243·31 = 234·30 + 243·1=7020+243=7263;

3. Перестановка сомножителей.

2·93·5 = 2·5·93 = 10·93=930;

4·17·25 = 17·4·25 = 17·100=1700;

125·201·8 = 201·125·8 = 201·1000=201000.

Особые приемы умножения.

Умножение на 4 может быть сведено к двукратному последовательному умножению данного числа на 2.

48·4 = 48·2·2

157·4 = 157·2·2

Умножение на 5

42·5 = 21·2 5= 21·10 = 210

92·5 = 46·2 5 = 46 10 =460

Умножение на 6

При умножении на 6 можно применять два способа:

1) Последовательное умножение

52 · 6 = 52·2·3 = 104·3 = 312

2) Представление 6 в виде суммы 5 и 1

52 · 6 = 52 · (5+1) = 260 + 52 =312

Умножение на 7

52 · 7 = 52 · (5+2) = 260 + 104 = 364

Умножение на 9

52 · 9 = 52 · (10-1) = 520 – 52 = 468

Умножение на 11

52 · 11 = 52 · (10+1) = 520 + 52 = 572

Умножение на 25

36 · 25 = 36 : 4 100 = 9 ·100 = 900

52 · 25 = 52 : 4 100 = 13 100 =1300

Умножение на 50

52 · 50 = 52 : 2 · 100 = 26 · 100 =2600;

48 50 =48 : 2 · 100 = 24 · 100 = 2400.

Устный счет на уроках математики в 5 классе

Цели на уроках:

Образовательные:

– повторить, закрепить и расширить знания учащихся;

– проверить усвоение учащимися умения решать задачи с помощью уравнений.

Воспитательные:

– прививать интерес к изучению математики;

– воспитывать эстетический вкус, чувство коллективизма.

Развивающие:

– расширить кругозор учащихся, умение работать по заданному алгоритму;

– развивать моторику рук, ориентировку на плоскости и в пространстве, внимание.

Виды устного счета

«Кто быстрее?»

Устный счет заранее заготовлен на доске. Каждый ряд или команда получает свое задание.

Для х = 1,3, х = 1,8.

2) Для каждого ряда заготовлены столбики с примерами. Ученики по одному выходят к доске, решают и записывают один ответ.

Как эстафету передают друг другу решение следующего примера. После чего подводится итог работы по критериям:

а) дисциплина; б) первенство выполнения заданий; в) правильные ответы.

7² – 5²	10² – 4²	4² – 3²
· 3	:4	: 7
: 4	+27	· 100
+ 12	: 3	: 2
: 2	: 5	+ 25

3) «Четырехугольник с секретом»

1. Какой из числовых рядов лишний, то есть отличается от других?

2	5	8	11	14
1	4	7	10	13
3	4	5	6	7

1	2	4	8	16
2	6	12	24	48
5	10	20	40	80

2. Согласно закономерности, найденной между числами в первом четырехугольнике, определите недостающее число во втором.

3,2	5,1	1,9
2,6	2,6+4,5=7,1	4,5

0,8	1,5	2,3
1,7	2,2-1,7=0,5	2,2

4)Игра «Лучший счетчик».

Учитель объявляет, что на следующем занятии будет проходить игра под названием «Лучший счетчик». Дома каждый ученик должен подобрать по теме три – четыре примера для устного счета. Класс делится на три команды. В каждой команде выбирается «счетчик», который будет защищать честь команды. Примеры для устного счета предлагают «счетчику» члены других команд до тех пор, пока он не собьется. Затем его сменяет другой ученик из той же команды, и игра продолжается. Число «счетчиков» для одного тура определяется по договоренности. Побеждает команда, в которой было наименьшее число «счетчиков», решивших наибольшее количество примеров. Среди «счетчиков» устанавливается личное первенство.

Дополнительно можно дать еще такие задания:

а). Вычислите площадь квадрата, периметр которого равен 36 см.

1) 12 см²; 2) 18 см²; 3) 81 см²; 4) 36 см²; 5) 25 см².

б).Выберите самое маленькое четырехзначное число, в записи которого все цифры разные.

1) 1023; 2) 1234; 3) 1203; 4) 1032; 5) 1203.

в). Корень уравнения х – 12678 = 25349 равен:

1) 35428; 2) 12675; 3) 38027; 4) 2671; 5) 28027.

г). Найдите значение выражения CXXV – XXXV

1) CX; 2) CXI; 3) IC; 4) IICV; 5) XC.

5)Найдите ошибки и объясните их.

а) 0,5 > 0,724; 0,0013

7,6421 > 7,6429; 0,908

б) 2,7 + 3,651 = 6,351; 0,325 + 11,76 = 15,01; 0,17 + 1 = 0,18;

2 – 0,63 = 1,63; 117,7 – 10,07 = 107,77; 0,632 – 0,124 = 0,508.

в) Уравнение х + 3,75 = 6,9 решено тремя способами,

найти верное решение.

Способ I. х = 6,9 – 3,75, х = 3,25.

Способ II. х = 6,9 + 3,75, х = 4,44.

Способ III. х = 6,9 – 3,75, х = 3,15.

При изучении арифметических действий над положительными числами:

6. «Давайте посчитаем». На доске написано несколько целых чисел, некоторые написаны два–три раза, например: –4; 87; 36; –105; 87. Из суммы всех повторяющихся чисел нужно вычесть сумму чисел, встречающихся по одному разу, и сообщить результат.

7. «Найди пример по ответу».

Трое ребят становятся спиной к доске. На доске записываются примеры:

а) 8,5 + 4,6 – 1,6 + 0,5 = ?; б) 2,5 × 3,78 × 4 = ?; в) 4,7 + 3,9 + 5,3 – 2,9 = ?;
г) 7,47 × 125 × 0,2 × × 0,8 × 5 = ?.

Учитель показывает на один из них. Ученики устно считают, затем один из решивших громко произносит ответ. Стоящие у доски поворачиваются к ней и ищут подходящий пример.

Побеждает тот, кто нашел его первым.

8) Подумай! Сообрази!

Задание: За определенное время необходимо решить как можно больше задач.

Задание первой команде:

1) Торговка, направляясь на базар, соображала: « Если бы к моим яблокам прибавить половину их, да еще десяток, то у меня была бы

целая сотня!» Сколько яблок было у торговки?

2) Трехзначное число 87* делится на 5 и на 3. Какова последняя цифра?(0)

3) Хор, состоящий из 280 мальчиков и 105 девочек исполняет задушевную песню. К счастью, только четвертая часть мальчиков и третья часть девочек орет во все горло. Остальные только открывают рот. Найдите разность между мальчиками и девочками, орущими во все горло.

4) Что всегда увеличивается и никогда не уменьшается? (Возраст)

5) Чем больше из нее берут, тем больше она становится? (Яма).

Задание 2-й команде:

1) Внук спросил деда: «Сколько тебе лет?» Дед ответил: «Если проживу еще половину того, что я прожил, да еще 1 год, то мне будет 100 лет». Сколько лет деду?

2) Число яблок в корзине – двузначное число. Яблоко можно разделить поровну между двумя, тремя и пятью детьми, но нельзя разделить между четырьмя детьми. Сколько яблок в корзине? (30яблок).

3)40 человек вошли в автобус. Пятая часть купила билеты. А остальные заявили, что у них проездной. На самом деле проездной был только у 7 человек. Сколько человек поехали «зайцем»? (25 человек)

4)Как может кошка зайти в погреб с одной головой, а выйти с двумя? (Если поймает мышь).

5) Одно яйцо варят 4 минуты. Сколько минут нужно варить 5 яиц?. (4 минуты).

9)Озеро «Ребусное»

Дети очень любят придумывать и решать ребусы. Можно учителю предложить свои ребусы, а потом решать ребусы, которые придумали дети.

1.Расшифруйте «закодированные» слова:

1) и100рия;

2) про100р;

3) кис. ;

4) 3тон;

5) о3цание.

2.Попробуй и отгадай!.

1
	Правильный ответ: Ромб. Комментарий: Бомба, заменяем букву Б на букву Р. Удаляем последнюю букву в слове.
2
	Правильный ответ: Угол. Комментарий: Первая буква У. Далее идет слово «глобус» где меняем местами буквы «гол». Три последние буквы удаляем
3
	Правильный ответ: Отрезок. Комментарий: В слове «кот» удаляем первую букву. Остается «ОТ».В слове «Зеркало» меняем местами буквы р, е, з. Удаляем последние 4 буквы. Дописываем «ок».
4
	Правильный ответ: Задача. Комментарий: В слове» заяц» убираем две последние буквы. А дальше подбираются слова по смыслу: дом, дача. Подходит «дача».
5
	Правильный ответ: Аксиома. Комментарий: В слове «такси» убирается буква «т». В слове «дома». Убирается первая буква «д».
6
	Правильный ответ: Транспортир. Комментарий: К слову «транспорт» добавляется «ир»
7
	Правильный ответ: Знаменатель. Комментарий: Подбираем слова «флаг» или «знамя». В слове «знамя» убирается буква «я». Далее читаем «е на т». Дальше снова подбираем слово «елка» , «ель».
8
	Правильный ответ: Квадрат. Комментарий: Первое слово будет не лягушка, а звук «ква», издаваемый лягушкой. Далее идет буква «д». В слове «рак» букву «к» заменим на букву «т».

Решение олимпиадных задач.

Задача 1. Разрежьте квадрат на 4 равные части. Затем такой же разрежьте на 16 равных частей. А теперь такой же квадрат – 17 равных частей.

Решение

Задача 2. Найти площадь прямоугольника, если его длина на 5см больше ширины, а половина периметра равна 19см.

Решение: пусть х см – ширина прямоугольника, (х+5)см – длина, тогда

х+(х+5) =19

2х=14, х=7. 7+5= 12(см), Площадь равна 7·12=84 см². Ответ:84 см².

Задача 3.

Площадь квадрата 25см², сторону квадрата увеличили на 3см. Найти площадь полученного квадрата.

Задачи в стихах.

Задача 1. (про хвосты).

По тропинке вдоль кустов шли 11 хвостов.

Сосчитать я так же смог, что шагало 30 ног.

Это вместе шли куда-то петухи и поросята.

А теперь вопрос таков: Сколько было петухов?

И узнать я был бы рад, сколько было поросят?

Ты сумел найти ответ?

До свиданья, вам привет.

Решение: пусть х было поросят. (11-х) петухов. Тогда 4х=2(11-х) =30, х=4,11-4=7. Ответ: 4 поросенка, 7 петухов.

Математическая шутка.

Как доказать, что ученики ничего не делают?
Доказательство:

1. По ночам занятий нет, значит, половина суток свободна. Остается

365 – 182 =183 (дня).

2. В школе ученики занимаются половину дня, значит. Вторая половина(или четвертая часть суток) может быть свободна. Остается

183 – 183:4 = 137 (дней).

3. В году 52 воскресенья. Из них на каникулы приходится приблизительно 15 дней, таким образом выходных в учебном году 52 – 15 = 37 (дней). Итого остается 137 – 37 = 100 (дней).

4. Но есть еще каникулы: осенние (5дней), зимние (10 дней), весенние (7 дней), летние (78 дней). Всего 5 + 10 + 7 +78 = 100 (.дней)

5. Значит, школьники заняты в году 100 – 100 = 0.

Когда же учиться? Где ошибка в рассуждениях? (Каникулы и воскресенья подсчитаны дважды).

Чтобы ученики относились к устному счету серьезно, желательно проводить учет вычислительных навыков и обязательно выставлять оценки. С целью поощрения учащихся, которые отлично владеют приемами устного счета, можно давать им проводить занятия с группой ребят, плохо справляющихся с устными вычислениями.

Итак, цель всех приемов устных вычислений – пробудить интерес к математике. Вызывая интерес и прививая любовь к математике с помощью различных видов устных упражнений, учитель будет помогать ученикам активно действовать с учебным материалом, пробуждать у них стремление совершенствовать способы вычислений и решения задач, менее рациональные заменять более совершенными. А это – важнейшее условие сознательного усвоения материала и одна из главных задач Федерального образовательного стандарта нового поколения.

Ссылки на источники

1. Гельфан Е. М. Арифметические игры и упражнения. – М.: Просвещение, 1968. – 112 с.

2. Ройтман П. Б., Минаев С. С., Прокофьева Н. С. и др. Повышение вычислительной культуры учащихся. – М.: Просвещение, 1985. – 48 с.

3. Минаев С. С. Вычисления на уроках и внеклассных занятиях по математике. – М.: Просвещение, 1983. – 128 с.

4. Автайкина А. К. Некоторые формы организации устного счёта // Математика в школе. – 1991. – № 3. – С. 10–12.

5. Борткевич Л. К. Повышение вычислительной культуры учащихся // Математика в школе. – 1995. – № 5. – С. 13–19.

6. Хэндли Б. Считайте в уме как компьютер. – Минск: Попурри, 2006. – 352 с.

7. Формирование вычислительной культуры учащихся на уроках математики // Учительский портал. – URL: http://www.uchportal.ru/publ/23-1-0-1913.

8. Шершакова Т. А. Формирование вычислительных навыков на уроках математики // Социальная сеть работников образования. – URL: http://nsportal.ru/shkola/algebra/library/formirovanie-vychislitelnykh-navykov-na-urokakh-matematiki.

9. Иванова Н. В. Устный счет на уроках математики в 5-6 классах // Социальная сеть работников образования. – URL: http://nsportal.ru/shkola/algebra/library/ustnyi-schet-na-urokakh-matematiki-v-5-6-klassakh.

10. Аскарова Б. Ш. Устные упражнения в обучении математике 5–6-х классов // Коллеги – педагогический журнал. – URL: http://collegy.ucoz.ru/publ/39-1-0-3061.

11.Н.М. Ляшова и др. Математика. Открытые уроки. 5,6,7,9,11 классы. Волгоград, Издательство «Учитель»., 2007.

12. Фарков А.В.Математические кружки. 5-8 классы. ООО «Издательство «АЙРИС – пресс», 2008.

6 стратегий обучения счету пропусков

Давайте поговорим о счете пропусков! Этот навык иногда рассматривается как произвольный математический навык или что-то, что вы повторяете на игровой площадке. Подсчет пропусков — это гораздо больше. Это помогает учащимся увидеть закономерности в числах, а также закладывает отличную основу для понимания чисел и изучения фактов умножения.

1. ИСПОЛЬЗУЙТЕ КАЛЬКУЛЯТОР

Учителя обычно не думают об использовании калькулятора. Тем не менее, они могут быть забавным и полезным инструментом при обучении этому навыку.

Совет учителю:

Покажите классу, как изменить начальное число, продолжая нажимать знак равенства (пример 8 + 2 =, =, =, =). Объедините учеников в пары с партнером. Один партнер называет новую сумму до того, как другой партнер нажмет кнопку =. Они по очереди пытаются назвать число, следующее за числом, прежде чем нажать кнопку. Это весело для детей, потому что это соревнование, и эта стратегия помогает развить беглость чисел.

2. ИГРАТЬ

Дети ОБОЖАЮТ игры! Это очень простая игра, в которую дети могут играть, чтобы научиться считать с пропусками весело. Попросите учащихся сесть или встать в круг. Учитель начинает со случайного числа, и ученики пропускают счет от этого числа, пока не пройдут весь круг.

Совет учителя:

Лучшее в этой игре то, что вы можете изменять ее в соответствии со своими потребностями. Например, чтобы перейти на более высокий уровень, начните с числа, которое не входит в обычную последовательность подсчета пропусков. Например, вместо того, чтобы просто пропускать счет до 2-х (например, 2, 4, 6, 8 и т. д.), начните с нечетного числа и пропустите счет до 2-х (например, 7, 9)., 11, 13 и т. д.) или пропускайте счет нетрадиционными числами, такими как 7 или 9.

3. ВОПРОСЫ

Иногда задавать вопросы – это стратегия обучения, которой часто пренебрегают. Есть много типов вопросов, которые вы можете задать, чтобы заставить ваших детей критически подумать о пропуске счета. Например, чаще всего учеников просят сделать: «Пропустить счет до 2». Попробуйте спросить: «Сколькими способами вы можете сосчитать до 36?» Вместо того чтобы просить учащихся сосчитать до 50 по 10, спросите: «Можете ли вы сосчитать до 50 по 11? Почему или почему нет?”

Ознакомьтесь с моими карточками “Пропустить счет” и “Четные/нечетные числа, перевернуть и перейти к математике”. Они отлично подходят для предоставления вопросов в целой группе или небольшой группе.

4. ИСПОЛЬЗУЙТЕ КЛИПКИ С ДИАГРАММОЙ 100

Использование стикеров может быть очень интересным и интерактивным способом попрактиковаться в счете с пропусками. Одним из примеров может быть использование увеличенной таблицы чисел и закрытие определенных чисел стикером. На каждом стикере напишите по одной букве алфавита. Затем попросите учащихся записать пропущенные числа на отдельном листе для записей. В приведенном ниже примере попросите учащихся начать с числа 9.и пропустить счет на 3 с.

Если вы любите использовать стикеры, обязательно ознакомьтесь с моим постом «10 способов преподавать математику с помощью стикеров».

5. ПОЮ ПЕСНИ

Все мы знаем, что дети любят песни. Существует так много бесплатных ресурсов о подсчете пропусков, которые заставят ваших детей двигаться и обучать математическим понятиям одновременно. Ознакомьтесь с одним из моих любимых ниже:

Skip Count (…и затем добавьте) от Harry Kindergarten Music — Harry Kindergarten Music содержит отличные музыкальные видеоклипы, которые включают в себя целый ряд навыков и концепций. Это видео с подсчетом пропусков имеет отличные визуальные эффекты. Он показывает, как пропустить счет, используя стержни с основанием десять, а затем добавляя единицы, чтобы вычислить общую сумму. Это отличный инструмент для обучения математике концептуально!

6. Используйте Манипуляторы

Студенты чувствуют себя очень достигнутыми, когда они способны считать 2S, 5S, 10S и т. Д. Может показаться, что учащиеся понимают эту стратегию, потому что они могут назвать последовательность цифр, но действительно ли они понимают цель пропуска счета? Вытащите манипуляторов. Используйте кубики оснастки, конфеты. скрепки или любые другие предметы, которые вы можете найти.

Обязательно задавайте наводящие вопросы, например: 1) Что вы заметили? 2) Как меняется сумма? или 3) Если вы продолжите этот шаблон, каково будет общее количество объектов в 10-й, 11-й или 12-й модели?

Нажмите на фотографию ниже, чтобы ознакомиться с информативным постом от Math Coach’s Corner о том, почему нам все еще нужно использовать эти конкретные объекты при ознакомлении с этим математическим навыком.

Есть ли у вас другие способы обучения счету в классе? Пожалуйста, поделитесь в разделе комментариев.

Соединение InLinkz

912

Занятия и уроки, которые сделают обучение увлекательным — гордимся тем, что учимся в начальной школе

Математические советы и стратегии для изучения чисел до 100 или 120 в детском саду, первом и втором классе. Включен обширный список действий до 100 и ресурсы: книги, материалы, идеи для уроков и БЕСПЛАТНЫЕ занятия!

Математические советы и стратегии, необходимые для изучения чисел до 100 (или 120), находятся прямо здесь. У вас будет все, что вам нужно, чтобы легко внедрить множество занятий, игр и центров, связанных с числами, в свой класс или домой.

Занятия, книги, предложения ресурсов (в том числе БЕСПЛАТНЫЕ) охватывают массу понятий о смысле чисел до 100/120 и идеально подходят для начальных классов. Кроме того, вы найдете ценные действия с числами до 100, а также материалы, манипулятивные предложения и бесплатные подарки, которые вы можете получить сегодня.

Почему так важно учить считать до 100?

Детям необходимо множество возможностей для обучения и опыта чисел. Научиться считать, определять числа и понимать количество — это лишь некоторые из важных понятий, которые они должны освоить. Повторяющийся опыт способствует пониманию и свободному обращению с числами. Этот опыт помогает расширить понимание и изучить новые концепции. Сильное чувство числа жизненно важно для понимания более сложных математических тем.

Приведенные ниже действия успешно использовались. Используйте их так, как они описаны, или адаптируйте их к своим потребностям. Быть гибким. Обсуждайте числа и поощряйте вопросы. Когда есть возможность заказать, посчитать, сопоставить или описать вместе с ребенком, дерзайте! Им выгодно видеть числа естественным и плавным образом. Ежедневно находите время для веселых и увлекательных занятий с числами и наблюдайте за развитием беглости речи.

Счет до 100

Для детей очень важно считать каждый день. Повторяющийся устный счет помогает им услышать, как звучат числа, и запомнить их порядок. Использование математических манипуляций, таких как подсчет фишек, может помочь установить связь с устным счетом и счетом предметов. Этот счет один к одному является важным навыком, который необходимо часто практиковать.

Счет до 100 Упражнения

Прогуляйтесь со счетом. Найдите вещи на природе, на игровой площадке или в школьном здании, чтобы считать их по мере прохождения.
Игра «Вокруг света» с использованием чисел — это быстрая и простая игра, в которую все вовлечены и внимательны. Начните с определенного числа и продолжайте считать устно по кругу.
Вы всегда можете использовать небольшие предметы (например, палочки от эскимо), чтобы дети могли легко держать их в руках и манипулировать ими во время счета.
Удобно иметь много мелких предметов, таких как мини-ластики, шарики, сухие бобы, полированные камни и пластиковые драгоценности. Дети могут использовать их для тренировки счета.
Счет на числовой прямой помогает увидеть прогрессию чисел. Поместите числовую линию на стене в классе и используйте указатель, чтобы считать вдоль линии.

Использование кубиков с основанием 10 — отличный способ визуально усвоить смысл чисел до 100. Пусть дети потренируются заменять десятки единицами, сотни — десятками и ставить единицы на 100-блоке.

Пропуск счетных действий до 100

Пропуск счетных диаграмм, показывающих группы предметов, для визуального пропуска подсчета творит чудеса. Диаграммы, показывающие руки и ноги (для 5 или 10), очки (для 2) и трехколесные велосипеды (для 3), полезны для визуализации.

Сосчитайте по 2 с помощью ершиков и бусин. Переместите две бусины до конца, пока считаете.

На графике 100 следует отметить важные модели. Если дети раскрашивают все двойки, пятерки, десятки и т. д., это отличный способ помочь им визуально понять счет с пропусками.
Если вы пропускаете счет вслух в классе или во время обучения, убедитесь, что считаете таким образом, чтобы дети могли слышать имеющиеся словосочетания и ритм. Это помогает им не забывать пропускать счет, даже если они еще не усвоили смысл чисел.
Картинные пазлы — отличный способ помочь детям попрактиковаться в счете. Собирая картинку в пазле, они могут самостоятельно проверить, правильно ли они считают.

Использование небольших предметов или инструментов, таких как бобы, мазки, наклейки или кубики, может помочь учащимся научиться пропускать счет. Группируясь для подсчета, они контролируют свое визуальное понимание и могут практиковаться в своем собственном темпе.

Чтение и запись чисел до 100

Учителя часто так усердно пытаются найти «веселые» и «новаторские» способы обучения и иногда пренебрегают простым актом чтения и написания во время явного обучения . Однако после того, как вы это сделаете, определенно появятся другие способы, которые оживят ваши уроки, пока вы тренируетесь в чтении и написании чисел до 100. Вот несколько идей:

Занятия

Такое простое занятие, как написание числа на доске и предоставление классу возможности назвать это число, работает хорошо. Для интересного поворота пусть дети по очереди напишут число, а их одноклассники попытаются назвать его.

Карточная игра «У меня есть, у кого есть» — забавная игра, в которую можно играть с картами. Детям нравится эта игра, которая держит их в напряжении и готова реагировать.

Раскрашивание — это занятие, которое многие дети находят расслабляющим и радостным. Используйте лист «Найди и раскрась», чтобы просмотреть числа до 100.

Популярная игра в бинго — это увлекательный способ попрактиковаться в числах. Следите за тем, чтобы ученики меняли свои карточки после каждого раунда, чтобы во время игры они могли практиковать множество разных чисел.

Развесьте номера в разных местах комнаты и устройте охоту за ними!

Запись чисел — это окончательный способ, с помощью которого мозг учится запоминать форму и детали каждого числа. Не пренебрегайте этой важной практикой, которая помогает детям узнавать их.

Сотни карт Количество действий до 100

С сотней карт можно делать так много всего! Вот почему учителя часто используют его в первую очередь при обучении числам до 100. Задания бесконечны, но вот некоторые из них, которые понравятся вам и вашим ученикам.

Занятия

Простые игры, такие как Roll to 100 и Race to 100, можно сыграть после урока по числам, чтобы развлечься.

Используйте гигантскую таблицу чисел, чтобы расположить карточки с числами по порядку. Дети могут помочь вам расположить их в нужном квадрате на схеме.
Проще всего предложить детям разрезать свою собственную таблицу сотен, а затем попытаться собрать их снова, как пазл. Это дает им практику резки, а также практики чисел!

Дайте детям пустую таблицу с числами и попросите их написать правильные числа. Вы можете опубликовать большую диаграмму классной комнаты для справки, если они в ней нуждаются.

Заламинируйте таблицу с числами и попросите детей вместе с партнерами закрывать и угадывать числа в игре «Угадай мой номер».

Нарисуйте на доске сетку 10×10 и предложите детям заполнить ее.
Дайте каждому ребенку по сто карточек и фишек для счета. Вызовите случайные числа и попросите их закрыть их счетными фишками.

Упорядочивание и сравнение чисел Занятия до 100

Предоставьте детям возможность упорядочивать числа. Располагая числа или объекты с числами в правильном порядке, они считают и формируют чувство числа. По мере знакомства с числами растет и способность сравнивать числа друг с другом. Обеспечьте возможность сравнивать числа ежедневно. Задайте вопросы о том, какое число больше, меньше или одинаково. И добавьте несколько из этих занятий, чтобы сделать уроки увлекательными!

Занятия

Использование картинок-пазлов, в которых числа упорядочиваются от меньшего к большему или от большего к меньшему, отлично подходит для того, чтобы дети могли практиковаться в упорядочивании и сравнении.
Распечатайте карточки с числами и заламинируйте их. Предложите детям вытянуть две карточки и сравнить, какая из них больше, а какая меньше. Пусть они вытянут более двух карт и разложат их по порядку.
Используйте карточки с вырезками, которые просят детей прикрепить зажим к самому большому числу или к числу, которое идет первым в последовательности. Это позволяет быстро оценить понимание.

Числовая линия — отличное наглядное пособие для обучения и отработки порядка и сравнения. Пусть дети укажут или отметят числа, которым они принадлежат на линии.
Для этих уроков еще раз принесите таблицу сотен. Их также можно использовать для упорядочивания и сравнения, попросив детей отметить, где числа находятся выше или ниже на диаграмме. Разрежьте диаграмму на полоски и предложите детям поставить числа сверху.

Изучите визуальное правило «аллигатор» с помощью сравнений. Нарисуйте зубы внутри символов, чтобы показать, что «аллигатор» очень голоден и любит есть только большее количество.

Подпишите кубики или используйте карточки с цифрами, чтобы дать детям физический предмет, который они могут держать и манипулировать, чтобы упорядочивать и сравнивать. Попробуйте расставить количество поездов до 100 по порядку в карманной таблице ( Возьмите это БЕСПЛАТНОЕ задание ниже! )

Сыграйте в карточную игру с колодой карт, в которой дети случайным образом выбирают два числа. Попросите их сравнить их с партнером или расположить их по порядку, на числовой прямой и т. д.

Разрядное значение Число Действия до 100

Обучение детей разрядному значению должно начинаться с обучения их видеть десять разными способами. После того, как вы научили числа до 100, используя несколько из вышеперечисленных способов, вы можете перейти к иллюстрированию чисел с помощью блоков с основанием 10 и к другим занятиям, которые обучают порядковому значению. Вот несколько идей, которые можно использовать в классе, чтобы научить и закрепить эту концепцию.

Занятия

Снэп-кубики — обычное средство манипулирования, которое можно найти почти в каждом классе. Это отличный способ научить детей отношениям между единицами и десятками.

Если у вас есть блоки с основанием 10, они созданы в первую очередь для обучения разрядности. Используйте их усердно и последовательно, чтобы визуальным образом развить чувство числа, обучая разряду.

Десять рамок — полезная картинка для многих детей. Добавьте их в свою инструкцию, чтобы показать детям еще одно полезное наглядное пособие.

Потренируйтесь размещать значение на диаграмме сотен, называя число, и они находят его на диаграмме. Сыграйте в игру и дайте подсказки, такие как «4 в разряде десятков и 6 в разряде единиц», и посмотрите, смогут ли они найти правильное число.
Ручные предметы, такие как палочки от эскимо, бобы и мини-ластики, можно использовать для отображения единиц и десятков.

Опять же, просто написать число и нарисовать, сколько десятков и единиц оно содержит, — это простой, но эффективный способ научить разрядному значению.

100-й день школьных занятий

Зимние месяцы часто бывают унылыми, и учителям приходится скучать. Вот почему 100-й день — это такой огромный успех. Учителя и ученики любят устраивать вечеринки, а что может быть лучше вечеринки, чем празднование большого числа — 100! Оно представляет собой проделанную большую работу и обучение, и вы можете использовать его в своих интересах, чтобы научить понимать число и его значение.

Мероприятия

Обязательно ознакомьтесь с этой подборкой из 100 дней школьных мероприятий, которые сделают ваше празднование огромным успехом.

Наденьте корону на их головы! Правильно, они будут гордиться тем, что целый день празднуют число 100, и заберут эту милую шапочку домой, чтобы показать своим родителям.
Цветные изображения, содержащие 100 элементов или требующие счета до ста (например, страница с точками).
Оденься как столетний! Детям понравится притворяться, что им 100 лет, и ходить с тростями, носить седые парики и одеваться в «старом» стиле.

Съешьте закуску из 100 штук (например, 100 семечек или 100 конфет Nerds).

Сделать ожерелья 100-го дня. На этих ожерельях должно быть 100 бусин или других предметов.

Попросите детей принести коллекцию из 100 вещей, чтобы поделиться ими со своими одноклассниками.

Количество действий до 100 Ресурсы

Действия, представленные в этом посте, можно найти в различных ресурсах на сайте Teachers Pay Teachers. Нажмите на изображения выше, чтобы перейти к устройству, деятельность которого показана на фотографии. Узнайте, почему учителям нравится программа Mindful Math для детского сада, первого и второго классов.

Счет до 100 для детского сада

Учебная программа Mindful Math для детского сада

Числа до 100/120 для первого класса

Учебная программа Mindful Math для первого класса

Чувство чисел (100 и 1000) для второго класса

Учебная программа Mindful Math для второго класса

БЕСПЛАТНАЯ 100-дневная школьная тренировка на поезде

Это печатное задание — отличный способ попрактиковаться в числах до 100. Постройте поезд чисел!

Щелкните изображение ниже, чтобы получить бесплатную копию.

Книги от чисел до 100

Одно арбузное семечко Селии Лоттридж. В этой красочной книге ученики учатся считать до десяти, пока Макс и Жозефина сажают семена в своем саду. Далее учащийся считает десятками до ста по мере сбора урожая. Наконец, учащимся предлагается найти в книге определенные картинки на тему сада. Эта простая книга — отличный способ познакомиться с числами от 1 до 100, а также рассказать о том, как выращивают и собирают урожай.
«Сто голодных муравьев» Элинор Пинчес и Бонни Макейн. Изучение чисел от 1 до 100 включает в себя больше, чем просто подсчет по порядку. Учащиеся должны прийти к пониманию того, как отдельные числа соотносятся с целым. Эта книга помогает учащимся с этой концепцией, поскольку она следует за линией из ста муравьев на пикник. Чтобы ускорить путь на пикник, муравьи объединяются в разные группы — 2 группы по 50, затем 4 группы по 25 и так далее. Это интересный способ лучше развить представление о числах от 1 до 100.
100 Snowmen by Jen Arena. Эта зимняя история использует для подсчета снеговиков и их приключения, но в то же время представляет более сложную концепцию сложения. Каждая страница содержит задачу на сложение, соответствующую числам в рассказе. В конце к веселью присоединяются 100 снеговиков.
1-2-3 Горох Кита Бейкера. Используя красочные картинки и простые стишки, учащиеся изучают числа от 1 до 100. Сначала числа увеличиваются на единицу, но как только будет достигнуто двадцать, числа будут считаться по 10, пока не достигнут 100.
Любопытный Джордж учится считать от 1 до 100 от H.A. Рей – В этой книге учащиеся учатся считать вместе со своей любимой любопытной обезьянкой. По пути, конечно же, Джордж попадает в шалости. Учащиеся много тренируются, считая различные предметы, с которыми Джордж сталкивается в рассказе.
«Считай обезьян» Мака Барнетта и Кевина Корнелла. Эта забавная книга заставит учеников листать страницы в поисках обезьян! По пути ученики будут встречать различных животных, которых нужно считать. Это отличная интерактивная история, которая развлечет школьников.
100 жуков!: Счетная книга. Учащимся понравится наблюдать за разнообразием жуков в этой книге, когда они будут двигаться от 1
до 100. Они также узнают, как составлять группы по 10 особей по-разному.
100 животных на параде! Масуюки Себе
Мисс Биндергартен празднует 100-летие детского сада Джозефа Слейта
100 школьных дней Энн Рокуэлл
Ночь перед 100-м днем в школе, Наташа Винг
100 способов сделать мир лучше! Лиза М. Джерри
Первые 100 номеров Роджера Придди
Спорим! Стюарт Дж. Мерфи
Счет Генри Плакроуза
100 вещей, которые делают меня счастливым Эми Шварц
100 Дэвида Картера: поднимите закрылки и научитесь считать! Дэвид Картер
Оставайся в очереди Тедди Слейтер
Place Value Дэвида А. Адлера
Сотня туфель многоножки Тони Росс
Ширли Дьюк «Какова стоимость места»
От одного до ста Тери Слоут

Материалы для обучения числам до 100

Кубики Mathlink — полезны для учащихся, практикующих переписку один на один и счет до 100 единицами и десятками.
Магнитная числовая строка 1-100 — это хороший инструмент для работы с порядковыми номерами, нечетными/четными числами и идентификацией чисел.
Сто ламинированных досок, вспомогательное средство для подсчета с помощью сухого стирания. Учащимся всегда нравятся занятия на доске. Эти сотни досок позволяют учащимся самим взаимодействовать с диаграммами.
Numbers Bingo Game – Сделайте процесс распознавания чисел увлекательным с этой игрой в бинго, которая понравится всем! Попросите учеников назвать номера, а также сыграть в игру.
School Zone – карточки с числами 1–100 – это базовый набор карточек, которые можно использовать с учениками по-разному. Практикуйтесь в идентификации, пропуске счета, нечетных/четных числах и играйте в игру, входящую в комплект.
Eureka Classroom Supplies Научитесь считать. Считайте животных с помощью емкости для хранения. Используйте этих красочных животных, чтобы укрепить соответствие, сортировку и счет один на один.
Number Slap Jack — забавная карточная игра с распознаванием и подсчетом чисел — забавная игра для тренировки чисел от 1 до 20. Ориентирован на К-1 класс.
Учебные ресурсы Большие магнитные числа — эти магнитные числа можно использовать различными способами для поддержки практики счета, идентификации чисел и решения простых математических уравнений.
ThinkFun Math Dice Junior Game — это увлекательная математическая игра, которая также бросает вызов учащимся, используя «умственную математику». Студентам будет так весело, что они даже не поймут, что тренируют свои математические навыки!
Карманная диаграмма Eamay Hundred — простое наглядное пособие, которое учителя могут использовать различными способами в своих классах. Студенты также могут взаимодействовать с числами.

Учить больше о номерах

Номер здания Смысл бесплатный серия электронной почты

Номер дневных мероприятий

Число зданий.

Некоторые приёмы устного счёта на уроках математики в 5-6 классах | Статья по математике (5, 6 класс) на тему:

2018_”Приемы устного счета в 5 классе” | Статья по математике (5 класс) по теме:

6 стратегий обучения счету пропусков

Занятия и уроки, которые сделают обучение увлекательным — гордимся тем, что учимся в начальной школе

Почему так важно учить считать до 100?

Счет до 100

Счет до 100 Упражнения

Пропуск счетных действий до 100

Чтение и запись чисел до 100

Занятия

Сотни карт Количество действий до 100

Занятия

Упорядочивание и сравнение чисел Занятия до 100

Занятия

Разрядное значение Число Действия до 100

Занятия

100-й день школьных занятий

Мероприятия

Количество действий до 100 Ресурсы

БЕСПЛАТНАЯ 100-дневная школьная тренировка на поезде

Книги от чисел до 100

Материалы для обучения числам до 100

Учить больше о номерах

Оставить комментарий Отменить ответ