Интерференция и дифракция радиоволн
Явления интерференции и дифракции оказывают существенное влияние на распространение радиоволн от источника к приемнику. Эти явления играют важную роль в формировании диаграммы направленности приемно-передающих антенн.
Дальность радиосвязи наземных объектов в пределах прямой видимости ограничена расстояниями в несколько десятков километров. При большей дальности прямое прохождение радиоволн от передатчика к приемнику оказывается невозможным вследствие кривизны земной поверхности, влияния рельефа местности, наличия на пути волны различных препятствий (зданий, сооружений и т. д.). Поэтому при большой дальности радиолинии радиоволны приходят на приемную антенну после отражения от земной поверхности и слоев атмосферы, дифракции и рассеяния на неоднородностях атмосферы и местных предметах.
В результате явления дифракции радиоволны огибают земную поверхность, что используется для радиосвязи абонентов в отсутствие прямой видимости (рис.
На пути радиоволн встречаются различные препятствия, такие как здания, элементы конструкций, складки рельефа местности и т. д. Для длинных волн (метрового диапазона) размеры этих препятствий оказываются соизмеримы с длиной волны, и такие волны способны огибать препятствия в результате дифракции. Для коротких волн, наоборот, размеры препятствий оказываются значительно больше длины волны, поэтому за препятствиями могут возникать области геометрической тени (“мертвые зоны”), где уровень сигнала значительно уменьшается.
Для обеспечения устойчивой, надежной радиосвязи необходимо учитывать эти факторы при размещении на местности приемной и передающей аппаратуры.
Излучение многих радиопередающих устройств имеет высокую степень когерентности и это создает предпосылки для возникновения интерференционных эффектов.
Особенностью распространения радиоволн в тропосфере и ионосфере является то, что на приемную антенну приходит не одна, а несколько волн, идущих разными путями. Из-за случайных изменений длин путей волн при их интерференции возникают искажения и хаотичные изменения принимаемого сигнала, называемые быстрыми замираниями. На эти замирания накладываются медленные флуктуации сигнала, обусловленные изменениями параметров среды распространения.
При радиосвязи наземных объектов, находящихся в пределах прямой видимости или в системах спутниковой связи, когда ретранслятор находится на небольшом возвышении над линией горизонта, на приемную антенну вместе с прямой волной приходит волна, отраженная от земной поверхности. Распространение этих волн подобно ходу лучей в схеме с зеркалом Ллойда (рис. 51.1, б). Интерференция прямой и отраженной волн приводит к изменению мощности принимаемого сигнала. В процессе движения спутника-ретранслятора принимаемая мощность периодически изменяется во времени от максимального до минимального значений.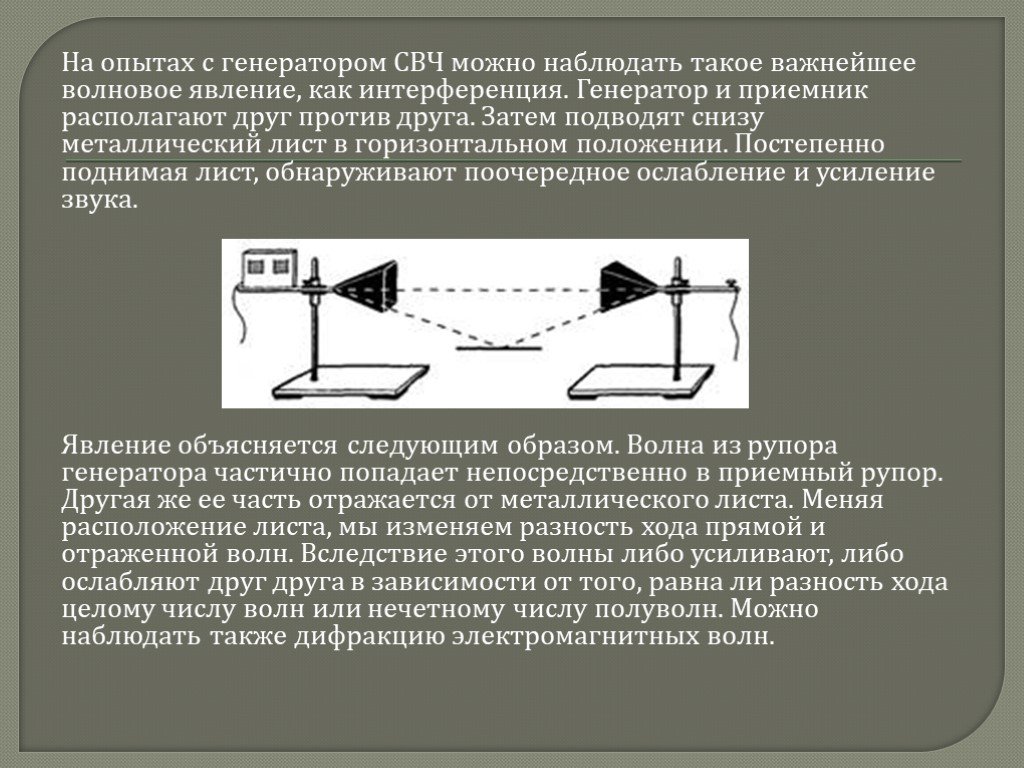
Явления интерференции и дифракции оказывают определяющее влияние на формирование диаграммы направленности приемно-передающих антенн радиодиапазона. Так, диаграмма направленности антенны определяется дифракцией плоской волны на ее апертуре. Путем расчета можно синтезировать антенны с заданной диаграммой направленности.
В § 42 была рассмотрена диаграмма направленности дипольного излучателя. Излучатели других типов (штыревые, рамочные и др.) также имеют сравнительно широкую диаграмму направленности. Однако если несколько таких излучателей расположить на определенных расстояниях друг от друга, то излучаемые ими волны в результате интерференции будут усиливать друг друга по некоторым выделенным направлениям, а по всем другим направлениям – подавлять. Тем самым осуществляется управление формой и пространственной ориентацией диаграммы направленности фазированных антенных решеток, обладающих высокими техническими характеристиками.
|
Дата добавления: 2014-01-05; Просмотров: 4131; Нарушение авторских прав?; Мы поможем в написании вашей работы!
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Явления влияющие на прохождение радиоволн
Дифракция – отклонение радиоволн вблизи края непрозрачного (для радиоволн) препятствия от первоначального направления движения.
Проходя возле края препятствия, волна как бы огибает его вершину, в результате чего часть энергии радиоволн попадает в зону тени. Край препятствия является повторным источником радиоволн, своеобразным пассивным ретранслятором. В случае световых волн наблюдается аналогичные явления, поэтому говорят, что край препятствия “светится”.
Атмосферная рефракция радиоволн – так называется (преломление), искривление траектории радиоволн. Рефракция происходит в основном в нижних слоях атмосферы, которую называют тропосферой. Тропосфера окружает землю слоем толщиной примерно 12 км. (8 км. у полюсов, 16 км. у экватора). Диэлектрическая проницаемость воздуха зависит от его влажности, температуры и давления, С увеличением высоты диэлектрическая проницаемость уменьшается, стремясь к единице. Незначительное изменение 
Могут возникать условия, когда искривление волны в сторону земли будет сильнее, чем обычно, это повышенная положительная рефракция. При возрастании e траектория изменится, волна отклоняется от земной поверхности. Такой случай называют отрицательной рефракцией. Все эти явления приводят к тому, что при многократном отражении радиоволн от отражающего слоя и земли, корреспонденты имеющие одинаковую мощность передатчиков и одинаковые антенны, имеют разную оценку силы приходящего сигнала. В большей мере это проявляется при проведении радиосвязи в направлениях север-юг или юг-север.
Интерференция (наложение) радиоволн. Одна волна-прямая, распространяется по кратчайшему пути, другая проходит более длинный путь отражаясь от земли или больших предметов.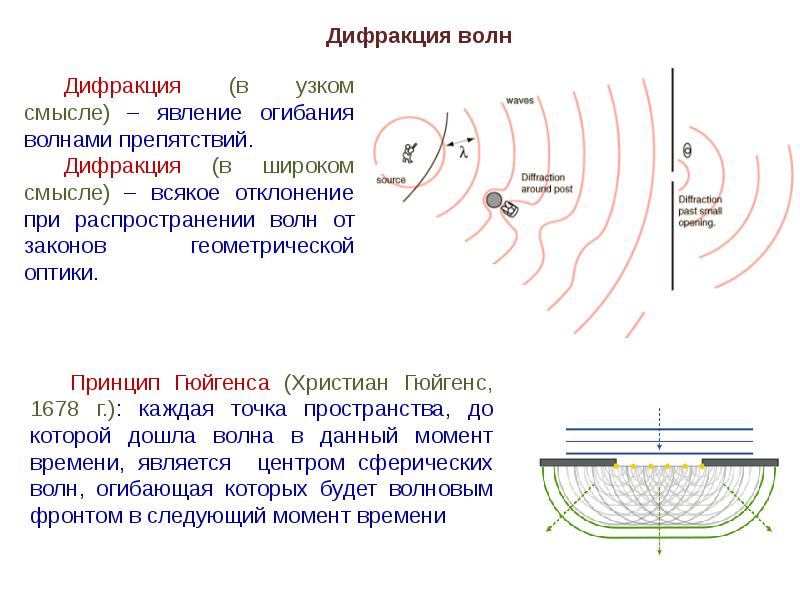
Для устранения интерференции, для данной частоты можно передвинуть антенну дальше или ближе к передающей станции или изменить высоту. Это справедливо лишь при условии прямой видимости.
Для диапазонов KB экспериментально установлено, что для трасс протяженностью 1500 км. наиболее вероятные углы прихода радиоволн 20-30°, для трасс 2000 – 3000 км. в пределах 12-20°, для трасс 3000-5000 км. в пределах 3-18°, а для более длинных трасс в пределах 3-12°. Эти углы являются оптимальными и для передачи. Таким образом, для создания оптимальных условий связи максимум вертикальной диаграммы направленности антенны, используемой для связи за счет отражения от ионосферы должен быть направлен на отражающий слой и менять свой наклон при изменении высоты этого стоя. Это можно реализовать, применяя двухэтажную синфазную решетку из двух антенн с управляемой диаграммой направленности в вертикальной плоскости.
Управление диаграммой направленности осуществляется фазовращателем в тракте запитка одной из антенн. При применении одной направленной антенны ширина диаграммы направленности в вертикальной плоскости должна быть порядка 30-40° с прижатым к земле лепестком. Отражающей слой ионосферы находится в постоянном движении при более узкой диаграмме направленности в вертикальной плоскости сигнал подвержен большим замираниям, так как при изменении высоты отражающего слоя отраженный от ионосферы луч сканирует по земле, изменяется напряженность поля в месте приема, и мы наблюдаем глубокие замирания сигнала
EW8AU, Владимир Приходько, 246027, г. Гомель – 27, а/я 68 БЕЛАРУСЬ
| Наверх |
17.1 Понимание дифракции и интерференции
Цели обученияДифракция и интерференцияРасчеты с учетом дифракции и интерференцииУчебные задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Объяснять волновое поведение света, включая дифракцию и интерференцию, включая роль конструктивной и деструктивной интерференции в экспериментах Юнга с одной и двумя щелями
- Выполнение расчетов с учетом дифракции и интерференции, в частности длины волны света с использованием данных двухщелевой интерференционной картины
The first row reads diffraction, Huygens’s principle, monochromatic. The second row reads wavefront.”>Дифракция и интерференция
Мы знаем, что видимый свет — это электромагнитная волна, на которую реагируют наши глаза. Как мы видели ранее, свет подчиняется уравнению
с=fλ,c=fλ,
где c=3,00×108c=3,00×108 м/с – скорость света в вакууме, f – частота электромагнитной волны в Гц (или с –1 ), λλ – ее длина волны в м . Диапазон видимых длин волн составляет приблизительно от 380 до 750 нм. Как и для всех волн, свет распространяется прямолинейно и действует как луч, когда взаимодействует с объектами, в несколько раз превышающими его длину волны. Однако, когда он взаимодействует с более мелкими объектами, он заметно проявляет свои волновые характеристики.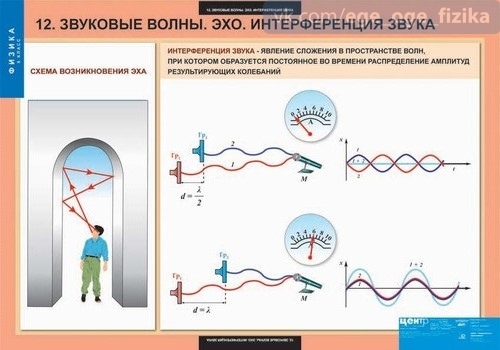
Интерференция – это идентифицирующее поведение волны.
На рис. 17.2 можно увидеть как лучевые, так и волновые характеристики света. Лазерный луч, испускаемый обсерваторией, отражает поведение луча, поскольку он движется по прямой линии. Пропускание чистого одноволнового луча через вертикальные щели шириной, близкой к длине волны луча, обнаруживает волновой характер света. Здесь мы видим, как луч распространяется горизонтально в виде узора из ярких и темных областей, которые вызваны систематической конструктивной и деструктивной интерференцией. Поскольку это характерно для волнового поведения, интерференция наблюдается для водяных, звуковых и световых волн.
Рис. 17.2 (а) Луч света, испускаемый лазером в обсерватории Параналь (часть Европейской южной обсерватории в Чили), действует как луч, движущийся по прямой линии. (кредит: Юрий Белецкий, Европейская южная обсерватория) (б) Лазерный луч, проходящий через сетку вертикальных щелей, создает интерференционную картину, характерную для волны.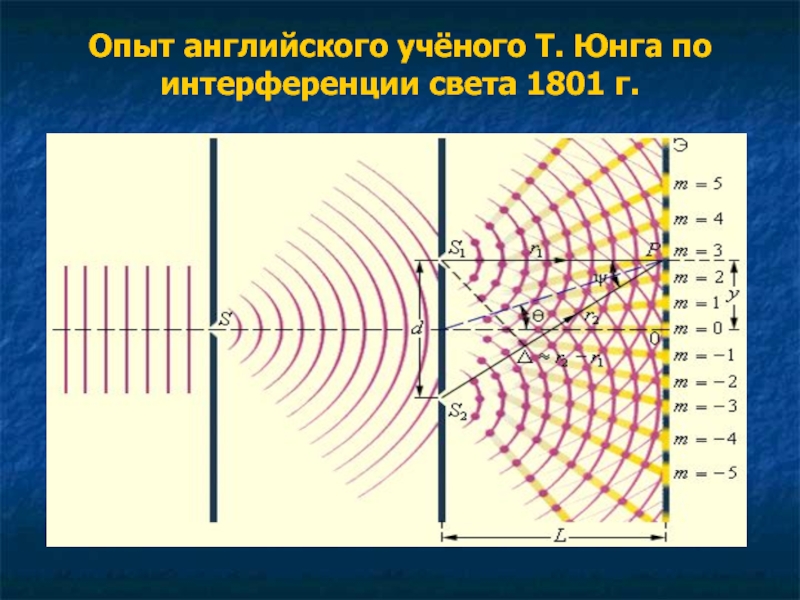
(кредит: Шимон и Слава Рыбка, Wikimedia Commons)
То, что интерференция является характеристикой распространения энергии волнами, более убедительно демонстрируется волнами на воде. На рис. 17.3 показаны водные волны, проходящие через щели между некоторыми камнями. Вы можете легко увидеть, что ширина зазоров аналогична длине волны, и это вызывает интерференционную картину, когда волны проходят за зазоры. Поперечное сечение волн на переднем плане показало бы гребни и впадины, характерные для интерференционной картины.
Рис. 17.3 Входящие волны (вверху рисунка) проходят через щели в скалах и создают интерференционную картину (на переднем плане).
Свет имеет волновые характеристики в различных средах, а также в вакууме. Когда свет переходит из вакуума в какую-либо среду, например воду, его скорость и длина волны меняются, но его частота f остается неизменной. Скорость света в среде v=c/nv=c/n, где n — его показатель преломления.
Если вы разделите обе части уравнения c=fλc=fλ на n , вы получаете c/n=v=fλ/nc/n=v=fλ/n. Следовательно, v=fλnv=fλn, где λnλn — длина волны в среде, а
λn=λn,λn=λn,
, где λλ — длина волны в вакууме, а n — показатель преломления среды. Отсюда следует, что длина волны света в любой среде меньше, чем в вакууме. Например, в воде, у которой n = 1,333, диапазон видимых длин волн составляет от (380 нм)/1,333 до (760 нм)/1,333, или λn=λn=285–570 нм. Хотя длины волн меняются при перемещении из одной среды в другую, цвета не меняются, поскольку цвета связаны с частотой.
Голландский ученый Христиан Гюйгенс (1629–1695) разработал полезную технику для детального определения того, как и где распространяются волны. Он использовал волновые фронты, которые представляют собой точки на поверхности волны, имеющие одну и ту же постоянную фазу (например, все точки, составляющие гребень водной волны).
Принцип Гюйгенса гласит: «Каждая точка на фронте волны является источником вейвлетов, которые распространяются в прямом направлении с той же скоростью, что и сама волна. Новый волновой фронт — это линия, касательная ко всем вейвлетам».
На рис. 17.4 показано, как применяется принцип Гюйгенса. Фронт волны — это длинный фронт, который движется; например, гребень или корыто. Каждая точка волнового фронта излучает полукруглую волну, которая движется со скоростью v . Они нарисованы позже в момент времени t , так что они переместились на расстояние s=vts=vt. Новый волновой фронт представляет собой линию, касательную к вейвлетам, и находится там, где волна находится в момент времени t . Принцип Гюйгенса работает для всех типов волн, включая волны воды, звуковые волны и световые волны. Это будет полезно не только при описании того, как распространяются световые волны, но и как они интерферируют.
Рис. 17.4 Применение принципа Гюйгенса к прямолинейному волновому фронту. Каждая точка на фронте волны излучает полукруглый вейвлет, который перемещается на расстояние s=vts=vt. Новый волновой фронт представляет собой линию, касательную к вейвлетам.
Что происходит, когда волна проходит через отверстие, например свет проникает через открытую дверь в темную комнату? Что касается света, вы ожидаете увидеть резкую тень от дверного проема на полу комнаты, и вы ожидаете, что свет не будет огибать углы в другие части комнаты. Когда звук проходит через дверь, вы слышите его повсюду в комнате и, таким образом, понимаете, что звук распространяется при прохождении через такой проем. Чем отличается поведение звуковых волн от световых в этом случае? Ответ заключается в том, что длины волн, из которых состоит свет, очень короткие, поэтому свет действует как луч. Звук имеет длину волны порядка размера двери, поэтому он огибает углы.
Если свет проходит через меньшие отверстия, часто называемые щелями, вы можете использовать принцип Гюйгенса, чтобы показать, что свет изгибается так же, как и звук (см.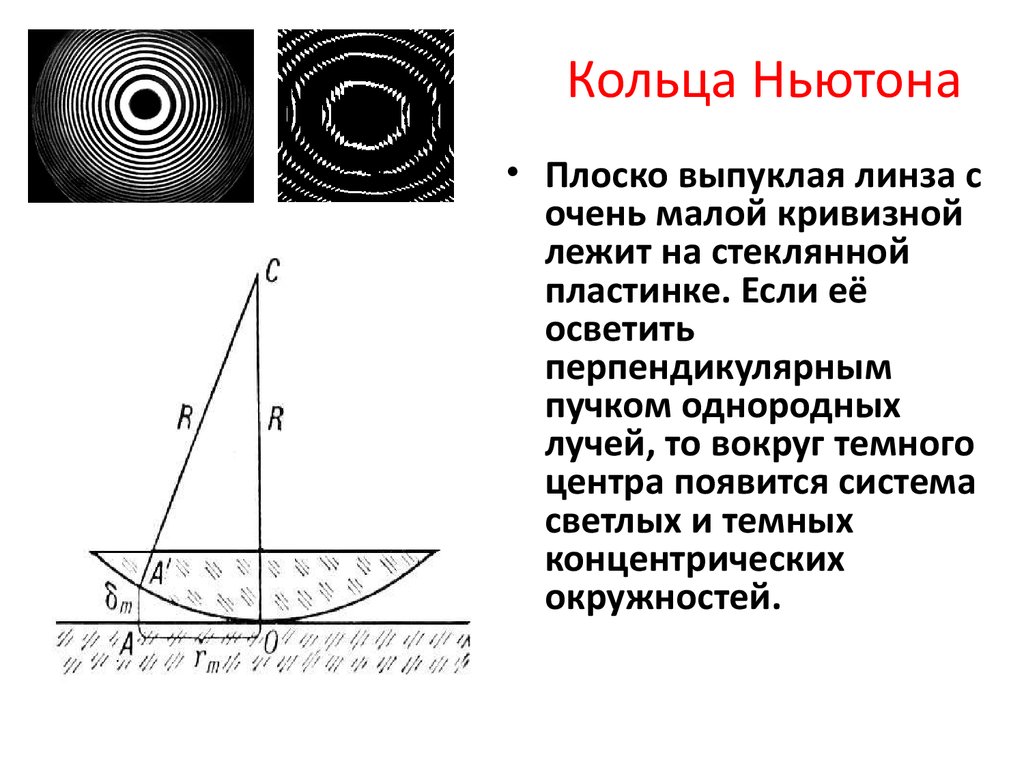
рис. 17.5). Огибание волной краев отверстия или препятствия называется дифракцией. Дифракция — это волновая характеристика, которая имеет место для всех типов волн. Если для явления наблюдается дифракция, это свидетельствует о том, что явление вызвано волнами. Таким образом, горизонтальная дифракция лазерного луча после прохождения через щели на рис. 17.2 свидетельствует о том, что свет обладает свойствами волны.
Рис. 17.5. Применение принципа Гюйгенса к прямому волновому фронту, падающему на отверстие. Края волнового фронта изгибаются после прохождения через отверстие, этот процесс называется дифракцией. Величина изгиба является более экстремальной для небольшого отверстия, что согласуется с тем фактом, что волновые характеристики наиболее заметны при взаимодействии с объектами примерно того же размера, что и длина волны.
И снова волны на воде представляют собой знакомый пример волнового явления, которое легко наблюдать и понимать, как показано на рис. 17.6.
Рис.
17.6 Океанские волны проходят через отверстие в рифе, образуя дифракционную картину. Дифракция возникает из-за того, что ширина отверстия аналогична длине волны.
Watch Physics
Интерференция с одной щелью
В этом видео используются математические расчеты, необходимые для прогнозирования дифракционных картин, вызванных интерференцией с одной щелью.
Щелкните для просмотра содержимого
Какие значения m обозначают место деструктивной интерференции на однощелевой дифракционной картине?
- целых чисел, кроме нуля
- целых чисел
- вещественных чисел без нуля
- действительные числа
Тот факт, что принцип Гюйгенса работал, не считался достаточным доказательством того, что свет является волной. Люди также не хотели принимать волновую природу света, потому что это противоречило идеям Исаака Ньютона, который все еще пользовался большим уважением.
Признание волнового характера света пришло после 1801 г., когда английский физик и врач Томас Юнг (1773–1829 гг.) провел ставший уже классическим эксперимент с двумя щелями (см. рис. 17.7).
Рис. 17.7 Двухщелевой эксперимент Юнга. Здесь свет одной длины волны проходит через пару вертикальных щелей и создает на экране дифракционную картину — многочисленные вертикальные светлые и темные линии, разбросанные по горизонтали. Без дифракции и интерференции свет просто образовал бы две линии на экране.
Когда свет проходит через узкие щели, он преломляется в полукруглые волны, как показано на рис. 17.8 (а). Чистая конструктивная интерференция возникает там, где волны выстраиваются в линию гребень к гребню или впадина к впадине. Чисто деструктивное вмешательство происходит там, где они выстраиваются от гребня к впадине. Свет должен падать на экран и рассеиваться в наших глазах, чтобы рисунок был виден. Аналогичная картина для волн на воде показана на рис. 17.8 (b). Обратите внимание, что области конструктивной и деструктивной интерференции выходят из щелей под определенными углами к исходному лучу.
Эти углы зависят от длины волны и расстояния между щелями, как вы увидите ниже.
Рис. 17.8 Двойные щели создают два интерферирующих источника волн. (а) Свет распространяется (дифрагирует) от каждой щели, потому что щели узкие. Волны перекрываются и интерферируют конструктивно (светлые линии) и деструктивно (темные области). Вы можете увидеть эффект, только если свет падает на экран и рассеивается в ваших глазах. (b) Двухщелевая интерференционная картина волн на воде почти идентична таковой для света. Волновое воздействие больше всего в областях конструктивной интерференции и наименьшее в областях деструктивной интерференции. в) Когда свет, прошедший через двойные щели, падает на экран, мы видим такую картину.
Виртуальная физика
Интерференция волн
Рисунок 17.9 Щелкните здесь для моделирования интерференции волн.
Это моделирование демонстрирует большинство волновых явлений, обсуждаемых в этом разделе.
Во-первых, наблюдайте интерференцию между двумя источниками электромагнитного излучения без добавления щелей. Посмотрите, как волны воды, звук и свет демонстрируют интерференционные картины. Оставайтесь со световыми волнами и используйте только один источник. Создайте дифракционные картины с одной щелью, а затем с двумя. Возможно, вам придется отрегулировать ширину щели, чтобы увидеть рисунок.
Визуально сравните ширину щели с длиной волны. Когда вы получаете наиболее четкую дифракционную картину?
- когда ширина щели больше длины волны
- , когда ширина щели меньше длины волны
- , когда ширина щели сравнима с длиной волны
- , когда ширина щели бесконечна
Расчеты с учетом дифракции и интерференции
Тот факт, что длина волны света одного цвета или монохроматического света может быть рассчитана по его двухщелевой дифракционной картине в экспериментах Юнга, подтверждает вывод о том, что свет обладает волновыми свойствами.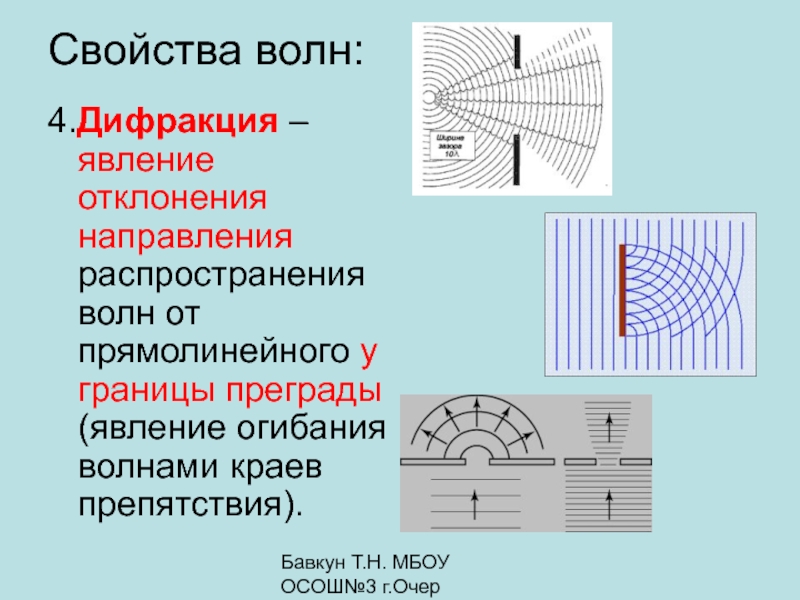
Чтобы понять основу таких расчетов, рассмотрим, как две волны проходят от щелей к экрану. Каждая щель находится на разном расстоянии от заданной точки на экране. Таким образом, на каждый путь укладывается разное количество длин волн. Волны начинаются от щелей в фазе (гребень к гребню), но заканчиваются в противофазе (гребень к впадине) на экране, если пути различаются по длине на половину длины волны, создавая деструктивные помехи. Если пути различаются на целую длину волны, то волны приходят на экран синфазно (гребень к гребню), конструктивно интерферируя. В более общем случае, если пути, по которым проходят две волны, отличаются на любое полуцелое число длин волн (12λ, 32λ, 52λ и т. д.) (12λ, 32λ, 52λ и т. д.), то возникает деструктивная интерференция. Точно так же, если пути, по которым проходят две волны, отличаются на любое целое число длин волн (λ, 2λ, 3λ и т. д.) (λ, 2λ, 3λ и т. д.), возникает конструктивная интерференция.
На рис. 17.10 показано, как определить разность длин пути для волн, идущих от двух щелей к общей точке экрана.
Если экран находится на большом расстоянии по сравнению с расстоянием между щелями, то угол θθ между траекторией и линией от щелей, перпендикулярной экрану (см. рисунок), для каждой траектории примерно одинаков. Это приближение и простая тригонометрия показывают, что разность длин ΔLΔL равна dsinθdsinθ, где d — расстояние между щелями,
ΔL=dsinθ. ΔL=dsinθ.
Чтобы получить конструктивную интерференцию для двойной щели, разность длин пути должна быть целым числом, кратным длине волны, или
dsinθ=mλ, для m=0,1,−1,2,−2,… (конструктивный).dsinθ=mλ, для m=0,1,−1,2,−2,…(конструктивный).
Точно так же, чтобы получить деструктивную интерференцию для двойной щели, разность длин пути должна быть кратной половине длины волны, или
dsinθ=(m+½)λ, для m=0,1,−1,2,−2,… (разрушающий).dsinθ=(m+½)λ, для m=0,1,−1,2 ,−2,…(деструктивный).
Число м порядок помех.
Например, м = 4 — это помехи четвертого порядка.
Рис. 17.10 Пути от каждой щели до общей точки на экране отличаются на величину d sin θd sin θ, если предположить, что расстояние до экрана намного больше, чем расстояние между щелями (здесь не в масштабе).
На рис. 17.11 показано, как уменьшается интенсивность полос конструктивной интерференции с увеличением угла.
Рисунок 17.11 Интерференционная картина для двойной щели имеет интенсивность, которая падает с углом. На фотографии видно множество ярких и темных линий или полос, образованных светом, проходящим через двойную щель.
Свет, проходящий через одинарную щель, образует дифракционную картину, несколько отличную от той, что образуется от двойных щелей. На рис. 17.12 показана картина дифракции от одной щели. Обратите внимание, что центральный максимум больше, чем с обеих сторон, и что интенсивность быстро уменьшается с обеих сторон.
Рис. 17.12 (а) Однощелевая дифракционная картина.
Монохроматический свет, проходящий через одну щель, дает центральный максимум и множество меньших и более тусклых максимумов по обеим сторонам. Центральный максимум в шесть раз выше показанного. (b) На рисунке показан яркий центральный максимум и более тусклые и тонкие максимумы по бокам. (c) Расположение минимумов показано через λλ и D .
Анализ однощелевой дифракции показан на рис. 17.13. Если предположить, что экран находится очень далеко по сравнению с размером щели, лучи, направляющиеся к общей цели, почти параллельны. Это приближение допускает ряд тригонометрических операций, которые приводят к уравнениям для минимумов, создаваемых деструктивной интерференцией.
Dsinθ=mλDsinθ=mλ
или
DyL=mλDyL=mλ
Когда лучи движутся прямо вперед, они остаются в фазе, и получается центральный максимум. Однако, когда лучи проходят под углом θθ относительно первоначального направления луча, каждый луч проходит разное расстояние до экрана, и они могут приходиться в фазе или в противофазе.
Таким образом, луч из центра проходит на расстояние λ/2λ/2 дальше, чем луч от верхнего края щели, приходят в противофазе и деструктивно интерферируют. Точно так же для каждого луча между вершиной и центром щели существует луч между центром и низом щели, который проходит расстояние λ/2λ/2 дальше от общей точки на экране и, таким образом, деструктивно интерферирует. . Симметрично ниже прямого луча будет еще один минимум под тем же углом.
Рисунок 17.13 Уравнения для однощелевой дифракционной картины, где λ — длина волны света, D — ширина щели, θθ — угол между линией от щели до минимума и линией, перпендикулярной экрану , L — расстояние от щели до экрана, y — расстояние от центра шаблона до минимума, а m — ненулевое целое число, указывающее порядок минимума.
Ниже мы суммируем уравнения, необходимые для последующих расчетов.
Скорость света в вакууме c , длина волны света λλ и его частота f связаны следующим образом.
с=fλc=fλ
Длина волны света в среде, λnλn, по сравнению с его длиной волны в вакууме, λλ, равна
17.1λn=λn.λn=λn.
Чтобы рассчитать положение конструктивной интерференции для двойной щели, разность длин пути должна быть целым числом, кратным м длины волны. λλ
dsinθ=mλ, для m=0,1,−1,2,−2,… (конструктивно), dsinθ=mλ, для m=0,1,−1,2,−2,…(конструктивно),
, где d — расстояние между щелями, а θθ — угол между линией от щелей до максимума и линией, перпендикулярной к преграде, в которой расположены щели. Чтобы рассчитать положение деструктивной интерференции для двойной щели, разность длин пути должна быть кратной половине длины волны:
dsinθ=(m+½)λ, для m=0,1,−1,2,−2,… (разрушающий).dsinθ=(m+½)λ, для m=0,1,−1,2 ,−2,…(деструктивный).
Для однощелевой дифрактограммы ширина щели, D , расстояние до первого ( м = 1) минимума деструктивной интерференции, y , расстояние от щели до экрана, L , а длина волны λλ определяется как
DyL=λ.DyL=λ.
Также для однощелевой дифракции
Dsinθ=mλ,Dsinθ=mλ,
, где θθ — угол между линией от щели до минимума и линией, перпендикулярной экрану, а м это порядок минимума.
Рабочий пример
Двухщелевая интерференция
Предположим, вы пропускаете свет гелий-неонового лазера через две щели, разделенные расстоянием 0,0100 мм, и обнаруживаете, что третья яркая линия на экране формируется под углом 10,95º относительно падающий пучок. Какова длина волны света?
СТРАТЕГИЯ
Третья светлая линия обусловлена конструктивной интерференцией третьего порядка, что означает, что м = 3.
Вам дано d = 0,0100 мм и θθ = 10,95º. Таким образом, длину волны можно найти, используя уравнение dsinθ=mλdsinθ=mλ для конструктивной интерференции.
Решение
Уравнение dsinθ=mλdsinθ=mλ. Решение для длины волны λλ дает
17,2λ=dsinθm.λ=dsinθm.
Подстановка известных значений дает
17,3λ=(0,0100 мм)(sin 10,95°)3=6,33×10−4 мм=633 нм.λ=(0,0100 мм)(sin 10,95°)3=6,33×10−4 мм=633 нм.
Обсуждение
В трехзначном выражении 633 нм — это длина волны света, излучаемого обычным гелий-неоновым лазером. Не случайно этот красный цвет похож на тот, который излучают неоновые огни. Однако более важным является тот факт, что интерференционные картины можно использовать для измерения длины волны. Янг сделал это для видимых длин волн. Его аналитический метод до сих пор широко используется для измерения электромагнитных спектров. Для данного порядка угол конструктивной интерференции увеличивается с увеличением λλ, поэтому можно получить спектры (измерения интенсивности в зависимости от длины волны).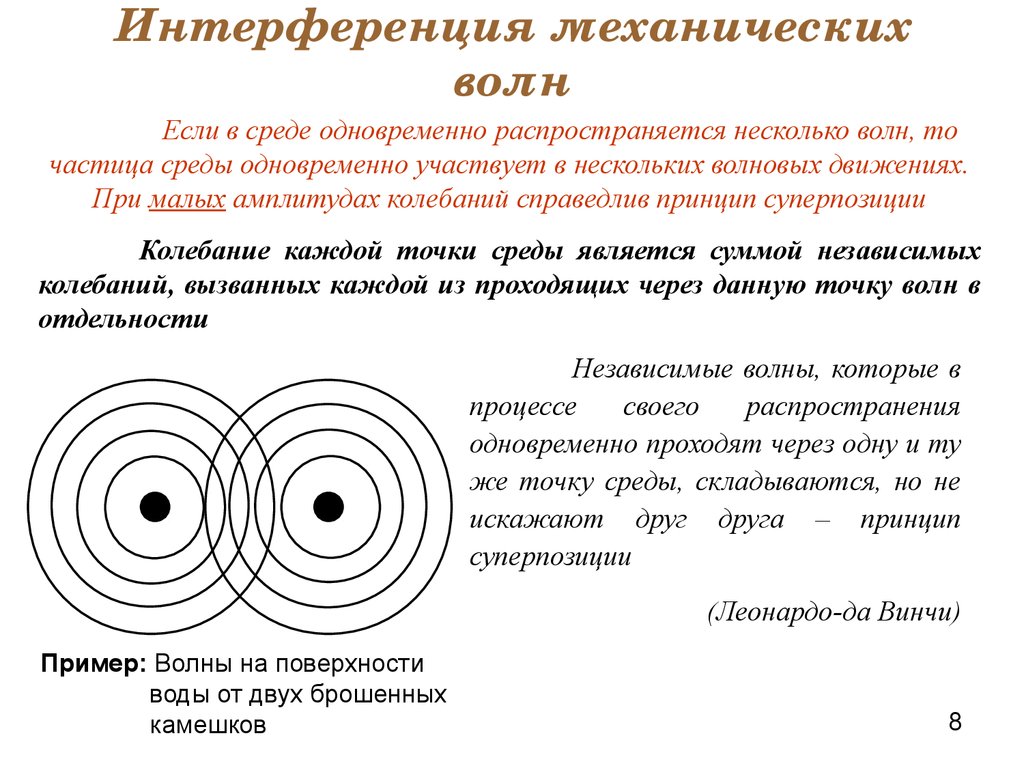
Рабочий пример
Дифракция с одной щелью
Видимый свет с длиной волны 550 нм падает на одну щель и дает второй минимум дифракции под углом 45,0° к направлению падения света. Какова ширина щели?
СТРАТЕГИЯ
Исходя из данной информации и предполагая, что экран находится далеко от щели, вы можете использовать уравнение Dsinθ=mλDsinθ=mλ, чтобы найти D .
Раствор
Приведены количества λλ = 550 нм, м = 2, а θ2θ2 = 45,0°. Решение уравнения Dsinθ=mλDsinθ=mλ для D и подстановка известных значений дает
17,4D=mλsinθ=2(550 нм)sin45,0°=1,56 × 10–6 м.D=mλsinθ=2(550 нм)sin45. 0°=1,56×10-6 м.
Обсуждение
Вы видите, что щель узкая (всего в несколько раз больше длины волны света). Это согласуется с тем фактом, что свет должен взаимодействовать с объектом, сравнимым по размеру с его длиной волны, чтобы проявлять значительные волновые эффекты, такие как эта дифракционная картина с одной щелью.
Практические задачи
Монохроматический свет от лазера проходит через две щели, разделенные расстоянием 0,00500 мм. Третья яркая линия на экране формируется под углом 18,0∘ к падающему лучу. Какова длина волны света?
- 51,5 нм
- 77,3 нм
- 515 нм
- 773 нм
Какова ширина одиночной щели, через которую проходит оранжевый свет с длиной волны 610 нм, образуя первый дифракционный минимум под углом 30,0°?
- 0,863 мкм
- 0,704 мкм
- 0,610 мкм
- 1,22 мкм
Проверьте свое понимание
Упражнение 1
Какой аспект луча монохроматического света изменяется, когда он попадает из вакуума в воду, и как он изменяется?
- Длина волны сначала уменьшается, а затем увеличивается.
- Длина волны сначала увеличивается, а затем уменьшается.
- Длина волны увеличивается.
- Длина волны уменьшается.
Упражнение 2
Выйдите на улицу на солнечный свет и понаблюдайте за своей тенью. У него нечеткие края, даже если у вас их нет. Это дифракционный эффект? Объяснять.
- Это эффект дифракции. Все ваше тело действует как источник нового волнового фронта.
- Это эффект дифракции. Каждая точка на краю вашей тени действует как источник нового волнового фронта.
- Это эффект преломления. Все ваше тело действует как источник нового волнового фронта.
- Это эффект преломления. Каждая точка на краю вашей тени действует как источник нового волнового фронта.
Упражнение 3
Какой аспект монохроматического зеленого света меняется, когда он переходит из вакуума в алмаз, и как он меняется?
- Длина волны сначала уменьшается, а затем увеличивается.
- Длина волны сначала увеличивается, а затем уменьшается.
- Длина волны увеличивается.
- Длина волны уменьшается.
- Печать
- Поделиться
Сегмент D: Звук: дифракция и интерференция
Тег:
- Образование
- Физика в движении
- Модуль 6: Волны и оптика
Возвращаемся в студию звукозаписи, чтобы изучить интерференцию и дифракцию звуковых волн. Мы качественно исследуем, как дифракция влияет на звуковые волны различных частот. Мы также исследуем, как создаются конструктивные и деструктивные интерференционные паттерны и что это означает для того, что мы слышим от источника звука.
Сегмент D: Звук: дифракция и интерференция
From Physics in Motion, Unit 6
Сегмент D: Звук: дифракция и интерференция
Мы возвращаемся в студию звукозаписи, чтобы изучить интерференцию и дифракцию звуковых волн. Мы качественно исследуем, как дифракция влияет на звуковые волны различных частот. Мы также исследуем, как создаются конструктивные и деструктивные интерференционные паттерны и что это означает для того, что мы слышим от источника звука.
Дополнительный сегмент
Наука
Получайте, оценивайте и сообщайте информацию о свойствах и применении волн.
Разработка и использование математических моделей для объяснения механических и электромагнитных волн как распространяющихся возмущений, переносящих энергию.
Разработка и использование моделей для описания и расчета характеристик, связанных с интерференцией и дифракцией волн (одна и две щели).
Придумайте аргумент, который анализирует производство и характеристики звуковых волн.
Планирование и проведение исследований для описания изменений в дифракционных картинах, связанных с геометрией и длиной волны механических и электромагнитных волн.
Получение, оценка и передача информации для объяснения свойств волн.
SPS9.c
Разработка моделей на основе экспериментальных данных, иллюстрирующих явления отражения, преломления, интерференции и дифракции.
Получение, оценка и передача информации в поддержку утверждения о том, что электромагнитные (световые) волны ведут себя иначе, чем механические (звуковые) волны.
S8P4.a
Задавайте вопросы, чтобы объяснить сходства и различия между электромагнитными и механическими волнами.
S8P4.d
Разработайте и используйте модель для сравнения и сопоставления того, как световые и звуковые волны отражаются, преломляются, поглощаются, дифрагируют или проходят через различные материалы.
– Дайте определение терминам дифракция и интерференция.
-Объясните, как дифракция на две щели создает интерференционные картины внутри звуковых волн.
-Опишите, как на амплитуду влияют звуковые волны, интерферирующие друг с другом конструктивно и деструктивно.
-Понять, как частота звуковой волны влияет на ее дифрагию.
-Опишите принцип суперпозиции.
– Объяснить, что такое биение, и уметь рассчитать его для двух заданных волн, которые интерферируют друг с другом.
beat – то, что слышно как изменение амплитуды, когда звуковые волны с почти одинаковыми частотами интерферируют друг с другом.
сжатие – сжатые области повышенного давления в звуковой волне.
конструктивная интерференция – когда две волны одинаковы по частоте и, в случае звуковой волны, их сжатия и разрежения совпадают по фазе.
деструктивная интерференция – когда две волны интерферируют и находятся в противофазе друг с другом на 180º.
дифракция – огибание волн вокруг преграды.
интерференция – комбинация двух или более волн для формирования результирующей волны, в которой смещение либо усиливается, либо нейтрализуется.
принцип суперпозиции – когда волны в пространстве интерферируют друг с другом, они объединяются, образуя большие или меньшие волны.
разрежение – области пониженного давления в звуковой волне.
реверберация – соединение множества отраженных друг от друга звуковых волн в пространстве.
Набор инструментов для учителя Physics in Motion содержит инструкции и ключи к ответам на учебные вопросы, практические задачи и лабораторные работы по всем семи блокам обучения. GPB предлагает набор инструментов для учителей бесплатно для преподавателей Грузии. Чтобы заказать набор инструментов для учителей, заполните и отправьте эту форму, чтобы запросить набор инструментов для учителей.