Курс физики (Грабовский Р.И.)
Курс физики (Грабовский Р.И.)
ОглавлениеПредисловиеВведение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III.  Работа и энергия Работа и энергия§ 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика  Основные положения молекулярно-кинетической теории Основные положения молекулярно-кинетической теории§ 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50.  Внутреннее трение (вязкость) Внутреннее трение (вязкость)Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 66. Испарение и конденсация. Кипение § 67. 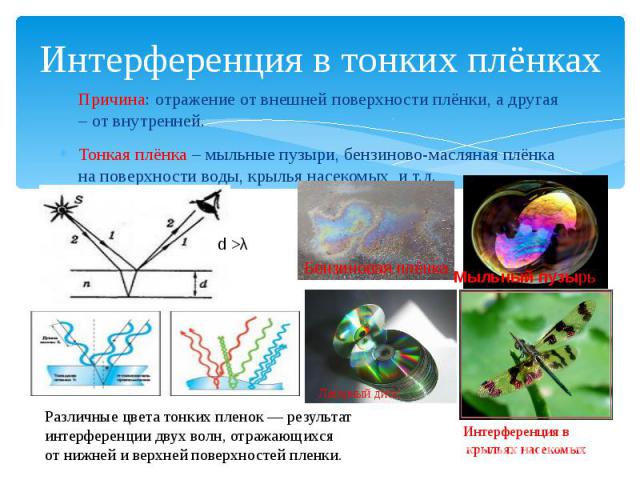 Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором§ 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле.  Поляризация диэлектриков Поляризация диэлектриков§ 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток.  Магнитные поля магнитов и токов Магнитные поля магнитов и токов§ 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106.  § 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122.  Об интерференции света, отраженного от прозрачных пленок Об интерференции света, отраженного от прозрачных пленок§ 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору).  Объяснение спектров излучения и поглощения водорода Объяснение спектров излучения и поглощения водорода§ 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии |
StudyPort.
 Ru – Интерференция света
Ru – Интерференция светаСтраница 1 из 2
41. Определите длину отрезка l1, на котором укладывается столько же длин волн монохроматического света в вакууме, сколько их укладывается на отрезке l2 = 5 мм в стекле. Показатель преломления стекла n = 1,5.
42. Два параллельных световых пучка, отстоящих друг от друга на расстоянии d = 5 см, падают на кварцевую призму (n = 1,49) с преломляющим углом α = 25° . Определите оптическую разность хода d этих пучков на выходе их из призмы.
43. В опыте Юнга расстояние между щелями d = 1 мм, а расстояние l от щелей до экрана равно 3 м. Определите: 1) положение первой светлой полосы; 2) положение третьей темной полосы, если щели освещать монохроматическим светом с длиной волны λ = 0,5 мкм.
44. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0,5 мм, расстояние l от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равна 6 мм.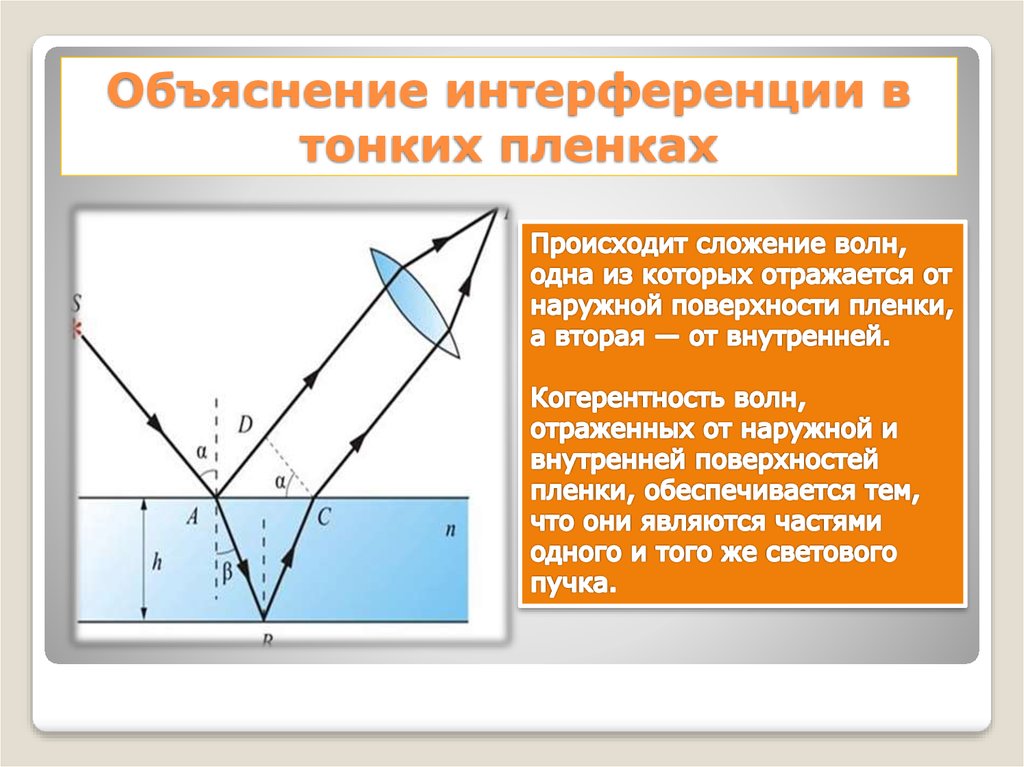 Определите длину волны желтого света.
Определите длину волны желтого света.
45. Расстояние между двумя щелями в опыте Юнга d = 0,5 мм (λ = 0,6 мкм). Определите расстояние l от щелей до экрана, если ширина Δх интерференционных полос равна 1,2 мм.
46. В опыте Юнга расстояние l от щелей до экрана равно 3 м. Определите угловое расстояние между соседними светлыми полосами, если третья световая полоса на экране отстоит от центра интерференционной картины на 4,5 мм.
47. Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (n = 1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны λ = 0,5 мкм. Определите толщину пластинки.
48. Определите, во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалом Френеля, если фиолетовый светофильтр (0,4 мкм) заменить красным (0,7 мкм).
49. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равно a = 30 см и b = 1,5 м.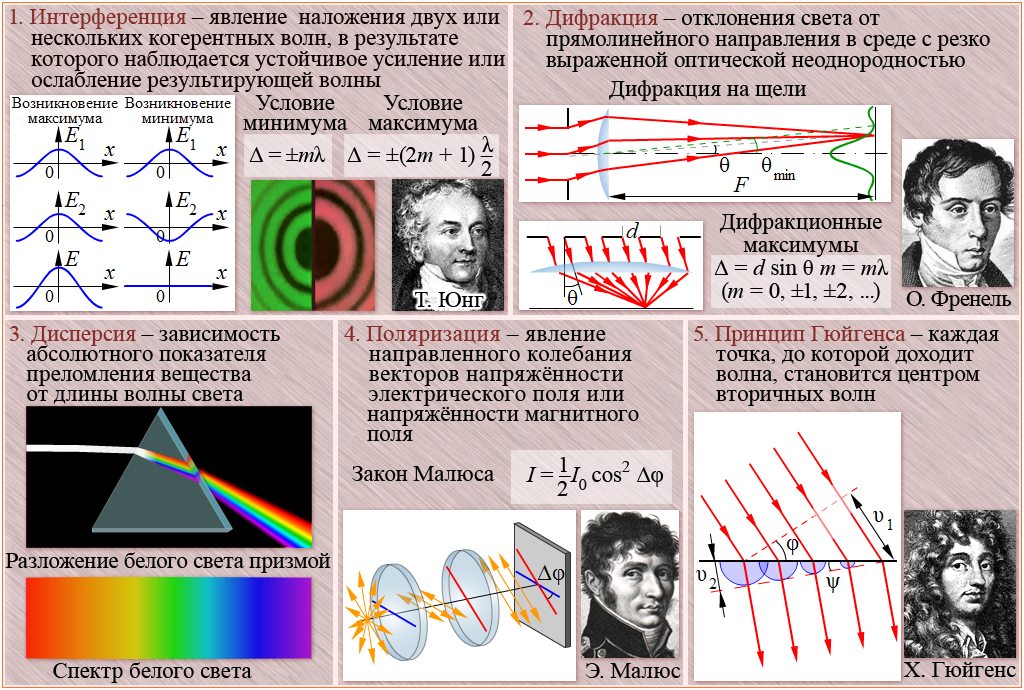 Бипризма стеклянная (n = 1,5) с преломляющим углом ν = 20′. Определите длину волны света, если ширина интерференционных полос Δx = 0,65 мм.
Бипризма стеклянная (n = 1,5) с преломляющим углом ν = 20′. Определите длину волны света, если ширина интерференционных полос Δx = 0,65 мм.
50. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равно a = 48 см и b = 6 м. Бипризма стеклянная (n = l,5) с преломляющим углом ν = 10′. Определите максимальное число полос, наблюдаемых на экране, если λ = 600 нм.
51. На плоскопараллельную пленку с показателем преломления n = 1,33 под углом i = 45° падает параллельный пучок белого света. Определите, при какой наименьшей толщине пленки зеркально отраженный свет наиболее сильно окрасится в желтый цвет (λ = 0,6 мкм).
52. На стеклянный клин (n = 1,5) нормально падает монохроматический свет (λ = 698 нм). Определите угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм.
53. На стеклянный клин (n = 1,5) нормально падает монохроматический свет. Угол клина равен 4′. Определите длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.
Угол клина равен 4′. Определите длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.
54. На тонкую мыльную пленку (n = 1,33) под углом i = 30° падает монохроматический свет с длиной волны λ = 0,6 мкм. Определите угол между поверхностями пленки, если расстояние b между интерференционными полосами в отраженном свете равно 4 мм.
55. Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами Δx1 = 0,4 мм. Определите расстояние Δx2 между интерференционными полосами, если пространство между пластинками, образующими клин, заполнить прозрачной жидкостью с показателем преломления n = 1,33.
56. Плосковыпуклая линза радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определите длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм.
57. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,55 мкм, падающим нормально. Определите толщину воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой в том месте, где в отраженном свете наблюдается четвертое темное кольцо.
58. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,6 мкм, падающим нормально. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение ведется в проходящем свете. Радиус кривизны линзы R = 4 м. Определите показатель преломления жидкости, если радиус второго светлого кольца r = 1,8 мм.
59. Плосковыпуклая линза с показателем преломления n = 1,6 выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в отраженном свете (λ = 0,6 мкм) равен 0,9 мм. Определите фокусное расстояние линзы.
60. Плосковыпуклая линза с радиусом сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметр десятого темного кольца Ньютона в отраженном свете равен 1 мм. Определите длину волны света.
Диаметр десятого темного кольца Ньютона в отраженном свете равен 1 мм. Определите длину волны света.
61. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определите показатель преломления жидкости.
Помехи в тонких пленках
Помехи в тонких пленкахДалее: Примеры работы Вверх: Волновая оптика Предыдущий: Двухщелевой эксперимент Янга В повседневной жизни интерференция света чаще всего вызывает легко наблюдаемые эффекты при свет падает на тонкую пленку какого-либо прозрачного материала. Например, яркие цвета, видимые в мыльных пузырях, в масле пленки, плавающие на лужах воды и в перьях павлина хвост, обусловлены интерференцией этого типа.
Предположим, что между двумя
кусочки стекла, как показано на рис. 88. Если монохроматический свет
( например , желтый свет натриевой лампы) падает почти
обычно на пленку, то часть света отражается от
поверхность раздела между нижней частью верхней пластины и воздухом, и
часть отражается от границы между воздухом и верхней частью
нижняя плита. Глаз фокусирует эти два параллельных световых луча в одном месте.
пятно на сетчатке. Два луча производят либо разрушительные, либо созидательные
интерференция, в зависимости от того, равна ли их разность хода
на нечетное или четное число полуволн соответственно.
88. Если монохроматический свет
( например , желтый свет натриевой лампы) падает почти
обычно на пленку, то часть света отражается от
поверхность раздела между нижней частью верхней пластины и воздухом, и
часть отражается от границы между воздухом и верхней частью
нижняя плита. Глаз фокусирует эти два параллельных световых луча в одном месте.
пятно на сетчатке. Два луча производят либо разрушительные, либо созидательные
интерференция, в зависимости от того, равна ли их разность хода
на нечетное или четное число полуволн соответственно.
Пусть – толщина воздушной пленки. Разница в длине пути
между двумя световыми лучами, показанными на рисунке, четко
.
Наивно можно было бы ожидать, что конструктивное вмешательство и, следовательно, яркость ,
произойдет, если
, где целое число,
и деструктивной интерференции, а значит, темнота , произойдет, если .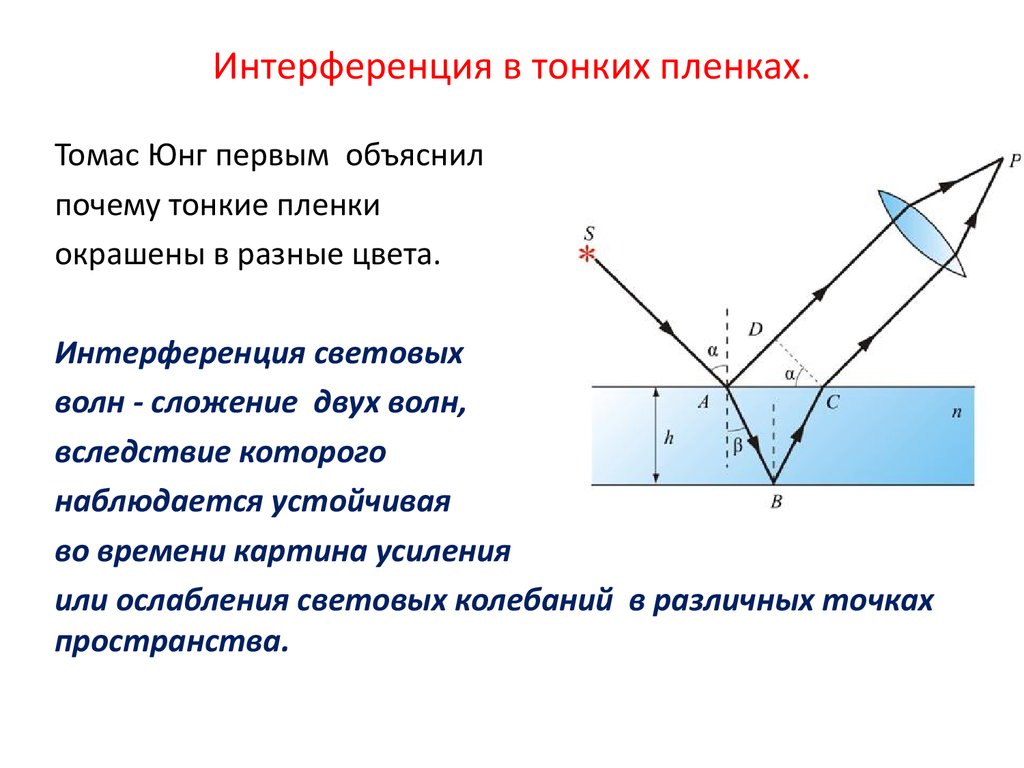 Однако это не тот
всю картину, так как вводится дополнительная разность фаз между
два луча при отражении. Первый луч отражается на границе раздела
между оптически плотной средой (стеклом), через которую
распространяется луч и менее плотная среда (воздух).
При отражении от такого интерфейса нет изменения фазы, просто
так как нет изменения фазы, когда волна на струне отражается от
свободный конец строки. (Как волны на струнах, так и электромагнитные
волны поперечные волны , а значит, имеют аналогичные
характеристики.)
Второй луч отражается на границе раздела
между оптически менее плотной средой (воздухом), через которую
распространяется луч и плотная среда (стекло). Eсть
изменение фазы при отражении от такого интерфейса, как и
есть изменение фазы, когда волна на струне
отражается от фиксированного конца. Таким образом, дополнительный фазовый переход
вводится между двумя лучами, что эквивалентно
дополнительная разность путей . Когда это дополнительное
фазового перехода условие конструктивного
вмешательство становится
Однако это не тот
всю картину, так как вводится дополнительная разность фаз между
два луча при отражении. Первый луч отражается на границе раздела
между оптически плотной средой (стеклом), через которую
распространяется луч и менее плотная среда (воздух).
При отражении от такого интерфейса нет изменения фазы, просто
так как нет изменения фазы, когда волна на струне отражается от
свободный конец строки. (Как волны на струнах, так и электромагнитные
волны поперечные волны , а значит, имеют аналогичные
характеристики.)
Второй луч отражается на границе раздела
между оптически менее плотной средой (воздухом), через которую
распространяется луч и плотная среда (стекло). Eсть
изменение фазы при отражении от такого интерфейса, как и
есть изменение фазы, когда волна на струне
отражается от фиксированного конца. Таким образом, дополнительный фазовый переход
вводится между двумя лучами, что эквивалентно
дополнительная разность путей . Когда это дополнительное
фазового перехода условие конструктивного
вмешательство становится
| (377) |
где целое число.
 Аналогично условие для
деструктивная интерференция становится
Аналогично условие для
деструктивная интерференция становится | (378) |
Для белого света вышеуказанные критерии дают конструктивную интерференцию для одни длины волн и деструктивные помехи для других. Таким образом, свет, отраженный от пленки, демонстрирует эти цвета для которых имеет место конструктивная интерференция.
Если тонкая пленка состоит из воды, масла или другого прозрачного материала
показателя преломления, то результаты в основном такие же, как и для
воздушная пленка, за исключением того, что длина волны света в
пленка уменьшается от (длины волны в вакууме) до .
Отсюда следует, что модифицированные критерии конструктивного и деструктивного
помехи
| (379) |
и
| (380) |
соответственно.

Далее: Примеры работы Вверх: Волновая оптика Предыдущий: Двухщелевой эксперимент Янга Ричард Фицпатрик 2007-07-14
12.7 Интерференция в тонкой пленке – Колледж Дугласа, физика 1207
Глава 12 – Волновая оптика
Цель обучения
- Обсудить образование радуги тонкими пленками.
Яркие цвета нефтяного пятна, плавающего на воде, или мыльного пузыря, освещенного солнцем, вызваны интерференцией. Самые яркие цвета — это те, которые конструктивно мешают. Эта интерференция возникает между светом, отраженным от разных поверхностей тонкой пленки; таким образом, эффект известен как тонкопленочная интерференция. Как отмечалось ранее, интерференционные эффекты наиболее заметны, когда свет взаимодействует с чем-то, размер которого равен его длине волны. Тонкая пленка – это пленка толщиной t в несколько раз меньше длины волны света, λ . Поскольку цвет косвенно связан с λ и поскольку все интерференции каким-то образом зависят от отношения λ к размеру вовлеченного объекта, мы должны ожидать увидеть разные цвета для пленок разной толщины, как на рис. 1.
Поскольку цвет косвенно связан с λ и поскольку все интерференции каким-то образом зависят от отношения λ к размеру вовлеченного объекта, мы должны ожидать увидеть разные цвета для пленок разной толщины, как на рис. 1.
Что вызывает интерференцию тонкой пленки? На рис. 2 показано, как может интерферировать свет, отраженный от верхней и нижней поверхностей пленки. Падающий свет лишь частично отражается от верхней поверхности пленки (луч 1). Остаток попадает на пленку и сам частично отражается от нижней поверхности. Часть света, отраженного от нижней поверхности, может выходить из верхней части пленки (луч 2) и мешать свету, отраженному сверху (луч 1). Поскольку луч, попадающий на пленку, проходит большее расстояние, он может быть в фазе или не в фазе с лучом, отраженным сверху. Однако снова рассмотрим на мгновение пузырьки на рис. 1. Пузырьки темнее всего там, где они самые тонкие. Более того, если вы внимательно понаблюдаете за мыльным пузырем, то заметите, что он темнеет в том месте, где лопается. Для очень тонких пленок разница в длинах пути лучей 1 и 2 на рис. 2 незначительна; так почему же они должны вмешиваться деструктивно, а не конструктивно? Ответ заключается в том, что изменение фазы может произойти при отражении. Правило следующее:
1. Пузырьки темнее всего там, где они самые тонкие. Более того, если вы внимательно понаблюдаете за мыльным пузырем, то заметите, что он темнеет в том месте, где лопается. Для очень тонких пленок разница в длинах пути лучей 1 и 2 на рис. 2 незначительна; так почему же они должны вмешиваться деструктивно, а не конструктивно? Ответ заключается в том, что изменение фазы может произойти при отражении. Правило следующее:
Когда свет отражается от среды, показатель преломления которой больше, чем у среды, в которой он распространяется, происходит изменение фазы 180 o (или λ/2). «Выше значит половина».
Рисунок 2. Свет, падающий на тонкую пленку, частично отражается (луч 1) и частично преломляется на верхней поверхности. Преломленный луч частично отражается от нижней поверхности и выходит как луч 2. Эти лучи будут интерферировать так, как это зависит от толщины пленки и показателей преломления различных сред. Если пленка на рис. 2 представляет собой мыльный пузырь (по сути, вода с воздухом с обеих сторон), то для луча 1 имеется сдвиг λ/2 , а для луча 2 отсутствует. Таким образом, когда пленка очень тонкая, разница в длине хода между двумя лучами незначительна, они точно не совпадают по фазе, и деструктивная интерференция будет происходить на всех длинах волн, поэтому мыльный пузырь здесь будет темным.
2 представляет собой мыльный пузырь (по сути, вода с воздухом с обеих сторон), то для луча 1 имеется сдвиг λ/2 , а для луча 2 отсутствует. Таким образом, когда пленка очень тонкая, разница в длине хода между двумя лучами незначительна, они точно не совпадают по фазе, и деструктивная интерференция будет происходить на всех длинах волн, поэтому мыльный пузырь здесь будет темным.
Толщина пленки по отношению к длине волны света является другим решающим фактором интерференции тонких пленок. Луч 2 на рисунке 2 проходит большее расстояние, чем луч 1. Если свет падает перпендикулярно поверхности, луч 2 проходит расстояние примерно 2t дальше луча 1. Когда это расстояние является целым или полуцелым кратным длины волны в среде λ n = λ/n , где λ — длина волны в вакууме, а n — показатель преломления), возникает конструктивная или деструктивная интерференция, в зависимости также от того, есть ли изменение фазы в том или ином луче.
Пример 1. Расчет неотражающего покрытия линз с использованием интерференции тонкой пленки
В сложных камерах используется серия из нескольких линз. Свет может отражаться от поверхностей этих различных линз и ухудшать четкость изображения. Чтобы ограничить эти отражения, линзы покрыты тонким слоем фторида магния, который вызывает деструктивную интерференцию тонкой пленки. Какой самой тонкой может быть эта пленка, если ее показатель преломления равен 1,38 и она предназначена для ограничения отражения света с длиной волны 550 нм, обычно самой интенсивной видимой длины волны? Показатель преломления стекла 1,52.
Стратегия
См. рис. 2 и используйте n 1 = 1,00 для воздуха, n 2 = 1,38 и 5
n 3 2
. И луч 1, и луч 2 будут иметь сдвиг λ/2 при отражении, поскольку они отражаются от вещества с более высоким показателем преломления или «более высокий означает половину». Таким образом, для получения деструктивной интерференции луч 2 должен будет пройти на половину длины волны дальше, чем луч 1. Для лучей, падающих перпендикулярно, разница в длине пути составляет 2т.
Таким образом, для получения деструктивной интерференции луч 2 должен будет пройти на половину длины волны дальше, чем луч 1. Для лучей, падающих перпендикулярно, разница в длине пути составляет 2т. Решение
Для получения деструктивной интерференции здесь
где λ n2 это длина волны в пленке и определяется как λ n2 9015 λ/n 2 .
Таким образом,
Решение для t и ввод известных значений дает
Обсуждение
Пленки, подобные пленке в этом примере, наиболее эффективны для создания деструктивной интерференции, когда используется самый тонкий слой, поскольку свет проходит через более широкий диапазон углов падения будет уменьшаться по интенсивности. Эти пленки называются неотражающими покрытиями; однако это лишь приблизительно правильное описание, поскольку другие длины волн будут нейтрализованы лишь частично. Неотражающие покрытия используются в автомобильных стеклах и солнцезащитных очках.
Неотражающие покрытия используются в автомобильных стеклах и солнцезащитных очках.
Тонкопленочная интерференция является наиболее конструктивной или наиболее деструктивной, когда разность длин пути для двух лучей составляет целую или полуцелую длину волны соответственно. То есть для лучей, падающих перпендикулярно, 2t = λ n , 2λ n , 3λ n …. . Чтобы узнать, является ли интерференция конструктивной или деструктивной, вы должны также определить, происходит ли изменение фазы при отражении. Таким образом, интерференция тонкой пленки зависит от толщины пленки, длины волны света и показателей преломления. Для белого света, падающего на пленку различной толщины, вы будете наблюдать радужные цвета конструктивной интерференции для различных длин волн при изменении толщины.
Пример 2: мыльные пузыри: более одной толщины может быть конструктивной
(a) Каковы три наименьших толщины мыльного пузыря, которые создают конструктивную интерференцию для красного света с длиной волны 650 нм? Показатель преломления мыла принимают равным показателю преломления воды. б) Какие три наименьшие толщины дадут деструктивную интерференцию?
б) Какие три наименьшие толщины дадут деструктивную интерференцию?
Стратегия и концепция
Используйте рисунок 2, чтобы визуализировать пузырек. Обратите внимание, что n 1 = n 3 = 1,00 для воздуха и n 2 = n мыло = n вода = 1,333 для мыла (эквивалентно воде). Для луча 1, отраженного от верхней поверхности пузырька, имеется сдвиг λ/2 , а для луча 2, отраженного от нижней поверхности, смещения нет. Таким образом, чтобы получить конструктивную интерференцию, разность длин пути ( 2t ) должна быть полуцелым кратным длины волны — первые три равны λ n /2 . 3 λ n /2 и 5 λ n /2 . Чтобы получить деструктивную интерференцию, разность длин пути должна быть целым кратным длины волны — первые три равны 0, λ n и 2 λ n .
Решение для (a)
Конструктивная интерференция возникает здесь, когда
Наименьшая конструктивная толщина t c , следовательно,
t c = λ n /4 = (650 нм) / ( (1.33) (4)) = 122 нм
и /4.
t’ c = 366 нм
Наконец, третья толщина, создающая конструктивную интерференцию, равна t” c = 5 λ n /4. так, что
t”c = 610 нм
Решение для (b)
Для деструктивной помехи разность длин пути здесь является целым кратным длины волны. Первый возникает при нулевой толщине, так как на верхней поверхности происходит фазовый переход. То есть
t d =0 м
Первая ненулевая толщина, создающая деструктивную интерференцию, равна Замена известных значений дает
Наконец, третья деструктивная толщина равна
2t” d = 2 λ n
t” d = λ n / 6 n 901 (6 n 901 50 нм) / (1,333) = 488 нм
Обсуждение
Если бы пузырек освещался чистым красным светом, мы бы увидели яркие и темные полосы с очень равномерным увеличением толщины. Сначала будет темная полоса с толщиной 0, затем яркая с толщиной 122 нм , затем темная с толщиной 244 нм , яркая с толщиной 366 нм , темный 488 нм и яркий 610 нм. Если бы пузырек плавно менялся по толщине, как гладкий клин, то полосы располагались бы равномерно.
Сначала будет темная полоса с толщиной 0, затем яркая с толщиной 122 нм , затем темная с толщиной 244 нм , яркая с толщиной 366 нм , темный 488 нм и яркий 610 нм. Если бы пузырек плавно менялся по толщине, как гладкий клин, то полосы располагались бы равномерно.
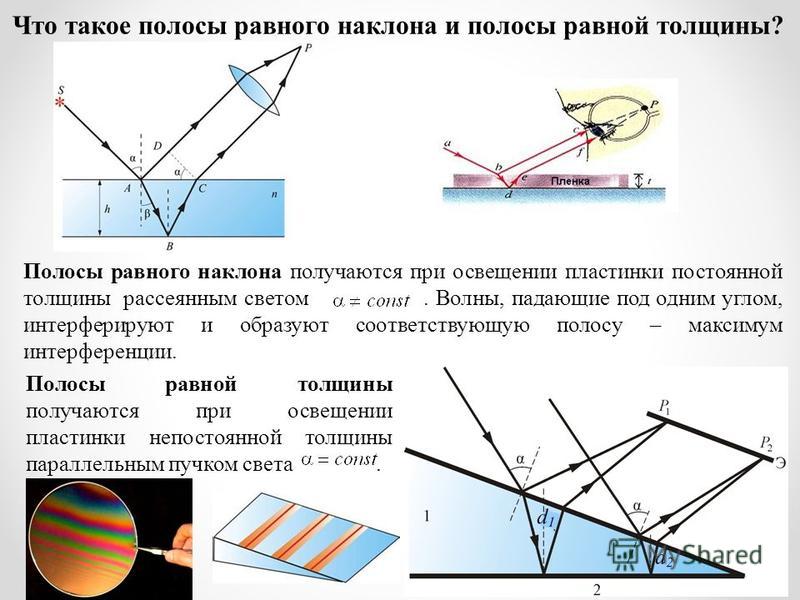
Другой пример тонкопленочной интерференции можно увидеть при разделении предметных стекол микроскопа (см. рис. 3). Горки очень плоские, так что клин воздуха между ними очень равномерно увеличивается в толщине. Фазовый переход происходит на второй поверхности, но не на первой, поэтому в месте соприкосновения слайдов появляется темная полоса. Цвета радуги конструктивной интерференции повторяются, снова и снова переходя от фиолетового к красному по мере увеличения расстояния между слайдами. По мере увеличения слоя воздуха полосы становится труднее увидеть, потому что небольшие изменения угла падения больше влияют на различия в длине пути. Если вместо белого света используется свет чистой длины волны, то получаются яркие и темные полосы, а не повторяющиеся цвета радуги.
Важным применением тонкопленочной интерференции является производство оптических приборов. Линзу или зеркало можно сравнить с мастером, когда он шлифуется, что позволяет придать ему форму с точностью менее длины волны по всей его поверхности. Рисунок 4 иллюстрирует явление, называемое кольцами Ньютона, которое возникает, когда плоские поверхности двух линз помещаются вместе. (Круговые полосы называются кольцами Ньютона, потому что Исаак Ньютон подробно описал их и их использование. Ньютон их не открыл; открыл Роберт Гук, и Ньютон не верил, что они возникли из-за волнового характера света.) Каждое последующее кольцо данный цвет указывает на увеличение расстояния между линзой и бланком только на одну длину волны, так что можно получить большую точность. Как только объектив станет идеальным, колец не будет.
Крылья некоторых мотыльков и бабочек имеют почти радужный цвет из-за интерференции тонкой пленки. Помимо пигментации, на цвет крыла большое влияние оказывает конструктивная интерференция определенных длин волн, отраженных от его пленочной поверхности. Производители автомобилей предлагают специальные покрасочные работы, в которых используется тонкопленочная интерференция для получения цветов, меняющихся под углом. Этот дорогостоящий вариант основан на изменении разности длины пути тонкой пленки в зависимости от угла. Защитные элементы на кредитных картах, банкнотах, водительских правах и подобных предметах, которые могут быть подделаны, используют интерференцию тонких пленок, дифракционные решетки или голограммы. Австралия лидировала в выпуске долларовых банкнот, напечатанных на полимере с защитным элементом в виде дифракционной решетки, что затрудняет подделку валюты. Другие страны, такие как Новая Зеландия и Тайвань, используют аналогичные технологии, в то время как валюта Соединенных Штатов включает эффект интерференции тонкой пленки.
Австралия лидировала в выпуске долларовых банкнот, напечатанных на полимере с защитным элементом в виде дифракционной решетки, что затрудняет подделку валюты. Другие страны, такие как Новая Зеландия и Тайвань, используют аналогичные технологии, в то время как валюта Соединенных Штатов включает эффект интерференции тонкой пленки.
Установление соединений: домашний эксперимент — интерференция на тонкой пленке
Одной из особенностей интерференционных и дифракционных решеток на тонкой пленке является то, что рисунок смещается при изменении угла, под которым вы смотрите или двигаете головой. Найдите вокруг себя примеры тонкопленочных интерференций и решеток. Объясните, как меняются закономерности для каждого конкретного примера. Найдите примеры, когда толщина изменяется, что приводит к изменению цвета. Если вы можете найти два предметных стекла микроскопа, попробуйте наблюдать эффект, показанный на рисунке 3. Попробуйте разделить один конец двух предметных стекол волосом или, может быть, тонким листом бумаги и наблюдайте за эффектом.
Шаг 1. Изучите ситуацию, чтобы определить наличие помех . Определите, учитываются ли в задаче щели или интерференция тонкой пленки.
Шаг 2. Если используются щели , обратите внимание, что дифракционные решетки и двойные щели дают очень похожие интерференционные картины, но решетки имеют более узкие (острые) максимумы. Однощелевые картины характеризуются большим центральным максимумом и меньшими максимумами по бокам.
Шаг 3. Если имеет место интерференция тонкой пленки, обратите внимание на разность длин пути между двумя интерферирующими лучами . Обязательно используйте длину волны в рассматриваемой среде, поскольку она отличается от длины волны в вакууме. Обратите также внимание на дополнительный фазовый сдвиг на 1/2 длины волны, когда свет отражается от среды с большим показателем преломления.
Шаг 4. Точно определить, что необходимо определить в задаче (определить неизвестные) . Письменный список полезен. Нарисуйте схему ситуации. Надписи на диаграмме полезны.
Письменный список полезен. Нарисуйте схему ситуации. Надписи на диаграмме полезны.
Шаг 5. Составьте список того, что дано или может быть выведено из сформулированной проблемы (укажите известное) .
Шаг 6. Решите соответствующее уравнение для определяемой величины (неизвестной) и введите известные . Щели, решетки и предел Рэлея включают уравнения.
Шаг 7. В случае тонкопленочной интерференции у вас будет конструктивная интерференция для полного сдвига, равного целому числу длин волн. У вас будет деструктивная интерференция на суммарный сдвиг на полуцелое число длин волн . Всегда имейте в виду, что гребень к гребню конструктивен, тогда как гребень к впадине деструктивен.
Шаг 8. Проверьте, разумен ли ответ: Имеет ли смысл? Например, углы в интерференционных картинах не могут превышать 90 градусов.
- Интерференция в тонкой пленке возникает между светом, отраженным от верхней и нижней поверхностей пленки.
 В дополнение к разнице длины пути может иметь место изменение фазы.
В дополнение к разнице длины пути может иметь место изменение фазы. - Когда свет отражается от среды, показатель преломления которой выше, чем у среды, в которой он распространяется, происходит изменение фазы на 180 градусов (или сдвиг длины волны на 1/2).
Задачи и упражнения
1: Мыльный пузырь имеет толщину 100 нм и освещен белым светом, падающим перпендикулярно его поверхности. Какая длина волны и цвет видимого света наиболее конструктивно отражается, при условии того же показателя преломления, что и у воды?
2: Нефтяное пятно на воде имеет толщину 120 нм и освещено белым светом, падающим перпендикулярно его поверхности. Какого цвета появляется масло (какая длина волны наиболее конструктивно отражается), если его показатель преломления равен 1,40?
3: Рассчитайте минимальную толщину нефтяного пятна на воде, которое выглядит голубым при освещении белым светом перпендикулярно ее поверхности. Примите длину волны синего цвета равной 470 нм, а показатель преломления масла — 1,40.
Примите длину волны синего цвета равной 470 нм, а показатель преломления масла — 1,40.
4: Найдите наименьшую толщину мыльного пузыря, который кажется красным при освещении белым светом перпендикулярно его поверхности. Возьмем длину волны 680 нм и примем тот же показатель преломления, что и у воды.
5: Пленка мыльной воды n = 1,33 поверх пластиковой разделочной доски n = 1,66 имеет толщину 233 нм . Какой цвет сильнее всего отражается, если его освещать перпендикулярно его поверхности?
6: Каковы три наименьшие ненулевые толщины мыльной воды n = 1,33 на оргстекле, если оно выглядит зеленым (конструктивно отражая свет с длиной волны 520 нм) при перпендикулярном освещении белым светом? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для волновой оптики».
7: Предположим, у вас есть система линз, предназначенная в первую очередь для красного света с длиной волны 700 нм. Какое второе самое тонкое покрытие из флюорита (фторида магния) не будет отражать свет для этой длины волны? См. разработанный пример ранее в этом разделе. Показатель преломления для фторида магния представляет собой число типа «поищите», в данном случае n = 1,38. Он на стекле с показателем преломления 1,52. Неотражающий означает, что это будет тёмная, разрушительная интерференция.
Какое второе самое тонкое покрытие из флюорита (фторида магния) не будет отражать свет для этой длины волны? См. разработанный пример ранее в этом разделе. Показатель преломления для фторида магния представляет собой число типа «поищите», в данном случае n = 1,38. Он на стекле с показателем преломления 1,52. Неотражающий означает, что это будет тёмная, разрушительная интерференция.
8: (a) По мере того, как мыльный пузырь становится тоньше, он становится темным, потому что разница в длине пути становится малой по сравнению с длиной волны света, а на верхней поверхности наблюдается фазовый сдвиг. Если становится темно, когда разница в длине пути составляет менее одной четверти длины волны, какой максимальной толщины может быть пузырек, чтобы он казался темным на всех видимых длинах волн? Примите тот же показатель преломления, что и у воды. (b) Обсудите хрупкость пленки с учетом найденной толщины.
9: Масляная пленка на воде будет казаться темной, когда она очень тонкая, потому что разница в длине пути становится малой по сравнению с длиной волны света, а на верхней поверхности имеется фазовый сдвиг. Если становится темно, когда разность длин пути составляет менее одной четверти длины волны, какой может быть самая густая нефть, которая кажется темной на всех видимых длинах волн? Нефть имеет показатель преломления 1,40.
Если становится темно, когда разность длин пути составляет менее одной четверти длины волны, какой может быть самая густая нефть, которая кажется темной на всех видимых длинах волн? Нефть имеет показатель преломления 1,40.
10: На рисунке 3 показаны два предметных стекла, освещенные светом чистой длины волны, падающим перпендикулярно. Верхний слайд одним концом касается нижнего слайда, а другим концом опирается на волосок диаметром 0,100 мм, образуя воздушный клин. а) На каком расстоянии друг от друга находятся темные полосы, если предметные стекла имеют длину 7,50 см и 589-нм свет используется? (b) Есть ли разница в том, сделаны ли предметные стекла из коронки или бесцветного стекла? Объяснять.
11: На рисунке 3 показаны два предметных стекла длиной 7,50 см, освещенные чистым светом с длиной волны 589 нм, падающим перпендикулярно. Верхний ползун касается нижнего ползуна одним концом и упирается в мусор другим концом, образуя воздушный клин.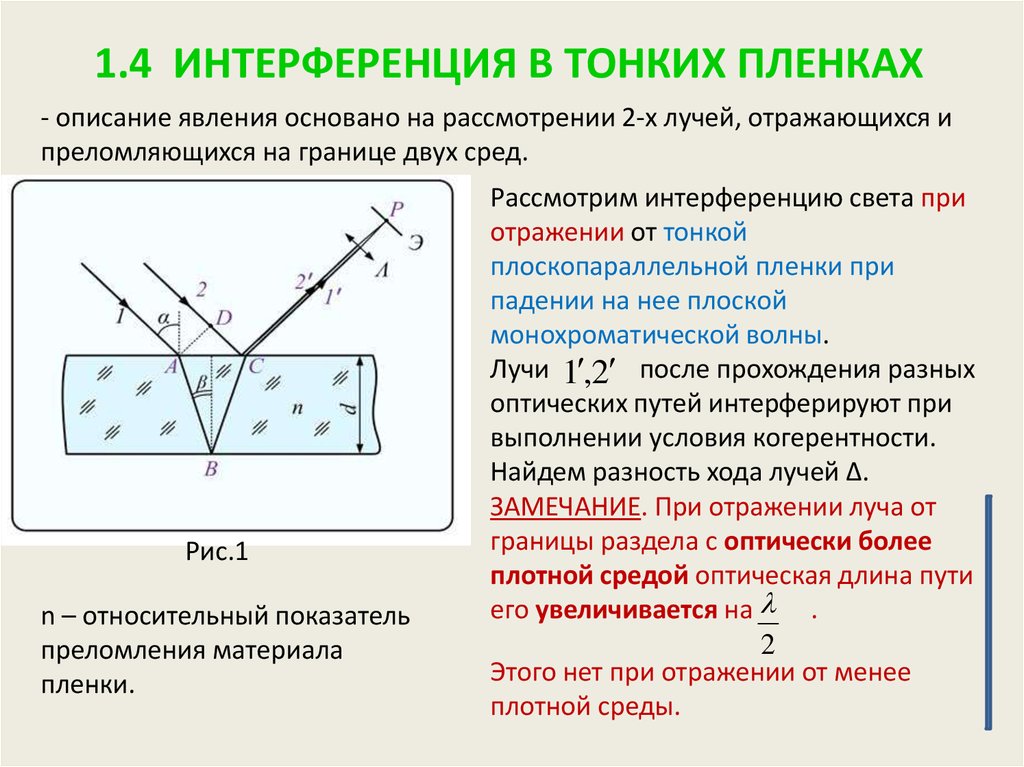


 В дополнение к разнице длины пути может иметь место изменение фазы.
В дополнение к разнице длины пути может иметь место изменение фазы.