Используя правило лопиталя найти предел онлайн: Решение пределов · oнлайн с подробным решением - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Задание для практической работы “Вычисление пределов с помощью правила Лопиталя ” по учебной дисциплине ЕН.01 Элементы высшей математики

Практическая работа №16

Вычисление пределов с помощью правила Лопиталя

Цель: научиться вычислять пределы с помощью правила Лопиталя.

Краткая теоретическая справка

Теорема Лопиталя (правило Лопиталя): Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x₀ за исключением быть может, самой точки x₀. Кроме того, пусть , причем в указанной окрестности точки x₀. Тогда если существует предел отношения (конечный или бесконечный), то существует и предел , причем справедлива формула:

Эта теорема верна и если х→±∞. Правило Лопиталя можно применять повторно, если и удовлетворяют тем же требованиям, что и исходные функции f(x) и g(x).

Если имеет место неопределенность , то правило Лопиталя остается справедливым при замене условия на условие .

Неопределенности вида 0∙∞ и ∞-∞ можно свести к неопределенностям вида и .

Практические задания для аудиторной работы

Найти пределы, используя правило Лопиталя:

а) ; б) ;

в) ; г) .

_{Самостоятельна работа}

_{Вариант 1}

Найти пределы, используя правило Лопиталя:

а) ; б) ;

в) ; г) ;

д) ; е) .

_{Вариант 2}

Найти пределы, используя правило Лопиталя:

а) ; б) ;

в) ; г) ;

д) ; е) .

_{Вариант 3}

Найти пределы, используя правило Лопиталя:

а) ; б) ;

в) ; г) ;

д) ; е) .

_{Вариант 4}

Найти пределы, используя правило Лопиталя:

а) ; б) ;

в) ; г) ;

д) ; е) .

Правило бернулли лопиталя примеры с решениями. Правило Лопиталя: теория и примеры решений

Правило Лопиталя (п. Л.) облегчает вычисление пределов функций. Например, надо найти предел функции, которая является отношением функций стремящихся к нулю. Т.е. отношение функций это неопределенность 0/0. Раскрыть ее поможет . В пределе отношение функций можно заменить отношением производных этих функций. Т.е. надо производную числителя разделить на производную знаменателя и от этой дроби взять предел.

1. Неопределенность 0/0. Первое п.Л.

Если = 0, то , если последний существует.

2. Неопределенность вида ∞/∞ Второе п. Л.

Нахождение пределов такого типа называется раскрытием неопределенностей.

Если = ∞, то , если последний существует.

3. Неопределенности 0⋅∞, ∞- ∞, 1 ∞ и 0 0 сводятся к неопределенностям 0/0 и ∞/∞ путем преобразований. Такая запись служит для краткого указания случая при отыскании предела. Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности. Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.

0⋅∞ произведение двух функций, первая стремится к нулю, вторая к бесконечности;
∞- ∞ разность функций, стремящихся к бесконечности;
1 ∞ степень, ее основание стремится к единице, а показатель к бесконечности;
∞ 0 степень, ее основание стремится к бесконечности, а степень к нулю;
0 0 степень, ее основание стремится к 0 и показатель тоже стремятся к нулю.

Пример 1. В этом примере неопределенность 0/0

Пример 2. Здесь ∞/∞

В этих примерах производные числителя делим на производные знаменателя и подставляем предельное значение вместо х.

Пример 3. Вид неопределенности 0⋅∞ .

Неопределенность 0⋅∞ преобразуем к ∞/∞, для этого х переносим в знаменатель в виде дроби 1/x , в числителе пишем производную от числителя, а в знаменателе производную от знаменателя.

Пример 4 Вычислить предел функции

Здесь неопределенность вида ∞ 0 Сначала логарифмируем функцию, затем найдем от нее предел

Для получения ответа надо е возвести в степень -1, получим e -1 .

Пример 5. Вычислить предел от если x → 0

Решение. Вид неопределенности ∞ -∞ Приведя дробь к общему знаменателю перейдем от ∞-∞ к 0/0. Применим правило Лопиталя, однако снова получим неопределенность 0/0, поэтому п. Л. надо применить второй раз. Решение имеет вид:

= = = =
= =

Пример 6 Решить

Решение. Вид неопределенности ∞/∞, раскрыв ее получим

В случаях 3), 4), 5) сначала логарифмируют функцию и находят предел логарифма, а затем искомый предел е возводим в полученную степень.

Пример 7. Вычислить предел

Решение. Здесь вид неопределенности 1 ∞ . Обозначим A =

Тогда lnA = = = = 2.

Основание логарифма е, поэтому для получения ответа надо е возвести в квадрат, получим e 2 .

Иногда бывают случаи, когда отношение функций имеет предел, в отличие от отношения производных, которое не имеет его.

Рассмотрим пример:

Т.к. sinx ограничен, а х неограниченно растет, второй член равен 0.

Эта функция не имеет предела, т.к. она постоянно колеблется между 0 и 2, к этому примеру неприменимо п. Л.

Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).

Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

Перейдём к формулировкам правил Лопиталя.

Правило Лопиталя для случая предела двух бесконечно малых величин . Если функции f (x ) и g (x a a , причём в этой окрестности g “(x a равны между собой и равны нулю

().

Правило Лопиталя для случая предела двух бесконечно больших величин

. Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки a , за исключением, может быть, самой точки a , причём в этой окрестности g “(x )≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности

(),

то предел отношения этих функций равен пределу отношения их производных

().

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

Замечания .

1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .

2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).

3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”

Пример 1.

x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

В числителе вычисляли производную многочлена, а в знаменателе – производную сложной логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо икса двойку.

Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.

Применить правило Лопиталя самостоятельно, а затем посмотреть решение

Раскрытие неопределённостей вида “ноль умножить на бесконечность”

Пример 12. Вычислить

Решение. Получаем

В этом примере использовано тригонометрическое тождество .

Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”

Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида

Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .

Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.

Пример 13.

Решение. Получаем

Пример 14. Вычислить, пользуясь правилом Лопиталя

Решение. Получаем

Вычисляем предел выражения в показателе степени

Пример 15. Вычислить, пользуясь правилом Лопиталя

Представьте стаю воробьёв с выпученными глазами. Нет, это не гром, не ураган и даже не маленький мальчик с рогаткой в руках. Просто в самую гущу птенчиков летит огромное-огромное пушечное ядро. Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость или .

Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя ». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений , Замечательные пределы . Методы решения пределов , Замечательные эквивалентности , где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.

Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.

Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.

Первое правило Лопиталя

Рассмотрим функции , которые бесконечно малЫ в некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости можно взять две производные – от числителя и от знаменателя. При этом: , то есть .

Примечание : предел тоже должен существовать, в противном случае правило не применимо.

Что следует из вышесказанного?

Во-первых, необходимо уметь находить производные функций , и чем лучше – тем лучше =)

Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного !!!

И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость .

Вернёмся к Примеру 5 первой статьи о пределах , в котором был получен следующий результат:

К неопределённости 0:0 применим первое правило Лопиталя:

Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!

Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах :

На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:

Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции . После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).

Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные , следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам . Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.

Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности .

Второе правило Лопиталя

Брат-2 борется с двумя спящими восьмёрками . Аналогично:

Если существует предел отношения бесконечно больших в точке функций: , то в целях устранения неопределённости можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется .

Примечание : предел должен существовать

Опять же, в различных практических примерах значение может быть разным , в том числе, бесконечным. Важно, чтобы была неопределённость .

Проверим Пример №3 первого урока: . Используем второе правило Лопиталя:

Коль скоро речь зашла о великанах, разберём два каноничных предела:

Пример 1

Вычислить предел

Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:

Таким образом, линейная функция более высокого порядка роста , чем логарифм с основанием бОльшим единицы ( и т. д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция растёт достаточно медленно и её график является более пологим относительно того же «икса».

Пример 2

Вычислить предел

Ещё один примелькавшийся кадр. В целях устранения неопределённости , используем правило Лопиталя, причём, два раза подряд:

Показательная функция, с основанием, бОльшим единицы ( и т.д.) более высокого порядка роста , чем степенная функция с положительной степенью .

Похожие пределы встречаются в ходе полного исследования функции , а именно, при нахождении асимптот графиков . Также замечаются они и в некоторых задачах по теории вероятностей . Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.

Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел .

Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:

Для разминки разберёмся с парой небольших воробушков:

Пример 3

Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:

В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .

Рассмотренный пример разруливается и через замечательные пределы , похожий случай разобран в конце статьи Сложные пределы .

Пример 4

Вычислить предел по правилу Лопиталя

Это пример для самостоятельного решения. Нормально пошутил =)

Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:

Пример 5

Вычислить предел, используя правило Лопиталя

Напрашивается применение замечательной эквивалентности , но путь жёстко предопределён по условию:

После дифференцирования настоятельно рекомендую избавляться от многоэтажности дроби и проводить максимальные упрощения . Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.

Пример 6

Вычислить предел, используя правило Лопиталя

Пример 7

Вычислить предел, используя правило Лопиталя

Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.

И, упрощения совершенно необходимы, когда после дифференцирования неопределённость не устранена .

Пример 8

Вычислить предел, используя правило Лопиталя

Поехали:

Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.

На днях мне попалось любопытное задание:

Пример 9

Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.

Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….

В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .

Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урока Методы решения пределов . Давайте для проформы ещё один:

Пример 10

Вычислить предел функции, используя правило Лопиталя

На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:

Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.

Неопределённость тоже не сопротивляется превращению в или :

Пример 11

Вычислить предел функции с помощью правила Лопиталя

Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций . Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.

Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:

После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:

Готово.

Исходный предел можно было попытаться свести к двум бубликам:

Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.

Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».

В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен.

Пусть при $x\to a$ функции $f(x)$ и $\varphi(x)$ обе бесконечно малые или обе бесконечно большие. Тогда их отношение не определено в точке $x=a$ , и в этом случае говорят, что оно представляет собой неопределенность типа $\left[\frac{0}{0}\right]$ или соответственно. Это отношение может иметь конечный или бесконечный предел в точке $x=a$ . Нахождение этого предела называется раскрытием неопределенности.

t_E1_p217_1
Теорема (Теорема Лопиталя-Бернулли. )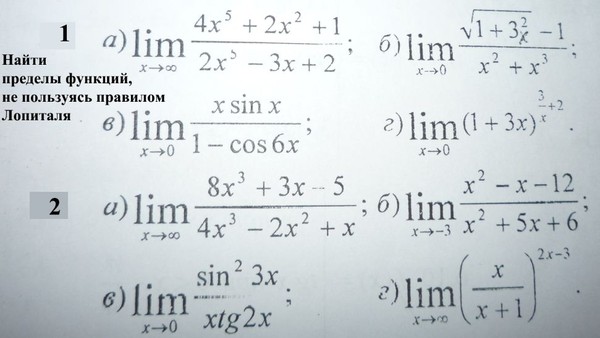
Пусть в некоторой окрестности $P$ точки $x=a$ функции $f(x)$ и $g(x)$ дифференцируемы всюду, кроме, может быть, самой точки $x=a$ , и пусть $g”(x)\neq0$ на $P$ . Если функции $f(x)$ и $\varphi(x)$ являются одновременно либо бесконечно малыми, либо бесконечно большими при $x\to a$ и при этом существует предел отношения $\frac{f”(x)}{\varphi”(x)}$ их производных при $x\to a$ , то тогда существует также и предел отношения $\frac{f(x)}{g(x)}$ самих функций, причем

(1)

\begin{align} \lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a}\frac{f”(x)}{g”(x)}. \end{align}

Правило () применимо и в случае, когда $a=\infty$ .

m_KR_p156_1
Метод (Правило Лопиталя. Раскрытие неопределенностей типа $\left[\frac{0}{0}\right]$ и $\left[\frac{\infty}{\infty}\right]$ .)
В силу теоремы () существует общий способ нахождения предела отношений двух функций, основанный на равенстве
$$\lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a}\frac{f”(x)}{g”(x)}. 2}=\lim\limits_{x\to0}\frac{\sin x}{2x}.$$
Используя первый замечательный предел, получаем окончательный ответ $\frac{1}{2}$ , уже не прибегая к правилу Лопиталя.

m_E1_p219_1
Метод (Правило Лопиталя. Раскрытие неопределенности типа $\left$ .)
Для вычисления $\lim\limits_{x\to a}f(x)g(x)$ , где $f(x)$ — бесконечно малая, а $g(x)$ — бесконечно большая функции при $x\to a$ , следует преобразовать произведение к виду $\frac{f(x)}{1/g(x)}$ (неопределенность типа $\left[\frac{0}{0}\right]$ ) или к виду $\frac{g(x)}{1/f(x)}$ (неопределенность типа $\left[\frac{\infty}{\infty}\right]$ ) и далее использовать правило Лопиталя.

e_E1_p219_1

Пример
Найти $$\lim\limits_{x\to1}\sin(x-1)\cdot\tan\frac{\pi x}{2}.$$
Имеем: $$\begin{array}{c}\lim\limits_{x\to1}\sin(x-1)\cdot\tan\frac{\pi x}{2}=\left=\lim\limits_{x\to1}\frac{\sin(x-1)}{\cot\frac{\pi x}{2}}=\left[\frac{0}{0}\right]=\\=\lim\limits_{x\to1}\frac{\cos(x-1)}{-\frac{\pi}{2}\frac{1}{\sin^2\frac{\pi x}{2}}}=-\frac{2}{\pi}\lim\limits_{x\to1}\cos(x-1)\sin^2\frac{\pi x}{2}=-\frac{2}{\pi}. 2.$$

Решение пределов функции онлайн . Найти предельное значение функции либо функциональной последовательности в точке, вычислить предельное значение функции на бесконечности. определить сходимость числового ряда и многое другое можно выполнить благодаря нашему онлайн сервису – . Мы позволяем находить лимиты функций онлайн быстро и безошибочно. Вы сами вводите переменную функции и предел, к которому она стремится, анаш сервис проводит все вычисления за вас, выдавая точный и простой ответ. Причем для нахождения предела онлайн вы можете вводить как числовые ряды, так и аналитические функции, содержащие константы в буквенном выражении. В этом случае найденный предел функции будет содержать эти константы как постоянные аргументы в выражении. Нашим сервисом решаются любые сложные задачи по нахождению пределов онлайн , достаточно указать функцию и точку в которой необходимо вычислить предельное значение функции . Вычисляя пределы онлайн , можно пользоваться различными методами и правилами их решения, при этом сверяя полученный результат с решением пределов онлайн на www. сайт, что приведет с успешному выполнению задачи – вы избежите собственных ошибок и описок. Либо вы полностью можете довериться нам и использовать наш результат в своей работе, не затрачивая лишних усилий и времени на самостоятельные вычисления предела функции. Мы допускаем ввод таких предельных значений, как бесконечность. Необходимо ввести общий член числовой последовательности и www.сайт вычислит значение предела онлайн на плюс или минус бесконечности.

Одним из основных понятий математического анализа является лимит функции и предел последовательности в точке и на бесконечности, важно уметь правильно решать пределы . С нашим сервисом это не составит никакого труда. Производится решение пределов онлайн в течение нескольких секунд, ответ точный и полный. Изучение математического анализа начинается с предельного перехода , пределы используются практически во всех разделах высшей математики, поэтому полезно иметь под рукой сервер для решения лимитов онлайн , каковым является сайт.

Правило Лопиталя

Теорема (правило Лопиталя раскрытия неопределенностей вида
$\frac{0}{0}$ или $\frac{\infty}{\infty}$).

Пусть функции $f(x)$ и $g(x)$ :

а) дифференцируемы в окрестности точки $a,$ за исключением, быть
может, самой точки $a,$ причем $g'(x)\neq 0$ в этой окрестности;

б) функции $f(x)$ и $g(x)$ являются одновременно либо бесконечно
малыми либо бесконечно большими при $x\rightarrow a;$

в) существует конечный $\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$

Тогда существует $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}$ и
выполняется равенство $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$

Если функции $f(x)$ и $g(x)$ дифференцируемы в точке $a,$

$g(a)=f(a)=0,$ $ g'(a)\neq ,0$ то $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\frac{f'(a)}{g'(a)}.$

Примеры:

1. $\lim\limits_{x\rightarrow 1}\frac{x^5-1}{2x^3-x-1}$

Имеем неопределенность вида $\frac{0}{0}. 2

Правило L’Hopital

Правило Л’Опиталя предоставляет метод оценки неопределенных форм типа \ (\ frac {0} {0} \) или \ (\ frac {\ infty} {\ infty}.\)

Пусть \ (a \) либо конечное число, либо бесконечность.

Если \ (\ lim \ limits_ {x \ to a} f \ left (x \ right) = 0 \) и \ (\ lim \ limits_ {x \ to a} g \ left (x \ right) = 0 ,\) тогда
\ [\ lim \ limits_ {x \ to a} {\ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}}} = \ lim \ limits_ {x \ to a} {\ frac {{f ‘\ left (x \ right)}} {{g’ \ left (x \ right)}}}; \]

Если \ (\ lim \ limits_ {x \ to a} f \ left (x \ right) = \ infty \) и \ (\ lim \ limits_ {x \ to a} g \ left (x \ right) = \ infty, \), то аналогично

\ [\ lim \ limits_ {x \ to a} {\ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}}} = \ lim \ limits_ {x \ to a} {\ frac {{f ‘\ left (x \ right)}} {{g’ \ left (x \ right)}}}.x} = \ ln a \ cdot 1 = \ ln a. \ prime}}} = \ lim \ limits_ {x \ to 2} \ frac {{\ frac {1} {{2 \ sqrt {7 + x}}}}} { 1} = \ frac {1} {2} \ lim \ limits_ {x \ to 2} \ frac {1} {{\ sqrt {7 + x}}} = \ frac {1} {2} \ cdot \ frac {1} {3} = \ frac {1} {6}.2}}} \ cdot 0 = 0. \]

См. Другие проблемы на странице 2.

Интернет-ресурсы для правила L’Hopital

Wolfram MathWorld

На этом веб-сайте представлена предыстория правила L’Hopital. Вам дается определение, которое, по сути, просто берет данные вам функции и находит их производные, чтобы увидеть, действительно ли предел бесконечен. Это также дает вам историческую справку, которая, я думаю, является отличным инструментом для учителей, которые они могут показать своим ученикам.Согласно сайту, там говорится, что правило Л’Опиталь было разработано в 1696 году. Я думаю, что это хорошая возможность объяснить, что Л’Опиталь и братья Бернулли на самом деле придумали это без использования компьютеров и калькуляторов. Этот сайт также показывает сумасшедшую математику, которая может быть не очень полезна учителю. Так что применять все здесь – не лучшая идея. Определение и краткая историческая справка этого правила – вот что меня запомнило. Поэтому я рекомендую этот сайт всем, кто ищет определение и краткую историю правила.

Правило Л’Опиталя – Введение

Это было единственное хорошее видео, в котором кто-то объясняет правило Л’Опиталя. Это видео с YouTube, но используется SchoolTrainer, которая использует видео для обучения студентов. Я подумал, что это дает учащимся лучшее понимание вне школы, если им нужно лучше понять это правило. Он показывает определение правила L’Hopital и показывает, какие типы ограничений применяются к этому правилу. Мне нравится это краткое объяснение правила L’Hopital, потому что, как я уже сказал, оно помогает понять значение правила L’Hopital.Студенты могут видеть, как применяется правило. Учителя могут использовать это как полезный ресурс в своем обучении, чтобы перейти к теме неопределенных функций и Правил Л’Опиталь. Я определенно рекомендую это видео, чтобы разъяснить правило.

Правило L’Hopital

Вот ресурс о том, что такое Правило L’Hopital, и он предоставляет доказательство правила. Что мне нравится в этом ресурсе, так это то, что он дает вам простой пример того, как работает правило. Друзья пытались объяснить мне это правило по-разному, и мне пришлось искать его самому, чтобы по-настоящему понять.Мне жаль, что я сначала не нашел эту ссылку, потому что она дает вам простое объяснение того, что вы должны делать, когда у вас есть проблемы, связанные с неопределенным пределом. Он говорит вам простыми фразами, что упрощает понимание правила. Однако есть доказательство, показанное на правиле. Я не знаю, правильное доказательство или нет, но я скажу, что если кто-то застрял на том, как использовать правило L’Hopital, тогда у них есть этот ресурс, который поможет выяснить, как его применить.

Правило Л’Опиталя (Википедия)

Это веб-сайт Википедии.Это дает краткую историю того, как возникло правило, но в то же время дает определение и пару доказательств. Однако я никогда не смотрю на доказательства, которые нахожу в Интернете, потому что многие доказательства, найденные в Интернете, неверны или содержат много ошибок. В любом случае, он дает некоторые хорошие вещи, такие как простые примеры, но также дает примеры, которые вы, вероятно, никогда не использовали бы в классе. Я считаю, что это полезный сайт для определения и истории, стоящей за ним, но не очень полезный для примеров и доказательств.Цель изучения этого правила – применить его к задачам, которые будут полезны учащимся. Я предлагаю просто использовать это для истории и определения.

Вот несколько полезных руководств!

Правило Л’Опиталя (онлайн-руководство)

Я знаю, что это название имеет то же название, что и предыдущее, но на этом веб-сайте есть правило и множество примеров. Во-первых, он дает регулярные примеры некоторых простых предельных задач, но затем он дает неопределенные формы, что является идеей 0 над 0 или бесконечности над бесконечностью. Эти примеры показывают, как на самом деле применять правило L’Hopital, потому что оно предназначено для этого. Учитель может просматривать этот сайт и применять идеи к обучению, показывая простые ограничения, а затем показывая более жесткие ограничения, чтобы показать правило L’Hopital. Внизу этого сайта рассматриваются ключевые концепции, а именно, что правило L’Hopital используется для определения пределов неопределенностей. Опять же, это очень полезный сайт, где можно найти примеры для обучения.

Использование правила L’Hopital

Это YouTube видео о Правиле L’Hopital.Это парень, известный как доктор Фил (не тот терапевт), показывает примеры того, как применять правило Л’Опиталя. Этот видео очень полезно для студентов и отличная ссылка для учителей, своим ученикам, которые борются с правилом L’Hopital. Доктор Фил показывает задачи, с которыми студенты могут столкнуться в математике. Он объясняет все четко и медленно, что очень хорошо. В то же раз, если студент не понимает, что было сказано, то они могут пойти назад и посмотрите на это еще раз. Мне очень нравится это видео с объяснением о применении правила L’Hopital, потому что я даже не видел, как L’Hopital Правило сработало, когда я впервые о нем услышал.Профессор предположил, что все знали об этом. Итак, это мой способ вернуть ученику и учителя, имея видео, которое они могут посмотреть и посмотреть, как это Правило применяется к некоторым функциям ограничения.

Пример правила L’Hopital 1 (Есть и другие примеры)

Это еще одно онлайн-видео от SchoolTrainer с использованием видео YouTube. Цель этого видео – помочь учащимся понять, когда следует использовать правило L’Hopital. Он показывает неопределенные функции, чтобы показать, что когда вы видите 0/0, вам нужно использовать правило L’Hopital, чтобы найти предел.Это очень полезно для студентов, которым нужна дополнительная помощь в поиске того, когда использовать правило L’Hopital. Это также хороший ресурс для учителей. Вот еще два примера:
Пример 2
Пример 3

Неопределенные формы и правило L’Hopital

Это очень интересный сайт. Он показывает пример правила Л’Опиталя с использованием графика. Вы можете взаимодействовать с графиком, перемещая точки, чтобы показать, что когда вы применяете правило L’Hopital (в данном случае они применяют правило дважды), они достигают предела.Причина, по которой я поместил его здесь, в раздел руководств, заключается в том, что он показывает, что вы можете использовать это правило несколько раз, что является хорошей возможностью показать студентам. У некоторых проблем может быть такая функция. Я бы использовал это, чтобы показать, что правило работает несколько раз, но вы также можете увидеть, как графики сходятся до предела. Это отличная возможность, и поэтому я бы использовал ее на уроках. Они показывают только один пример, и вы также не можете изменить проблему.Так что это можно использовать как отличную возможность для обучения студентов.

Калькуляторы

Апплет Calculus: Правило L’Hopital

У этого сайта двойная функция! Сначала он дает определение, как и некоторые из предыдущих сайтов, но затем он дает график с настройкой типа калькулятора. Угадай, что?! Вы действительно можете использовать функцию калькулятора! Это то, что мне нравится в этом сайте! Вы можете применить правило L’Hopital, посмотрев на график, который он дает вам с вашей функцией, но затем он дает вам график после того, как вы найдете производную плюс предел.Все готово для вас. Вы вводите f (x), g (x) и ваш предел, равный части, и вы получаете свой ответ. Под частью калькулятора приводится объяснение использованных ими примеров, но кроме этого, вы можете поиграть с самим калькулятором! Кнопка «Запустить презентацию» помогает расширить калькулятор в более крупную перспективу. Это очень хорошая возможность, так что вы можете просто сосредоточиться на проблемах. Это было бы очень хорошо для учителей, если бы они показывали графики и примеры, но как учитель я бы скрывал функцию вычисления, потому что хочу, чтобы мои ученики сами научились применять правило.Однако это очень полезный сайт!

Онлайн-калькулятор: решение предельных задач с помощью правила L’Hopital

Это интересный калькулятор для использования в Интернете. Вы вводите функцию, для которой нужно найти предел, а затем вводите предельную точку. Нажмите Enter, и вы увидите пошаговый процесс решения проблемы и ответ. Вы должны быть осторожны при вводе функции, но у них есть небольшие полезные подсказки для ввода функций. Это хороший сайт, чтобы увидеть, как решать функции с помощью правила Л’Опиталя, но я бы очень осторожен, позволяя студентам знать, что это существует, потому что студенты могут стать слишком зависимыми от этого калькулятора, поскольку он действительно объясняет пошаговые процедуры.Однако это хороший калькулятор. Я рекомендую учителям использовать это с учениками, чтобы объяснить, как решаются задачи. Это был бы лучший способ использовать этот ресурс.

Примеры проблем

Drill – Правило L’Hopital

На этом сайте вы найдете проблемы, которые нужно решить самостоятельно. Учитель определенно может найти здесь некоторые проблемы и использовать их в качестве примеров или реальных домашних заданий в отношении Правила L’Hopital. На сайте также есть решения, которые очень важно иметь.Решения также показывают, как правило применяется к проблеме, что является хорошей основой для объяснения проблем учащимся, у которых есть и проблемы с ответами. Этот сайт лучше использовать учителям, которым нужны дополнительные задачи или домашние задания для своих учеников.

L’Hopital’s Rule Problems

На этом сайте вы найдете несколько более сложных проблем, которые нужно решить, с ответами для каждой проблемы на вкладках. Это дает учащимся возможность изучить некоторые более сложные проблемы, связанные с Правилом L’Hopital, и дает им возможность подумать и развить свои производные навыки.Однако я бы использовал эти задачи, когда вы чувствуете, что ваши ученики готовы к такого рода задачам. Хороший способ включить эти типы проблем – пройти тест в качестве дополнительной кредитной задачи. По крайней мере, ученики получают хороший вызов, усваивая это правило. В то же время они также расширяют свои производные навыки. Так что эти проблемы почти беспроигрышны для учителя. В любом случае, мне нравятся эти задачи, потому что они заставили меня задуматься над проблемами и бросили мне вызов.Эти проблемы – определенно хороший вызов.

Правило Л’Оспиталя – Исчисление 2

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects. org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Правило госпиталя

Правило Л’Оспиталя полезно при определении поведения функции, имеющей предел неопределенной формы.

Это обсуждение будет сосредоточено на двух типах неопределенных форм.

Первый тип возникает, когда предел функции приводит к пределу 00 и считается пределом в неопределенной формы 00.

УКАЗАТЬ ФОРМУ 00:

limx → 1logxx − 1 = log11−1 = 00

Второй тип возникает, когда предел функции приводит к пределу ∞∞ и называется пределом неопределенной формы ∞∞.

ОПРЕДЕЛЕННАЯ ФОРМА ∞∞:

limx → ∞logxx − 1 = log∞∞ − 1 = ∞∞

Пусть f (x) и g (x) – две функции, дифференцируемые на открытом интервале с точкой s , кроме, может быть, в s, и первая производная g (x) не равна нулю.Если предел f (x) g (x) по мере приближения x к s имеет неопределенную форму 00 или ∞∞, то можно применить правило Л’Оспиталя.

Правило Л’Оспиталя гласит, что предел частного двух функций равен пределу частных их первых производных.

ПРАВИЛО БОЛЬНИЦЫ:

Если f (x) и g (x) дифференцируемы на открытом интервале, который содержит s (кроме, возможно, s), и предел имеет неопределенную форму 00 или ∞∞, то есть:

limx → sf (x) = 0ANDlimx → sg (x) = 0

limx → ∞f (x) = ∞ ANDlimx → ∞g (x) = ∞

Тогда применяется следующее правило :

limx → sf (x) g (x) = limx → sf ′ (x) g ′ (x)

Давайте рассмотрим несколько примеров.

Для работы этих примеров требуется использование различных производных правил. Если вы не знакомы с правилом, перейдите к соответствующей теме для обзора.

Пример 1. Найдите limx → 2×2−2xx3 + x − 10.

Шаг 1. Убедитесь, что лимит имеет неопределенную форму 00 или ∞∞.

Возьми предел:

limx → 2×2−2xx3 + x − 10

limx → 2 (2) 2−2 (2) (2) 3+ (2) −10 = 00

Шаг 2: Примените правило L’Hospital

Поскольку предел имеет неопределенную форму 00, можно применить правило Л’Оспиталя.

limx → sf (x) g (x) = limx → sf ′ (x) g ′ (x)

limx → 2×2−2xx3 + x − 10

limx → 22x − 23×2 + 1 Возьмем производную

limx → 22 (2) −23 (2) 2 + 1 = 213 Взять предел

Пример 1: Найти limx → ∞lnxx3 + 1.

Шаг 1: Убедитесь, что предел имеет неопределенную форму 00 или ∞∞.

Возьми предел:

limx → ∞lnxx3 + 1

limx → ∞lnx∞ (∞) 3 + 1 = ∞∞

Шаг 2: Примените правило L’Hospital

Поскольку предел имеет неопределенную форму ∞∞, можно применить правило Л’Оспиталя.

limx → sf (x) g (x) = limx → sf ′ (x) g ′ (x)

limx → ∞lnxx3 + 1

limx → ∞1 / x3x2 = 13×3 Возьмем производную

limx → ∞13×3 = 13 (∞) 3 = 0 Предел

Что такое правило L’Hospital? – Magoosh Blog

Правило L’Hospital – это метод определения значений определенных видов лимитов с использованием производных финансовых инструментов. Правило названо в честь Guillaume de l’Hospital (или l’Hôpital), французское название которого произносится как low-pee-tal (НЕ le Hoss-pih-tal ).

Guillaume de l’Hospital

Правило L’Hospital

Если f ( x ) / г ( x ) имеет вид 0/0 или ∞ / ∞, если x = a подключается, затем:

Другими словами, возьмите производную числителя (вверху) и производную знаменателя (внизу), а затем попробуйте вычислить предел.

Использование правила L’Hospital

Чтобы использовать правило L’Hospital, вы должны сначала убедиться, что ваш лимит имеет правильную форму.

Прежде всего, это должно быть частью двух функций, f ( x ) / g ( x ), чтобы применить правило.

Во-вторых – и это главное! – когда вы вставляете заданное значение x , дробь должна быть равна 0/0 или ∞ / ∞. Это два типа неопределенных форм . Если ваша проблема с лимитом не является неопределенной, вы не можете использовать этот метод напрямую.

Примеры

Давайте посмотрим, как работает правило больницы, на следующих двух примерах.

Пример 1

После вставки x = 0 мы находим неопределенную форму 0/0. Так что можно использовать Правило больницы. Просто возьмите производную от вершины и производную от основания. После этого попробуйте снова подключить значение x .

Пример 2

Правило L’Hospital работает так же хорошо в определенных пределах, как x → ± ∞.Обратите внимание, неопределенная форма на этот раз – ∞ / ∞.

Но в этом примере есть еще одна интересная особенность. После однократного использования правила предел все еще остается неопределенным (∞ / ∞). Следовательно, мы можем снова использовать это правило.

Как правило, Правило госпиталя может повторяться столько раз, сколько необходимо, при условии, что на каждом этапе присутствует неопределенная форма.

Функции, не являющиеся дробями

Иногда возникает проблема ограничения, которую кажется невозможным.Стандартные алгебраические методы могут не работать. Если бы функция имела дробную форму, мы могли бы использовать l’Hospital. Но что, если функция даже не дробь?

Есть определенные алгебраические манипуляции, которые могут заставить выражение быть дробью. Если все сделано правильно, можно использовать l’Hospital.

Форсирование дроби

Вот пример, в котором мы преобразуем произведение в дробь, используя стандартный алгебраический трюк.

Пример 3

На этот раз мы начали не с дроби.Но если вы перепишете x ² = 1/ x ^-2, используя отрицательные показатели степени, то мы можем заставить функцию принять форму дроби. Затем воспользуйтесь Правилом больницы для получения результата.

Заключение

Если задача ограничения включает в себя часть двух функций, попробуйте правило L’Hospital. Не забудьте сначала проверить, не является ли это неопределенной формой. С этим мощным инструментом в вашем наборе инструментов ограничения на экзамены AP Calculus стали намного проще!

Гарантированно улучшите свой результат SAT или ACT.Начните 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep уже сегодня!

Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (Go Bucks !!). В 2002 году он получил степень бакалавра математики и информатику в Оберлинском колледже. Кроме того, Шон получил степень бакалавра искусств. из Консерватории Оберлина в том же году по специальности “музыкальная композиция”. Шон по-прежнему любит музыку – почти так же сильно, как математику! – и он (думает, что он) может играть на пианино, гитаре и басу.Шон обучал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!
Просмотреть все сообщения

Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!

4.4: Неопределенные формы и правило госпиталя

В этом разделе мы исследуем мощный инструмент для оценки пределов. Этот инструмент, известный как правило L’Hôpital, использует производные для расчета пределов.С помощью этого правила мы сможем оценить многие пределы, которые мы еще не смогли определить. Вместо того, чтобы полагаться на числовые свидетельства, чтобы предположить, что предел существует, мы сможем окончательно показать, что предел существует, и определить его точное значение.

Применение правила L’Hôpital

Правило Л’Опиталя можно использовать для оценки пределов, включающих частное двух функций. Рассмотрим

\ [\ lim_ {x → a} \ dfrac {f (x)} {g (x)}. \]

Если \ (\ displaystyle \ lim_ {x → a} f (x) = L_1 \) и \ (\ displaystyle \ lim_ {x → a} g (x) = L_2 ≠ 0, \), то

\ [\ lim_ {x → a} \ dfrac {f (x)} {g (x)} = \ dfrac {L_1} {L_2}.2−4} {x − 2} = \ lim_ {x → 2} \ dfrac {(x + 2) (x − 2)} {x − 2} = \ lim_ {x → 2} (x + 2) = 2 + 2 = 4. \ nonumber \]

Для \ (\ displaystyle \ lim_ {x → 0} \ dfrac {\ sin x} {x} \) мы смогли показать, используя геометрический аргумент, что

\ [\ lim_ {x → 0} \ dfrac {\ sin x} {x} = 1. \ nonumber \]

Здесь мы используем другую технику для оценки таких пределов. Этот метод не только обеспечивает более простой способ оценки этих пределов, но также, что более важно, дает нам возможность оценить многие другие пределы, которые мы не могли вычислить ранее.

Идея правила Л’Опиталя может быть объяснена с помощью локальных линейных приближений. Рассмотрим две дифференцируемые функции \ (f \) и \ (g \) такие, что \ (\ displaystyle \ lim_ {x → a} f (x) = 0 = \ lim_ {x → a} g (x) \) и т. Д. что \ (g ′ (a) ≠ 0 \) Для \ (x \) около \ (a \) мы можем записать

\ [f (x) ≈f (a) + f ′ (a) (x − a) \]

\ [g (x) ≈g (a) + g ′ (a) (x − a). \]

Следовательно,

\ [\ dfrac {f (x)} {g (x)} ≈ \ dfrac {f (a) + f ′ (a) (x − a)} {g (a) + g ′ (a) (x −a)}. \]

Рисунок \ (\ PageIndex {1} \): Если \ (\ displaystyle \ lim_ {x → a} f (x) = \ lim_ {x → a} g (x) \), то соотношение \ (f (x ) / g (x) \) примерно равно отношению их линейных приближений вблизи а.

Поскольку \ (f \) дифференцируем в \ (a \), то \ (f \) непрерывно в \ (a \), и, следовательно, \ (\ displaystyle f (a) = \ lim_ {x → a} f (х) = 0 \). Точно так же \ (\ Displaystyle g (a) = \ lim_ {x → a} g (x) = 0 \). Если мы также предположим, что \ (f ′ \) и \ (g ′ \) непрерывны в \ (x = a \), то \ (\ displaystyle f ′ (a) = \ lim_ {x → a} f ′ ( Икс) \) и \ (\ Displaystyle г ‘(а) = \ lim_ {х → а} г’ (х) \). Используя эти идеи, мы заключаем, что

\ [\ lim_ {x → a} \ dfrac {f (x)} {g (x)} = \ lim_ {x → a} \ dfrac {f ′ (x) (x − a)} {g ′ ( x) (x − a)} = \ lim_ {x → a} \ dfrac {f ′ (x)} {g ′ (x)}.\]

Обратите внимание, что предположение, что \ (f ′ \) и \ (g ′ \) непрерывны в \ (a \) и \ (g ′ (a) ≠ 0 \), можно ослабить. Формально формулируем правило Л’Опиталя для неопределенной формы \ (\ dfrac {0} {0} \). Также обратите внимание, что запись \ (\ dfrac {0} {0} \) не означает, что мы фактически делим ноль на ноль. Скорее, мы используем обозначение \ (\ dfrac {0} {0} \) для представления частного пределов, каждый из которых равен нулю.

Правило L’Hôpital (дело 0/0)

Предположим, что \ (f \) и \ (g \) – дифференцируемые функции на открытом интервале, содержащем \ (a \), за исключением, возможно, точки \ (a \).Если \ (\ displaystyle \ lim_ {x → a} f (x) = 0 \) и \ (\ displaystyle \ lim_ {x → a} g (x) = 0, \), то

\ [\ lim_ {x → a} \ dfrac {f (x)} {g (x)} = \ lim_ {x → a} \ dfrac {f ′ (x)} {g ′ (x)}, \ ]

при условии, что предел справа существует или равен \ (∞ \) или \ (- ∞ \). Этот результат также верен, если мы рассматриваем односторонние пределы или если \ (a = ∞ \) или \ (a = −∞. \)

Проба

Мы даем доказательство этой теоремы в частном случае, когда \ (f, g, f ′, \) и \ (g ′ \) все непрерывны на открытом интервале, содержащем a.В этом случае, поскольку \ (\ lim_ {x → a} f (x) = 0 = \ lim_ {x → a} g (x) \) и \ (f \) и \ (g \) непрерывны в \ (a \), то \ (f (a) = 0 = g (a) \). Следовательно,

\ [\ begin {align *} \ lim_ {x → a} \ dfrac {f (x)} {g (x)} & = \ lim_ {x → a} \ dfrac {f (x) −f (a )} {g (x) −g (a)} & & \ text {Поскольку} \, f (a) = 0 = g (a) \\ [4pt]
& = \ lim_ {x → a} \ dfrac {\ dfrac {f (x) −f (a)} {x − a}} {\ dfrac {g (x) −g (a)} {x − a}} & & \ text {Умножьте числитель и знаменатель на } \, \ frac {1} {xa} \\ [4pt]
& = \ frac {\ displaystyle \ lim_ {x → a} \ dfrac {f (x) −f (a)} {x − a}} {\ displaystyle \ lim_ {x → a} \ dfrac {g (x) −g (a)} {x − a}} & & \ text {Предел частного – это частное от пределов.} \\ [4pt]
& = \ dfrac {f ′ (a)} {g ′ (a)} & & \ text {По определению производной} \\ [4pt]
& = \ frac {\ displaystyle \ lim_ {x → a} f ′ (x)} {\ displaystyle \ lim_ {x → a} g ′ (x)} & & \ text {По непрерывности} \, f ′ \, \ text {and} \, g ′ \\ [4pt]
& = \ lim_ {x → a} \ dfrac {f ′ (x)} {g ′ (x)}. & & \ text {Предел частного} \ end {align *} \]

Обратите внимание, что правило Л’Опиталя гласит, что мы можем вычислить предел частного \ (\ dfrac {f} {g} \), рассматривая предел частного производных \ (\ dfrac {f ′} {g ′} \).2} \)

Решение

a .. Поскольку числитель \ (1− \ cos x → 0 \) и знаменатель \ (x → 0 \), мы можем применить правило Л’Опиталя для оценки этого предела. У нас

\ [\ lim_ {x → 0} \ dfrac {1− \ cos x} {x} = \ lim_ {x → 0} \ dfrac {\ dfrac {d} {dx} \ big (1− \ cos x \ big)} {\ dfrac {d} {dx} \ big (x \ big)} = \ lim_ {x → 0} \ dfrac {\ sin x} {1} = \ frac {\ displaystyle \ lim_ {x → 0 } \ sin x} {\ displaystyle \ lim_ {x → 0} 1} = \ dfrac {0} {1} = 0. \ nonumber \]

г. При \ (x → 1, \) числитель \ (\ sin (πx) → 0 \) и знаменатель \ (\ ln (x) → 0.2x \)

Ответ: \ (1 \)

Мы также можем использовать правило Л’Опиталя для оценки пределов частных \ (\ dfrac {f (x)} {g (x)} \), в которых \ (f (x) → ± ∞ \) и \ (g ( х) → ± ∞ \). Пределы этой формы классифицируются как неопределенные формы типа \ (∞ / ∞ \). Опять же, обратите внимание, что на самом деле мы не делим \ (∞ \) на \ (∞ \). Поскольку \ (∞ \) не является действительным числом, это невозможно; скорее \ (∞ / ∞ \). используется для представления отношения пределов, каждый из которых равен \ (∞ \) или \ (- ∞ \).

Правило Л’Опиталя (случай \ (∞ / ∞ \))

Предположим, что \ (f \) и \ (g \) – дифференцируемые функции на открытом интервале, содержащем \ (a \), за исключением, возможно, точки \ (a \). Предположим, \ (\ displaystyle \ lim_ {x → a} f (x) = ∞ \) (или \ (- ∞ \)) и \ (\ displaystyle \ lim_ {x → a} g (x) = ∞ \) ( или \ (- ∞ \)). Затем,

\ [\ lim_ {x → a} \ dfrac {f (x)} {g (x)} = \ lim_ {x → a} \ dfrac {f ′ (x)} {g ′ (x)} \]

при условии, что предел справа существует или равен \ (∞ \) или \ (- ∞ \). Этот результат также верен, если предел бесконечен, если \ (a = ∞ \) или \ (- ∞ \), или предел односторонний.+} \ dfrac {\ ln x} {\ cot x} \)

Решение

а. Поскольку \ (3x + 5 \) и \ (2x + 1 \) – многочлены первой степени с положительными старшими коэффициентами, \ (\ displaystyle \ lim_ {x → ∞} (3x + 5) = ∞ \) и \ (\ displaystyle \ lim_ {х → ∞} (2x + 1) = ∞ \). Поэтому мы применяем правило Л’Опиталя и получаем

\ [\ lim_ {x → ∞} \ dfrac {3x + 5} {2x + 1} = \ lim_ {x → ∞} \ dfrac {3 + 5 / x} {2x + 1} = \ lim_ {x → ∞} \ dfrac {3} {2} = \ dfrac {3} {2}. \ Nonumber \]

Обратите внимание, что этот предел также можно рассчитать без применения правила L’Hôpital.+} \ dfrac {\ ln x} {\ cot x} = 0. \ nonumber \]

Упражнение \ (\ PageIndex {2} \)

Вычислить \ [\ lim_ {x → ∞} \ dfrac {\ ln x} {5x}. \ nonumber \]

Подсказка: \ (\ dfrac {d} {dx} \ big (\ ln x \ big) = \ dfrac {1} {x} \)

Ответ: \ (0 \)

Как уже упоминалось, правило L’Hôpital – чрезвычайно полезный инструмент для оценки пределов. 2−5) = ∞.∞ \) – все неопределенные формы. Сами по себе эти выражения бессмысленны, потому что мы не можем на самом деле оценить эти выражения, как мы оценили бы выражение, содержащее действительные числа. Скорее, эти выражения представляют собой формы, возникающие при нахождении пределов. Теперь мы исследуем, как правило Л’Опиталя можно использовать для оценки пределов, связанных с этими неопределенными формами.

Поскольку правило Л’Опиталя применяется к частным, мы используем функцию натурального логарифма и ее свойства, чтобы уменьшить задачу вычисления предела, включающего показатели, к связанной задаче, включающей предел частного.{g (x)}) = g (x) \ ln (f (x)). \]

Следовательно,

\ [\ lim_ {x → a} [\ ln (y)] = \ lim_ {x → a} [g (x) \ ln (f (x))]. \]

Поскольку \ (\ displaystyle \ lim_ {x → a} f (x) = ∞, \) мы знаем, что \ (\ displaystyle \ lim_ {x → a} \ ln (f (x)) = ∞ \). Следовательно, \ (\ displaystyle \ lim_ {x → a} g (x) \ ln (f (x)) \) имеет неопределенную форму \ (0⋅∞ \), и мы можем использовать методы, обсужденные ранее, чтобы переписать выражение \ (g (x) \ ln (f (x)) \) в форме, позволяющей применить правило Л’Опиталя. 3 \) оба стремятся к бесконечности при \ (x → ∞ \).2 + 4x + 1 \) растут с той же скоростью, что и \ (x → ∞. \)

В более общем смысле, предположим, что \ (f \) и \ (g \) – две функции, которые стремятся к бесконечности при \ (x → ∞ \). Мы говорим, что \ (g \) растет быстрее, чем \ (f \) при \ (x → ∞ \), если

\ [\ lim_ {x → ∞} \ dfrac {g (x)} {f (x)} = ∞ \ quad \ text {или, что то же самое,} \ quad \ lim_ {x → ∞} \ dfrac {f ( x)} {g (x)} = 0. \]

С другой стороны, если существует константа \ (M ≠ 0 \) такая, что

\ [\ lim_ {x → ∞} \ dfrac {f (x)} {g (x)} = M, \]

мы говорим, что \ (f \) и \ (g \) растут с той же скоростью, что и \ (x → ∞ \).2 \) растет быстрее, чем \ (\ ln x \) при \ (x → ∞ \) (см. Рисунок \ (\ PageIndex {4} \) и таблицу \ (\ PageIndex {4} \)).

Таблица \ (\ PageIndex {4} \): Темпы роста степенной функции и логарифмической функции

\ (х \)

100

1000

10 000

\ (\ ln (x) \)

2.p \) для любого \ (p> 0 \) при \ (x → ∞ \).

Таблица \ (\ PageIndex {6} \): логарифмическая функция растет медленнее, чем любая корневая функция
\ (х \)	10	100	1000	10 000
\ (\ ln (x) \)	2.303	4.605	6,908	9.210
\ (\ sqrt [3] {x} \)	2.154	4.642	10	21,544
\ (\ sqrt {x} \)	3,162	10	31,623	100

Оставить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.