Главная
Исследование теплоотдачи при вынужденном движении воздуха в трубе: Исследование теплоотдачи при вынужденном движении воздуха в трубе

Исследование теплоотдачи при вынужденном движении воздуха в трубе: Исследование теплоотдачи при вынужденном движении воздуха в трубе

Содержание

Исследование теплоотдачи при вынужденном движении воздуха в трубе

В качестве определяющего размера при расчете теплоотдачи в трубах и каналах принимают внутренний диаметр трубы ( R0 d ).

Определяющую скорость находят из уравнения неразрывности:

где G – расход флюида, кг/c; – плотность, кг/м3; f – площадь попе-

речного сечения для прохода теплоносителя, м2.

Конкретный вид функциональной зависимости в уравнениях подобия принимает ученый – автор формулы. В принципе для аппроксимации экспериментальных данных можно использовать любую полиноминальную зависимость. В отечественной литературе, как правило, в качестве аппроксимирующих уравнений применяют степенные функции вида:

— ламинарный режим течения флюида

 

 

 

 

 

Nu C Gr k Ren Prm t ;

(12)

— переходный и турбулентный режимы течения флюида

(13)

где С, n, m, k – эмпирические коэффициенты, которые находят путем статистической обработки экспериментальных данных по методу наименьших квадратов; t – поправка, учитывающая зависимость фи-

зических свойств флюида от температуры; f ( / d) – поправка,

учитывающая влияние начального участка гидродинамической и тепловой стабилизации потока.

Для расчета поправочного коэффициента t академик М.А. Михеев предложил формулу:

 

 

 

Pr

 

0,25

 

 

 

 

f

 

,

(14)

t

 

 

 

 

 

 

 

 

 

 

Prw

 

 

где Prf – критерий Прандтля, который находят по таблицам физических свойств флюида при определяющей температуре; Prw – критерий

Прандтля, который находят по таблицам физических свойств флюида при температуре стенки.

В зависимости от значения критерия Рейнольдса в трубах и каналах существует ламинарный ( Ref ,d 2300 ), турбулентный ( Ref ,d 104 )

и переходный ( 2300 Ref ,d 104 ) от ламинарного к турбулентному режимы течения.

Теплоотдача при вынужденном движении – Энциклопедия по машиностроению XXL

ТЕПЛООТДАЧА ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ ЖИДКОСТИ В ТРУБАХ  [c.186]

Используя метод конечных разностей, решить обратною задачу теплопроводности с целью определения локальных коэффициентов теплоотдачи на начальном участке трубы, нагреваемой электрическим током. По данным экспериментального исследования теплоотдачи при вынужденном движении воздуха в трубе температура внутренней  

[c.206]


Теплоотдача при вынужденном движении воздуха в трубе  [c.147]

Теплоотдача при вынужденном движении жидкости вдоль плоской поверхности. При движении жидкости вдоль плоской поверхности профиль распределения продольной скорости поперек потока изменяется по мере удаления от передней кромки пластины. Если скорость в ядре потока и о, то основное изменение ее происходит в пограничном слое толщиной б, где скорость уменьщается от vvo до и,. = О на поверхности пластины. Течение в пограничном слое может быть как ламинарным, так и турбулентным. Режим течения определяется критическим значением критерия Рейнольдса, нижний предел которого для ламинарного пограничного слоя равен Re p = 8 Ю , а при Re > 3 10 вдоль пластины устанавливается устойчивый турбулентный режим течения. При значениях 8 10 режим течения — переходный (рис. 2.30).  

[c.170]

Размерное уравнение (12-9) коэффициента конвективной теплоотдачи при вынужденном движении в трубах может быть, как будет показано ниже, приведено к безразмерному виду  [c.159]

Глава 13 КОНВЕКТИВНАЯ ТЕПЛООТДАЧА ТЕПЛООТДАЧА ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ ЖИДКОСТИ И ГАЗОВ Теплоотдача при движении среды в трубах  

[c. 163]

Поясним это на следующем примере. Пусть для определенного процесса теплоотдачи при вынужденном движении теплоносителя в итоге обобщения опытных данных получена зависимость  [c.58]

Теплоотдача при вынужденном движении жидкости  [c.143]

На рис. 1 приведено сопоставление известных из литературы опытных данных по теплоотдаче при вынужденном движении до-гретого до температуры насыщения двухфазного пароводяного потока в трубах и кольцевых щелях. Из графика видно, что опытные точки вполне удовлетворительно группируются вокруг осредняющей кривой (2).  

[c.196]

В уравнениях (19), (21) и (22) о — коэффициент теплоотдачи при вынужденном движении жидкости в трубе оо коэффициент теплоотдачи при кипении в большом объеме Nu =  [c.222]

К настоящему времени выполнено большое число работ, посвященных исследованию кризиса теплоотдачи при вынужденном движении жидкости. Однако вводу большой сложности процессов тепло- и массо-переноса в потоке теплоносителя, приводящих к возникновению кризиса, до сих пор отсутствует достаточно надежная теория этого явления.

Опытные данные и построенные на их основе расчетные соотношения для определения критических тепловых нагрузок не всегда согласуются между собой даже качественно.  [c.72]


ИССЛЕДОВАНИЕ ТЕПЛООТДАЧИ ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ ЖИДКОСТИ ВНУТРИ ТРУБ И КАНАЛОВ  [c.163]

В настояш,ее время накоплен обширный экспериментальный материал по кризису теплоотдачи при вынужденном движении. Наиболее подробно изучен кризис теплоотдачи при подъемном движении воды в трубах с равномерным обогревом. Результаты этих опытов могут служить в качестве стандартных условий для выявления особенностей возникновения кризиса в каналах другой геометрии, при различных профилях тепловой нагрузки, в динамических условиях и пр.  

[c.127]

Теплоотдача при вынужденном движении  [c.71]

Для расчета теплоотдачи при вынужденном движении жидкости внутри или снаружи круглой трубы (рис. 3.4, а, б) применяются критериальные уравнения типа  [c.72]

На основании обработки результатов многих экспериментов академик М. А. Михеев составил формулу для определения среднего коэффициента теплоотдачи при вынужденном движении жидкости в трубе  

[c.208]

Для определения локального коэффициента теплоотдачи при вынужденном движении жидкости получена формула, учитывающая как конвективный, так и радиационный перенос теплоты, она имеет следующий вид  [c.314]

Теплоотдача при вынужденном движении. Вынужденное движение среды играет основную роль в современных тепловых устройствах. Для организации этого движения используют дымовые трубы, дымососы, эжекторы и т. п. Если при свободном движении скорость потока не находит своего отражения в  [c.73]

При вынужденной конвекции интенсивность теплоотдачи определяется прежде всего характером движения. Теплоотдача при вынужденном движении в трубах.

 [c.172]

С изменением температуры стенки трубы коэффициент теплоотдачи при вынужденном движении однофазной жидкости  [c.217]

Как записывается в общем виде критериальное уравнение для расчета теплоотдачи при вынужденном движении жидкости  [c.276]

В предыдущих гл. 7 и 8 были рассмотрены способы теоретического анализа процессов теплоотдачи на основе теории пограничного слоя на примере продольно и поперечно-омываемой пластины и вынужденного движения жидкости в гладкой круглой трубе. При этом физические константы К, ji,, р, с), от которых зависит способность жидкости переносить теплоту, принимались постоянными. Кроме того, не учитывалось влияние свободной конвекции, которая может либо усиливать теплоотдачу при вынужденном движении жидкости, либо ослаблять ее. Однако теоретическое определение теплоотдачи при наружном омывании тел более слоя ной формы или при вынужденном движении в трубах некруглого сечения с шероховатыми стенками (практически внутренние стенки труб всегда имеют шероховатую поверхность) с учетом переменности физических констант жидкости и свободной конвекции пока невозможно.

Следует отметить, что значительная часть сведений о процессах переноса теплоты, которыми мы располагаем, была получена экспериментально. Поэтому инежерные расчеты теплоотдачи в основном построены на экспериментальных сведениях.  
[c.185]

Для определения локального к оэфсЬициента теплоотдачи при вынужденном движении жидкости с малой скоростью и заданном температурном напоре АТ =Т, —Т получена формула [44], учи-  [c.269]

При ламинарном режиме течения (Red=a>d/vвынужденном движении оказывает влияние свободная конвекция, что и учитывается в (10.9) введением в число независимых аргументов критерия Сг. Однако влияние свободной конвекции на теплоотдачу ощущается лишь в том случае, когда имеет место так называемый вязкостногравитационный режим течения теплоносителя (GrPr S-10 ).  [c.136]

Целью настоящей статьи является анализ проблемы теплоотдачи при вынужденном движении (проблемы Грэтца) с учетом вязкой диссипации и внутреннего тенловыделения с помощью вариационного метода. Вариационные методы и раньше использовались для решения ряда задач теплообмена [3,]. Пользуясь математической терминологией, можно сказать, что основное дифференциальное уравнение чаще всего является самосопряженным. Вариационные формулировки обычно могут быть построены по образцу принципа Гамильтона, который приводит к уравнениям Эйлера — Лагран-н[c.325]


Монография освещает роль атомных электростанций. Рассматриваются закономерности обменных процессов в основном оборудовании атомных станций. Анализируются процессы тепло- и массообмена в докризисной области парогенерирующих каналов с непроницаемой поверхностью и в-каниллярно-пористых структурах, особенно кризиса теплоотдачи при вынужденном движении и теплообмене в закризисной области. Обобщаются данные по гидродинамике двухфазных потоков в прямых и криволинейных каналах. Говорится о безопасности атомных электростанций, о нестационарном теплообмене при разгерметизации и аварийному захолажи-ванию.  [c.143]

Естественно, что каждому режиму течения соответствуют определенные закономерности теплоотдачи, зависящие от режимных параметров потока и прежде всего от тепловой нагрузки и паросодержания. На картограмме теплоотдачи при вынужденном движении теплоносителя, изображенной на рис. 2.6, схематически показаны все режимы теплоотдачи. Здесь же штрихпунктиром нанесена область кризиса второго рода (высыхания пленки), существующая в узком диапазоне параметров. Как видно из картограммы, режим теп.лоотдачи за счет испарения жидкости при вынужденной кон-  [c.42]

Режим подавленного кипения в пленке и начало кинения. Анализ опытных данных по теплоотдаче при вынужденном движении показывает, что для начала кипения на стенке жидкость в пристенном слое б  [c.103]

Теплоотдача при свободном и вынужденном движении жидкости

 

содержание   ..  20  21  22   . .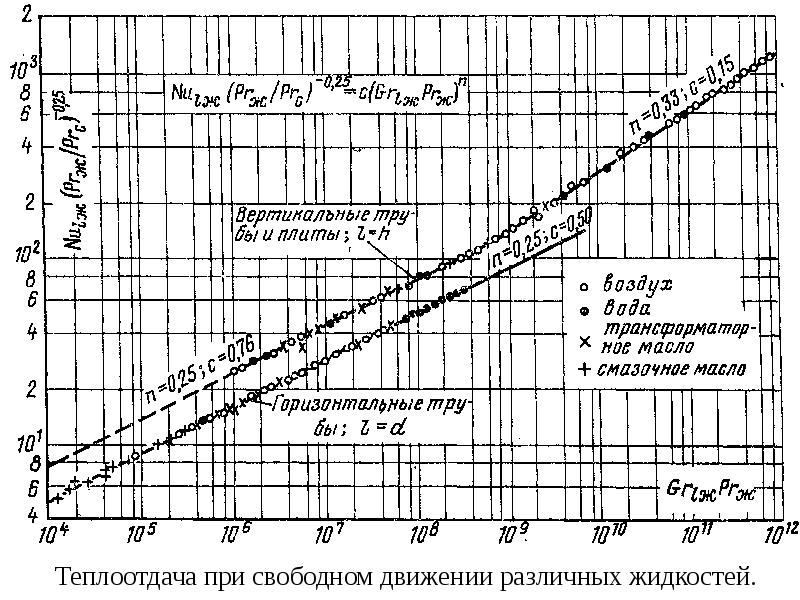

 

 

3.6.4.

Теплоотдача при свободном и вынужденном движении жидкости

 

 Свободное движение жидкости происходит под действием разности плотностей нагретых и холодных частей жидкости. Эта разность температур зависит от разности температур теплообменной поверхности и жидкости. Форма поверхности имеет второстепенное значение, поэтому уравнение подобия для естественной конвекции имеет вид

.

Константы  зависят от режима движения жидкости, т.е. от произведения :

для ламинарного режима (=1,18,  =0,125;

для переходного режима (=0,54,  =0,25;

для турбулентного режима (=0,135,  =0,33.

В качестве определяющих геометрических размеров  при вычислении чисел Грасгофа приняты: для цилиндрических или сферических тел – диаметр; для плоских поверхностей – высота.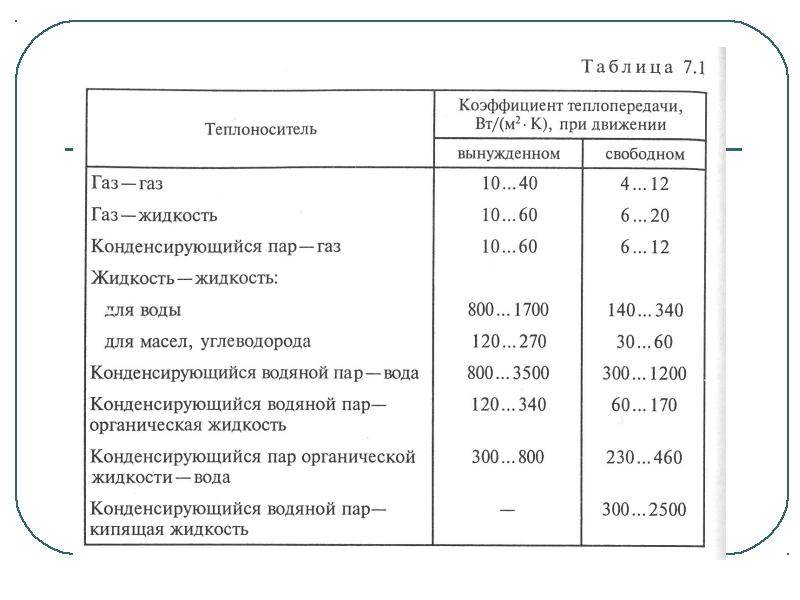

 В качестве определяющей температуры, т.е. температуры, при которой вычисляются значения физических параметров, входящих в критерии подобия, принята средняя температура пограничного слоя, равная 0,5().

Теплоотдача при вынужденном движении жидкости. Интенсивность теплоотдачи при вынужденном движении жидкостей в первую очередь зависит от режима течения жидкости. Соответственно этому рассматривается теплоотдача в условиях установившегося турбулентного, ламинарного и переходного режимов течения жидкости.

В условиях установившегося турбулентного течения () теплоотдача зависит от характера движения и свойств жидкости:

.

Физические параметры в критериях   определены при средней температуре жидкости, а в критерии   при температуре стенки. Отношением критериев  учитывается влияние на теплоотдачу направления теплового потока и температурного перепада. Определяющим геометрическим размером принят эквивалентный диаметр канала, равный учетверенной площади поперечного сечения канала, деленной на смоченный периметр. Зависимость справедлива для случаев движения жидкости по прямым каналам любой формы поперечного сечения.

В коротких каналах коэффициент теплоотдачи выше, чем в длинных. Его величина снижается с увеличением  от 1 до 50. Дальнейшее увеличение  не приводит к снижению коэффициента теплоотдачи. Если отношение , в критериальное уравнение вводится коэффициент , численные значения которого меняются в пределах от 1 до 1,65 в зависимости от  и критерия Рейнольдса. Значение величины поправочного коэффициента  можно найти в технической литературе.

При движении жидкости по изогнутой трубе или каналу с радиусом кривизны  теплообмен гораздо интенсивнее, чем при движении по прямому каналу.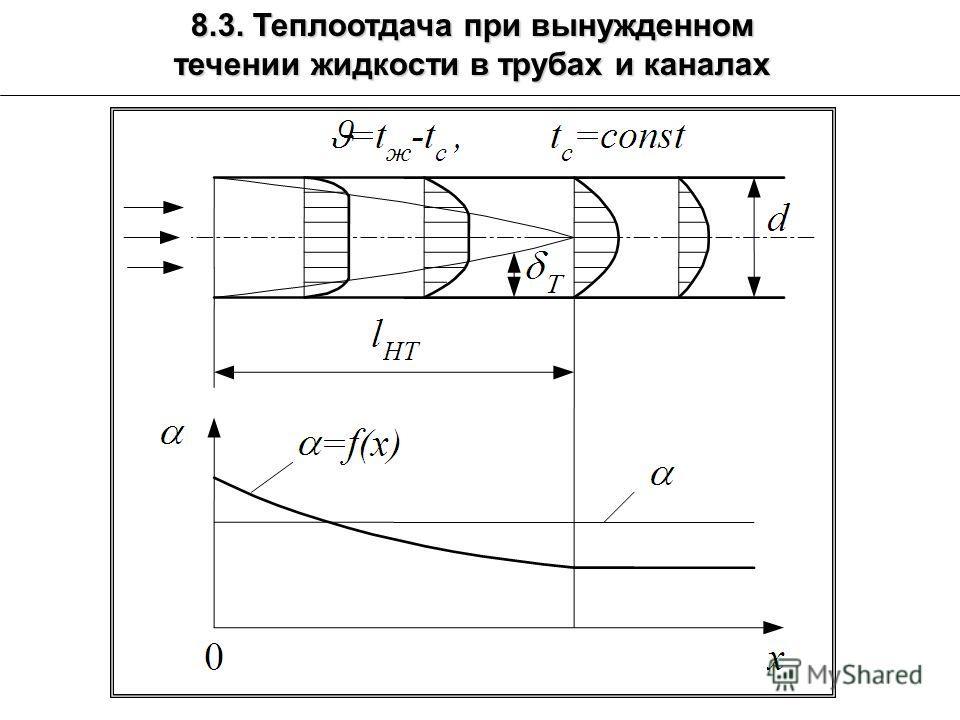 Увеличение интенсивности теплообмена в этом случае учитывается поправочным коэффициентом:

.

В условиях ламинарного течения () теплоотдача определяется как вынужденным, так и свободным движением жидкости.

На теплоотдачу при ламинарном режиме существенное влияние оказывает естественная циркуляция. В результате ее влияния коэффициент теплоотдачи иногда может изменяться в пять раз. Для горизонтальных круглых труб при расчете a может быть использована эмпирическая формула Михеева, учитывающая естественную конвекцию:

.

Коэффициент e, учитывающий изменение коэффициента теплоотдачи в зависимости от длины трубы, указан в таблице:

 

l/d

1

2

5

10

15

20

30

40

50

e

1,9

1,7

1,44

1,28

1,18

1,13

1,05

1,02

1,00

 

При ламинарном  режиме, когда влияние свободной конвекции невелико (Gr×Pr £5×105 ),   критериальные уравнения имеют вид:

при  (Re×Pr×d/l >12)              ;

при  (Re×Pr×d/l  £12)              ,

где mст, – коэффициент динамической вязкости теплоносителя принимается при температуре стенки.

Для расчета теплоотдачи при движении теплоносителя, не меняющего своего фазового состояния, по трубам и каналам при переходном режиме (104>Re>2300) могут быть использованы зависимости:

.

(для   P r= 20¸140)

Экспериментальные данные при поперечном обтекании труб и трубных пучков обобщаются в виде эмпирических уравнений:

для коридорного пучка

при 10< Re <150 

;

при 103< Re <105  

;

для шахматного пучка

 

при 10< Re <200 

;

при 103< Re <105  

.

При течении теплоносителя в межтрубном пространстве кожухотрубного теплообменника с сегментными перегородками могут быть использованы зависимости

  (при Re ³103),

   (при Re <103).

В них определяющую скорость потока рассчитывают для  наименьшего сечения межтрубного пространства.

 

3.6.5. Теплоотдача при изменении агрегатного состояния

 

Довольно часто в процессе теплообмена нагреваемые или охлаждаемые вещества изменяют агрегатное состояние: испаряются, конденсируются, плавятся или кристаллизуются. Особенности процессов теплообмена состоят в том, что тепло к ним подводится или отводится при постоянной температуре и распространяется не в одной, а двух фазах. Эти особенности могут быть учтены путем введения в уравнения подобия конвективного переноса тепла дополнительного критерия подобия, учитывающего теплоту изменения агрегатного состояния.

Рассмотрим процесс теплообмена при конденсации пара. Выберем на поверхности раздела жидкой и паровой фаз элементарную площадку . Пар, непрерывно конденсируясь, переходит в жидкую фазу. Обозначим скорость жидкости, образующейся при конденсации пара и протекающей через элементарную площадку , плотность этой жидкости  и теплоту парообразования. . Очевидно, что количество тепла, передаваемого жидкости от пара при его конденсации через площадку в единицу времени, составит

.

Это количество тепла отводится от площадки   в массу жидкости теплопроводностью и в соответствии с законом Фурье может быть определено как

.

Сопоставление двух равенств дает

 или  .

Заменив в последнем равенстве   произведением температуропроводности  жидкости на ее теплоемкость  , получим уравнение, характеризующее условия на границе раздела фаз при изменении агрегатного состояния

.

После деления правой части уравнения на левую получим безразмерный комплекс  .

Вычеркнув в полученном комплексе символы дифференцирования и направления (замена   на неориентированный в определенном направлении линейный размер ), получим критерий подобия . Этот критерий представляют в виде произведения  двух безразмерных комплексов, причем в первом критерии температуру   заменяют некоторой разностью температур:

.

В этом равенстве критерий равен

.

Этот безразмерный комплекс называют критерием Кутателадзе. Равенство этих критериев для различных систем характеризует подобие систем при изменении агрегатного состояния. Величина  представляет собой разность между температурой фазового превращения и температурой одной из фаз, а произведение   представляет собой теплоту перегрева или переохлаждения рассматриваемой зоны относительно температуры фазового превращения. Критерий Кутателадзе является мерой отношения тепла, идущего на изменение агрегатного состояния вещества, к теплоте перегрева или переохлаждения одной из фаз относительно температуры фазового превращения.

Из различных случаев теплоотдачи при изменении агрегатного состояния наибольшее значение, для процессов пищевых производств, имеет теплоотдача при конденсации паров и при кипении жидкостей.

Теплоотдача при конденсации паров. Расчетные зависимости по теплоотдаче при конденсации паров можно получить с помощью теории подобия и на основе теплового анализа процесса конденсации. Эти два пути дают одинаковые результаты при одинаковой схеме процесса.

Наиболее удовлетворительной схемой процесса считается схема, предложенная Нуссельтом, согласно которой на поверхности твердого тела, воспринимающего тепло от пара, происходит пленочная конденсация. Пленка жидкости, образующаяся на поверхности твердого тела, стекает с него и по мере движения книзу утолщается в результате конденсации пара на всей поверхности твердого тела.

При пленочной конденсации термическое сопротивление практически полностью сосредоточено в пленке конденсата, температура которой принимается равной со стороны стенки , а со стороны пара – температуре насыщения пара .

Анализ этого процесса на основе теории подобия позволяет установить следующую зависимость:

.

В расчетной практике для вертикальных труб и стенок рекомендуется применять следующие критериальные уравнения:

при  ламинарном режиме течения пленки жидкости на вертикальных поверхностях  

;

при  турбулентном режиме  

.

Для горизонтальных труб

,

где  К= – критерий Кутателадзе;   DТ=(Тн–Тст) – температурный напор.

Формулы получены для конденсации неподвижного пара. Для движущегося пара значение коэффициента теплоотдачи может быть либо больше, либо меньше в сравнении с неподвижным паром. Коэффициент теплоотдачи увеличивается, если его поток уменьшает толщину пленки или срывает ее. При создании препятствий движению пленки движущимся паром увеличение скорости способствует росту толщины пленки и уменьшению коэффициента теплоотдачи.

Для шероховатых поверхностей коэффициенты теплоотдачи меньше, чем для гладких, т.к. шероховатые поверхности оказывают большее сопротивление течению жидкой пленки. В этой связи скорость течения пленки уменьшается,  ее толщина увеличивается.  

Наличие воздуха или газов в насыщеном паре приводит к резкому снижению интенсивности теплоотдачи при конденсации из-за большого термического сопротивления слоя газов, скапливающихся у стенок. Для приближенных расчетов теплоотдачи вводят поправочные коэффициенты, величина которых зависит от концентрации неконденсирующихся газов.

Для расчета   коэффициентов теплоотдачи внутри горизонтальных труб, когда режим течения пленки конденсата турбулентный и влияние гравитационных сил пренебрежимо мало по сравнению с силами межфазного взаимодействия (Re > 5×103),  рекомендуется формула Н.Г. Кружилина

 

,

где  – коэффициент теплоотдачи, рассчитанный  по формулам для теплоотдачи без изменения агрегатного состояния; x1, x2– паросодержание потока на входе и выходе участка конденсации.

Если конденсируется смесь паров, образующая раствор из нескольких веществ, то конденсация протекает аналогично конденсации паров индивидуальных веществ. В этом случае при вычислении коэффициента теплоотдачи по формулам принимаются значения физических параметров растворов.

Если же смесь паров образует жидкость, состоящую из несмешивающихся компонентов, то теплоотдача обуславливается физическими свойствами того компонента, содержание которого больше. Конденсация паров с составом постоянно кипящей смеси может протекать с коэффициентами теплоотдачи как большими, так и меньшими, чем для чистых компонентов смеси, в зависимости от характера смачивания поверхности образующимся конденсатом.

Теплоотдача при кипении жидкостей. Этот вид теплоотдачи относится к числу особенно сложных процессов, поэтому до последнего времени никому из исследователей еще не удалось сделать теоретических обобщений, позволяющих вполне надежно вычислять коэффициенты теплоотдачи.

Исследования процесса кипения жидкостей показывают, что при кипении образуется пар в виде пузырьков в определенных местах (центрах) поверхности нагрева. При хорошей смачиваемости жидкостью поверхности нагрева (рис. 3.4) и небольшом угле   жидкость подтекает под пузырьки и облегчает их отрыв от поверхности нагрева.

При плохой смачиваемости пузырьки пара имеют широкое основание (большой угол ) и достигают при отрыве больших размеров. Фактически отрывается только вершина пузырька, а у поверхности нагрева остается паровая прослойка.

При большом числе центров парообразования поверхность нагрева может покрыться сплошной паровой пленкой. В этом случае из-за плохой теплопроводности пара коэффициенты теплоотдачи при кипении имеют малые значения. Режим кипения, когда еще нет сплошной паровой прослойки у поверхности нагрева, называется  пузырьковым, когда она появляется – пленочным. Эти режимы характерны при кипении жидкостей, хорошо смачивающих и плохо смачивающих поверхности.

 

 

Рис. 3.4. Форма паровых пузырьков при кипении на смачиваемой (а)

 и несмачиваемой (б) поверхностях нагрева

 

Измерение температур в неподвижном объеме кипящей жидкости показывает следующий характер температурного поля. Непосредственно на поверхности нагрева жидкость имеет температуру, равную этой поверхности. На расстоянии 2–3 мм от поверхности температура резко уменьшается до значения, превышающего на 0,3–0,5 температуру образующегося пара. Эта температура сохраняется во всем объеме жидкости, т.е. жидкость в основной своей массе незначительно перегрета.

Отрывающийся от поверхности нагрева пузырек пара имеет в момент отрыва диаметр  , обусловленный поверхностным натяжением жидкости, краевым углом смачиваемости (в градусах) и плотностями жидкости и пара:

.

Расчет по этой формуле показывает, что пузырьки водяного пара при атмосферном давлении имеют диаметр 2-3 мм.

По мере продвижения вверх через слой жидкости пузырек пара значительно увеличивается в объеме. Это свидетельствует о том, что пузырек пара при движении через слой жидкости получает от нее дополнительное количество пара и тепла. Обычно объем пузырька при движении вверх увеличивается в несколько десятков раз, а значит основное количество тепла воспринимается не от поверхности нагрева, а от жидкости. Таким образом, из рассмотренного механизма парообразования при кипении жидкостей следует, что теплоотдача при кипении состоит в передаче тепла от поверхности нагрева к жидкости, а от жидкости к пузырькам пара и вместе с ними это тепло переходит в паровую фазу.

Число центров образования паровых пузырей, частота их отрыва и, следовательно, интенсивность теплоотдачи при кипении зависят от перепада температур от поверхности нагрева и кипящей жидкости. На рис. 3.5 представлена зависимость коэффициента теплоотдачи и плотности теплового потока от разности температур.

 

 

 

 

 

 

 

 

Рис. 3.5. Плотности тепловых потоков и коэффициентов теплоотдачи при кипении воды в зависимости от температур поверхности нагрева и кипящей жидкости: I – пузырьковое      кипение; II – пленочное кипение

 

Как следует из графика, плотность теплового потока и коэффициент теплоотдачи с ростом разности температур растут до некоторых значений, а затем резко снижаются. Разность температур, соответствующая максимальным значениям коэффициента теплоотдачи и плотности теплового потока, называется критической разностью температур. При критической разности температур имеет место переход от пузырькового режима к пленочному.

Критическая разность температур зависит от природы жидкости, температуры, давления и характера поверхности нагрева.

По данным, полученным С.С. Кутателадзе при исследовании процесса кипения воды и других жидкостей в неограниченном объеме, зависимость для расчета коэффициента теплоотдачи имеет вид:

.

Коэффициент теплоотдачи при пузырьковом кипении однокомпонентных жидкостей в большом объеме можно также определять по следующей зависимости:

,

где rж, rп – плотность жидкости и пара, соответственно; l, u, s – коэффициент теплопроводности, кинематическая вязкость и поверхностное натяжение жидкости; q – плотность теплового потока.

Плотность теплового потока может быть определена по величине теплового потока, соответствующего первому кризису кипения чистых жидкостей:

,

где r –  теплота парообразования.

При расчетах этими уравнениями не всегда можно пользоваться из-за отсутствия необходимых значений физических параметров жидкости и пара, соответствующих определенной температуре кипения. Поэтому для расчетов применяют приведенные в справочниках опытные зависимости вида

.

 

 

 

3.7. Сложный теплообмен

 

В тепловых процессах в большинстве случаев распространение тепла осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением. Такой вид процесса, как было сказано выше, называется сложным теплообменом.

Передача тепла одновременно конвекцией и тепловым излучением является одним из важнейших процессов теплообмена.

Для установившегося процесса количество тепла, отдаваемое стенкой за счет теплопроводности, составляет

,

а за счет теплового излучения

.

 

Если ввести обозначение для коэффициента теплоотдачи излучением

,

количество тепла, отдаваемое стенкой за счет теплового излучения,          составит

.

Тогда общее количество тепла, отдаваемое стенкой, равно:

или

,

где  – приведенный коэффициент теплоотдачи, учитывающий одновременно конвективный теплообмен и теплообмен излучением.

Теплопередача, как было сказано выше, также относится к сложным видам теплообмена между теплоносителями через разделяющую перегородку.

Количество передаваемого тепла определяется основным уравнением теплопередачи

.

В этом уравнении коэффициент теплопередачи   является коэффициентом скорости процесса, учитывающим перенос тепла теплоотдачей от теплоносителя к  стенке, теплопроводностью через стенку и от стенки теплоотдачей к другому теплоносителю. Коэффициент теплопередачи определяет количество тепла, которое передается от одного теплоносителя к другому через единицу площади разделяющей их стенки в единицу времени при разности температур между теплоносителями в один град.

 

 
 


Соотношение для расчета коэффициента теплопередачи можно получить из схемы процесса, приведенной на рис. 3.6. 

 

Рис. 3.6. Характер изменения температур при теплопередаче через плоскую стенку

 

При установившемся процессе количество тепла, которым обмениваются теплоносители, остается неизменным для процессов теплоотдачи от одного теплоносителя к стенке и от стенки к другому теплоносителю, а также теплопроводности по толщине стенки

;

;

.

После решения этих уравнений относительно разностей температур получим

;

;

.

В результате сложения правых и левых частей уравнение примет вид

,

откуда

.

При сопоставлении последнего уравнения с уравнением теплопередачи получим выражение для коэффициента теплопередачи

.

Величина, обратная коэффициенту скорости, представляет собой сопротивление, называемое термическим сопротивлением теплопередаче. Это сопротивление складывается из суммы термических сопротивлений теплоотдачи со стороны теплоносителей и самой стенки:

.

При расчете термического сопротивления многослойной стенки (например, при наличии загрязнений с той и другой стороны поверхности теплообмена) необходимо учитывать термические сопротивления всех слоев, составляющих стенку:

.

Движущая сила процесса теплопередачи при прямоточном и противоточном движении теплоносителей вычисляется по уравнению

,

где   – наибольшая и наименьшая разности температур между теплоносителями на концах теплообменника, соответственно.

При небольших изменениях температур теплоносителей, когда , среднюю разность температур вычисляют как среднеарифметическую:

.

При перекрестном и смешанном токе теплоносителей среднюю разность температур определяют из формулы для прямоточного и противоточного движения теплоносителей с учетом поправочного коэффициента , определяемого из справочной литературы, т.е. 

.

 

 

 

 

 

 

 

 

 

 

содержание   ..  20  21  22   ..

 

 

 

ТОТ Дьяконов Владимир Германович – Механический факультет КГТУ   TOT Daykonov Vladimir Germanovich

В.Г.Дьяконов, О.А.Лонщаков. Исследование теплоотдачи при плёночной конденсации пара смеси этилацетат-вода в вертикальной трубе. Тепло- и массоб. в хим. техн.: межвуз. сб. науч. тр.: КХТИ.
Исследование местной теплоотдачи при вынужденном турлентном движении воздуха в трубе. Метод. пособие к лабор. работе. Казань, КХТИ, 1993.
В.Г.Дьяконов, О.А.Лонщаков, А.Г.Усманов. Теплоотдача при кипении несмешивающихся жидкостей (этилацетат-вода). Отчётная научно-технич. Конф. КГТУ, январь 1994.
В.Г.Дьяконов, О.А.Лонщаков, А.Г.Усманов. Теплоотдача при кипении несмешивающихся жидкостей (этилацетат-вода). Отчётная научно-технич. Конф. КГТУ, январь 1994.
В.Г.Дьяконов, А.Г.Усманов, В.П.Большов, А.А.Мухамадиев. Проблема сочетания университетского уровня образования и профилизации.
В.Г.Дьяконов, М.С.Курбангалеев. Теплообмен при вынужденной конвекции в высокочастотном электромагнитном поле. Тепло- и массообмен в хим. техн. КГТУ межвуз. сб. 1994, с.18-25.
В.Г.Дьяконов, О.А.Лонщаков. Исследование теплоотдачи при плёночной конденсации пара смеси этилацетат-вода в вертикальной трубе. КГТУ межвуз. сб. 1994, с.49-56.
Исследование местной теплоотдачи при вынужденном поперечном омывании одиночного цилиндра воздухом. Метод. пособие с.14-23 к лабор. работам. КГТУ, 1994.
Основы теории конвективного теплообмена. Метод. пособие к лабор. работам. Теория теплообмена. 1994г., с.4-7.
В.Г.Дьяконов, М.С.Курбангалеев, А.Г.Усманов, Теплообмен в насадочном слое в условиях высокочастотного электромагнитного поля. Отчётная научно-техн. конф. КГТУ, январь 1995 г.
В.Г.Дьяконов, О.А.Лонщаков, А.Г.Усманов. Конденсация паров бинарных смесей в ограниченной растворимостью компонентов. г.Москва, ВИНИТИ, 1995. Номер гос. рег. 2295-В95, от 25.07.95.
В.Г.Дьяконов, О.А.Лонщаков, А.Г.Усманов. Конденсация паров бинарных смесей с ограниченной растворимостью компонентов в вертикальной трубе. г.Москва, ВИНИТИ, 1995. Номер гос. рег. 2295-В95, от 25.07.95.
В.Г.Дьяконов, О.А.Лонщаков, А.Г.Усманов, А.А.Мухамадиев. Теплообмен при кипении смеси этилацетат-вода. Тепло- и массообмен в хим. техн. Казань, КГТУ межвуз. сб. 1995, с.3-13.
В.Г.Дьяконов, О.А.Лонщаков, А.Г.Усманов. Теплообмен при кипении и конденсации смесей этилацетата и воды. Науч. конф. КГТУ, февраль. 1997.

Поляков А.Ф. – список статей

  • Затухание пристенной генерации турбулентности при дополнительных воздействиях на поток жидкости
    Поляков А.Ф.
  • Вязкостно-термогравитационная конвекция и теплообмен в вертикальной полости при различных тепловых условиях
    Поляков А.Ф.
  • Установившееся вязкостно-термогравитационное течение капельной жидкости и теплообмен в вертикальной полости при ассимметричных тепловых условиях
    Поляков А.Ф.
  • Численное моделирование температурной стратификации в аккумуляционной солнечной водонагревательной установке
    Поляков А.Ф., Фрид С.Е.
  • Тепловое состояние и теплообмен в пористой металлической оболочке при проникающем охлаждении
    Поляков А.Ф.
  • Свободная конвекция и теплообмен при околосверхкритических давлениях жидкости в горизонтальной квадратной полости с боковым нагревом
    Артемов В.И., Поляков А.Ф.
  • Численная реализация вязкостно-термогравитационных режимов в микроканалах и в условиях микрогравитации при околокритических свойствах жидкости
    Поляков А.Ф.
  • Теплопередача через пористую пластину при асимптотическом отсосе охлаждающего газа
    Леонтьев А.И., Поляков А.Ф.
  • Гидравлические характеристики пористых материалов для системы проникающего охлаждения
    Зубков Н.Н., Поляков А.Ф., Шехтер Ю.Л.
  • Обобщенные зависимости для расчета теплообмена газа на входе в пористый слой
    Поляков А.Ф.
  • Неустойчивость ламинарного течения газа в трубе относительно определенного класса осесимметричных возмущений с учетом сжимаемости
    Синкевич О.А., Поцепкин В.М., Поляков А.Ф.
  • Устойчивость неизотермического ламинарного течения газа в плоском канале
    Синкевич О.А., Поцепкин В.М., Поляков А.Ф.
  • Моделирование внутреннего теплообмена в пористой проницаемой оболочке при малых числах Рейнольдса
    Леонтьев А.И., Поляков А.Ф.
  • Экспериментальное исследование поведения твердых частиц при их движении в гладкой и формованной лунками трубах
    Вараксин А.Ю., Протасов М.В., Иванов Т.Ф., Поляков А.Ф.
  • Тепловое состояние пористой стенки при проникающем охлаждении
    Леонтьев А.И., Поляков А.Ф.
  • Анализ возможности использования лазерного доплеровского анемометра для исследования сильнозапыленных потоков
    Протасов М.В., Вараксин А.Ю., Иванов Т.Ф., Поляков А.Ф.
  • Численное моделирование конвективно-кондуктивного теплообмена в блоке прямоугольных микроканалов
    Артемов В.И., Леонтьев А.И., Поляков А.Ф.
  • Постановка и решение задачи о конвективно-кондуктивном теплообмене в блоке щелевых микроканалов при однородной температуре каркаса
    Леонтьев А.И., Поляков А.Ф.
  • Исследование течения вблизи затупления из пористого материала на цилиндрическом обтекаемом теле
    Вараксин А.Ю., Поляков А.Ф., Ревизников Д.Л., Стратьев В.К., Третьяков А.Ф.
  • Структура ламинарного выхода газа из пористой сетчатой вставки
    Поляков А.Ф., Сухорученко С.Ю., Шехтер Ю.Л.
  • Распределения скоростей бидисперсных частиц в нисходящем турбулентном потоке воздуха в трубе
    Вараксин А.Ю., Поляков А.Ф.
  • Некоторые проблемы экспериментального исследования структуры гетерогенных потоков
    Вараксин А.Ю., Поляков А.Ф.
  • Экспериментальное исследование пульсаций скоростей частиц в турбулентном потоке воздуха в трубе
    Вараксин А.Ю., Поляков А.Ф.
  • Влияние концентрации частиц на интенсивность пульсаций их скоростей при турбулентном течении газовзвеси в трубе
    Вараксин А.Ю., Полежаев Ю.В., Поляков А.Ф.
  • Численное моделирование сопряженного тепломассообмена при конвективно-завесном охлаждении
    Поляков А.Ф., Ревизников Д.Л.
  • Особенности теплозащиты передней кромки при сочетании пористого проникающего и конвективно-кондуктивного охлаждения
    Поляков А.Ф., Ревизников Д.Л.
  • Уравнения пульсационного движения и пульсационного теплообмена нестоксовых частиц в турбулентных потоках
    Вараксин А.Ю., Полежаев Ю.В., Поляков А.Ф.
  • Структура осредненного течения за обратным уступом в щелевом канале
    Комаров П.Л., Поляков А.Ф.
  • Численное моделирование сопряженного тепломассообмена при проникающем пористом охлаждении цилиндрической передней кромки
    Поляков А.Ф., Ревизников Д.Л.
  • Экспериментальное исследование влияния твердых частиц на турбулентное течение воздуха в трубе
    Вараксин А.Ю., Полежаев Ю.В., Поляков А.Ф.
  • Стенд “Турбина” ИВТ РАН для исследований теплового состояния высокотемпературных элементов газовых турбин
    Бойко А.Л., Долинский Ю.Л., Зейгарник Ю.А., Низовский В.Л., Нусс В.П., Поляков А.Ф., Тетерин В.Ю., Толчинский Л.С., Шехтер Ю.Л.
  • Тепловые режимы пористой стенки при проникающем охлаждении. Постановка и решение задачи
    Полежаев Ю.В., Поляков А.Ф., Поцепкин В.М., Репин И.В.
  • Параметрический анализ тепловых режимов пористой стенки при проникающем охлаждении
    Полежаев Ю.В., Поляков А.Ф.
  • Гидравлические характеристики оболочек из пористых сетчатых материалов
    Зейгарник Ю.А., Поляков А.Ф., Сухорученко С.Ю., Шехтер Ю.Л.
  • Численное моделирование сопряженного теплообмена при обтекании лопаток газовых турбин
    Кузьмин Р.Б., Полежаев Ю.В., Поляков А.Ф., Ревизников Д.Л.
  • Измерения полей скоростей газа и твердых частиц в пограничном слое турбулизированного гетерогенного потока
    Вараксин А.Ю., Михатулин Д.С., Полежаев Ю.В., Поляков А.Ф.
  • Экспериментальное исследование локальной структуры течения над стационарным слоем засыпки
    Зейгарник Ю.А., Поликовский М.В., Поляков А.Ф., Шехтер Ю.Л.
  • Реализация устойчивой термической стратификации в трубах и подавление пристенной турбулентности
    Поляков А.Ф.
  • Развитие вторичной турбулентной циркуляции в горизонтальных трубах при локальной устойчивой стратификации плотности
    Поляков А.Ф.
  • Экспериментальное исследование теплообмена при вязкостно-гравитационном течении жидкости в горизонтальной трубе
    Петухов Б.С., Поляков А.Ф.
  • О влиянии свободной конвекции на теплоотдачу при вынужденном течении в горизонтальной трубе
    Петухов Б.С., Поляков А.Ф.
  • Температурное поле в кольце с источником тепла и переменными граничными условиями третьего рода
    Поляков А.Ф.
  • Международная летняя школа “Тепло- и массоперенос в турбулентном пограничном слое”
    Поляков А.Ф., Ковалев С.А.
  • Распределение температуры в вязкостно-гравитационном потоке воды в горизонтальных трубах
    Поляков А.Ф., Барковский В.В.
  • Границы режимов с “ухудшенной” теплоотдачей при сверхкритическом давлении теплоносителя
    Петухов Б.С., Поляков А.Ф.
  • Влияние стенки на пульсации температуры в вязком подслое
    Поляков А.Ф.
  • Границы и характер начала влияния термогравитации на турбулентное течение и теплообмен жидких металлов в вертикальных трубах
    Поляков А.Ф.
  • Расчет турбулентного переноса импульса и тепла при течении в трубах газа с переменными физическими свойствами
    Максин П.Л., Петухов Б.С., Поляков А.Ф.
  • Теплоотдача в трубах при сверхкритических давлениях теплоносителя и переменной по длине тепловой нагрузке
    Григорьев В.С., Поляков А.Ф., Росновский С.В.
  • Экспериментальное исследование поля температуры при турбулентном стратифицированном течении воздуха в плоском канале
    Кулешов В.А., Поляков А.Ф., Цыпулев Ю.В.
  • Экспериментальное исследование полей скорости и температуры при турбулентном течении воздуха с переменными свойствами
    Кулешов В.А., Поляков А.Ф., Шехтер Ю.Л.
  • Турбулентное течение и теплообмен в поле силы тяжести
    Петухов Б.С., Поляков А.Ф., Шехтер Ю.Л.
  • Экспериментальное исследование вероятностных характеристик пульсаций скорости и температуры при турбулентном течении воздуха в плоском несимметрично обогреваемом канале
    Петухов Б.С., Поляков А.Ф., Цыпулев Ю.В.
  • Экспериментальное исследование влияния поля силы тяжести на турбулентное течение воздуха в плоском горизонтальном несимметрично обогреваемом канале
    Цыпулев Ю.В., Петухов Б.С., Поляков А.Ф.
  • Баланс интенсивности пульсаций температуры при турбулентном течении жидкости
    Максин П.Л., Петухов Б.С., Поляков А.Ф.
  • Об особенностях частотного анализа структуры пристенной турбулентности
    Поляков А.Ф., Цыпулев Ю.В., Шиндин С.А.
  • Трение и теплоотдача при турбулентном течении в горизонтальных трубах в поле силы тяжести
    Петухов Б.С., Поляков А.Ф., Троицкий В.В., Шехтер Ю.Л.
  • Экспериментальное исследование тепловых потоков в МГД-канале
    Петухов Б.С., Карпухин А.В., Кириллов В.В., Плавинский А.И., Поляков А.Ф., Семенов В.Д., Соколов Ю.Н., Цыпулев Ю.В.
  • Применение методов распознавания образов для исследования структуры турбулентных течений
    Поляков А.Ф., Шиндин С.А.
  • Cнижение турбулентности в вертикальных трубах в условиях термогравитации и в слабозапыленном потоке газа
    Поляков А.Ф.
  • Турбулентный теплоперенос при подавлении пристенной турбулентности и соотношение между теплоотдачей и сопротивлением трения
    Поляков А.Ф.
  • Границы и характер начала влияния термогравитационных сил на турбулентное течение и теплообмен в вертикальных трубах
    Поляков А.Ф.

принудительная конвекция по цилиндрической трубе и потоку в воздуховоде

Выводы и перспективы

В этой статье мы обсудили метод исследования процессов теплопередачи

, который предназначен для академического обучения, но может быть полезен и в практических

ситуации. Он имеет аналогию с так называемой функциональной оптимизацией

, см. [3] и цитируемые там ссылки.

Этот подход фокусируется на теоретическом анализе соответствующих уравнений,

и позволяет узнать поведение критических величин априори,

, до проведения каких-либо эмпирических тестов.Это повышает осведомленность о физическом процессе у

студентов и эффективно помогает исследователям.

Мы применили этот метод к двум общим процессам теплопередачи,

, а именно к 1. потоку жидкости через цилиндр и 2. потоку по трубе. В обоих случаях

мы обсудили поведение числа Рейнольдса и коэффициента конвекции

в зависимости от таких переменных, как температура жидкости и диаметр трубы

, используя реалистичные значения испытаний.

Наши результаты, перечисленные в ряде графиков и таблиц, могут быть непосредственно использованы

в качестве справочного материала для студентов академических курсов. В Приложении мы также

показываем, как использовать метод наименьших квадратов для вычисления кривых интерполяции.

Ссылки

[1] Х. Хенс, «Строительная физика – тепло, воздух и влажность», Ernst & Sohn,

2007.

[2] Q. Chen, «Прогноз эффективности вентиляции для зданий: метод

. Обзор

и недавние приложения », Building and Environment, 44 (4),

848-858 (2009).

[3] А. Феррантелли, П. Мелуа, М. Ряиккёнен и М. Вильянен, «Энергетическая оптимизация

в хоккейных залах I. Системный COP как многопараметрическая функция

. рассол и выбор дизайна », материалы конференции Sustainable

Building Conference sb13 munich,« Внедрение устойчивого развития – Bar-

riers and Chances », Fraunhofer IRB Verlag, 2013. Электронная версия:

http://arxiv.org/abs /1211.3685.

[4] Роберт К. Рид и Томас К.Шервуд, «Свойства газов

и жидкостей», McGraw-Hill, 2006; Ф. Дж. Маккуиллан, Дж. Р. Калхэм и

М. М. Йованович (1984), «Свойства сухого воздуха в одной атмосфере».

Отчет ”UW / MHTL 8406, G-01”, Лаборатория теплопередачи микроэлектроники,

Университет Ватерлоо, Ватерлоо, Онтарио, Канада.

35

Что такое теплопередача? | Документация SimWiki

В общем, теплопередача описывает поток тепла (тепловой энергии) из-за разницы температур и последующего распределения и изменений температуры.

Изучение явлений переноса касается обмена импульсом, энергией и массой в форме проводимости, конвекции и излучения. Эти процессы можно описать математическими формулами.

Основы этих формул находятся в законах сохранения количества движения, энергии и массы в сочетании с основными законами, соотношениями, которые описывают не только сохранение, но и поток величин, участвующих в этих явлениях. Для этого используются дифференциальные уравнения, чтобы наилучшим образом описать упомянутые законы и определяющие соотношения.Решение этих уравнений – эффективный способ исследования систем и прогнозирования их поведения.

Рисунок 1: Охлаждение радиатора с помощью SimScale, показывающее распределение температуры

История и терминология

Без внешней помощи тепло всегда будет течь от горячих объектов к холодным, что является прямым следствием второго закона термодинамики .

Мы называем это тепловым потоком . В начале девятнадцатого века ученые считали, что все тела содержат невидимую жидкость, называемую калорической (безмассовая жидкость, которая, как считается, течет от горячих объектов к холодным).Калорийности были присвоены свойства, некоторые из которых оказались несовместимыми с природой (например, у нее был вес, и ее нельзя было создать или уничтожить). Но самой важной его особенностью было то, что она могла перетекать из горячих тел в холодные. Это был очень полезный способ думать о тепле.

Томпсон и Джоуль показали, что теория калорийности неверна. Тепло – это не вещество, как предполагалось, а движение на молекулярном уровне (так называемая кинетическая теория , ).5 \).

Поток тепла происходит постоянно от любого физического объекта к окружающим его объектам. Тепло постоянно течет от вашего тела в окружающий вас воздух. Небольшое плавучее (или конвективное) движение воздуха будет продолжаться в комнате, потому что стены никогда не могут быть идеально изотермическими, как в теории. Единственная область, свободная от теплового потока, должна быть изотермической и полностью изолированной от любой другой системы, допускающей передачу тепла. Такую систему создать практически невозможно.1 \).

Феноменология

Теплопередача – это передача тепловой энергии за счет градиента температуры.

Методы теплопередачи

Рисунок 2: Проводимость, конвекция и излучение происходят одновременно.

Проводимость

Закон Фурье : Жозеф Фурье (см. Рисунок 3) опубликовал свою книгу «Аналитическая теория Шалера» в 1822 году.

Рисунок 3: Жозеф Фурье – французский математик и физик

В этой книге он сформулировал полную теорию теплопроводности.Он заявил эмпирический закон, а именно. закон Фурье, который гласит, что тепловой поток (\ (q \), возникающий в результате теплопроводности, прямо пропорционален величине температурного градиента. Если мы назовем константу пропорциональности \ (k \), это означает

$$ q = -k \ frac {dT} {dx} \ tag {1} $$

Константа \ (k \) называется теплопроводностью с размерами \ (\ frac {W} {m * K} \) или \ (\ frac {J} {m * s * K}. \).

Учтите, что тепловой поток – величина векторная! Уравнение (1) говорит нам, что если температура уменьшается с \ (x \), \ (q \) будет положительным i.е. он будет течь в положительном \ (x \) – направлении. Если \ (T \) увеличивается с \ (x \), \ (q \) будет отрицательным; он будет течь в отрицательном \ (x \) – направлении. В любом случае \ (q \) будет течь от более высоких температур к более низким температурам, как уже упоминалось. Уравнение (1) представляет собой одномерную формулировку закона Фурье. Трехмерная эквивалентная форма:

$$ \ overrightarrow {q} = -k \ nabla T $$

, где \ (\ nabla \) обозначает градиент.

В одномерных задачах теплопроводности нет проблемы с определением направления теплового потока.1 \).

Теплопроводность газов можно понять с помощью воображения молекул. Эти молекулы перемещаются в результате теплового движения из одного положения в другое, как показано на рисунке ниже:

Рисунок 4: Теплопроводность газа

Внутренняя энергия молекул передается посредством удара с другими молекулами. 6 \).Теплопроводность не зависит от давления и увеличивается корнем от температуры.

Эту теорию довольно сложно понять для других объектов, кроме металлов. А для жидкостей это еще сложнее, потому что не существует простой теории. В неметаллических компонентах тепло передается посредством колебаний решетки (Фонон). Теплопроводность , передаваемая фононами, также существует в металлах, но ее превосходит проводимость электронов.

Низкая теплопроводность изоляционных материалов, таких как полистирол или стекловата, основана на принципе низкой теплопроводности воздуха (или любого другого газа).В следующей таблице перечислены некоторые из часто используемых элементов / материалов и их теплопроводность:

0,0171 0,0171 9017 905 9017 9017 901 9017 9017 9017 901 9017
Материал Теплопроводность \ (Вт / (мК) \)
Кислород 0,023
Пар 0,0248
0,0248
Полистирол
Вода 0,5562
Стекло 0,76
Бетон 2.1
Сталь высоколегированная 15
Сталь нелегированная 48-58
Железо 80,2
Медь чистая
Таблица 1: Теплопроводность различных материалов

Аналогичные определения

Теплопередача: Плотность теплового потока \ (\ propto \) grad T (теплопроводность)

Диффузия: Частичная плотность тока \ (\ propto \) grad x (Коэффициент диффузии)

Электропровод: Плотность тока \ (\ propto \) grad \ (U_ {el} \) (Электропроводность)

Радиация

Радиация описывает явление передачи энергии от одного тела к другому при распространении независимо от среды.Все тела постоянно излучают энергию электромагнитным излучением. Интенсивность такого потока энергии зависит не только от температуры тела, но и от характеристик поверхности. 1 \).7 \).

Электромагнитное излучение можно рассматривать как поток фотонов, каждый из которых движется волнообразно, движется со скоростью света и несет энергию. Различные электромагнитные излучения классифицируются по энергии фотонов в них. Важно иметь в виду, что если мы говорим об энергии фотона, поведение может быть либо волной, либо частицей, называемой световым дуализмом « волна-частица ».

Каждый квант лучистой энергии имеет длину волны \ (\ lambda \) и частоту \ (\ nu \), связанную с ним.{-34} Js) \).

В таблице ниже показаны различные формы в диапазоне длин волн. Тепловое излучение от 0,1 до 1000 мкм.

свет свет 3-400 \ (нм \)
Характеристика Длина волны
Гамма-лучи 0,3 100 \ (пм \)
Рентгеновские лучи 0,01-30 \ (нм \)
Видимый свет 0,4-0,7 \ (мкм \)
Ближнее инфракрасное излучение 0. S \), однородные для всех длин волн.2 \).

Конвекция

Рассмотрим ситуацию с конвективным охлаждением. Холодный газ проходит мимо теплого тела, как показано на рисунке ниже:

Рисунок 6: Конвективное охлаждение нагретого тела происходит в результате теплообмена между двумя телами аналогично теплопроводности.

Жидкость образует тонкую замедленную область, называемую пограничным слоем, непосредственно прилегающую к телу. В этот слой передается тепло, который исчезает и смешивается с потоком. Мы называем этот процесс отвода тепла от тела движущейся жидкостью конвекцией .1 \).

Стационарная форма закона Ньютона охлаждения, определяющая свободную конвекцию, описывается следующей формулой:

$$ Q = h (T_ {body} – T_ \ infty) $$

, где \ (h \) – коэффициент теплопередачи . Этот коэффициент можно обозначить полосой \ (\ overline {h} \), которая указывает среднее значение по поверхности тела. \ (h \) без черты обозначает «локальные» значения коэффициента.

В зависимости от того, как инициируется движение жидкости, мы можем классифицировать конвекцию как естественная (свободная) или принудительная конвекция . Естественная конвекция вызвана, например, эффектами плавучести (теплая жидкость поднимается, а холодная опускается из-за разницы в плотности). В другом случае принудительная конвекция заставляет жидкость перемещаться с помощью внешних средств, таких как вентилятор, ветер, охлаждающая жидкость, насос, всасывающие устройства и т. Д.

Перемещение твердого компонента в жидкость также можно рассматривать как принудительную конвекцию. Естественная конвекция может создать заметную разницу температур в доме или квартире. Мы осознаем это, потому что одни части дома теплее других.3 \).

Моделирование теплопередачи – структурная теплопередача

Рисунок 8: Структурный анализ теплопередачи в сравнении с анализом жидкость-твердое тело

Программное обеспечение для структурной теплопередачи используется, когда:

  • Можно предположить, что температура жидкости вокруг твердой детали однородна
  • Исследование поведения конструктивных элементов только при нагревании
  • Исследование напряжения и деформации детали, вызванной тепловой нагрузкой (анализ термического напряжения)

Сопряженный Анализ теплопередачи (жидкость-твердое тело) используется, когда:

  • Необходимо изучить распределение жидкости вокруг твердого тела
  • Исследование влияния объекта на жидкость
  • Исследование естественного охлаждения

Анализ теплопередачи – линейный статический анализ

Проведите быстрое сравнение двух анализов в таблице ниже:

90 ( k )
Категория Структурный анализ (линейный статический) Анализ теплопередачи (установившееся состояние)
Свойства материала
Модуль Юнга ( E

84)
Законы Закон Хука \ (\ sigma = E \ cdot \ frac {du} {dx} \) Закон Фурье \ (q = -k \ cdot \ frac {dT} { dx} \)
Степень свободы
(DOF)		 Смещение ( u ) Температура ( T )
Градиент DOF Напряжение \ (\ epsilon \) Напряжение \ (\ epsilon \) \ sigma \) Температурный градиент \ ((\ nabla T) \)
Сходства Осевая сила на единицу длины: Q Площадь поперечного сечения: A Модуль Юнга: E Внутренний тепловыделение на единицу длины: Q Площадь поперечного сечения: A Теплопроводность: k
Таблица 3: Анализ теплопередачи в сравнении со структурным анализом

Применение теплового моделирования

Термический – структурный анализ

Heat Transfer учитывает энергетический баланс исследуемых систем.При исследовании термомеханических компонентов также могут быть включены деформации конструкции, вызванные воздействием тепловых нагрузок на твердые тела. Моделирование реакции напряжения на тепловые нагрузки и отказы важно для многих промышленных приложений. Примером приложения является анализ теплового напряжения печатной платы.

Рисунок 9: Печатная плата – смоделирована с помощью SimScale. Области, отмеченные красным, являются «горячими» точками и могут деформировать материал.

Сопряженная теплопередача

Моделирование сопряженной теплопередачи (CHT) анализирует сопряженную теплопередачу в жидкостях и твердых телах.Прогнозирование потока жидкости с одновременным анализом теплопередачи, которая имеет место на границе жидкость / твердое тело, является важной особенностью моделирования CHT. Одна из областей, в которой он может использоваться, – охлаждение электроники (см. Рисунок 1).

Проводимость

Теоретически тепло передается от горячего объекта к холодному. Электропроводность – это передача тепла от горячего к холодному объекту, находящемуся в непосредственном контакте друг с другом. Теплопроводность различных объектов определяет, сколько тепла передается в данный момент времени.Примеры включают лампы накаливания CFL.

Конвекция

Конвективная теплопередача – это передача тепла между двумя зонами без физического контакта. Конвективные токи возникают, когда молекулы поглощают тепло и начинают двигаться. Как вы понимаете, эти эффекты трудно предсказать, поэтому для получения надежных результатов моделирования требуется высокая вычислительная мощность. Одно из таких приложений – охлаждение материнской платы Raspberry pi.

Радиация

Электромагнитные волны являются источником передачи тепла посредством излучения.Обычно они играют роль при высоких температурах. Количество тепла, излучаемого излучением, зависит от типа поверхности материала. Общее правило состоит в том, что чем больше поверхность, тем выше излучение. Применение, в котором используется моделирование излучения, – это лазерная сварка.

Термический анализ SimScale

Многие материалы и продукты имеют температурно-зависимые характеристики, что делает анализ нагрева и управление температурным режимом критически важным процессом при разработке продукта.Модуль теплопередачи онлайн-платформы моделирования SimScale позволяет прогнозировать воздушный поток, распределение температуры и теплопередачу. Это включает в себя конвекцию, теплопроводность и излучение, чтобы обеспечить производительность, долговечность и энергоэффективность ваших конструкций.

Анимация 1: тепловое моделирование с использованием SimScale, показывающее движущуюся горячую лазерную точку на зубе.

Последнее обновление: 28 мая 2021 г.

Решила ли эта статья вашу проблему?
Как мы можем добиться большего?

Мы ценим и ценим ваши отзывы.

Отправьте свой отзыв