Главная
Измеряется момент инерции: В чем измеряется момент инерции?

Измеряется момент инерции: В чем измеряется момент инерции?

Содержание

Центробежный момент инерции – это… Что такое Центробежный момент инерции?

Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

Моментом инерции механической системы относительно неподвижной оси a («осевой момент инерции») называется физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

  • mi — масса i-й точки,
  • ri — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси

a подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

где:

  • dm = ρdV — масса малого элемента объёма тела dV,
  • ρ — плотность,
  • r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Гюйгенса-Штейнера

Момент инерции данного тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера),

момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Если  — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии от неё, равен

,

где  — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Осевые моменты инерции некоторых тел

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке

O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения, пропорциональная площади сечения и квадратно пропорциональная расстоянию до этого сечения. Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости и взаимного расположения различных элементов конструкции.

Геометрический момент инерции двух стержней диаметром d на расстоянии L:

J = 2dL2

Центральный момент инерции

Центральный момент инерции (или момент инерции относительно точки O) — это величина

,

где:

  •  — масса малого элемента объёма тела dV,
  •  — плотность,
  •  — расстояние от элемента dV до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .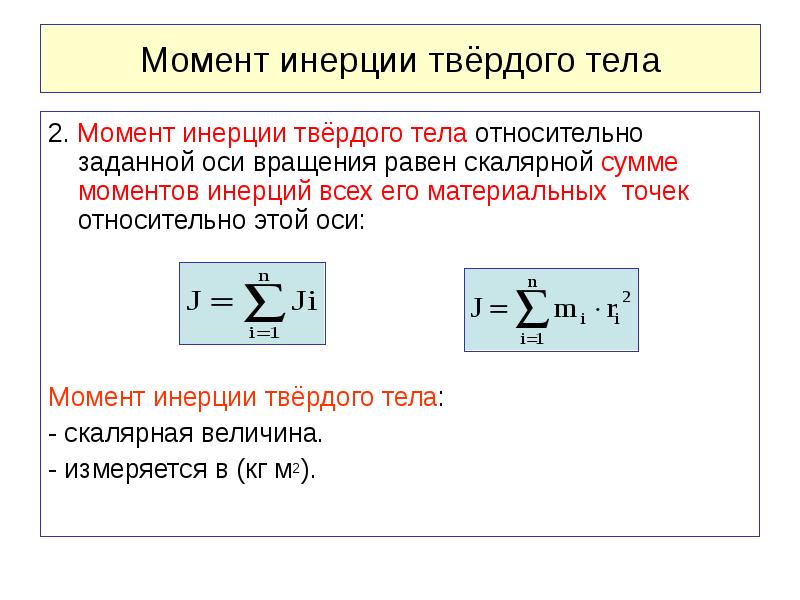

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы :

(1),

где  — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

,

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :

Где,  — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины  — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

.

Откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на


и произведя замены:

,

получаем канонический вид уравнения эллипсоида в координатах :

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой проходящей через центр эллипсоида и эту точку:


См. также

Литература

  • Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
  • Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
  • Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
  • Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002.
     — 392с. http://www.alleng.ru/d/phys/phys99.htm
  • Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
  • Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm

Ссылки

Wikimedia Foundation. 2010.

простое пояснение, значении в физике, формулы, примеры

Что такое инерция?
  • Определение момента инерции

  • Формула

  • Теорема Гюйгенса – Штейнера

  • Моменты инерции простейших объектов

  • Рекомендованная литература по теме и полезные ссылки

  • Видео

    • Что такое инерция?

    Инерция в физике – способность тел определенное время сохранять состояние движения при отсутствии действия внешних сил. Впрочем, понятие инерции имеет частое применение не только в физике, но и в нашей повседневной жизни. Так обычно «инертным» называют человека, который совершенно не проявляет никакой инициативы, делают только то, что ему скажут другие, и делает это крайне медленно, без какого-либо энтузиазма. «Движется по инерции», – говорим мы, когда хотим подчеркнуть, что что-то делается без какого-либо смысла, а просто потому, что так было заведено когда-то или в силу наработанной годами привычки. И если с понятием инерции все более-менее понятно, благодаря таким вот житейским примерам, то термин «момент инерции» требует более детального пояснения, чем мы и займемся в нашей статье.

    Определение момента инерции

    Со школьной программы по физике мы прекрасно знаем, что масса тела является мерой его инертности. Например, если в супермаркете сильно толкнуть две тележки, одна из которых будет пустой, а вторая нагруженной разными товарами, то впоследствии остановить будет труднее тележку, нагруженную товарами в силу ее большей массы. Другими словами, чем больше у тела масса, тем большее на него воздействие инерции и тем больше нужно сил, чтобы изменить движение такого тяжелого тела.

    В приведенном примере тележка движется по прямой линии, то есть иными словами совершает поступательное движение. И если при поступательном движении какого-либо теле его масса является мерой его инерции, то при вращательном движении тела вокруг своей оси мерой его инерции будет величина, которая собственно и называется – момент инерции.

    Момент инерции – скалярная физическая величина, мера инертности тела при его вращении вокруг оси. Обычно обозначается буквой J и измеряется в килограммах, умноженных на квадратный метр. Такое академическое определение того, что такое момент инерции.

    Формула

    Как рассчитать точное значение момента инерции? Для этого есть общая формула, помогающая физикам определять момент инерции любого тела. Если тело разбить на бесконечно маленькие кусочки с массой dm, то момент инерции будет равным сумме произведения этих элементарных масс на квадрат расстояния до оси вращения. Формула будет иметь такой вид:

    J – момент инерции, r – расстояние до оси вращения.

    Для материальной точки массы m, которая вращается вокруг оси на расстоянии r, данная формула будет иметь такой вид:

    Теорема Гюйгенса – Штейнера

    Говоря о моменте инерции невозможно не упомянуть о теореме двух математиков Гюйгенсе и Штейнере, которые дали формулировку определению характеристики параллельных осей.

    Теорема Гюйгенса – Штейнера гласит: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

    Если записать вышесказанное математической формулой, то получится следующее:

    Где d – расстояние между осями

    Эта теорема значительно облегчает решения многих физических задач, связанных с инерцией. К примеру, у Вас имеется объект произвольной формы, центробежная сила которого известна. При помощи формулы Штейнера можно вычислить момент инерции тела относительно любой оси параллельной линии, которая проходит через середину фигуры.

    Моменты инерции простейших объектов

    Несмотря на внешнюю простоту, вычисление моментов инерции для разных предметов предполагает знание интегралов, этих важных инструментов высшей математики. Для упрощения задачи создана таблица с вычислениями инерции для простых геометрических фигур: круга, квадрата, цилиндра и т. д.

    Так выглядят математические расчеты вычисления моментов инерции для круга и кольца.

    Аналогичным образом будет рассчитываться момент инерции цилиндра.

    Предлагаем вашему вниманию более детальную таблицу с формулами для расчета момента инерции для основных геометрических фигур: шара, сферы, диска, цилиндров, и т. д.

    Рекомендованная литература и полезные ссылки

    • Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
    • Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ. ) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — DOI:10.1126/science.286.5437.77. — PMID 10506564.
    • Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.)русск. : journal. — 2012. — Vol. 117. — DOI:10.1029/2012JE004161.
    • Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
    • Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
    • Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
    • Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
    • Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
    • Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М. : Дрофа, 2002, 800с. ISBN 5-7107-5956-3

    Видео

    И в завершение образовательное видео по теме нашей статьи.


    Эта статья доступна на английском языке – Moment of Inertia.

    1.2. Осевые моменты инерции Jx ; Jy

    Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.

    (7)

    (8)

    Единица измерения [см4], [мм4].

    Знак всегда «+».

    Не бывает равным 0.

    Свойство:Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения.

    Чем дальше площадь удалена от центральной оси, тем осевой момент инерции сечения больше. Жесткость конструкции повышается.

    Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.

    1.3. Полярный момент инерции сечения Jρ

    Рис. 3

    (9)

    Взаимосвязь полярного и осевого моментов инерции:

    (10)

    (11)

    Полярный момент инерции сечения равен сумме осевых моментов.

    Свойство:

    при повороте осей в любую сторону, один из осевых моментов инерции возрастает, а другой убывает (и наоборот). Сумма осевых моментов инерции остается величиной постоянной.

    1.4. Центробежный момент инерции сечения Jxy

    Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей

    (12)

    Единица измерения [см4], [мм4].

    Знак «+» или «-».

    , если координатные оси являются осями симметрии (пример – двутавр, прямоугольник, круг), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).

    Таким образом для симметричных фигур центробежный момент инерции равен 0.

    Координатные оси uиv, проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называютсяглавными центральными осями инерции сечения. Главными они называются потому, что центробежный момент относительно них равен нулю, а центральными – потому, что проходят через центр тяжести сечения.

    У сечений, не обладающих симметрией относительно осей xилиy, например у уголка,не будет равен нулю. Для этих сечений определяют положение осейuиvс помощью вычисления угла поворота осейxиy

    (13)

    Центробежный момент относительно осей uиv–

    Формула для определения осевых моментов инерции относительно главных центральных осей uиv:

    (14)

    где – осевые моменты инерции относительно центральных осей,

    – центробежный момент инерции относительно центральных осей.

    1.5. Момент инерции относительно оси, параллельной центральной (теорема Штейнера)

    Теорема Штейнера:

    Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.

    (15)

    Рис. 4

    Доказательство теоремы Штейнера.

    Согласно рис. 5 расстояние удо элементарной площадкиdF

    Рис. 5

    Подставляя значение ув формулу, получим:

    Слагаемое , так как точка С является центром тяжести сечения (см. свойство статических моментов площади сечения относительно центральных осей).

    Для прямоугольника высотой h и шириной b :

    Осевой момент инерции:

    Момент сопротивления изгибу:

    момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:

    т. к. , то

    Для круга:

    Полярный момент инерции:

    Осевой момент инерции:

    Момент сопротивления кручению:

    Т.к. , то

    Момент сопротивления изгибу:

    Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx.

    Рис. 6

    Решение. Разобьём площадь прямоугольника на элементарные прямоугольники с размерами b(ширина) иdy(высота). Тогда площадь такого прямоугольника (на рис. 6 заштрихована) равна dF=bdy. Вычислим значение осевого момента инерции Jx

    По аналогии запишем

    – осевой момент инерции сечения относительно центральной

    оси у

    Центробежный момент инерции

    , так как оси Сxи Сyявляются осями симметрии.

    Пример 3. Определить полярный момент инерции круглого сечения.

    Рис. 7

    Решение. Разобьём круг на бесконечно тонкие кольца толщиной радиусом, площадь такого кольца. Подставляя значениев выражение для полярного момента инерции интегрируя, получим

    Учитывая равенство осевых моментов круглого сечения и

    , получаем

    Осевые моменты инерции для кольца равны

    с – отношение диаметра выреза к наружному диаметру вала.

    Лекция №2 «Главные оси иглавные моментыинерции

    Рассмотрим, как изменяются моменты инерции при повороте координатных осей. Положим, даны моменты инерции некоторого сечения относительно осей 0х, 0у(не обязательно центральных)- ,- осевые моменты инерции сечения. Требуется определить,- осевые моменты относительно осейu,v, повёрнутых относительно первой системы на угол(рис. 8)

    Рис. 8

    Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:

    (15)

    Исключим uиvв выражениях моментов инерции:

    Тогда

    Откуда

    (16)

    (17)

    (18)

    Рассмотрим два первых уравнения. Складывая их почленно, получим

    Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла и при повороте осей остается постоянной. Заметим при этом, что

    Где – расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом

    Где – уже знакомый нам полярный момент инерции:

    Определим осевой момент инерции круга относительно диаметра.

    Так как в силу симметрии но, как известно,

    Следовательно, для круга

    С изменением угла поворота осей значения моментов именяются, но сумма остается неизменной. Следовательно существует такое значение, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражениепо углуи приравнивая производную к нулю, находим

    (19)

    При этом значении угла один из осевых моментов будет наибольшим, а другой – наименьшим. Одновременно центробежный момент инерции обращается в нуль, что можно легко проверить, приравнивая к нулю формулу для центробежного момента инерции .

    Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главнымиосями.Если они к тому же являются центральными (точка начала координат совпадает с центром тяжести сечения), то тогда они называютсяглавными центральными осями (u; v).Осевые моменты инерции относительно главных осей называютсяглавными моментами инерции –и

    И их значение определяется по следующей формуле:

    (20)

    Знак плюс соответствует максимальному моменту инерции, знак минус – минимальному.

    Существует ещё одна геометрическая характеристика – радиус инерциисечения.Эта величина часто используется в теоретических выводах и практических расчётах.

    Радиусом инерции сечения относительно некоторой оси, например 0x,называется величина ,определяемая из равенства

    (21)

    F– площадь поперечного сечения,

    – осевой момент инерции сечения,

    Из определения следует, что радиус инерции равен расстоянию от оси 0хдо той точки, в которой следует сосредоточить (условно) площадь сеченияF, чтобы момент инерции одной этой точки был равен моменту инерции всего сечения. Зная момент инерции сечения и его площадь, можно найти радиус инерции относительно оси 0х :

    (22)

    Радиусы инерции, соответствующие главным осям, называютсяглавными радиусами инерциии определяются по формулам

    (23)

    Лекция 3. Кручение стержней круглого поперечного сечения.

    Момент – инерция – материальная точка

    Момент – инерция – материальная точка

    Cтраница 1

    Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния от нее до этой оси.  [1]

    Моментом инерции материальной точки Р с массой m относительно какой-либо оси называется произведение массы на квадрат расстояния точки Р от этой оси.  [2]

    Согласно определению момента инерции материальной точки.  [3]

    Следовательно, моментом инерции материальной точки относительно некоторой оси вращения называется произведение массы материальной точки на квадрат ее расстояния до этой оси.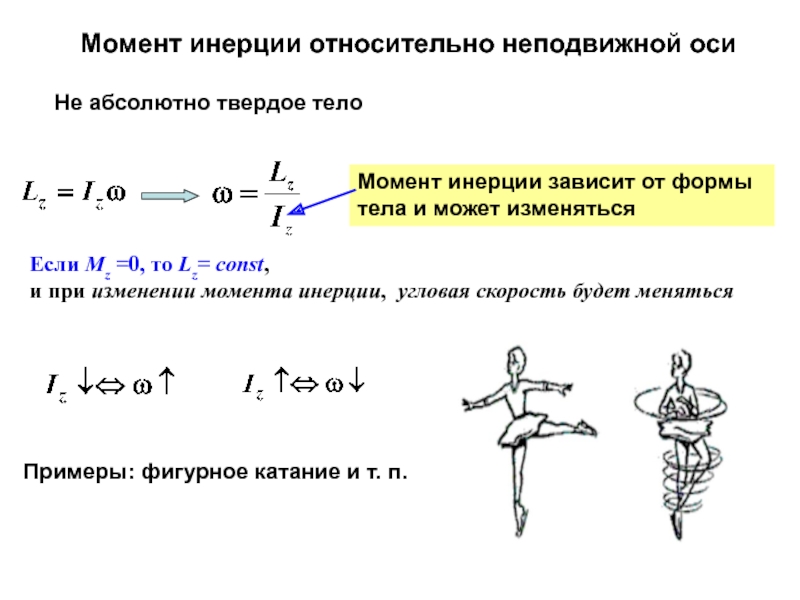  [4]

    Исходя из определений момента инерции материальной точки и системы материальных точек, получить выражение для момента инерции однородного сплошного цилиндра массой т и радиусом R относительно оси, совпадающей с осью цилиндра.  [5]

    Величина mr2 называется моментом инерции материальной точки массой m относительно оси вращения, находящейся на расстоянии г от материальной точки.  [6]

    Зная, что моментом инерции материальной точки называется произведение массы материальной точки и квадрата расстояния от оси вращения до данной материальной точки, получить выражение для момента инерции однородного тонкого диска массой т и радиусом R относительно оси, проходящей через его центр масс перпендикулярно к плоскости диска.  [7]

    Килограмм-метр в квадрате равен моменту инерции материальной точки массой 1 кг, находящейся на расстоянии 1 м от оси вращения.  [8]

    Килограмм-метр в квадрате равен моменту инерции материальной точки массой 1 кг, находящейся на расстоянии 1 м от оси инерции.  [9]

    Какая физическая величина называется моментом инерции материальной точки и тела. Что называется моментом силы. Какая физическая величина называется импульсом момента силы.  [10]

    Считая известным выражение для определения момента инерции материальной точки, получить выражение для момента инерции однородного тонкостенного цилиндра массой т и радиусом R относительно оси, совпадающей с осью цилиндра.  [11]

    Из курса механики известно, что моментом инерции материальной точки М с массой m относительно некоторой оси называется произведение массы на квадрат расстояния от точки М до этой оси. Момент инерции относительно оси системы материальных точек равен сумме моментов инерции всех точек относительно той же оси. G относительно осей координат.  [12]

    Каждое слагаемое внутри скобок последнего равенства представляет собой момент инерции материальной точки твердого тела. Сумма моментов инерции всех отдельных точек тела называется моментом инерции тела и обозначается через /, как уже было указано на стр.  [13]

    Каждое слагаемое внутри скобок последнего равенства представляет собой момент инерции материальной точки твердого тела. Сумма моментов инерции всех отдельных точек тела называется моментом инерции тела и обозначается через I, как уже было указано на стр.  [14]

    Единицей измерения моментов инерции в технической системе единиц является момент инерции материальной точки, имеющей массу, равную одной технической единице массы, и находящейся на расстоянии одного метра от данной оси или от данной точки.  [15]

    Страницы:      1    2

    Экспериментальное определение моментов инерции ротора электродвигателя

    Не всегда значение маховых моментов или моментов инерции роторов или якорей электрических машин можно найти в каталогах электрооборудования. Также в данный момент на предприятиях эксплуатируется большое количество электрических машин, данные на которые могут потеряться в ходе эксплуатации. Если данные о маховом моменте электрической машины отсутствуют, то их можно определить экспериментально с помощью методов:

    • Крутильных колебаний;
    • Маятниковых колебаний;
    • Падающего груза;
    • Свободного выбега;

    Содержание:

    Метод крутильных колебаний

    Суть данной методики заключается в следующем: ротор электромашины подвешивают на  стальной проволоке за конец вала. Второй конец проволоки жестко закрепляют на опоре, как показано на рисунке ниже (а):

    При таком определении момента инерции нужно строго обеспечить вертикальность оси вала ротора. После чего ротор, подвешенный на проволоке, закручивают на определенный угол и подсчитывают количество полных колебаний z, которые ротор совершит за какой – то промежуток времени t. Период полного колебания, если пренебречь затуханием, можно представить:

    Где k – направляющий момент проволоки (момент, вызывающий закручивание проволоки на 1 радиан). Если мы знаем k, то момент инерции ротора можно определить из следующего выражения:

    k можно определить исходя из размеров проволоки:

    Где Е – модуль кручения для материала проволоки в кГ/см2;

    r и l – радиус и длина проволоки в см соответственно.

    Так как формула не дает точного значения k, более точно можно определить его из опыта. Для этого нужно измерять вращающий момент М, необходимый для закручивания проволоки на угол α. Тогда:

    Но еще проще произвести определение момента инерции на основе двух опытов крутильных колебаний ротора. Для этого измеряют продолжительность полного колебания как указано выше. Второе измерение периода колебания ротора производят с прикрепленным к нему телом, момент инерции которого известен Jдоб. Как вариант, это может быть диск с известными геометрическими размерами и весом или рычаг с грузами на концах (рис. выше б). если Т – период колебаний одного ротора, а Т/ — с добавочным грузом, тогда получим выражение:

    Благодаря пропорциональности между углом отклонения и направляющим моментом угол первоначального закручивания может быть взят произвольным.

    Метод маятниковых колебаний

    Ротор машины крепят проволокой к куску угловой стали так, чтоб вершину уголка можно было использовать в качестве призмы, относительно которой ротор электромашины смог бы выполнять колебания. После чего оба конца полученного таким образом маятника опирают на металлические горизонтальные опоры так, чтоб ротор мог относительно точек опоры совершать колебания. Момент его инерции относительно оси, совпадающей с вершиной уголка, при пренебрежении инерцией последнего будет равен:

    Где: G – это вес ротора машины в кг;

    е – расстояние между осью ротора и осью качания, измеряется в м;

    Т – период одного колебания в сек.

    Зная JN, определяют по общему правилу инерцию ротора относительно оси, проходящей через центр тяжести:


    Метод падающего груза

    Самым главным недостатком методик, описанных выше, является то, что для определения инерции необходима разборка электромашины. Метод падающего груза позволит определить момент инерции электродвигателя без разборки последнего.

    На конец вала или шкив, сидящий на валу, навивают несколько витков шнура. К другому концу шнура прикрепляют груз и опускают его через направляющие блоки, либо непосредственно, как показано ниже:

    При опускании груз поворачивает ротор, преодолевая трение в подшипниках электромашины, при этом измеряют время t, за которое груз опустится на величину h.

    В таком случае инерция ротора может быть вычислена по формуле:

    Где: m – масса груза 

     

    r – радиус вала или шкива, на который навивается шнур;

    t и h – время, и соответственно высота опускания груза;

    g – ускорение свободного падения равное 9,81;

    Метод свободного выбега

    Перечисленные выше методы определения инерции электрической машины больше подходят к электрическим машинам относительно малой мощности. При значительных габаритных и массовых показателей машин большой мощности определение инерции методами маятниковых колебаний и падающего груза становятся практически не пригодными, и тем более не пригодны в системе электродвигатель – рабочий орган. Поэтому зачастую применяют метод свободного выбега.

    Когда  двигатель отключают от сети, то за счет накопленной кинетической энергии, двигатель и соединенный с ним рабочий орган будет вращаться замедляясь постепенно. Чем больше тормозящее усилие сил трения и чем меньше запас кинетической энергии, тем быстрее будет замедлятся система. Имея кривую самоторможения, показанную ниже, которая представляет собой график зависимости скорости от времени.

    По данной кривой можно сделать вывод о величине тормозных усилий. Мощность торможения в данном случае будет равна уменьшению кинетической энергии во времени:

    Подставив в формулу значение кинетической энергии , которая представлена в джоулях, тогда получим:

    Из данного выражения можно определить момент инерции:

    Величину поднормали   определяют из кривой торможения для точки, в которой известны потери энергии при торможении. Если масштабы выбраны, то для построения кривой самоторможения: µn = об/мин/см – скорость, µt = сек/см – времени. В таком случае масштаб поднормали будет равен: , то есть , где СВ выражена в см.

    Таблица. Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур.


    		 Навигация по справочнику TehTab.ru:  главная страница  / / Техническая информация / / Материалы – свойства, обозначения / / Сопротивление материалов. Сопромат.  / / Таблица. Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур.

    Таблица. Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур.

    (Моменты инерции J даны для главных центральных осей. Радиус инерции i=(J/F)1/2, где F – площадь сечения).

    Легенда:
    • π – математическая константа (3,14)
    • d, D – диаметр
    • r – радиус
    • с – отношение 2х диаметров друг к другу
    • s – толщина
    		 Легенда:
    • h – высота
    • α – диаметр
    • b – ширина, длина
    • О – центр

    Форма поперечного сечения

    Осевой момент инерции, J, см4

    Момент сопротивления W, см3

    Радиус инерции i, см

    Круг
    Кольцо

    c=d1/d
    Тонкостенное кольцо

    s≤(D/10)
    Полукруг

    Vo=2d/3π=0,2122d=0,4244r
    Круговой сегмент
    Круговой сектор

    		 —
    Круговое полукольцо
    Сектор кругового кольца

    		 —
    Профиль с симметричными закруглениями
    		 —

    Эллипс

    Квадрат

    Полый квадрат  

    Полый тонкостенный квадрат

     

    s<(B/15)
    Квадрат, поставленный на ребро

    Срез верхнего и нижнего углов увеличивает Wx; при срезе углов на С=1/18 диагонали с каждой стороны момент сопротивления увеличивается до Wx=0,124b3
    Полый квадрат, поставленный на ребро

    Прямоугольник

     
    Прямоугольник повернутый

    Полый прямоугольник

    Полый тонкостенный прямоугольник

    Сечение из двух равных прямоугольников

    Треугольник 

    		 При вычислении напряжения в вершине треугольника

    при вычислении напряжения в точке основания

    Поставленный на ребро треугольник

    Трапеция

    		 При вычислении напряжений в точках верхнего основания

    в точках нижнего основания

    Трапеция

    Тавр

    		 Для нижних волокон

    Для верхних волокон

    Корытное сечение 

    Крестообразное сечение

    Правильный шестиугольник

    Правильный восьмиугольник



    Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
    TehTab.ru

    Реклама, сотрудничество: [email protected]

    		 Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

    Как измерить MOI с помощью CG

    Как измерить момент инерции через центр тяжести: даже не зная местоположения центра тяжести

    1. Зачем измерять момент инерции (MOI) через центр тяжести (CG)?

    Когда объект может свободно вращаться, он будет вращаться вокруг оси, проходящей через его центр тяжести. Поэтому важно знать момент инерции через центр тяжести, чтобы оценить летные характеристики полезной нагрузки.

    MOI вокруг оси A, проходящей через CG, является наименьшим MOI вокруг любой оси, параллельной A.Как только вы знаете MOI через CG, вы можете экстраполировать на MOI по любой оси, параллельной ей, при условии, что вы знаете расстояние между CG и вашей осью.

    Формула:

    MOI через ось A = MOI через CG + Md 2

    Где:
    M – масса объекта
    d – расстояние между CG и осью A

    2. Как измерить MOI с помощью CG, не зная местоположения CG?

    Конечно, самый простой способ измерить момент инерции через центр тяжести – это использовать инструмент, который измеряет как CG, так и MOI.Наша серия KSR – это высокоточные инструменты, которые измеряют CG и MOI с точностью 0,1%. На этом приборе одна установка полезной нагрузки позволяет измерять две координаты местоположения центра тяжести и один момент инерции. Инструмент показывает момент инерции непосредственно через центр тяжести.

    Наши прядильные машины (серия POI) также измеряют CG и MOI и, следовательно, определяют момент инерции через центр тяжести. Наша серия MP – это инструменты, которые также измеряют как CG, так и MOI, хотя и с меньшей точностью.

    Но не обязательно знать положение центра тяжести, чтобы измерить момент инерции через центр тяжести. Измеряя MOI относительно нескольких параллельных осей, можно рассчитать MOI через CG.

    Оптимальное количество измерений момента инерции (лучший компромисс между точностью и временем) – 6. Чем больше измерений, тем больше точность не будет. Меньшее количество измерений значительно снизит точность.

    Точность момента инерции зависит от нескольких факторов, в том числе:

    • Позиции, используемые для каждого измерения
    • Точность прибора
    • Точность приспособления

    В зависимости от полезной нагрузки вы получите точность в порядок 1.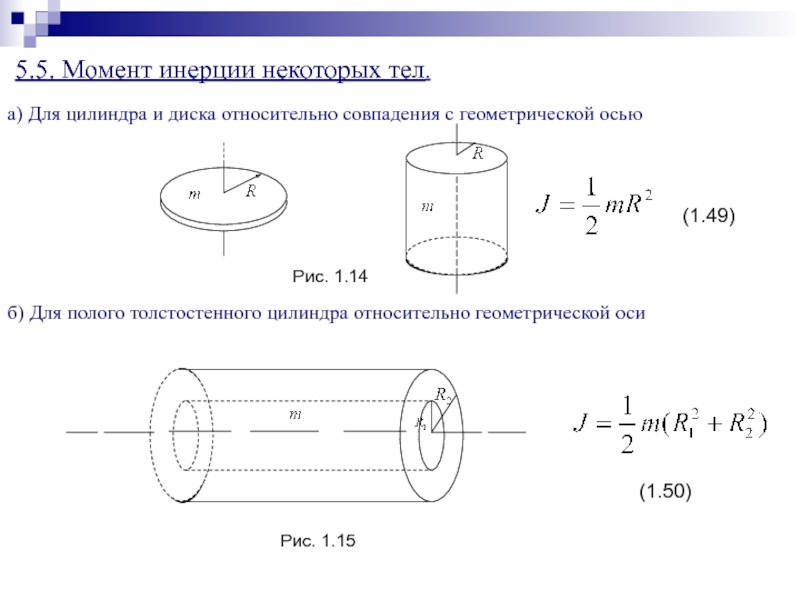 В 5–3 раза хуже, чем точность вашего прибора. Другими словами, если ваш прибор для измерения момента инерции имеет точность 0,1%, вы получите MOI через CG с точностью от 0,15% до 0,3%.

    От одного измерения к другому полезная нагрузка должна перемещаться в горизонтальной плоскости без изменения ее ориентации. Измерения момента инерции дают наилучшие результаты, когда центр тяжести полезной нагрузки расположен близко к центральной линии машины. Следовательно, позиции измерения должны выбираться осторожно, чтобы оставаться в пределах допуска инструмента для опрокидывающего момента, но чтобы обеспечить как можно больший разброс от одного положения к другому.

    Крепление имеет решающее значение для этих измерений. Использование двухосевой таблицы трансляции позволяет проводить измерения без повторной фиксации полезной нагрузки.

    3. Могу ли я определить местоположение центра тяжести с помощью этого метода? На какую точность я могу рассчитывать?

    Этот метод даст вам приблизительную оценку местоположения центра тяжести, но погрешность очень велика. Не полагайтесь на этот метод для определения местоположения центра тяжести, которое вы можете использовать в расчетах или для балансировки.

    Точность зависит от вашей полезной нагрузки.Например, на головке клюшки для гольфа вы можете установить центр тяжести с точностью +/- 0,25 дюйма (+/- 6 мм). Для других полезных нагрузок погрешность может составлять +/- 1 дюйм (+/- 2,54 см) или более.

    4. Как Space Electronics реализует этот метод?

    Приборы для измерения момента инерции Space Electronics поддерживают метод измерения множественных значений MOI для нахождения MOI с помощью компьютерной графики. Мы разрабатываем индивидуальное программное обеспечение и приспособления, которые автоматизируют процесс измерения и расчета.

    Наши приборы для измерения момента инерции также позволяют вручную вводить центр тяжести и переводить результаты MOI на любую ось.

    ОБСУЖДЕНИЕ: Момент инерции

    ОБСУЖДЕНИЕ: Момент инерции

    Анализ движения в плоскости динамики транспортного средства, включая повороты, момент инерции каждого Автомобиль должен вращаться вокруг вертикальной оси через его центр тяжести.

    Момент инерции твердое тело во вращательном движении аналогично его массе в поступательном движении. Он равен сумме произведений каждой массовой частицы тела m, умноженное на квадрат соответствующего расстояния r от оси вращение.

    (1)

    Момент инерции обычно дается в одной из единиц, перечисленных в. (Обратите внимание, что Компьютерные программы SMAC / EDSMAC используют блоки LB-SEC 2 -IN.)

    Таблица 1 Моменты инерции (единицы и пересчет Факторы)

    Умножить

    по

    Получить

    Ударные ножки 2

    LB-SEC 2 -FT

    12. 000

    LB-SEC 2 -IN

    0,13832

    Килопонд-метр-сек 2

    1,35691

    Килограмм-метр 2

    Килограмм-метр 2

    8.84362

    LB-SEC 2 -IN

    Килопонд-метр-сек 2

    0,73697

    Ударные ножки 2

    LB-SEC 2 -IN

    0. 011527

    Килопонд-метр-сек 2

    0,11308

    Килограмм-метр 2

    0,08333

    Ударные ножки 2

    Килопонд-метр-сек 2

    86.75595

    LB-SEC 2 -IN

    0,10194

    Килограмм-метр 2

    7.22966

    Ударные ножки 2

    Если момент инерция, определяемая уравнением (1), делится на общую массу тело, квадрат среднего r, называемый радиусом вращения, равен полученный.Таким образом, радиус инерции определяется как расстояние от ось вращения, на которой можно принять всю массу тела равной сконцентрированы для целей вращения.

    Относительно простой подход к аппроксимации инерции рыскания автомобиля представлен в Ссылка [36]. Это рассчитывается, как если бы через вагон проходил прямоугольный блок форменной одежды. плотность:

    (2)

    где a и b – длина и ширина и

    M – это масса автомобиля.

    k 2 = радиус вращения в квадрате

    в ссылках 36 и 37 , процедуры аппроксимации для представлена ​​инерция рыскания, основанная на измерениях, выполненных под состояние снаряженной массы. Подгоняемые линейные функции снаряженной массы: отображается графически на Рис. 33.

    Для удобства в приложения к автомобилям, где вес включает пассажиров и / или ограниченный веса груза, подогнанные отношения Ссылки [37] и [38] были преобразованы для получения квадрата радиуса инерции, соответствующего заданному бордюру. масса.Для простоты предполагается, что радиус инерции остается приблизительно постоянный при нормальных условиях занятости и / или ограниченного груза загрузка. Таким образом, общую массу можно умножить на снаряженную массу. Квадрат радиуса инерции для аппроксимации момента инерции.

    Радиус Квадрат инерции аппроксимируется следующими соотношениями:

    ( Номер ссылки 36 )

    ( Номер ссылки 37 )

    где W c = Снаряженная масса, фунт

    В таблице 2 приблизительное значения, полученные с помощью уравнений (1), (2) и (3), сравниваются с заявленными результаты измерений для ряда конкретных автомобилей (Ссылка 37 ).Хотя всегда желательно, где это возможно, использовать измеренные значения для свойств транспортного средства, это можно увидеть из таблицы 2 , что уравнения (2) и (3) дают разумные точные приближения. Чувствительность общей реконструкции результаты к ± вариации приблизительных значений, конечно, могут быть оценены чтобы определить потребность в большей точности.

    Дополнительная литература:

    В 1997 г. MacInnis, et.аль ( Ссылка [39]) в презентация обзора методов оценки момента инерции показала, что «Метод идеализированной автомобильной призмы и практическое правило« mab »часто приводили к очень хорошие результаты ».

    • Уравнение (2) на предыдущей странице – это метод, описанный в Артикул 38 как «модель автомобильной призмы».

    • Методика оценки «mab» упоминается в статье как «наиболее часто цитируемая оценка момента рыскания ».Они цитируют Bastow ( Ссылка ). [40]) как источник для описания и вывода уравнения (они не могли установить первоисточник уравнения).

    Краткое описание других источников для измерения свойств транспортного средства следующие:

    • Bixel (, ссылка [41]) включает в Приложении 1 измерения прибл. 14 автомобилей, произведенных на ВИМФ (Автомобиль Установка для измерения инерции).

    • Гарротт ( Ссылка [42]) включает измерения, выполненные на IPMD (устройство измерения инерционных параметров), которое расположен в VRTC (Центр исследований и испытаний транспортных средств).Инерциальные данные и / или компьютерная графика В документ включены данные о высоте из 356 измерений.

    • Керзон ( Ссылка [43]) включает измеренные свойства некоторых транспортных средств как а также сравнение различных методов оценки.

    Таблица 2 Пример момента инерции Результаты расчетов

    * Ссылка 3, Снаряженная масса, как есть; Момент инерции измеряется.

    ** Технические характеристики автомобилей для Канады (1998)

    Рисунок 53 Общая инерция автомобиля по рысканью О стихах CG Снаряженная масса

    Система измерения момента инерции

    K-KMAM-BC Системы измерения момента инерции

    Наши системы измерения массовых характеристик (масса, центр тяжести и момент инерции), которые превосходно используются во всем мире, точно измеряют различные подсистемы, оборудование, контейнеры, боеприпасы, ракеты, ракеты, радары, наземная техника, самолеты и многие другие товары оборонной промышленности.Системы, которые мы разработали до сих пор, использовались для измерения многих образцов. от 60 граммов до 40 тонн.

    К превосходным качествам, по которым наши измерительные системы отдают предпочтение во многих странах мира, можно отнести следующее:

  • Запатентованный алгоритм измерения драгоценного центра тяжести
  • Соединения и механизмы особой степени свободы
  • Конструкция измерительного стола сводит к минимуму ошибку позиционирования
  • Уникальное электронное оборудование, разработанное специально для измерения массовых характеристик
  • Высокочастотные оптические датчики и алгоритмы расчета для измерения момента инерции
  • Алгоритм эвристической калибровки
  • Программное обеспечение с удобным интерфейсом

    • K-KOC Системы измерения момента инерции и массовых свойств

    Системы измерения момента инерции и массовых характеристик K-KOC – это продукты с расширенными функциями и пользовательским интерфейсом, которые могут измерять массы, центры масс, моменты инерции и моменты произведения объектов различного веса и размеров по всем осям и с помощью одного приспособления.

  • В этой системе исполнительные механизмы обеспечивают движения по осям крена, тангажа и рыскания. При использовании одного приспособления Ixx, Iyy, Izz и их произведения должны быть рассчитаны в конце измерительных перемещений.
  • Дружественная и понятная панель управления обеспечивает перемещение элемента управления в простом интерфейсе.Кроме того, результаты измерений отображаются на панели управления по окончании процесса. В случае возникновения нежелательных и аварийных ситуаций с помощью аварийного пульта ручного типа система может быть остановлена.
  • Используются приборы до 1000 кг, инфраструктура однофазного электричества. Возможность подключения RJ45, TCP-соединение используется для связи с панелью управления и приводами.
  • В дополнение к системе измерения K-KOC, услуга измерения массовых свойств также может быть предоставлена ​​для больших платформ.

    • KAM_DataSheet (EN) ->

    Необходимость измерения момента перекрестных произведений инерции

    Момент инерции и матрица умножения являются важным параметром, используемым в различных механических, кинематических и динамических расчетах.

  • Инерционное взвешивание и структурный анализ
  • Автомобиль Dynamic
  • Механик, управление и моделирование полетов
  • Анализ аэроупругости
  • Проверка конструкции
  • Контроль симметрии и баланса

    • Методы измерения момента инерции

    Для измерения момента инерции используются четыре основных метода:

  • Измерение силы и движения
  • Поворотно-платформенный метод
  • Маятниковый метод
  • Метод многоосного маятника

    • Метод измерения мощности и движения
  • Используется самая простая формула момента инерции: T = Iα
  • Приводы необходимы для перемещения объекта измерения.
  • Измерение можно проводить по всем осям с помощью одного приспособления.
  • Чем тяжелее становится измеряемый объект, тем выше мощность и мощность приводов.

    • Маятниковый метод
  • Это самый простой метод измерения момента инерции.
  • Измерение выполняется с помощью маятника сверху.
  • Большие объекты можно легко измерить.
  • Простая формула: I = (mgb 2 T 2 ) / (4π 2 h)

    • Поворотно-платформенный метод
  • Он использует ту же теорию, что и метод маятника.
  • Измерение можно проводить снизу с помощью пневматического подшипника и торсионной пружины.
  • Измерение можно проводить только по одной оси.
  • Для каждой оси требуется различное приспособление.
    • Метод многоосного маятника

    Измерительная платформа подвешена на пружинах с разных точек.В результате платформа может двигаться в каждом направлении и по каждой оси. Полученные измерения мощности исследуются в частотной области, Благодаря разработанным методам расчета частоты разделяются и рассчитываются моменты инерции.

    Но каждый раз можно измерить момент инерции только одной оси.После каждого измерения предел должны быть изменены. Но переделывать приспособление не нужно. Его чувствительность ниже по сравнению с другой метод fs. Измерение можно производить снизу с помощью пневматического подшипника и торсионной пружины. Измерение можно сделать только на одной оси. Для каждой оси требуется приспособление.

    Измерение момента инерции для летательных аппаратов

    Маятниковый метод – это старый метод, используемый в основном для измерения момента инерции воздушных транспортных средств. воздушные платформы, ракеты и контейнеры.Первый ход может быть сделан человеком или автоматически линейным привод. Не будет необходимости в сложных приспособлениях. Вопрос разработки системы измерения момента инерции для воздушных, морских и наземных транспортных средств, платформ и контейнеров. Главный Характеристики системы следующие:

  • Конструкция со структурным расчетом и проведенным анализом
  • Разработанное оборудование и датчики
  • Блок передачи, обработки и оценки данных в реальном времени
  • Точное измерение момента инерции транспортного средства по трем основным осям

    • Помимо этого, мы можем разработать систему благодаря следующим характеристикам:

  • Конструкция по индивидуальному заказу
  • Графический интерфейс пользователя разработан по желанию заказчика
  • Местная система, имеющая ценовое преимущество по сравнению с зарубежной
  • Бесперебойная техническая поддержка
  • Измерение через нижний воздушный подшипник и торсионную пружину.
  • Измерение можно проводить только по одной оси.
  • Для каждой оси требуется различное приспособление.

    • Лаборатория 7 – инерция вращения

    Введение

    Когда вы были моложе, у вас могли быть игрушечные машинки, которые вы несколько раз быстро терли по полу, чтобы «разогнать их».«Затем, когда вы их опускаете, они проносятся на некоторое расстояние. Или, может быть, вы видели по телевизору автокатастрофу, когда колеса перевернутой машины продолжали вращаться некоторое время. Возможно, вы видели, как приземлился вертолет. , и заметили, что лопасти продолжают вращаться после того, как пилот выключит двигатель. Все это примеры инерции вращения. У игрушечной машинки есть небольшое колесо внутри, называемое маховиком, которое прикреплено к колесам автомобиля. Когда вы “Увеличь обороты”, маховик начинает вращаться.Затем, когда вы отпускаете машину, маховик продолжает вращаться из-за инерции вращения и, таким образом, поворачивает колеса. Колеса перевернутого автомобиля и лопасти вертолета продолжают вращаться до тех пор, пока трение не преодолеет их инерцию вращения. Вы уже узнали об инерции линейных систем; движущийся объект будет продолжать движение до тех пор, пока на него не будет действовать результирующая сила. Вращательная инерция – это аналогичное понятие, применяемое к объектам, движение которых является вращательным, а не линейным.Инерция вращения объекта – это сопротивление объекта изменению его угловой скорости. То есть, если объект вращается, он имеет тенденцию продолжать вращаться до тех пор, пока на него не воздействует чистый крутящий момент. Это просто еще одно проявление второго закона Ньютона.

    Обсуждение принципов

    Во втором законе Ньютона

    F = ma

    масса м объекта является мерой его инерции. Очевидно, что чем меньше масса, тем меньше силы требуется для изменения линейной скорости объекта.При вращательном движении именно инерция вращения, часто называемая моментом инерции I , определяет крутящий момент

    τ ,

    , необходимый для изменения угловой скорости объекта

    ω .

    Аналог второго закона Ньютона для вращательного движения есть

    (1)

    τ net = I α где τ net – чистый крутящий момент , а α – угловое ускорение.Момент инерции объекта зависит от формы объекта и распределения его массы относительно оси вращения объекта. Однородный диск массой м не так сложно привести во вращательное движение, как «гантель» той же массы и радиуса. Для симметричного сплошного тела (например, твердого диска), которое вращается вокруг оси симметрии, например, оси, проходящей через центр и перпендикулярной диску, момент инерции вычисляется путем выполнения интеграла

    (2)

    I =
    r 2 дм
    где

    дм

    – крошечный кусочек массы, расположенный на расстоянии r от оси вращения.Для набора из n точечных масс момент инерции вычисляется путем выполнения суммы

    (3)

    I =
    n m i r i 2
    i = 1
    где

    m i

    и

    r i

    – масса и положение, соответственно, i -й частицы. Таким образом, для гантели

    n = 2

    и массой м на каждом конце, разделенной расстоянием d , момент инерции равен

    (4)

    I = 2 м
    2
    = м

    Информацию о моментах инерции различных симметричных тел см. В этом списке.В этом эксперименте вы будете использовать диск почти однородной массы и прикладывать крутящий момент, добавляя вес к струне, прикрепленной к ступенчатому шкиву в центре диска. См. Рис. 1. Используя полученные результаты, вы определите момент инерции диска.

    Рисунок 1 : Эскиз и фотография аппарата

    Несмотря на то, что колесо расположено горизонтально и струна проходит через второй шкив, на рис. 1а мы показываем колесо в вертикальном положении. При падении подвешенной массы колесо вращается против часовой стрелки.Это вращение происходит в первую очередь из-за крутящего момента, создаваемого силой натяжения в струне, которая возникает из-за веса подвешенной массы. Колесо имеет подшипники на оси, и в их движении присутствует некоторое трение. Крутящий момент, связанный с этой силой трения f , действует, чтобы противодействовать крутящему моменту, создаваемому силой T натяжения в колонне. Если мы рассмотрим только колесо, мы можем изучить два действующих момента: момент трения

    τ f

    и момент напряжения

    τ растяжение .

    Величина крутящего момента от натяжения равна где r – радиус ступенчатого шкива. Чистый крутящий момент – это векторная сумма этих двух крутящих моментов.

    (6)

    τ net = rT – τ f

    Применяя уравнение. (1) τ net = I α получаем Здесь мы следуем соглашению о знаках, согласно которому крутящий момент против часовой стрелки положительный, а крутящий момент по часовой стрелке отрицательный. Теперь рассмотрим висящую массу м. На рис. 2 показана диаграмма свободного тела для подвешенной массы. Мы видим, что натяжение противостоит силе тяжести.

    Рисунок 2 : Диаграмма свободного тела для подвешенной массы

    Тогда второй закон Ньютона, записанный для висячей массы, имеет вид где a – это ускорение висящей массы, и мы выбрали направление вниз, , как положительное. Решение для T , Если предположить, что струна не проскальзывает, тогда a – это также тангенциальное ускорение точки на ступенчатом шкиве.Точно так же

    a ‘

    – тангенциальное ускорение точки на краю колеса. Именно здесь мы и будем измерять ускорение с помощью Smart Pulley . Угловое ускорение колеса связано с этими касательными ускорениями соотношением С уравнениями. Уравнение (9)

    T = m (g – a)

    и (10)

    , мы можем переписать уравнение. (7)

    rT – τ f = I α

    как

    (11)

    m (г – а) r – τ f = I

    Анализ методом линеаризации

    Есть два момента, которые следует учитывать в отношении уравнения.(11) m (g – a) r – τ f = I

    : он не является линейным в m и a , и мы не делаем знать

    τ f .

    В этом анализе мы сделаем приближение, которое приведет к формуле. (11) m (g – a) r – τ f = I

    становится линейным.Мы предполагаем, что

    г >> a,

    и, следовательно,

    T ≈ мг.

    Как следствие, уравнение. (11) m (g – a) r – τ f = I

    становится

    (12)

    mgr – τ f = I

    Решение уравнения. (12) mgr – τ f = I

    для a дает Таким образом, если мы определим ускорение a для различных висящих масс м и построим график зависимости ускорения от массы, то наклон будет равен

    gr 2 / I

    , а интервал y будет равен

    τ r f / I.

    Примечание : Если мы определили ускорения,

    a 1

    и

    a 2 ,

    только для двух масс

    м 1

    и

    м 2 ,

    , тогда и поэтому

    (15)

    I =
    (м 2 – м 1 ) gr 2
    (a 2 – a 1 )

    Анализ точным методом

    Как и в примечании выше, предположим, что процедура повторяется с двумя разными массами,

    м 1

    и

    м 2 ,

    , что приводит к ускорениям

    a 1

    и

    a 2 ,

    соответственно.

    (16)

    m 1 (g – a 1 ) r – τ f = I

    (17)

    m 2 (g – a 2 ) r – τ f = I

    Теперь можно математически исключить

    τ f

    .Решение двух одновременных уравнений. (16) m 1 (g – a 1 ) r – τ f = I

    и (17) m 2 (g – a 2 ) r – τ f = I

    для I , мы имеем

    (18)

    I =
    (m 2 – m 1 ) gr 2 + (m 1 a 1 – m 2 a 2 ) r 2
    (a 2 – а 1 )
    Сравните уравнения.(15) I =
    (m 2 – m 1 ) gr 2
    (a 2 – a 1 )
    и (18) I =
    (m 2 – m 1 ) gr 2 + (m 1 a 1 – m 2 a 2 ) r 2
    (a 2 – a 1 )
    .

    Цель

    В этом эксперименте вы будете использовать колесо со ступенчатым шкивом, чтобы измерить ускорение вращающегося колеса и определить момент инерции колеса.Вы также определите момент инерции удлинителя, который вы добавите к колесу.

    Оборудование

    • Колесо со ступенчатым шкивом
    • Smart Pulley с фотозатвором
    • Нить
    • Масса с вешалкой
    • Программное обеспечение DataStudio
    • Каверномер
    • Остаток средств
    • Метрическая палка
    • Обруч
    • Пластина

    Процедура

    Аппарат (см. Рис.1) состоит из колеса, в центре которого установлен небольшой ступенчатый шкив. Струна, намотанная на этот шкив и прикрепленная к подвешенной массе, обеспечивает необходимый крутящий момент, необходимый для вращения колеса. Установлен небольшой шкив с фотозатвором, так что он контактирует с ободом колеса. При вращении колеса этот интеллектуальный шкив также будет вращаться. Спицы вращающегося шкива прерывают инфракрасный луч от фотозатвора, и фотозатвор отправляет эти сигналы на компьютер.Компьютер использует информацию для измерения скорости вращения шкива. Компьютер измеряет скорость вращения шкива и вычисляет сначала тангенциальную скорость кромки колеса, а затем тангенциальное ускорение

    a ‘

    на ободе колеса. Исходя из этого, вы рассчитаете тангенциальное ускорение на ободе ступенчатого шкива, используя уравнение. (10)

    . К колесу можно добавить удлинение, например обруч или прямоугольную пластину, и измерить момент инерции комбинации.Поскольку удлинитель имеет ту же ось вращения, что и колесо, момент инерции комбинации будет

    (19)

    I всего = I колесо + I удлинитель .

    Отсюда можно определить момент инерции удлинителя.

    1

    Взвесьте колесо и запишите это значение в рабочий лист. Вешалку включать не нужно.

    2

    Используйте измерительную палочку, чтобы измерить диаметр колеса.Как только вы найдете диаметр, используйте его, чтобы найти радиус R колеса, и запишите это значение в рабочий лист.

    3

    Рассчитайте принятое значение момента инерции вашего колеса, используя

    (20)

    I диск = (1/2) MR 2 .

    4

    Используйте штангенциркуль, чтобы измерить диаметр ступенчатого шкива. Это самый маленький шкив, вокруг которого наматывается струна. См. Приложение D. Используйте диаметр для вычисления радиуса r ступенчатого шкива и запишите это значение в рабочий лист.

    5

    Откройте файл DataStudio , связанный с этой лабораторной работой. Отобразится экран, аналогичный показанному на рис. 3.

    Рисунок 3 : Начальный экран для лаборатории инерции вращения

    6

    С помощью весов определите массу подвески

    м 1

    и запишите это значение в рабочий лист. Это будет масса для первой точки данных.

    7

    Намотайте струну на ступенчатый шкив наименьшего диаметра.Затем пропустите веревку через второй шкив и прикрепите крючок к концу веревки так, чтобы она свешивалась над краем стола.

    8

    Нажмите кнопку Start один раз и позвольте колесу начать вращаться. Нажмите Stop после того, как груз упадет на пол или когда у вас закончится веревка, и колесо начнет вращаться в противоположную сторону. Необязательно пытаться отпустить колесо и щелкать мышью в одно и то же время, вы можете щелкнуть мышью примерно за полсекунды перед тем, как отпустить колесико.Обязательно остановите колесо от вращения, когда у него закончится веревка. Таблица времени, скорости и ускорения, подобная показанной на рис. 4, заполняется автоматически.

    Рисунок 4 : Таблица данных для пробного прогона

    9

    Прокрутите данные, чтобы выбрать десять последовательных ускорений ближе к середине пробега, а не в самом начале или в самом конце. Запишите эти десять значений в таблицу данных на листе.

    10

    Используя функцию суммирования , расположенную в верхнем левом углу окна таблицы данных, определите среднее значение этих десяти измерений ускорения и введите результат в рабочий лист. Возможно, вам придется повторить запуск, если числа очень нестабильны.

    11

    Повторите шаги с 7 по 9 еще три раза, добавляя массу к вешалке с шагом 50 граммов. Примечание : Вам может потребоваться повысить точность ускорений по мере добавления новых серий данных.Вы можете сделать это, щелкнув Увеличить точность в меню в правом верхнем углу окна таблицы данных. См. Рис.4.

    Контрольно-пропускной пункт 1:
    Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.

    Процедура A: Метод линеаризации

    12

    Используя Excel, создайте график зависимости ускорения от подвешенной массы. См. Приложение G.

    13

    Используя функцию Linest, определите наклон и точку пересечения.Запишите эти значения на листе. См. Приложение J.

    14

    Из значений наклона и пересечения рассчитайте момент инерции и момент трения, используя уравнение. (13)

    . Запишите эти значения на листе.

    15

    Вычислите разницу в процентах между моментом инерции, который вы только что рассчитали, и моментом инерции, вычисленным на шаге 3. См. Приложение B.

    Контрольно-пропускной пункт 2:
    Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.

    Процедура B: Точный метод

    18

    Вычислите разницу в процентах между моментом инерции, который вы только что рассчитали, и моментом инерции, вычисленным на шаге 3.

    Контрольно-пропускной пункт 3:
    Попросите своего технического специалиста проверить ваши расчеты, прежде чем продолжить.

    Процедура C: Определение момента инерции добавочного номера

    19

    Выберите либо пяльцы, либо пластину в качестве расширения, которое нужно добавить к колесу.Измерьте размеры и массу пристройки и запишите эти значения на листе.

    20

    Рассчитайте принятое значение момента инерции удлинителя (используйте формулы, приведенные в таблице).

    22

    Установите удлинитель на колесо и выполните шаги с 7 по 9 с подвешенной массой

    200 г.

    23

    Найдите ускорение

    a ‘

    колеса и ускорение a ступенчатого шкива.Запишите эти значения на листе.

    24

    Используя момент трения τ f , определенный на этапе 17, и формулу, полученную на этапе 21, вычислите общий момент инерции удлинителя и колеса. Запишите это значение в рабочий лист.

    25

    Используя момент инерции колеса, полученный точным методом из шага 16, и уравнение. (19)

    I всего = I колесо + I удлинитель .

    найти момент инерции удлинителя самостоятельно.Запишите это значение на листе.

    26

    Найдите процентную разницу между этим значением и принятым значением, вычисленным на шаге 20. Запишите это значение в рабочий лист.

    Контрольно-пропускной пункт 4:
    Попросите вашего ТА проверить ваши расчеты.

    Copyright © 2011 Advanced Instructional Systems Inc. и Государственный университет Северной Каролины | Кредиты

    Измерение момента инерции на основе крутильного маятника

    [1] Чжан Х М, Ван Л И, Лю Дж Х и др.Китайский журнал научных инструментов, Vol. 29 (2008), стр 212-215. (На китайском языке).

    [2] Ли Г. К., Чен Ю. К., Ю З. Ю. Механика в машиностроении, Vol.29 (2007), стр. 54-57.

    [3] Чжан Д. С., Ху X Л., Юань Л. Транзакции Китайского общества сельскохозяйственной техники, Vol.39 (2008), стр 34-40. (На китайском языке).

    [4] Су Кью, Лу З. Х. Инженерная механика, Vol. 24 (2007), стр 59-65.

    [5] Тан В. И, Ли Х. П, Чжан С. Ф.Журнал Нанкинского университета науки и технологий, Vol. 32 (2008), стр 69-72. (На китайском языке).

    [6] Ли Х И, Чжан И Ц, Ли Б Х.Автоматизация вооружения, Vol. 22 (2003), стр. 4-6. (На китайском языке).

    1. НАЗНАЧЕНИЕ:

    (1) Чтобы продемонстрировать применение принципов энергии и импульса к вращающемуся система.

    (2) Для измерения момента инерции различных распределений массы с помощью динамического метода и проверить равенство I = mr 2 для момента инерция.

    2. АППАРАТ:

      Ротационный аппарат Welch с шарикоподшипниковым валом.
      Момент крепления стержня инерции.
      Гири с прорезями по 100 и 50 грамм.
      Секундомер 1/10 секунды.
      Весовая вешалка, веревка.

    3. КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРИИ:

    Момент инерции тела – это мера его инерции вращения вокруг оси. Он определяется распределением массы тела вокруг этой оси.Важность момента Инерция заключается в ее влиянии на динамическое поведение тела. В частности, крутящий момент, приложенный к тело вызовет угловое ускорение тела по

    где τ – приложенный крутящий момент, I – момент инерции тела, а α – его угловое ускорение. [И τ, и I должны быть выражены относительно одной и той же оси .]

    Момент инерции локализованной или “точечной” массы относительно оси

    где m – масса, а r – перпендикулярное расстояние, измеренное от оси до масса.Момент инерции распределенной массы находится путем разделения тела на бесконечно малые массы точки и интегрирование по всему объему массы. Самый В учебниках есть таблицы моментов инерции тел простой геометрической формы. Вам нужно будет свериться с этой таблицей, и вы также должны будете уметь применять Теорема о параллельной оси.

    4. ЭКСПЕРИМЕНТАЛЬНАЯ СТРАТЕГИЯ:

    Рис.1. Аппарат инерции вращения.

    Аппарат имеет вертикальный вал (D), вращающийся на высококачественных шарикоподшипниках (B). А горизонтальный рычаг прикрепляется к верхней части вала. Грузы с прорезями (C 1 и C 2 ) могут быть размещены на этом рычаге с разным радиусом и закреплены барашковыми гайками. Вы будете динамично измерить момент инерции распределителей веса, размещенных на этом плече, относительно к вертикальной оси вращения.Вы также сверите эти результаты с проведенными расчетами. по формулам из учебника для моментов инерции простых форм.

    Вращение производится таким образом, чтобы можно было измерить ускорение система. Вокруг вертикального вала наматывается струна, проходит через шкив (H) до груза. вешалка. На вешалку помещают грузы (W), которые позволяют падать на определенное расстояние. В время падения измеряется.

    Падающий груз преодолевает расстояние y за t секунд, поэтому

    Используйте уравнение.3 для расчета линейного ускорения падающего груза. Чистая сила на падающем теле –

    .

    Таким образом, чистый крутящий момент на вращающемся валу составляет

    .

    τ f – это тормозящий момент из-за всех сил трения, прежде всего в шкиве и коренном подшипнике.

    Угловое и линейное ускорения связаны соотношением

    Из уравнения. 4–6 можно исключить натяжение T и угловое ускорение α.Результат можно решить на данный момент инерции, I:

    Уравнение 3 можно использовать для экспериментального определения a. Уравнение 7 дает момент инерции в с точки зрения измеряемых величин.

    Полный момент инерции, I может быть записан как сумма инерции из-за добавленной веса, MR 2 , и внутренней инерции вертикального вала и траверсы, I o .

    Чтобы исследовать уравнение.8 систематически преобразовать его алгебраически в форму, подходящую для графического анализа. Оставив детали в качестве упражнения по алгебре, получим:

    График зависимости MR 2 от (1 / a) должен быть прямой линией. Величина [mr 2 g – τ f r] представляет собой наклон линия, по которой может быть определен крутящий момент из-за трения τ f . Величина [I o + mr 2 ] является точкой пересечения на оси MR 2 , из которой может быть определено I o .

    Величину [mr 2 g – τ f r] можно записать [r (mgr – τ f )], что более четко показывает, что момент трения τ f противостоит ускоряющему моменту mgr.

    Эта форма уравнения предлагает подходящую стратегию сбора данных. Чтобы получить прямолинейный график, значения в квадратных скобках должны оставаться постоянными. Все количества в квадратных скобках – констант, кроме m, но m можно легко сохранить постоянная при изменении M и R.

    5. МЕТОДИКА ЭКСПЕРИМЕНТА:

    Момент инерции вертикального вала и горизонтального рычага можно измерить, но не может быть легко рассчитан непосредственно из геометрии. Может возникнуть соблазн напрямую измерить момент инерции за счет ускорения траверсы без дополнительных грузов. Это бы требуется очень маленький метр на вешалке, чтобы достичь времени падения, достаточного для измерения точно. Это также сделало бы приложенную силу на валу настолько малой, что момент трения может вызвать систематическую ошибку.

    Еще одна серьезная проблема заключается в том, является ли крутящий момент из-за трения постоянным для всех случаев. Трение, как известно, обычно зависит от силы, прижимающей поверхности друг к другу ( сила нагрузки.) Здесь сила нагрузки – это полная сила, действующая на подшипник, т.е. общий вес вала, траверсы и любых масс на плече. Единственный способ удержать константа трения должна поддерживать постоянные значения M и m, позволяя изменять R.

    Таким образом, вы будете поддерживать m постоянным во всех случаях по причинам, указанным выше.потом систематически изучать кейсы с разными значениями М и Р.

    Всегда полезно иметь четкую стратегию анализа данных. С до вы начинаете сбор данных. Тогда у вас обязательно будет достаточно данных в правильная форма для анализа.

    Ваша цель – экспериментально проверить, что момент инерции движущейся массы в круге радиуса R пропорционален массе и пропорционален квадрату радиуса круга.Поэтому хорошей стратегией будет изучить достаточное количество случаев, когда M является постоянным и R меняется, и еще один набор случаев, когда R остается постоянным, а M меняется. Вам следует изучить следующий раздел, АНАЛИЗ ДАННЫХ, от до на самом деле. снимаю любые данные!

    В общем, процедура такова: поместите соответствующее количество гирь с прорезями в вес, чтобы ускорение было достаточно медленным, чтобы точно рассчитать время. Запись:

      ч, расстояние “опускается” вешалка
      t, время, за которое пролетит это расстояние
      м, общая масса грузов и подвески
      радиус и длина вертикального стального вала
      длина и масса горизонтального вала
      R – расстояние грузов на горизонтальном плече от оси вращения.
      M – общая масса грузов, добавленных к горизонтальному рычагу.

    Необходимо определить следующие количества:

      I o , момент инерции вращающегося узла
      τ f , момент трения в подшипнике

    Поместите одинаковые гири на равных радиусах по обе стороны от горизонтального рычага для обеспечения хорошей статики. и динамический баланс. Надежно затяните барашковые гайки.

    Рассмотрим значение Р.Его необходимо измерять от оси вращения до эффективного центра масс. Где эффективный центр? Это , а не центр масс. Это местоположение точечной массы, которая имела бы тот же момент инерции, что и распределенная масса. «Эффективный» радиус называется «радиусом вращения». оно несколько больше, чем расстояние до центра масс.) Если у вас был расчет, вы должны вывести уравнение для радиуса вращения для цилиндрической массы, ориентированной так же, как и ваши цилиндрические грузы.Если у вас не было исчисления, просто измерьте от геометрического центра и поймите, что вы вносите небольшую систематическую ошибку, делая это.

    (1) Возьмите данные для различных значений массы M, удерживая R постоянным на значении около 12 см. Используйте эти данные, чтобы построить график зависимости M от (1 / a). Включите массу крыла орехи в М.

    (2) Возьмите данные для различных значений R с постоянной M. Постройте график зависимости R 2 от (1 / а).

    6.АНАЛИЗ ДАННЫХ

    (1) Посмотрите на график MR 2 в зависимости от (1 / a) из шага процедуры (1), где R оставалось постоянным. Из уравнений (8) и (9) вы ожидаете, что график должен быть прямой (с некоторые отклонения из-за неопределенных ошибок). Если отклонения соответствуют вашей ошибке оценки, проведите лучшую прямую линию через данные. С перехвата этого На оси MR 2 рассчитайте момент инерции вала и стержня, I o , когда нет добавленной массы.Наклон линии позволяет вычислить τ f , крутящий момент, обусловленный трением. Будьте особенно внимательны, чтобы определить, значимы ли значения момента трения; что есть, вычислить пределы погрешности по значению.

    (2) Посмотрите на график зависимости R 2 от (1 / a) данных из процедуры (2), где R оставалось постоянным. Это тоже должна быть прямая линия. Имеет ли он тот же наклон и точку пересечения, что и другой график? Должен ли он? Если нет, о чем это вам говорит?

    (3) Вы также можете нанести все данные на один график.Предложение: График R 2 в зависимости от (1 / a) с M в качестве параметра. Вы ожидаете, что для каждого значения M вы получите другой график прямой линии, но все прямые линии будут параллельны. Такое бывает?

    (4) Вы также можете построить график всех данных, построив график зависимости M от (1 / a) с R в качестве параметра. Обсудите значимость (если таковая имеется) наклонов и пересечений этого графика.

    (5) τ f – интересная величина в этом эксперименте. Конечно, это будет зависеть от вашего конкретный аппарат и качество коренного подшипника.Это может быть слишком маленьким, чтобы влияют на ваши измерения и поэтому слишком малы для измерения, но не предполагайте этого. Пусть ваш Анализ данных покажет, является ли оно значительным. Если это , это влияет на ваши данные в измеримым способом, вы можете обнаружить, что трение не является постоянным, а зависит от общая массовая нагрузка подшипника (2М). Показать эту зависимость может быть реальным вызов!

    (6) Уравнения, использованные в этом эксперименте, не разделяют различные эффекты трения.Величина τ f фактически включает трение в шкиве, которое, вероятно, больше, чем у коренного подшипника. Можно ожидать, что это трение шкива будет зависеть от массовой нагрузки шкива, которая пропорциональна падающему весу, мг. Ваши данные подтверждают это?

    7. ВОПРОСЫ:

    (1) Определите долю мг, рассеиваемую за счет трения.

    (2) Ученик предполагает, что натяжение тетивы просто равно весу висения. от него.(Это, конечно, не так.) Сколько ошибок вызовет эта ошибка (в%) в этом студенческом экспериментальном определении момента инерции?

    (3) Покажите полный вывод уравнения (7).

    (4) Насколько велика была бы систематическая ошибка момента инерции, если бы масса барашковые гайки не были учтены в расчетах?

    (5 *) Выведите уравнение для момента инерции, выраженного как функцию экспериментально измеренные величины, указанные в процедуре (1).

    (6 *) Выведите уравнение для полной энергии, потерянной на нагрев за счет трения, в терминах экспериментально измеренных величин, перечисленных в процедуре (1).

    (7 *) Уравнение (8) использовалось для расчета моментов инерции. Это уравнение не явно включать количество потерь энергии на трение. Тем не менее трение, безусловно, влияет на данные – падающее тело ускорилось бы немного быстрее, если бы трение было устранено. Тогда почему трение «игнорировать» при использовании уравнения (8)?

    (8 *) Рассматривая вращающиеся грузы как цилиндры, составьте уравнение для экспериментального определить их радиус вращения.

    Текст и рисунок © 1998, 2004 Дональд Э. Симанек.

    10.6: Расчет моментов инерции

    В предыдущем подразделе мы определили момент инерции, но не показали, как его рассчитать. В этом подразделе мы покажем, как рассчитать момент инерции для нескольких стандартных типов объектов, а также как использовать известные моменты инерции, чтобы найти момент инерции для смещенной оси или для составного объекта. Этот раздел очень полезен для того, чтобы увидеть, как применить общее уравнение к сложным объектам (навык, который имеет решающее значение для более продвинутых курсов физики и инженерии).2 \]

    для всех точечных масс, составляющих объект. Поскольку \ (r \) – это расстояние до оси вращения от каждой части массы, составляющей объект, момент инерции для любого объекта зависит от выбранной оси. Чтобы убедиться в этом, возьмем простой пример двух масс на конце безмассового (пренебрежимо малая масса) стержня (рис. \ (\ PageIndex {1} \)) и вычислим момент инерции относительно двух разных осей. В этом случае суммирование по массам является простым, потому что две массы на конце штанги могут быть аппроксимированы как точечные массы, и поэтому в сумме есть только два члена.{2} \ ldotp \]

    Из этого результата можно сделать вывод, что вращать штангу вокруг конца в два раза сложнее, чем вокруг ее центра.

    Рисунок \ (\ PageIndex {1} \): (a) Штанга с осью вращения, проходящей через ее центр; (б) штанга с осью вращения, проходящей через один конец.

    В этом примере у нас было две точечные массы, и сумму было просто вычислить. Однако, чтобы иметь дело с объектами, которые не являются точечными, нам нужно тщательно продумать каждый член уравнения.Уравнение просит нас суммировать каждый «кусок массы» на определенном расстоянии от оси вращения. Но что именно означает каждый «кусок массы»? Напомним, что при выводе этого уравнения каждая часть массы имела одинаковую величину скорости, что означает, что вся часть должна находиться на одном расстоянии r от оси вращения. Однако это невозможно, если мы не возьмем бесконечно малый кусок массы dm, как показано на рисунке \ (\ PageIndex {2} \).

    Рисунок \ (\ PageIndex {2} \): Использование бесконечно малой массы для вычисления вклада в общий момент инерции.{2} dm \ ldotp \ label {10.19} \]

    Фактически, это форма, которая нам нужна для обобщения уравнения для сложных форм. Лучше всего подробно проработать конкретные примеры, чтобы понять, как рассчитать момент инерции для конкретных форм. Этому посвящена большая часть остальной части этого раздела.

    Однородный тонкий стержень с осью через центр

    Рассмотрим однородный (по плотности и форме) тонкий стержень массы M и длины L, как показано на рисунке \ (\ PageIndex {3} \). Нам нужен тонкий стержень, чтобы мы могли предположить, что площадь поперечного сечения стержня мала, и стержень можно представить как набор масс вдоль одномерной прямой линии.В этом примере ось вращения перпендикулярна стержню и для простоты проходит через среднюю точку. Наша задача – вычислить момент инерции относительно этой оси. Ориентируем оси так, чтобы ось z была осью вращения, а ось x проходила через длину стержня, как показано на рисунке. Это удобный выбор, потому что затем мы можем интегрировать по оси x.

    Рисунок \ (\ PageIndex {3} \): Расчет момента инерции I для однородного тонкого стержня вокруг оси, проходящей через центр стержня.

    Мы определяем dm как небольшой элемент массы, составляющий стержень. Интеграл момента инерции является интегралом по распределению масс. Однако мы знаем, как интегрироваться по пространству, а не по массе. Поэтому нам нужно найти способ связать массу с пространственными переменными. Мы делаем это, используя линейную массовую плотность \ (\ lambda \) объекта, которая является массой на единицу длины. Поскольку массовая плотность этого объекта однородна, мы можем написать

    \ [\ lambda = \ frac {m} {l} \; или\; m = \ lambda l \ ldotp \]

    Если мы возьмем дифференциал каждой части этого уравнения, мы найдем

    \ [dm = d (\ lambda l) = \ lambda (dl) \]

    , поскольку \ (\ lambda \) постоянно.Для удобства мы решили сориентировать стержень по оси x – именно здесь такой выбор становится очень полезным. Обратите внимание, что кусок стержня dl полностью лежит вдоль оси x и имеет длину dx; фактически, в этой ситуации dl = dx. {2} \ lambda dx \ ldotp \]

    Последний шаг – быть осторожным с нашими пределами интеграции.{2} \ ldotp \ end {split} \]

    Затем мы вычисляем момент инерции для того же однородного тонкого стержня, но с другим выбором оси, чтобы мы могли сравнить результаты. Мы ожидаем, что момент инерции будет меньше относительно оси, проходящей через центр масс, чем ось конечной точки, как это было в примере со штангой в начале этого раздела. Это происходит потому, что больше массы распределяется дальше от оси вращения.

    Унифицированный тонкий стержень с осью на конце

    Теперь рассмотрим тот же однородный тонкий стержень массы \ (M \) и длины \ (L \), но на этот раз переместим ось вращения к концу стержня.{2} \ ldotp \ label {ThinRod} \ end {align} \]

    Обратите внимание, что инерция вращения стержня вокруг его конечной точки больше, чем инерция вращения вокруг его центра (в соответствии с примером со штангой) в четыре раза.

    Теорема о параллельных осях

    Сходство между процессом определения момента инерции стержня вокруг оси, проходящей через его середину, и вокруг оси, проходящей через его конец, поразительно и позволяет предположить, что существует более простой метод определения момента инерции стержня, проходящего через его середину. {2} \ nonumber \]

    Единый тонкий диск вокруг оси, проходящей через центр

    Интегрирование для определения момента инерции двумерного объекта немного сложнее, но на этом уровне исследования обычно делается одна форма – однородный тонкий диск вокруг оси, проходящей через его центр (Рисунок \ (\ PageIndex {5 } \)).

    Рисунок \ (\ PageIndex {5} \): Расчет момента инерции тонкого диска вокруг оси, проходящей через его центр.

    Поскольку диск тонкий, мы можем считать массу распределенной полностью в плоскости xy. Мы снова начнем с соотношения для плотности поверхностной массы , которая является массой на единицу площади поверхности. Поскольку он однороден, поверхностная плотность массы \ (\ sigma \) постоянна:

    \ [\ sigma = \ frac {m} {A} \] или \ [\ sigma A = m \], поэтому \ [dm = \ sigma (dA) \]

    Теперь мы используем упрощение для области.{2} \ ldotp \ end {split} \]

    Обратите внимание, что это соответствует значению, приведенному на рисунке 10.5.4.

    Расчет момента инерции составных объектов

    Теперь рассмотрим составной объект, подобный изображенному на рисунке \ (\ PageIndex {6} \), который изображает тонкий диск на конце тонкого стержня. Это не может быть легко интегрировано, чтобы найти момент инерции, потому что это объект неоднородной формы. Однако, если мы вернемся к первоначальному определению момента инерции как суммы, мы можем заключить, что момент инерции составного объекта может быть найден из суммы каждой части объекта:

    \ [I_ {total} = \ sum_ {i} I_ {i} \ ldotp \ label {10.21} \]

    Важно отметить, что моменты инерции объектов в уравнении \ (\ PageIndex {6} \) равны относительно общей оси . В случае этого объекта это был бы стержень длиной L, вращающийся вокруг своего конца, и тонкий диск радиуса \ (R \), вращающийся вокруг оси, смещенной от центра на расстояние \ (L + R \) , где \ (R \) – радиус диска. Определим массу стержня как m r , а массу диска как \ (m_d \).

    Рисунок \ (\ PageIndex {6} \): Составной объект, состоящий из диска на конце стержня.{2} \ ldotp \]

    Применение расчета момента инерции для решения задач

    Теперь давайте рассмотрим некоторые практические применения расчета момента инерции.

    Пример \ (\ PageIndex {1} \): человек на карусели

    Ребенок весом 25 кг стоит на расстоянии \ (r = 1.0 \, m \) от оси вращающейся карусели (рисунок \ (\ PageIndex {7} \)). Карусель можно представить как сплошной однородный диск массой 500 кг и радиусом 2,0 м. Найдите момент инерции этой системы.

    Рисунок \ (\ PageIndex {7} \): Расчет момента инерции ребенка на карусели.

    Стратегия

    Эта задача связана с вычислением момента инерции. Нам даны масса и расстояние до оси вращения ребенка, а также масса и радиус карусели. Поскольку масса и размер ребенка намного меньше, чем у карусели, мы можем аппроксимировать ребенка как точечную массу. Используемые обозначения: m c = 25 кг, r c = 1.{2} \ ldotp \ nonumber \]

    Значение

    Значение должно быть близко к моменту инерции карусели, потому что она имеет гораздо большую массу, распределенную от оси, чем ребенок.

    Пример \ (\ PageIndex {2} \): стержень и твердая сфера

    Найдите момент инерции стержня и твердой сферы вокруг двух осей, как показано ниже. Удочка имеет длину 0,5 м и массу 2,0 кг. Радиус сферы 20.0 см и имеет массу 1,0 кг.

    Стратегия

    Поскольку в обоих случаях у нас есть составной объект, мы можем использовать теорему о параллельных осях, чтобы найти момент инерции относительно каждой оси. В (а) центр масс сферы расположен на расстоянии \ (L + R \) от оси вращения. В (b) центр масс сферы расположен на расстоянии \ (R \) от оси вращения. В обоих случаях момент инерции стержня действует относительно оси на одном конце.{2} \ ldotp \ end {split} \]

    Значение

    Использование теоремы о параллельных осях упрощает вычисление момента инерции составных объектов. Мы видим, что момент инерции больше в (а), чем в (б). Это потому, что ось вращения находится ближе к центру масс системы в (b). Простая аналогия – это стержень. Момент инерции относительно одного конца равен \ (\ frac {1} {3} \) mL 2 , но момент инерции, проходящий через центр масс по его длине, равен \ (\ frac {1} {12} \ ) мл 2 .

    Пример \ (\ PageIndex {3} \): угловая скорость маятника

    Маятник в форме стержня (рис. \ (\ PageIndex {8} \)) выходит из состояния покоя под углом 30 °. Он имеет длину 30 см и массу 300 г. Какова его угловая скорость в самой низкой точке?

    Рисунок \ (\ PageIndex {8} \): Маятник в виде стержня выходит из состояния покоя под углом 30 °.

    Стратегия

    Используйте сохранение энергии для решения проблемы. В момент срабатывания маятник обладает гравитационной потенциальной энергией, которая определяется по высоте центра масс над его самой низкой точкой при качании.{2}) \ left (\ dfrac {3} {0,3 \; m} \ right) (1 – \ cos 30)} = 3,6 \; рад / с \ ldotp \ nonumber \]

    Значение

    Обратите внимание, что угловая скорость маятника не зависит от его массы.

    Оставить комментарий