ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23. 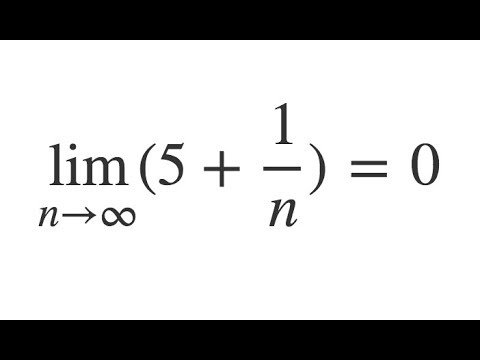 Упражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 2.  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратовУпражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла |
примеры пределов x стремится к бесконечности
Пределы/ Предел функции
| → | ↑ Функция f(x) ? |
|---|
Примеры
Для конечных точек:
———Слева (x0-)Справа (x0+)
График:
от до
Ввести:
{ кусочно-заданную функцию можно здесь.
2
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- 15/7
- – дробь
3Другие функции:
- asec(x)
- Функция – арксеканс от x
- acsc(x)
- Функция – арккосеканс от x
- sec(x)
- Функция – секанс от x
- csc(x)
- Функция – косеканс от x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция – округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция – гиперболический арксеканс от x
- csch(x)
- Функция – гиперболический косеканс от x
- sech(x)
- Функция – гиперболический секанс от x
- acsch(x)
- Функция – гиперболический арккосеканс от x
Постоянные:
- pi
- Число “Пи”, которое примерно равно ~3. 14159..
- e
- Число e – основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности – знак для бесконечности
14159... Что означает, что $f(x)$ стремится к пределу, когда $x$ стремится к бесконечности?
спросил
Изменено 7 лет, 2 месяца назад
Просмотрено 4к раз
$\begingroup$
Я не ожидаю получить точный ответ, но некоторые аргументы будут оценены. Спасибо.
- исчисление
- пределы
$\endgroup$
1
$\begingroup$
$f(x)$ — это функция, и мы помещаем числа в эту функцию, и она возвращает нам числа.
Если $f(x)$ стремится к пределу, когда $x$ стремится к бесконечности, то это означает, что если мы введем в функцию действительно большое число, она будет вести себя определенным образом. Так что же произойдет, если мы будем вводить в функцию все большие и большие числа? Вот что такое предел.
Например, давайте посмотрим на $f(x) = 0$. Это постоянная функция, и независимо от того, какой $x$ мы выберем, она выдает $0$. Если мы вложим действительно большой $x$, то это не имеет значения, мы все равно получим $0$ обратно. Поскольку $x$ стремится к бесконечности, это все равно не влияет на вывод, функция по-прежнему возвращает $0$. Таким образом, предел функции при стремлении $x$ к бесконечности равен просто $0$.
Теперь рассмотрим $f(x)= 1/x$. Если мы вложим, скажем, 1000 долларов, то обнаружим, что $f(1000) = 1/1000$. Это довольно мало, но если мы выберем еще большее значение $x$, то сможем сделать его еще меньше. Например, $f(10000) = 1/10000$. Оказывается, чем большее число мы выбираем, тем ближе к $0$ становится эта функция.
Это говорит нам о том, что по мере того, как число, которое мы вводим в функцию, $x$, приближается к бесконечности (становясь все больше и больше), функция выдает числа, которые становятся все ближе и ближе к $0$. Таким образом, предел функции равен $0$.
$\endgroup$
$\begingroup$
Представьте, что у вас есть торт объемом $C$, а $f(x)$ — это объем куска торта, если его разрезать на $x$ кусочков. Итак, $f(x) = \frac{C}{x} $.
Что произойдет с объемом кусочка торта, если количество кусочков увеличится? Оно будет становиться все меньше и меньше, и если бы $x$ могло достигать бесконечности, $f(x)$ было бы равно 0.
Другими словами, хотя $x$ стремится к бесконечности, $f(x)$ стремится к $0$ . Или хотя $x$ стремится к бесконечности, $f(x)$ стремится к пределу. Или в символическом выражении: 92$ Теперь предположим, что вы приближаете $x$ к $2$. Когда $x = 1,9, f(x) = 3,61$ Когда $x = 1,999, f(x) = 3,996001$
Так как $x\to 2, \f(x)\to 4$ что также может быть альтернативно выражено как: $\lim_{x\to2} f(x) = 4$
Аналогично, пусть существует функция $f(x) = 1/x$.
\mathbb{R} \times \mathbb{R} \rightarrow \{\mathrm{true},\mathrm{false}\}$ следующим образом: 9\mathbb{R}\rightarrow \{\mathrm{true},\mathrm{false}\}$ следующим образом:
$$Q(f) = \mathop{\exists}_{y\in \mathbb{R }} R(f,y)$$
Тогда фраза “$f(x)$ стремится к пределу, когда $x$ стремится к бесконечности” является способом сказать, что выполняется $Q(f)$.
$\endgroup$
0
$\begingroup$
$\fbox{$\text{Предел — это значение, к которому “приближается” функция, когда индекс приближается к некоторому значению}$.}$
Если функция приближается к бесконечности в пределе, то индекс будет увеличиваться бесконечно, пока не будет достигнуто значение, если конечное значение не достигнуто, мы говорим, что предел расходится.
Вот графическое производное определение, включающее пределы, оно может немного отточить вашу интуицию, но не является прямым ответом на ваш вопрос.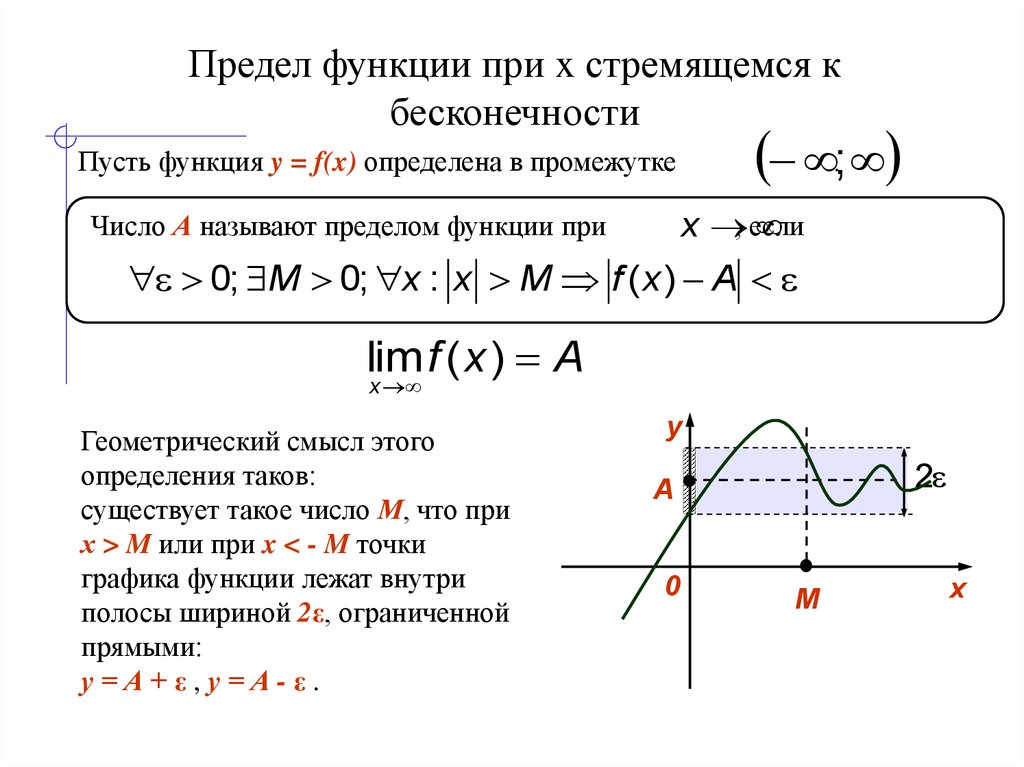
Вот точное $(\varepsilon, \delta)$ определение предела функции; Пусть $f : D \rightarrow \mathbb{R}$ — функция, определенная на подмножестве $D \subseteq \mathbb{R}$ , пусть $c$ — предельная точка $D$, и пусть $L$ быть действительным числом. Тогда функция $f$ имеет предел $L$ в точке $c$, что означает, что для всех $\varepsilon \gt 0$ существует $\delta \gt 0$ такое, что для всех $x$ в $D $, которые удовлетворяют $0 \lt | х – с | \lt \delta$ , неравенство $|f(x) – L| \lt \varepsilon$ выполняется. 92$ в знаменателе будет равно нулю в пределе, когда $x$ стремится к бесконечности.
Это означает, что функция $f(x)$ приближается к значению или пределу, если вы предпочитаете (в данном случае к $4$), когда $x$ стремится к бесконечности.
$\endgroup$
исчисление– Следует ли использовать «стремится к» или «равно» при работе с бесконечностью?
$\begingroup$
Это совершенно верно:
$$\lim_{x\to0}\frac{1}{x}=\infty \tag{1}$$
или я должен использовать:
$$\frac{1}{x}\to\infty\quad\text{as}\quad x\to0 \tag{2}$$
или аналогично:
$$\lim_{x\to0}\frac{1}{x}\to\infty \tag{3}$$
все действительны? Меня всегда учили, что вы никогда не должны помещать бесконечность в уравнение или в качестве ответа, скорее вы должны говорить «f (x) стремится к бесконечности», потому что ничто не может «равно» бесконечности, однако в моем учебнике используется первый пример, как и во многих ресурсы, которые я просматривал в Интернете.
-}\frac{1}{x}=-\infty$, где первое означает приближение к $0$ справа и последний слева. Пределы разные, поэтому говорить $\lim_{x\to 0}\frac{1}{x}=\infty$ неверно. 9+}{\frac 1x}=\infty$$
“Предел, когда x стремится к 0 с положительной стороны от 1 над x, равен бесконечности”
Короче говоря, используйте “стремится к”, когда не используется обозначение предела, используйте равные, когда вы.
$\endgroup$
$\begingroup$
Вас неправильно учили. “$\lim_{x \to 0} f(x) = \infty$” имеет точное значение, такое же, как “$f(x) \to \infty$ as $x \to 0$”. С другой стороны, вы никогда не должны говорить $\lim_{x \to 0} f(x) \to \infty$.
Однако ваш конкретный пример неверен. $\lim_{x \to 0} 1/x$ не существует, поскольку он включает как положительные, так и отрицательные значения $x$. $\lim_{x \to 0+} 1/x = +\infty$, но $\lim_{x \to 0-} 1/x = -\infty$.
$\endgroup$
$\begingroup$
Первые два верны и означают одно и то же, третий не имеет особого смысла.