K физика: Колебания груза на пружине — урок. Физика, 9 класс.

Константы и единицы

Константы и единицы

Обозначение	Название	Величина
e	единица заряда	1.6·10-19 Кл
1/α = ћс/e2	постоянная тонкой структуры	137.0
c	скорость света в вакууме	2.998·1010 см/с
h	постоянная Планка	6.626·10-27 эрг .с
ћ	приведенная постоянная Планка	6.582·10-22 МэВ·с
ћс	константа конверсии	197.3 Мэв·Фм
k	константа Больцмана	8.617·10-11 МэВ/град
re	классический радиус электрона	2.818 Фм
ћ/mec	комптоновская длина волны электрона	386. 2 Фм
ћ/mpc	комптоновская длина волны протона	0.210 Фм
	комптоновская длина волны пиона	1.414 Фм
	атомная единица массы	931.5 МэВ/c2
me	масса электрона	0.511 МэВ/c2
mn	масса нейтрона	939.6 МэВ/c2
mp	масса протона	938.3 МэВ/c2
	масса π−, π +	139.6 МэВ/c2
	масса π0	135.0 МэВ/c2
	масса W–,W+-бозонов	80.2 ГэВ/c2
	масса Z-бозона	91.2 ГэВ/c2
NA	число Авогадро	6. 02 .1023
μN = ћe/2mpc	ядерный магнетон	3.152·10-18 МэВ/Г
	магнитный момент протона	2.793μN
	магнитный момент нейтрона	1.913μN

1 Фм = 10-13 см	1 а.е.м. = 1.66 .10-24 г	1 Гр = 1 Дж/кг = 100 рад
1 барн = 10-24 см2	1 эВ = 1.602 .10-19 Дж	1 P = 2.58 .10-4 Кл/кг
1 эВ/c2 = 1.783 .10-33 г	1 Ки = 3.7 .1010 Бк	1 Зв = 100 бэр
1 мэВ = 10-3 эВ, 1 кэВ = 103 эВ, 1 МэВ = 106 эВ, 1 ГэВ = 109 эВ, 1 ТэВ = 1012 эВ, 1 ПэВ = 1015 эВ,

Физика и техника полупроводников

Физика и техника полупроводников

• Журналы
• Поиск
• Войти

Физика и техника полупроводников

• Описание журнала
• Редакционная коллегия
• Статистика
• Переводная версия

Авторам

• Правила оформления публикаций

Вышедшие номера

• 2022
  • 1 2 3 4 5 6 7 8 9 10 11
• 2021
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2020
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2019
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2018
  • 1 2 3 4 5 6 7 8 9 10 11 12 13
• 2017
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2016
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2015
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2014
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2013
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2012
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2011
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2010
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2009
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2008
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2007
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2006
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2005
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2004
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2003
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2002
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2001
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 2000
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1999
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1998
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1997
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1996
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1995
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1994
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1993
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1992
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1991
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1990
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1989
  • 1 2 3 4 5 6 7 8 9 10 11 12
• 1988
  • 1 2 3 4 5 6 7 8 9 10 11 12

Home » Физика и техника полупроводников » Год 1992, выпуск 3

<<<>>>

Физика и техника полупроводников, 1992, том 26, выпуск 3

Горфинкель В. Б., Филатов И.И.

Высокочастотная модуляция выходной мощности полупроводникового лазера на двойной гетероструктуре n⁺-AlGaAs-GaAs-p^*-AlGaAs греющим электрическим полем

Соловьева А.Е.

Образование шнура проводимости и пробоя в поликристаллическом оксиде индия

Иванов-Омский В.И., Смирнов В.А., Юлдашев Ш.У., Гадаев О.А., Стрэдлинг Р.А., Фергюсон И.

Фотолюминесценция эпитаксиального слоя InSb на квазиполуизолирующей подложке p-InSb

Иванов-Омский В.И., Кутехов Н.В., Смирнов В.А., Юлдашев Ш.У., Гадаев О.А.

Нейтронное облучение Cd_xHg_1-xTe

Баграев Н.Т., Мирсаатов Р.М., Половцев И.С., Сирожов У., Юсупов А.

Метастабильность центров марганца в твердых растворах кремний-германий

Забродский А.Г., Андреев А.Г., Алексеенко М.В.

Прыжковая проводимость K=0.3-серии образцов Ge : Ga : эффект насыщения, перскоки по ближайшим соседям и переход к прыжкам с переменной длиной

Бабич В.М., Баран Н.П. , Доценко Ю.П., Зотов К.И., Ковальчук В.Б., Максименко В.М.

Образование и свойства термодоноров при отжигах ниже 550^oC в кристаллах кремния, выращенных по методу Чохральского

Торчинская Т.В., Бердинских Т.Г., Смиян О.Д.

Природа нестабильности свечения в светоизлучающих CaP : N-структурах

Логвинов Г.Н.

Термоэдс в полупроводниковых субмикронных пленках

Боднарук О.А., Горбатюк И.Н., Остапов С.Э., Раренко И.М.

Концентрация собственных носителей и эффективная масса электронов в Mn_xHg_1-xTe

Шматов А.А.

К вопросу о корреляции функции в релаксационной спектроскопии глубоких уровней

Еремин В.К., Иванов А.М., Строкан Н.Б.

Ложные пики в спектрах DLTS планарных диодных структур

Баграев Н.Т., Мирсаатов Р.М., Половцев И.С., Юсупов А.

Цинк в кремнии: фотоиндуцированные реакции

Серженко Ф.Л., Шадрин В.Д.

Теория инфракрасных фотоприемников на основе структур n-Si-Si_1-xGe_x с квантовыми ямами

Абрамов А. А., Захарикова Л.П., Микуленок А.В., Стоянова И.Г.

Распределение концентрации мелких и глубоких заряженных центров в ионно-легированных бериллием слоях фосфида индия

Рудь В.Ю., Рудь Ю.В., Сергинов М.

Усиление фотоплеохроизма в структурах n-p-CdSiAs₂-n-In₂O

3

Горшкова О.В., Дрозд И.А., Стафеев В.И.

Фотоэлектрические свойства эпитаксиальных пленок Pb_1-xSn_xS и структур на их основе, обусловленные микро- и макронеоднородностями

Алешкин В.Я., Аншон А.В., Бабушкина Т.С., Батукова Л.М., Демидов Е.В., Звонков Б.Н., Кунцевич Т.С., Малкина И.Г., Янькова Т.Н.

Межподзонное поглощение ИК излучения в напряженных структурах In_xGa_1-xAs-GaAs с квантовыми ямами

Дубровский Ю.В., Ларкин И.А., Морозов С.В.

“Энергетическая квазибаллистика” в микроструктурах с двумерным электронным газом

Гукасян А.М., Ушаков В.В., Гиппиус А.А., Марков А.В.

Фотоиндуцированное образование центров поверхностной рекомбинации в арсениде галлия

Прима Н. А.

Упругое рассеяние в многодолинных полупроводниках и его роль в релаксации энергии неравновесных электронов

Карачевцева Л.А., Любченко А.В., Маловичко Э.А.

Особенности магнитополевых зависимостей кинетических коэффициентов в двухслойных структурах Cd_xHg_1-xTe

Гусев Г.М., Квен З.Д., Бесман В.Б., Вильмс П.П., Коваленко Н.В., Мошегов Н.Г., Торопов А.И.

Осцилляции Шубникова-де-Гааза двумерного электронного газа в двумерном периодическом потенциале

Гусинский Г.М., Дьяконова Н.В., Левинштейн М.Е., Румянцев С.Л.

Шум 1/f, электрические и фотоэлектрические свойства GaAs, подвергнутого облучению ионами высокой энергии

Бурлак А.В., Зотов В.В., Игнатов А.В., Тюрин А.В., Цукерман В.Г.

Особенности электрофизических характеристик тонких слоев PbS с низким содержанием окислителя

Арутюнян В.М., Варданян С.Х., Димаксян М.Л., Маргарян А.Л., Меликсетян В.А., Саруханян Р.Э.

О возможности обнаружения поверхностных состояний из спектров фотопроводимости

Аждаров Г. Х., Кязимзаде Р.З., Мир-Багиров В.В.

Акцепторные уровни замещающих атомов примеси меди в кристаллах Ge_1-xSi_x

Магомедов М.А., Медведкин Г.А., Рудь В.Ю., Рудь Ю.В.

Получение и свойства изотипных гетероструктур на основе n-CuInSe₂

Константинова Н.Н., Магомедов М.А., Рудь В.Ю., Рудь Ю.В.

Оптические гетероконтакты на основе пленок CuInSe₂

Вирт И.С., Кузьма М.С., Шерегий Е.М., Шкумбатюк П.С.

Твердофазное лазерное легирование монокристаллов Cd_xHg_1-xTe

Вирт И.С., Белотелов С.В.

Свойства n⁺-p-переходов на основе Cd_xHg_1-xTe, подвергнутых локальной деформации

Бойко М.П., Засавицкий Е.А.

Низкотемпературные аномалии термоэдс PbTe<Tl>

Савицкий В.Г., Соколовский Б.С., Новак В.И.

Рекомбинационное излучение варизонных полупроводников в условиях магнитоконцентрационного эффекта

Голубев В.Г., Емцев В.В., Клингер П.М., Кропотов Г. И., Шмарцев Ю.В.

Процессы образования радиационных дефектов в Si : Ge при 4.2, 78 и 300 K

Катана П.К.

Многофотонное межзонное поглощение лазерного излучения в полупроводниках с участием примесных уровней

Учредители

• Российская академия наук

• Физико-технический институт им. А.Ф.Иоффе Российской академии наук

Издатель

• Физико-технический институт им. А.Ф.Иоффе Российской академии наук

© 2023 Физико-технический институт им. А.Ф. Иоффе Российской академии наук
Powered by webapplicationthemes.com – High quality HTML Theme

Учебник по физике: Закон Кулона

Взаимодействие между заряженными объектами представляет собой бесконтактную силу, действующую на некотором расстоянии друг от друга. Заряд, заряд и расстояние. Каждое электрическое взаимодействие включает в себя силу, которая подчеркивает важность этих трех переменных. Будь то пластиковая трубка для гольфа, притягивающая кусочки бумаги, два одинаково заряженных шарика, отталкивающие друг друга, или заряженная пластина из пенополистирола, взаимодействующая с электронами в куске алюминия, всегда есть два заряда и расстояние между ними как три критические переменные, влияющие на прочность. взаимодействия. В этом разделе урока 3 мы рассмотрим важность этих трех переменных.

Сила как вектор Величина

Электрическая сила, как и все силы, обычно выражается в единицах измерения Ньютон. Будучи силой, сила электрического взаимодействия является векторной величиной, имеющей как величину, так и направление. Направление электрической силы зависит от того, заряжены ли заряженные объекты одинаковым или противоположным зарядом, а также от их пространственной ориентации. Зная тип заряда на двух объектах, направление силы на любой из них можно определить с небольшими рассуждениями. На приведенной ниже диаграмме объекты A и B имеют одинаковый заряд, из-за чего они отталкиваются друг от друга.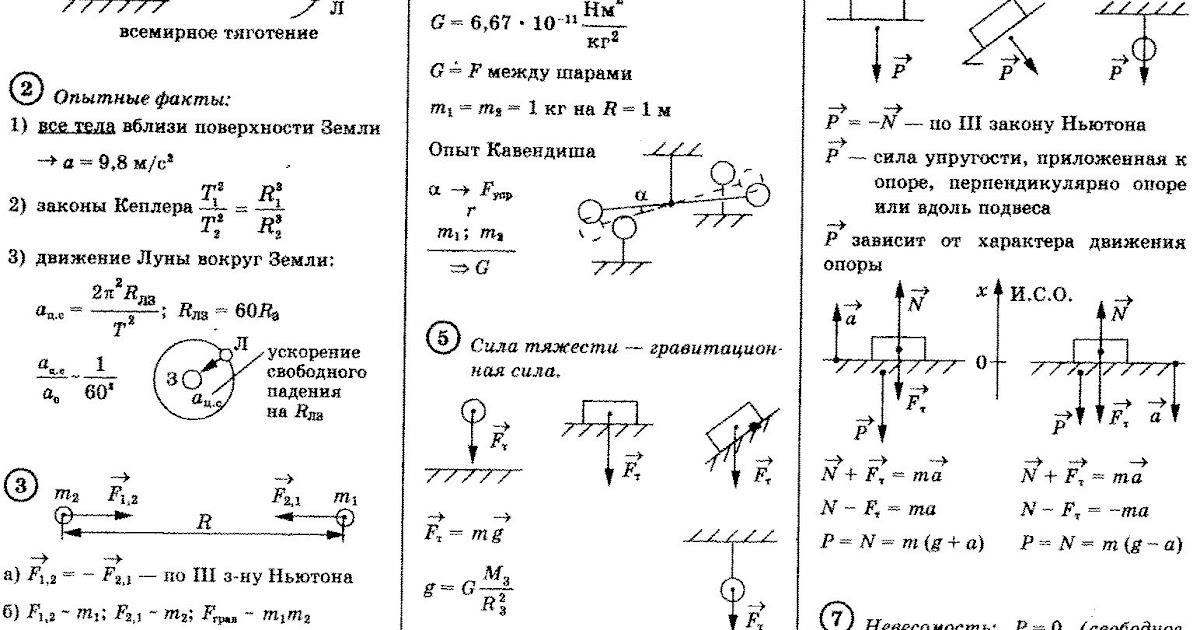 Таким образом, сила на объекте А направлена ​​влево (от В), а сила на объекте В направлена ​​вправо (от А). С другой стороны, объекты C и D имеют противоположный заряд, поэтому они притягиваются друг к другу. Таким образом, сила на объекте C направлена ​​вправо (к объекту D), а сила на объекте D направлена ​​влево (к объекту C). Когда дело доходит до вектора электрической силы, возможно, лучший способ определить его направление — это применить фундаментальные правила взаимодействия зарядов (противоположности притягиваются, а подобные отталкиваются), используя небольшие рассуждения.

Электрическая сила также имеет величину или силу. Как и для большинства типов сил, существует множество факторов, влияющих на величину электрической силы. Два шара с одинаковым зарядом будут отталкивать друг друга, и силу их отталкивания можно изменить, изменив три переменные. Во-первых, на силу отталкивания будет влиять количество заряда одного из шаров. Чем сильнее заряжен воздушный шар, тем больше сила отталкивания. Во-вторых, количество заряда второго шара будет влиять на силу отталкивания. Аккуратно потрите два шарика шерстью животных, и они немного оттолкнутся. Энергично потрите два шарика, чтобы придать им обоим больше заряда, и они сильно отталкиваются. Наконец, расстояние между двумя шарами будет иметь значительное и заметное влияние на силу отталкивания. Электрическая сила наиболее сильна, когда воздушные шары находятся ближе всего друг к другу. Уменьшение разделительного расстояния увеличивает силу. Величина силы и расстояние между двумя шарами равны обратно пропорционально .

Уравнение закона Кулона

Количественное выражение влияния этих трех переменных на электрическую силу известно как закон Кулона. Закон Кулона гласит, что электрическая сила между двумя заряженными объектами прямо пропорциональна произведению количества заряда на объектах и ​​обратно пропорциональна квадрату расстояния между двумя объектами. В форме уравнения закон Кулона можно сформулировать как

где Q ₁ представляет количество заряда на объекте 1 (в кулонах), Q ₂ представляет количество заряда на объекте 2 (в кулонах), а d представляет расстояние расстояния между двумя объектами (в метрах). Символ k представляет собой константу пропорциональности, известную как константа закона Кулона. Значение этой константы зависит от среды, в которую погружены заряженные объекты. В случае воздуха значение составляет примерно 9.0 x 10 ⁹ Н • м ² / C ² . Если заряженные объекты присутствуют в воде, значение k может быть уменьшено в 80 раз. Стоит отметить, что единицы измерения k таковы, что при подстановке в уравнение единицы на заряд (кулоны) и единицы расстояния (метры) будут отменены, оставив Ньютон в качестве единицы силы.

Уравнение закона Кулона обеспечивает точное описание силы между двумя объектами всякий раз, когда объекты действуют как точечные сборы . Заряженный проводящий шар взаимодействует с другими заряженными объектами так, как если бы весь его заряд был сосредоточен в его центре. Хотя заряд равномерно распределен по поверхности сферы, центр заряда можно считать центром сферы.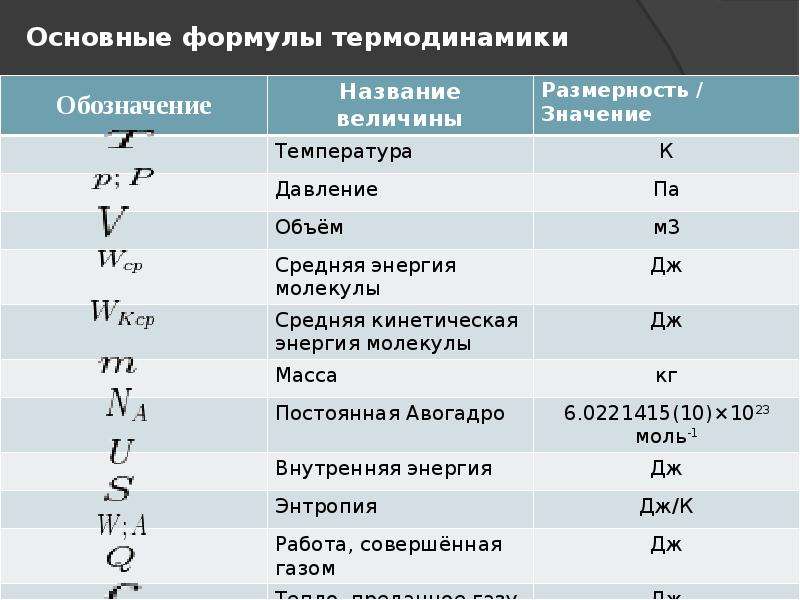 Сфера действует как точечный заряд с избыточным зарядом, расположенным в ее центре. Поскольку закон Кулона применим к точечным зарядам, расстояние d в уравнении — это расстояние между центрами заряда обоих объектов (а не расстояние между их ближайшими поверхностями).

Символы Q ₁ и Q ₂ в уравнении закона Кулона представляют количество зарядов на двух взаимодействующих объектах. Поскольку объект может быть заряжен положительно или отрицательно, эти величины часто выражаются как значения «+» или «-». Знак заряда просто показывает, имеет ли объект избыток электронов (отрицательно заряженный объект) или недостаток электронов (положительно заряженный объект). Может возникнуть соблазн использовать знаки «+» и «-» при расчете силы. Хотя эта практика не рекомендуется, в этом, безусловно, нет никакого вреда. При использовании знаков «+» и «-» при расчете силы результатом будет то, что значение «-» для силы является признаком силы притяжения, а значение «+» для силы означает силу отталкивания. Математически значение силы должно быть положительным, когда Q ₁ и Q ₂ имеют одинаковый заряд – либо оба “+”, либо оба “-“. И значение силы будет отрицательным, когда Q ₁ и Q ₂ имеют противоположный заряд – один «+», а другой «-». Это согласуется с концепцией о том, что противоположно заряженные объекты взаимодействуют притягивающе, а заряженные объекты отталкиваются. В конце концов, если вы мыслите концептуально (а не просто математически), вы вполне сможете определить природу силы — притягивающей или отталкивающей — без использования знаков «+» и «-» в уравнении.

 

Вычисления с использованием закона Кулона

В курсах физики закон Кулона часто используется в качестве алгебраического рецепта для решения физических задач. Здесь показаны три таких примера.

Пример А Предположим, что два точечных заряда, каждый с зарядом +1,00 Кулона, находятся на расстоянии 1,00 метра друг от друга. Определить величину электрической силы отталкивания между ними.

Это не самая сложная математическая задача, которую можно было выбрать. Он определенно не был выбран из-за его математической строгости. Используемая здесь стратегия решения проблем может показаться ненужной, учитывая простоту данных значений. Тем не менее, эта стратегия будет использоваться, чтобы проиллюстрировать ее полезность для любой проблемы закона Кулона.

Первым шагом стратегии является идентификация и перечисление известной информации в переменной форме. Здесь мы знаем заряды двух объектов (Q ₁ и Q ₂ ) и расстояние между ними (d). Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о силе. Итак, F _Elect — это неизвестная величина. Результаты первых двух шагов представлены в таблице ниже.

Дано: Ом 1 = 1,00 С Q 2 = 1,00 С d = 1,00 м

Найти: F избранный = ???

Следующий и последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации.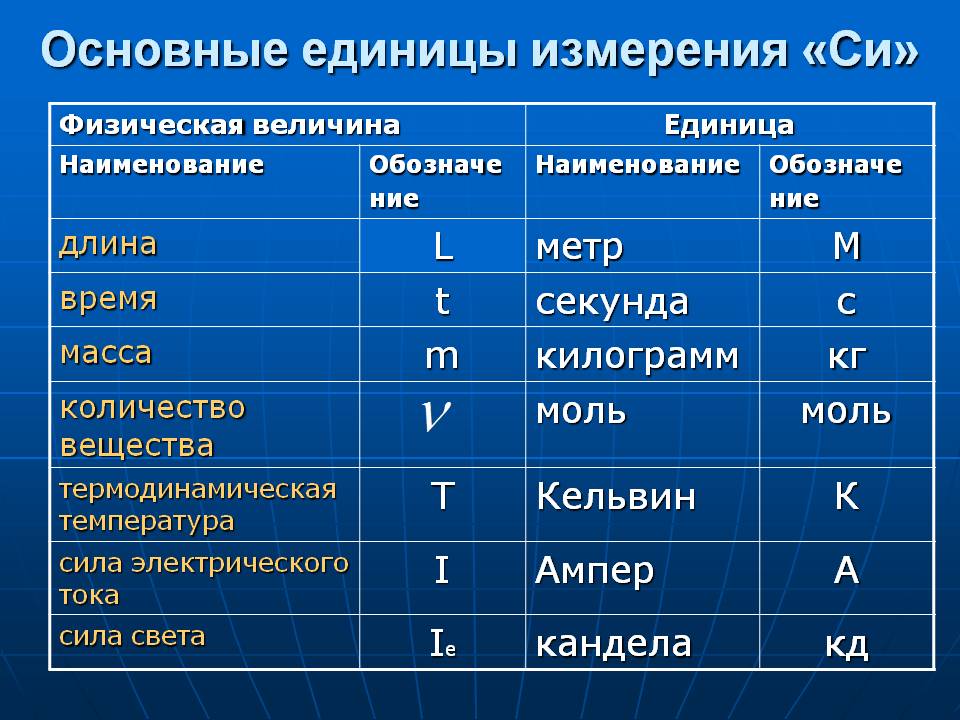 Этот шаг показан ниже.

F _{избранный} = к • Q ₁ • Q ₂ / д ²

F _Elect = (9,0 x 10 ⁹ Н•м ² /C ² ) • (1,00 C) • (1,00 C) / (1,00 м) ²

F _{избранный} = 9,0 x 10 ⁹ N

 

Сила отталкивания двух зарядов +1,00 Кулон, находящихся на расстоянии 1,00 м друг от друга, составляет 9 миллиардов ньютонов. Это невероятно большая сила, по величине сравнимая с весом более 2000 реактивных лайнеров.

Эта задача была выбрана прежде всего из-за ее концептуального сообщения. Объекты просто не приобретают зарядов порядка 1,00 кулона. На самом деле более вероятно, что значения Q составляют порядка 10 ^-9 или, возможно, 10 ^-6 кулонов. По этой причине перед кулоновской единицей заряда часто используется греческий префикс. Заряд часто выражается в микрокулонах (мкКл) и нанокулонах (нКл). Если в задаче указан заряд в этих единицах, рекомендуется сначала преобразовать в кулоны перед подстановкой в ​​уравнение закона Кулона. Следующие единицы эквивалентности помогут в таких преобразованиях.

 1 Кулон = 10 ⁶ микроКулон

 1 Кулон = 10 ⁹ наноКулон

 

Стратегия решения проблем, использованная в примере А, включала три шага:

1. Определение и перечисление известной информации в переменной форме.
2. Перечислите неизвестную (или желаемую) информацию в переменной форме.
3. Подставьте известные значения в уравнение закона Кулона и, используя соответствующие алгебраические шаги, найдите неизвестную информацию. (В некоторых случаях и для некоторых учащихся может быть проще сначала выполнить алгебраические вычисления с использованием переменных, а затем выполнить подстановку в качестве последнего шага.)

Эта же стратегия решения проблем демонстрируется в Примере B ниже.

 

Пример В Два баллона заряжены одинаковым количеством и типом заряда: -6,25 нКл. Они разнесены на расстояние 61,7 см. Определить величину электрической силы отталкивания между ними.

В задаче указано значение Q ₁ и Q ₂ . Поскольку эти значения выражены в единицах нанокулонов (нКл), необходимо выполнить преобразование в кулоны. В задаче также указывается разделительное расстояние (d). Поскольку расстояние указывается в сантиметрах (см), необходимо также выполнить преобразование в метры. Эти преобразования необходимы, поскольку единицами заряда и расстояния в постоянной Кулона являются кулоны и метры. Неизвестной величиной является электрическая сила (F). Результаты первых двух шагов представлены в таблице ниже.

Дано: Ом 1 = -6,25 нКл = -6,25 х 10 -9 Кл Q 2 = -6,25 нКл = -6,25 x 10 -9 C д = 61,7 см = 0,617 м

Найти: F избранный = ???

Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. Эта замена и алгебра показаны ниже.

F _{избранный} = k • Q ₁ • Q ₂ / d ²

F _Elect = (9,0 x 10 ⁹ Н•м ² /C ² ) • (6,25 x 10 ^-9 C) • (6,25 x 10 ^{-9 9004,2 C)17 (/9004,2 C) м) 2}

F _{избранный} = 9,23 x 10 ^-7 N

 

Обратите внимание, что перед подстановкой в ​​уравнение закона Кулона знак «-» был удален из значений Q ₁ и Q ₂ . Как упоминалось выше, использование знаков «+» и «-» в уравнении приведет к положительному значению силы, если Q ₁ и Q ₂ одинаково заряжены, и к отрицательному значению силы, если Q ₁ и Q ₂ заряжены противоположно. Полученные в результате знаки «+» и «-» на F означают, является ли сила притягательной (значение «-» F) или отталкивающей (значение «+» F).

Пример С Два шарика с зарядами +3,37 мкКл и -8,21 мкКл притягиваются друг к другу с силой 0,0626 ньютона. Определите расстояние между двумя шарами.

В задаче указано значение Q ₁ и Q ₂ . Поскольку эти значения выражены в микрокулонах (мкКл), будет выполнено преобразование в кулоны. В задаче также указывается электрическая сила (F). Неизвестной величиной является разделительное расстояние (d). Результаты первых двух шагов представлены в таблице ниже.

Дано: Q 1 = +3,37 мкКл = +3,37 x 10 -6 С Q 2 = -8,21 мкКл = -8,21 x 10 -6 C F избрать = -0,0626 Н (используйте значение силы, так как оно является привлекательным)

Найти: д = ???

Как упоминалось выше, использование знаков «+» и «-» необязательно. Однако, если они используются, то они должны использоваться последовательно для значений Q и значений F. Их использование в уравнении показано в этой задаче.

Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. В этом случае алгебра выполняется первой, а подстановка выполняется последней. Эта алгебра и замена показаны ниже.

F _{избранный} = k • Q ₁ • Q ₂ / d ²

d ² • F _{избранный} = k • Q ₁ • Q ₂

d ² = k • Q ₁ • Q ₂ / F _{избранный}

d = SQRT(k • Q ₁ • Q ₂ ) / F _{избранный}

d = SQRT [(9,0 x 10 ⁹ Н•м ² /C ² ) • (-8,21 x 10 ^-6 C) • (+3,37 x 10 ^-6 C) / ( -0,0626 Н)]

d = Кв. [ +3,98 м ² ]

d = +1,99 м

 

Сравнение электрических и гравитационных сил

Электрическая сила и гравитационная сила — это две бесконтактные силы, обсуждаемые в учебном пособии The Physics Classroom. Уравнение закона Кулона для электрической силы очень похоже на уравнение Ньютона для всемирного тяготения.

Эти два уравнения имеют очень похожую форму. Оба уравнения показывают обратную квадратичную зависимость между силой и разделяющим расстоянием. И оба уравнения показывают, что сила пропорциональна произведению величины, вызывающей силу, — заряда в случае электрической силы и массы в случае гравитационной силы. Тем не менее, между этими двумя силами есть некоторые поразительные различия. Во-первых, сравнение констант пропорциональности – k и G – показывает, что константа закона Кулона (k) значительно больше, чем ньютоновская постоянная всемирного тяготения (G). Следовательно, единица заряда будет притягивать единицу заряда со значительно большей силой, чем единица массы притягивает единицу массы. Во-вторых, гравитационные силы действуют только притягивающе; электрические силы могут быть как притягивающими, так и отталкивающими.

Зависимость обратного квадрата между силой и расстоянием, вплетенная в уравнение, является общей для обеих бесконтактных сил. Эта взаимосвязь подчеркивает важность разделяющего расстояния, когда речь идет об электрическом взаимодействии между заряженными объектами. Этому посвящен следующий раздел Урока 3.

 

 

 

Мы хотели бы предложить…

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного закона Кулона. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный закон Кулона позволяет учащимся исследовать влияние заряда и разделяющего расстояния на величину электрической силы между двумя заряженными объектами.

Посетите:  Закон Кулона 

Проверьте свое понимание

Используйте свое понимание, чтобы ответить на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.

1. Q в уравнении закона Кулона означает _____.

а. масса заряженного объекта	б. # избыточных электронов на объекте
с. ток заряженного объекта	д. расстояние между заряженными объектами
эл. заряд заряженного объекта

 

 

2. Символ d в уравнении закона Кулона представляет собой расстояние от ___.

 

а. от А до Б	б. от А до Д	с. от В до С	д. от В до Д
эл. С-D	ф. от А до G	г. от В до F	ч. от С до Е

 

3. Определить электрическую силу притяжения между двумя воздушными шарами с отдельными зарядами +3,5 х 10 ^-8 Кл и -2,9 х 10 ^-8 Кл при расстоянии 0,65 м друг от друга.

 

4. Определите электрическую силу притяжения между двумя шариками, заряженными противоположным типом заряда, но одинаковым количеством заряда. Заряд аэростатов составляет 6,0 х 10 ^-7 Кл, расстояние между ними 0,50 м.

 

5. Джоанна натерла шарик шерстью, чтобы придать ему заряд -1,0 x 10 ^-6 C. Затем она приобрела пластиковую трубку для гольфа с зарядом +4,0 x 10 ^-6 C локализован в данной позиции. Она держит место заряда на пластиковой трубке для гольфа на расстоянии 50,0 см над баллоном. Определить электрическую силу притяжения между трубкой для гольфа и шариком.

 

 

6. Баллон с зарядом 4,0 мкКл держат на расстоянии 0,70 м от второго баллона с таким же зарядом. Вычислите величину силы отталкивания.

 

7. На каком расстоянии друг от друга должны находиться два заряда в 1,00 мкК, чтобы сила отталкивания между ними была эквивалентна весу (на Земле) груза массой 1,00 кг?

Следующий раздел:

Перейти к следующему уроку:

Электричество – Закон Кулона – Физика 299

Электричество – Закон Кулона – Физика 299

“Когда человек захотел сделать машину, которая ходить он создал колесо, которое не похоже на ногу”
Гийом Аполлинер

• Величина силы притяжения (или отталкивания), Ф ₁₂ между двумя точечными зарядами q ₁ и q ₂  составляет дается законом Кулона.





где R ₁₂   — расстояние между обвинения. k — константа пропорциональности, известная как кулоновская постоянная, имеющая значение 9Икс 10 ⁹   Н.м ² / C ²  в вакуум.

Обратите внимание, что постоянная Кулона k равна часто заменяется на (1/4π ε ₀ ), где ε ₀ — диэлектрическая проницаемость вакуума (подробнее позже).


• Направление этой силы вдоль линии, соединяющей два обвинения со смыслом, определяемым относительными знаками зарядов
• Обратите внимание, что сила, действующая на каждый заряд, имеет одинаковую величину (как требуется третьим законом Ньютона).


• Для двух зарядов по 1 Кулону, разнесенных на 1 метр, величина силы определяется,
  F = (9 x 10 ⁹   x 1 x 1 )/ 1  =  9 x 10 ⁹ Ньютоны

  Это чрезвычайно большая сила (достаточная для переместиться на гору Эверест с ускорением 1 см/с ² ). Кулон очень большой блок. Типичные макроскопические заряды измеряются в микрокулонах (10 ^-6 С).

• Чтобы справиться с ситуациями с более чем одним зарядом, заряды должны рассматривать попарно, так что общая сила на один заряд будет векторная сумма силы из-за каждого из других обвинений. Например сила на q ₁ в связи со всеми другими расходами q ₂ , q ₃ , q ₄ … было бы быть данный по,

Ф ₁ = Ф ₂₁ + F ₃₁ + F ₄₁ + …

• Уведомление в сходство из Закон Кулона к закону всемирного тяготения Ньютона

оба являются законами обратных квадратов. Заменить заряд на массу и «k» вместо «G», и у вас есть закон Кулона.
Относительные величины Кулона постоянная k = 9 x 10 ⁹ и гравитационная постоянная G = 6,67 x 10 ^-11 , является показателем относительной силы две силы.