К какому виду приводится система при решении методом гаусса: Метод Гаусса. Примеры решения систем линейных алгебраических уравнений методом Гаусса.

Гауссоанская ликвидация – Wikiwand

• Введение Гауссоанское устранение
• Определения и пример Algorithmrow Operations. также
• СсылкиПроцитированные работы
• Внешние ссылки

В математике Исключение Гаусса , также известное как редукция строк , представляет собой алгоритм решения систем линейных уравнений. Он состоит из последовательности операций, выполняемых над соответствующей матрицей коэффициентов. Этот метод также можно использовать для вычисления ранга матрицы, определителя квадратной матрицы и обратной обратимой матрицы. Метод назван в честь Карла Фридриха Гаусса (1777–1855), хотя некоторые частные случаи метода, хотя и представленные без доказательств, были известны китайским математикам еще около 179 г.н.э.[1]

Чтобы выполнить сокращение строк в матрице, используется последовательность элементарных операций со строками для изменения матрицы до тех пор, пока нижний левый угол матрицы не будет заполнен нулями, насколько это возможно.

Существует три типа операций с элементарными строками:

• Замена двух строк местами,
• Умножение строки на ненулевое число,
• Добавление кратного одной строки к другой строке. (вычитание можно выполнить, умножив одну строку на -1 и прибавив результат к другой строке)

С помощью этих операций матрицу всегда можно преобразовать в верхнюю треугольную матрицу, причем в виде эшелона строк. Когда все старшие коэффициенты (крайний левый ненулевой элемент в каждой строке) равны 1, а каждый столбец, содержащий старший коэффициент, имеет нули где-либо еще, говорят, что матрица имеет форму сокращенного эшелона строк. Эта окончательная форма уникальна; другими словами, он не зависит от последовательности используемых операций над строками. Например, в следующей последовательности операций со строками (где две элементарные операции над разными строками выполняются на первом и третьем шагах) третья и четвертая матрицы являются ступенчатыми матрицами строк, а конечная матрица представляет собой единственную сокращенную строку эшелонированная форма.

[131911−11311535]→[13190−2−2−80228]→[13190−2−2−80000]→[10−2−301140000]{\displaystyle {\begin{bmatrix}1&3&1&9\\1&1&-1&1 \\3&11&5&35\end{bmatrix}}\to {\begin{bmatrix}1&3&1&9\\0&-2&-2&-8\\0&2&2&8\end{bmatrix}}\to {\begin{bmatrix}1&3&1&9\\0&-2& -2&-8\\0&0&0&0\end{bmatrix}}\to {\begin{bmatrix}1&0&-2&-3\\0&1&1&4\\0&0&0&0\end{bmatrix}}}

Использование операций со строками для преобразования матрицы в сокращенную эшелонированную форму строк иногда называют исключением Гаусса-Жордана . В этом случае термин Исключение по Гауссу относится к процессу до тех пор, пока он не достигнет своей верхней треугольной или (нередуцированной) формы эшелона строк. Из вычислительных соображений при решении систем линейных уравнений иногда предпочтительнее остановить операции со строками до того, как матрица будет полностью уменьшена.

сокращение строки

Сокращение строк , также известное как Исключение Гаусса , представляет собой алгоритм решения системы линейных уравнений

an⁢m⁢xm=bn

Для описания редукции строк удобно сформулировать линейную система как одно матрично-векторное уравнение A⁢x=b, где

A=[a11a12⋯a1⁢ma21a22⋯a2⁢m⋮⋮⋱⋮an⁢1an⁢2⋯an⁢m],b=[b1b2⋮bn],x=[x1x2⋮xm]

– соответственно n×m-матрица коэффициентов линейная система, n-местный вектор-столбец скаляров из правая часть уравнений, и m-местный вектор-столбец неизвестные.

Метод состоит в объединении матрицы коэффициентов A с правый вектор b для формирования «расширенной» матрицы n×(m+1)

[Ab]=[a11a12⋯a1⁢mb1a21a22⋯a2⁢mb2⋮⋮⋱⋮⋮an⁢1an⁢2⋯an⁢mbn]=[R1R2⋮Rn,]

, где каждый Ri представляет собой m+1-местный вектор-строку, соответствующий строке i расширенной матрицы.

Затем к этой матрице применяется последовательность операций с элементарными строками. чтобы преобразовать его в форму эшелонированного ряда. Элементарные операции таковы:

Обратите внимание, что эти операции «законны», потому что x является решением преобразованная система тогда и только тогда, когда она является решением исходной системы.

Если количество уравнений равно количеству переменных (m=n) и если матрица коэффициентов A невырожденная (http://planetmath.org/singular), то алгоритм будет заканчиваются, когда расширенная матрица имеет следующий вид:

[a11′a12′⋯a1⁢n′b10a22′⋯a2⁢n′b2′⋮⋮⋱⋮⋮00⋯an⁢n′bn′]

При этих предположениях существует единственное решение, которое может быть полученный из приведенной выше матрицы обратной заменой.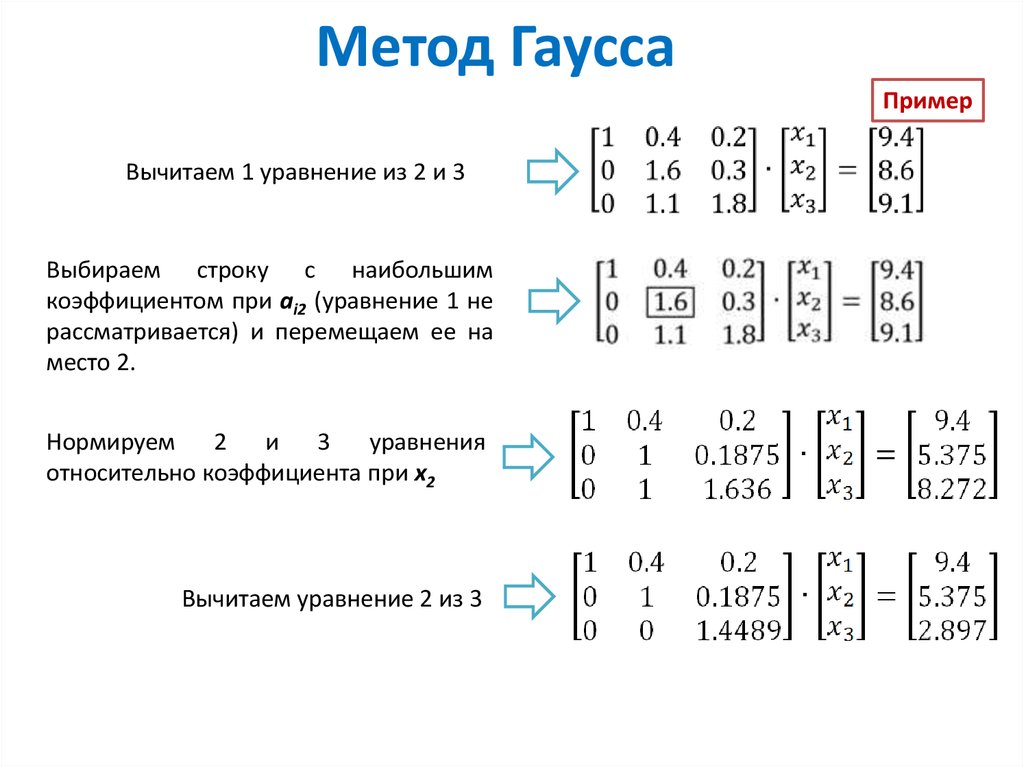

В общем случае процедура расторжения несколько сложнее. сложный. Сначала напомним, что матрица имеет ступенчатую форму, если каждый строка имеет больше начальных нулей, чем строки над ней. Поворот — это ведущий ненулевой элемент некоторой строки. Тогда у нас есть

• •

  Если в последнем столбце есть сводка, система непоследовательный; решений не будет.

• •

  Если это не так, то общее решение будет иметь d степеней свободы, где d — количество столбцов от 1 до м, у которых нет стержня. Точнее, общее решение будет иметь вид одного частного решения плюс произвольная линейная комбинация линейно независимых n-векторов.

  Если говорить еще более прозаично, то переменные в неосновном столбцы должны считаться «свободными переменными» и должны «переместился» в правую часть уравнения. Генерал затем решение получается путем произвольного выбора значений свободной переменные, а затем решение для оставшихся «несвободных» переменных которые находятся в сводных столбцах.