Как быстро делить в уме: Как делить в уме 🚩 как быстро делить числа 🚩 Математика

Как быстро разделить число на 5?

Говорят: «Математика – гимнастика ума». Воистину, верные слова. Вычисления, производимые в уме, без калькулятора, карандаша и других «подручных инструментов», прекрасно развивают мозг. Кроме того, вы приобретаете уверенность в том, что в случае непредвиденных обстоятельств, спокойно обойдетесь собственными силами.

Еще несколько десятков лет назад в школах был такой предмет – «Устный счет», на занятиях школьники учились вычислять в уме – умножать, делить, складывать и вычитать числа. Из собственного опыта все мы знаем, что делить в уме намного сложнее, чем, например, умножать. Для того чтобы делить устно, нужно знать методику сокращенного деления и, естественно, таблицу умножения. Например, есть способ, который поможет вашему ребенку научиться быстро делить на 5.

Как это делается?

Метод быстрого деления на 5 очень прост. Естественно, он подразумевает, что ребенок таблицу умножения помнит «на зубок». Для примера мы не будем брать числа, которые в таблице умножения есть, и ваш ученик их хорошо помнит. Возьмем что-то более сложное. Например:

• 165
• 238
• 482
• 1026

Как мы помним, умножать легче, чем делить. А умножать на 2 – под силу практически всем школьникам. Так вот, чтобы быстро разделить любое число на 5, его нужно сначала умножить на 2! То, что получится в результате умножения, является почти ответом на вопрос: «Сколько будет, если разделить число на 5?» Только нужно в числе произведения последнюю цифру отделить запятой.

Проверим?

Берем число 165, умножаем его на 2, в результате получаем 330. Отделяем в этом числе последнюю цифру, то есть ноль, и получаем число 33. Именно это число и является результатом деления числа 165 на 5. Вот так просто, можете проверить на калькуляторе.

Продолжаем.

• 238х2 = 476.

47,6

238:5 = 47,6.

• 482х2 = 964.

96,4

482:5 = 96,4.

• 1026х2 = 2052.

205,2

1026:5 = 205,2.

Просто, как все гениальное.

И еще одно. Если уже мы говорим об устном счете, то для таких вычислений нужно тренировать память: это необходимо, чтобы удерживать в голове все расчеты.

Кстати, если у вашего школьника хорошо развита зрительная память, он может попробовать мысленно делить «в столбик». Этот метод не такой «скоростной», как предыдущий, но как вариант может использоваться.

Улучшить навыки счета поможет IQКлуб

Развить навыки счета, улучшить память, внимание, мышление, расширить кругозор вашего ребенка поможет интернет-сервис IQКлуб. Команда профессионалов, в которую вошли ученые, программисты, дизайнеры, педагоги, психологи, разработали специальные, очень увлекательные игры для детей. С учетом их возраста рассчитана нагрузка в обучающих программах.

Разработчики игр позаботились о том, чтобы они не содержали рекламы и платного контента. Интерактивное обучение, без сомнения, заинтересует современного ребенка. Его досуг будет интересным и, главное, полезным. А родители смогут контролировать процесс обучения в режиме онлайн.

Как же воспользоваться услугами сервиса IQКлуб?

1. Зарегистрируйтесь в системе.
2. Ваш ребенок проходит несложный, но занимательный тест.
3. Специальный алгоритм оценивает способности вашего малыша.
4. Для вашего ребенка формируется индивидуальная программа обучения.

Все! Заниматься можно в любом месте, где есть доступ к сети Интернет. Развивающие игры на сайте предназначены для детей от 3 до 14 лет. 13 тысяч родителей уже сотрудничают с новым интернет-сервисом IQКлуб, который имеет в своем арсенале более 90 полезных игр.

Можно ли быстро научиться вычитать и делить без калькулятора?

Чтобы научиться считать быстрее калькулятора, надо лишь обогатить свой ум новыми шаблонами, в дополнение к уже имеющимся.

Павел Горбачев

Freepik

Например, вы быстро ответите на вопрос 10−5=?, потому что у вас в голове уже есть шаблон про это. Также вы сходу ответите на вопрос 55−5=?, ведь и тут все просто.

• Но, отвечая на вопрос 44−8=?, вам придется уже задуматься. Хотя можно представить число 44 как сумму 14+30, затем вы вычитаете из числа 14 число 8, получаете 6, и прибавляете к числу 30. То есть надо сложное число разделить на два более простых , одно из них вы мысленно откладываете по левую руку от себя, а со вторым числом проводите простое вычисление, чтобы результат прибавить к отложенному числу: 44−8=30+6=36

Точно так же можно производить расчеты и с трехзначными числами. Например, 138+176=? Вы разделяете первое число на сумму 130+8, а второе число на сумму 170+6. Откладываете мысленно слева от себя 130 и 170, которые уже легко складываются в число 300. Затем вы легко складываете 8+6=14, а затем складываете все полученные числа друг с другом: 300+14=314

Многие из нас хорошо помнят таблицу умножения, в том числе и двузначных чисел, поэтому вопрос о том, сколько будет 11х11=? не вызывает затруднений, ответ будет 121.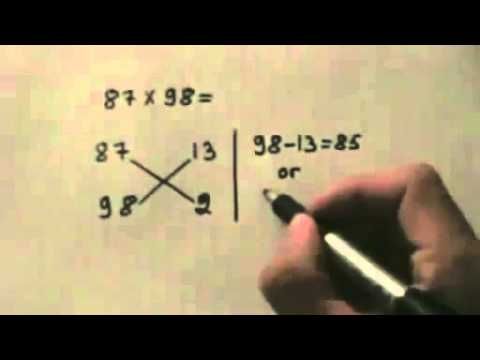

Также не сложно вспомнить, что 12х12=144. Но как быть, если двузначные числа иные?

• Давайте разберем пример, как можно легко умножать такие числа. Итак, 21х33=? Эти числа можно представить как 20+1 и 30+3. Теперь первую пару цифр нужно перемножить со второй парой цифр. Итак: 20х30=600, 20х3=60, 1х30=30, 1х3=3. И все полученные результаты надо сложить по порядку: 600+60+30+3=693

Потренировавшись на этом и легко манипулируя сначала двузначными цифрами в вычитании и сложении, а затем набив руку и отточив мозг в умножении трехзначных числе, можете переходить к делению двузначных и трехзначных чисел.

• При делении двузначных числе на двузначное важно сразу понять, что это число делится без остатка, то есть в результате получится только целое число, а не дробное. Например, 81:27=? В этом случае нам надо смотреть на вторые цифры в каждом числе, то есть на 1 и 7.   Теперь вспоминаем таблицу умножения и проверяем, в каком случае при умножении на 7 получается двузначное число с 1 на конце. Это число 3 (7х3=21). Оно и есть ответ: 81:27=3

• Этим же самым способом можно трехзначные числа легко делить на двузначные, но нам для этого надо удостовериться, что в результате получится однозначное число. Например, как узнать, какие трехзначные числа можно использовать для делителя в виде числа 29? Для этого надо число-делитель умножить на 10: 29х10=290 Все числа, которые меньше этого числа, можно разделить на 29. В любом случае ответ будет однозначным числом, то есть меньше 10 (хотя во многих случаях он будет дробным). Например, 145:29=? Смотрим на последние две цифры в трехзначном числе (45) и на вторую цифру в двузначном числе (9). Помним из таблицы умножения, что 5х9=45, и это число 5 и есть ответ: 145:29=5

Эти четыре простых правила позволят экономить время в простых расчетах и тренируют память, что позволяет ум оставаться гибким и цепким в любом возрасте.

Как делить на длинные числа в Mental Math – World Mental Calculation

Наиболее распространенный метод деления подходит только при делении на маленькие числа или при использовании ручки и бумаги. Умственный расчет более продвинутых делений требует другого метода.

Например, при использовании стандартного метода « деление на » для вычисления в уме 1829 ÷ 7,6543 нам потребуется вычислить кратные 7,6543, например 7,6543 × 3 = 22,9629, и вычесть каждое кратное из остатка, хранящегося в наша рабочая память.

Учитывая, что у всех людей ограниченная рабочая память, это становится неуправляемо трудным по мере увеличения объема вычислений.

К счастью, существует альтернативный метод , основанный на перекрестном умножении, который лишь умеренно нагружает нашу рабочую память и, следовательно, позволяет быстро делить числа произвольного размера с произвольной точностью. Вы можете использовать этот метод для вычисления 123 ÷ π с точностью до ста знаков после запятой, если хотите.

Я (пере)открыла для себя этот метод при подготовке в 2015 году к конкурсу Мемориада, и в этой статье я покажу вам, как это сделать самостоятельно.

Примечание: , когда достаточно оценки, а не многих цифр точности, тогда методы оценки более полезны.

 

Метод перекрестного деления

Чтобы решить 1829 ÷ 7,6543 методом перекрестного деления, мы сначала берем первые 1-2 цифры — в данном случае 76 — которые мы будем использовать для деления. Если ваш умственный расчет силен, вы должны использовать 2 цифры. Если для вас это очень сложно, при некоторых обстоятельствах вы можете использовать только 1 цифру (

7 ).

Цифры после 76 — в данном случае 543 — будут использоваться для шага перекрестного деления.

Масштаб

765,43 < 1829  < 7654,3 , поэтому ответ будет между 100 и 1000, а первые цифры будут стоять на месте сотен.

Первая цифра

Для получения каждой новой цифры ответа выполняем те же действия — делим текущее число на

76 , вычислив остаток , а затем вычтя некоторые дополнительные условия для учета 543 .

• Потому что 76 × 2 < 182 < 76 × 3 , первая цифра- 2 [Ответ 2 00-чем-то]
• Остаток равен 182 – ( 76 × 2 ) = 30
• Умножьте на 10 и добавьте следующую цифру от 1829 , что равно 9 , чтобы дать 309
• Поперечное деление: вычесть 309 –
  5 ×  2 = 299

[В следующем шаге я объясню, почему мы вычли 5 × 2 ]

Следующая цифра — с объяснением

Мы просто повторяем те же шаги для каждой новой цифры: 3 6 Потому что 76 × 3 < 299  < 76 × 4 , следующая цифра 3 [ответ 23 0-кое-что]

Остаток равен 299  – ( 76 × 3 ) = 71

Умножьте на 10 и добавьте следующую цифру от 1829 . 000…, что равно 0 , чтобы получить 710

Поперечное деление: вычесть 710 – 5 × 3 – 4 × 2  = 687

Вот как найти вычитание на шаге перекрестного деления:

• Начните со старшей цифры, на которую мы не делим — в данном случае это 5 из 543 , и умножьте это на самая новая цифра ответа — в данном случае это 3 из 23 0 с чем-то.
• Далее продолжайте по цифрам делителя, двигаясь к младшим значащим цифрам ( 4 , затем 3 ) в паре с цифрами ответа (пока только 2 ), продвигаясь к более старым цифрам. Итак, для этого примера у нас есть просто 4 × 2 , но позже у нас может быть больше вычитаний.
• Остановиться, когда либо в ответе больше нет цифр, либо все оставшиеся цифры в делителе равны 0. В этом случае в делителе есть еще одна ненулевая цифра ( 3 ), но нет более ранних цифр в ответ, так что мы уже остановимся.

Поначалу вам потребуется много практики, чтобы научиться разделению крестов, но оно довольно механическое.

Следующая цифра – пример с переполнением выпуска

Продолжение, как и раньше:

• , потому что 76 × < 687 , следующая цифра [Ответ 239 .SMATEL]
• Остаток равен 687  – ( 76 × 9 ) = 3
• Умножить на 10 и добавить следующую цифру от 1829 .000…, что равно 0 , чтобы получить 30
• Поперечное деление: вычесть 30 – 5 × 9 – …

Здесь у нас проблема, потому что ответ отрицательный! Когда это происходит, это означает, что мы должны были взять меньшее кратное 76 и допустить « неправильный » остаток, больший, чем 76 . Это редко, но случается, когда остаток ( 3 ) очень мал, поэтому с некоторым опытом вы сможете быстро обнаружить такие ситуации! Давайте попробуем:

• Попробуйте использовать 8 для следующей цифры [ответ: 238 .something]
• Остаток равен 687  – ( 76 × 8 ) = 79
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 790
• Поперечное деление: вычесть 790 – 5 × 8  – 4 × 3 – 3 × 2 = 732

Следующая цифра

Продолжение, как и раньше:

• Потому что 76 × < 732 , следующая цифра – [Ответ 238,9 …]
.
• Остаток равен 732  – ( 76 × 9 ) = 48
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 480
• Cross Division: Вычитание 480 – 5 × – 4 × 8 – 3 × 3 = 394

Следующая цифра

• Потому что 76 × 5 < 394 < 76 × 6 , следующая цифра 5 [Ответ 38.95 ]
.
• Остаток 394  – ( 76 × 5 ) = 14
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 140
• Cross Division: Вычитание 140 – 5 × 5 – 4 × – 3 × 8 = 55

Следующая цифра

• Потому что 55  < 76 × 1 , следующая цифра 0  [ответ 238,950 …]
• Остаток всего 55
• Умножьте на 10 и добавьте следующую цифру от 1829 . 000…, что равно 0 , чтобы получить 550
• Cross Division: Вычитание 550 – 5 × 0 – 4 × 5 – 3 × = 503

Следующая цифра

• Потому что 76 × 6 < 503 < 76 × 7 , следующая цифра – 6 [Ответ 238.9506 …]
• Остаток равен 503  – ( 76 × 6 ) = 47
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 470
• Поперечное деление: вычесть 470  – 5 × 6 – 4 × 0 – 3 × 5  =  425

И так далее, пока не будет достигнута требуемая точность.

 

Наглядный пример

Один из наших читателей представил наглядную иллюстрацию описанного выше метода с тем же примером. Спасибо Эльке Куге — коллеге-тренеру по умственным вычислениям в JMCWC и эксперту по Hectoc!

 

Советы и подсказки

Одноразрядные делители

Для новичков в ментальной арифметике лучше использовать одноразрядный делитель (например, 76,543 ), а не оставшийся шаг 06, чтобы упростить шаг 3 90.0. Однако это означает, что проблема с переполнением возникает гораздо чаще!

В этом случае 76 является хорошим приближением к 76.543 , поэтому проблема переполнения возникает редко. Но 7 0 намного дальше от 76.543 , так что у вас будут проблемы очень часто.

Поэтому я рекомендую как можно больше использовать двузначные делители.

Подсчет остатков

На первый взгляд, решение, например, 503 – ( 76 × 6 ) = 47 кажется очень сложным, как 76 × 6 = 456 – это сложно, а затем выполнять 503 – 456 без тоже сложно.

Тем не менее, более простой способ подумать об этом заключается в том, что 76 × 6 = 75 × 6 + еще 6 , так:

503 – ( 76 × 6 6. ) = ( 503 – 450 ) – 6 = 53 – 6 = 47

Разделение этих вычислений остатка в уме значительно облегчает такие вычисления.

Лучшие исполнители

Самые быстрые люди в мире могут вычислить с точностью до десяти цифр менее чем за одну минуту!

Обучение

Для начала предлагаю написать свои вопросы, разделив их на 4 или 5 цифр, но выбрав легкие первые две цифры. Например, 45,123 легко разделить, потому что 45 — это удобное число для умножения, а цифры 123 маленькие, поэтому вы, вероятно, автоматически избегаете проблем с переполнением.

Чтобы связаться со мной (Дэниелом Тиммсом) по поводу обучения умственным вычислениям, коучинга или чего-то еще на этом сайте, вы можете связаться со мной здесь.

Умственное деление больших чисел

Как разделить число путем разбиения

Чтобы разделить число путем разбиения, запишите число как сумму двух или более меньших чисел, которые можно точно разделить. Разделите эти числа, а затем сложите результаты, чтобы найти ответ.

Разбиение просто означает запись числа в виде двух или более меньших чисел, сложенных вместе.

Например, в 44 ÷ 2 44 можно записать как 40 + 4.

Мы решили разбить 44 на 40 и 4, потому что и 40, и 4 легко делятся на 2.

4 ÷ 2 = 2 и, следовательно, 40 ÷ 2 = 20.

Мы можем просто разделить цифры по одной.

44 ÷ 2 = 22

Обе цифры числа 44 можно просто разделить на 2, чтобы получить цифры ответа.

Число можно легко разделить в уме, если цифры можно сгруппировать в числа, которые делятся точно.

Например, вот 63 ÷ 3. Мы видим, что обе цифры 6 и 3 можно разделить на 3.

6 ÷ 3 = 2 и, следовательно, цифра десятков в ответе равна 2.

3 ÷ 3 = 1, значит, первая цифра ответа равна 1.

Цифры в числе можно точно разделить, а значит, это деление можно произвести в уме.

Если все цифры числа можно разделить точно, то деление можно выполнить, разделив каждую цифру по отдельности. Если это невозможно, можно сгруппировать цифры в числа, которые точно делятся.

Например, вот 128 ÷ 2.

Глядя на первую цифру, 1 не делится на 2 точно. Если первую цифру числа нельзя разделить точно, соедините ее со следующей цифрой и посмотрите, делится ли это новое число точно.

Первые две цифры числа 128 — 12. 12 можно разделить на 2.

12 ÷ 2 = 6, значит, в ответе 6 десятков.

Теперь осталось только разделить 8 на 2.

8 ÷ 2 = 4, значит, в ответе 4 единицы.

Последним шагом является объединение цифр ответа. 128 ÷ 2 = 64.

Вот еще один пример 105 ÷ 5.

1 не делится на 5, поэтому мы объединяем его со следующей цифрой, чтобы получить 10.

10 ÷ 5 = 2, значит, в ответе 2 десятка.

Оставшаяся цифра 5. 5 ÷ 5 = 1, значит, в ответе 1 единица.

105 ÷ 5 = 21

Стратегия разделения для подразделения

Стратегия разделения для деления — это метод, используемый для деления больших чисел путем записи их в виде суммы меньших чисел. Сначала разделите меньшие числа, а затем сложите результаты, чтобы найти ответ.

Стратегия разделения для разделения — это другое название разделения путем разделения. При обучении этим методам может быть полезно начать с разбиения чисел на десятки и единицы.

Например, 86 ÷ 2 можно записать как 80 + 6.

Так как 8 ÷ 2 = 4, 80 ÷ 2 = 40.

6 ÷ 2 = 3.

>

40 + 3 = 43 и так, 86 ÷ 2 = 43.

При использовании стратегии разделения не имеет значения, как разбивается номер. Например, мы могли бы записать 86 как 60 + 26.

Затем делим эти два числа. 60 ÷ 2 = 30 и 26 ÷ 2 = 13.

Складываем результаты так, чтобы 30 + 13 = 43. Мы все равно получаем тот же ответ.

Вот еще один пример 729 ÷ 9.

Мы можем разделить 729 на 720 + 9.

72 ÷ 9 = 8 и так, 720 ÷ 9 = 80.

9 ÷ 9 = 1.

80 + 1 = 81 и так, 729 ÷ 9 = 81.

Опять же, мы могли бы разделить 729 на любую другую комбинацию чисел, если они делятся на 9..

Например, 729 можно записать как 630 + 99.

630 ÷ 9 = 70 и 99 ÷ 9 = 11.

70 + 11 = 81 и так, ответ тот же.

Разделение путем разделения или стратегия разделения учит учащихся разбивать большие числа на управляемые фрагменты.