Как быстро решать примеры: Хотите быстро научиться считать в уме? 22 лучших способа!

10 СПОСОБОВ как БЫСТРО СЧИТАТЬ В УМЕ!

Способность мгновенно, легко и быстро считать – одна из определяющих вашего успеха. Мы научим вас считать в уме, как компьютер. Удивите скептических знакомых и вредных учителей!

Талантливый российский ученый Михайло Ломоносов, блиставший во многих научных областях, всегда считал математику своей любимой наукой, отлично приводящей в порядок ум. Современным людям в условиях ускоренных темпов жизни умение считать устно может здорово пригодиться.

Согласитесь, намного удобнее производить вычисления, не прибегая к помощи специальных устройств – это всегда экономия времени и денежных затрат. Более того, регулярные устные вычисления – отличная гимнастика для ума, а владение быстрым счетом обычно производит впечатление на тех, кто такой способности лишен.

Содержание

Научиться считать в уме просто!

Некоторые из нас прекрасно справляются устно с такими математическими операциями, как: умножение двузначных чисел на однозначные, нахождение произведения в пределах 20 и перемножение несложных двузначных чисел. Для кого-то подобные быстрые вычисления составляют определенную трудность, и таких людей большинство. Часто человека к этому вынуждают обстоятельства, когда без навыка быстро считать в уме не обойтись. Обычно это математики по образованию или те, кому ежедневно приходится производить ставшие уже привычными арифметические расчеты.

Разнообразные способности, которые заложены практически в каждом при рождении, нуждаются в развитии и постоянной тренировке. Однако не так часто встречаются отдельные личности, поражающие быстротой решения сложных примеров, состоящих из трехзначных чисел. Обычному человеку бывает сложно совершить подобные действия даже в письменном варианте.

Дотянуться до таких высот реально, если научиться применять определенные разработанные учеными методики быстрого счета в уме. Чтобы в будущем радоваться результату, поражать окружающих живостью мышления, а также с целью выработки навыка устных вычислений — важны следующие элементы:

1. Приобретенные способности
Большую роль играют хорошая концентрация внимания и одновременное запоминание нескольких фактов, врожденные математические наклонности и способность логически мыслить (выделять важное, обращая внимание на второстепенное, приходя к выводам и имея доказательства).

2. Знание математических алгоритмов
Понимание математических законов, эффективные схемы вычитания и умножения должны быть заложены в памяти как результат многократного опыта. Такие алгоритмы должны при необходимости «вспоминаться» и оперативно использоваться.

3. Опыт, полученный путем регулярных тренировок
На скорость и успешный результат устного счета влияет постоянная тренировка внимания и памяти, постепенно усложняющаяся для решения задач.

Феноменальные способности и знание определенных формул не будут эффективно действовать без регулярного применения на практике. Потому «тренируйтесь» регулярно.

Методика визуального представления

Производя устные вычисления, можно помочь себе, как бы мысленно записывая их в воздухе перед собой. Запоминание промежуточных результатов в представляемых образах намного облегчает задачу счета. Эффективность будет достигаться с практикой не без следующих важных условий и умений:

• Условие игры.  Когда изобретательные родители хотят от ребенка успешного и более быстрого выполнения какой-то скучной задачи, им достаточно превратить обычный ежедневный учебный процесс в игру. Результат такой «игры» будет потрясающим. Если попытаться отыскать что-то необычное в любом самом привычном действии (в решении математических примеров в том числе), то заниматься умножением будет гораздо проще и эффективнее. При этом не забывайте, что игра должна всегда быть увлекательной и пробуждать у ребенка желание возвращаться к ней снова и снова.
• Условие азарта. Чтобы во время игры не пропадала первоначальная увлеченность (азарт), важны ее установленные четкие правила.
• Условие соперничества. Занимаясь в одиночку, труднее достигнуть нужного эффекта, чем соревнуясь с достойными соперниками. Осознание того, что кто-то сможет сделать лучше, заставляет стремиться к новым достижениям. Упражнения в устном счете формате небольшого коллектива дают результаты на порядок выше, чем зубрежка в одиночестве.
• Условие фиксации личных достижений. Желание превзойти свои прежние достижения также толкает к новым вершинам. В связи с этим, фиксировать можно и скорость вычисления, и количество, и сложность примеров, решенных за определенную единицу времени.
• Умение справляться со скучной работой. Необходимо научиться нормально воспринимать скучную, однообразную работу. Психологи рекомендуют находить разные методы борьбы со скукой. Подойдет даже изучение событий за окошком или переключение внимание на движение часовой стрелки.
• Умение не воспринимать помехи.  Если приучить себя не отвлекаться на окружающие шумы и помехи, концентрация внимания намного повысится. Есть люди, которые привыкли выполнять задания различной сложности и в небольших густонаселенных шумных квартирах, и в общежитиях, где невозможно остаться одному. Они не обращают внимания на помехи и способны выполнять решать все задачи, что от них требуются. Тренировать такую способность можно, специально — пытаясь делать вычисления при включенной музыке, телевизоре, в шумной компании.

Существует такое особое состояние (транс), когда вошедший в него человек концентрируется на чем-то определенном и перестает отвлекаться на окружающую обстановку и даже на сигналы собственного организма. В трансе возможно сохранение самой неудобной позы в течение длительного промежутка времени. Человек, увлеченный интересным чтением или сёрфингом в интернете, может не заметить, как затекла нога или шея. Повышенное внимание к содержанию книги или интернетной статьи отвлекло от сигналов, подаваемых организмом.

Чтобы быстро справляться с устным счетом, нужно уметь пользоваться целым набором коротких, но эффективных математических правил. Решение более сложных примеров упроститься, если использование представленных ниже правил станет автоматическим, практически мгновенным.

Полезные арифметические правила:

1. Вычитание

+ При отнимании 9 от любого числа из него вычитают 10 и добавляют 1:
N-10+1
321-9 = 321-10+1 = 312

+ При отнимании 8 от любого числа из него вычитают 10 и добавляют 2:
N-10+2
321-8 = 321-10+2 = 313

+ При отнимании 7 от любого числа из него вычитают 10 и добавляют 3:
N-10+3
321-7 = 321-10+3 = 314

2. Умножение и деление

+ Любые числа умножаются на 9 легко и просто: следует умножить заданное число на 10 (или просто приписать ноль), а от полученного числа отнять исходное:
Nх9 = Nx10 – N
63х9 = 630 – 63 = 567

Это самый быстрый способ произвести подобные вычисления. Его рекомендуем довести до полного втомата.

+ Некруглые числа умножаются на 2 таким нехитрым способом:
сначала их округляют до удобных для умножения ближайших значений. Например, если необходимо посчитать 149х2, то проще для начала умножить 150 на 2, а после вычесть из результата 2 (1х2 = 2 – ведь это 1 не хватало нам до 150). Итого получаем пример:
149х2 = 150х2 — (1х2) = 298

+ По схожему принципу можно делить на 2 некруглые числа: округляется число, которое делят на 2, и из него вычитают. Делим это число на 2-ку, отнимаем 1 (последняя цифра получена в процессе деления прибавленной 2-ки на 2-ку.
В результате деление 198 на 2 равняется: 200:2 – 2:2 = 100 – 1 = 99!

+ Умножение, как и деление на 4 и 8, соответствуют двукратному и трехкратному умножению и делению на 2 в каждом случае конкретном случае. Действия производятся последовательно, например:
26х4 = 26х2х2 = 52х2 = 104
88/8 = 88/2/2/2 = 44/2/2 = 22/2 = 11

+ Математики вывели закономерность, по которой умножение на 5 практически приравнивается к делению на 2. Пример: 33х5 = 165, 33:2 = 16,5
Из этого следует, что при умножении на 5 любого из чисел, его стоит разделить на 2, а после этого умножить на 10:
68х5 = 68:2х10 = 34х10 = 340

+ Чтобы умножить какое-то число на 25, иногда проще его разделить на 4, а после увеличить в 100 раз (или приписать два нуля). Ведь умножение на 25 отчасти эквивалентно делению на 4:

8х25 = 8:4х100 = 200

+ Неслабые трудности при вычислениях в уме представляет умножение двузначных и трехзначных чисел на однозначные. Чтобы справиться и с этим, необходимо разряды многозначных чисел перемножать по очереди (начиная слева направо). При умножении 54 на 3 для начала перемножаем 5 и 3, дописывая ноль (учтем, что это разряд десятков). После этого складываем результат с произведением 4х3.
54х3 = 5х3х10+4х3 = 150+12 = 162

Попробуем умножить на однозначное трехразрядное число:
541х3 = 5х3х100+4х3х10+1х3 = 1500+120+3 = 1623

Прогнозирование конечного результата при счете в уме

В операциях умножения, особенно если приходится оперировать многозначными числами, можно легко сбиться с толку и ошибиться с результатом. Во избежание этого нужно грамотно «прогнозировать» ответ.

• Перемноженные между собой однозначные числа не дадут произведения, большего 81. Ведь 9х9 = 81.
• При умножении двузначных чисел конечный итог не превысит 10 000, так как 99х99 = 9801.
• Произведение двух трехзначных чисел не будет больше 1 000 000. Ведь 999х999 = 998001.
• Важно помнить деление 1000 на 2, 4, 8, 16. Всегда пригодится держать в голове результат деления чисел, кратных 10 и чисел, кратных 2: 1000 = 2х500 = 4х250 = 8х125 = 16х62,5.

Перечисленные выше формулы являются основными для устного счета. Преодоление трудностей со сложными примерами — в регулярных упражнениях. Доведение до автоматизма арифметических операций позволит вам решать просто неподъемные для обычного человека математические задачки. Восхищайте своими интеллектуальными способностями окружающих!

Как научить ребенка считать в уме: быстрый и проверенный способ

Несмотря на то, что в школе не требуют, чтобы к первому классу ребенок освоил навык устного счета, часть родителей стремится начать обучение как можно раньше. В каком возрасте ребенок должен считать в уме, с чего начинать обучение и какие методы обучения выбрать, «Газете.Ru» рассказали преподаватель математики и специалист по ментальной арифметике.

Умение хорошо и быстро считать не влияет напрямую ни на умственные способности, ни на способность к обучению школьным дисциплинам, объяснил преподаватель по математике и анализу данных Школы программистов МШП Дмитрий Коняев. Тем не менее, по мнению эксперта, такой навык крайне полезен и сильно облегчает жизнь, так что не будет лишним приобрести его уже в дошкольном возрасте.

«Устный счет можно сравнить с навыком скоростной печати на клавиатуре. Сам по себе этот навык почти ни на что не влияет, но облегчает жизнь каждый день, потому что в современном мире мы постоянно что-то печатаем. Также каждый день мы что-то считаем, и тянуться каждый раз за телефоном просто неудобно», – объяснил Коняев.

В каком возрасте ребенок должен считать в уме

«Оптимальный возраст для начала устного счета – от трех до пяти лет. Можно начать и раньше, если ребенок проявляет интерес к арифметике и довольно быстро осваивает навыки», – подчеркнул преподаватель математики и ментальной арифметики онлайн-школы «Коалиция» Арсений Кузнецов.

Преподаватель Коняев считает, что в среднем ребенок способен считать в уме уже с четырех лет. Однако, по его мнению, торопить события не стоит. «Если это произойдет позже — ничего страшного тут нет. Давить на неразвитый мыслительный аппарат гораздо хуже», – предупредил специалист.

Как научить ребенка складывать и вычитать

Как быстро научить ребенка считать

Изучение цифр, понятий сложения и вычитания дети, как правило, осваивают в дошкольном возрасте. ..

31 мая 19:54

Сложение и вычитание – базовые арифметические действия, которые дошкольник вполне способен освоить. Арсений Кузнецов советует на первых стадиях производить счет на пальцах, в игровой форме с палочками и картинками.

Дмитрий Коняев поддерживает коллегу в том, что в освоении счета взрослым стоит опираться на игровую механику. «Гуляя по улице, предлагайте ребенку посчитать котов/окна/машины/деревья. Это прекрасный способ вовлечь в игру и развить навык», – объяснил Коняев.

Понятия «больше» и «меньше» также поможет освоить практикоориентированный подход, так как, по мнению специалистов, дети лучше воспринимают информацию, которая проецируется на реальную жизнь. «Первое время можно объяснять на примере конфет, кубиков, раскладывая большее количество в правую сторону, меньшее – в левую. Так у ребенка возникнут ассоциации, что меньшее число всегда находится левее», – рассказал Кузнецов. Он отметил, что ребенка важно обучить последовательности счета, и тогда с крепким фундаментом знаний дошкольнику будет проще переходить на более высокие уровни сложности.

close

100%

Как научить ребенка решать примеры с переходом через десяток

«Дети начинают чувствовать себя растерянно, когда помимо привычных примеров, где ответ получается не более 10, появляются вычисления, выходящие за рамки первого десятка», – поделился наблюдениями преподаватель Кузнецов.

Эксперт посоветовал обратиться к самому комфортному и действенному методу обучения – рисованию схем. Это поможет развеять страх и продемонстрирует, что новые цифры учить не придется, так как все базируется на значениях от 0 до 9.

«При сложении с переходом через десяток нужно дополнять первое слагаемое до 10, а затем прибавлять оставшиеся единицы, – рассказал математик. – Пример: 9 + 7 = ? 9 + 1 + 6 = 16».

Объяснить это ребенку эксперт посоветовал следующим образом: для округления цифры 9 до десятки не хватает 1. Значит, из 7 вычитаем 1 и прибавляем эту единицу к 9, чтобы получить круглое число. После вычитания 1 из 7 осталась шестерка. К 10 прибавляем 6 и находим ответ.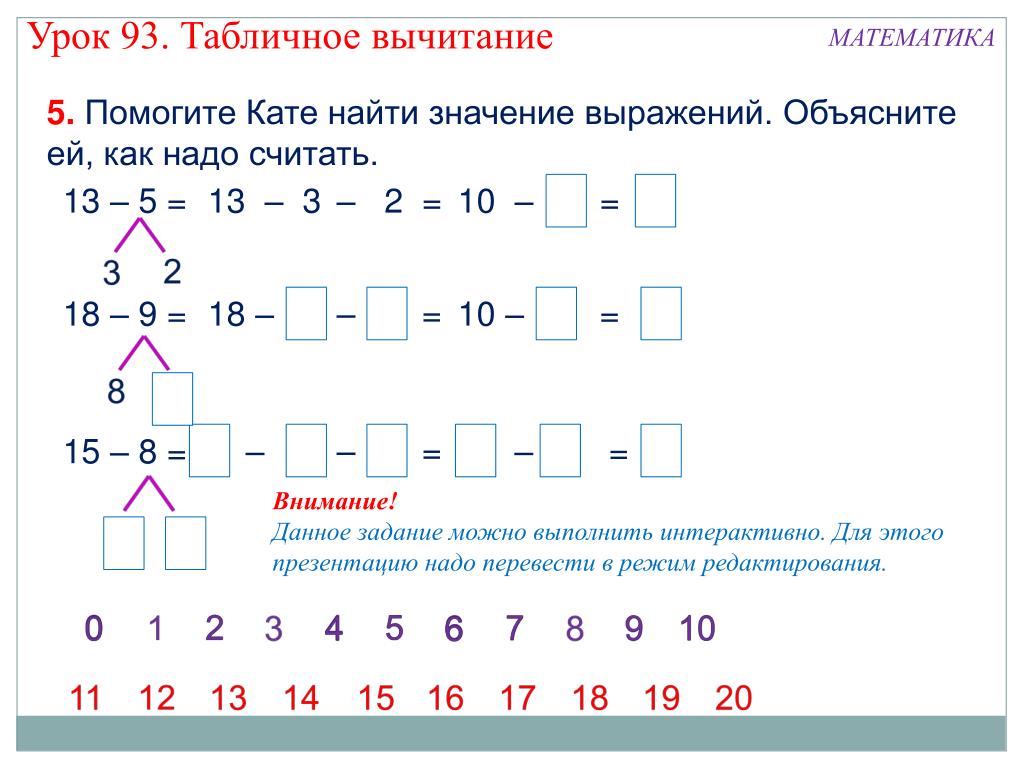

Как научить ребенка считать в уме двузначные числа

До перехода к устному счету необходимо отработать умение складывать и вычитать двузначные числа на бумаге. Эту задачу, по мнению преподавателя Коняева, стоит оставить школе.

Как научить ребенка читать: методики от опытного педагога

Ребенок, который научился читать в три года — гордость родителей. Но стоит ли торопить события и…

21 апреля 12:31

Если же родителям не терпится обучить ребенка этому навыку, то можно воспользоваться счетом в столбик. «Столбики дают наглядное представление о десятках и единицах, об операциях, производимых с ними. Когда ребенок начнет безошибочно проводить письменные вычисления, можно приступать к устным расчетам. Стоит начинать с круглых чисел, вычитать из них десятки, затем пятерки, а после усложнять примеры, добавляя в них разнообразия», – рассказал Арсений Кузнецов.

Специалист объяснил, что для освоения навыка дошкольнику может потребоваться больше времени, чтобы он научился представлять в уме ранее используемых столбцов, но занятия каждый день решат эту проблему.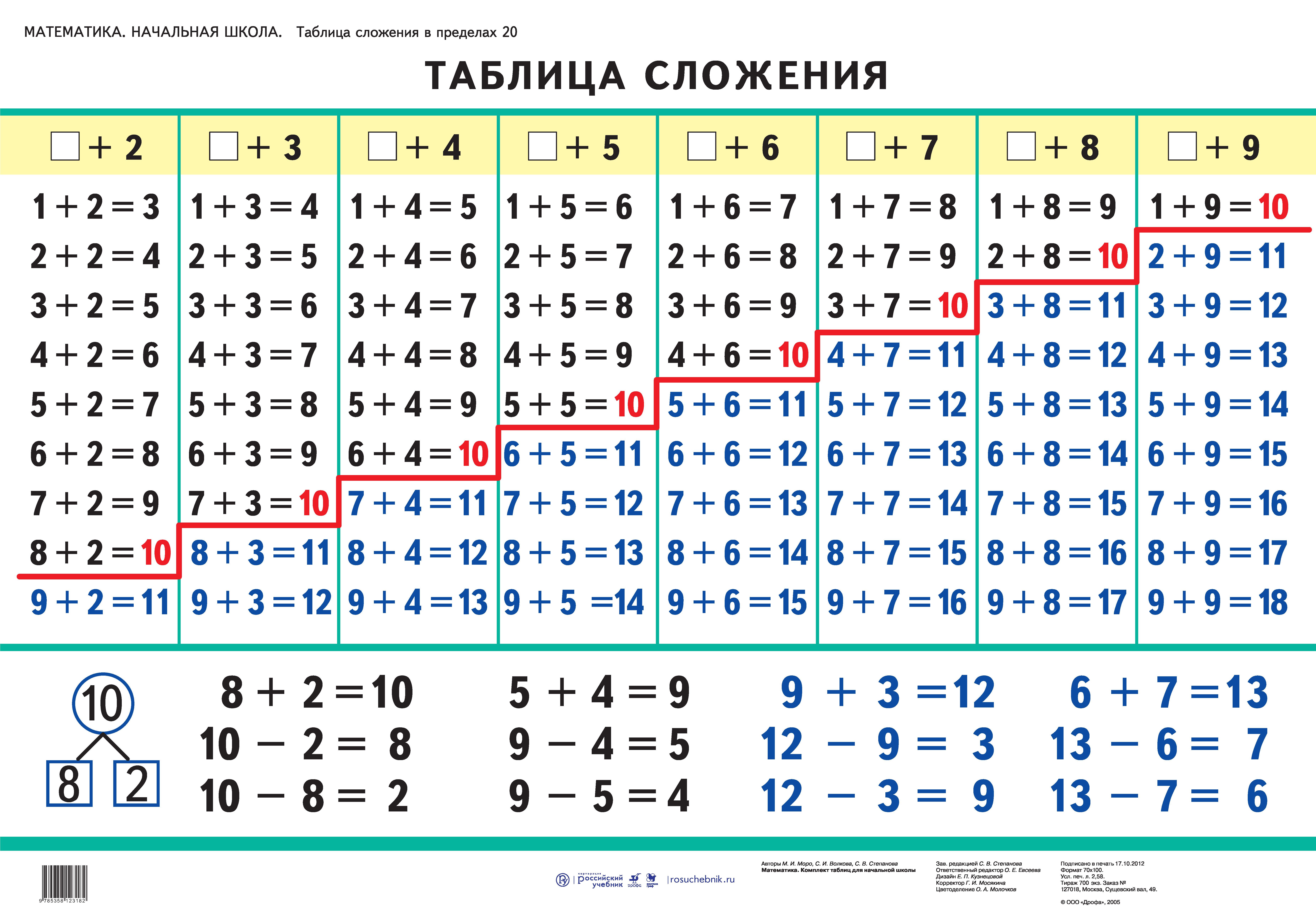

close

100%

Подходит ли ментальная арифметика для обучения быстрому счету

Школы ментальной арифметики сейчас есть почти в любом российском городе, поэтому родителей не может не интересовать вопрос, поможет ли этот метод ребенку научиться быстро считать в уме.

Математик Кузнецов порекомендовал осваивать этот метод тем, кто готов к немалому вложению энергии и времени. Также обучение потребует от дошкольника терпения. Но наградой за труды станет способность к высокой концентрации внимания, гибкость мышления и памяти.

«Ментальная арифметика направлена на развитие умственных способностей ребенка и мелкой моторики рук. За данной методикой обучения скрываются усиленные тренировки и упорство, ее освоение займет около двух лет и первое время будет сопряжено с неверными расчетами. Сдвиги в лучшую сторону начнутся после пары месяцев занятий», – отметил эксперт.

Он объяснил, что для освоения ментальной арифметики достаточно знать цифры от 0 до 9. Обучение протекает постепенно, и уровни сложности повышаются по мере прохождения предыдущих этапов.

3 хитрости для решения проблем быстрее и лучше

Вы когда-нибудь придумывали отличную идею для кого-то другого, но оказывались в тупике из-за собственной проблемы?

Недавнее исследование, проведенное Эваном Полманом из Нью-Йоркского университета и Кайлом Дж. Эмичем из Корнелла, может пролить свет на то, почему. В ходе трех серий экспериментов они обнаружили, что, когда люди решали проблемы от имени других, они находили более быстрые и творческие решения, чем когда они решали те же проблемы для себя.

В первом эксперименте Полман и Эмих попросили участников нарисовать инопланетянина для рассказа, который они собирались написать сами, или для рассказа кого-то другого. Инопланетяне, которых люди рисовали для других, были более творческими, чем те, которых они рисовали для себя.

Во втором исследовании участников попросили придумать идеи подарков для себя, для близкого или далекого человека. Результат: чем дальше получатель, тем оригинальнее подарок.

А в третьем исследовании участники должны были решить следующую задачу:

Заключенный пытался сбежать из башни. Он нашел в своей камере веревку, которой вдвое меньше, чтобы он мог безопасно спуститься на землю. Он разделил веревку пополам, связал две части вместе и сбежал. Как он мог это сделать?

Испытуемые с большей вероятностью придумывали ответ от имени другого человека, чем от себя; чем дальше предполагалось, что другой человек находится, тем больше вероятность того, что участники дадут правильный ответ.

Полман и Эмих говорят, что принцип работы — это то, что называется «теорией концептуального уровня», что, говоря простым языком, означает, что мы думаем более абстрактно о далеких проблемах (или проблемах, принадлежащих далеким людям) — и думаем более абстрактно. уровень дает более творческие решения.

Итак, учитывая, что мы часто более творчески подходим к решению чужих проблем, что мы можем сделать, чтобы более эффективно решать свои собственные? Вот три идеи:

1. Обменивайтесь проблемами с кем-нибудь. Если вы застряли, перестаньте копаться в проблеме и найдите коллегу, с которым можно было бы обменяться мнениями.

2. Решать проблемы от имени кого-то другого. Создайте некоторую психологическую дистанцию ​​от своего проекта, притворившись, что делаете это от имени кого-то другого. Здесь используйте свое воображение: «другой человек» может быть женщиной напротив, родственницей или незнакомцем на другом конце мира. Чем дальше, тем лучше.

3. Держите дистанцию ​​между собой и вашим проектом. Писатели знают, что происходит что-то волшебное, когда вы убираете рукопись в ящик стола. Когда вы возвращаетесь к ней через неделю, месяц или полгода, у вас появляется более свежий и творческий взгляд на работу. Когда есть возможность, внесите в свои дедлайны небольшой запас и постарайтесь убрать свою работу с глаз долой столько, сколько сможете.

Вы пробовали этот подход? Кто-нибудь создал веб-сайт, чтобы люди могли обмениваться проблемами? (Похоже на перспективное дело. ) И как, черт возьми, заключенный сбежал? Если у вас есть ответы, ответьте в разделе «Комментарии».

---

Как решать проблемы на работе

Содержание

Проблемы — это не что иное, как призыв к творчеству.

— Герхард Гшвандтнер

 

Вся жизнь — это решение проблем.

—Карл Поппер

 

Если подумать, большинство работ связано с решением проблем.

У клиентов или клиентов есть проблема, и бизнес и сотрудники должны ее решить.

Эти проблемы могут быть относительно простыми («Я голоден и мне нужно что-нибудь вкусное») или очень сложными («Я не знаю, что делать со своей жизнью, и мне нужен кто-то, кто меня научит»).

Где бы вы ни работали в будущем, знание того, как справляться с проблемами и решать их, сослужит вам хорошую службу.

На самом деле, решение проблем является одним из самых важных социальных навыков для многих работодателей, а это означает, что если вы отточите свою способность эффективно и разумно решать сложные проблемы, вам будет намного легче продвигаться по карьерной лестнице.

И если вы когда-нибудь планируете начать свой собственный бизнес, вам лучше поверить, что ваши навыки решения проблем вам пригодятся.

Вот в чем загвоздка: не существует единого метода решения проблем, который можно было бы применить к каждой проблеме, с которой вы столкнетесь на работе. Разные проблемы требуют разных решений.

В этой статье я собираюсь показать вам некоторые из наиболее распространенных методов решения проблем и то, как вы можете сразу же начать применять их в своей работе (или повседневной жизни).

 

1. Решение проблем с резиновыми утками

В разработке программного обеспечения отладка резиновых уточек или резиновых уточек — это метод отладки кода.

Название отсылает к истории из книги Прагматик-программист, , где программист носил с собой резиновую утку и отлаживал свой код, заставляя себя объяснять его утке строчка за строчкой.

Для этой техники существует много других терминов, часто связанных с различными неодушевленными предметами. Тем не менее, суть та же: потратить время на то, чтобы объяснить свою проблему вслух — резиновой утке, собаке или просто себе — это хороший способ увидеть проблему под новым углом и в конечном итоге решить ее. Если разговор вслух с самим собой не помогает, попробуйте подробно описать проблему.

Секрет в том, чтобы притормозить и обдумать проблему, прежде чем бежать к кому-то за решением.

Ваши будущие начальники будут любить вас за это. Когда вы сталкиваетесь с проблемой на работе, если вы работаете над ней и думаете о решениях, прежде чем сообщить о ней своему боссу, вы будете практиковать тонкое искусство управления. (Еще один отличный способ продвинуться по карьерной лестнице.) 

Важнейшая часть решения задач с резиновыми утками – это задавать подробные и подробные вопросы воображаемому человеку или неодушевленному предмету.

Попробуйте этот процесс: 

1. Подробно опишите проблему. Представьте, как бы вы объяснили проблему другу или коллеге. Пока не думайте о решениях — просто изложите проблему.

2. Объясните, что вы уже узнали. Предполагая, что вы уже изучили проблему, объясните все, что вы уже знаете, что повлияет на решение.

3. Перечислите вопросы, которые у вас остались. Теперь объясните неодушевленному предмету, где отсутствует информация — что разве вы не знаете или не понимаете, что мешает вам добраться до сути проблемы?

4. Объясните, почему некоторые решения не работают. Какие решения вашей проблемы можно исключить, потому что они не будут работать? Что вы уже пробовали и почему не получилось?

Теперь сделайте перерыв и вернитесь, чтобы прочитать свои записи. Если вы еще этого не сделали, вас, вероятно, поразят несколько идей (и, возможно, даже полные решения), о которых вы раньше не думали.

 

2. Латеральное мышление

Вот обычная головоломка, созданная в книге Шейна Сноу Smartcuts : 

«Представьте, что вы ведете машину в разгар грозы, и вдруг вы на трех человек на обочине дороги.

Одна из них – хрупкая старушка, которая выглядит на грани обморока. Еще один друг, который когда-то спас тебе жизнь. Другой — романтический интерес вашей мечты, и это уникальная возможность встретиться с ними.

У вас есть только одно место в машине.

Кого вы забираете?

Есть веская причина выбрать любой из трех.

Старушке нужна помощь.

Друг заслуживает твоей расплаты.

И очевидно, что счастливое будущее с человеком вашей мечты будет иметь огромное долгосрочное влияние на вашу жизнь.

Итак, кого выбрать?

[Драматическая пауза]

Старуха, конечно. Затем отдайте ключи от машины своему другу и оставайтесь с романтическим интересом, чтобы дождаться автобуса! »

Эта головоломка является одним из лучших примеров метода решения проблем, известного как латеральное мышление. Это причудливый термин для использования творческих, неожиданных решений проблемы, а не более традиционных и прагматичных методов.

Латеральное мышление может быть сложным, потому что оно требует от вас отбрасывания предположений (и не всегда легко узнать, когда вы сделали предположение).

Но если вы сможете это сделать, появятся новые решения проблемы, с которой вы столкнулись. В приведенном выше примере вы, возможно, предположили, что можете посадить в свою машину только одного человека или что только вы можете водить машину. Удалите эти предположения, и вдруг проблему станет намного легче увидеть.

Итак, как это применить на практике? Возьмем пример, связанный с работой.

Представьте, что ваш начальник поручил вам руководить проектом, который требует от вас координации встреч между отделом маркетинга и группой технической поддержки.

Но есть проблема: отдел маркетинга находится в Дубае, а отдел технической поддержки — в Далласе. В этих двух командах более 100 человек, и нет простого способа собрать их в одной комнате, не говоря уже о том же часовом поясе.

Эта проблема может показаться невозможной, пока вы не сделаете паузу и не рассмотрите некоторые из уже сделанных предположений:

Предположение 1: Встречи должны проводиться лично.

Предположение 2: Встречи должны проходить в прямом эфире.

Предположение 3: Все члены команды должны присутствовать на всех встречах.

Предположение 4: Эти встречи необходимы для завершения проекта.

Теперь возьмите каждое из этих предположений и посмотрите, что произойдет, если исключить их из уравнения.

Что было бы, если бы встречи проводились виртуально? Или с помощью программного обеспечения для совместной работы?

Не могли бы вы заранее записать некоторые из сессий, чтобы сократить количество совещаний?

Что, если бы ваша компания отправила нескольких представителей от каждой команды в центральное место, а не заставляла всех путешествовать?

Что, если бы вы вообще пропустили эти встречи, а вместо этого… 

Вы поняли. Чем больше предположений вы найдете в проблеме, подойдя к ней, тем больше решений вы сможете найти, пока не найдете правильное.

 

3. Метод проб и ошибок

До сих пор тактика из этого списка требовала от вас терпения и вдумчивости, но метод решения проблем, широко известный как метод проб и ошибок, гораздо более ориентирован на действия ( даже если это более утомительно и занимает много времени).

Применяя метод проб и ошибок, вы обязуетесь просто идти вперед и пробовать различные варианты решения любой конкретной проблемы. Когда один терпит неудачу, вы останавливаетесь и начинаете заново с другим вариантом.

Метод проб и ошибок невероятно распространен, и иногда вы можете использовать его, даже не осознавая этого. Например, давайте представим, что вы начинаете новую работу и пытаетесь найти наиболее эффективный способ добраться туда вовремя.

Первый день прогулки по парку…

На следующий день вы берете свой велосипед…

Затем вы пробуете автобусный маршрут… 

В конце концов, вы перепробовали все варианты (это испытание) и обнаружили, какие из них занимают слишком много времени (это ошибка).

Предупреждение: держитесь подальше от этого метода, если в вашей ситуации слишком много вариантов, потому что невозможно протестировать каждое отдельное решение. В зависимости от задачи метод проб и ошибок может быть либо самым быстрым, либо самым медленным способом сделать что-либо. Так что хорошенько подумайте, прежде чем решить, как именно вы хотите решить проблему.

Хотя метод проб и ошибок дает множество шансов найти решение, он не предназначен для того, чтобы понять, почему что-то работает определенным образом. При этом основная причина часто может проявиться, как только вы найдете правильное решение.

Так кто использует эту технику?

• Химики. Так они открывают новые лекарства, такие как антибиотики. Они просто пробуют химикаты случайным образом, пока не найдут тот, который дает желаемый эффект.
• Геймеры. Игроки в видеоигры часто используют метод проб и ошибок, чтобы добиться успеха в игре.
• Спортивные команды. Они используют его, чтобы пройти квалификацию и/или пройти через плей-офф и выиграть чемпионат, проверяя различные тактики — игры, составы и схемы — чтобы победить  всех на пути к победе. Это особенно важно в сериях плей-офф, в которых для продвижения требуется несколько побед. У команды, проигравшей игру, будет возможность попробовать новую тактику, чтобы найти способ победить, если она не вылетит.
• Ученые. Научный метод считается стратегией проб и ошибок, потому что ученые создают и проверяют гипотезы.

 

4. 5 «почему?» возможно.

Но есть причина, по которой маленькие дети постоянно спрашивают , почему . Они относительно новые здесь, на планете Земля, и есть МНОГО проблем, которые нужно понять и решить!

Вопрос «почему» — один из самых эффективных способов решить сложную проблему, и он даже превратился в официальную технику решения проблем, известную как «5 почему».

Концепция была первоначально разработана Сакичи Тойода для Toyota Industries Corporation, согласно отчету Азиатского банка развития.

В отличие от метода проб и ошибок, метод «5 почему» направлен на то, чтобы добраться до самой основной причины любой проблемы, чтобы вы могли решить ее раз и навсегда.