Как быстро умножать двузначные числа в уме картинки: Как быстро научиться умножать в уме двузначные числа? — Блог Викиум

Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.

Как умножить двузначное число на однозначное?

Начнем с простой задачи – как умножать двузначные числа на однозначные.

Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.

Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.

Умножение двузначных чисел на десятки

Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:

• Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
• Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
• Единственное, что отличает этот пример от предыдущего – в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.

Как перемножить два двузначных числа?

После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.

• Выписываем данные числа в столбец – единицы под единицами, десятки под десятками.
• Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.
• После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами – это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
• Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.

Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.

Как умножать в уме

Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.

Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм.

• Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
• Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.

Некоторые хитрости при умножении двузначных чисел

Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?

Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.

• При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.

Ставим 7 в середину, 374. Это и есть ответ.

Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.

• Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.

14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.

• Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
• Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.

Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.

Умножение в столбик позволяет быстро выдавать решение примеров даже с многозначными числами.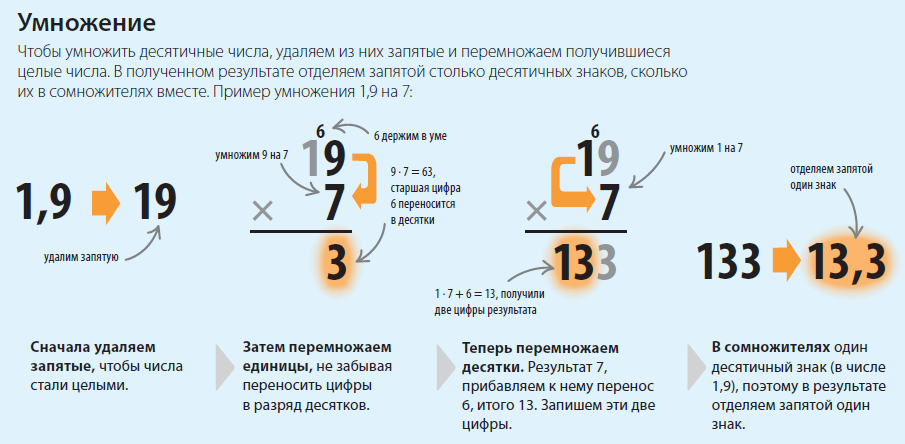 Для счёта нужно только знать наизусть таблицу умножения.

Как правильно умножать столбиком

Как и в случае со сложением и вычитанием в столбик, при умножении числа записываются друг под другом. Каждый разряд на своём месте: единицы под единицами, десятки под десятками и т. д. Внизу рисуется горизонтальная черта, ответ пишется под ней.

Возьмём числа 78 и 12. Для лучшего понимания: пишем 78 наверху, 12 – внизу. Начинаем с единицы нижнего числа, то есть с цифры 2.

Сперва считаем 8×2=16. Число получилось больше 10, значит, как и в сложении, пишем последнюю цифру (6), а единицу держим в уме. Теперь переходим к десятку, то есть считаем 7×2=14. Единицу мы держали в уме, значит, сейчас прибавляем её к результату, получается 14+1=15. Цифра 5 пишется под десятками, а 1 переходит в новый разряд – сотни. Другими словами, под горизонтальной чертой должно быть написано «156».

Переходим к следующему разряду. Теперь наш ответ будет записываться иначе: последняя цифра ответа должна быть ровно под верхними десятками, то есть под цифрой 5.

Считаем 8×1=8. Цифра меньше 10, пишем 8 под пятёркой в числе «156». Считаем 7×1=7. Семёрка переходит в разряд сотен, то есть она должна быть написана под единицей в ответе «156». Под шестёркой ничего не написано, для удобства туда можно поставить ноль.

Полученное выражение складываем в столбик: 156+78. К 6 ничего не прибавляется (0), значит, переписываем её в прежнем виде. Затем считаем 5+8=13, пишем 3, один в уме. Наконец, 1+7=8, прибавляем единицу – получается 9.

Таким образом, ответ: 936.

Тренироваться лучше на листе в клеточку, чтобы привыкнуть к расположению разрядов множителей

Точно так же умножаются и другие многозначные числа.

Если в множителях есть нули, они не перемножаются, а просто переносятся в правую часть окончательного ответа.

Варианты карточек

Для наглядности можно распечатать карточки с примерами разного уровня сложности. Так детям будет проще запомнить принцип счёта. Примеры для практики можно использовать и при первом изучении умножения, и для повторения после каникул.

Поначалу решение примеров будет занимать много времени, но постепенно скорость повысится. Даже при наличии калькулятора лучше считать вручную: это развивает умственную деятельность.

Фотогалерея: примеры карточек для урока

Видео: умножение чисел в столбик

Постоянная практика – залог успеха, и со временем можно научиться перемножать в уме даже большие числа. Но начинать, конечно, лучше с простых примеров, постепенно увеличивая уровень сложности.

Перемножать большие числа, записывая их в строку, рано или поздно становится довольно сложным и утомительным процессом. Гораздо проще воспользоваться специальным алгоритмом по умножению в столбик: вам не придется держать числа в своей голове и что-либо запоминать. Вы можете делать пометки над столбиком, чтобы всегда видеть, как числа вам нужно перенести. Если вы пытаетесь обучить такому способу ребенка, то очень важно, чтобы таблица умножения отскакивала у него от зубов, иначе, процесс затянется надолго, а сам малыш совершит много ошибок, которые вереницей потянутся по всему примеру. Внимательно прочитайте статью и возьмите такой алгоритм себе на вооружение.

Запишите пример по такому принципу, как указано на картинке ниже.

• Сверху напишите большее число.
• Слева поставьте знак умножения в виде крестика.
• Снизу запишите меньшее число.
• Проведите прямую черту под примером.

• Ноли нужно выносить за пример.
• Числа пишите под числами.

В таком случае, вы просто переносите это количество нолей сразу в ответ. Если ноли имеются и у первого множителя, и у второго, то сложите их количество и запишите в ответ.

• Всё верхнее число вы умножаете на последнюю цифру нижнего. Помните, что на последние ноли умножение не производится.
• Чтобы вам было удобнее, записывайте числа, которые нужно перенести, сверху над всем примером. Позднее вы можете их просто стереть, зато в процессе вам не придется запоминать числа переноса.
• Как только вы закончите расчет, запишите полученное число под чертой.

Как только вы перемножите верхнее число на последнюю цифру нижнего и запишите свой ответ, начинайте перемножать следующее.

Как вы уже догадались, вам нужно перемножить верхнее число на все цифры нижнего, начиная с конца. Каждый раз запись ответа переносится на одну клетку левее.

Перемножьте таким образом все числа между собой. Теперь снова проведите черту под столбиком. Между всеми решениями поставьте знак сложения.

• Складывайте все числа, находящиеся на одной вертикальной линии.
• Если число получается двухзначным, то число десятков вы переносите в следующую вертикальную полосу.

Под некоторыми числами вовсе не будет других – в таком случае, вы просто записываете это число в ответ. Не забывайте переносить в ответ все нули, которые стоят в конце множителей.

Выполнять умножение в столбик очень удобно и быстро, особенно, если требуется перемножить большие числа. Вы легко можете проверить правильность умножения, просто разделив ответ на один из множителей. Для этого используйте калькулятор, либо способ деления уголком. На первых порах такое умножение занимает значительную долю времени, но с опытом, всё действие происходит всего за пару секунд.

Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга. В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.

Первый способ – раскладка на десятки и единицы

Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Например: 63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 + 3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:

• Первое действие: 60*80 = 4800 – запоминаем
• Второе действие: 60*5+3*80 = 540 – запоминаем
• Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.

Второй способ – арифметические подгонки

Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:

Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.

Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.

Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.

Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.

Третий способ – мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик.

Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков

Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.

Второе действие: 56*6=300+36=336 (ну или 392-56)

Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.

Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.

Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.

«Мне не дали почивать на лаврах» – Огонек № 44 (5454) от 07.11.2016

“Огонек” поговорил с лауреатом Филдсовской премии — “Нобеля для математиков” — Григорием Маргулисом о его научной карьере, советской “кружковости” и американской открытости, а также о будущем математики

— В одном из интервью вы заметили, что математикой вас заинтересовал отец.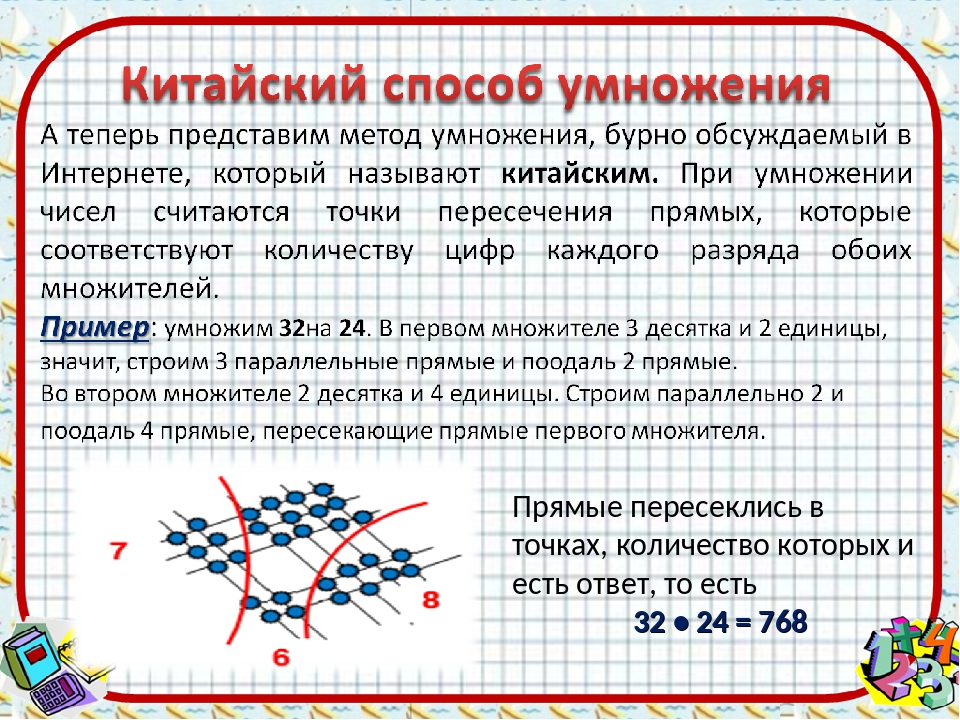 То есть любовь к этому предмету прививается не столько в школе, сколько в семье?

— Существует довольно много математических династий, так что для некоторых математиков — это действительно фамильное дело. В моем случае это так только частично. Папа был по образованию математик, и он защитил кандидатскую диссертацию по педагогике математики под руководством знаменитого математика Хинчина. После войны он работал доцентом на кафедре математики в различных московских и подмосковных вузах и продолжал интересоваться педагогикой, но не занимался научной работой в области теоретической математики. Папа вовремя заметил мои склонности: я с ранних лет умел умножать двузначные числа в уме, легко решал школьные задачки, причем, заметим, особых матшкол еще не было, я учился в обычной школе. В 7-м классе я стал ходить на так называемые математические кружки при мехмате МГУ, где и получил все необходимые мне навыки, исправно посещая кружковые занятия вплоть до 10-го класса. На кружках с нами занимались студенты и аспиранты мехмата, что создавало атмосферу доверительности — действительно атмосферу особого “ближнего круга”. Уже после появилась система физматшкол. Но, замечу, именно кружки первыми способствовали развитию математического сообщества в стране.

— При этом, будучи школьником, вы еще и очень серьезно увлекались шахматами. Почему оставили спорт?

— Математику, конечно, можно играть в шахматы, но после какого-то периода совмещать эти два занятия — науку и шахматы — чрезвычайно трудно. Одно отвлекает от другого и нужно делать выбор. Конечно, бывают исключения. Так, второй чемпион мира по шахматам Эммануил Ласкер был также известным математиком. Я же скоро после поступления в МГУ понял, что не могу серьезно заниматься и тем и другим.

— Зато спортивный темперамент, видимо, помогал вам хорошо выступать на Олимпиадах…

— Это интересная тема: достижения на Олимпиадах далеко не всегда отражают реальный уровень способностей человека. Мой учитель, лауреат премии Абеля, прославленный математик Яков Синай, например, так и не стал призером математических Олимпиад. Просто, чтобы победить на Олимпиаде, нужно иметь особый темперамент, уметь собраться и за 4-5 часов показать все, на что способен. В 1962 году я получил первую премию на Всесоюзной олимпиаде и благодаря этому попал на Международную математическую олимпиаду в Чехословакию, где оказался в числе призеров.

— А потом вы поступили в МГУ и попали в ученики к Синаю? Как вы выбирали научного руководителя?

— Может, не очень верится, но к человеку, с которым я знаком более 50 лет и который на меня очень сильно повлиял, я попал скорее по счастливому стечению обстоятельств. Мехмат МГУ тогда был очень творческим местом, и поощрялось всякое живое общение, самоорганизация, поэтому я посещал многие семинары, и очень многие люди на меня влияли, формировали математический кругозор. Пожалуй, в этом и есть секрет русской матшколы — в большом внимании к среде. На Западе все устроено несколько иначе: там у человека есть определенный научный руководитель, с ним плотно общаются, а вокруг мало смотрят. Нас-то как раз призывали смотреть вокруг, искать приложение своим талантам в разных областях математики. Научный руководитель поэтому был очень важным человеком, но, скажем так, не ограничивающим твой поиск.

— Уже в 20 лет вы написали свою первую научную работу. Такой ранний старт — это норма?

— Да, для русской школы вполне. Скажем, у математика Владимира Арнольда первая работа была опубликована еще в 19 лет, у Синая работы тоже начали появляться еще в студенческом возрасте. Замечу, что в мое время, чтобы поступить в аспирантуру в МГУ, нужно было, как правило, иметь опубликованную научную работу или, по крайней мере, работу, представленную к публикации. В США, конечно, система другая: диссертация там — это, как правило, первая научная работа, и она появляется, соответственно, в 26-27 лет.

— Вы предполагали, что то, чем вы занимались сначала в МГУ, а потом в Институте проблем передачи информации, заслуживает Филдсовской медали, которую еще называют “Нобелем для математиков”?

— Ну как предполагал. .. Были в окружении люди, которые говорили, что я, может быть, сделал что-то стоящее медали. Но нельзя же здесь быть уверенным. Потом за полгода до вручения награды мне сообщили, что она мне присуждена, но что официально об этом будет объявлено только во время международного математического конгресса в Хельсинки в августе 1978 года. Несмотря на присуждение Филдсовской медали, на лаврах мне не дали почивать. Так, в течение более 3 лет мою докторскую диссертацию не пропускали к защите на мехмате МГУ, пользуясь различными отговорками. Потом в конце концов я защитил докторскую в Белоруссии, в минском Институте математики. Так или иначе, на родине моя медаль вызвала резкое неудовольствие среди значительной части математического начальства.

— И ведь вам не дали ее получить?

— Да, меня не выпустили из страны в 1978 году. Нужно было получить характеристику от института, написать обоснование отъезда, потом идти в райком партии, потом в саму академию — в общем, существовал многоступенчатый отбор, на каждом этапе которого тебя могли отбраковать. В моем случае, по-видимому, “выбраковщиком” оказался национальный комитет советских математиков, который в то время возглавлял Виноградов. Было обидно, конечно, что не пустили. В 1979 году мне дали выехать в Западную Германию, в Бонн, на три месяца, как мне кажется, в качестве компенсации. Потом опять долго не выпускали на Запад. Только в 1987 году я оказался в Норвегии, но тогда уже и сама государственная система стала стремительно меняться.

— При такой оторванности от западного мира вам удавалось узнавать о его научных достижениях?

— Конечно, о многом мы знали. Но писать письма, поддерживать общение с заграничными коллегами — все это было очень трудно. Публикация статьи за границей считалась нежелательной и требовала специальных обоснований. За счет чего русская школа выживала? По моему мнению, просто в СССР было очень мало областей, куда талантливые молодые люди могли идти, чтобы сохранить себя и заниматься творчеством, и главные области — это, конечно, теоретическая физика и математика. При такой концентрации талантов в этих двух областях мы могли долгое время существовать за счет внутренних ресурсов. Заметим, экспериментальной физике требовалось большее участие государства для развития (что влекло за собой и больший контроль со стороны государства), и, думаю, именно поэтому она у нас оказалась слабее теоретической.

Я посещал многие семинары и очень многие люди на меня влияли, формировали математический кругозор. Пожалуй, в этом и есть секрет русской матшколы — в большом внимании к среде

— Зато в 90-х перед вами открылся целый мир…

— Да, в 1990-1991 годах мне почти одновременно сделали предложение стать профессором в Йельском университете, в Гарварде, в Принстоне и в Чикагском университете. Но в Йеле было больше математиков, которые интересовали меня в научном смысле, поэтому я выбрал его и до сих пор там работаю. Официально мой тогдашний отъезд воспринимался как командировка, и, пожалуй, я до сих пор нахожусь в командировке. .. Мне легко возвращаться в Москву. Это совсем не то ощущение, с которым уезжали ученые в 1970-е: тогда их проводы напоминали похороны, никто не ожидал повторной встречи. Сейчас повторные встречи возможны, я с удовольствием посещаю родной ИППИ РАН.

— У вас не было культурного или, скажем, научно-культурного барьера в общении с зарубежными коллегами, от которых вы до того были фактически изолированы?

— Сложности возникали, все-таки научная культура там немного другая. Потом, я на родине никогда не преподавал, а в Йеле пришлось читать лекции студентам, и мне нужно было к ним очень долго готовиться. Важно еще учесть, что американские студенты гораздо более требовательные, чем русские: если они чего-то не понимают, то считают, что это ты плохо преподаешь, а не они плохо понимают.

— Вы остались представителем русской школы математики, стали американским математиком или “математиком мира”?..

— Смотря что считать американской математикой. Скажем, в Йеле я был научным руководителем где-то у 20 аспирантов, и среди них вообще не нашлось американцев по рождению. Были люди из Ирана, Кореи, Франции, России, Швеции… Поэтому я бы назвал аспирантуру ведущих американских вузов не собственно американской, а аспирантурой мира — туда принимают лучших студентов отовсюду. В противовес русской школе, долго (и вынужденно) остававшейся закрытой, американская школа работала на полную открытость. Думаю, в США меня уже не считают русским математиком, потому что национальности там не играют большой роли, там все “неместные”. Потом, в США почти отсутствует понятие “школы такого-то математика”. В СССР всегда существовали живые сообщества учеников, объединенных вокруг своего учителя. На Западе такое редкость. Аспирант работает со своим научным руководителем, но, как я и говорил, мало заинтересован в образовании “кружков”. С одной стороны, это умаляет живое общение, с другой стороны, “кружковость” тоже склонна к вырождению. Скажем, были у какого-то выдающегося математика ученики, у этих учеников — свои ученики, но постепенно сообщество замыкается, люди со стороны не приходят, и творчество в “кружке” угасает.

— Вам приходилось объяснять, чем вы занимаетесь, гуманитариям?

— Нет, и не только гуманитариям, но и представителям других наук. Есть не так много представителей чистой математики, которые способны доходчиво объяснять внешним людям предмет своего научного интереса. Вероятно, Владимир Арнольд умел это делать лучше многих. А если говорить обо мне, то все получится очень общо и неконкретно. Скажем, группы Ли — многомерные объекты, которые меня интересуют,— связаны с областью дифференциальных уравнений и находят применение как в научно-технической сфере, то есть в computer science, так и в квантовой физике. Вообще лет 40 или 50 физики с математиками взаимодействовали мало, потому что считали современную им математику не очень интересной и релевантной. А вот в последние 20 лет взаимодействие между двумя науками усилилось, произошло даже слияние некоторых областей. И к подчас странным задумкам математиков, к тому, что называется general nonsense, вроде как ерундой, появилось больше терпимости. Наши открытия теперь часто интересуют коллег-физиков.

— То есть в математике есть классические, а есть и “странные” направления исследований? Может ли случиться, что специалисту будет “неудобно перед коллегами” заниматься какой-то проблемой?

— Вполне может. Скажем, Эндрю Уайлс 6 или 7 лет работал над доказательством так называемой последней теоремы Ферма, скрывая это от коллег, потому что заниматься таким безнадежным делом всем казалось не лучшим приложением сил. Математика все время развивается, есть мейнстрим, есть что-то периферийное. Плохо, когда приоритетные направления задаются начальством сверху, как часто случается в России, это давление блокирует возможность свободного поиска. Но и в США случаются конфликты, потакание общим интересам, рая же нигде нет. О спорах между учеными существует один популярный в нашей среде анекдот, состоящий из вопроса и ответа: “Почему академические конфликты такие ожесточенные? — Потому что ставки очень низкие”. Однако не эти будни определяют будущее математики. Оно все-таки всегда связано с творческим прорывом, который может случиться на любом из направлений, каким бы неожиданным оно ни казалось.

Беседовала Ольга Филина

Григорий Александрович Маргулис родился в 1946 году в Москве. В 1967 году окончил механико-математический факультет МГУ, под руководством Якова Синая защитил кандидатскую диссертацию по эргодической теории. Основная область научных интересов — теория групп Ли, за достижения в которой в 1978 году был удостоен премии Дж. Филдса. Защитил докторскую в минском Институте математики. Работал и продолжает работать в Институте проблем передачи информации им. Харкевича, однако в начале 90-х уехал на постоянное место жительства в США, став профессором Йельского университета. В 2001 году избрал членом Национальной академии наук США, с 2012 года — действительный член Американского математического общества.

* Интервью продолжает совместный медиапроект “Огонька” с Институтом проблем передачи информации им.  А.А. Харкевича РАН “Математические прогулки”. “Огонек” уже опубликовал беседы с математиками Михаилом Гельфандом (N 9), Юлием Ильяшенко (N 12), Александром Кулешовым (N 19), Андреем Соболевским (N 27), Александром Буфетовым (N 30-31), Никитой Введенской (N 40).

Как правильно сделать умножение столбиком. Умножение. Как быстро умножать двузначные числа в уме

Если вы уже запамятовали, как умножать цифры в столбик, то прочитайте статью. Тут вы найдете всю информацию об этом математическом действии.

Даже некоторые взрослые не освоили в школе, как можно умножать числа в столбик. А ведь это умение может и пригодиться в жизни, если не будет под рукой калькулятора или мобильного телефона.

Тем более, что это совсем не трудно, если вы знаете таблицу умножения и поняли, как правильно располагать цифры при данном процессе. Умножение в столбик всегда начинают изучать с умножения многозначного числа на однозначное, чтобы понять правила данного действия. Далее подробней.

Правила и алгоритм умножения в столбик

Математические занятия многим детям даются не с первого раза. Это непростая наука, требующая особого внимания, понимания. И ученикам в начальных классах в обязательном порядке необходима помощь мамы и папы в решении сложных примеров, задач. В частности нельзя все оставлять на самотеке, если ваше чадо не поняло, что такое умножение, деление чисел и т.п. Надо помочь разобраться в теме и выучить таблицу умножения, чтобы потом не получать плохие оценки, и не расстраиваться.

Освоить умножение в столбик будет легко, если:

• Школьник отлично знает таблицу умножения. Не путается в значениях произведения.
• Уяснил, в какой последовательности следует перемножать цифры многозначного числа.
• Ребенок понял, где их правильно писать. И умеет производить сложение многочленов в столбик.

Нужно знать, правило, что от перемены мест множителей произведение не меняется. Точнее, если умножить 56 ⋅ 2 = 112 и 2 ⋅ 56 = 112 — произведение будет 112.

ВАЖНО : Когда перемножают цифры в столбик. Под низом пишут то число, которое имеет меньше цифр в своем составе.

Как правильно умножать в столбик трехзначные числа на однозначные, двузначные, трехзначные

Любое умножение — это сложение одинаковых цифр необходимое количество раз. Точнее 725 ⋅ 2 = 725 + 725 = 1450. Но такой пример можно сделать устно, если второе число — 2,3,4. А если это — 8, то перемножать уже лучше в столбик. Для этого:

1. Вверху нужно написать цифру 725 , а внизу под цифрой — 5 написать число — 8 .
2. Теперь нужно поочередно, начиная с 5 , все значения трёхзначного числа перемножить на 8 .
3. Точнее: 5 ⋅ 8 = 40 (ноль пишем ниже под восьмеркой и пятеркой, а — 4 запоминаем ).
4. Далее умножаем: 2 ⋅ 8 = 16 (к 16 прибавляем — 4 = 20, опять 0 пишем, только уже под двойкой, а — 2 запоминаем ).
5. Остается умножить: 7 ⋅ 8 = 56 (к 56 прибавляем — 2 = 58, восьмерку пишем под семеркой, а пять впереди ).
6. В результате такого умножения (725 ⋅ 8 ) получатся — 5800 . И этот расчет получен вручную, без каких-либо машинок, калькуляторов.

Умножение в столбик — трехзначное на трехзначное

Умножить многочлен на многочлен несколько сложнее. Однако, если вы уже в первом примере уяснили, как происходит процесс, то вам не составит труда перемножить и трехзначные числа, а потом сложить в столбик, получившиеся значения.

Рассмотрим в подробностях, как умножить 125 на 32

1. Вверху на листке напишите трехзначное число 125, под ним 32, причем расположите его следующим образом: тройку под двойкой первого числа , а двойку второго под пятеркой первого числа — это очень важно.
2. Начните перемножать с конца. То есть: перемножьте все цифры трехзначного числа (125) вначале на двойку .
3. У вас получится 250 , ноль напишите под двойкой , остальные цифры впереди.
4. Далее перемножайте 125 на три . И располагайте на листике значение произведения (375 ), начиная с цифры — 3 .
5. Теперь остается сложить 250 и 375(0) , получится 250 + 3750 = 4000.

ВАЖНО : Как перемножить трёхзначные числа наглядно можно увидеть на рисунке выше. Цифры перемножаются в строгой последовательности, начиная с конца, а потом все получившиеся значения складываются.

Как правильно умножать в столбик числа с нулями?

Уже из математики начальных классов любой ученик знает, что, если умножить любое число на ноль, то произведение будет тоже 0. Именно поэтому, когда производится умножение в столбик, то на цифру ноль умножение не производится, его выносят за рамки, а в произведении приписывают ноль или несколько нулей — смотрите на изображении ниже.

Как объяснить ребенку умножение столбиком?

• Если вы дома решили провести урок по математике, изучить, как производить умножение в столбик, то превратите ваше занятие в игру.
• Постепенно, терпеливо объясняя, как это делается. Отвечайте на все вопросы школьника, чтобы ему было понятно, что и за чем делать.
• Дайте вначале для примеров несложные примеры, а потом уже выбирайте задания потруднее.

ВАЖНО : Уделяйте больше времени своим детям, не игнорируйте их просьбы о помощи. В школе учитель соблюдает программные требования. На закрепление материала дается не много времени. Поэтому не все школьники успевают освоить программу, тем более в таком сложном деле, как умножение, деление в столбик.

Видео: Примеры умножения многозначных чисел в столбик с пояснениями

Как умножать столбиком

Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.

Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить 846 на 5:

Умножить 846 на 5 – значит, сложить 5 чисел, каждое из которых равно 846. Для этого достаточно взять сначала 5 раз по 6 единиц, потом 5 раз по 4 десятка и наконец 5 раз по 8 сотен.

5 раз по 6 единиц = 30 единиц, т. е. 3 десятка. Пишем 0 под чертой на месте единиц, а 3 десятка запоминаем. Для удобства, чтобы не запоминать можно написать 3 над десятками множимого:

5 раз по 4 десятка = 20 десятков, прибавляем к ним ещё 3 десятка = 23 десятка, т. е. 2 сотни и 3 десятка. Пишем 3 десятка под чертой на месте десятков, а 2 сотни запоминаем:

5 раз по 8 сотен = 40 сотен, прибавляем к ним ещё 2 сотни = 42 сотни. Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:

Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить 3826 на 472:

Умножить 3826 на 472 – значит, сложить 472 одинаковых числа, каждое из которых равно 3826. Для этого надо сложить 3826 сначала 2 раза, потом 70 раз, потом 400 раз, т. е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.

2 раза по 3826 = 7652. Пишем полученное произведение под чертой:

Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением . Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.

Умножаем 3826 на 7. Это будет второе частичное произведение (26782):

Умножаем множимое на 4. Это будет третье частичное произведение (15304):

Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение (1 805 872):

Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:

Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.

Например, необходимо вычислить 23 000 · 4500. Сначала умножим 23 на 45, не обращая внимание на нули:

И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится 103 500 000.

Калькулятор умножения столбиком

Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку Вычислить.

Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.

Как умножить двузначное число на однозначное?

Начнем с простой задачи – как умножать двузначные числа на однозначные.

Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.

Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.

Умножение двузначных чисел на десятки

Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:

• Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
• Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
• Единственное, что отличает этот пример от предыдущего – в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.

Как перемножить два двузначных числа?

После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.

• Выписываем данные числа в столбец – единицы под единицами, десятки под десятками.
• Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.
• После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами – это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
• Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.

Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.

Как умножать в уме

Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.

Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.

• Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
• Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.

Некоторые хитрости при умножении двузначных чисел

Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?

Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.

• При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.

Ставим 7 в середину, 374. Это и есть ответ.

Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.

• Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.

14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.

• Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
• Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.

Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.

>> Урок 13. Умножение на трёхзначное число

Главная » Здоровье ребенка » Как правильно сделать умножение столбиком. Умножение. Как быстро умножать двузначные числа в уме

Способы быстрого устного умножения чисел

Некоторые способы быстрого устного умножения мы уже с Вами разобрали, теперь давайте подробнее разберемся, как быстро умножать числа в уме, используя различные вспомогательные способы. Некоторые способы Вы, возможно, уже знаете, а некоторые из них довольно экзотические, например, древний китайский способ умножения чисел.

Раскладка по разрядам

Является самым простым приемом быстрого умножения двухзначных чисел. Оба множителя нужно разбить на десятки и единицы, а затем все эти новые числа перемножить друг на друга.

Данный способ требует умения удерживать в памяти одновременно до четырех чисел, и делать с этими числами вычисления.

К примеру, нужно перемножить числа 38 и 56. Делаем это следующим образом:

38 * 56 = (30 + 8 ) * (50 + 6) = 30 * 50 + 8 * 50 + 30 * 6 + 8 * 6 = 1500 + 400 + 180 + 48 = 2128 Еще проще будет делать устное умножение двухзначных чисел в три действия. Сначала нужно перемножить десятки, затем прибавить два произведения единиц на десятки, и затем прибавить произведение единиц на единицы. Выглядит это так: 38 * 56 = (30 + 8 ) * (50 + 6) = 30 * 50 + (8 * 50 + 30 * 6) + 8 * 6 = 1500 + 580 + 48 = 2128 Для того, чтобы успешно пользоваться этим способом, нужно хорошо знать таблицу умножения, уметь быстро складывать двухзначные и трехзначные числа, и переключаться между математическими действиями, не забывая промежуточные результаты. Последнее умение достигается с помощью тренировки зрительной памяти и визуализации.

Данный способ не самый быстрый и эффективный, потому стоит изучить еще и другие способы устного умножения.

Подгонка чисел

Можно попробовать привести арифметическое вычисление к более удобному виду. Например, произведение чисел 35 и 49 можно себе представить таким образом: 35 * 49 = (35 * 100) / 2 — 35 = 1715
Этот способ может оказаться более эффективным, чем предыдущий, но он не универсальный, и подходит не ко всем случаям. Не всегда можно найти подходящий алгоритм для упрощения задачи.

На эту тему вспомнился анекдот про то, как математик проплывал по реке мимо фермы, и заявил собеседникам, что ему удалось быстро подсчитать количество овец в загоне, 1358 овец. Когда его спросили, как ему это удалось, он сказал, что все просто — нужно подсчитать количество ног, и разделить на 4.

Визуализация умножения в столбик

Этот один из самых универсальных способов устного умножения чисел, развивающий пространственное воображение и память. Для начала следует научиться умножать в столбик в уме двухзначные числа на однозначные. После этого Вы легко сможете умножать двухзначные числа в три действия. Сначала двухзначное число нужно умножить на десятки другого числа, затем умножить на единицы другого числа, и после этого просуммировать полученные числа.

Выглядит это таким образом: 38 * 56 = (38 * 5) * 10 + 38 * 6 = 1900 + 228 = 2128

Визуализация с расстановкой чисел

Очень интересный способ перемножения двухзначных чисел следующий. Нужно последовательно перемножить цифры в числах, чтобы получились сотни, единицы и десятки.

Допустим, Вам нужно умножить 35 на 49.

Сначала перемножаете 3 на 4, получаете 12, затем 5 и 9, получаете 45. Записываете 12 и 5 , с пробелом между ними, а 4 запоминаете.

Получаете: 12 __ 5 (запоминаете 4).

Теперь умножаете 3 на 9, и 5 на 4, и суммируете: 3 * 9 + 5 * 4 = 27 + 20 = 47.

Теперь нужно к 47 прибавить 4, которое мы запомнили. Получаем 51.

Пишем 1 в середине, а 5 прибавляем к 12, получаем 17.

Итого, число, которое мы искали, 1715, оно является ответом:

35 * 49 = 1715
Попробуйте таким же образом перемножить в уме: 18 * 34, 45 * 91, 31 * 52.

Китайское, или японское, умножение

В азиатских странах принято умножать числа не в столбик, а рисуя линии. Для восточных культур важно стремление к созерцанию, и визуализации, поэтому, наверное, они и придумали такой красивый метод, позволяющий перемножать любые числа. Сложен этот способ только на первый взгляд. На самом деле, большая наглядность позволяет использовать этот способ гораздо эффективнее, чем умножение в столбик.

Кроме того, знание этого древнего восточного етода повышает Вашу эрудицию. Согласитесь, не каждый может похвастаться тем, что знает древнюю систему умножения, которой китайцы пользовались еще 3000 лет назад.

Видео о том, как китайцы перемножают числа

Более подробные сведения Вы можете получить в разделах “Все курсы” и “Полезности”, в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.

Также Вы можете подписаться на блог, и узнавать о всех новых статьях.
Это не займет много времени. Просто нажмите на ссылку ниже:
    Подписаться на блог: Дорога к Бизнесу за Компьютером

Проголосуйте и поделитесь с друзьями анонсом статьи на Facebook:  

Как научить ребёнка считать в уме? . Ментальная арифметика: обучение ребенка устному счету с помощью абакуса

Не секрет, что ключевые навыки, определяющие успех детей в будущем, закладываются в дошкольном возрасте и в начальных классах. В мире, где всё решают цифры, а решения оцениваются через призму данных, пожалуй, нет лучших навыков, чем умение быстро считать в уме и анализировать. Как научить ребенка устному счету и сохранить навык быстрого счета на всю жизнь?

Научить ребёнка считать в уме — это целая наука, однако ничто не поможет ему в будущем больше. Родители могут поинтересоваться: а стоит ли заставлять ребёнка учиться устному счёту в уме, если он сам этого не просит или не осознаёт такой необходимости?

На мой взгляд — стоит. Умение считать в уме поможет ребёнку со временем покорить любые высоты в учёбе или творчестве, поскольку ничто не развивает оба полушария мозга лучше. Данная способность стимулирует работу всего мозга в процессе обучения и усвоения материала. Дети преуспевают в арифметике и других предметах, поскольку у них значительно увеличивается память, а также способность к восприятию информации.

Обучение счету: с чего начать?

Интерес к счёту в уме просыпается у детей рано, ещё в дошкольном возрасте, и его нужно продолжать подпитывать, чтобы он не угас. Его можно стимулировать через различные обучающие игры: начать с простого пересчёта игрушек, а в начальных классах сфокусироваться на таблице умножения, или же по мере прогресса перейти на изучение ментальной арифметики.

В самом начале пути и ещё до школьной скамьи, нужно учить ребёнка считать в пределах 10, дальше уже переходить к счёту двузначных цифр. Для обучения можно использовать картинки, игрушки или другие однородные предметы, которые бы откладывались в памяти у ребёнка и помогали бы ему в дальнейшем.

Однако при обучении ребёнка важно контролировать, чтобы он не считал с помощью пальцев или палочек. Освоить этот способ легко, а чтобы отучиться он него, потребуются усилия, поскольку механизм памяти задействован не будет. Это так же, как и с калькулятором: люди, которые привыкли на нём считать, впоследствии тяжело отучаются, а способности считать в уме в результате страдают.

Выучили таблицу умножения — что дальше?

Все мы когда-то учили таблицу умножения в начальных классах. Это опыт, который был одним из самых ранних примеров счёта в уме. В результате почти все пользуются навыками умножения, которые выучили в детстве, до сих пор. Нужно ли посчитать что-то на работе или в магазине — таблица умножения незамедлительно всплывает в нашей памяти.

Учить таблицу умножения можно по-разному. Можно прибегнуть к тому же способу пересчёта игрушек или картинок, можно нарисовать примеры и демонстрировать ответы на обратной стороне. Обучение также должно вызывать положительные эмоции и не должно идти из-под палки.

Но не стоит останавливаться на одной лишь таблице умножения — есть ещё более интересные способы развить способность считать в уме. Когда таблица умножения освоена, можно переходить на следующую ступень — ментальную арифметику.

Представьте, что вместо привычных «дважды два» или «девятью девять» ваш ребёнок со временем сможет с лёгкостью перемножать двузначные или даже трёхзначные числа. Я уже давно обучаю детей по данной методике, и для меня важнее всего видеть, как дети со временем преуспевают в школах и в кружках, а также превосходят своих сверстников.

Что такое ментальная арифметика

Для многих в нашей стране ментальная арифметика остаётся чем-то новым и пока неизведанным. Однако она существует тысячи лет, а сегодня широко практикуется в странах Азии и Западной Европы. Данная методика примечательна тем, что стимулирует развитие качества и скорости мышления посредством арифметического счёта в уме и тем самым улучшает работу обоих полушарий мозга.

Математика — наука, которая сложно даётся некоторым детям отчасти из-за абстрактности передаваемой информации. Многие не могут что-то посчитать, пока не представят или не увидят предметы счёта. Ментальная же арифметика, как и любое обучение устному счёту, разрешает данную проблему благодаря использованию «абакуса» (счётов), который позволяют детям «прочувствовать» числа.

Таким образом, методика учитывает особенности восприятия детей и позволяет многим развить навыки, которые зачастую невозможно получить в школах.

На занятиях по ментальной арифметике дети изначально осваивают четыре основные арифметические операции: вычитание и сложение, деление и умножение. По мере продвижения многие учатся выполнять операции с дробями, возводить в квадрат, извлекать квадратный корень и даже комбинировать в уме.

Учить ментальной арифметике не так сложно: как только ребёнок начинает представлять абак в уме, сразу же начинают проявляться его арифметические способности. После закрепления основ у детей постепенно ослабевает привязка к счётам, что позитивно влияет на развитие интеллектуальных способностей. Дети начинают представлять графические счёты в уме, подобно рисунку. Потом — воображать, как двигают косточки «абакуса», в результате чего появляются ответы.

Ментальная арифметика

Лидирующей компанией в мире по обучению ментальной арифметике на данный момент является ALOHA, которая расшифровывается как «Abacus Learning Of Higher Arithmetic» (обучение высшей арифметике с помощью «абакуса»). Организация является основоположником обучения ментальной арифметике во всём мире и совсем недавно открыла представительство в России, а многие методики, накопленные за почти четверть века работы, представлены в открытом доступе в интернете.

Возраст начала обучения, как правило, начинается с пяти лет и обусловлен тем, что дети уже способны считать, понимают значение чисел от 0 до 9 и определяют большее и меньшее число. Начав же изучение ментальной арифметики в возрасте 13 лет, ученики после двух-трех лет достигают пика обучаемости.

Как быстро умножать большие числа без калькулятора 06.

06 марта 2017, 14:18

Эта техника поможет сдать ВНО по математике

На ВНО по математике запрещено пользоваться калькулятором, и если вам нужно быстро умножить большие числа, не тратьте время на то, чтобы высчитывать результат в столбик.

При умножении двузначных чисел ответ будет четырехзначным. Пример – 99 х 83. Ваши действия:

1. Начертите таблицу из 4-х клеток
2. От 100 отнимаем число, дающее первый множитель: в нашем случае 100 – 1 = 99.
3. От 100 отнимаем число, дающее второй множитель: у нас 100 – 17 = 83.
4. От первого множителя (у нас – 99) отнимаем число, которого не хватало до 100 второму множителю (у нас – 17): 99 – 17 = 82. Либо от второго множителя (у нас 83) – число, не достающее до 100 первому множителю (у нас – 1): 83 – 1 = 82. Учтите, что результаты обоих путей вычисления должен совпадать.
5. Полученный результат (у нас – 82) запишите в первые две клетки.
6. Умножаем числа, недостающие до 100 обоим множителям (у нас – 1 и 17): 1 х 17 = 17 и записываем полученное число в третью и четвертую клетку соответственно.
7. Итого получаем, что 99 х 83 = 8217.

Если перемножать необходимо трехзначные числа и выше, то, во-первых, количество клеток в таблице должно быть равно сумме цифр обоих множителей, во-вторых – результат, полученный в действии № 6 записываем с конца таблицы. А если между результатом из действий № 5 и № 6 остаются пустые клетки, в них выписываем нули. Обратите внимание, что в пункте № 2 для трехзначных множителей и выше вычитать необходимо из числа, в котором на один ноль больше: для трёхзначных из 1000, четырехзначных – из 10000, из пятизначных – из 100000, шестизначных – из миллиона и т.д.

Пример – 999973 х 999990

1. Клеток чертим 12 (6-значный первый множитель и 6-значный второй множитель).
2. 1000000 – 27 = 999973.
3. 1000000 – 10 = 999990.
4. 999973 – 10 = 999963 или 999990 – 27 = 999963.
5. Записываем полученный результат в действии № 4 в первые клетки таблицы (в нашем примере – в первые шесть).
6. 10 х 27 = 270. Записываем этот результат в последние три клетки таблицы.
7. В действии № 4 мы получили шестизначное число, а в действии № 6 – трехзначное. Но наша таблица состоит из 12 клеток. То есть клетки 7-9 – пусты, а значит в них мы должны вписать ноли.
8. Итого получаем, что 999973 х 999990 = 999963000270.

3 НОМЕР: ЧТО ЕСТЬ ЗНАТЬ? | Сложим: помощь детям в изучении математики

Бер, М.Дж., Харел, Г., Пост, Т., и Леш, Р. (1992). Рациональное число, соотношение и пропорция. В D.A.Grouws (Ed.), Справочник по исследованиям по преподаванию и изучению математики (стр. 296–333). Нью-Йорк: Макмиллан.

Bruner, J.S. (1966). К теории обучения . Кембридж, Массачусетс: Belknap Press.

Куоко, А.(Ред.). (2001). Роли представления в школьной математике (Ежегодник Национального совета учителей математики 2001 г.). Рестон, Вирджиния: NCTM.

Дюваль Р. (1999). Представление, видение и визуализация: когнитивные функции в математическом мышлении. Основные вопросы для обучения. В F.Hitt & M.Santos (Eds.), Proceedings of the двадцать первого ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (т.1. С. 3–26). Колумбус, Огайо: Информационный центр ERIC по естествознанию, математике и экологическому образованию. (Служба размножения документов ERIC № ED 433 998).

Фройденталь, Х. (1983). Дидактическая феноменология математических структур . Дордрехт, Нидерланды: Рейдел.

Грино, Дж. Г., и Холл, Р. (1997). Практика репрезентации: изучение репрезентативных форм и о них. Дельта Фи Каппан , 78 , 1–24.Доступно: http://www.pdkintl.org/kappan/kgreeno.htm. [10 июля 2001 г.].

Капут,]. (1987). Системы представлений и математика. В C.Janvier (Ed.), Проблемы представления в преподавании и изучении математики (стр. 19–26). Хиллсдейл, Нью-Джерси: Эрлбаум.

Knuth, D.E. (1974). Информатика и ее отношение к математике. Американский математический ежемесячник , 81 , 323–343.

Лакофф, Г., & Núñez, R.E. (1997). Метафорическая структура математики: наброски когнитивных основ математики, основанной на разуме. В L.D.English (Ed.), Математическое рассуждение: аналогии, метафоры и изображения (стр. 21–89). Махва, Нью-Джерси: Эрлбаум.

Морроу, Л.Дж., и Кенни, М.Дж. (ред.). (1998). Преподавание и изучение алгоритмов в школьной математике (Ежегодник Национального совета учителей математики 1998 г.). Рестон, Вирджиния: NCTM.

Пимм, Д.(1995). Символы и значения в школьной математике . Лондон: Рутледж.

Рассел Б. (1919). Введение в математическую философию . Нью-Йорк: Макмиллан.

Сфард А. (1997). Комментарий: О метафорических корнях концептуального роста. В L.D. English (Ed.), Математические рассуждения: аналогии, метафоры и изображения (стр. 339–371). Махва, Нью-Джерси: Эрлбаум.

2-й и 3-й классы Построение двузначного числа – мышление 101

Grade 2 & Grade 3 Двухзначное число

Значение числа для 2- и 3-значного числа ничем не отличается от значения для числа до 10.

• Определите количество и выразите несколько способов с помощью единиц разряда

слов, единицы умножения, расширенные выражения, карты расширения, блоки до 100 сеток в числовые строки. ОСТАНОВИТЕ картинки счетчиков и кругов. Создавайте образы, которые связаны с числами, чтобы учащиеся могли использовать выражения. ДОБАВИТЕЛЬНАЯ КОМПОЗИЦИЯ, для начала сосредоточьтесь только на частях внутри целого.

записывать выражения и соединять выражения несколькими способами. Появляются ассоциативные и коммутативные свойства.

Насколько близко к? Как далеко от? Относитесь к другим числам.Используйте ссылки на декады (кратные 5 и 10), 50 и 100 и язык более, чем, чем, между, рядом, около. Растяните модели площадей на числовые линии. СРАВНИТЬ

понять взаимосвязь и как ее записать, используя знаки сложения и вычитания. Недостающие части можно объяснить, если у вас есть твердое ощущение чисел. Используйте сетку и объясните пространство. Используйте числовую прямую и объясните расстояния между ними.

Книги о двухзначных и трехзначных числах содержат мастеров черной линии и вспомогательные страницы, которые помогут вам разработать индивидуальные и целые занятия в классе. Заказываются отдельно. Просто укажите, что вы хотите, в электронном письме на адрес [email protected].

Деки цветные, ламинированные. Ваша стоимость 12 долларов за колоду. Двухзначная книга стоит 39,99 долларов, а трехзначная книга – 29,99 долларов. Я принимаю Visa, электронный перевод и школьный заказ на покупку или личные чеки.

Возьмите за привычку составлять списки выражений по мере того, как учащиеся объясняют то, что они видят, а затем поощряйте учащихся искать закономерности в списках, чтобы сосредоточиться на организации данных.

Страница ниже предназначена для предоставления вам руководства при работе с двузначным числом. Здесь есть еще несколько страниц с пояснениями. СТО СЕТКА Раздача апрель 2018.

Это часть буклета, который я разрабатываю. Пожалуйста, уважайте мои авторские права и не воспроизводите для других .. Спасибо.

Загрузите лист выше здесь.

ЗНАЧЕНИЕ НОМЕРОВ СТРОК

Я перемещаю студентов между моделями площадей (сетками) и числовыми линиями.Цель состоит в том, чтобы поддержать их в развитии умственных способностей для манипулирования числовыми композициями и управления ими в своем воображении. Другими словами, цель – отойти от рисования и письма к эффективному выражению своих мыслей на бумаге. Если можете сложить, используйте это для вычитания. Все, что вам действительно нужно, это бумага, чтобы не сбиться с пути.

Числовая линия не является волшебной и не заслуживает особых отметок. Это инструмент для развития здравого смысла числа и точности вычислений.

Примеры, представленные ниже, являются мыслителями 2-го класса, решающими задачи, состоящие из двухзначных чисел. Это мышление развилось из понимания образов сетки.

Нравится:

Нравится Загрузка…

Японский ученый-преподаватель начальных классов учит нас, как решить сложный математический недостаток

Урок умножения открывает нам глаза на совершенно новый образ мышления.

Между Японией и западным миром существует множество вариаций, и одна из многих вариаций – это того, как детей учат умножать числа .

В Японии тактика более заметна и включает в себя гораздо больше умеренного подсчета, чем простое умножение, что означает, что , как только молодые люди узнают, как полагаться, не будет конца разнообразию многозначных чисел, которые они будут умножать. .

Здесь, чтобы показать нам, как это закончилось, – первокурсник начального факультета , который недавно шокировал свою маму, дав ей правильный ответ на вопросы двузначного умножения, такие как 14 экземпляров 14, время и время еще раз.

Его мама, подписавшаяся в Твиттере с @shiorinenglish, попросила сына указать ей, как он это делает, поэтому он достал карандаш и бумагу и подтвердил ей это:

Как видите, ответ на 14 x 14 равен 196.Как также можно видеть, – лучший способ, который он нашел на этот ответ, – это что-то вроде головокружительного триллера .

Однако, изучив его в течение некоторого времени, вы можете увидеть логику, лежащую в основе этого, и это действительно интеллектуальный метод, устраняющий серьезный недостаток.

Умножаемые числа сначала делятся на два элемента, поэтому в этом случае, вместо того, чтобы рассматривать проблему как 14 x 14, вы видите ее как 10 и 4 x 10 и 4 . Затем вы умножаете каждое из этих чисел, что подразумевает: 10 x 10, 10 x 4, 4 x 10 и 4 x 4.Затем все, что осталось сделать, это сложить решения, что даст вам 196.

Еще один способ взглянуть на это:

14 × 14
= （10 + 4） × （10 + 4）
= 10 × 10 + 4 × 10 + 4 × 10 + 4 × 4
= 100 + 40 + 40 + 16
= 196

Обозначив проблему визуально с помощью диаграммы, подобной приведенной выше, вы даже не должны знать, как умножить, чтобы получить ответ, хотя, поскольку блоки, нарисованные этим сыном, означают сумму меньших блоков.

Например:

Включая 4 блока выше ( 1 00 + 40 + 40 + 16), вы получите 196, и это именно то, что этот умный сын проиллюстрировал на фотографии, которую его гордая мама опубликовала в Твиттере.

小 1 息 子 が 14✖️14 と か の の か け 算 の 答 え で サ ク サ い る の で

気 に な っ て ど う や っ て 考 え て い る か 聞 い た ら

マ マ な ん で 分 か ら な い の？ 😤

と ブ ツ ブ ツ 言 い な が ら 図 解 し て く れ ま し た。 pic.twitter.com/W6g7alPKoM

– し お り ん @ ゆ る り お う ち 英語 7 年 目 (@shiorinenglish) 9 ноября 2021 г.

Некоторые клиенты Twitter сравнили методику умножения, которую использует младший мальчик, с методикой, которой обучают в Numberblocks , британской молодежной телевизионной коллекции, созданной с использованием компьютерной графики, которая дополнительно размещает клипы на своем официальном канале YouTube.Этот приятный учебный сборник разбивает числа на блоки, при этом совершенно разных символов отображают совершенно разные формы блоков, которые изменяются при добавлении, вычитании или при умножении или делении.

▼ Изменение того, как молодежь «видит» числа, по одному блоку за раз.

Этому младшему мальчику, вероятно, не семь, но, однако, отзывы, которые он получил в Твиттере, показывают, что он уже заслужил награду и восхищение взрослых по всей стране.

«Гений!»
«Какая красивая методика – я должен это вспомнить!»
“Мне нужен калькулятор для устранения этого математического недостатка!”
«Ух ты, он нарисовал его наилучшим образом, чтобы все было просто вычислить!»
“Это просто указывает на то, что есть несколько способов получить соответствующий ответ!”

Эта методология действительно открывает нам глаза на совершенно новый образ мышления, и лучший способ, которым этот ребенок разбивает сложные проблемы на более мелкие, дополнительные управляемые элементы, – это метод, который мы применим ко всем типам общих проблем в жизни.

Так что спасибо, математики, за то, что еще раз дали нам все ответы на вселенную. Теперь нам просто нужно поразмыслить над этими арифметическими задачами, каждая из которых является правильной, но, к сожалению, не подходит для японских преподавателей математики.

Поставка: Twitter / @ shiorinenglish через Hachima Kikou
Главное изображение: Twitter / @ shiorinenglish
Вставить фотографии: Twitter / @ shiorinenglish, SoraNews24
● Хотите узнавать о новейших статьях SoraNews24 так же быстро, как они напечатаны? Следуйте за нами в Facebook и Twitter!

Как это:

Нравится Загрузка…

3-й класс по математике | Бесплатные онлайн-математические игры

Детский сад

1 класс

2 класс

3 класс

4 класс

5 класс

6 класс

Веселые игры для детей

Математические игры для 3-го класса

Обзор игры: Пингвин в прыжке