Урок 6. Умножение в уме любых чисел до 100
Чтобы умножать любые числа до 100 в уме важно быстро подобрать нужный алгоритм. Для удобства этого подбора в данном уроке выделены наиболее удобные случаи для каждой методики умножения.
Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).
Универсальные методики
Применимость универсальных методик умножения чисел до 100 такова:
Использование одного опорного числа (Урок 5):
- все числа в диапазонах до 30, 40-60, 85-100 – если оба множителя рядом с опорным числом.
Например: 13*17, 18*23, 29*22, 53*61, 88*97 и т.д.
- если одно число очень близко к удобному опорному (+/- 3 от 10, 20, 50, 100), второе может быть любым.
Например: 21*67 (21 близко к 20), 48*33 (48 близко к 50), 98*32 (98 близко к 100)
Использование двух опорных чисел (Урок 5):
- Если одно опорное число является кратным другому и если одно из опорных чисел является удобным (10, 20, 50, 100)
Иные числа удобно умножать традиционными методами из третьего урока, когда разряды десятков и единиц не очень большие (Урок 3). Кроме того, традиционный метод удобен, когда вы не знаете, какой другой метод вам применить.
Кроме того, традиционный метод удобен, когда вы не знаете, какой другой метод вам применить.
- Например: 42*32 = 12 (2*4+3*2) 4 = 1344
Частные методики
Также полезно помнить о частных методиках, существенно упрощающих решение некоторых примеров:
Умножение на 10, 20, 25, 50 – должно осуществляться практически на автомате (Урок 2):
- Например: 88*25 = 2200 (деление на 4)
Умножение на 11 всегда по методике из урока 4
- Например: 57*11= 5 (5+7) 7 = 627
Числа, заканчивающиеся на 5 удобно возводить в квадрат по методу из четвёртого урока
- Например: 65*65 = (6*7)25 = 4 225
Любые числа удобно возводить в квадрат используя формулы сокращенного умножения четверного урока
- Например: 69*69 = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Теперь, вы имеете серьезный алгоритмический аппарат для решения примеров на умножение чисел до 100.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Евгений Буяновумножаем большие числа в уме — Блог Викиум
 А если мозг не тренировать, он ленится, что приводит к ухудшению всех его функций и нашей продуктивности. Еще до времен повсеместного распространения вычислительных машин люди изобрели несколько лайфхаков устного счета. Рассмотрим их подробнее.
А если мозг не тренировать, он ленится, что приводит к ухудшению всех его функций и нашей продуктивности. Еще до времен повсеместного распространения вычислительных машин люди изобрели несколько лайфхаков устного счета. Рассмотрим их подробнее.Гаусс — не только распределение
Достаточно одной таблицы
Чтобы научиться перемножать любые числа, нам необходимо помнить таблицу умножения. Хитрость заключается в том, что любое большое число можно разложить на маленькие — те, что представлены в этой таблице. Суть умножения двух чисел заключается в многократном повторении одного из них.
Если перед нами стоит задача умножить однозначное число на многозначное, то достаточно разложить больше на маленькие по разрядам, т.е. сначала сотни, потом десятки, потом единицы. И по очереди их умножить на заданное число. Далее останется сложить эти произведения. Например, 254*7 = 200*7 + 50*7 + 4*7 = 1400 + 350 + 28 = 1778. Как мы видим, каждый разряд представляет собой однозначное число с определенным количеством нулей. Таким образом, нам нужно лишь помнить таблицу умножения, чтобы легко справиться с этой задачей.
Этот же способ применим для умножения двух двузначных чисел — их нужно так же разбить на однозначные и выполнить операцию последовательно. Допустим, наша задача умножить 67 на 43. 43 — это 40 + 3. А значит, 67 нужно умножить сначала на 40, затем на 3, и сложить эти произведения. Далее раскладываем 67 и производим ту же операцию. Получаем: 67*40 + 67*3 = 60*40 + 7*40 + 60*3 + 7*3 = 2400 + 280 + 180 + 21 = 2881.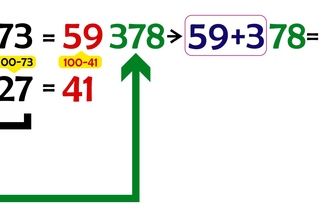
Одиннадцать друзей умножения
Самый простой и интересный способ умножения двузначного числа — с использованием числа 11. Нужно всего лишь сложить между собой цифры, из которых состоит двузначное число. А по бокам поставить те же самые исходные 2 числа, которые мы складывали. Что получится, если 35 умножить на 11? Складываем 3 + 5 = 8, а по бокам ставим 3 и 5 — 385. Проверяем на калькуляторе. Но что делать, если сумма двух этих чисел больше 10? Куда что ставить? Нужно сделать все ровно так же, только при помощи наложения. Посмотрим на примере 83*11: 8 + 3 = 11. Посередине у нас стоит 11, справа 3, а к первому месту прибавляется 8, итого: 8 + 1 = 9 — это первое число. Далее у нас стояла единица, последней тройка. Собираем: 913. Проверяем. Вуаля!
Лайфхаки не тренировка
Конечно, само слово «лайфхак» подразумевает, что мы используем определенный прием, чтобы меньше напрягать мозг. При таком счете мозг тоже тренируется — ведь нам надо удерживать всю раскладку в голове, да еще и складывать эти элементы.
Викиум разработал более 75 специальных — когнитивных тренажеров. Они развивают базовые (когнитивные) функции мозга комплексно, по запатентованной технологии. Программа составляет вам персональный план тренировок, следит за прогрессом, постепенно повышает нагрузку. Сами тренажеры выглядят как игровые задания с понятным интерфейсом — на них могут заниматься даже дети от 7 лет. В результате регулярных тренировок существенно увеличивается работоспособность мозга и ваша общая продуктивность. Занимайтесь каждый день всего по 10 минут и будьте в тонусе!
Как научить ребенка считать в уме
Детям в школе приходится несладко: то сменку забыл, то домашки много задали.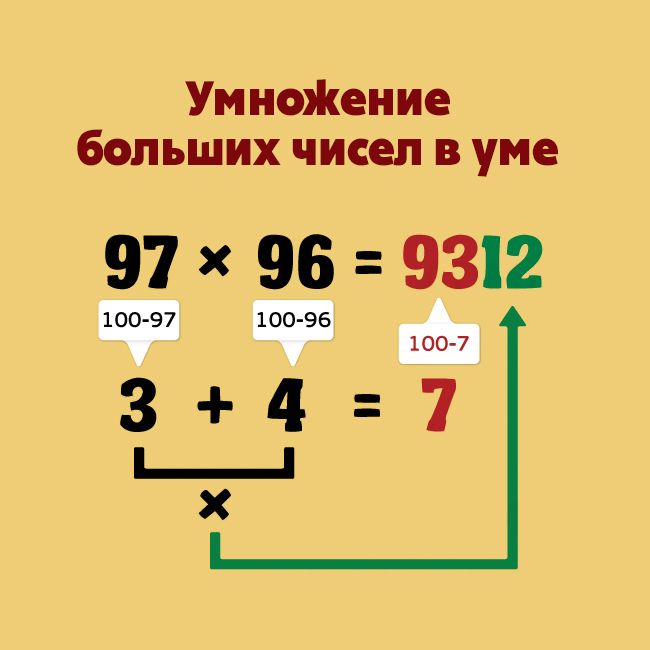
Но есть несколько приемов, которые смогут хоть немного упростить жизнь любого школьника, особенно, если на уроках запрещают пользоваться калькуляторами. Именно о них мы тебе сейчас и расскажем.
© Depositphotos1. Возведение в квадрат чисел, которые оканчиваются на 5
Любое двузначное число, оканчивающееся на 5, легко возвести в квадрат, нужно лишь первую цифру числа (десятки) умножить на цифру большую на единицу, а потом к полученному значению приписать в конце 25. Например, в квадрат нужно возвести 65: Первый шаг: 6 х 7 = 42. Второй шаг: дописываем 25, получаем 4 225.
2. Возведение в квадрат двузначных чисел
Квадрат сложного двузначного числа можно найти без особого труда, если оно находится рядом с тем, квадрат которого посчитать совсем просто.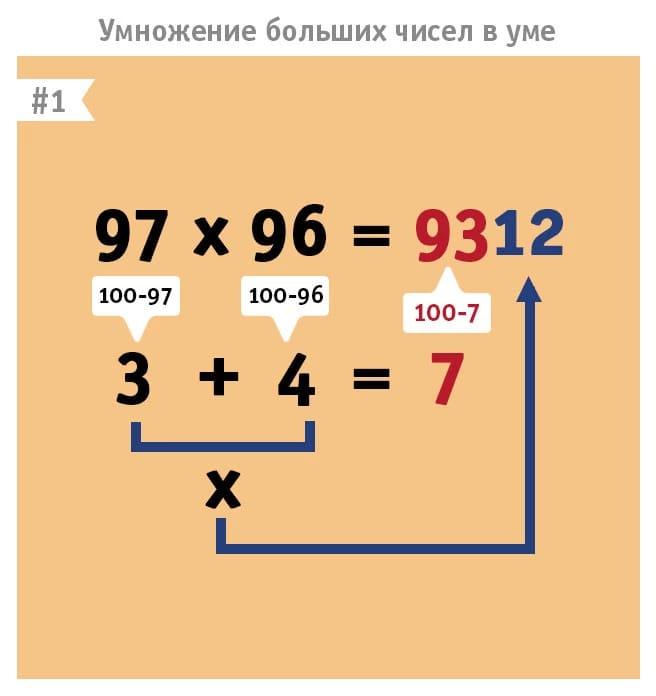 2 + 40 + 41 = 1 600 + 81 = 1 681.
2 + 40 + 41 = 1 600 + 81 = 1 681.
3. Умножение двузначных чисел на 11
Чтобы быстро умножить двузначное число на 11, нужно просто сложить его цифры. Если сумма получается однозначной, то мы просто вписываем ее между цифрами исходного числа. Например, 63 х 11 = 693 (9 = 3 + 6).
Если сумма получается двузначной, то алгоритм усложняется на 1 шаг. Последнюю цифру суммы мы так и вписываем между цифрами исходного числа, а первая цифра суммы — всегда единица, поскольку сумма любых двух цифр не может превышать 18 (9 + 9). И эту единицу мы просто прибавляем к первой цифре исходного числа. Например: 93 х 11 = 9(12)3 = 1 023.
4. Сложное умножение
В некоторых ситуациях перемножить числа между собой помогает разложение их на простые множители. Например, 16 х 225 = (2 х 2 х 2 х 2) х 225. Дальше каждую двойку по отдельности умножаем на число, и найти результат оказывается не так уж сложно.
(2 х 2 х 2) х (2 х 225) = (2 х 2) х (2 х 450) = 2 х (2 х 900) = 2 х 1 800 = 3 600.
5. Умножение чисел, состоящих из единиц, на самих себя
Чем объяснять закономерность словами, проще проследить ее наглядно на этой таблице. Главное — правильно посчитать количество единиц в числе.
6. Умножение трехзначных чисел на однозначные
Всё гениальное просто, тебе нужно лишь разбить «страшное» трехзначное число на составляющие попроще. Например, 284 х 3 = (200 + 80 + 4) х 3 = (200 х 3) + (80 х 3) + (4 х 3) = 600 + 240 + 12 = 852.
© Depositphotos7. Как найти процент от большого числа
Чтобы упростить себе задачу, и число, и сам процент раздели на 10, а потом перемножь результаты между собой. Например, 70 % от 300: 7 х 30 = 210.
8. Табличка умножения на 9
Если трудно зазубрить значения, нам на помощь приходят руки. Смотрим на ладони и загибаем палец, который по счету соответствует цифре-множителю. Количество пальцев перед ним — это десятки, а после него — единицы в результате умножения. Например, 6 х 9 = 54 (5 пальцев до и 4 после загнутого пальца).
Например, 6 х 9 = 54 (5 пальцев до и 4 после загнутого пальца).
9. Деление чисел на 5
Чтобы быстро и легко поделить большое число на 5, нужно просто умножить его на 2 и запятой «отодвинуть» последний знак. Например, нам нужно 341 разделить на 5. Умножаем 341 на 2 и получаем 682. Переносим запятую на один знак вперед и получаем 68,2.
© Depositphotos10. Магическое число 1 089
Ну и напоследок, не столько лайфхак, сколько интересная закономерность, которой можно лишний раз заинтересовать ребенка математикой.
Нужно взять любое трехзначное число, цифры которого идут в порядке убывания (например, 431 или 863), и отнять от него число, записанное теми же цифрами, но в обратном порядке. Потом к полученной разнице нужно прибавить число, записанное в обратном порядке, но уже ее цифрами разницы. И полученная сумма всегда будет равна 1 089.
Проверим цифры с нашего примера: 431 – 134 = 297. Прибавляем к результату его «зеркальное» значение: 297 + 792 = 1 089. Второй пример: 863 – 368 = 495. 495 + 594 = 1 089. И так можно продолжать бесконечно, результат всегда будет 1 089.
Второй пример: 863 – 368 = 495. 495 + 594 = 1 089. И так можно продолжать бесконечно, результат всегда будет 1 089.
Вот так, благодаря нескольким хитростям математика вмиг может стать любимой наукой не только для ребенка, но и для взрослого.
Учеба в школе была бы куда проще и увлекательнее, если бы такие закономерности показывали и объясняли на уроках. Не зря математику называют царицей наук, в ней сокрыто множество удивительных, но при этом абсолютно логичных вещей.
Редакция Офигенно
Это творческая мастерская, работники которой не спят днем и ночью, генерируя новые идеи. Если судьба занесла тебя на «Офигенно», значит, ты попал в особый мир, который заставит тебя переживать самые разнообразные эмоции — от желания разбить монитор до слёз восторга! Как бы то ни было, заверяем тебя: здесь ты найдешь миллион уникальных историй со всех уголков мира!
Как быстро умножать двузначные числа в уме?
Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека. Точные вычисления без применения специальных устройств существенно экономят время, позволяют постоянно тренировать свою память и, что скрывать, вызывают восхищение у людей, не наделенных такими способностями.
Точные вычисления без применения специальных устройств существенно экономят время, позволяют постоянно тренировать свою память и, что скрывать, вызывают восхищение у людей, не наделенных такими способностями.
Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.
Что поможет в быстром обучении
Дотянуться до высот вундеркиндов вполне реально. Особенно, если грамотно использовать данные природой способности.
- Неплохо, если вы наделены логическим мышлением, концентрацией внимания и способностью выделять важные факторы.
- Хорошим стартом будет знание эффективных способов сложения и вычитания, понимание алгоритмов.

- На качество обучения влияет способность ежедневно тренировать память и внимание, усложняя задачи.
Какие же способы наиболее эффективны, чтобы научиться как можно быстрее умножать двузначные числа в уме?
Выбираем традиционные методы
Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Умножение с помощью разложения чисел
Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются.
Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.
Например, для умножения 38 на 57 необходимо:
- разложить число на (30+8)*(50+7);
- 30*50 = 1500 – запомнить результат;
- 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
- (1500 + 610) + 8*7 = 2110 + 56 = 2166
Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.
Умножение в столбик в уме
Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
- 47*1 = 47 – запомнить;
- 47*8 = 376 – запоминаем;
- 376*10 + 47 = 3807.
Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.
Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.
Умножение на 11
Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.
Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143
Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308
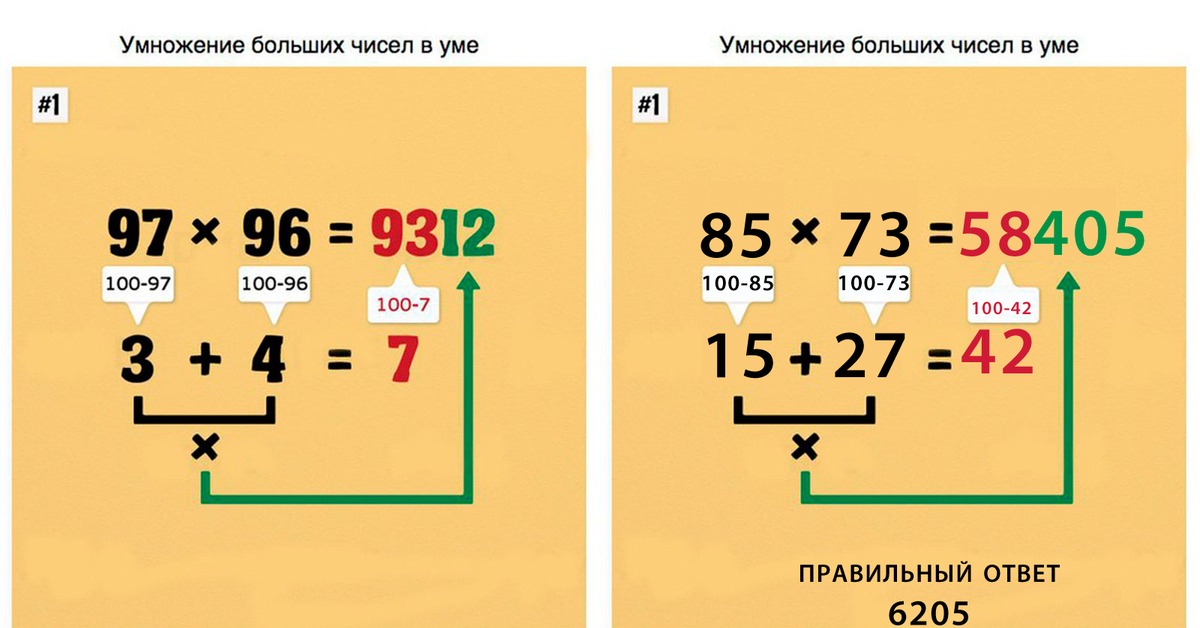
Умножение больших чисел
Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.
Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.
Как научиться считать деньги в уме быстро. Считаем в уме.
Каждый родитель желает своему ребенку, чтобы вырос умным, хорошо развитым и проявлял заинтересованность к учебе. Тем не менее, существует сложность в проявлении интереса у малыша в получении новых знаний. Одним их первых проявлений интереса к знаниям у детей дошкольного возраста является счет.
Одним их первых проявлений интереса к знаниям у детей дошкольного возраста является счет.
Именно в этот момент очень важно создать из математических заданий игру, которая увлечет малыша.
О том, как быстро научить ребенка складывать в уме, пойдет речь в этой статье. Мы приведем не только упражнения, но и расскажем, с чего следует начинать занятия и как перевести их в игровую форму.
Первой ступенью в образовательном процессе является изучение порядкового счета, иными словами цифр их расположения. Начальным этапом можно взять повседневные занятия, т.е. внедрение счета, когда вы идете с малышом по лестнице, застегиваете ему куртку или кушаете. Остальные этапы обучения также плавно идут один за другим, поэтому в таких занятиях важно соблюдать последовательность и систематичность.
Основными заданиями на первичных этапах являются:
- обучить малыша различать множественные предметы от единичных, т.е. «много» и «один»;
- научить разделять такие понятия, как «равно», «больше» и «меньше»;
- порядковый и количественный счет;
- научить пониманию, как количество предметов относится к конкретной цифре;
- изучите состав чисел – сначала от одного до десяти, затем от 10 до 20 и т.
 д.;
д.; - простейшие задачи по арифметике.
Когда вы дойдете до задач по математике, следует применять не один способ решения, а несколько. При таком подходе, ребенку в дальнейшем будет легче искать иные пути решения, а ум его станет более гибким.
Отвечая на вопрос, «как научиться считать в уме?», отметим, что обучение следует начинать планомерно, при достижении ребенком возраста 3-х, 4-х лет. Помните, что процесс должен быть игровым. В противном случае, у малыша можно заблокировать желание учиться.
Презентация: “Устный счет на уроках математики”
Процесс счета
Умственный процесс, касающийся счёта всегда начинается с простых действий. Как правило, они подразделены на два компонента – речевой и двигательный.
- Речевое действие развивается по схеме – сначала говорим о том, что делаем, затем шепчем, а после счет происходит про себя. И лишь после этого этапа можно переходит на быстрый счет. К примеру, при сложении единиц 1+1, называется следующая цифра в ряду, т.
 е. в уме ребенок сразу будет добавлять 1,2,3,4…
е. в уме ребенок сразу будет добавлять 1,2,3,4… - Двигательный элемент развивается с обычного перекладывания предметов из стороны в сторону. Таким образом, в игровой форме предметы будут увеличиваться или уменьшаться. Поначалу ребенок будет следить за счетом пальчиком, затем только глазами, в уме совершая математические действия.
При счете на пальцах или палочках, малыши не стремятся запомнить результат. Ввиду этого, когда при счете не хватит пальцев и палочек, у ребенка возникают трудности.
Если родитель желает научить ребенку счета, то предмет следует как можно быстрее снизить их участие в процессе, однако убрать их полностью не получится. Как научиться быстро считать в уме? Об этом читайте в следующих разделах.
Главный компонент обучения – игра
Развитие каждого человека происходит индивидуально. Совершение ошибок в процессе ознакомления с материалом – нормально. Тем не менее, многие родители не понимают, отчего смышленый ребенок не способен понять простых вещей, с точки зрения взрослого.
Отметим, что мозг ребенка отличен по своей структуре от мозга взрослого человека. Малыши не хотят и не могут запоминать то, что не вызывает их интереса.
Память у детей устроена таким образом, что она хранит только то, что вызывает эмоциональный ответ. При этом не имеет значение позитивные это эмоции, или негативные.
Так как же научить считать в уме ребенка? Игра поможет усваивать математические основы можно начинать считать котят на улице, пока, например, вы идете в детский сад. Обучив ребенка цифрам от 1 до 10 можно предложить ему искать их по дороге в магазин, а придя домой, посчитать, сколько цифр было найдено, и сложить их в уме.
Методик существует множество и с наиболее популярными предлагаем ознакомиться в следующем разделе.
Умение считать важно не только при подготовке к школе, но и в дальнейшей жизни любого человека. Счет до 10 важен, но осилить его сразу, у малыша вряд ли получится, поэтому необходимо начинать с 1 до 5, а затем усложнять задачу по нарастающей.
Для того чтобы освоить счет быстро и успешно, рекомендуем пользоваться подсказками, но только в начале обучения. Далее их постепенно нужно убирать, чтобы малыш учился считать в уме.
- пальцы рук;
- развивающие ТВ-передачи;
- обучающие игры и счёты;
- стишки с цифрами или считалочки;
- ежедневно считать с малышом всё, что видите.
Приемы быстрого счета:
- Карточки. В период изучения цифр, карточки очень важно. Их можно купить, или смастерить с ребенком самостоятельно. Последнее будет более интересным для ребенка. В начале показывайте их малышу последовательно, затем меняйте очередность.
- Магазин. Одна из самых любимых игр у малышей. На столе следует разложить «товары для продажи», придумать «валюту» и назначить на каждый предмет ценник. Ваше чадо следует назначить кассиром. При общении с сотрудником магазина нужно не обращать внимание на ценники, пусть ребенок сам рассказывает, и считает, сколько стоят предметы.
- Пластилин.
 Игра, в которой необходимо попросить ребенка слепить мишке 4 лапки, или котику два ушка. Попутно следует показывать ему карточки с этими цифрами.
Игра, в которой необходимо попросить ребенка слепить мишке 4 лапки, или котику два ушка. Попутно следует показывать ему карточки с этими цифрами.
Как научить ребенка считать в уме? Обучить ребенку счету достаточно непросто, при этом все родители стремятся, чтобы он делал не задумываясь. Ежедневные упражнения, увлекательные формы занятий вкупе с вашим упорством и терпеливостью помогут ребенку освоить королеву наук – математику.
Как научиться быстро считать в математике, волнует не только многих детей, но и их родителей. Даже с дошкольниками часто проводят специальные занятия, направленные на развитие навыка оперирования цифрами в уме. Это умение, безусловно, пригодится и в средней, и в старшей школе, и даже во взрослой жизни. Так как научиться быстро считать ребенку и можно ли вообще добиться каких-либо результатов? Конечно, если регулярно заниматься с малышом, обучая его приемам устного счета, то со временем скорость выполнения математических операций резко возрастет. Из этого можно сделать вывод, что следует запастись терпением.
Из этого можно сделать вывод, что следует запастись терпением.
Информация для учеников средней и старшей школы
Если вы учитесь в школе, а на уроках математики отнимает у вас много драгоценного времени, то самое время научиться быстро считать. Примеры, которые вы решали ранее с большим трудом, будут отнимать у вас вдвое меньше сил. Для развития способности быстро считать в уме воспользуйтесь такими советами:
- Развивайте краткосрочную память. Это позволит вам удержать в поле своего внимания несколько больших цифр одновременно.
- Подберите литературу, в которой описаны различные алгоритмы устного счета, и изучите их все.
- Регулярные тренировки помогут быстро развить способности считать в уме и закрепить полученные результаты.
Как вы уже догадались, нужно часто совершать математические операции в уме. Любой человек при наличии регулярных тренировок научится быстро считать. Числа для развития этого умения подбирайте таким образом, чтобы они подходили вашему уровню подготовки. Начинайте с простых задач, постепенно усложняя их.
Начинайте с простых задач, постепенно усложняя их.
Информация для родителей дошкольников и младших школьников
Если речь идет о маленьких детях, которые еще не переступили порог средней школы, то в обучении быстрому устному счету без помощи родителей им не обойтись. Одним из первых вопросов, которым задаются родители, является рассуждение о том, с какого возраста нужно учить ребенка проводить манипуляции с цифрами.
Если вы вовремя начнете заниматься с малышом, то он никогда не будет задаваться вопросом о том, как быстро научиться считать устно, потому что математические действия будут даваться ему легко.
Первый опыт обращения с цифрами ребенок получает примерно в возрасте одного года, когда играет с матрешками. Конечно, считать он не учится, но у него просыпается интерес к математике, поскольку он стремится узнать количество игровых фигурок.
Примерно в 4 года необходимо объяснить ребенку, что существует определенный цифровой ряд. Также не забудьте сказать, что каждая цифра в нем больше предыдущей.
В 5 лет малыш должен различать цифры визуально. Тут незаменимыми помощниками станут карточки с их изображением, которые ребенок должен запомнить.
В 6 лет ребенок должен научиться оперировать простыми математическими действиями. Для этого складывайте и отнимайте цифры вместе с ним. Но помните, что должен всегда быть перед глазами у ребенка.
Основные ошибки родителей
Ребенок никогда не поймет, как научиться быстро считать, если родители будут совершать такие ошибки при обучении малыша:
- Учить ребенка считать на пальцах или при помощи Так малыш будет уметь складывать цифры, только если у него перед глазами будут вспомогательные предметы. Конечно, память и логика развиваться не будут.
- Проводить занятия с ребенком, подобные школьным урокам. Маленькие дети эффективно усваивают материал только в том случае, если он представлен в игровой форме. Проще говоря, первое, что вам нужно сделать, – это вызвать интерес у ребенка. Только в этом случае занятия будут продуктивными.

Математические операции бывают разной степени сложности, в этом и состоит проблема для родителей.
Как научиться быстро считать: складываем и вычитаем
Научить ребенка считать можно с помощью простых игровых приемов. Например, приобретите в магазине или сделайте самостоятельно игрушечный домик и нескольких маленьких человечков. Поместите одну фигурку в домик и спросите у ребенка, сколько в нем теперь игрушек. Когда малыш ответит, положите в дом еще одного человечка и спросите об их количестве снова.
Когда ребенок свободно будет отвечать на ваши вопросы, усложните задачу. Помещайте в домик по нескольку человечков сразу, пусть ребенок подумает об их количестве. Те же манипуляции можно проделать и с вычитанием.
Умножаем и делим
Если возникает вопрос о том, как научиться быстро считать, нельзя обойти стороной и другие математические действия. Умножение и деление – достаточно сложные цифровые манипуляции для ребенка, в отличие от сложения и вычитания. Но вам на помощь снова придут игровые упражнения.
Но вам на помощь снова придут игровые упражнения.
Возьмите 2 коробочки и несколько предметов, которые могут поместиться в них. Попросите ребенка заполнить одну емкость и сосчитать, сколько в ней фигурок. Такие же манипуляции он должен провести и со второй коробочкой. Сперва пользуйтесь только двумя предметами в каждой емкости. Подведите ребенка к мысли, что два раза по два – это четыре. Постепенно увеличивайте количество предметов.
Если умножение освоить легко, то деление – это трудная задача. Ему ребенок научится в школе. Приступать к делению чисел можно только тогда, когда будет изучена таблица умножения. Главная ваша задача состоит в том, чтобы привить ребенку способность считать в уме, а совершенствовать свои навыки в дальнейшем он будет самостоятельно.
Выводы
Таким образом, научиться быстро считать можно, но для этого нужны постоянные тренировки. Если речь идет о маленьком ребенке, то занимайтесь с ним регулярно, даже если уроки в школе кажутся вам эффективными. Если же речь идет о человеке с уже сформировавшимися способностями и характером, то единственной методикой, которая способна ему помочь, являются постоянные манипуляции с цифрами в уме. Поставьте себе четкую цель, выделите время для тренировок, чтобы в будущем упростить себе задачу и сократить время на раздумья при решении контрольных работ.
Если же речь идет о человеке с уже сформировавшимися способностями и характером, то единственной методикой, которая способна ему помочь, являются постоянные манипуляции с цифрами в уме. Поставьте себе четкую цель, выделите время для тренировок, чтобы в будущем упростить себе задачу и сократить время на раздумья при решении контрольных работ.
Приемы быстрого счета: магия, доступная всем
Для того чтобы понять, какую роль в нашей жизни играют цифры, поставьте простой эксперимент. Попробуйте некоторое время обойтись без них. Без цифр, без вычислений, без измерений… Вы окажетесь в странном мире, где почувствуете себя абсолютно беспомощным, связанным по рукам и ногам. Как успеть на встречу вовремя? Отличить один автобус от другого? Позвонить по телефону? Купить хлеб, колбасу, чай? Сварить суп или картошку? Без чисел, а значит, без счета жизнь невозможна. Но как тяжело иногда дается эта наука! Попробуйте быстро перемножить 65 на 23? Не получается? Рука сама тянется за мобильником с калькулятором. А, между тем, полуграмотные русские крестьяне 200 лет назад спокойно делали это, пользуясь лишь первым столбиком таблицы умножения – умножением на два. Не верите? А зря. Это – реальность.
А, между тем, полуграмотные русские крестьяне 200 лет назад спокойно делали это, пользуясь лишь первым столбиком таблицы умножения – умножением на два. Не верите? А зря. Это – реальность.
“Компьютер” каменного века
Даже не зная чисел, люди уже пытались считать. Если нашим предкам, обитавшим в пещерах и носившим шкуры, нужно было поменяться чем-либо с соседним племенем, они поступали просто: расчищали площадку и выкладывали, например, наконечник стрелы. Рядом ложилась рыба или горсть орехов. И так до тех пор, пока не заканчивался один из обменных товаров, или глава “торговой миссии” не решал, что уже хватит. Примитивно, но по-своему очень удобно: и не запутаешься, и не обманут.
С освоением скотоводства задачи усложнились. Большое стадо нужно было как-то считать, чтобы знать, все ли козы или коровы на месте. “Счетной машиной” неграмотных, но умных пастухов стала долбленая тыква с камешками. Как только животное покидало загон, пастух клал в тыкву камешек. Вечером стадо возвращалось, и пастух вынимал по камешку с каждым входившим в загон животным. Если тыква пустела, он знал, что со стадом все в порядке. Если оставались камешки – шел искать потерю.
Если тыква пустела, он знал, что со стадом все в порядке. Если оставались камешки – шел искать потерю.
Когда появились цифры, дело пошло веселее. Хотя еще долго у наших предков в ходу было лишь три числительных: “один”, “пара” и “много”.
Можно ли считать быстрее компьютера?
Обогнать устройство, выполняющее сотни миллионов операций в секунду? Невозможно… Но тот, кто говорит так, жестоко лукавит, или просто кое-что умышленно упускает из вида. Компьютер – это лишь набор микросхем в пластике, он не считает сам по себе.
Поставим вопрос по-другому: может ли человек, считая в уме, обогнать того, кто выполняет вычисления на компьютере? И здесь ответ – да. Ведь, чтобы получить ответ от “черного чемоданчика”, данные в него необходимо сначала ввести. Это будет делать человек при помощи пальцев или голосом. А все эти действия имеют ограничения по времени. Непреодолимые ограничения. Сама природа поставила их человеческому телу. Всему – кроме одного органа. Мозга!
Калькулятор умеет выполнять лишь две операции: сложение и вычитание. Умножение для него – это множественное сложение, а деление – множественное вычитание.
Умножение для него – это множественное сложение, а деление – множественное вычитание.
Наш мозг поступает по-другому.
Класс, где учился будущий король математики, Карл Гаусс, как-то получил задание: сложить все числа от 1 до 100. Карл написал на своей доске абсолютно правильный ответ, как только учитель закончил объяснять задание. Он не стал прилежно складывать числа по порядку, как поступил бы любой уважающий себя компьютер. Он применил открытую им самим формулу: 101 х 50 = 5050. И это далеко не единственный прием, ускоряющий вычисления в уме.
Простейшие приемы быстрого счета
Их изучают в школе. Самое простое: если вам нужно прибавить к любому числу 9, прибавляете 10 и вычитаете 1, если 8 (+ 10 – 2), 7 (+ 10 – 3) и т.д.
54 + 9 = 54 + 10 – 1 = 63. Быстро и удобно.
Двухзначные числа складываются так же легко. Если во втором слагаемом последняя цифра больше пяти, число округляется до следующего десятка, а потом “лишнее” вычитается. 22 + 47 = 22 + 50 – 3 = 69.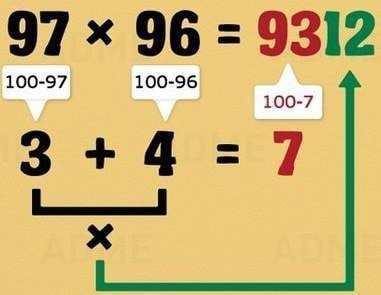 Если ключевая цифра меньше пятерки, то надо сложить сперва десятки, затем единицы: 27 + 51 = 20 + 50 + 7 + 1 = 78.
Если ключевая цифра меньше пятерки, то надо сложить сперва десятки, затем единицы: 27 + 51 = 20 + 50 + 7 + 1 = 78.
С трехзначными числами точно так же не возникает никаких трудностей. Складываем их, как читаем, слева на право: 321 + 543 = 300 + 500 + 20 + 40 + 1 + 3 = 864. Гораздо проще, чем в столбик. И гораздо быстрее.
А вычитание? Принцип тот же: вычитаемое округляем до целого и добавляем недостающее: 57 – 8 = 57 – 10 + 2 = 49; 43 – 27 = 43 – 30 + 3 = 16. Быстрее чем на калькуляторе – и никаких претензий от учителя даже во время контрольной!
Нужно ли учить таблицу умножения?
Дети этого, как правило, терпеть не могут. И правильно делают. Ни к чему ее учить! Но не спешите возмущаться. Никто не утверждает, что таблицу не нужно знать.
Ее изобретение приписывают Пифагору, но, скорее всего, великий математик лишь придал законченную, лаконичную форму тому, что уже было известно. На раскопках древней Месопотамии археологи нашли глиняные таблички с сакраментальным: “2 х 2”. Люди давно пользуются этой в высшей степени удобной системой вычислений и открыли множество способов, которые помогают постичь внутреннюю логику и красоту таблицы, понять – а не тупо, механически зазубрить.
Люди давно пользуются этой в высшей степени удобной системой вычислений и открыли множество способов, которые помогают постичь внутреннюю логику и красоту таблицы, понять – а не тупо, механически зазубрить.
В древнем Китае таблицу начинали учить с умножения на 9. Так проще, и не в последнюю очередь потому, что умножать на 9 можно “на пальцах”.
Положите обе руки на стол ладонями вниз. Первый слева палец – 1, второй – 2 и т.д. Допустим, вам нужно решить пример 6 х 9. Поднимите шестой палец. Пальцы слева покажут десятки, справа – единицы. Ответ 54.
Пример: 8 х 7. Левая рука – первый множитель, правая – второй. На руке пять пальцев, а нам нужно 8 и 7. Загибаем на левой руке три пальца (5 + 3 = 8), на правой 2 (5 + 2 = 7). Загнутых пальцев у нас пять, значит пять десятков. Теперь перемножим оставшиеся: 2 х 3 = 6. Это единицы. Всего 56.
Это лишь один из наипростейших приемов “пальцевого” умножения Их много. “На пальцах” можно оперировать числами до 10 000!
У “пальцевой” системы есть бонус: ребенок воспринимает ее как веселую игру. Занимается охотно, испытывает массу положительных эмоций и в итоге очень скоро начинает проделывать все операции в уме, без помощи пальцев.
Занимается охотно, испытывает массу положительных эмоций и в итоге очень скоро начинает проделывать все операции в уме, без помощи пальцев.
Делить так же можно при помощи пальцев, но это немного сложнее. Программисты до сих пор пользуются руками, чтобы перевести числа из десятичной системы в двоичную – это удобнее и гораздо быстрее, чем на компьютере. Но в рамках школьной программы научиться быстро делить можно даже без пальцев, в уме.
Допустим, нужно решить пример 91: 13. Столбик? Нет нужды пачкать бумагу. Делимое заканчивается на единицу. А делитель – на тройку. Что там в таблице умножения самое первое, где задействована тройка, а заканчивается на единицу? 3 х 7 = 21. Семерка! Вот и все, мы ее поймали. Надо 84: 14. Вспоминаем таблицу: 6 х 4 = 24. Ответ – 6. Просто? Еще бы!
Волшебство числа
Большинство приемов быстрого счета похоже на фокусы. Взять хотя бы известнейший пример умножения на 11. Чтобы, например, 32 х 11 нужно написать 3 и 2 по краям, а в середину поставить их сумму: 352.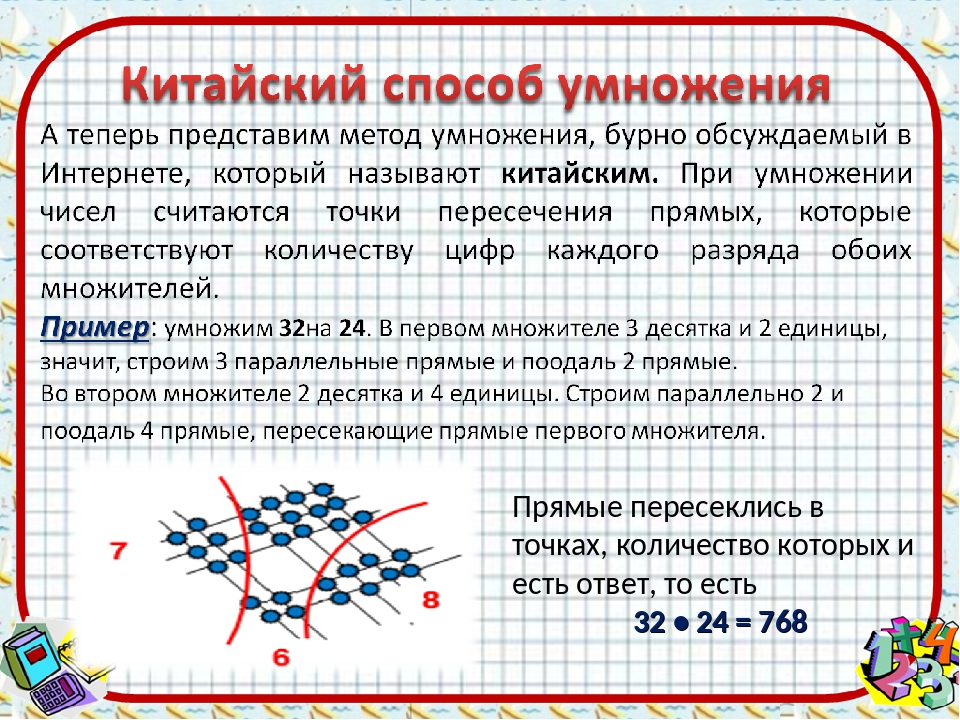
Для умножения двузначного числа на 101 надо просто записать число два раза. 34 х 101 = 3434.
Для умножения числа на 4 нужно два раза умножить его на 2. Для деления – дважды разделить на 2.
Много остроумных и, главное, быстрых приемов помогают возводить число в степень, извлекать квадратный корень. Знаменитые “30 приемов Перельмана” для математически мыслящих людей будут покруче шоу Коперфильда, потому что они еще и ПОНИМАЮТ что происходит, и как оно происходит. Ну а остальные могут просто наслаждаться красивым фокусом. Например, нужно перемножить 45 на 37. Напишем числа на листе и разделим их вертикальной чертой. Левое число делим на 2, отбрасывая остаток, пока не получим единицу. Правое – умножаем до тех пор, пока число строчек в столбике не сравняется. Затем вычеркиваем из ПРАВОГО столбика все те числа, напротив которых в ЛЕВОМ столбике получился четный результат. Оставшиеся числа из правого столбика складываем. Получится 1665. Перемножьте числа привычным способом. Ответ сойдется.
Ответ сойдется.
“Зарядка” для ума
Приемы быстрого счета способны здорово облегчить жизнь и ребенку в школе, и маме в магазине или на кухне, и папе на производстве или в офисе. Но мы предпочитаем калькулятор. Почему? Не любим напрягаться. Нам тяжело держать числа, даже двухзначные, в голове. Почему-то не держатся.
Попробуйте выйти на середину комнаты и сесть на шпагат. Почему-то “не сажается”, да? А гимнаст делает это совершенно спокойно, не напрягаясь. Тренироваться нужно!
Самый простой способ тренировки и, одновременно, разминки мозга: устный счет вслух (обязательно!) через число до ста и обратно. Утром, стоя под душем, или готовя завтрак, посчитайте: 2.. 4.. 6.. 100… 98.. 96. Можно считать через три, через восемь – главное, делать это вслух. Всего через пару недель регулярных занятий вы удивитесь, насколько ПРОЩЕ станет обращаться с числами.
Эта статья навеяна топиком и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:Т.к. на 10 , 100 , 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10 . Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190 .
Еще пример:
31 x 29 = (30 + 1) x (30 – 1) = 30 x 30 – 1 x 1 = 900 – 1 = 899.
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2 , а 50 в виде 100:2 ):68 x 50 = (68 x 100) : 2 = 6800: 2 = 3400; 3400: 50 = (3400 x 2) : 100 = 6800: 100 = 68.
Аналогично выполняется умножение или деление на 25 , ведь 25 = 100:4 .
 Например,
Например,600: 25 = (600: 100) x 4 = 6 x 4 = 24; 24 x 25 = (24 x 100) : 4 = 2400: 4 = 600.
Теперь не кажется невозможным умножить в уме 625 на 53 :
625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = = (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125.
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25 . Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50 -ю. 2 = 17000 + 19000 + 2000 + 25 = 38025.
2 = 17000 + 19000 + 2000 + 25 = 38025.
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.Пусть даны два двузначных числа, у которых сумма единиц равна 10:
M = 10m + n, K = 10a + 10 – n.
Составив их произведение, получим:
Например, вычислим 77 x 13 . Сумма единиц этих чисел равна 10 , т.к. 7 + 3 = 10 . Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77 .
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77 . Теперь перемножим новые числа 80 x 10 , а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10 :
13 x 77 = 10 x 80 + 3 x (77 – 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001. 2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 =
= 10000 + 19000 + 1000 + 8000 + 25 = 38025.
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.Использованная литература :
«1001 задача для умственного счёта в школе С.А. Рачинского» .
В наши дни существует большое многообразие всевозможных счетных устройств электронного образца. Несмотря на это устный счет все еще актуален для человека. Благодаря несложным вычислениям в уме можно решать многие бытовые задачи, не говоря уже о рабочих моментах. К тому же, если вы научитесь быстро считать в уме, то это существенно улучшит ваш имидж. Особенно важно это тем, кто имеет престижную работу, которая связана с вычислением. Приемы устного счета, которым может обучиться каждый желающий, помогут научиться организовывать себя во всевозможных жизненных ситуациях.
Приемы устного счета, которым может обучиться каждый желающий, помогут научиться организовывать себя во всевозможных жизненных ситуациях.
От чего зависит возможность быстро считать в уме
Многие люди умеют считать в уме двузначные числа, но когда речь заходит о трехзначных цифрах и сложных математических действиях, то справиться с этим в уме уже может не каждый. Такой навык нужно развивать и тренировать. Научитесь вы или нет, будет зависеть от трех важных составляющих:
- Способность. Чтобы действительно научиться быстро считать в уме, нужно иметь предрасположенность к математике и уметь логически мыслить. Кроме того человек должен уметь концентрировать внимание и держать в краткосрочной памяти сразу несколько вещей. Не каждый это может делать.
- Алгоритмы. Нужно знать специальные алгоритмы, а также уметь их быстро подобрать в нужный момент. При этом необходимо быстро сориентироваться и выбрать именно максимально эффективный алгоритм в зависимости от конкретной ситуации.
 Этому со временем можно научиться.
Этому со временем можно научиться. - Тренировка и опыт. Только при многочисленных тренировках можно выработать навыки устного счета. Нужно ставить себе задачи и выполнять их. Постепенно их следует усложнять и упражняться. Это поможет быстро набраться опыта и улучшить качество устного счета.
Каждая из этих составляющих имеет большое значение. Особое внимание уделите тренировкам, ведь именно они имеют ключевое значение.
Правила подсчета
Существует несколько правил устного подсчета, которые помогут облегчить это дело. Так, для начала можно воспользоваться легким способом умножения двухзначных чисел на 11. Это сделать очень просто, зная одну хитрость. Так, для примера можно взять число 69 и умножить его 11. Нужно в уме представить, что между 6 и 9 свободное место. Теперь нужно посчитать, какая сумма этих двух цифр получится. Если это однозначное число, то его мысленно нужно поместить между двумя числами. Если же это двухзначное значение, как в нашем примере, то нужно вставить в пустое место между числами только вторую цифру.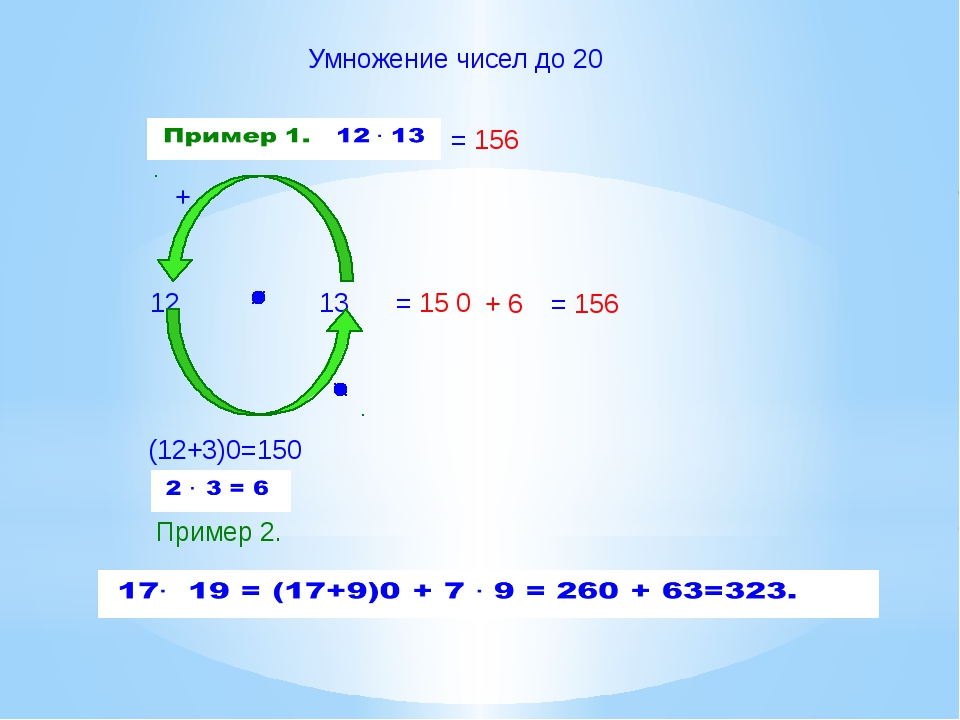 Первую при этом следует добавить к первой цифре множителя. Таким образом, получается, что 6+9=15, а значит, что между ними будет стоять 5. В итоге получается 659. Теперь добавляем оставшуюся от 15 единицу к 6 и получаем, что 69 умноженное на 11 будет 759. Это может показаться сложным, учитывая, что считать нужно в уме, но всего несколько тренировок и вы сможете быстро справляться с подобными задачами.
Первую при этом следует добавить к первой цифре множителя. Таким образом, получается, что 6+9=15, а значит, что между ними будет стоять 5. В итоге получается 659. Теперь добавляем оставшуюся от 15 единицу к 6 и получаем, что 69 умноженное на 11 будет 759. Это может показаться сложным, учитывая, что считать нужно в уме, но всего несколько тренировок и вы сможете быстро справляться с подобными задачами.
Есть еще один несложный способ, с помощью которого можно умножать числа на 11. Для этого понадобиться умножать любое нужное число на 10, а после этого прибавлять к нему еще одно исходное значение. В примере с тем же числом 69 получится так: 69 мы умножаем на 10 и получаем 690. Теперь к нему прибавляем исходное значение, т.е. 69 и получаем такой же ответ 759.
Еще одна хитрость и легкое правило позволит вам быстро освоить умножение любых чисел на 4. Вам нужно лишь умножить любое число на 2, что не составит особого труда, а затем еще один раз на 2. Это гораздо легче, чем сразу умножать какую-либо цифру на 4.
Есть простое правило, помогающее считать в уме проценты. Можно научиться с легкостью высчитывать 15 % от любого числа. Чтобы это сделать нужно сначала взять 10 % от числа, осуществив деление его на 10. После этого следует добавить еще половину от того, что получилось. Чтобы легче было разобраться, можно рассмотреть это на примере. Так, чтобы определить 15 % от 490, нужно просчитать в уме несколько действий: 490 разделить на 10, из чего получится 49. Это и будет 10 %. Дальше 49 следует разделить на пополам, из чего выходит 24,5 и прибавить их к тем же 10%, то есть к 49. В итоге получаем 24,5+49=73,5. Именно это значение будет составлять 15 % от числа 490.
Не каждый сможет осуществить такие математические действия в уме сразу, поэтому нужно как можно больше тренироваться. Сначала можно решать подобные задачки на бумаге, а со временем выработаются навыки и быстрого устного счета.
Подобных «хитрых» приемов существует довольно много. С их помощью осуществлять сложные математические операции в уме будет гораздо легче. Следует знать хотя бы основные из них, чтобы можно было освоить устный счет.
Следует знать хотя бы основные из них, чтобы можно было освоить устный счет.
Устный счет в повседневной жизни
Умение считать в уме играет большую роль. Это хорошо пригодиться в жизни каждого человека. При этом самым важным аспектом будет выступать хорошее знание таблицы умножения. Ее нужно повторять как можно чаще, чтобы не забывать, и применять ее на практике. Не стоит пользоваться калькулятором при вычислении легких значений.
Многим умение быстро считать в уме пригодится и при устройстве на работу. Даже в организациях, в которых не занимаются непосредственно математическими расчетами, при собеседовании могут попросить высчитать какие-либо действия в уме. Если человек справляется, у него будет больше шансов на получение хорошей должности, ведь это будет говорить об аналитическом складе ума.
Еще одним доказанным фактом выступает то, что люди, которые часто считают в уме, а не прибегают к калькулятору при каждой возможности, меньше подвергаются раннему слабоумию, а также старческому маразму.
Таким образом, если у вас есть возможность и желание научиться быстрому устному счету, обязательно воспользуйтесь этим. Это хорошо помогает в жизни и некоторых бытовых ситуациях. К тому же, учитывая удобные алгоритмы и небольшие хитрости, научиться этому можно довольно быстро.
Быстрый счёт в уме: умножение
Числа окружают нас везде. Мы почти каждый день ходим в магазин, планируем расходы, переводим рубли в доллары, наконец.
Конечно же, сложение и вычитание небольших чисел большинство выполняет в уме, например, при покупке батона за 22 рубля мы сразу смекаем, что с отданных 50 должны получить 28 сдачи. Но иногда требуется более сложные операции — умножения (3 батона) или деления (500 граммов сыра).
Я, конечно, не в состоянии научить вас счёту в уме для любых чисел, тем более, что для этого есть калькулятор, но попытаюсь донести, что неплохо владея навыками сложения и вычитания, можно так же успешно, а главное быстро, умножать в уме. Конечно, речь не идёт о дробных или двузначных числах. Но с умножение на цифры в состоянии справится любой.
Конечно, речь не идёт о дробных или двузначных числах. Но с умножение на цифры в состоянии справится любой.
Если для вас является проблемой сложение и вычитание даже небольших чисел, не отчаивайтесь. Небольшая практика быстро заставит мозг «шуршать», а продолжив занятия, можно будет с каждым разом оперировать всё большими числами и за меньшее время. Именно эти простейшие арифметические опреции лежат в основе более сложных — умножения и деления, поэтому прежде, чем переходить к следующему шагу крайне желательно подтянуть азы.
Умножение
На 2
Для умножения на 2 достаточно сложить число само с собой: 123 × 2 = 123 + 123 = 246
На 3
Тоже довольно тривиальная задача. В простейшем случае можно трижды сложить число самим с собой: 123 × 3 = 123 + 123 + 123 = 369
Но иногда проще сделать поразрядное умножение: 123 × 3 = 100 × 3 + 20 × 3 + 3 × 3 = 300 + 60 + 9 = 369
На 4
Так как 4 это не что иное, как 2 × 2, достаточно умножаемое число сложить сперва самим с собой, а затем ещё раз сложить полученную сумму: 123 × 4 = (123 + 123) × 2 = 246 + 246 = 492
На 5
Данная цифра ровно в 2 раза меньше 10, сделовательно, можно сначала разделить на 2, а затем умножить на 10, либо поступить наоборот: умножить на 10 и разделить на 2 (смотря что проще): 123 × 5 = 123 × 10 / 2 = 1230 / 2 = 615
На 6
Цифру 6 можно представить с помощью произведения 2 × 3, а это мы уже разобрали: 123 × 6 = 123 × 3 × 2 = 369 × 2 = 738
На 7
Наиболее простой способ — поразрядное умножение: 123 × 7 = 100 × 7 + 20 × 7 + 3 × 7 = 700 + 140 + 21 = 861
На 8
Цифра 8 получается при тройном умножении двойки на себя: 123 × 8 = 123 × 2 × 2 × 2 = 246 × 2 × 2 = 492 × 2 = 984
Иногда проще бывает исходное число умножить на 10 и отнять удвоенное исходное числа: 123 × 8 = 123 × 10 — 123 × 2 = 1230 — 246 = 984
На 9
Несмотря на то, что цифру 9 можно получить, умножив тройку саму на себя, есть способ намного легче: нужно к умножаемому числу прибавить ноль (т. е. умножить на 10) и отнять от получившегося значения исходное число: 123 × 9 = 123 × 10 — 123 = 1230 — 123 = 1107
е. умножить на 10) и отнять от получившегося значения исходное число: 123 × 9 = 123 × 10 — 123 = 1230 — 123 = 1107
Вот мы и разобрались (я надеюсь) с цифрами. В качестве небольшого бонуса приведу ещё несколько вариантов умножения, на этот раз, с числами.
Умножение на 10, 100, 1000 и т. д.
Т. к. мы оперируем десятичной системой счисления, наиболее простое умножения как раз будет на числа, начинающие следующие разряды. Для умножения необходимо просто добавить 1 (2, 3, …) ноль в конец множителя: 123 × 100 = 12300
На 11
По аналогии с умножением на 9, только в данном случае необходимо прибавить исходное число: 123 × 11 = 123 × 10 + 123 = 1230 + 123 = 1353
На 20, 30, …
Здесь достаточно представить число в виде множителей, для которых нам известен порядок действий, например, 20 = 2 × 10, 300 = 3 × 100 и т. п.: 123 × 500 = 123 × 5 × 100 = ( 123 × 100 / 2 ) × 100 = 615 × 100 = 61500
Как видим, некоторые числа вполне можно представить в виде произведения и выполнить ряд более простых действий. А поупражнявшись некоторое время с удивлением обнаружите, что калькулятор будет нужен всё реже. В заключении, приведу ещё один интересный способ, который может быть полезен при перемножении двух чисел.
А поупражнявшись некоторое время с удивлением обнаружите, что калькулятор будет нужен всё реже. В заключении, приведу ещё один интересный способ, который может быть полезен при перемножении двух чисел.
Умножение по формуле «разность квадратов»
Если кто-то не помнит эту формулу из школьного курса математики, вот она:
a2 — b2 = (a + b) × (a — b)
Допустим, нужно умножить 123 на 117. Данное произведение удобно разложить по этой формуле, т. к. 123 = 120 + 3, а 117 = 120 — 3. Составим простое выражение и убедимся, что можно легко «вертеть» в уме даже такими значениями, для которых, казалось бы, необходим калькулятор: 123 × 117 = (120 + 3) × (120 — 3) = 1202 — 32 = 14400 — 9 = 14391
Ещё пример, на этот раз попроще, для двузначных чисел: умножим 28 на 32. Снова раскладываем множители на составляющие: 28 = 30 — 2 и 32 = 30 + 2. Итоговая формула принимает вид: 28 × 32 = (30 + 2) × (30 — 2) = 302 — 22 = 900 — 4 = 896
Элементарно, не так ли? 😉
Автор публикации
2 070не в сети 7 дней
x64 (aka andi)
Комментарии: 2893Публикации: 405Регистрация: 02-04-2009 Загрузка. ..
..Как найти x и зачем это нужно
Среди читателей наверняка найдутся те, кто, познакомившись с этими примерами, скажет: «Ух ты, здо?рово! Но какая от всего этого польза?» Здесь в любом математике проснулся бы художник, и в ответ вы услышали бы: «Разве нужно красоте оправдание иное, нежели сама красота?» Ведь чем лучше мы понимаем числовые закономерности, тем глубже постигаем их красоту. И все-таки иногда они приносят практическую пользу.
Вот простая закономерность, которую мне посчастливилось обнаружить в юности (даже если я и не был первооткрывателем). Я смотрел на пары чисел, которые в сумме давали 20 (10 и 10, например, или 9 и 11), и думал, а какие из них надо перемножить, чтобы получить наибольшее произведение? Логика подсказывала, что это 10 на 10, и моя схема эта подтвердила.
Эта закономерность была несомненна. Чем дальше отстояли друг от друга числа, тем меньше становилось произведение. И насколько они отдалялись от 100? На 1, на 4, на 9, 16, 25… То есть на 1?, 2?, 3?, 4?, 5? и т. д. А потом мне стало интересно, работает ли эта закономерность для чисел, дающих другую сумму. Я решил попробовать 26:
д. А потом мне стало интересно, работает ли эта закономерность для чисел, дающих другую сумму. Я решил попробовать 26:
И я снова увидел, что наибольшее произведение дало умножение двух одинаковых чисел. А потом произведение стало уменьшаться с интервалом сначала 1, потом 4, потом 9 и т. д. Еще несколько подобных примеров убедили меня, что закономерность была строгой (ее алгебраическое выражение я покажу чуть позже). Выяснил я и то, что ее можно применять для быстрого возведения чисел в квадрат.
Допустим, нам нужно знать квадрат 13. Вместо того чтобы умножать 13 ? 13, можно сделать умножение попроще: 10 ? 16 = 160. До правильного ответа уже рукой подать, и чтобы его получить, достаточно будет прибавить возведенное в квадрат 3 – число, составляющее разницу между 13 и числами, которые мы перемножили. То есть:
13? = 10 ? 16 + 3? = 160 + 9 = 169
Можно взять еще один пример, скажем, 98 ? 98. Для удобства к первому числу добавим 2 до 100, а от второго отнимем 2 до 96. Значит, к их произведению нужно будет прибавить 2?. Вот наше уравнение:
Значит, к их произведению нужно будет прибавить 2?. Вот наше уравнение:
98?= 100 ? 96 + 2? = 9600 + 4 = 9604
Особенно легко применять эту схему к числам, которые заканчиваются на 5: если уменьшить и увеличить их на 5, оперировать придется круглыми числами. Например:
35? = 30 ? 40 + 5? = 1200 + 25 = 1225
55? = 50 ? 60 +5? = 3000 + 25 = 3025
85? = 80 ? 90 + 5? = 7200 + 25 = 7225
Теперь попробуем возвести в уме в квадрат 59. Увеличив и уменьшив это число на единицу, получим 59? = (60 ? 58) + 1?. Но как умножить в уме 60 на 58? Простой совет из двух слов: слева направо. Забудем на время про 0 и подсчитаем 6 ? 58: 6 ? 50 = 300 и 6 ? 8 = 48. Потом сложим эти два результата (опять же, слева направо) и получим 348. И добавим ноль в конце, то есть 60 ? 58 = 3480. Поэтому:
59? = 60 ? 58 + 1? = 3480 + 1 = 3481
Отступление
А вот алгебраическое доказательство этого метода (перечитайте это отступление после того, как во второй главе мы поговорим о разнице квадратов):
А? = (A + d) (A–d) + d?
где A – число, возводимое в квадрат, d – разность с ближайшим круглым числом (формула, кстати, справедлива для любого d). Для примера возведем в квадрат 59: А = 59, d = 1, значит, формула превращается в (59 + 1) ? (59 – 1) + 1?, как и в предыдущем вычислении.
Для примера возведем в квадрат 59: А = 59, d = 1, значит, формула превращается в (59 + 1) ? (59 – 1) + 1?, как и в предыдущем вычислении.
Теперь, когда вы профессионально возводите в квадрат двузначные числа, можно попробовать и трехзначные. Если помните, 12? = 144, значит:
112? = (100 ? 124) + 12? = 12 400 + 144 = 12 544
Есть еще одна подобная формула, которая работает для любых двух чисел, близких к сотне. Человек, который становится случайным свидетелем таких вычислений, испытывает чувство, будто наблюдает за трюком фокусника. Вот, например, 104 ? 109. Рядом с каждым из них пишем число, на которое оно превышает сотню (см. пример ниже). В левом столбце сложим первое число со второй разностью и запишем результат: 104 + 9 = 113. В правом столбце перемножим две разности: 4 ? 9 = 36. «Соединим» эти числа, то есть запишем их одно за другим и – тадам! – волшебным образом получим ответ: 11 336.
Другие примеры и алгебраическую формулу такого вычисления я приведу чуть позже, в главе 2. И, раз уж мы об этом заговорили, кое-что еще о вычислениях в уме. Мы тратим уйму времени на то, чтобы научиться считать столбиком, хотя научиться делать это в уме куда быстрее. Задумайтесь: как часто в обычной жизни у нас есть время и возможность достать бумагу и провести все необходимые подсчеты? Для сложных вычислений можно воспользоваться калькулятором, но не будете же вы доставать его в магазине, читая данные об энергетической ценности на упаковке продуктов, или сидя в зале собрания, или дома, включив выпуск экономических новостей. Вот здесь-то, в оценке по-настоящему важных для вас цифр, и становятся очевидными все плюсы устного счета. Увы, в школе нас хорошо учат считать на бумаге, со счетом в уме дела обстоят плохо.
И, раз уж мы об этом заговорили, кое-что еще о вычислениях в уме. Мы тратим уйму времени на то, чтобы научиться считать столбиком, хотя научиться делать это в уме куда быстрее. Задумайтесь: как часто в обычной жизни у нас есть время и возможность достать бумагу и провести все необходимые подсчеты? Для сложных вычислений можно воспользоваться калькулятором, но не будете же вы доставать его в магазине, читая данные об энергетической ценности на упаковке продуктов, или сидя в зале собрания, или дома, включив выпуск экономических новостей. Вот здесь-то, в оценке по-настоящему важных для вас цифр, и становятся очевидными все плюсы устного счета. Увы, в школе нас хорошо учат считать на бумаге, со счетом в уме дела обстоят плохо.
Строго говоря, эта тема достойна отдельной книги, но, раз уж мы говорим о магии, а не о способностях человеческого мозга, коснемся ее вскользь, обозначив лишь самые основные положения. Главный прием, о котором я не устаю говорить: считайте слева направо. Подсчеты в уме – это процесс постоянного упрощения. Вы начинаете с проблемы огромной, неподъемной, кажущейся непомерно сложной, и расщепляете ее на несколько элементарных и очевидных вопросов, пока не получите искомый результат.
Подсчеты в уме – это процесс постоянного упрощения. Вы начинаете с проблемы огромной, неподъемной, кажущейся непомерно сложной, и расщепляете ее на несколько элементарных и очевидных вопросов, пока не получите искомый результат.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесКак умножать большие числа в уме (перекрестное умножение) – World Mental Calculation
Основной метод – для малых чиселПри вычислении умножения, где одно из чисел маленькое, например 68435 × 18 , может быть самым быстрым просто сложить кратные меньшего числа:
- 5 × 18 = 90 ⇒ ………… 0
- 9 + 3 × 18 = 63 ⇒ ……… .30
- 6 + 4 × 18 = 78 ⇒ ……..830
- 7 + 8 × 18 = 151 ⇒ …… 1830
- 15 + 6 × 18 = 123 ⇒ 1231830
Фактически, когда я обучаю новичков ментальной математике, одна из первых вещей, над которыми я работаю, – это расширение знаний о таблицах умножения на другие полезные числа, такие как 18, чтобы упростить выполнение этой задачи.
Но при использовании этого базового метода для больших умножений, например 29136 × 5847 , у нас не хватает рабочей памяти для вычисления каждого кратного e.г. 5847 , не забывая уже вычисленные числа! Итак, нам нужен другой метод – более эффективный с точки зрения памяти.
Ниже я покажу вам метод перекрестного умножения, который используют для умножения самые продвинутые ментальные калькуляторы.
Метод перекрестного умноженияНекоторые приятные моменты в этом методе:
- Вам нужно знать только таблицу умножения до 9 × 9
- Какими бы большими ни были умножения, вам никогда не придется запоминать сразу много чисел
- Это очень просто, если вы знаете простой шаблон
Чтобы увидеть, как это работает, возьмем в нашем примере 29136 × 5847 :
1-я цифра – место единиц:
Для начала просто умножим 6 × 7 = 42 . Тогда самая правая цифра ответа – 2, и мы можем «перенести» 4 для следующего шага:
Тогда самая правая цифра ответа – 2, и мы можем «перенести» 4 для следующего шага:
29136
× 5847
2 (несет 4 из 42) 2-я цифра – множители с 10:
Далее мы рассматриваем 40 × 6 и 7 × 30, поскольку это произведения цифр (4 × 6 и 7 × 3), которые имеют коэффициент 10, точно так же, как 40, которое мы запомнили из предыдущего шага.
Самый быстрый способ – начать с 4 из 40, которые у нас есть, затем добавить 4 × 6 и 7 × 3:
- 4 + 4 × 6 = 28
- 28 + 7 × 3 = 49
Эти пары сложение-умножение быстро применимы на практике.
Опять же, мы можем записать «9» вместо десятков в окончательном ответе и оставить 4 для следующего шага.
29136
× 5847
92 (неся 4 из 49) 3-я цифра – множители на 100:
Мы продолжаем с 800 × 6, 40 × 30 и 7 × 100, так как это цифровые продукты с коэффициентом 100.
Опять же – начните с 4 из 400, которые у нас есть, затем добавьте к остальным товарам:
- 4 + 8 × 6 = 52
- 52 + 4 × 3 = 64
- 64 + 7 × 1 = 71
Запишите «1» в разряде сотен окончательного ответа и сохраните 7 для следующего шага:
29136
× 5847
192 (несет 7 из 71) Обратите внимание, что на каждом шаге порядок цветов вверху является зеркальным отображением цветов внизу, поскольку каждая совпадающая пара цифр должна представлять одну и ту же степень 10.
Вы можете складывать цифры в любом порядке, но я считаю полезным всегда начинать с нижнего левого и верхнего правого произведения (здесь 8 × 6) и систематически перемещаться одновременно вправо по нижнему числу и влево по номеру. верхний номер.
4-я цифра – множители с 1000:
К настоящему времени картина должна быть достаточно ясной, поэтому я продолжу с минимальными комментариями:
- 7 + 5 × 6 = 37
- 37 + 8 × 3 = 61
- 61 + 4 × 1 = 65
- 65 + 7 × 9 = 128
29136
× 5847
8192 (с 12 из 128) 5-я цифра – множители с 10,000:
На этот раз обратите внимание, что цифра «6» уже умножена на каждую цифру нижнего числа, поэтому не будет активна до конца вычисления:
- 12 + 5 × 3 = 27
- 27 + 8 × 1 = 35
- 35 + 4 × 9 = 71
- 71 + 7 × 2 = 85
29136
× 5847
58192 (несет 8 из 85) 6-я цифра – множители на 100000:
С этого момента расчет становится проще, так как продуктов той же величины становится все меньше и меньше:
- 8 + 5 × 1 = 13
- 13 + 8 × 9 = 85
- 85 + 4 × 2 = 93
29136
× 5847
358192 (несет 9 из 93) 7-я цифра – множители с 1,000,000:
- 9 + 5 × 9 = 54
- 54 + 8 × 2 = 70
29136
× 5847
0358192 (несёт 7 из 70) 8-я цифра – множители с 10,000,000:
Поскольку это заключительный этап, нам не нужно ничего нести, а просто записываем оставшиеся цифры:
29136
× 5847
170358192 Сводка Итак, это стандартный метод перекрестного умножения, используемый людьми-любителями-калькуляторами, а также нынешними и прошлыми мировыми рекордсменами по умножению, такими как Фреддис Рейес и Марк Джорнет Санс! (Jeonghee Lee предпочитает метод письма справа налево).
В заключение – метод в целом:
- Начинайте с крайней правой цифры каждого числа:
- рассчитать свой продукт
- запишите цифру единиц
- переносит разряд десятков для следующего этапа
- За каждую последующую цифру ответа:
- возьмите перенесенный номер до
- систематически добавляйте все продукты той же величины
- запишите цифру единиц в окончательном ответе
- отнести остальное к следующему этапу
На соревнованиях Memoriad и на Кубке мира по интеллектуальным вычислениям участники должны умножить 8-значные числа, например, 12345678 × 98702468, и самые быстрые участники могут сделать это за 15-30 секунд!
Чтобы попрактиковаться в этом, вы можете использовать программное обеспечение Memoriad – хотя я рекомендую начать с продуктов меньшего размера, состоящих из 3- и 4-значных чисел, прежде чем двигаться дальше.
Чтобы связаться со мной (Дэниел Тиммс) по поводу тренировки мысленных вычислений или чего-либо на этом сайте, вы можете связаться со мной здесь.
Ненавижу математику? Эти умственные уловки заставят вас размножаться быстрее, чем когда-либо мог Эйнштейн! «Mind Hacks :: WonderHowTo
2 + 2 = 4.
Это примерно столько математики, с которой я могу справиться без калькулятора каждый день. Я ненавижу заниматься математикой больше всего в жизни, в основном потому, что у меня это плохо получается – и я ненавижу делать то, что у меня не получается.
Итак, когда я натыкаюсь на классную математическую уловку в Интернете, которая утверждает, что облегчает жизнь таким людям, как я, я все слышу. Хотя вычисления (в основном) бесполезны для повседневной жизни среднего человека, умножение, сложение, вычитание и проценты – это все, что мы должны уметь делать – и без калькулятора.
Как большой поклонник TED Talks, я наткнулся на следующее видео, где Гаурав Текривал демонстрирует преимущества того, что называется ведической математикой, которая является базовым набором стратегий, помогающих упростить сложные вычисления.
Хотя происхождение этих учений несколько загадочно, стратегии весьма эффективны, и я буду помнить это каждый день. Может быть, математика все-таки не так уж сложна?
Вот несколько советов и приемов.
Как умножить двузначные числа на 11
Моя таблица умножения остановилась на 10, поэтому, помимо этого, я делаю вычисления, основываясь на памяти или подсчете в уме.Однако, используя ведическую математику, умножить на 11 совсем несложно.
Все, что вам нужно сделать, это сложить цифры числа, которое вы умножаете, на 11 и поместить его в середину исходного числа. Если сумма цифр 10 или больше, просто перенесите ее. Лучше увидеть, чем написать.
Видите, как легко это было? В принципе, если вы умеете складывать, вы знаете, как умножать на 11.
Теперь давайте посмотрим на другой пример.
Просто разделите число, умноженное на 11 (в данном случае также 11 ), чтобы между ними оставалось место для вашего числа.Теперь просто сложите две цифры этого числа вместе ( 1 + 1 = 2 ) и бросьте сумму в то место, которое вы оставили открытым. Это дает вам 121 .
Просто добавьте 5 + 8 , что даст вам 13 . Вставьте его между 5 и 8 , и вы получите 5138 . Но это неправильно, так как вам нужно перенести это. Перенесите его, и вы получите 638 .
Излишне говорить, что теперь, когда я это знаю, я чувствую себя полным задирой.
Как умножать числа, близкие к степени 10
В этом базовом методе используются степени 10 (десятки, сотни, тысячи и т. Д.), А также перекрестное вычитание и умножение сумм. Опять же, гораздо лучше видеть, что я говорю, чем пытаться это прочитать. Вот пример умножения двух двузначных чисел (основание сотен).
То, что делает Гаурав, на самом деле довольно просто.
Он берет разность каждого числа из 100 и помещает эти числа в правый столбец ( 99-100 = -01 и 97-100 = -03 ).
Затем он складывает один набор чисел (подойдет любая пара), чтобы получить первое число ответа. Итак, 99 + -03 или 97 + -01 = 96 . Итак, это будет первая часть ответа.
Теперь умножьте два меньших числа ( -01 x -03 ), чтобы получить вторую часть ответа. -01 х -03 = 03 . Итак, получаем ответ 9603 .
Итак, получаем ответ 9603 .
Довольно круто, правда?
Тот же метод работает для любого основания из десяти. 999 x 987 или 9 878 x 9 999 все будут работать с базой 1000 и 10000 соответственно. Вы можете увидеть это примерно на отметке 3:45 на видео.
Как умножить двузначные числа на любые другие двузначные числа
Самое интересное в математике – это наблюдение за тем, как кажущиеся невозможными комбинации кажутся идеальными в конце. Выполняя определенные операции, вы можете превратить чрезвычайно сложные уравнения в простые пошаговые решения.
Используя вертикальный и крестообразный паттерны, мы можем легко умножать большие двузначные числа, как на изображении ниже.
Вместо того, чтобы использовать метод умножения стоя, мы собираемся разделить и победить.
Сначала умножаем вертикально на правую сторону. 2 х 4 = 8 . Итак, 8 будет последней цифрой в нашем ответе.
Далее перемножаем крест-накрест. 3 x 2 = 6 и 4 x 1 = 4 . Теперь добавьте 6 + 4 , чтобы получить 10 . Перенесите 1 , как обычно, и у вас останется 0 , которое будет перед 8 , которые у нас уже есть.
Итак, теперь у вас должно быть 08 в строке ответа.
Наконец, мы вертикально умножаем левую часть. 3 x 1 = 3 и прибавляем перенесенное 1 . Поместите это перед строкой ответа, и мы получим 408 .
Как умножать, используя линии вместо чисел
Если вы больше визуальный ученик, который действительно ненавидит числа, вы также можете использовать их на японском языке и заменить эти цифры на строки, как это делает YouTuber kimelicious.Я не буду объяснять это – просто посмотрите, и вы увидите.
Разве вы не любите математику сейчас?
Есть несколько действительно удивительных математических трюков с использованием ведической математики, поэтому обязательно посмотрите полное видео, чтобы лучше понять это и начать использовать в своей повседневной жизни.
У вас есть какие-нибудь прикольные математические трюки? Дайте нам знать в комментариях.
Хотите освоить Microsoft Excel и вывести свои перспективы работы на дому на новый уровень? Начните свою карьеру с помощью нашего пакета обучения Microsoft Excel Premium от А до Я из нового магазина гаджетов и получите пожизненный доступ к более чем 40 часам инструкций от базового до расширенного по функциям, формулам, инструментам и многому другому.
Купить сейчас (97% скидка)>
Другие выгодные предложения, которые стоит проверить:
Оригинальные изображения обложек Джеймса Вестона / Shutterstock, Photosync / ShutterstockКак быстро умножить большие числа | by Maths and Musings
Алгоритм Тоома-Кука
Здесь мы узнаем о гениальном применении алгоритма «разделяй и властвуй» в сочетании с линейной алгеброй для быстрого умножения больших чисел. И введение в нотацию с большим О!
На самом деле этот результат настолько противоречит интуиции, что великий математик Колмогоров предположил, что такого быстрого алгоритма не существовало.
Часть 0: Длинное умножение – это медленное умножение. (И введение в нотацию Big-O)
Мы все помним, как в школе учились умножать. На самом деле, я должен признаться. Помните, это зона без суждения 😉
В школе у нас была «игра по мокрой дороге», когда шел дождь, слишком сильный для игры на детской площадке. В то время как другие дети (нормальные / веселые / позитивно-избранные) играли в игры и возились, я иногда брал лист бумаги и умножал большие числа, просто ради удовольствия.Настоящая радость вычислений! У нас даже было соревнование по умножению, «Супер 144», где нам нужно было как можно быстрее умножать скремблированные 12 на 12 сетку чисел (от 1 до 12). Я практиковал это неукоснительно до такой степени, что у меня были свои собственные заранее подготовленные листы практики, которые я делал фотокопии, а затем использовал по очереди. В конце концов я сократил свое время до 2 минут и 1 секунды, когда был исчерпан физический предел каракулей.
В то время как другие дети (нормальные / веселые / позитивно-избранные) играли в игры и возились, я иногда брал лист бумаги и умножал большие числа, просто ради удовольствия.Настоящая радость вычислений! У нас даже было соревнование по умножению, «Супер 144», где нам нужно было как можно быстрее умножать скремблированные 12 на 12 сетку чисел (от 1 до 12). Я практиковал это неукоснительно до такой степени, что у меня были свои собственные заранее подготовленные листы практики, которые я делал фотокопии, а затем использовал по очереди. В конце концов я сократил свое время до 2 минут и 1 секунды, когда был исчерпан физический предел каракулей.
Несмотря на эту одержимость умножением, мне никогда не приходило в голову, что мы можем сделать это лучше.Я потратил столько часов на умножение, но никогда не пытался улучшить алгоритм.
Рассмотрим умножение 103 на 222.
Вычислим 2 раза 3 раза 1 +2 раза 0 раз 10 + 2 раза 1 раз 100 + 20 раз 3 раза 1 + 20 раз 0 раз 10 + 20 раз 1 раз 100 = 22800
Как правило, для умножения на n-значные числа требуется O (n²) операций. Обозначение «большой О» означает, что если бы мы изобразили график числа операций как функцию от n, то значение n² действительно имеет значение.(1/3) то же самое? », И их, вероятно, вырвет в чашку с кофе, и они начнут плакать, и бормочут что-нибудь о топологии. По крайней мере, такова была моя реакция (сначала), а я почти ничего не знаю о топологии.
Обозначение «большой О» означает, что если бы мы изобразили график числа операций как функцию от n, то значение n² действительно имеет значение.(1/3) то же самое? », И их, вероятно, вырвет в чашку с кофе, и они начнут плакать, и бормочут что-нибудь о топологии. По крайней мере, такова была моя реакция (сначала), а я почти ничего не знаю о топологии.
Ок. Они не одинаковы. Но наш компьютер не заботится о топологии. Компьютеры различаются по производительности во многих отношениях, что я даже не могу описать, потому что я ничего не знаю о компьютерах.
Но настраивать каток нет смысла. Если две функции при больших значениях их входных данных растут на один и тот же порядок величины, то для практических целей это содержит большую часть важной информации.x при x = 100 уже намного больше, чем количество атомов во Вселенной. (10¹⁰⁰ >>>> 10⁸⁰, что является оценкой, числом Эддингтона, числа атомов во Вселенной согласно моему поиску в Google *).
* на самом деле я использовал DuckDuckGo.
Записывать целые числа как полиномы очень естественно и очень неестественно. Написание 1342 = 1000 + 300 + 40 + 2 очень естественно. Запись 1342 = x³ + 3x² + 4x + 2, где x = 10, немного странно.
В общем, предположим, что мы хотим умножить два больших числа с основанием b на n цифр в каждом.Мы записываем каждое n-значное число в виде многочлена. Если мы разделим n-значное число на r частей, этот многочлен будет содержать n / r членов.
Например, пусть b = 10, r = 3, и наше число 142,122,912
Мы можем превратить это в
Это очень хорошо работает, когда r = 3 и наше число, записанное в базе 10, состояло из 9 цифр. Если r не делит n идеально, мы можем просто добавить несколько нулей впереди. Опять же, лучше всего это проиллюстрировать на примере.
27134 = 27134 + 0 * 10⁵ = 027134, что мы представляем как
Почему это может быть полезно? Чтобы найти коэффициенты многочлена P, если многочлен имеет порядок N, то путем выборки его в N + 1 точках мы можем определить его коэффициенты.
Например, если полином x⁵ + 3x³ + 4x-2, который имеет порядок 5, выбирается в 6 точках, мы можем вычислить весь полином.
Интуитивно понятно, что многочлен 5-го порядка имеет 6 коэффициентов: коэффициент при 1, x, x², x³, x⁴, x⁵. Учитывая 6 значений и 6 неизвестных, мы можем узнать значения.
(Если вы знаете линейную алгебру, вы можете рассматривать различные степени x как линейно независимые векторы, создать матрицу для представления информации, инвертировать матрицу и вуаля )
Выборочные полиномы для определения коэффициентов (необязательно)
Здесь мы более подробно рассмотрим логику выборки многочлена для вывода его коэффициентов.Не стесняйтесь переходить к следующему разделу.
Мы покажем, что если два полинома степени N совпадают в N + 1 точках, то они должны быть одинаковыми. Т.е. N + 1 точек однозначно определяют полином порядка N .
Рассмотрим полином порядка 2. Он имеет вид P (z) = az² + bz + c . Согласно фундаментальной теореме алгебры – бесстыдство, вставьте сюда, я потратил несколько месяцев, собирая доказательство этого, а затем записывая его, вот – этот многочлен можно факторизовать.Это означает, что мы можем записать его как A (z-r) (z-w)
Согласно фундаментальной теореме алгебры – бесстыдство, вставьте сюда, я потратил несколько месяцев, собирая доказательство этого, а затем записывая его, вот – этот многочлен можно факторизовать.Это означает, что мы можем записать его как A (z-r) (z-w)
Обратите внимание, что при z = r и при z = w полином оценивается как 0 . Мы говорим, что w и r являются корнями полинома.
Теперь покажем, что P (z) не может иметь более двух корней. Предположим, у него есть три корня, которые мы называем w, r, s . Затем мы факторизуем многочлен. P (z) = A (z-r) (z-w). Тогда P (s) = A (s-r) (s-w). Это делает не равным 0, так как умножение ненулевых чисел дает ненулевое число.Это противоречие , потому что наше исходное предположение состояло в том, что s было корнем многочлена P.
Этот аргумент может быть применен к многочлену порядка N по существу идентичным образом.
Теперь предположим, что два полинома P и Q порядка N совпадают с N + 1 точками. Тогда, если они разные, P-Q является полиномом порядка N , который равен 0 при N + 1 точек.По предыдущему, это невозможно, так как полином порядка N имеет не более N корней. Таким образом, наше предположение должно быть ошибочным, и если P и Q совпадают по N + 1 точкам, они являются одним и тем же многочленом.
Увидеть – значит поверить: рабочий пример
Давайте посмотрим на действительно огромное число, которое мы называем p. В базе 10 p состоит из 24 цифр (n = 24), и мы разделим его на 4 части (r = 4). n / r = 24/4 = 6
p = 292 103 243 859 143 157 364 152.
И пусть представляющий его многочлен будет называться P,
P (x) = 292,103 x³ + 243,859 x² +143,157 x + 364,152
с P (10⁶) = p.
Поскольку степень этого полинома равна 3, мы можем вычислить все коэффициенты из выборки в 4 местах. Давайте почувствуем, что происходит, когда мы попробуем это в нескольких точках.
Давайте почувствуем, что происходит, когда мы попробуем это в нескольких точках.
- P (0) = 364,152
- P (1) = 1,043,271
- P (-1) = 172,751
- P (2) = 3,962,726
Поразительно то, что все они имеют 6 или 7 цифр.Это по сравнению с 24 цифрами, изначально найденными на стр.
Умножим p на q. Пусть q = 124,153,913,241,143,634,899,130 и
Q (x) = 124,153 x³ + 913,241 x² + 143,634 x + 899,130
Вычисление t = pq может быть ужасным. Но вместо того, чтобы делать это напрямую, мы пытаемся вычислить полиномиальное представление t, которое мы обозначаем T. Поскольку P является полиномом порядка r-1 = 3, а Q – полиномом порядка r-1 = 3, T равно полином порядка 2r-2 = 6.
T (10⁶) = t = pq
T (10⁶) = P (10⁶) Q (10⁶)
Хитрость в том, что мы вычислим коэффициентов T вместо прямого умножения p и q вместе.Тогда вычислить T (1⁰⁶) легко, потому что для умножения на 1 мы просто наклеиваем 6 нулей на обороте. Подвести итог по всем частям также легко, потому что добавление – очень дешевое действие для компьютеров.
Подвести итог по всем частям также легко, потому что добавление – очень дешевое действие для компьютеров.
Чтобы вычислить коэффициенты T, нам нужно выбрать его в 2r-1 = 7 точках, потому что это полином порядка 6. Мы, вероятно, захотим выбрать маленькие целые числа, поэтому мы выбираем
- T (0) = P ( 0) Q (0) = 364,152 * 899,130
- T (1) = P (1) Q (1) = 1,043,271 * 2,080,158
- T (2) = P (2) Q (2) = 3,962,726 * 5,832,586
- T (-1) = P (-1) Q (-1) = 172751 * 1544584
- T (-2) = P (-2) Q (-2) = -1,283,550 * 3,271,602
- T (3) = P (-3) Q (-3) = –5,757,369 * 5,335,266
Обратите внимание на размер P (-3), Q (-3), P (2), Q (2) и т.д. примерно n / r = 24/4 = 6 цифр.Некоторые из них 6-значные, некоторые – 7. По мере увеличения n это приближение становится все более и более разумным.
До сих пор мы свели проблему к следующим шагам или алгоритму:
(1) Сначала вычислите P (0), Q (0), P (1), Q (1) и т. Д. (малозатратное действие )
Д. (малозатратное действие )
(2) Чтобы получить наши 2r-1 = 7 значений T (x), мы должны теперь умножить 2r-1 числа приблизительного размера n / r цифр. А именно, мы должны вычислить P (0) Q (0), P (1) Q (1), P (-1) Q (-1) и т. Д. ( Действие с высокими затратами )
(3) Восстановить T (x) из наших точек данных.(n / r)) в целом для базы b и длины n]
Это хорошо ведет к анализу времени выполнения этого подхода.
Время выполнения
Из вышеизложенного мы выяснили, что, временно игнорируя действия low cost (1) и (3), стоимость умножения двух n-значных чисел с помощью алгоритма Тоома будет подчиняться:
Это то, что мы видели в отработанном примере. Умножение каждого P (0) Q (0), P (1) Q (1) и т. Д. Стоит T (n / r), потому что мы умножаем два числа длины примерно n / r.Мы должны сделать это 2r-1 раз, так как мы хотим выбрать T (x) – многочлен порядка 2r-2 – в 2r-1 местах.
Насколько это быстро? Мы можем решить подобные уравнения явно.
Теперь все, что осталось, – это некоторая беспорядочная алгебра
Поскольку были некоторые другие затраты, связанные с процессом умножения (‘повторной сборки’) матриц и сложением, мы не можем сказать, что наше решение является точным временем выполнения, поэтому вместо этого мы заключаем что мы нашли большой O среды выполнения
Оптимизация r
Эта среда выполнения все еще зависит от r.Исправьте r, и все готово. Но наше любопытство еще не удовлетворено!
Когда n становится большим, мы хотим найти приблизительно оптимальное значение для нашего выбора r. Т.е. мы хотим выбрать значение r, которое изменяется для разных значений n.
Ключевым моментом здесь является то, что при изменении r нам нужно обратить внимание на стоимость повторной сборки – матрица, которая выполняет эту операцию, имеет стоимость O (r²). Когда r было фиксированным, нам не нужно было на это смотреть, потому что по мере увеличения n при фиксированном r именно члены, содержащие n, определяли рост количества требуемых вычислений. Поскольку наш оптимальный выбор r будет увеличиваться с увеличением n, мы больше не можем игнорировать это.
Поскольку наш оптимальный выбор r будет увеличиваться с увеличением n, мы больше не можем игнорировать это.
Это различие очень важно. Первоначально наш анализ выбрал значение r, может быть, 3, возможно, 3 миллиарда, а затем посмотрел на большой размер O, когда n стало на произвольно большим. Теперь мы смотрим на поведение, когда n растет произвольно большим и r растет с n с некоторой скоростью, которую мы определяем . Это изменение перспективы рассматривает O (r²) как переменную, тогда как, когда r оставалось фиксированным, O (r²) было константой, хотя мы и не знали.
Итак, мы обновляем наш анализ по сравнению с предыдущим:
, где O (r²) представляет собой стоимость матрицы повторной сборки. Теперь мы хотим выбрать значение r для каждого значения n, что приблизительно минимизирует это выражение. Чтобы минимизировать, сначала попробуем дифференцировать по r. Это дает несколько отвратительно выглядящее выражение
Обычно, чтобы найти точку минимума, мы устанавливаем производную равной 0. Но это выражение не имеет хорошего минимума. Вместо этого мы находим «достаточно хорошее» решение.sqrt (logN), которое было нашим предполагаемым значением. «X» заменяет «r», и на каждом из трех изображений используется различное значение N.
Но это выражение не имеет хорошего минимума. Вместо этого мы находим «достаточно хорошее» решение.sqrt (logN), которое было нашим предполагаемым значением. «X» заменяет «r», и на каждом из трех изображений используется различное значение N.
Меня убедило, что наш выбор был удачным. Выбрав r, мы можем подключить его и посмотреть, как наш алгоритм получает последний большой O:
, где мы просто вставили наше значение для r и использовали приближение для log (2r-1) / log (r), которое очень точен для больших значений r.
Возможно, я не заметил этого алгоритма, когда был маленьким мальчиком и делал умножение, и это было разумным.На графике ниже я даю коэффициент нашей функции большого O равный 10 (в демонстрационных целях) и делю его на x² (поскольку исходный подход к умножению был O (n²). Если красная линия стремится к 0, то это будет показывать наше новое время работы асимптотически работает лучше, чем O (n²).
И действительно, хотя форма функции показывает, что наш подход на , в конечном итоге на быстрее, и в конечном итоге намного быстрее, мы должны подождите, пока у нас не будет почти 400-значных чисел, чтобы это имело место! Даже если бы коэффициент был всего 5, числа должны были бы состоять примерно из 50 цифр, чтобы увидеть улучшение скорости.
Для моего 10-летнего «я» умножение 400-значных чисел было бы непростой задачей! Отслеживать различные рекурсивные вызовы моей функции также было бы довольно сложно. Но для компьютера, выполняющего задачу в области искусственного интеллекта или физики, это обычная проблема!
Что мне нравится в этой технике, так это то, что она , а не ракетостроение . Это не самая ошеломляющая математика, которую когда-либо можно было открыть. Оглядываясь назад, возможно, это кажется очевидным!
И все же в этом блеск и красота математики.Я читал, что Колмогоров на семинаре выдвинул гипотезу о том, что умножение – это, по сути, O (n²). Колмогоров в основном изобрел множество современной теории вероятностей и анализа. Он был одним из величайших математиков 20 века. Но когда дело дошло до этой несвязанной области, оказалось, что целый массив знаний, ждущих своего открытия, сидит прямо у него и у всех под носом!
Фактически, алгоритмы Divide and Conquer и сразу приходят в голову сегодня, поскольку они так широко используются. Но они являются продуктом компьютерной революции в том смысле, что человеческий разум сосредоточился именно на скорости вычислений как области математики, достойной изучения как таковой, только благодаря огромной вычислительной мощности.
Но они являются продуктом компьютерной революции в том смысле, что человеческий разум сосредоточился именно на скорости вычислений как области математики, достойной изучения как таковой, только благодаря огромной вычислительной мощности.
Вот почему математики не хотят просто признать, что гипотеза Римана верна только потому, что кажется, что она может быть правдой, или что P не равно NP только потому, что это кажется наиболее вероятным. Прекрасный мир математики всегда сохраняет способность опровергать наши ожидания.
Фактически, вы можете найти еще более быстрые способы умножения. Современные лучшие подходы используют быстрое преобразование Фурье. Но я приберегу это на другой день 🙂
Дайте мне знать, что вы думаете ниже. Я недавно в Твиттере под именем ethan_the_mathmo , вы можете подписаться на меня здесь .
Я столкнулся с этой проблемой в замечательной книге, которую использую, под названием «Природа вычислений» физиков Мура и Мертенса, где одна из задач проведет вас через анализ алгоритма Тоома.
10 советов по совершенствованию своих умственных математических способностей
Иллюстрация: Елена Скотти / Gizmodo, Shutterstock
Калькуляторы прекрасны, но не всегда удобны. Более того, никто не хочет, чтобы его видели, когда он тянется к калькулятору на своем мобильном телефоне, когда приходит время рассчитывать 15-процентное вознаграждение. Вот десять советов, которые помогут вам вычислить числа в своей голове.
Мысленная математика не так сложна, как может показаться, и вы можете быть удивлены тем, насколько легко производить, казалось бы, невозможные вычисления, используя только свой прекрасный мозг.Вам просто нужно запомнить несколько простых правил.
Сложить и вычесть слева направо Помните, как в школе вас учили складывать и вычитать числа справа налево (не забывайте носить одно!)? Это нормально, когда вы занимаетесь математикой с карандашом и бумагой, но при выполнении мысленной математики лучше делать это, двигаясь слева направо. Переключение порядка таким образом, чтобы вы начинали с самых больших значений, делает его немного более интуитивным и более простым для понимания.Итак, прибавляя 58 к 26, начните с первого столбца и вычислите 50 + 20 = 70, затем 8 + 6 = 14, что в сумме дает 84. Легко, легко.
Переключение порядка таким образом, чтобы вы начинали с самых больших значений, делает его немного более интуитивным и более простым для понимания.Итак, прибавляя 58 к 26, начните с первого столбца и вычислите 50 + 20 = 70, затем 8 + 6 = 14, что в сумме дает 84. Легко, легко.
Столкнувшись со сложным расчетом, попробуйте найти способ упростить задачу, временно изменив значения. Например, при вычислении 593 + 680 прибавьте 7 к 593, чтобы получить 600 (более управляемо). Вычислите 600 + 680, что составляет 1280, а затем уберите эти дополнительные 7, чтобы получить правильный ответ – 1273.
То же самое можно сделать и с умножением. Для 89×6 вместо этого вычислите 90×6, а затем вычтите эти дополнительные 6, так что 540-6 = 534.
Запоминание строительных блоков
Запоминание таблиц умножения – важный аспект умственной математики, и его нельзя сбрасывать со счетов.
Спенсер Гринберг, математик и основатель ClearerThinking. org, говорит, что, запоминая эти базовые «строительные блоки» математики, мы можем мгновенно получить ответы на простые задачи, которые встроены в более сложные.Так что, если вы забыли эти таблицы, было бы полезно поскорее освежить их в памяти. Пока вы это делаете, запоминайте свои таблицы 1 / n, чтобы вы могли быстро вспомнить, что 1/6 – это 0,166, 1/3 – это 0,333, а 3/4 – это 0,75.
org, говорит, что, запоминая эти базовые «строительные блоки» математики, мы можем мгновенно получить ответы на простые задачи, которые встроены в более сложные.Так что, если вы забыли эти таблицы, было бы полезно поскорее освежить их в памяти. Пока вы это делаете, запоминайте свои таблицы 1 / n, чтобы вы могли быстро вспомнить, что 1/6 – это 0,166, 1/3 – это 0,333, а 3/4 – это 0,75.
Чтобы помочь вам выполнить простое умножение, важно запомнить некоторые изящные приемы. Одно из наиболее очевидных правил состоит в том, что любое число, умноженное на 10, просто должно иметь ноль в конце. При умножении на 5 ваш ответ всегда будет оканчиваться либо на 0, либо на 5.
Кроме того, при умножении числа на 12 всегда получается 10 умножить на два больше этого числа. Например, при вычислении 12×4 сделайте 4×10 = 40 и 4×2 = 8, а затем 40 + 8 = 48. Один из моих любимых – умножение на 15: просто умножьте свое число на 10, а затем добавьте половину к ответу (например, 4×15 = 4×10 = 40, плюс половина этого ответа, 20, что даст вам 60).
Есть еще хитрый способ умножения на 16. Сначала умножьте рассматриваемое число на 10, а затем умножьте половину числа на 10.Затем сложите эти два результата вместе с самим числом, чтобы получить окончательный ответ. Итак, чтобы вычислить 16 x 24, сначала вычислите 10 x 24 = 240, затем вычислите половину 24, которая равна 12, и умножьте на 10, получив 120. Простая математика завершает это: 240 + 120 + 24 = 384.
Подобные уловки существуют и для других номеров, о которых вы можете прочитать здесь.
Квадраты – ваши друзья
Эти простые приемы хороши и хороши, но большие числа представляют собой другую проблему. Для этого физик из аскаматематика.com говорит, что это хорошая идея – использовать разницу квадратов (квадрат – это число, умноженное на само себя).
«Возьмите два числа, которые вы умножаете, и думайте о них как об их среднем, x, плюс и минус разница между каждым и их средним значением, ± y», – говорит он. «Эти два числа возведены в квадрат, поэтому вместо запоминания целых таблиц умножения вы запоминаете только квадраты».
Это может показаться сложной задачей, но запомнить все квадраты от 1 до 20 не так уж и плохо, как кажется.В конце концов, это всего лишь 20 чисел. Вооружившись этими предварительными знаниями, вы можете выполнять довольно невероятные вычисления.
Вот как это работает. Начнем с простого примера. Предположим на мгновение, что мы не знаем ответа на вопрос 10×4. Первый шаг – вычислить среднее число между этими двумя числами, которое равно 7 (т. Е. 10-3 = 7 и 4 + 3 = 7). Затем определите квадрат 7, который равен 49. Теперь у нас есть близкое, но недостаточно близкое число. Чтобы получить правильный ответ, мы должны возвести в квадрат разницу между средним (в данном случае 3) и получить 9.Последний шаг – выполнить простое вычитание, 49–9 = 40, и разве вы не знаете, что у вас есть правильный ответ.
Это может показаться окольным способом вычисления 10×4 (это так), но тот же метод работает для больших чисел. Возьмем, к примеру, 15×11. Еще раз, мы должны найти среднее число между этими двумя, которое равно 13. Квадрат 13 равен 169. Квадрат разницы среднего (2) равен 4. Наконец, 169-4 = 165, правильный ответ. .
Квадрат 13 равен 169. Квадрат разницы среднего (2) равен 4. Наконец, 169-4 = 165, правильный ответ. .
Приблизительно
При мысленном вычислении, особенно для больших чисел, часто бывает хорошей идеей сделать осознанную оценку и не беспокоиться о получении точного ответа.Например, еще во время Манхэттенского проекта физик Энрико Ферми хотел приблизительно оценить мощность атомного взрыва до получения диагностических данных. С этой целью он ронял листы бумаги, когда взрывная волна ударила его (с безопасного расстояния, курс). Измерив пройденное расстояние, он оценил силу взрыва примерно в 10 килотонн в тротиловом эквиваленте. Эта оценка была довольно точной, так как истинный ответ был 20 килотонн в тротиловом эквиваленте.
Этот метод, теперь известный как «оценка Ферми», работает, оценивая числа в степени десяти (подробнее см. Видео TED-Ed выше).Поэтому, когда вы пытаетесь придумать, казалось бы, невозможное решение, полезно разбивать элементы таким образом, а затем разбивать их на части. Например, при попытке оценить количество настройщиков пианино в вашем городе, сначала оцените население вашего города (например, 1000000), затем оцените количество пианино (10000), а затем количество настройщиков фортепиано (например, 100). Вы не получите точного ответа, но получите ответ быстро, причем часто достаточно близкий.
Например, при попытке оценить количество настройщиков пианино в вашем городе, сначала оцените население вашего города (например, 1000000), затем оцените количество пианино (10000), а затем количество настройщиков фортепиано (например, 100). Вы не получите точного ответа, но получите ответ быстро, причем часто достаточно близкий.
Если сомневаетесь, переставьте
Чтобы преобразовать сложные задачи в более простую форму, рекомендуется использовать математические правила.Например, вычисление задачи 5x (14 + 43) само по себе является сложной задачей, но ее можно разбить на три довольно управляемых вычисления. Помня ваш порядок действий, эту задачу можно перефразировать как (5×14) + (5×40) + (5×3) = 285.
Превратите большую проблему в кучу мелких
Если есть сомнения, разбейте ее на части. «Для многих проблем способ быстро решить их – разбить их на подзадачи и решить их», – говорит Гринберг. «Когда вы сталкиваетесь с проблемой, которая кажется сложной, часто бывает полезно найти способы разбить ее на более простые проблемы, которые вы уже знаете, как решать. ”
”
Например, вы можете умножить на 8, удвоив три раза. Поэтому вместо того, чтобы пытаться вычислить 12×8, просто удваиваю 12 три раза: 24, 48, 96. Или при умножении на 5 я начинаю с умножения на 10, так как это легко, а затем делю на 2, поскольку это тоже обычно довольно легко. Например, для 5×18 вместо этого вычислите 10×18 и разделите на 2, где 180/2 = 90.
Используйте научную запись для неоправданно больших чисел
При вычислении больших чисел в уме помните, что вы можете сначала преобразовать их в экспоненциальную запись.Что получится 44 миллиарда разделить на 400 000? Простой способ справиться с этим – преобразовать 4 миллиарда в 10 9 и 400000 в 10 5 . Теперь мы можем выразить это как 44/4 и 10 9 /10 5 . Как указывает Гринберг, правило деления показателей требует от нас их вычитания (легко!), Поэтому мы получаем 11 x 10 (9-5) = 11 x 10 4 = 110 000.
Простейший способ расчета чаевых
Наконец, несколько советов о том, как рассчитать чаевые в уме. Если вы можете подсчитать 10-процентные чаевые в уме (легко), то вы можете рассчитать и 20-процентные, и 15-процентные чаевые.
Если вы можете подсчитать 10-процентные чаевые в уме (легко), то вы можете рассчитать и 20-процентные, и 15-процентные чаевые.
При расчете 10-процентных чаевых за обед, который стоит 112,23 доллара, просто переместите десятичную запятую на одну позицию влево, получив 11,22 доллара. При подсчете 20-процентных чаевых сделайте то же самое, но просто удвойте ответ (20-процентные чаевые вдвое больше, чем 10-процентные чаевые), который в данном случае составляет 22,44 доллара.
Для 15-процентных чаевых еще раз вычислите 10-процентные чаевые, а затем прибавьте половину (дополнительные 5 процентов составляют лишь половину от 10-процентной суммы).Итак, $ 11,22 + (11,22 / 2). Не волнуйтесь, если вы не можете получить точный ответ. Если не особо беспокоиться о десятичных точках, мы можем быстро подсчитать, что чаевые в размере 15 процентов в размере 112,23 доллара равны 11 + 5,50 доллара, что составляет 16,50 доллара. Достаточно близко. Добавьте четверть или две, если вы беспокоитесь о снижении производительности сервера.
Поделитесь, пожалуйста, другими интересными советами в комментариях!
Умножение × | Основы арифметики
На этой странице описаны основы умножения (×) .
См. Другие наши арифметические страницы для обсуждения и примеров: Сложение (+), Вычитание (-) и Деление ( ÷ ).
Умножение
При записи общий знак умножения – « × ». В электронных таблицах и некоторых других компьютерных приложениях символ « * » (или звездочка) используется для обозначения операции умножения.
Чтобы выполнять вычисления умножения без калькулятора или электронной таблицы, вам необходимо знать, как складывать числа.См. Нашу страницу добавления, чтобы узнать, как добавить.
Когда вы «умножаете» или «умножаете» число, вы добавляете его к самому себе несколько раз, например, умножение 4 на 3 – это то же самое, что сказать 4 + 4 + 4 = 12. Следовательно, умножение – это более быстрый способ сложения одно и то же число много раз, например 3 × 4 = 12. Этот расчет аналогичен выражению, если у меня есть 3 пакета по 4 яблока, сколько всего яблок у меня есть?
Этот расчет аналогичен выражению, если у меня есть 3 пакета по 4 яблока, сколько всего яблок у меня есть?
Основные правила умножения:
- Любое число, умноженное на 0, равно 0.200 × 0 = 0
- Любое число, умноженное на 1, остается неизменным. 200 × 1 = 200.
- Когда число умножается на два, мы удваиваем число. 200 × 2 = 400.
- Когда целое число умножается на 10, мы можем просто написать 0 в конце (один ноль из 10, потому что это 1 × 10). 200 × 10 = 2000.
- При умножении на 100 мы записываем два нуля в конце, на тысячу записываем три нуля в конце и так далее. Например, 4 × 2000 – это 4 × 2 = 8 с 3 нулями: 8000.
Для простого и быстрого умножения полезно запомнить умножение или «таблицу умножения », как показано ниже. Эта таблица дает ответы на все умножения до 10 × 10. Чтобы получить ответ на 4 × 6, например, найдите 4 в верхней (заштрихованной красным) строке и найдите 6 в левом (заштрихованном красным) столбце – столбец точка пересечения двух линий и есть ответ: 24 .
Неважно, с какой стороны искать числа; если вы найдете 4 в первом столбце и 6 в первой строке, вы получите тот же ответ, 24.
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Приведенная выше таблица может помочь нам быстро вычислить ответ на следующую проблему. Меган ведет в кинотеатр троих братьев, всего ей нужно купить 4 билета, каждый стоит 8 фунтов. Во сколько обойдется поездка? Нам нужно вычислить 4 лота по 8 фунтов стерлингов, что написано 4 × 8.
Меган ведет в кинотеатр троих братьев, всего ей нужно купить 4 билета, каждый стоит 8 фунтов. Во сколько обойдется поездка? Нам нужно вычислить 4 лота по 8 фунтов стерлингов, что написано 4 × 8.
Найдите 4 в вертикальном красном столбце и 8 в горизонтальном красном столбце, ответ находится в ячейке, где пересекаются две линии: 32 . Стоимость похода в кинотеатр составит 32 фунтов стерлингов.
Часто бывает необходимо умножать числа больше 10.В этом случае приведенная выше таблица умножения не может дать немедленного ответа. Однако мы все еще можем использовать его, чтобы упростить расчет.
Лиза занимается ресторанным бизнесом. Она должна доставить бутерброды 23 предприятиям, в каждом из которых работает 14 сотрудников. Если предположить, что каждый сотрудник съедает один бутерброд, сколько бутербродов нужно приготовить Лизе?
23 предприятиям нужно 14 бутербродов, что составляет 23 лота по 14 или, другими словами, 23, умноженные на 14. Как мы уже обнаружили, мы можем записать расчет наоборот.14 × 23. Ответ будет таким же.
Как мы уже обнаружили, мы можем записать расчет наоборот.14 × 23. Ответ будет таким же.
Нам нужно найти ответ на расчет 23 × 14.
Сначала запишите свои числа в столбцы, представляющие сотни, десятки и единицы (за помощью см. Нашу страницу Числа ).
| Сот | Десятки | шт. |
| 2 | 3 | |
| 1 | 4 |
Шаг 1: Начиная с правого столбца (единицы), умножьте 4 на 3.При необходимости вы можете обратиться к приведенной выше таблице умножения. Напишите ответ (12) под своими вычислениями, стараясь поставить 1 в столбце десятков и 2 в столбце единиц.
Синие числа – это те, над которыми мы сейчас работаем, а розовые числа – это первая часть нашего ответа.
| Сотни | Десятки | шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 |
Шаг 2: Затем мы умножаем 4 на следующее число, равное 2 (или 20, потому что оно находится в столбце десятков). Напишите свой ответ внизу в столбце десятков: мы напишем 8 в столбце десятков (4 раза по 2 десятка) и ноль в столбце единиц (4 раза по 2 десятка это то же самое, что 4 × 20 = 80).
Напишите свой ответ внизу в столбце десятков: мы напишем 8 в столбце десятков (4 раза по 2 десятка) и ноль в столбце единиц (4 раза по 2 десятка это то же самое, что 4 × 20 = 80).
| Сотни | Десятки | шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 |
Шаг 3: В приведенных выше шагах мы умножили единицы нижнего числа (4) на верхнее число (23).Затем нам нужно умножить десятки в нижнем числе (1) на верхнее число (23). Теперь мы работаем с цифрой в столбце десятков нижнего числа и повторяем шаги, описанные выше. Оглядываясь на наши основные правила умножения, приведенные выше, мы знаем, что, умножая число на 10, мы пишем ноль в конце. На этом этапе, поскольку мы переместились по столбцу и работаем с десятками, мы должны не забыть записать нули в первый столбец (единицы).
Выполните 1 × 3. Как и выше, мы записываем наш ответ (3) в столбец десятков и (0) в столбец единиц.
| Сотни | Десятки | шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 |
Шаг 4: Последнее умножение, которое нам нужно выполнить, – 1 × 2.Оба числа находятся в столбце десятков, поэтому мы умножаем один лот из 10 на два лота по 10. Используя правила, которые мы узнали на предыдущих шагах, нам нужно записать ноль в столбец единиц и ноль в столбец десятков. Наш ответ (1 × 2 = 2) записан в столбце сотен, потому что мы фактически вычислили 10 × 20 = 200.
| Сотни | Десятки | шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 | |
| 2 | 0 | 0 |
Этап 5: На этом этапе мы закончили умножение; остается только сложить все наши ответы (розовые числа), чтобы найти общее количество необходимых бутербродов. См. Нашу страницу Дополнение , если вам нужна помощь с суммированием чисел.
См. Нашу страницу Дополнение , если вам нужна помощь с суммированием чисел.
| Сот | Десятки | шт. | |
| 2 | 3 | ||
| 1 | 4 | ||
| 1 | 2 | ||
| 8 | 0 | ||
| 3 | 0 | ||
| 2 | 0 | 0 | |
| Всего: | 3 | 2 | 2 |
12 + 80 + 30 + 200 = 322. Мы подсчитали, что Лизе нужно сделать в общей сложности 322 бутербродов.
В приведенном выше примере показано, как выполнить умножение, разделенное на все возможные части, но по мере повышения уверенности можно пропустить шаги.
Мы могли бы, например, умножить 4 на 23, разбив сумму на две части:
4 × 20 = 80
4 × 3 = 12
80 + 12 = 92
| Сотни | Десятки | шт. |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 |
То же для второго столбца:
10 × 23 = 230
| Сот | Десятки | шт. |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 | |
| 2 | 3 | 0 |
Наконец, мы складываем два наших ответа:
| Сот | Десятки | шт. | |
| 2 | 3 | ||
| 1 | 4 | ||
| 9 | 2 | ||
| 2 | 3 | 0 | |
| Всего: | 3 | 2 | 2 |
92 + 230 = 322.
Умножение более двух чисел
Если вам нужно перемножить более двух элементов, обычно проще перемножить первые два элемента, получить результат, а затем умножить следующее число на первое число. Например, если Джо хотел вычислить, сколько часов он проработал за четырехнедельный период, то расчет выглядел бы так:
Джо работает 7 часов в день 5 дней в неделю в течение четырех недель.
Шаг первый:
7 × 5 = 35 (количество часов, которые Джо работает за одну неделю).
Шаг второй:
Чтобы узнать, сколько часов Джо работает за четыре недели, мы можем затем умножить этот ответ (35) на 4. 35 × 4 = 140.
Если мы знаем, что Джо платят 12 фунтов в час, мы можем затем подсчитать, сколько денег он заработал за четырехнедельный период: 12 × 140.
Быстрый способ решить это – вычислить:
10 × 140 = 1400 (помните, что если мы умножаем на 10, мы просто добавляем ноль в конец числа, на которое мы умножаем).
2 × 140 = 280 то же, что 2 × 14 (с нулем на конце) или 140 + 140.
Мы складываем наши ответы вместе: 1400 + 280 = 1680.
Таким образом, Джо заработал 1 680 фунтов стерлингов за четырехнедельный период.
Умножение отрицательных чисел
Умножение отрицательного числа на положительное всегда дает отрицательный ответ:
15 × (−4) = −60
Умножение отрицательного числа на другое отрицательное число всегда дает положительный ответ:
(−15) × (−4) = 60
Как умножать большие числа | Более быстрый способ умножить
- Умножать большие числа сложно.В 1971 году два немецких профессора предсказали алгоритм, который упростит задачу, но никто так и не доказал его.
- До сих пор.
- Математики из Австралии и Франции говорят, что их алгоритм может сделать умножение и другие виды арифметики намного более эффективными.
Начиная с начальной школы, сложное умножение было головной болью. Но доцент из Сиднейского университета Нового Южного Уэльса в Австралии разработал новый метод умножения гигантских чисел, который более эффективен, чем «длинное умножение», которому многих учат в раннем возрасте.
Но доцент из Сиднейского университета Нового Южного Уэльса в Австралии разработал новый метод умножения гигантских чисел, который более эффективен, чем «длинное умножение», которому многих учат в раннем возрасте.
«Технически мы доказали гипотезу Шёнхаге и Штрассена 1971 года о сложности целочисленного умножения», – говорит доцент Дэвид Харви в видео ниже.
Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.
Алгоритм Шёнхаге – Штрассена, разработанный двумя немецкими математиками, на самом деле был самым быстрым методом умножения с 1971 по 2007 год.Хотя более быстрый метод был разработан в 2007 году, сегодня он используется редко.
Шёнхаге и Штрассен предсказали, что должен существовать алгоритм, умножающий n -значных чисел с использованием основных операций n * log ( n ), говорит Харви. Его статья – первое известное доказательство того, что это так.
Харви берет пример 314, умноженного на 159 – большое уравнение, конечно, но гораздо более крупные уравнения используются каждый день в реальных сценариях. Чтобы решить эту проблему, большинство людей учат умножать каждое отдельное число вместе, а затем складывать суммы:
9 умножается на 4, 1 и 3; затем 5 умножается на 4, 1, 3 и так далее.В результате получается 9 продуктов с цифрой за цифрой.
Этот метод называется n 2 или n в квадрате, потому что нужно умножить n на n несколько раз. Ответ будет правильный, но Шёнхаге и Штрассен разработали более быстрый метод. Он смог перейти от n 2 к чему-то меньшему, но проблема все же возникла в виде n * log ( n ).
Некоторым может быть достаточно увидеть слово в середине математической задачи, чтобы глаза потускнели, как на уроке алгебры.Напоминаем: log – это сокращение от logarithm, которое помогает людям расшифровывать показатели, которые возводят числа в квадрат или куб, или даже что-то большее. Итак, 2⁵ равно 32, но при логарифмическом выражении это будет выглядеть как log₂ (32) = 5. Хотя это может показаться скучным, логарифмы имеют решающее значение, когда числа становятся намного больше.
Итак, 2⁵ равно 32, но при логарифмическом выражении это будет выглядеть как log₂ (32) = 5. Хотя это может показаться скучным, логарифмы имеют решающее значение, когда числа становятся намного больше.
По словам Харви, метод Шёнхаге-Штрассена очень быстр. Если бы компьютер применил метод возведения в квадрат, которому учат в школе, для решения задачи, где у двух чисел есть миллиард цифр каждое, на это потребовались бы месяцы.Компьютер, использующий метод Шенхаге-Штрассена, мог сделать это за 30 секунд.
Но если цифры будут продолжать расти до триллионов и более, алгоритм, разработанный Харви и его соавтором Йорисом ван дер Хувеном из Политехнической школы во Франции, сможет найти решения быстрее, чем алгоритм Шёнхаге-Штрассена 1971 года.
«Это означает, что вы можете более эффективно выполнять всевозможные арифметические операции, например деление и извлечение квадратного корня», – говорит он. «Вы также можете вычислять цифры числа Пи более эффективно, чем раньше. У него даже есть приложения к задачам, связанным с огромными простыми числами.
У него даже есть приложения к задачам, связанным с огромными простыми числами.
«Люди охотились за таким алгоритмом почти 50 лет», – продолжает он. Вывод о том, что кто-то в конечном итоге добьется успеха, нельзя было игнорировать. Может оказаться, что Шёнхаге и Штрассен ошибались и что такого алгоритма не было возможно.
«Но теперь мы знаем лучше», – говорит он. Дэвид Гроссман Дэвид Гроссман – штатный автор PopularMechanics.com.
Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти дополнительную информацию об этом и подобном контенте на сайте piano.io.
12 математических приемов, которые помогут вам решать задачи без калькулятора | Автор: Эндрю Джеймисон
Разбираем в голове
Фото Крисси Джарвис на Unsplash1. Дополнение
Первый трюк – упростить задачу, разбив ее на более мелкие части.Например, можно переписать
567 + 432
= 567 + (400 + 30 + 2)
= 967 + 30 + 2
= 997 + 2
= 999
Switch
Часто проще работать с добавив меньшее число, чтобы вместо 131 + 858 поменять местами числа
858 + 131
= 858 + 100 + 30 + 1
= 989
2.
 Вычитание
ВычитаниеИспользование дополнения числа может помочь сделать вычитание проще. Дополнение – это разница между исходным числом и круглым числом, например 100, 1000.
Вот несколько примеров с числом и его дополнением по сравнению с 100:
67:33, 45:55, 89:11, 3:97
Обратите внимание, что вторая цифра в сумме дает 10, а первая цифра добавляет до 9.
Вот как это помогает
721–387
# дополнение 87 равно 13, поэтому мы можем поменять местами 387 на 400 - 13
-> 721 - (400-13)
= 321 - - 13
= 321 + 13
= 334
Другой способ – записать большее число, чтобы оно оканчивалось на 99.В том же примере:
721 -> (699 + 22)Фотография Криса Ливерани на Unsplash
= 699 - 387 + 22
= 312 + 22
= 334
3. Elevens
Для двузначного числа число, сложите цифры и поместите ответ в середину числа, которое вы умножаете:
35 x 11
-> 3 _ 5
-> 3 + 5 = 8
-> 3 8 5
Если сумма больше 10, добавьте цифру десятков в следующий столбец слева и запишите цифру единиц в ответ. Например, 4 + 8 = 12, запишите 2 и перенесите 1 в следующий столбец.
Например, 4 + 8 = 12, запишите 2 и перенесите 1 в следующий столбец.
48 x 11
-> 4_8
-> 4 + 8 = 12
-> 4,12,8
-> 528
Процесс немного сложнее для трехзначных и больших чисел, но он работает аналогичным образом. На этот раз сохраните первую и последнюю цифру и просуммируйте цифры попарно
725 X 11
-> 7__5
-> 7 _, (7 + 2 = 9), (2 + 5 = 7), _5
-> 7975 51973 x 11
-> 5__3
-> 5 _, (5 + 1 = 6), (1 + 9 = 10), (9 + 7 = 16), (7 + 3 = 10), _3
# где сумма больше десяти, мы перемещаем цифру десятков в следующий столбец
-> 5, (6 + 1), (0 + 1), (6 + 1), (0), 3
-> 571703
4.Девятки
Умножение на девять можно упростить, умножив на 10 и вычтя исходное число
799 x 9
= 799 x (10-1)
= 7990-799
= 7191
Используйте тот же метод для всего оканчивается на 9
72 x 89
= 72 x (90–1)
= (70 x 90) + (2 x 90) - 72
= 6300 + 180–72
= 6408
5.
 2
2 # мы прибавляем 3 к 57, так как 60 легче умножить, чем 57, и вычтите 3 из второго 57
-> 60 x 54 + 9
= 3000 + 240 + 9
= 3249
Конечный пример – когда вы возводите в квадрат число, заканчивающееся на 5, а затем округляете одно число в большую сторону до ближайшего 10, другое число до ближайшего 10 и прибавить 25.2
= 4200 + 25
= 4225
6. Метод близкого совпадения
Аналогичный метод работает для умножения близких чисел. Формула работает для всех чисел, но не может хорошо упрощаться, если числа не похожи.
Вот формула. n – «базовое» число
(n + a) (n + b) = n (n + a + b) + ab
Пример:
47 x 43
= (40 + 7) (40 + 3)
= 40 x (40 + 3 + 7) + (7 x 3)
= (40 x 50) + (7 x 3)
= 2000 + 21
= 2021
В этом примере единицы цифры в сумме дают десять, поэтому наше «базовое» число и множитель – круглые числа (40 и 50).
Вот еще пример. Уменьшите меньшее число, чтобы получить ближайшее круглое число – наше базовое число, в данном случае 40. Добавьте разницу к большему числу. Умножьте основание на большее число. Наконец, добавьте произведение разницы между исходными числами и основным числом.
47 x 42
= (40 + 7) x (40 + 2)
= (40 + 7 + 2) x 40 + (7 x 2)
= (49 x 40) + (7 x 2)
= (40 x 40) + (40 x 9) + (7 x 2)
= 1600 + 360 + 14
= 1974
Вы также можете округлить до основного числа.Поскольку исходные числа меньше основания, мы складываем произведение двух отрицательных чисел.
47 x 42
= (50 x 39) + (-3 x -8)
= (50 x 30) + (50 x 9) + (-3 x -8)
= 1500 + 450 + 24
= 1974
Это работает и для трехзначных чисел. В этом случае базовое число находится между нашими числами, поэтому произведение является отрицательным числом.
497 x 504Фотография Сандро Шу на Unsplash
= (500-3) x (500 + 4)
= (500) x (500 + 4-3) + (-3 x 4)
= 500 x 501 - 12
= 250,000 + 500 - 12
= 250,488
7.
 Упростите вычисления
Упростите вычисленияВы можете упростить некоторые уравнения еще до того, как начнете. Например, разделите делитель и делимое на два.
898/4
= 449/2
= 224 и ½
Обратите внимание, что с помощью этого метода вы должны записать остаток в виде дроби:
898/4 имеет остаток 2 - деленный на 4
449/2 остаток равен 1 - делится на 2
Дробь такая же, но абсолютное число другое.
При делении на 5 измените уравнение, умножив на 2.Гораздо проще разделить на 10. Например:
1753/5
= 3506/10
= 350,6
8. Проверка на делимость
Есть много способов быстро определить, является ли число множителем.
2 : Число четное.
Пример 28790 четный, поэтому он делится на 2.
3 : Сумма цифр делится на 3.
Пример: 1281 -> 1 + 2 + 8 + 1 = 12
-> 12 кратно 3, поэтому 1281 делится на 3
4 : Последние две цифры делятся на 4. Почему это работает? 100 кратно 4, поэтому нам нужно проверить только две последние цифры.
Почему это работает? 100 кратно 4, поэтому нам нужно проверить только две последние цифры.
Пример: 1472, 72 делится на 4, поэтому 1472 делится на 4.
5 : Число заканчивается на 5 или 0.
Пример: 575 заканчивается на 5, поэтому оно делится на ноль
6 : Число четное, а сумма цифр делится на 3. 6 равно 3 x 2, поэтому применяются правила 2 и 3.
Пример: 774 четно и 7 + 7 + 4 = 18
-> 18 делится на 3, поэтому 774 делится на 6.
7 : прибавьте или вычтите число, кратное 7, так, чтобы оно оканчивалось нулем. Отбросьте последнюю цифру с нулем и повторите процесс. Продолжайте, пока не определите, делится ли результат на 7.
Пример: 2702 прибавить 98 (7 x 14) -> 2800, отбросить нули
-> 28 кратно 7, поэтому 2702 делится на 7.
8 : последние три цифры делятся на 8.
Пример: 79256, 256 делится на 8, поэтому 79256 делится на 8.(Альтернативное правило: если цифра сотен , четная , последние 2 цифры делятся на 8, если цифра сотен нечетная , последние 2 цифры + 4 делятся на 8)
9 : то же правило, что и 3, но с 9. Если сумма цифр делится на 9, то число делится на 9.
Если сумма цифр делится на 9, то число делится на 9.
Пример: 13671 -> 1 + 3 + 6 + 7 + 1 = 18
-> 18 делится на 9, поэтому 13671 делится на 9
10 : Число заканчивается на 0.
Пример: 280 оканчивается на 0, 280 делится на 10
11 : Правило аналогично 3 и 9, начинайте с правой цифры и попеременно вычитая и складывая оставшиеся цифры. Если ответ равен нулю или кратен 11, то число делится на 11.
Пример: 12727 -> 1-2 + 7-2 + 7 = 11, поэтому 12727 делится на 11.
Можно ознакомьтесь с некоторыми дополнительными методами здесь.
9. Разделение больших чисел на 9
Пример:
-> 10520/9
Напишите первую цифру над уравнением и напишите букву «R» (остаток) над последней цифрой.Добавьте число, которое вы только что написали, и число по диагонали ниже и справа от него. Напишите этот новый номер во втором месте. Добавьте это число к числу по диагонали внизу и справа. Продолжайте этот процесс, пока не дойдете до R.
Наконец, добавьте последнюю цифру к числу под R, чтобы получить остаток.
10520/9
= 1168 R8
или 1168,889
Вот еще один пример:
-> 57423/9
На этот раз после того, как мы завершили первый шаг, сумма нашего первого числа и числа по диагонали внизу и справа больше десяти (5 + 7 = 12).Ставим единицу над первой цифрой и вычитаем из нее девять . (Мы делим на девять, поэтому мы вычитаем девять, а не десять). Поместите получившееся число на вторую позицию (12–9 = 3). Продолжайте тот же процесс.
В этом примере наш остаток больше 9 (9 + 3 = 12). И снова мы переносим единицу над предыдущей цифрой и вычитаем девять из остатка, в результате чего остается три. Теперь сложите результат и цифры переноса.
57423/9Фотография Элисон Панг на Unsplash
= 6380 R3
или 6380.333
10. Переверните вопрос
Проценты ассоциативны, поэтому иногда изменение порядка вопросов упрощает расчет.
Пример:
Что 36% от 25
-> то же самое, что 25% от 36
-> 25% равно ¼
-> 36/4 = 9
36% от 25 равно 9
11. Дроби
Как вы можете видеть, использование ¼ в последнем примере помогает узнать дроби и то, как они соотносятся с процентами.
1/2 = 50% 1/3 = 33,33%, 2/3 = 66,67%, 1/4 = 25%, 3/4 = 75% 1/5 = 20%, 2/5 = 40%… 1 / 6 = 16,67%, 5/6 = 83,33% (2/6 = 1/3, 3/6 = 1/2, 4/6 = 2/3) 1/7 = 14,2857%, 2/7 = 28,5714% , 3/7 = 42,8571%, 4/7 = 57,1428% (обратите внимание на повторяющийся образец .142857) 1/8 = 12,5%, 3/8 = 37,5%, 5/8 = 62,5%, 7/8 = 87,5% 1 / 9 = 11,11%, 2/9 = 22,22%, 3/9 = 33,33%… 1/10 = 10%, 2/10 = 20%… 1/11 = 9,09%, 2/11 = 18,18%, 3 / 11 = 27,27%… 1/12 = 8,33%, 5/12 = 41,67%, 7/12 = 58,33%, 11/12 = 91,67%
12. Правило 72
Правило 72 дает оценку того, как Чтобы удвоить стоимость при заданном процентном доходе, потребуется много лет.Он работает путем деления 72 на процент с ответом как количество лет, которое потребуется, чтобы удвоиться.


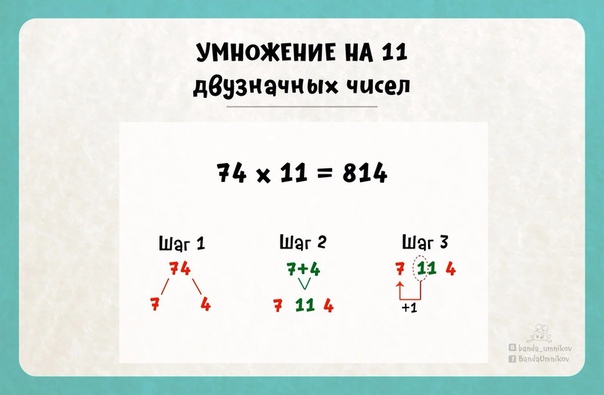 д.;
д.; е. в уме ребенок сразу будет добавлять 1,2,3,4…
е. в уме ребенок сразу будет добавлять 1,2,3,4… Игра, в которой необходимо попросить ребенка слепить мишке 4 лапки, или котику два ушка. Попутно следует показывать ему карточки с этими цифрами.
Игра, в которой необходимо попросить ребенка слепить мишке 4 лапки, или котику два ушка. Попутно следует показывать ему карточки с этими цифрами.