Как быстро в уме умножать числа: Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018?

Как научиться быстро считать в уме; как быстро умножать двузначные числа в уме; быстрый счет в уме методика

Умение складывать в уме – навык, который может показаться ненужным в современном информационном обществе. Но гаджеты в любой момент могут отказать, блокнота с ручкой не найдется, калькулятора не будет под рукой. И что тогда? Быстрый счет без подручных средств чаще нужен в быту, а не в школе, институте или на работе. Расскажем, как научиться быстро считать в уме взрослому и ребенку.

Содержание

1. Внимание и концентрация
2. Визуализация
3. Состязание
4. Погружение
5. Простые арифметические закономерности
6. Сложение в уме
7. Суммирование однозначных чисел
8. Суммирование многозначных чисел
9. Как научиться умножать и делить в уме
10. Умножение двузначных чисел
11. Деление на двузначное число

Внимание и концентрация

Концентрация – один из ментальных навыков, завязанный на способности мыслить абстрактными категориями. В наибольшей степени развит у математиков. Способность развивалась в разных частях света преимущественно различными философскими школами. Нам известна греческая школа пифагорейцев, в которой практиковалась герменевтика. И теория древнеегипетского жреца Гермеса Трижды Величайшего.

Основной принцип упражнения на концентрацию (именно оно является базовым, чтобы наработать фокусировку) – сосредоточение на точке – она расположена в центре круга. Через его границу проходят 4 стрелки, направленные к точке. Сами стрелки находятся на периферии, пересекают только кривую с 4-х сторон, по принципу расположения: С, Ю, З, В. Так получается мандала, которую необходимо удерживать во внимании. Затем происходит дальнейшее действие… Так, постепенно, с выполнением этой визуализации происходит обучение, нарабатывается базовое состояние концентрации. Оно необходимо для любой работы, связанной с повышенным вниманием.

Существуют более конкретные методики для обучения быстрому счету. Но это не значит, что они лучше – они просто не являются базовыми. Объяснение их будет куда проще. Далее предлагаются к рассмотрению наиболее популярные способы, как научиться концентрироваться и быть внимательным.

Визуализация

Очень важно научиться представлять решаемый пример прописью в виде образа, мысленно. Он может быть изображен “как бы” на мониторе компьютера, гаджета, на листе бумаги, в тетради или блокноте. Смысл упражнения заключается не только в легкости производимого действия, которое можно осуществить в игровой форме, без напряжения.

Но и в готовности приложить усилие, собраться, сконцентрироваться, “зацепиться” за образ. Способ применяется и в др. сферах. Это обучение игре в шахматы, на музыкальном инструменте, разучивание стихов и прозы.

Мысленно представляются шахматные фигуры, клавиши и струны, заучиваемые тексты. Все они задействованы в вымышленном пространстве.

Состязание

Хорошим стимулом для лучшего обучения может быть соревнование. Для этого необходим настоящий партнер, собеседник, оппонент, соперник. Состязание лучше проводить в тишине. Как на контрольной работе. Хорошей тренировкой будет и борьба с самим собой.

Можно поставить задачу на решение примера по исчислению и решить ее на определенном временном отрезке. Смысл состязания – бить временные рекорды, идти к цели, не останавливаясь на достигнутом.

В этом случае выбранный путь приведет к усложнению программы и к новым целям. И, конечно, принесет качественный рост в освоении техник на устные вычисления.

Погружение

В данном подходе нужен прежде всего неподдельный интерес либо определенные наработанные качества входа в определенное состояние. Многим знакомы спонтанные состояния увлеченности процессом. Например, чтением, музицированием, рисованием, занятием любимым делом. В этом случае человек словно забывает об окружающих людях, предметах, выпадает из временного потока. Происходит погружение. Если, тренируясь в упражнениях на математические операции в уме, человек входит в подобное состояние, приемы устных вычислений открываются быстрее.

Простые арифметические закономерности

Основой любых производимых действий для решения поставленной задачи является базовый принцип. Изучение закономерностей, состоящих из простых последовательностей, позволит решить примеры более сложные. Система быстрого счета предполагает увязывание воедино элементов, находящихся в определенной иерархической соподчиненности. Следуя правилам, нарабатывая опыт в обработке примитивных операций, доводя их до полного автоматизма, у вас получится решать в уме любые стандартные задачи.

Онлайн-тренажер по математике имеет функционал, отвечающий перечисленным выше требованиям. Необязательно работать на узкоспециализированном – для устного счисления. Главное – методика, которая делает обучение более эффективным. Ее можно найти в учебниках, тем самым выбрать для себя подходящую траекторию. Вот и ответ на вопрос, как научиться быстро считать в уме на тренажере.

Но он служит лишь вспомогательным средством. Далее будут представлены наиболее простые приемы устного счета.

Сложение в уме

Это – первоначальное арифметическое действие, которому дети обучаются после освоения цифр и правильного их перечисления в порядке возрастания и убывания. Вычисления производится (как и все в дальнейшем рассмотренные операции) от простого к сложному.

Суммирование однозначных чисел

Обучение целесообразно начать по системе школьного сложения – через 10. Такая тренировка пройдет быстро и просто:

1. Допустим, что к 5 нужно прибавить 9.
2. Нужно прикинуть недобор до 10 для одного из слагаемых. Обычно выбирают ближайшее. То 6сть: 9 + 1 = 10.
3. Теперь необходимо посмотреть, из чего складывается 5 через число 1, которое в свою очередь было добавлено до 10. Получается: 5 = 1 + 4.
4. В итоге, к 10 добавляется 4. Получается, что: 10 + 4 = 14.

Выходит, что 1 добавленная к 10, была также отнята у второго члена. То есть получился 0. Дальше, через 10 (по тому же принципу) складываются и 2-значные, 3-значные и многозначные числа.

Смысл – наработать качество. Оно заключается в скорейшем подсчете.

Суммирование многозначных чисел

Двузначные числа в этой статье пропускаются, но принцип их сложения ничем не отличается от приведенного выше примера. Сложить числа можно аналогичным способом, представленном ниже.

Как быстро считать в уме, если нужно осуществить счет в сложении многозначных чисел? Для устного счета таких чисел применяется принцип раскладки на разряды (единицы, десятки, сотни, тысячи и т. д.). Далее их складывают в порядке очередности с однотипными разрядами второго слагаемого:

1. Предположим, что необходимо прибавить 619 к 1233.
2. Поэтому, первое слагаемое нужно разложить на 3 разряда: 600 + 10 + 9. Второе – на 4. 1000 + 200 + 30 + 3.
3. Далее их складывают поочередно, согласно разрядам: 0 + 1000, 600 + 200, 10 + 30, 9 + 3.
4. На последнем этапе применяется наиболее удобная группировка. Например: 1000 + 800, 40 + 12. Получаем: 1800 + 52 = 1852.

Единственная трудность этого метода состоит в удержании промежуточных результатов в памяти.

Как научиться умножать и делить в уме

Деление и умножение – два противоположных действия, требующих для успешного исчисления знания таблицы умножения. Иначе придется складывать и вычитать. Поэтому ее учат наизусть. Но есть и вариант таблицы Пифагора, устроенной по другому принципу. Она полезнее для умения счета в уме, а не для банальной зубрежки. Умножение больших чисел на устный счет – 8 класс, алгебра.

Этот вариант намного лучше, нежели стандартный – в виде столбиков на каждую цифру. Он дает общее системное представление об умножении и делении.

Умножение двузначных чисел

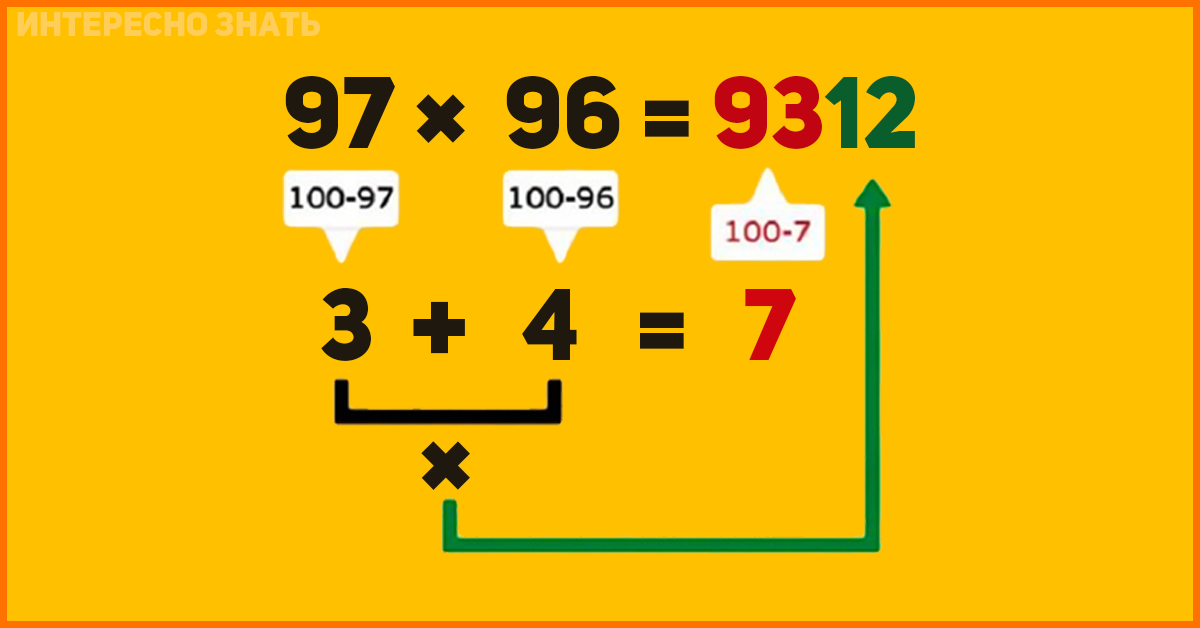
Как быстро умножать в уме двузначные числа? Для этого не нужно умножение в столбик. Достаточной будет разбивка на несколько шагов:

1. Нужно произвести умножение 47 на 32. Раскладка: 47 × 30 + 2, или 47 × 30 + 47 × 2.
2. Умножаем 47 на 30. 47 × 3 = 40 × 3 + 7 × 3 = 120 + 21 = 141. Приписывается справа нолик и выходит: 1410.
3. Далее: 47 × 2 = 40 × 2 + 7 × 2 = 80 + 14 = 94.
4. В итоге результаты складываются: 1410 + 94 = 1500 + 4 = 1504.

Деление на двузначное число

Делить в уме на 2-значное число – это высший пилотаж устного счета. Здесь используется метод “пристрелки”:

1. Делится 1128 на 24. Сколько раз 24 может поместиться в 1128? Очевидно, что для “пристрелки” берется множитель 50: 24 × 50 = 1200.
2. До 1200, делимому 1128, не хватает 72. Сколько раз 24 поместится в 72? Три раза. Следовательно: 1128 = 24 × 50 − 24 × 3 = 24 × (50 − 3) = 24 × 47. Стало быть: 1128 / 24 = 47.

Как перемножать в уме шестизначные числа

Математика — наука волшебная, просто в школе это от нас скрывают, заставляя считать в столбик и зубрить формулы. Профессор математики Артур Бенджамин не скрывает магию от своих учеников и широкой публики. Бенджамин выступает с научно-популярными лекциями и математическими шоу, на которых он перемножает и делит в уме шестизначные числа. Как ему удаётся делать невероятные вычисления в уме, Бенджамин рассказывает в книге «Магия математики: Как найти икс и зачем это нужно», которая вышла в июне в издательстве «Альпина Паблишер».

И с ходу несколько математических трюков из книги Артура Бенджамина.

Магия алгебры

1. Задумайте число от одного до десяти (хотя можно и больше)

2. Умножьте это число на два

3. Добавьте 10

4. Разделите на 2

5. Вычтите из результата изначально задуманное вами число

Уверен, получилось 5. Правильно?

Хотите узнать, в чем кроется секрет волшебства? В алгебре. Разберём фокус ещё раз, шаг за шагом, начиная с первого. Я понятия не имею, какое число вы загадали, поэтому давайте заменим его буквой N. Неизвестное число, обозначаемое буквой, называется переменной.

Шаг второй предлагает нам удвоить загаданное число, то есть мы, по сути, имеем 2N (знак умножения в алгебре принято опускать, в том числе и потому, что очень часто для обозначения переменной используется внешне похожая на него буква x). После третьего шага ваше число выглядит как 2N + 10. Четвёртая операция предлагает нам упростить пример, разделив все его части на 2: N + 5. И наконец, мы вычитаем загаданное число (то есть N): N + 5 — N = 5. Давайте соберём весь фокус в одну таблицу:

---

Магия счёта

Вот одна хитрость, с которой ещё в детстве столкнулся немецкий математик Карл Фридрих Гаусс. Как-то раз на уроке математики учитель попросил класс сложить между собой все числа от 1 до 100. Вряд ли он хотел развлечь учеников — скорее, отвлечь: заставить заняться чем-нибудь нудным и требующим полного сосредоточения, а самому спокойно сделать другую работу. Представьте себе его удивление, когда через несколько секунд Гаусс вышел к доске и написал ответ — 5050. Хотите знать, как он это сделал? Он просто представил все эти числа в виде двух рядов: верхний — от 1 до 50, нижний — от 51 до 100, причём в нижнем ряду числа шли в обратном порядке, вот так:

Гаусс заметил, что сумма чисел в каждом из пятидесяти столбцов одинаковая — 101, значит, чтобы получить искомый результат, нужно всего лишь умножить 101 на 50. Так у него и получилось 5050.

Собственно, благодаря такой вот способности — не быстро считать в уме, но заставлять числа плясать под свою дудку — Гаусс и стал одним из величайших математиков XIX столетия.

---

Магия геометрии

Большинство доказательств теоремы Пифагора основываются на перестановке частей одной геометрической фигуры с целью получения другой с той же площадью. Но смотрите, какой обнаруживается парадокс. Возьмём квадрат 8 на 8. Его, пожалуй, вполне можно разделить на четыре части, как на рисунке чуть ниже: длина одной стороны каждой части должна равняться 3, 5 или 8 (да-да, одному из чисел Фибоначчи!). Перегруппируем эти части так, чтобы получился прямоугольник 5 на 13 (обязательно попробуйте сделать это сами!). Но ведь площадь начальной фигуры равна 8 × 8 = 64, а конечной — 5 × 13 = 65! Как это возможно?

Разгадка этого парадокса заключается в том, что прямая линия, являющаяся «диагональю» прямоугольника 5 на 13, на самом деле не такая уж и прямая. Смотрите сами: треугольник, обозначенный буквой С, имеет гипотенузу с наклоном 3/8 = 0,375 (потому что значение её y-координаты увеличивается на 3, а значение x-координаты — на 8) при том, что верхняя грань фигуры (трапеции), обозначенной буквой D, имеет наклон 2/5 = 0,4 (потому что значение её y-координаты увеличивается на 2, а значение x-координаты — на 5). То же происходит и с нижними гранями трапеции и треугольника, находящихся в верхней части. Отрезки с разным наклоном никогда и ни за что не образуют прямую линию, а значит, если мы присмотримся к нашему прямоугольнику, то увидим небольшой зазор между двумя почти «прямыми» почти «диагоналями» (см. рисунок). И получается, что, будучи растянутой по всей площади, эта щель даёт нам лишнюю единицу общей площади.

---

Выступления Артура Бенджамина на TED:

---

Процент от числа с использованием вычислений в уме

Научитесь решать процентные задачи в уме! Поскольку 10% — это 1/10, а найти 1/10 любого числа очень просто, мы можем использовать это, чтобы быстро вычислить в уме определенные проценты величин. чтобы найти 20% числа, сначала найдите 10% и удвойте это число. И так далее.

Основные концепции и идеи этого урока также объясняются в этом видео:

100% чего-то означает все этого. 1% чего-то означает 1/100 этого.

Чтобы рассчитать процент от количества, мы используйте тот же метод, что и при вычислении дробной части этой величины потому что процентов просто означает сотые доли . Поэтому, проценты – это просто дроби.

Сколько стоит 1% от 200 кг?   Это означает, сколько составляет 1/100 от 200 кг? Это просто 2 кг. 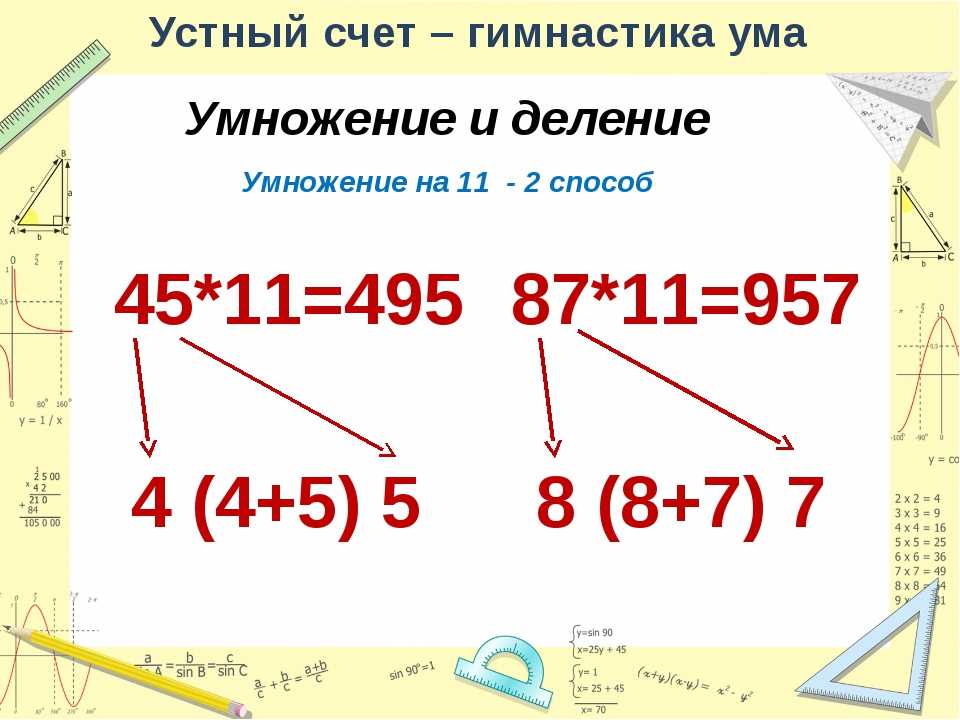Вы просто делите на 100, чтобы найти сотую часть! Чтобы найти 1% чего-то (1/100 чего-то), разделите на 100. Вспомните, как делить на 100 в уме: просто переместите запятую на два знака влево. Например, 1% от 540 — это 5,4. И 1% 8,30 это 0,083.

Чтобы найти 10% некоторого количества, разделите до 10. Почему это работает? 10% составляет 10/100. А 10/100 равно 1/10. Таким образом, мы просто находим 1/10 часть Например, 10% от 340 человек — это 34 человека. Точно так же 10% от 2,30 доллара составляют 0,23 доллара. (Делить на 10 мысленно, просто переместите запятую на одну позицию влево.)

1. Найдите 10% этих чисел.

а.  900   _______ б.  160   _______ в.  50   _______

2. Найдите 1% этих чисел.

а.  900  _______ б.  6 800  _______ в.  550  _______

3. Если 1% зарплаты Синди составляет 23 доллара, сколько у нее зарплата?

4. Десять процентов от стоимости бассейн стоит 430 долларов. Сколько стоит бассейн?

Чтобы найти 2% количества, сначала найти 1% от него, а затем удвоить это. Например, давайте найдем 2% от 6 долларов. С 1% из 6 составляет 0,06 доллара США, тогда 2% от 6 составляет 0,12 доллара США.

Можете ли вы придумать способ найти 20% числа? (Подсказка: начните с нахождения 10% числа.)

7. Заполните таблицу. Использовать умственная математика.

номер/ процент	400	60	78	8	4. 1
1% от числа
2% от числа
10% от числа
20% от числа

8. Заполните это руководство по арифметике в уме процентами:

Счет в уме и процент от числа
50% это 1/2. Чтобы найти 50% числа, разделите его на ______. 10% равно 1/     . Чтобы найти 10% числа, разделите на ______. 1% равно 1/     . Чтобы найти 1% числа, разделите его на ______.	50% от 244 составляет _______. 10% от 47 это ________. 1% от 530 составляет ________.
Чтобы найти 20 %, 30 %, 40 %, 60 %, 70 %, 80 % или 90 % числа, Первая находка _________% числа и , затем умножьте на 2, 3, 4, 6, 7, 8 или 9.	10% от 120 это _______. 30 % от 120 составляет _______. 60 % от 120 составляет _______.

9. Найти проценты. Используйте ментальную арифметику.

а. 10% от 60 кг ________ 20% от 60 кг   ________

б. 10% от 14 долларов США  ________ 30% от 14 долл. США ________

10. Дэвид платит 20% подоходный налог с его зарплаты в размере 2100 долларов. Сколько долларов составляет налог?

   Сколько денег у него осталось после уплаты налога?

 

12. Определите ошибки, которые допустили эти дети. Затем найдите правильные ответы.

Найти 90% от 55 долларов.     Решение Питера: 10% от 55 долларов США составляет 5,50 долларов США Итак, вычтите 100% – 5,50 доллара = 94,50 доллара  .

Еще немного математических трюков в уме:

90% от количества

Сначала найдите 10% количества, а затем вычтите эти 10% из 100%.

25% от количества

25% равно 1/4. Итак, чтобы найти 25% количества, разделите его на 4.

12% от количества

Сначала найдите 10%. Затем найдите 1% и используйте этот 1% найти 2% от него. Затем добавьте 10% и 2%.

75% от количества

75% составляет 3/4. Сначала найдите 1/4 количества и умножьте это на 3.

13. Найдите проценты. Используйте ментальную арифметику.

а. 25% от 48 миль   _______ 75% от 48 миль   ________

14. Найдите проценты от количества.

а. 50% от 26 дюймов

б. 25% от 40 футов

15. Введите метод вычисления в уме, чтобы найти 12% от 65 долларов.

10 % от 65 долларов – это ________ долларов.
1% от 65 долларов составляет _________ долларов.
2% от 65 долларов составляют _________ долларов.

Теперь добавьте, чтобы получить 12% от 54 долларов:
$_________ +  $_________  =  $________

18. В своем счете за мобильный телефон Ханна заметила, что 340 текстовых сообщений, которые она отправила в прошлом месяце, 15% были отправлены в более дешевый ночной тариф. Сколько сообщений отправила Ханна на ночь? В течение дня?

20. В картонной коробке 2 литра. тропического сока. Сок состоит из 25% сока манго, 30% ананасового сока и остальное – сок гуавы. Найдите сколько миллилитров каждого сока ушло в 2-х литровую коробку тропического сока.

См. также

Процент – бесплатный урок

Как считать проценты — бесплатный урок

Как вычислить проценты от чисел — бесплатный урок

Основы процентной сдачи – бесплатный урок

---

Этот урок взят из книги Марии Миллер Math Mammoth Percent и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторское право © Мария Миллер.

---

Меню уроков математики

Стратегии умственного умножения — орхидеи

Умственная математика

Стратегии умственного умножения

• Умственная арифметика определяется как способность решать арифметические вычисления. мысленно используя приемы.
• Решение проблемы занимает меньше времени.
• Повышает способность детей решать проблемы.
• Регулярная практика сложения в уме улучшает у ребенка чувство чисел.

Трюки с умножением

Умножение целого числа на кратное 10:

• Умножьте ненулевую часть обоих коэффициентов.
• Подсчитайте количество нулей в каждом множителе.
• Добавьте такое же количество нулей в произведение.

Пример 1:

Умножьте 2100 на 400.

Решение:

Шаг 1. Умножьте 21 на 4
    21 × 4 = 84.
Шаг 2: Общее количество нулей в каждом коэффициента = 4.
Шаг 3: Добавьте 4 нуля в произведение 84.
    840000
Следовательно, 21 × 4 = 8 40 000.

Пример 2:

Умножьте 100 на 1000.

Решение:

Шаг 1. Умножьте 1 на 1
    1 × 1 = 1
Шаг 2: Общее количество нулей в каждом коэффициента = 5.
Шаг 3: Добавьте 5 нулей в произведение 1.
    100000
Следовательно, 100 × 1000 = 1 00 000.

Умножение двузначного числа на двузначное:

Шаг 1: Умножьте цифру единицы оба числа.
Шаг 2: Умножьте цифру единицы измерения множитель на десятизначный знак множимого и на десять разрядов множителя на единичный разряд множимого. Добавьте их вместе.
Шаг 3. Умножьте десять цифр числа оба номер.

Пример:

Умножьте 57 на 62.

Решение:

Умножение двузначного числа на двузначное число, когда десять цифры одинаковые, а сумма единичных цифр равна 10:

Шаг 1: Умножьте обе единицы цифры.
Шаг 2: умножьте десять цифр на последующая цифра.
Шаг 3: Объедините оба результата.

Пример:

Умножьте 27 на 23.

Решение:

Сумма единичных цифр равна 10 = (7 + 3).
Умножить 3 на 7 = 3 × 7 = 21
Цифра в разряде десятков равна 2. Последующая цифра 2 равна 3.
Умножить 2 на 3 = 2 × 3 = 6.
Решение: 621.

Умножение трехзначного числа на двузначное:

Пример:

Умножьте 157 на 23.

Решение:

Умножение трехзначного числа на трехзначное:

Пример:

Умножьте 517 на 216.

Решение:

Следовательно, 517 × 216 = 1,11,672.

Умножение трехзначного числа на трехзначное число, когда десять цифры и сотни цифр одинаковы, а сумма единичных цифр равна 10:

Шаг 1: Умножьте обе единицы цифры.
Шаг 2: Умножьте десять на сто цифр следующей цифрой.
Шаг 3: Объедините оба результата.

Пример:

Умножьте 277 на 273.

Решение:

Сумма единичных цифр равна 10 = (7 + 3).
Умножить 3 на 7 = 3 × 7 = 21 28.
Умножить 27 на 28 = 27 × 28 = 756.
Решение: 75 621.

Трюки с умножением чисел

Правило умножения на 9:

• Умножьте число на 10.