Вопрос: Как делить матрицы? – Образование и коммуникации
Содержание статьи:
Как разделить матрицу на число онлайн
Видео взято с канала: Тонечка Математика видеоКонспект
§23 Приведение матрицы к каноническому виду
Видео взято с канала: Мемория Высшая Математика
Обратная матрица (2 способа нахождения)
Видео взято с канала: Valery Volkov
Математика без Ху%!ни. Метод Гаусса.
Видео взято с канала: Sergej Kuts
Как находить обратную матрицу bezbotvy
Видео взято с канала: bezbotvy
Как найти определитель матрицы 2х2, 3х3 и 4х4
Показать описаниеПо просьбам учащихся продолжаю рассказывать про матрицы. И сегодня расскажу о том, как находить определители матриц разных размеров: от матриц 2 на 2 до матрицы n x n.В ролике рассказывается про основные нюансы, которые важно помнить при нахождении детерминанта матриц, а также разбираются 3 примера, чтобы каждый способ был нагляден и понятен. Жду ваших комментариев к этому уроку и заявок на новые ролики. Всем успехов!
Жду ваших комментариев к этому уроку и заявок на новые ролики. Всем успехов!
—
Комментарии закрыты, ибо видео уже 6 лет. Его можно ругать, но мне оно дорого как память: такие видео я начинал записывать, будущие будут лучше! Есть вопросы? Пишите их на сайте specclass.ru на странице, посвященной матрице:.
—
СпецКласс это бесплатные видео уроки и онлайн вебинары, которые помогут вам в учебе, подготовке к ГИА и ЕГЭ и сдачи сессии. Видеоуроки длятся не более 5 минут, за которые вы сможете разобраться в решении сложных примеров или понять теорию. Все, что останется сделать это решить свой пример по аналогии!
—
Остались вопросы? Пишите их в комментариях где удобно!
Все уроки по порядку http://specclass.ru/.
Присылайте свои вопросы по решениям http://vk.com/specclass.
Видео взято с канала: bezbotvy
Можно ли делить матрицу на число.
 Деление матриц на число онлайн
Деление матриц на число онлайнВидео взято с канала: Тонечка Математика видеоКонспект
Изучаем матрицы в питоне и массивы NumPy в Python
Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:
Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.
Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:
A = [[1, 4, 5],
[-5, 8, 9]]
Этот список является матрицей на 2 строки и 3 столбца.
Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.
Давайте посмотрим, как работать с вложенным списком.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print("A =", A)
print("A[1] =", A[1]) # вторая строка
print("A[1][2] =", A[1][2]) # третий элемент второй строки
print("A[0][-1] =", A[0][-1]) # последний элемент первой строки
column = []; # пустой список
for row in A:
column. append(row[2])
print("3rd column =", column)
append(row[2])
print("3rd column =", column)
Когда мы запустим эту программу, результат будет следующий:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A [1] = [-5, 8, 9, 0] A [1] [2] = 9 A [0] [- 1] = 12 3-й столбец = [5, 9, 11]
Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .
NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,
- Ознакомьтесь: Как установить NumPy Python?
- Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.
После установки NumPy можно импортировать и использовать его.
NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:
Давайте рассмотрим приведенный ниже пример:
import numpy as np a = np.array([1, 2, 3]) print(a) # Вывод: [1, 2, 3] print(type(a)) # Вывод: <class 'numpy.ndarray'>
Как видите, класс массива NumPy называется ndarray.
Существует несколько способов создания массивов NumPy.
import numpy as np A = np.array([[1, 2, 3], [3, 4, 5]]) print(A) A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой print(A) A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел print(A)
Когда вы запустите эту программу, результат будет следующий:
[[1 2 3] [3 4 5]] [[1.1 2. 3.] [3. 4. 5.]] [[1. + 0.j 2. + 0.j 3. + 0.j] [3. + 0.j 4. + 0.j 5. + 0.j]]
import numpy as np zeors_array = np.zeros( (2, 3) ) print(zeors_array) ''' Вывод: [[0. 0. 0.] [0. 0. 0.]] ''' ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype print(ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2-31 до 2-31-1.
Следовательно, этот массив может принимать значения от -2-31 до 2-31-1.
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Вывод:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Узнайте больше о других способах создания массива NumPy .
Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.
Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.
import numpy as np A = np.array([[2, 4], [5, -6]]) B = np.array([[9, -3], [3, 6]]) C = A + B # сложение соответствующих элементов print(C) ''' Вывод: [[11 1] [ 8 0]] '''
Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .
Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.
import numpy as np A = np.array([[3, 6, 7], [5, -3, 0]]) B = np.array([[1, 1], [2, 1], [3, -3]]) C = a.dot(B) print(C) ''' Вывод: [[ 36 -12] [ -1 2]] '''
Мы используем numpy.transpose для вычисления транспонирования матрицы.
import numpy as np A = np.array([[1, 1], [2, 1], [3, -3]]) print(A.transpose()) ''' Вывод: [[ 1 2 3] [ 1 1 -3]] '''
Как видите, NumPy значительно упростил нашу задачу.
Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.
import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент
Когда вы запустите эту программу, результат будет следующий:
A [0] = 2 A [2] = 6 A [-1] = 10
Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).
import numpy as np A = np.array([[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]) # Первый элемент первой строки print("A[0][0] =", A[0][0]) # Третий элемент второй строки print("A[1][2] =", A[1][2]) # Последний элемент последней строки print("A[-1][-1] =", A[-1][-1])
Когда мы запустим эту программу, результат будет следующий:
A [0] [0] = 1 A [1] [2] = 9 A [-1] [- 1] = 19
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [0] = [1, 4, 5, 12] A [2] = [-6, 7, 11, 19] A [-1] = [-6, 7, 11, 19]
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [:, 0] = [1 -5 -6] A [:, 3] = [12 0 19] A [:, - 1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».
Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:
import numpy as np letters = np.array([1, 3, 5, 7, 9, 7, 5]) # с 3-го по 5-ый элементы print(letters[2:5]) # Вывод: [5, 7, 9] # с 1-го по 4-ый элементы print(letters[:-5]) # Вывод: [1, 3] # с 6-го до последнего элемента print(letters[5:]) # Вывод:[7, 5] # с 1-го до последнего элемента print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5] # список в обратном порядке print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
Теперь посмотрим, как разделить матрицу.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Вывод:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Вывод:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Вывод:
[ 5 9 11]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
[ 9 0 17]
[11 19 21]]
'''
Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Пожалуйста, оставьте ваши комментарии по текущей теме статьи. Мы очень благодарим вас за ваши комментарии, лайки, отклики, подписки, дизлайки!
Вадим Дворниковавтор-переводчик статьи «Python Matrices and NumPy Arrays»
Урок 21. Векторы и матрицы в Mathcad
С этими понятиями Вы могли сталкиваться, работая в Excel – столбец чисел называется вектор-столбцом, строка – вектор-строкой. Блок объектов является матрицей. Вычисления в Excel, по сути, являются операциями с векторами и матрицами. В этом уроке мы познакомимся с аналогичными вычислениями в Mathcad, и мы поймем, почему в Mathcad их проводить проще.
Введение
В предыдущих уроках наши векторы начинались с элемента с номером «0». В этом уроке для простоты сделаем номер первого элемента равным «1». Это можно сделать с помощью вкладки Расчет –> Параметры документа –> ORIGIN:
Это значение можно вывести прямо в документ, чтобы не забыть его и не запутаться:
Теперь рассмотрим несколько матриц:
Как видно, они могут включать в себя числа, символы и даже функции. Они также могут содержать текстовые элементы (строки).
Они также могут содержать текстовые элементы (строки).
Элемент матрицы можно вывести, используя подстрочные индексы:
Матрицы выше являются квадратными 2х2, но у них может быть любой размер по строкам и столбцам:
Запомните: первое число – номер строки (или их количество), второе – столбца.
Элементы, выделенные с помощью подстрочных индексов:
Для вектор-столбца второй индекс можно опустить, но не для вектор-строки:
Во вкладке Математика –> Операторы и символы –> Операторы –> Векторы и матрицы Вы найдете команды для выделения столбцов и строк:
Многие операции для векторов и матриц аналогичны операциям для обычных чисел, переменных и функций: сложение, вычитание, некоторые виды умножения. Поиск обратной матрицы близко к операции деления. Вы можете записать эти операторы, используя имена векторов и матриц. В качестве примера рассмотрим векторное произведение матрицы и вектора:
Мы рассмотрим эту операцию подробнее позже. Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.
Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.
Применение векторов очень широко. Вспомните пиксели на экране монитора – их могут быть миллионы. Они обрабатываются с помощью операций с матрицами.
В Mathcad
Для создания вектора или матрицы откройте вкладку Матрицы/таблицы. Когда курсор находится в пустой области щелкните по самой левой кнопке «Вставить матрицу». Появится сетка с маленькими квадратами:
Перемести указатель на сетку, выберите желаемый размер матрицы, затем щелкните левой кнопкой мыши. Появится пустая матрица:
Матрице можно присвоить имя, щелкнув на левую скобку, нажав [:] для оператора присваивания и введя имя:
Вставку и удаление строк и столбцов легко осуществлять с помощью команд из меню «Операторы с векторами/матрицами» на вкладке Матрицы и таблицы:
Операции с матрицами
Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:
Будем использовать две матрицы и два вектора:
Транспонирование
Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:
Щелкните по правой границе матрицы и примените оператор. Он работает как для символьных, так и для числовых матриц:
Поэлементные операции
Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:
Затем выберите все выражение и примените векторизацию:
Вычислите, чтобы посмотреть результат: первый элемент умножается на первый, второй – на второй, и т.д.:
Другие поэлементные операции:
Поэлементные операции применимы только к массивам одного размера.
Сложение и вычитание
Сложение и вычитание выполняется поэлементно:
Эта операция также применима лишь к массивам одного размера.
С помощью оператора суммирования можно найти сумму всех элементов вектора (не матрицы):
Скалярное произведение
Умножение на константу работает так:
При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:
Заметьте, что последовательность множителей играет роль:
Скалярное произведение не коммутативно, за исключением особых случаев:
Скалярное произведение двух векторов дает результат с комплексно-сопряженными числами (с чертой сверху). Для действительных чисел на это можно не обращать внимания:
Векторное произведение
Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:
Векторное произведение имеет широкое применение в механике, гидродинамике, электромагнетизме и в других областях.
Обратная матрица
Обратная матрица определяется только для квадратных матриц:
Произведение матрицы и ее обратной матрицы является единичной матрицей:
Произведение матрицы и единичной матрицы дает изначальную матрицу:
Определитель
Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:
Если определитель равен нулю, обратной матрицы не существует, а матрица является сингулярной. Вспомните деление на ноль в обычной алгебре. Mathcad сообщит, если матрица является сингулярной:
Для скаляра определитель равен его модулю:
Для вектора команда Определитель вычисляет длину вектора:
Резюме
В этом уроке мы рассмотрели векторы и матрицы (массивы).
- Элементы массива можно вывести с помощью подстрочного индекса – один индекс для вектор-столбца, два – для других массивов.
 Первое индекс – для строк, второй – для столбцов.
Первое индекс – для строк, второй – для столбцов. - Есть специальные команды для извлечения отдельных строк и столбцов.
- Векторы и матрицы создаются и редактируются с помощью команд со вкладки Матрицы/таблицы.
Операции над векторами и матрицами, которые мы рассмотрели:
- Транспонирование.
- Поэлементные операции.
- Сложение и вычитание.
- Скалярное произведение.
- Векторное произведение.
- Поиск обратной матрицы.
- Поиск определителя.
Другие интересные материалы
матрица приоритетов Эйзенхауэра (+ бланк для скачивания)
Это очень простой прием тайм-менеджмента, но со сложным названием. Сегодня мы поговорим о матрице приоритетов Эйзенхауэра. Уверена, что большинство читателей приходили к такому планированию времени и дел интуитивно, хотя, может, и оформляли список дел иначе.
Матрица приоритетов Эйзенхауэра помогает определить самые важные и срочные дела в течение дня.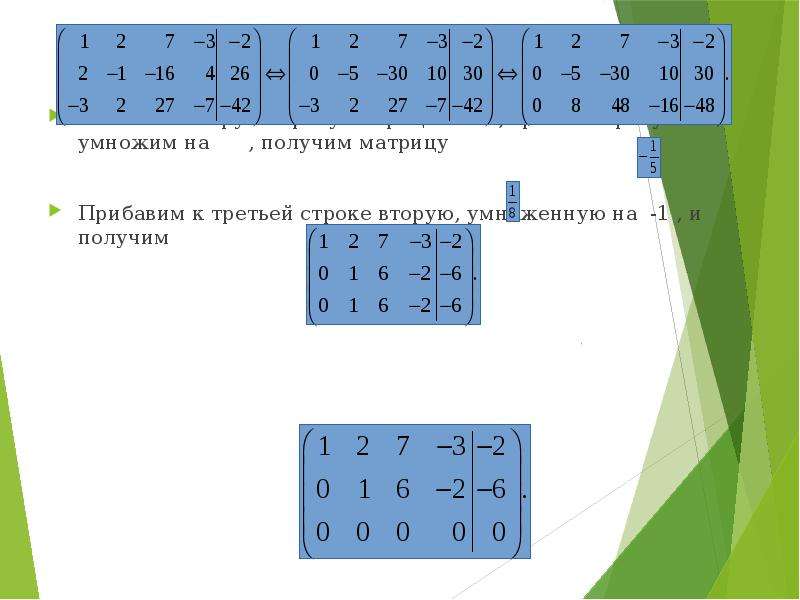
Кстати, почему Эйзенхауэра? Это фамилия одного из американских президентов, который, как считается, стал первым ее применять.
Скачайте шаблон матрицы приоритетов Эйзенхауэра здесь: вот готовый бланк – просто распечатайте и пользуйтесь!
Матрица: важное, срочное, неважное, несрочное
Использовать матрицу очень легко: запишите свои дела в нужный квадрат – и выполняйте)).
Уникальность приема в том, что человек учится осознавать, что является самым важным, а что можно вообще отбросить и не делать, ведь иногда важность/неважность дел бывает неочевидна.
Матрица Эйзенхауэра: как делить дела?
1. Срочное и важное (выполняем сразу!)
Наверняка, у вас появилось искушение почти все свои дела вписать в этот квадрат. На самом деле по-настоящему важных и срочных дел у нас немного – большинство может и подождать. Сюда заносим:
- дела, у которых подходит срок сдачи (сдача курсовой, отчета, статьи)
- экстренные походы к врачам (травматолог, стоматолог)
- срочные звонки
- форс-мажорные ситуации (вызов сантехника, если течет труба)
Лучший вариант – если поле матрицы «Срочное и важное» будет почаще пустым, а все дела можно отнести к следующему пункту.
Читайте также: «Правило 20 минут. Лучше мало, чем ничего!»
2. Несрочное и важное (планируем!)
В идеале у человека, знающего тайм-менеджмент, все важные дела записаны тут. В категорию «Срочное» задачи обычно переходят из-за лени, прокрастинации или форс-мажоров в быту или со здоровьем.
Последних избежать бывает трудно, но если регулярно бывать у врачей на профилактическом осмотре, то по крайней мере категорию «срочных дел, связанных со здоровьем», можно будет сократить.
Что касается прокрастинации, то стоит научиться не допускать в своей жизни горящих сроков, и матрица приоритетов Эйзенхауэра здорово в этом помогает (если ей, конечно, следовать).
Кстати, если научиться выполнять запланированное, пока оно еще не горит, можно сильно снизить количество стрессов: есть возможность качественно и без спешки выполнять каждое дело.
Что относим в эту категорию?
- плановая работа
- анализ и оценка рабочих моментов
- спортивные занятия
- приготовление пищи
- ремонт одежды, стирка
- уборка
Почитайте о том, зачем есть лягушку и о других необычных приемах для управления временем
3. Срочное и неважное (делегируем!)
Срочное и неважное (делегируем!)
Эти дела, как правило, никак не приближают нас к цели, а лишь тормозят рабочий процесс и отвлекают. К ним можно отнести:
- навязанные и не важные лично вам встречи
- празднование дней рождений неблизких знакомых или поздравление их по телефону
- уборка или готовка к незапланированному приходу гостей
- внезапно появившиеся бытовые проблемы: сломалась микроволновка, перегорела лампочка, разбилось большое зеркало. Эти неприятности огорчают и раздражают, но мир не рухнет, если вы не уделите им внимания сиюминутно.
Есть большая опасность – многие относят эти дела в категорию «Срочное и важное», поэтому старайтесь хорошо анализировать каждое дело, а затем заносите в нужную категорию матрицы Эйзенхауэра: возможно, дело окажется не столь важным, как вы думали.
Ну а поскольку дела из этого поля часто не приближают нас к цели, а только отвлекают, постарайтесь их минимизировать: некоторые можно просто не делать, а другие перепоручить: к примеру, заказать торт вместо того, чтобы печь его самой.
4. Несрочное и неважное (думаем: а нужно ли это?)
Такие дела мы обычно и не записываем: к примеру, время на соц.сети или телевизор, компьютерные игры, серфинг по сайтам без цели.
Узнайте о методиках для женского тайм-менеджмента
Куда отнести отдых?
Профессионалы в использовании матрицы приоритетов Эйзенхауэра советуют планировать даже отдых.
К примеру, такой пункт как получасовая прогулка вполне можно отнести к «Важным и срочным» делам – с указанием времени.
Если подразумевается поездка на отдых на несколько дней, то заносим это дело в категорию «Важное и несрочное».
Научившись планировать качественный отдых, меньше будет желания урвать час на неполезный и нерасслабляющий.
Читайте также: как научиться рано вставать?
Мои выводы после использования матрицы Эйзенхауэра:
- Срочных дел действительно немного! А бывали дни, когда их просто не было. Раньше все свои планы я считала срочными и важными, а потому мучила себя тем, что не выполняю их быстро.

- Теперь я стараюсь не допускать горящих сроков – мои планы в основном остаются в категории «важных и несрочных», а не переходят в «срочные». Матрица помогла отказаться от привычки делать всё в последнюю минуту.
- Задумалась вот над чем: если некоторые дела нет нужды заносить в список дел (типа посидеть вконтакте), то может и делать их можно пореже? Например, я начала контролировать своего «пожирателя» времени — время в соц.сетях.
P.S. Как провести расхламление и разобрать домашние завалы? Как легко расставаться с ненужными вещами? Как навести порядок, который сохраняется, а не исчезает через день?
Ответы — в бесплатном гиде 18 правил для расхламления и порядка. Получите его в подарок! — ВКонтакте или на свою электронную почту.
Как получить?
Разделение матриц в MatLab® (иллюстрированное выражение)
В этой статье мы покажем, как делить матрицы или можем ли мы делить матрицы в Matlab®. Как вы знаете, деление матриц имеет особое значение в линейной алгебре. Итак, есть несколько правил деления матриц в линейной алгебре. Эти правила также действуют в Matlab® при делении матриц. Вы можете взглянуть на приведенные ниже примеры, чтобы понять правила деления матриц в Matlab® и то, как разделить матрицы в Matlab® элемент за элементом.
Как вы знаете, деление матриц имеет особое значение в линейной алгебре. Итак, есть несколько правил деления матриц в линейной алгебре. Эти правила также действуют в Matlab® при делении матриц. Вы можете взглянуть на приведенные ниже примеры, чтобы понять правила деления матриц в Matlab® и то, как разделить матрицы в Matlab® элемент за элементом.
Кроме того, вы можете найти много контента о Matlab®, например, эту статью в Mechanical Base, чтобы полностью изучить Matlab®. Посетите главную страницу Механической базы!
Как разделить матрицы в Matlab®?
>> а = [1 3 5; 7 8 11; 100 1 4];
b = [1 4 5; 5 82 411; 1400 51 4];
с = а / б
d = a./b
c =
0,6632 0,0041 0,0002
1,8725 0,0039 0,0036
-1,1393 0,0229 0,0722
d =
1.0000 0,7500 1,0000
1,4000 0,0976 0,0268
0,0714 0,0196 1,0000
>> Деление матриц в Matlab® приводит к «an * inv (b)», которое является делением матриц одинаковых размеров в линейной алгебре. Итак, результат прямого деления матриц «a» и «b» показан выше.
Итак, результат прямого деления матриц «a» и «b» показан выше.
Значение «d» – это поэлементное деление матриц «a» и «b». Одни и те же пронумерованные элементы строка-столбец в матрицах «a» и «b» разделяются друг на друга.Мы ставим “.” Прямо перед математическим символом деления (./).
Заключение
Таким образом, разделить матрицы в Matlab® очень просто, как указано выше.
Не забывайте оставлять ниже свои комментарии и вопросы по разделению матриц в Matlab®.
Если вам нужны дополнительные примеры кодирования о разделении матриц в Matlab®, сообщите нам в комментариях.
Эта статья предназначена исключительно для образовательных и информационных целей.Изображения любезно предоставлены Matlab®
Ваши ценные отзывы очень важны для нас.
Обратная квадратная матрица
6.3 – Обратная квадратная матрицаРеальные числа
При работе с действительными числами уравнение ax = b может быть решено относительно x путем деления обоих
стороны уравнения на a, чтобы получить x = b / a, если a не было равным нулю. Поэтому казалось бы логичным
что при работе с матрицами можно взять матричное уравнение AX = B и разделить оба
сторон на A, чтобы получить X = B / A.
Поэтому казалось бы логичным
что при работе с матрицами можно взять матричное уравнение AX = B и разделить оба
сторон на A, чтобы получить X = B / A.
Однако это не сработает, потому что …
Нет матричного деления!
Хорошо, скажете вы. Вычитание было определено в терминах сложения, а деление – в терминах умножение. Поэтому вместо деления я просто умножу на обратное. Так оно и есть должно быть сделано.
Обратная матрица
Итак, что есть инверсия матрицы?
Ну, в реальных числах, обратное любому действительному числу a было числом a -1 , так что a умножить на a -1 равняется 1.Мы знали, что для действительного числа обратное число было обратным значению число, если число не было нулем.
Обратной квадратной матрице A, обозначенной A -1 , является матрица
так что произведение A
а -1 – это матрица идентичности. Идентификационная матрица, которая дает
будет того же размера, что и матрица A. Вау,
есть
а
много общего между действительными числами и матрицами. Это хорошо, правда
–
ты
не хочу
это быть
что-то совсем другое.
Вау,
есть
а
много общего между действительными числами и матрицами. Это хорошо, правда
–
ты
не хочу
это быть
что-то совсем другое.
A (A -1 ) = I или A -1 (A) = I
Но есть несколько исключений. Прежде всего, A -1 делает не значит 1 / A. Помните: «Матричного деления нет!» Во-вторых, A -1 делает не означает брать обратную величину каждого элемента в матрице А.
Требования к инверсу
- Матрица должна быть квадратной (одинаковое количество строк и столбцов).
- Определитель матрицы не должен быть нулевым (определители рассматриваются в разделе 6.4). Это вместо того, чтобы действительное число не равнялось нулю, чтобы иметь обратное значение, определитель не должен равняться нулю, чтобы иметь обратное.
Квадратная матрица, имеющая обратную, называется обратимой или невырожденной . Матрица, которая не
у инверсии называется в единственном числе .
Матрица не обязательно должна иметь обратную, но если она есть, то обратная матрица уникальна.
Трудный путь в поисках обратного
Матрица, обратная матрице A, будет удовлетворять уравнению A (A -1 ) = I.
- Присоедините единичную матрицу к правой части исходной матрицы, чтобы у вас есть A слева и единичная матрица справа. Это будет выглядеть так [A | I].
- Строка-уменьшить (предлагаю использовать поворот) матрицу пока в левой части не появится матрица идентичности. Когда левая сторона – это личность матрица правая сторона будет Обратной [I | А -1 ]. Если вы не можете чтобы получить единичную матрицу в левой части, тогда матрица сингулярна и не имеет обратного.
- Возьмите расширенную матрицу с правой стороны и назовите ее обратной.
Ярлык для поиска обратной матрицы 2 × 2
Матрица, обратная матрице 2 × 2, может быть найдена с помощью …
- Переключить элементы по главной диагонали
- Возьмите противоположность двух других элементов
- Делим все значения на определитель матрицы (так как мы
не говорили о детерминанте, для системы 2 × 2 это
произведение элементов на главной диагонали за вычетом произведения
двух других элементов).

Пример ярлыка
Поехали с оригинальной матрицей
Шаг 1, переключение элементов на главной диагонали повлечет за собой переключение 5 и 7.
Шаг 2, возьмите противоположность двух других элементов, но оставьте их там, где они есть.
Шаг 3, найдите определитель и разделите на него каждый элемент. Определитель это произведение элементов на главной диагонали за вычетом произведения элементы от главной диагонали.Это означает, что определитель этой матрицы равен 7 (5) – (-3) (2) = 35 + 6 = 41. Делим каждый элемент на 41.
Матрица, обратная исходной матрице …
| 5/41 | 2/41 | ||
| -3/41 | 7/41 |
Теперь, вы говорите, подождите минутку – вы сказали, что не было матричного деления.
Деления по матрице нет. Вы можете умножить или разделить матрицу на
скаляр (действительное число) и определитель
является скаляром.
Использование калькулятора
Теперь, когда вы знаете, как найти единичную матрицу вручную, поговорим о практичности. Калькулятор сделаю это за вас.
Вход в матрицу
- Нажмите клавишу Matrix (справа под клавишей X). На TI-83 + вам понадобится чтобы поразить 2 и Matrix.
- Стрелка к подменю Правка.
- Выберите матрицу для работы. У вас есть пять вариантов на выбор с TI-82 и десять на выбор. выбирайте из с TI-83.Обычно вы будете использовать [A]. Старайтесь избегать использования [E] для неуказанные причины, которые будут указаны, если вы изучаете конечную математику.
- Введите количество строк, нажмите клавишу ВВОД, а затем введите количество столбцов, а затем входить.
- Теперь вы вводите каждый элемент в матрицу, читая слева направо и сверху вниз. Нажмите введите после каждого числа. Вы можете использовать клавиши со стрелками для перемещения, если вы допустили ошибку.
- Закройте (режим 2 и ), когда закончите вводить все числа.

Использование матриц
Всякий раз, когда вам нужно получить доступ к созданной вами матрице, просто нажмите клавишу Matrix и выберите соответствующая матрица. Я бы посоветовал вам начать использовать Матрицу 1, Матрицу 2 и т. Д. Вместо Матрица, стрелка вниз, ввод. Это будет происходить быстрее, и вы будете много делать с этими матрицами.
Нахождение обратной матрицы на калькуляторе
Введите выражение [A] -1 , перейдя в Матрицу 1 и нажав клавишу x -1 .(-1).
Возможно, вам придется использовать клавиши со стрелками вправо или влево, чтобы пролистать всю матрицу, чтобы записать ее вниз. По возможности дайте точные ответы.
Один из способов дать точный ответ – это заставить калькулятор переводить десятичные дроби в дроби для
ты. В конце концов, дроби действительно ваши друзья (и я серьезно это имею в виду). Вы можете получить
Калькулятор выполняет преобразование десятичной дроби в дробную, нажимая Math, Enter, Enter.
Также, если вы получите ответ типа 1.2E-12, шансы действительно хорошо, что число равно нулю, и это из-за неточности в калькуляторе что вы получаете такой ответ. Преобразуйте число до нуля.
Зачем понадобился инверс?
Я так рад, что вы спросили об этом.
Одно из основных применений обратного преобразования – решение системы линейных уравнений. Вы можете записать систему в матричной форме как AX = B.
Теперь предварительно умножьте обе стороны на обратную величину A. Убедитесь, что вы соблюдаете эти два условия.
- Вы должны разместить инверсную матрицу рядом с матрицей. То есть потому что инверсии должны быть рядом друг с другом (математически очень расплывчато, но вернемся к функциям), чтобы уничтожить друг друга.
- Если
вы умножаете, помещая что-то перед левой стороной (предварительное умножение),
он должен идти впереди правой стороны. Если вы положите что-то позади
(пост-умножение) левой стороны, она должна идти позади правой стороны.

Умножение матриц НЕ коммутативно!
A -1 (AX) = A -1 (B)… предварительно умножить с обеих сторон по А -1
(A -1 A) X = A -1 B … используйте ассоциативный свойство для перегруппировки факторов
I X = A -1 B … при умножении на обратное вместе они становятся единичной матрицей
X = A -1 B … единичная матрица похожа на умножение на 1.
Если AX = B, то X = A -1 B
Итак, вы обычно цинично спрашиваете: «Вы только что решили другое уравнение, что это имеет какое-либо отношение? »
Решение систем линейных уравнений
Рассмотрим систему линейных уравнений
3x + 2y - 5z = 12 х - 3у + 2z = -13 5x - y + 4z = 10
Запишите коэффициенты в матрицу A.
| х | y | z | ||
|---|---|---|---|---|
| 3 | 2 | -5 | ||
| 1 | -3 | 2 | ||
| 5 | –1 | 4 |
Запишите переменные в матрицу X.
Запишите константы в матрицу B.
| 12 | ||
| -13 | ||
| 10 |
Убедитесь, что AX = B
Этот шаг на самом деле не нужен, но я хотел показать вам, что это действительно работает.
AX будет (3 × 3) × (3 × 1) = 3 × 1 матрица. Матрица B также является матрицей 3 × 1, поэтому, по крайней мере, размеры работать правильно.
Вот A, умноженное на X.
| 3 | 2 | -5 | х | 3x + 2y – 5z | ||||||||
| 1 | -3 | 2 | y | = | 1x – 3y + 2z | |||||||
| 5 | –1 | 4 | z | 5x – 1y + 4z |
Обратите внимание, что это левая часть системы уравнений. В
B – правая часть, значит, мы достигли равенства. Woohoo! Ты можешь написать
система линейных уравнений в виде AX = B.
В
B – правая часть, значит, мы достигли равенства. Woohoo! Ты можешь написать
система линейных уравнений в виде AX = B.
Итак, если вы можете записать систему линейных уравнений в виде AX = B, где A – коэффициент матрица, X – переменная матрица, а B – правая часть, вы можете найти решение системы X = A -1 B.
Поместите матрицу коэффициентов в [A] на калькуляторе и с правой стороны. стороной в [B].
Если вы попросили калькулятор найти обратный коэффициент матрица, это даст вам это для A -1
| 5/44 | 3/88 | 1/8 | ||
| -3/44 | -37/88 | 1/8 | ||
| -7/44 | -13/88 | 1/8 |
Вы можете сделать это, а затем умножить это на B, но было бы проще просто
поместить все выражение в калькулятор и сразу получить ответ. Даже то, что показано ниже, – это больше работы, чем необходимо.
Даже то, что показано ниже, – это больше работы, чем необходимо.
X = A -1 B = …
| х | 5/44 | 3/88 | 1/8 | 12 | 191/88 | |||||||||||
| y | = | -3/44 | -37/88 | 1/8 | -13 | = | 519/88 | |||||||||
| z | -7/44 | -13/88 | 1/8 | 10 | 111/88 |
Итак, x = 191/88, y = 519/88 и z = 111/88. Это было бы настоящим
боль
решать вручную.
Это было бы настоящим
боль
решать вручную.
Это просто, почему мы не всегда так делаем?
Основная причина в том, что это не всегда работает.
- Инверсии существуют только для квадратных матриц. Это означает, что если вы не то же самое количество уравнений в качестве переменных, то вы не можете использовать этот метод.
- Не каждая квадратная матрица имеет инверсию. Если матрица коэффициентов A равна единственное число (не имеет обратного), тогда решения может не быть или может быть много решений, но мы не можем сказать, что это такое.
- Перевертыши сложно найти вручную. Если у вас есть калькулятор, его нет так плохо, но помните, что калькуляторы не всегда дают вам ответ, который вы находясь в поиске.
(PDF) РАЗДЕЛЕНИЕ МАТРИЦ И ЗЕРКАЛЬНОЕ ИЗОБРАЖЕНИЕ СВОЙСТВА МАТРИЦ
7 ССЫЛКИ
[1] Bachmann, F .; Schmidt, E .: n-Ecke. B. I. Hochschultaschenbuch 471 / 471a, Mannheim,
Wien, Z¨urich 1970. Zbl 0208.23901
Zbl 0208.23901
[2] Radi´c, M .: Определение определителя прямоугольной матрицы.Glas. Мат. 1 (21) (1966),
17 – 22. Zbl 0168.02703
[3] Suˇsanj, R .; Радиц, М .: Геометрическое значение одной генерации определителя
квадратной матрицы. Glas. Матем., III. Сер. 29 (2) (1994), 217 – 233. Zbl 0828.15005
Math. 1356, Springer – Verlag, 1988
Math. Ежемесячно 62 (1955) 395-413.
[4] Яглом И. М .: Комплексные числа в геометрии. Перевод Э. Дж. Ф. Примроуза, Aca-demic Press, Нью-Йорк
1966.Zbl 0147.20201
[5] Нилам Дживан Кумар, «Деление матриц», Индия, том – 1, стр. 570-578, сентябрь. 2012, ISSN: 2278 – 8697
[6] WB Jurkat, HG Ryser, «Факторизация матриц и детерминанты перманентов», J algebra 3,1966,1-27
[7] Алстон С. матрицы в численном анализе »(Бласидель Джин и компания) Newyork,
Toronto, London, 1964
[8] Г. Бутри, М. Элад, Г. Голуб, П. Миланфар, Обобщенная проблема собственных значений для неквадратных карандашей
используя подход минимального возмущения, SIAM J. Матрица Анал. Прил.
Матрица Анал. Прил.
27 (2005), 582–601
[9] Д. Чу, Г. Голуб, Об одной обобщенной задаче на собственные значения для неквадратных пучков. SIAM
J. Matrix Anal. Прил. 28 (2006), 770 – 787
[10] Х. Фолькмер, Многопараметрические задачи на собственные значения и теоремы о разложении. Лект. Примечания.
JW Demmel, Applied Numerical
Linear Algebra, SIAM, Philadelphia, 1997
[12] GH Golub and CF Van Loan, Matrix Computations, Third Edition,
The Johns Hopkins University Press, Baltimore, 1996
[13 ] ГРАММ.W. Stewart, Introduction to Matrix Computations, Academic Press, New
York, 1973
[14] GW Stewart, Matrix Algorithms: Basic Decompositions, SIAM, Philadel – phia, 1998
[15] LN Trefethen and D. Bau , III, Численная линейная алгебра, SIAM, Филадельфия, 1997 г.
[16] Дж. Форсайт и CB Moler «Вычислительная система и линейные алгебраические системы» Прентис – холл
[17] JH Уилкинсон, Алгебраическая проблема собственных значений, Oxford University Press, Oxford, 1965
[18] Джоши В. А. Определитель для прямоугольных матриц // Изв. Остуаль. Математическое общество., 21, 1980, 107 – 122
А. Определитель для прямоугольных матриц // Изв. Остуаль. Математическое общество., 21, 1980, 107 – 122
[19] Radic.M «Определение прямоугольной матрицы», Гласник, Математицки, 1 (21), вып. 1, 1966, 17–22.
[20] Райнхарт, РФ., Эквивалентность определений матричной функции, Американский
Международный журнал достижений в области исследований и технологий, Том 2, выпуск 7, июль 2013 г.
ISSN 2278-7763
Авторские права © 2013 SciResPub. IJOART
FAQ: Поэлементные операции с матрицами
Как выполнять поэлементные операции с матрицами?
| Заголовок | Выполнение поэлементных операций с матрицами | |
| Автор | Аллен Макдауэлл, StataCorp |
Матричные манипуляции были значительно улучшены со времен Stata 9 с использованием Mata
язык.Одна из возможностей – поэлементный расчет.
с помощью оператора двоеточия. Например:
Например:
. мата
------------------------------------------------- мата (введите конец до выхода) ------
: х
1 2
+ --------- +
1 | 1 2 |
2 | 3 4 |
+ --------- +
: y
1 2
+ --------- +
1 | 3 5 |
2 | 7 9 |
+ --------- +
: г = х: / у
: z
1 2
+ ----------------------------- +
1 | .3333333333 .4 |
2 | .4285714286 .4444444444 |
+ ----------------------------- +
: конец
-------------------------------------------------- ------------------------------
Или, в Stata, предположим, что у меня есть следующие две матрицы, A и B,
. матрица A = (1,2,3,4,5 \ 6,7,8,9,10)
. список матов A
А [2,5]
c1 c2 c3 c4 c5
г1 1 2 3 4 5
г2 6 7 8 9 10
. матрица B = (11,12,13,14,15 \ 16,17,18,19,20)
.матричный список B
B [2,5]
c1 c2 c3 c4 c5
г1 11 12 13 14 15
г2 16 17 18 19 20
Я хочу выполнить поэлементное деление. То есть, предположим, я хочу
чтобы сгенерировать матрицу C, чтобы каждый элемент C был отношением
соответствующие элементы в A и B, так что C [1,1] = A [1,1] / B [1,1]; C [1,2] =
A [1,2] / B [1,2]; и т.п.
То есть, предположим, я хочу
чтобы сгенерировать матрицу C, чтобы каждый элемент C был отношением
соответствующие элементы в A и B, так что C [1,1] = A [1,1] / B [1,1]; C [1,2] =
A [1,2] / B [1,2]; и т.п.
Сначала я создаю матрицу C, чтобы она имела правильные размеры. я должен заполнить элементы некоторым значением, поэтому я выбрал нули.
. матрица C = J (2,5,0)
. список матриц C
С [2,5]
c1 c2 c3 c4 c5
г1 0 0 0 0 0
г2 0 0 0 0 0
Теперь я могу настроить вложенные циклы для значений с индексацией внешнего цикла. строки и внутренний цикл индексации столбцов.
для значений i = 1/2 {
для значений j = 1/5 {
матрица C [`i ',` j'] = A [`i ',` j'] / B [`i ',` j']
}
}
список матриц C
С [2,5]
c1 c2 c3 c4 c5
r1.009 .16666667 .23076923 .28571429 .33333333
r2 .375 .41176471 .44444444 .47368421 .5
Я могу легко изменить приведенный выше код, чтобы учесть другие алгебраические
выражения, включающие отдельные матричные элементы и матрицы любых
Габаритные размеры.
Матричная алгебра
Матричная алгебра Матричная алгебра
Что такое единичная матрица?
Что такое скаляр?
Что такое обратная матрица?
Когда (для какой матрицы) транспонированная матрица равна исходной матрице?
Произвести умножение матриц.
Учитывая матрицу и матричную операцию, определите содержимое результирующей матрицы (например, SSCP, ковариация, корреляция).
Определения
«Матрица – это прямоугольник размером n на k, состоящий из чисел или символов, обозначающих числа» (Pedhazur, 1997, p. 983). Размер матрицы называется ее порядком и обозначается строками и столбцами. По соглашению, строки всегда упоминаются первыми. Таким образом, матрица порядка 3 на 2 под названием A может выглядеть так:
A
= Матрица с именем B порядка 4 на 4 может выглядеть так:
B
= Обычно матрицы в тексте печатаются жирным шрифтом .
Элементы (элементы) матрицы упоминаются по имени матрицы в нижнем регистре с заданной строкой и столбцом (опять же, строка идет первой). Например, a 31 = 2, b 22 = 1. Как правило, a ij означает элемент A в i-й строке и j-м столбце. По соглашению, элементы напечатаны курсивом .
Преобразование матрицы получается путем обмена строками и столбцами, так что первая строка становится первым столбцом и так далее.Транспонирование матрицы обозначается одинарной кавычкой и называется простым числом. Например, A ‘(простое число):
A
= A ‘=
Обратите внимание, что A ‘- это не просто A , «опрокинутый» на бок (если это так, мы увидим в первом столбце 1 3 вместо 3 1). Это как если бы карточки или доски с номерами для каждого ряда были вытянуты 1 на 1 и размещены в порядке транспонирования. Транспонирование B:
B
= B ‘=
(Для некоторых матриц транспонирование равно исходной матрице. )
)
Если n = k, количество строк равно количеству столбцов, а матрица равна квадрату . Квадратная матрица может быть симметричной или асимметричной . Симметричная матрица обладает тем свойством, что элементы выше и ниже главной диагонали одинаковы, так что element (i, j) = element (j, i), как в нашей матрице B . (Главная или главная диагональ в матрице B состоит из элементов, все равны 1.) В случае квадратной симметричной матрицы транспонированная матрица является исходной матрицей.Корреляционная матрица всегда будет квадратной симметричной матрицей, поэтому транспонирование будет равно оригиналу.
Вектор-столбец – это числовая матрица размером n на 1. Например:
(я собираюсь использовать прямоугольники для матриц, а не стандартные скобки из-за проблем с форматированием.) Итак, b – вектор-столбец. Вектор-строка представляет собой числовую матрицу размером 1 на k. Например,
Итак, b ‘- вектор-строка. Обратите внимание, что b ‘ – это транспонирование b . По соглашению векторы печатаются строчными буквами жирным шрифтом, а векторы-строки представлены как транспонированные векторы-столбцы.
Обратите внимание, что b ‘ – это транспонирование b . По соглашению векторы печатаются строчными буквами жирным шрифтом, а векторы-строки представлены как транспонированные векторы-столбцы.
Диагональная матрица – это квадратная симметричная матрица с нулями везде, кроме главной диагонали. Например: С
= 12
0
0
0
10
0
0
0
5
C – диагональная матрица.
Особенно важная диагональная матрица называется единичной матрицей, I . Эта диагональная матрица имеет единицы на главной диагонали.
Эта диагональная матрица имеет единицы на главной диагонали.
Я
= 1
0
0
0
1
0
0
0
1
I – единичная матрица.Бывает, что корреляционная матрица, в которой все переменные ортогональны, является единичной матрицей.
Скаляр – это матрица с одним элементом. Например
d
– скаляр. Матричные операции
Сложение и вычитание
Матрицы можно складывать и вычитать тогда и только тогда, когда они одного порядка (идентичны по количеству строк и столбцов). Матрицы, на которых допустима операция, называются соответствующими операции.
Матрицы, на которых допустима операция, называются соответствующими операции.
Нам повезло, что сложение и вычитание матриц просто означает сложение или вычитание соответствующих элементов двух матриц.
Дополнение
4
+
6
=
10
1
2
3
5
3
8
x
л
z
Дополнение
1
2
+
3
4
=
4
6
1
2
5
6
6
8
1
2
7
8
8
10
Х
Y
Z
Вычитание
1
2
–
3
4
=
-2
-2
1
2
5
6
-4
-4
1
2
7
8
-6
-6
Х
Y
Z
Умножение
В отличие от сложения и вычитания матриц, умножение матриц не является прямым расширением обычного умножения. Умножение матриц включает как умножение, так и добавление элементов. Если мы умножим вектор-строку на вектор-столбец, мы получим скаляр.
Умножение матриц включает как умножение, так и добавление элементов. Если мы умножим вектор-строку на вектор-столбец, мы получим скаляр.
Чтобы получить это, мы сначала умножаем соответствующие элементы, а затем складываем их.
в1
=
а1
а2
a3
в2
a1b1
+ a2b2
+ a3b3
b3
а ‘
б
с
Для числового примера:
0
=
=
1
2
3
2
0 + 4 + 12
16
4
Результат умножения двух таких векторов называется скалярным произведением. Скалярные произведения имеют множество статистических приложений. Например, сумму переменной можно найти, поместив эту переменную в вектор-столбец и предварительно умножив ее на вектор-строку, состоящий из единиц.
Скалярные произведения имеют множество статистических приложений. Например, сумму переменной можно найти, поместив эту переменную в вектор-столбец и предварительно умножив ее на вектор-строку, состоящий из единиц.
Например,
7
1
1
1
8
=
7 + 8 + 9
=
24
9
1 дюйм x
= S X Мы можем найти сумму перекрестных произведений по таким операциям:
1
2
4
6
3
=
2 + 12 + 30
=
44
5
x’y
= S XY И если мы вычтем среднее значение из вектора-столбца, мы можем найти сумму квадратов:
–1
–1
0
1
0
=
1 + 0 + 1
=
2
1
x’x
= S x 2 В отличие от обычного умножения, матричное умножение не является симметричным, так что в целом x’y не равно y’x , то есть предварительное и последующее умножение обычно не дает одинакового результата. В общем, первая матрица будет порядка r1xc1, а вторая – порядка r2xc2.
В общем, первая матрица будет порядка r1xc1, а вторая – порядка r2xc2.
Чтобы соответствовать умножению, c1 должно быть равно r2. Порядок результирующей матрицы будет r1xc2. Внутренние числа должны быть равны, чтобы произошло умножение. Если да, то результат будет порядка внешних чисел. Некоторые примеры
А (1 ул )
Б (2 nd )
AB
рядов
Cols
рядов
Cols
рядов
Cols
1
5
5
1
1
1
1
10
10
1
1
1
1
6
5
1
DNC
5
1
1
5
5
5
3
2
2
3
3
3
3
3
2
3
DNC
2
4
4
3
2
3
То, что происходит при умножении матриц, зависит от порядка матриц (хотя последовательность шагов всегда одинакова).
Если мы умножим вектор-столбец на вектор-строку, мы получим матричное произведение векторов, а не скаляр.
Пример
1
1
-2
0
2
1
-2
0
=
2
-4
0
3
3
-6
0
а
б ‘
=
К
3×1
1×3
3×3
Возьмите первую строку a (1), умножьте на первый столбец b (1) установите результат на c 1,1 . Возьмите вторую строку a (2), умножьте на 1 st col b (1), установите результат как c 2,1 и т. Д.
Возьмите вторую строку a (2), умножьте на 1 st col b (1), установите результат как c 2,1 и т. Д.
Тот же самый шаблон используется для матриц большего порядка, за исключением того, что для каждой комбинации мы умножаем и складываем. Например
2
1
7
8
9
3
1
2
3
4
9
11
13
4
2
3
2
1
14
16
18
А
Б
К
3×2
2×3
3×3
Чтобы получить значения C
(2) 2+ (1) 3 = 7 (1,1)
(2) 3+ (1) 2 = 8
(1,2) (2) 4+ (1) 1 = 9
(1,3) (3) 2+ (1) 3 = 9
(2,1) (3) 3+ (1) 2 = 11
(2,2) (3) 4+ (1) 1 = 13
(2,3) (4) 2+ (2) 3 = 14
(3,1) (4) 3+ (2) 2 = 16
(3,2) (4) 4+ (2) 1 = 18
(3,3)
Идите по строкам первой матрицы и столбцам второй. Чтобы получить c (1,1), возьмите первую строку и первый столбец, умножьте соответствующие элементы и сложите.
Чтобы получить c (1,1), возьмите первую строку и первый столбец, умножьте соответствующие элементы и сложите.
Умножение матриц полезно для нахождения матрицы сумм квадратов и перекрестных произведений (матрица SSCP).
Мы можем найти либо исходную оценку, либо сумму оценок отклонений квадратов и перекрестных произведений. Первые необработанные баллы:
1
2
0
1
2
2
3
2
2
2
3
2
26
37
14
2
3
4
3
4
2
2
4
2
37
58
20
0
2
2
2
0
0
3
3
2
14
20
12
2
4
0
2
2
0
Х ‘
Х
SSCP
3х6
6×3
3×3
Содержимое матрицы SSCP
Теперь отклонение оценок от тех же данных:
-1
-1
-1
-1
0
0
1
0
0
0
0
1
2
1
2
-1
0
1
0
1
-1
0
1
1
1
4
2
-1
1
1
1
-1
-1
1
0
1
2
2
6
0
1
-1
0
-1
-1
Х ‘
Х
SSCP
3х6
6×3
3×3
Содержимое матрицы SSCP
Если мы умножаем или делим матрицу на скаляр, каждый элемент матрицы умножается (делится) на этот скаляр. Если мы разделим каждый элемент в приведенной выше матрице SSCP на 6 (размер выборки), мы получим
Если мы разделим каждый элемент в приведенной выше матрице SSCP на 6 (размер выборки), мы получим
2/6
1/6
2/6
0,33
,17
0,33
1/6
4/6
2/6
=
.17
,66
0,33
2/6
2/6
6/6
0,33
0,33
1
Матрица SSCP, деленная на N (или N-1), называется матрицей вариации-ковариации. В нем у нас есть дисперсии по диагонали и ковариации по главной диагонали.
В нем у нас есть дисперсии по диагонали и ковариации по главной диагонали.
Если мы дополнительно разделим на стандартное отклонение для каждой строки и каждого столбца, мы получим матрицу корреляции:
Корреляционная матрица для наших данных:
Детерминанты
Определитель – это необычное свойство или значение матрицы. Мы (ну, фактически, компьютер) будем находить детерминанты корреляции, дисперсии-ковариации или матриц суммы квадратов и перекрестных произведений (SSCP).Вы можете думать о детерминанте как о мере свободы изменения или отсутствия предсказуемости в матрице (я говорю это, чтобы дать вам некоторое представление о том, что это такое, даже если оно не совсем правильное или точное). Помимо общего представления о том, что это такое и окружающей его номенклатуре, вам необходимо знать (а) что определитель используется для нахождения обратной матрицы (обсуждается в следующем разделе) и (б) что это означает, когда определитель нуль.
Записан определитель матрицы A
det ( A ) = | A | или
Определитель обозначен вертикальными линиями вместо скобок.Определитель трудно вычислить, если матрица не имеет порядок 2×2. В этом случае определитель будет просто a 11 ( a 22 ) – a 21 ( a 12 ). В нашем примере выше определитель будет 1 (1) – (. 5) (. 5) = 0,75.
Большой детерминант означает, что есть свобода изменения; нулевой определитель означает, что нет свободы варьирования, в матрице есть полная предсказуемость.Например, если бы корреляция между двумя нашими показателями была 1,0, то определитель корреляционной матрицы был бы (1) (1) – (1) (1) = 0. Определитель нулевых результатов, когда существует линейная зависимость в матрица. То есть, если одна переменная является линейной комбинацией других переменных в матрице, определитель будет равен нулю. Например, предположим, что я хочу использовать удовлетворенность работой для прогнозирования текучести кадров. У меня есть пять шкал удовлетворенности работой из JDI (известный показатель описания работы): работа, оплата, продвижение по службе, супервизия и коллеги.Теперь предположим, что я хочу спрогнозировать текучесть кадров из этих пяти плюс общее удовлетворение. Если я суммирую пять шкал, чтобы обозначить общее удовлетворение, общая сумма будет линейной комбинацией пяти шкал (общая = работа + оплата + промо + супер + работа).
Например, предположим, что я хочу использовать удовлетворенность работой для прогнозирования текучести кадров. У меня есть пять шкал удовлетворенности работой из JDI (известный показатель описания работы): работа, оплата, продвижение по службе, супервизия и коллеги.Теперь предположим, что я хочу спрогнозировать текучесть кадров из этих пяти плюс общее удовлетворение. Если я суммирую пять шкал, чтобы обозначить общее удовлетворение, общая сумма будет линейной комбинацией пяти шкал (общая = работа + оплата + промо + супер + работа).
Если я помещу все шесть шкал в корреляционную матрицу, у нее будет нулевой определитель. Матрица с нулевым определителем называется сингулярным числом . Как скоро будет объяснено, это в некотором роде плохо. Сингулярные матрицы создают для нас неприятные проблемы.Матрица будет сингулярной, если любые две переменные в матрице идеально коррелированы (либо r = 1, либо r = -1). Матрица также будет сингулярной, если любая переменная в матрице идеально предсказывается любой комбинацией других переменных в матрице. То есть, если мы выберем любую одну переменную в качестве зависимой переменной и используем любую комбинацию других переменных в матрице для вычисления линейной регрессии и найдем R 2 равным 1,0, матрица будет сингулярной. У сингулярной матрицы нет обратной .
То есть, если мы выберем любую одну переменную в качестве зависимой переменной и используем любую комбинацию других переменных в матрице для вычисления линейной регрессии и найдем R 2 равным 1,0, матрица будет сингулярной. У сингулярной матрицы нет обратной .
1
0
0
0
1
0
| A |
= 1
0
0
1
А
1
. 5
5
,25
,5
1
,25
| B |
= 0,69
.25
,25
1
Б
1
1
0
1
1
0
| C |
= 0
0
0
1
К
Обратите внимание, что определитель для A больше, чем для B , потому что у A больше свободы для изменения, и, конечно, определитель для C равен нулю, потому что две из переменных идеально подходят коррелирован.
Инверсная матрица
Матричный аналог деления действительных чисел . В реальных числах x -1 равно 1 / x. А в действительных числах, если мы умножим x на x -1 , мы получим (x) (1 / x) = 1. Только квадратная матрица может иметь обратную. Обратное имеет свойство: когда мы умножаем матрицу на обратную, результатом является единичная матрица, I . Другими словами, AA -1 = A -1 A = I .Это особенное во многих отношениях. Во-первых, обычно бывает, что предварительное умножение и постумножение двух матриц дает один и тот же результат ( AX обычно не равно XA ). Во-вторых, единичная матрица обладает тем свойством, что ее умножение на любую соответствующую матрицу дает ту же матрицу. То есть AI = IA = A . Умножение матрицы на единичную матрицу аналогично действительной операции умножения числа или переменной на 1: результирующий вывод идентичен вводимым числам. Вот почему обратная матрица аналогична делению числа на себя в действительных числах. В вещественных числах, когда вы делите число на обратное (обратное), результат будет 1. Когда вы умножаете матрицу на обратную, результат будет I . В обоих случаях (1 и I ) при умножении на что-то исходное значение остается неизменным.
Вот почему обратная матрица аналогична делению числа на себя в действительных числах. В вещественных числах, когда вы делите число на обратное (обратное), результат будет 1. Когда вы умножаете матрицу на обратную, результат будет I . В обоих случаях (1 и I ) при умножении на что-то исходное значение остается неизменным.
1
,5
,25
1
0
0
1
.5
,25
,5
1
,25
0
1
0
,5
1
,25
,25
,25
1
0
0
1
. 25
25
,25
1
Б
Я
BI
1
. 5
5
,25
1,36
-.64
-.18
1
0
0
,5
1
,25
-.64
1,36
-.18
0
1
0
,25
,25
1
-.18
-. 18
18
1,36
0
0
1
Б
В -1
BB -1
Проверить умножение.
БИ (1,1) = 1 + 0 + 0; BI (2,1) = 0,5 + 0 + 0; BI (3,1) = 0,25 + 0 + 0 и т. Д. BB -1 (1,1) = (1) 1,36-5 (0,46) – 0,25 (0,18) = 1; BB -1 (2,1) = 0,5 (1,36) – (1) .64-0,25 (0,18) = 0 и т. Д.
Третья, основная причина, по которой мы заботимся об этом, заключается в том, что инверсия используется при нахождении весов b и b из матриц данных. Если мы умножим корреляционную матрицу на ее обратную, мы получим единичную матрицу, I . Это позволяет нам умножить обе части уравнения на обратное, чтобы решить матричное уравнение (точно так же, как деление обеих сторон уравнения в обычной алгебре).
Если мы умножим корреляционную матрицу на ее обратную, мы получим единичную матрицу, I . Это позволяет нам умножить обе части уравнения на обратное, чтобы решить матричное уравнение (точно так же, как деление обеих сторон уравнения в обычной алгебре).
Обратное выражение позволяет нам найти веса b .
Во всяком случае, обратного нет, когда матрица сингулярна (когда определитель равен нулю). Когда нет обратного, мы не можем найти веса b . Итак, если у нас есть сингулярная матрица, мы не можем выполнять множественную регрессию.
Как разделить в Google Таблицах (числа, ячейки или столбцы)
Google Таблицы теперь являются популярным инструментом для работы с электронными таблицами для большинства людей.Это бесплатное приложение, с которым очень легко сотрудничать, и в нем есть несколько замечательных функций и возможностей.
Даже если вы хотите сделать что-то столь же простое, как хранение данных или простые вычисления, такие как умножение или деление, вы можете легко сделать это в Google Таблицах.
В этом руководстве. Я покажу вам несколько способов делить числа в Google Таблицах.
Вы можете легко разделить числа в Google Таблицах, используя встроенную формулу или оператор деления (как мы увидим на примерах).
Итак, приступим!
Разделите две ячейки в Google Таблицах
Если вы хотите разделить два числа в Google Таблицах (или две ячейки с числами), то есть несколько способов сделать это в Google Таблицах.
Использование функции РАЗДЕЛ
Деление в Google Таблицах – настолько обычная задача, что существует встроенная функция, которая позволяет вам разделить два числа или числа, которые находятся в двух ячейках.
Это функция РАЗДЕЛИТЬ (без оценок для угадывания)!
Предположим, вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Для этого можно использовать приведенную ниже формулу РАЗДЕЛЕНИЯ:
= РАЗДЕЛЕНИЕ (A1, B1)
В приведенной выше формуле первым аргументом является делимое (число, которое нужно разделить) и делитель (число, на которое нужно разделить)
Я использовал ссылки на ячейки в приведенном выше примере, но вы также можете жестко закодировать значения в формуле. Например, вы также можете использовать следующую формулу:
Например, вы также можете использовать следующую формулу:
= РАЗДЕЛИТЬ (1200,15)
Преимущество использования ссылок на ячейки заключается в том, что результат формулы становится динамическим.Это означает, что если я изменю значение в ячейке A1 или B1, формула обновится автоматически.
Также помните, что делитель не может быть 0. Если ваш делитель равен 0, вы получите ошибку деления – # DIV / 0!
Использование оператора DIVIDE
Еще один быстрый способ делить числа в Google Таблицах – использовать оператор деления – косая черта (/)
Предположим, у вас есть данные, как показано ниже, и вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Для этого можно использовать приведенное ниже уравнение:
= A1 / B1
И если вы хотите быстро разделить числа (вместо ссылок на ячейки), вы также можете это сделать (как показано в формуле ниже):
= 1200/15
Также читайте: Как умножить в Google Таблицах
Порядок приоритета при делении клеток
При использовании арифметических операторов (таких как деление или умножение) в Google Таблицах важно знать порядок приоритета.
Позвольте мне попытаться объяснить это на примере.
Предположим, я использую следующую формулу:
= 1200/15 + 15
Вы можете угадать, что будет в результате?
Было бы 95.
Это происходит из-за того, что в Google Таблицах существует порядок приоритета, в котором деление выполняется перед добавлением. Следовательно, сначала он делит 1200 на 15, где результат равен 80. Затем он прибавляет 15 к этому результату, что дает вам общий результат как 95.
Теперь это несложно понять на нашем простом примере, но это может привести к проблемам при работе с большими сложными формулами.
В таких случаях лучше не беспокоиться о порядке приоритета, оставив вычисления в скобках (скобках).
Например, если вы хотите сначала выполнить сложение, а затем деление, вы можете использовать следующую формулу:
= 1200 / (15 + 15)
Это даст вам результат 40 (= 1200/30)
Разделение двух столбцов в Google Таблицах
В реальных сценариях вам не нужно открывать Google Таблицы для простого разделения. Вы можете легко сделать это с помощью калькулятора на своем смартфоне или с помощью простого поиска в Google.
Вы можете легко сделать это с помощью калькулятора на своем смартфоне или с помощью простого поиска в Google.
Google Таблицы можно использовать для быстрого разделения чисел на столбцы и получения результата для сотен ячеек за секунду.
Например, предположим, что у вас есть набор данных, показанный ниже, и вы хотите вычислить деление, когда значение в столбце A делится на соответствующую ячейку в столбце B
Ниже приведена формула, которая сделает это:
= ArrayFormula (A1: A20 / B1: B20)
Так как это формула массива, вам нужно только ввести эту формулу только в ячейку C1, и она даст вам результат, как показано выше.
Также нельзя удалить или отредактировать часть массива. Однако вы можете удалить весь массив, удалив содержимое ячейки C1.
Разделить без остатка в Google Таблицах
Допустим, у вас есть набор данных, показанный ниже, и вы хотите разделить значение в столбце A на значение в столбце B.
Если вы сделаете это, как показано в предыдущем разделе, вы получите целую часть, а также десятичную часть.
Если вам не нужен остаток при делении этих значений (где остаток является десятичной частью), вы можете использовать следующую формулу:
= ArrayFormula (INT (A1: A20 / B1: B20))
В приведенной выше формуле используется та же формула деления, но она заключена в функцию INT, которая возвращает только целую часть результата, а не десятичную часть.
Итак, вот несколько способов разделения в Google Таблицах. В зависимости от того, хотите ли вы разделить числа, ячейки или столбцы, вы можете использовать функцию РАЗДЕЛЕНИЕ или оператор деления.
Надеюсь, вы нашли этот учебник по Google Таблицам полезным!
Другие руководства по Google Таблицам, которые могут оказаться полезными:
Матрицы – тождественные и обратные матрицы
Тождественные и обратные матрицы
Обратные матрицы
Здесь у вас может возникнуть вопрос, почему Четвертый всадник математического апокалипсиса, разделение, кажется, упускается из виду. Что ж, дело в том, что делением по матрицам не сделаешь. Это нормально, потому что, например, если вы не можете разделить на x , вы можете умножить его на обратное:
Что ж, дело в том, что делением по матрицам не сделаешь. Это нормально, потому что, например, если вы не можете разделить на x , вы можете умножить его на обратное:
То же самое и с матрицами. Все, что нам нужно знать, это как найти обратное, верно?
Проверьте это в контексте решения уравнения:
2 x = 4
Обычно мы просто делим каждую сторону на 2, чтобы решить это:
2 x = 4
x = 2
Но что, если мы не можем разделить? Подумайте об этом так.Деление на 2 в этом примере то же самое, что умножение на обратное значение 2:
то же самое, что и потому, что это обратное значение 2.
Давайте подумаем над этим со всеми переменными.
Если это наше уравнение:
ab = c
… и нам нужно найти b без деления, нам нужно найти обратное к a и умножить обе части на это:
Разделения нет. Готовы сделать это с матрицами? Очень важное замечание, прежде чем мы начнем: сейчас мы будем беспокоиться только о том, чтобы найти обратные матрицы 2 × 2. С матрицами размером больше 2 × 2 становится немного сложнее, поэтому мы оставим это для предварительного расчета.
С матрицами размером больше 2 × 2 становится немного сложнее, поэтому мы оставим это для предварительного расчета.
Используя обычные числа, мы могли бы умножить любое число на обратное и получить 1. Верно? Примерно так:
2 × = 1
То же самое и с матрицами. Когда мы умножаем квадратную матрицу на ее обратную, мы должны получить в качестве продукта идентичную матрицу (поскольку единичная матрица – это матричная версия числа 1).
Допустим, мы хотим найти обратную матрицу:
Для этого мы возвращаем нашего старого приятеля, определителя.Запомнить его? Сначала находим определитель. Наш определяющий фактор в этом случае будет:
до н.э. – до н.э.
крест-накрест минус яблочное пюре. Затем мы бросаем это число в знаменатель дроби. Умножьте эту дробь на скрученную версию исходной матрицы, где мы меняем местами на и d (верхний левый и нижний правый входы) и меняем местами знаки плюс / минус на b и c .
