Второй закон ньютона в импульсной форме: формулировка, формула
Содержание
- 1 Второй закон Ньютона в импульсной форме
- 2 Второй закон ньютона в импульсной форме формула
- 3 В каких случаях применяют импульсную форму
- 4 Пример использования
Второй постулат динамики записывают несколькими способами, например, используя импульс. Указанная формулировка встречается гораздо реже обычного, однако решает ряд задач школьной, университетской механики.
Второй закон Ньютона в импульсной форме
В общем случае запись главного постулата динамики включает три составляющие:
- массу, m;
- ускорение, a;
- воздействие, F.
Второй закон Ньютона в импульсной форме записывают, определив изначально импульс тела
– величину, получаемую вследствие умножения массы на скорость движения:
Измеряется результатом деления произведения килограмма, метра на секунду –
Очевидно: описываемая мера механического движения — величина векторная, совпадающая с направлением
Физика использует понятие импульса силы
– величины, равной результату произведения существующего воздействия, времени:
Измеряется произведением ньютона, секунды –
Сформулируем 2 закон Ньютона через импульс:
Импульс действующей силы равен изменению импульса объекта.
Похожая формулировка:
Изменение импульса во времени равно величине действующей силы.
Второй закон ньютона в импульсной форме формула
Самостоятельно выразим требующуюся формулу, используя известную запись:
Определение ускорение гласит: данная величина характеризует увеличение, уменьшение скорости:
Аналогично:
– приобретённая, начальная скорости,
– изменение времени.
Зная стандартный вид постулата, выразим ускорение, приравняем к полученному выражению:
Части уравнения умножим на
, получим:
Правая часть уравнения равна
, преобразуем равенство, получим:
3.6 Импульская форма II закон Ньотона” src=”https://www.youtube.com/embed/xrHNFXZ2MqQ?feature=oembed&wmode=opaque” frameborder=”0″ allow=”accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””/>Глядя на получившуюся формулу сформулируем второй закон Ньютона через импульс.
Изменение импульса тела равно импульсу действовавшей на тело силы.
Формулировка аксиомы ньютоновской динамики, использующая понятие импульса, полностью соответствует виду, изначально выведенному учёным. Получить подобную запись возможно, учитывая оператор, называемый дифференциалом. Дифференциал функции d – приращение, изменение.
Формула a записывается видом:
Читается: «изменение скорости при изменяющемся времени».
Приравнивая правые части, получаем:
Умножаем части уравнения на m, сразу вносим массу под знак дифференциала:
Результат:
В каких случаях применяют импульсную форму
Некоторые задачи невозможно решить, применяя обычную формулу постулата динамики. Например, задания движения тела изменяющегося веса.
Русский механик, учёный Иван Всеволод Мещерский на основе импульсной формы вывел уравнение, позволяющее решать задачи перемещения объектов переменной массы. Уравнением Мещерского удобно выводить формулу Константина Эдуардовича Циолковского, использующуюся при проектировании баллистических, космических ракет. Указанные летательные аппараты — реальный пример тел, изменяющих вес.
Уравнением Мещерского удобно выводить формулу Константина Эдуардовича Циолковского, использующуюся при проектировании баллистических, космических ракет. Указанные летательные аппараты — реальный пример тел, изменяющих вес.
Более приземлённые, обыденные задачи применения описываемой записи 2 постулата – движение двух сталкивающихся шаров, движение одного шара, ударяющегося о препятствие.
Пример использования
Пусть шарик, обладающий массой m, неизменяющейся скоростью
, ударяется о стену под углом , спустя отлетает.
шарик перемещается с изменяющейся скоростью
Принимаем допущение: стена гладкая, трение отсутствует. Шарик, ударяясь, испытывает воздействие силы упругости N.
на шар воздействует сила упругости
Известно:
Сила, действующая на тело, является единственной, видоизменим запись:
Найдём
, используя правило сложения векторов – векторный треугольник.
векторный треугольник
Потери скорости отсутствуют, вес остаётся прежним, следовательно,
. Получившийся векторный треугольник равнобедренный. Неизвестный вектор:
N равна:
Второй закон Ньютона в импульсной форме позволяет решать задачи разного уровня значимости: школьные типовые задания, проекты космического масштаба.
Второй закон Ньютона – формула, применение и примеры решения
При решении задач с физико-математическим уклоном на движение тел используется базовая формула — второй закон Ньютона. С ее помощью можно вычислить ускорение, массу и силу, приложенную к объекту движения. Физики перед решением задач рекомендуют подробно ознакомиться с теорией, а затем переходить к практике.
Содержание
- Общие сведения
- Правило и высшая математика
- Основные величины
- Алгоритм перевода значений
- Пример решения задачи
Общие сведения
Знакомство с правилами Ньютона начинается в старших классах средних образовательных школах. Формулу 2 закона Ньютона можно сформулировать в таком виде: a = F / m, где F — результирующая сила, m — масса тела и a — ускорение. Расшифровка формулы (формулировка правила) следующая: ускорение тела в инерциальных системах отсчета прямо пропорционально зависит от результирующей силы, действующей на него, и обратно пропорционально его массе.
Правило и высшая математика
В высших учебных заведениях на уроках по физике (динамика) II правило Ньютона записывается в дифференциальной форме: d (p) / d (t) = F. В этом случае второй закон Ньютона, формулировка которого имеет вид: сила, действующая на материальную точку, прямо пропорционально зависит от ее производной импульса в определенный момент времени.
Исходя из формулы d (p) / d (t) = F, можно произвести некоторые математические преобразования для получения упрощенного соотношения. Импульс тела (p) определяется при помощи такого уравнения: p = m * v, где m — масса материальной точки (тела), а v — ее скорость. Если произвести подстановку этого соотношения в дифференциальную запись, то получится такое выражение: d (m * v) / d (t) = F. Используя свойства дифференциалов, константу (m) можно вынести: m * (d (v) / d (t)) = F.
Величина d (v) / d (t) является ускорением, следовательно, формула записывается следующим образом: m * a = F или a = F / m.
Основные величины
Один из элементов формулы II закона Ньютона — масса тела, показывающая реакцию тела на воздействие внешних сил и являющаяся количественным показателем инертных свойств вещества. Она обладает такими характеристиками:

Единицей измерения в международной системе является килограмм (кг). При решении задач рекомендуется переводить производные значения (тонны, граммы и т. д. ) в кг.
Следующим компонентом формулы является ускорение (а), которое показывает, какое будет изменение скорости движения тела или материальной точки в текущий момент. Если тело движется равномерно, а = 0. При равноускоренном движении объекта величина «а» растет до определенного значения с течением времени. Ускорение обладает такими характеристиками:
Единицей измерения является м/с 2 . Она вычисляется по формуле: a = v / t, где v — скорость в текущий момент времени t.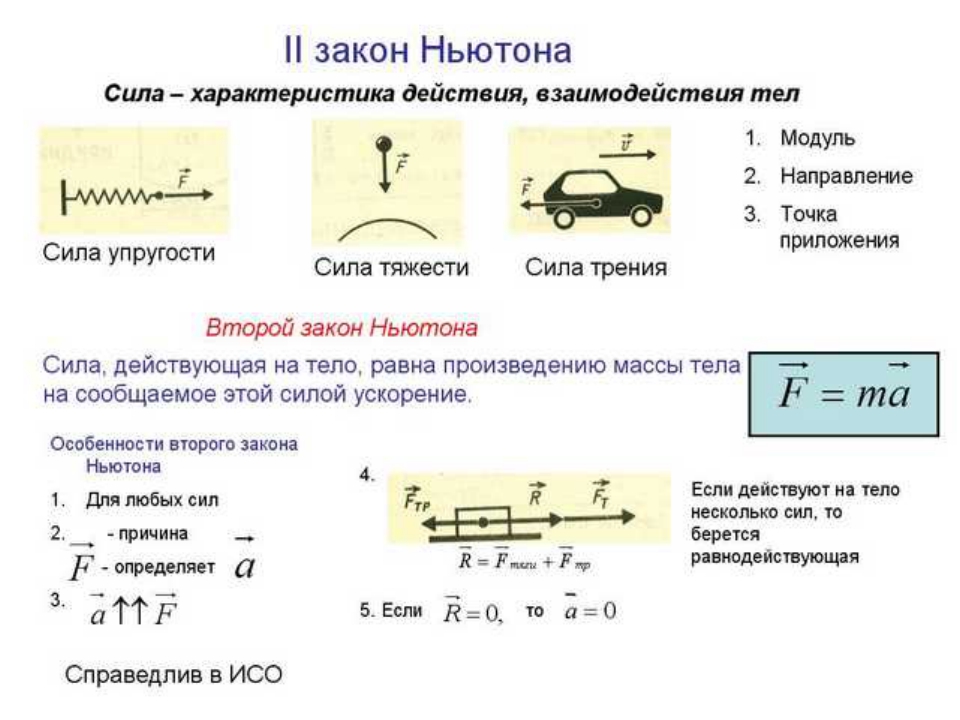 Физический смысл a: изменение скорости тела, равной 1 м/с за единицу времени 1 с. Кратко запись выглядит так: 1 м/с 2 = 1 м/с * 1 с.
Физический смысл a: изменение скорости тела, равной 1 м/с за единицу времени 1 с. Кратко запись выглядит так: 1 м/с 2 = 1 м/с * 1 с.
Силой называется векторная величина, которая воздействует на материальные объекты со стороны других тел. Она бывает результирующей и единичной. Первая состоит из группы сил — трения, тяжести, реакции опоры, тяги и т. д. Вторая представляет только одну единицу, т. е. силу тяжести или тяги, трения или реакцию опоры. Параметры, характеризующие F:
В учебниках по физике можно встретить понятие равнодействующей силы. Она эквивалентна результирующей. Например, в известной басне Крылова персонажи тянут воз в разные стороны, который не двигается. Из этого следует, что равнодействующая сила тяги равна сумме векторов всех сил, приложенных персонажами (Ft = -Ft1 + Ft2 — Ft3 + Ft4 = 0, т. к. по условию Ft1, Ft2, Ft3 и Ft4 имеют различные векторы воздействия). 2 = 1 м/c 2 / 60 (1 мин = 60 секунд).
2 = 1 м/c 2 / 60 (1 мин = 60 секунд).
Для примера требуется разобрать единицу измерения, равную 20 км/ч 2 . Воспользовавшись правилами перевода, можно записать следующее: 20 * 1000 / 3600 = 5,6 (м/с 2 ).
Пример решения задачи
Формула позволяет решать задачи простой и повышенной сложности. Последние относятся к тем, в которых не дано 2 элемента соотношения, а известен всего лишь один. Чтобы узнать практическое применение формулы, нужно решить задание. Например, требуется найти массу тела, которому сообщается сила (F), равная 2 кН. Кроме того, оно движется равноускоренно. Значение скорости (v) эквивалентно 57 км/ч в текущий момент времени (t), равный 2 с. Чтобы было понятно, необходимо решать задачу по такому алгоритму:
 Необходимо обратить внимание на запись единиц измерения величины при выполнении вычислений.
Необходимо обратить внимание на запись единиц измерения величины при выполнении вычислений.Необходимо отметить, что расчет ускорения в 4 пункте можно упустить, подставив «а» в конечную формулу: m = F / (v / t) = F * t / v.
Таким образом, применение II закона Ньютона позволяет решать практически любые задачи на движения, поскольку он является базовым соотношением динамики.
Предыдущая
ФизикаВращательное движение твердого тела – характеристика, формулы и уравнения
Следующая
ФизикаЭлектрический ток в газах – причины появления и применение
Физика Импульс материальной точки. Другая формулировка второго закона Ньютона
Материалы к уроку
Конспект урока
Введем новую физическую величину – импульс материальной точки. Дадим другую формулировку второго закона Ньютона.
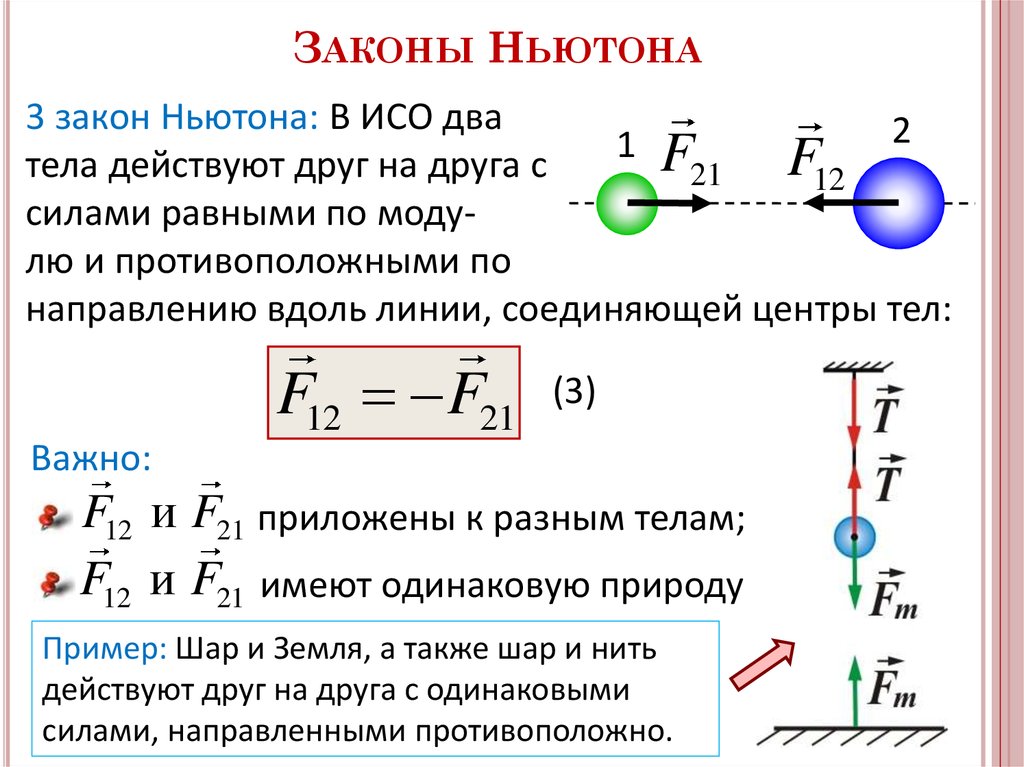
Второй закон Ньютона «произведение массы тела на его ускорение равно действующей на тело силе» можно записать в иной форме, которая приведена самим Ньютоном в его главном труде «Математические начала натуральной философии».
Если на тело (материальную точку) действует постоянная сила, то постоянным будет и ускорение тела, которое равно отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Подставив это значение ускорения во второй закон Ньютона, получим, что произведение массы тела и изменения скорости, деленное на промежуток времени, в течение которого это изменение произошло, равно силе, действующей на тело. Проведя некоторые математические преобразования, получим: разность между произведением массы тела и конечной скорости и произведением массы и начальной скорости равна произведению силы, действующей на тело, и промежутка времени, в течение которого произошло изменение скорости.
Импульсом тела (материальной точки) называется величина, равная произведению массы тела на его скорость.
Иногда импульс называют количеством движения.
Из формулы видно, что импульс – векторная величина. Так как масса тела всегда положительная величина, то импульс имеет такое же направление, как и скорость.
Обозначим через p1 импульс тела в начальный момент времени, а через p2 – его импульс в конечный момент времени.
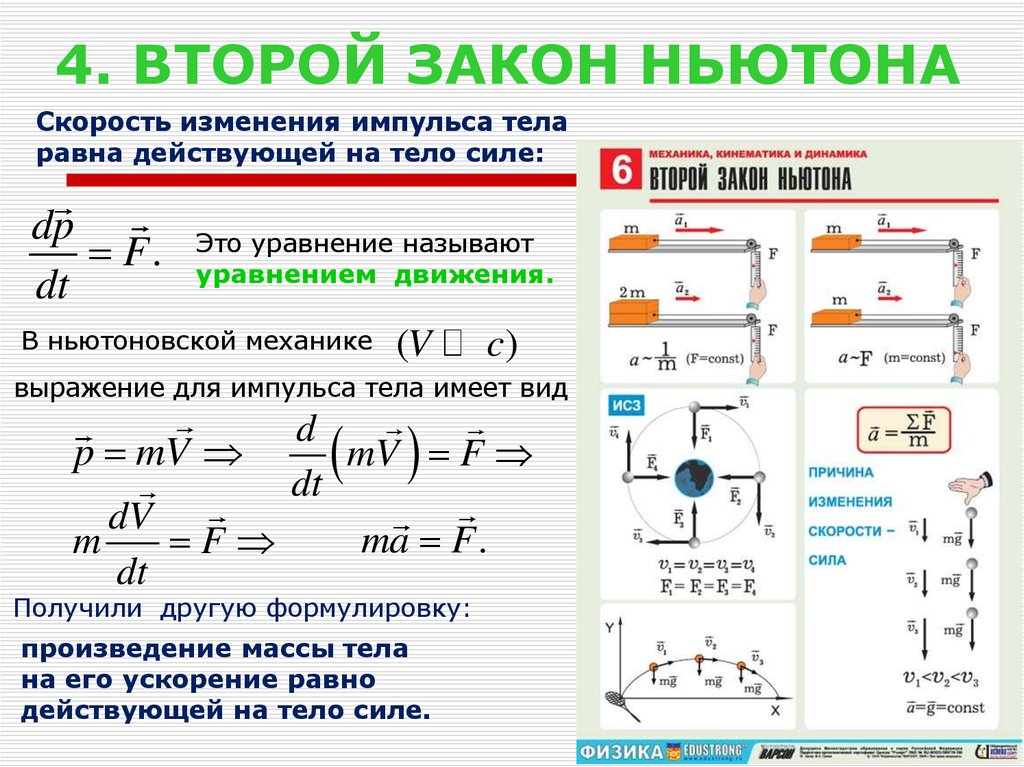
Так как промежуток времени – величина всегда положительная, то направления векторов импульса и силы совпадают.
Согласно полученной формуле, изменение импульса тела или материальной точки пропорционально приложенной к нему силе и имеет такое же направление, как и сила.
Произведение силы на время ее действия называют импульсом силы. Поэтому можно сказать, что изменение импульса тела равно импульсу действующей на него силы. Уравнение показывает, что одинаковые изменения импульса могут быть получены в результате действия большой силы в течение малого интервала времени или малой силы за большой промежуток времени.
В результате мы получили импульсную форму второго закона Ньютона: изменение импульса тела равно импульсу действующей на него силы.

Проиллюстрировать эту формулировку второго закона Ньютона можно с помощью опыта с гирей и двумя нитями. Подвесим гирю на тонкой нити. Снизу привяжем к гире вторую такую же нить.
Резко дернем за конец нижней нити, она при этом порвется, а гиря останется висеть. Если же медленно тянуть за конец нижней нити, то оборвется верхняя нить, и гиря упадет.
Если дергать за нижнюю нить резко, то время действия силы будет малым и импульса силы будет не достаточно для существенного изменения импульса гири. Если же за нижнюю нить тянуть медленно, то время действия силы увеличится, а значит, увеличится и ее импульс. В этом случае импульс силы может существенно изменить импульс гири.
Если картонку сдвигать медленно, то монета будет сдвигаться вместе с ней.
Но если резким ударом выбить картонку, то монета упадет в стакан. Объяснить этот опыт можно, применяя второй закон Ньютона в импульсной форме.
 Когда картонка движется медленно, время действия силы трения на монету достаточно для изменения импульса монеты, и монета приходит в движение вместе с картонкой. Если же картонка резко выбивается, то время действия силы трения оказывается крайне малым, и импульса силы недостаточно для того, чтобы сдвинуть монетку: она остается на месте. Но после того как картонка выбита, лишенная опоры монетка падает в стакан.
Когда картонка движется медленно, время действия силы трения на монету достаточно для изменения импульса монеты, и монета приходит в движение вместе с картонкой. Если же картонка резко выбивается, то время действия силы трения оказывается крайне малым, и импульса силы недостаточно для того, чтобы сдвинуть монетку: она остается на месте. Но после того как картонка выбита, лишенная опоры монетка падает в стакан.Импульс тела может быть равен нулю даже в том случае, когда это тело движется. В качестве примера можно привести вращающийся вокруг неподвижной оси однородный диск. Действительно, два диаметрально противоположных, равных по массе элемента A и B имеют одинаковые по модулю скорости.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Объяснение урока: Второй закон движения Ньютона
В этом объяснении мы научимся применять второй закон Ньютона закон движения, 𝐹=𝑚𝑎, чтобы найти ускорения, вызванные силами, которые действуют в различных направлениях.
Первый закон движения Ньютона объясняет, что объект не меняет скорость
если на него не действует результирующая сила и что скорость объекта должна измениться
если на него действует результирующая сила.
Второй закон движения Ньютона говорит нам, что изменение скорости объекта зависит от приложенной к нему силы. Чтобы объект изменил скорость, объект должен ускориться. Ускорение тела – это скорость, с которой скорость тела меняется с течением времени. секунда Ньютона Закон движения гласит, что ускорение тела прямо пропорционально силе, приложенной к объекту. Это можно выразить как 𝐹∝𝑎, где 𝐹 – приложенная сила и 𝑎 — ускорение объекта.
И сила, и ускорение являются векторными величинами; следовательно, ускорение объект находится в направлении действия приложенной к нему силы.
Второй закон движения Ньютона обычно выражается как
𝐹=𝑚𝑎,
где 𝑚 — константа пропорциональности между силой
применительно к объекту и полученному в результате ускорению объекта. Это
называется массой объекта. Чем больше масса объекта, тем больше
сила, необходимая для ускорения тела.
Чем больше масса объекта, тем больше
сила, необходимая для ускорения тела.
Масса объекта также связана с гравитационной силой, создаваемой объекта, но в этом объяснителе нас интересует только масса как константа пропорциональности между силой и ускорением. Это называется инерционная масса. Все упоминания о массе в этом толкователе относятся к инерционным масса.
Рассмотрим пример, в котором сила действует на объект, который изменяется скорость.
Пример 1. Определение силы, действующей на объект, изменяющий скорость
К объекту массой 22 кг приложена сила. На графике показано изменение скорости объекта при применяется сила. Какая сила приложена к объекту? Отвечать до ближайшего Ньютон.
Ответ
Сила, действующая на объект, находится по формуле 𝐹=𝑚𝑎, где масса объекта 𝑚 равна 22 кг и ускорение, 𝑎, не дано.
Ускорение объекта есть скорость изменения скорости как
Время проходит. На графике показано изменение скорости объекта
с течением времени.
На графике показано изменение скорости объекта
с течением времени.
График показывает, что скорость объекта изменяется от 5 м/с до 20 м/с. Таким образом, увеличение скорости определяется выражением Δ𝑣=20/−5/=15/.msmsms
График показывает, что время, необходимое для увеличения объекта в скорость 5 секунд.
Ускорение объекта есть скорость изменения скорости как время идет, так что это дается 𝑎=15/5=3/.mssms
Теперь, когда известны ускорение и масса объекта, сила на нем может быть определена как 𝐹=22×3/=66.kgmsN
Давайте теперь рассмотрим пример, в котором отношение между силой и ускорение указано более прямо.
Пример 2: Определение силы, действующей на ускоряющуюся частицу
Какая сила приложена к объекту массы 5 кг то есть ускоряется этой силой со скоростью 2 м/с 2 ?
Ответ
Сила, действующая на объект, находится по формуле
𝐹=𝑚𝑎,
где масса объекта 𝑚 равна
5 кг и
ускорение, 𝑎, равно
2 м/с 2 .
У нас есть то, что 𝐹=5×2/=10.kgmsN
Давайте теперь рассмотрим пример, в котором сила, действующая на реальный мир объект определен.
Пример 3. Определение силы, приложенной для ускорения системы объектов
Массовый скейтбордист 50 кг стоит на скейтборд массы 1,5 кг, близко к стене здания. Скейтбордист стоит одной ногой на доску и другой ногой отталкивается от стены. скейтборд ускоряется от стены в 4,66 м/с 2 . С какой силой скейтбордист прижался к стене? Дайте ответ ближайшему Ньютон.
Ответ
Сила, действующая на объект, находится по формуле 𝐹=𝑚𝑎, где 𝑚 — масса объекта, на который действует сила, и ускорение, 𝑎, равно 4,66 м/с 2 .
Скейтбордист стоит на скейтборде. Когда скейтборд ускоряется от стены, скейтбордист также ускоряется от стены с той же скоростью (иначе вопрос, по-видимому, упоминал бы что-то о падении скейтбордиста со скейтборда). Масса, которая ускоряется, является массой скейтборда и скейтбордиста. Эта масса определяется
𝑚=1,5+50=51,5.кгкгкг
Масса, которая ускоряется, является массой скейтборда и скейтбордиста. Эта масса определяется
𝑚=1,5+50=51,5.кгкгкг
У нас есть то, что 𝐹=51.5×4.66/=239.99.kgmsN
Вопрос касается силы с точностью до ближайшего Ньютон, который 240 Н.
Второй закон движения Ньютона, выраженный формулой 𝐹=𝑚𝑎, описывает связь между силой, действующей на тело, и массой объекта, и ускорение объекта, так что любая из этих величин может быть определяется по формуле. Чтобы найти массу или ускорение объекта, используя формулу для второго закона движения Ньютона, формула должна быть преобразована в изменить подлежащее формулы на определяемую величину.
Например, чтобы определить ускорение объекта по этой формуле, 𝑎 должно быть предметом формулы. Мы можем сделать это, сначала разделив формула по 𝑚: 𝐹𝑚=𝑚𝑎𝑚.
В правой части полученного уравнения есть член 𝑚 как в
числитель и знаменатель:
𝐹𝑚=𝑚𝑚𝑎.
Деление 𝑚 на 𝑚 дает результат 1: 𝐹𝑚=1𝑎.1𝑎 равно 𝑎, поэтому выражение для 𝑎 дается 𝑎=𝐹𝑚.
Теперь рассмотрим пример, в котором ускорение объекта равно определяется по второму закону Ньютона.
Пример 4. Определение ускорения объекта, на который действует сила
Массивный объект 1,5 кг есть к нему приложена сила 4,5 Н. С какой скоростью тело ускоряет сила?
Ответ
Второй закон движения Ньютона можно выразить формулой 𝐹=𝑚𝑎, где 𝐹 — сила, действующая на объект, 𝑚 — масса объекта, а 𝑎 — ускорение.
Чтобы определить ускорение объекта по этой формуле, 𝑎 должен стать предметом формулы. Мы можем сделать это, разделив формула по 𝑚: 𝐹𝑚=𝑚𝑎𝑚=𝑎𝑎=𝐹𝑚.
Подставляя значения в вопрос, мы видим, что 𝑎=4.51.5=3/.Nkgms
Теперь рассмотрим пример, в котором определяется масса объекта
используя второй закон Ньютона.
Пример 5. Определение массы объекта, на который действует сила
Объект ускоряется с 4 м/с 2 в то время как сила 20 Н применяется к Это. Какова масса объекта?
Ответ
Второй закон движения Ньютона можно выразить формулой 𝐹=𝑚𝑎, где 𝐹 – сила, действующая на объект, 𝑚 – масса объекта, а 𝑎 — ускорение.
Чтобы определить массу объекта по этой формуле, 𝑚 должно быть предметом формулы. Мы можем сделать это, разделив формула 𝑎: 𝐹𝑎=𝑚𝑎𝑎=𝑚𝑚=𝐹𝑎.
Подставляя значения в вопрос, мы видим, что 𝑚=204/=5.Nmskg
Давайте теперь рассмотрим пример, связанный с определением ускорения объект реального мира.
Пример 6. Определение ускорения объекта, на который действует сила
Мяч имеет массу 250 г. Мяч бьют ногой, и это применимо
сила 15 Н, чтобы
мяч, как показано на схеме. Насколько ускоряется мяч
в направлении удара?
Насколько ускоряется мяч
в направлении удара?
Ответ
Второй закон движения Ньютона можно выразить формулой 𝐹=𝑚𝑎, где 𝐹 – сила, действующая на объект, 𝑚 — масса объекта, а 𝑎 — ускорение.
Чтобы определить ускорение объекта по этой формуле, 𝑎 должно быть предметом формулы. Мы можем сделать это с помощью разделив формулу на 𝑚: 𝐹𝑚=𝑚𝑎𝑚=𝑎𝑎=𝐹𝑚.
Масса мяча 250 грамм, но формула 𝐹=𝑚𝑎 дает силу в ньютоны действует на массу в килограммов, необходимых для ускорить объект на несколько метров в секунду в квадрате.
Сила, действующая на мяч, указана в
ньютонов, поэтому для определения
ускорение мяча в
метров на секунду в квадрате, масса
мяч должен быть указан в килограммах. Масса
250 грамм эквивалентно
масса
0,250 кг.
Ускорение мяча в направлении удара определяется выражением 𝑎=𝐹𝑚𝑎=150,250=60/.Nkgms
На самом деле это не означает, что скорость мяча после его пинают 50 м/с.
Это было бы верно только в том случае, если бы бутса, которая ударила по мячу, ударила по нему средняя сила 15 ньютонов через 1 секунда и если нет другого во время удара по мячу действовала горизонтальная сила.
При ударе по мячу контакт между ударной ногой и мячом сохраняется гораздо меньше, чем 1 секунда. Кроме того, мяч, касающийся на землю действует трение, которое уменьшает ее скорость, как и сопротивление воздуха.
Сила и ускорение являются векторными величинами и поэтому имеют направление как ну и величина. Когда на объект действует только одна сила, направление ускорение объекта обязательно направлено в сторону действия силы.
На объект могут действовать несколько сил, и эти силы не обязательно действуют
в том же направлении. Ускорение объекта, на которое действует несколько сил
действие зависит от чистой силы, действующей на объект.
Ускорение объекта, на которое действует несколько сил
действие зависит от чистой силы, действующей на объект.
Рассмотрим пример, в котором на объект действуют несколько сил.
Пример 7. Определение массы объекта, на который действуют две силы
Объект имеет силы 30 Н и 55 Н приложено к Это. Силы действуют в противоположных направлениях друг к другу, как показано на рис. диаграмма. Объект ускоряется влево с 0,5 м/с 2 . Какова масса объекта?
Ответ
Второй закон движения Ньютона можно выразить формулой 𝐹=𝑚𝑎, где 𝐹 — сила, действующая на объект, 𝑚 — масса объекта, а 𝑎 — ускорение.
В этом случае сила, действующая на объект, является равнодействующей двух силы, действующие в противоположных направлениях: сила 30 Н, действующая на справа и 55 Н сила, действующая влево.
Заявлено, что объект ускоряется влево, что находится в том же
направление как 55 N
сила. Направление ускорения в сторону большей
сила.
Направление ускорения в сторону большей
сила.
Приняв левую сторону положительной, сила, действующая влево, имеет положительную величина, а сила, действующая вправо, имеет отрицательную величину.
Таким образом, величины сил, действующих на объект, равны 55 Н и –30 Н. Сумма этих сил равна 𝐹=55+(−30)=55−30=25.NNNNN
Теперь, когда сила определена, нужно определить массу объект по формуле 𝐹=𝑚𝑎,𝑚 необходимо сделать предметом формулы. Мы можем сделать это, разделив формула по 𝑎: 𝐹𝑎=𝑚𝑎𝑎=𝑚𝑚=𝐹𝑎.
Подставляя значения в вопрос, мы видим, что 𝑚=250,5/=50,Нм/кг
Давайте теперь рассмотрим пример с несколькими силами, действующими на объекты реального мира.
Пример 8. Определение ускорения объекта, на который действуют две силы
Пловец массы
48 кг использует ее
ноги, чтобы оттолкнуться от стенки бассейна, приложив силу
280 Н. Вода
что пловец ускоряется через применяется
160 Н силы в
направление, противоположное тому, в котором она ускоряется. Что это
ускорение пловца относительно воды?
Вода
что пловец ускоряется через применяется
160 Н силы в
направление, противоположное тому, в котором она ускоряется. Что это
ускорение пловца относительно воды?
Ответ
Второй закон движения Ньютона можно выразить формулой 𝐹=𝑚𝑎, где 𝐹 – сила, действующая на объект, 𝑚 – масса объекта, а 𝑎 — ускорение.
В этом случае сила, действующая на объект, является равнодействующей двух силы, действующие в противоположных направлениях: 280 Н действующая сила вдали от стенки бассейна и 160 Н действующая сила к стене бассейна.
Если принять направление от стенки бассейна за положительное, то сила, действующая от стенки бассейна имеет положительную величину, а сила, действующая в направлении стенка бассейна имеет отрицательную величину.
Таким образом, величины сил, действующих на объект, равны
280 Н и
–160 Н. Сумма этих сил равна
𝐹=280+(−160)=280−160=120.NNNNN
Сумма этих сил равна
𝐹=280+(−160)=280−160=120.NNNNN
Теперь, когда сила определена, нужно определить ускорение пловец по формуле 𝐹=𝑚𝑎,𝑎 должно быть предметом формулы. Мы можем сделать это, разделив формулу на 𝑚: 𝐹𝑎=𝑚𝑎𝑚=𝑎𝑎=𝐹𝑚.
Подставляя значения в вопрос, мы видим, что 𝑎=12048=2,5/.Nkgms
Вполне реально, что ноги пловца могут соприкасаться с стенка бассейна на одного за секунду до того, как ноги пловца потеряют контакт с стенки бассейна, если ноги пловца изначально были согнуты и они выпрямляется за одну секунду. Сила, действующая в противоположном направлении в расчет включено направление движения пловца, так что результат 2,5 м/с 2 в этом случае может разумно означать, что пловец имеет скорость 2,5 м/с при момент, когда ее ноги теряют контакт со стенкой бассейна.
Однако эта скорость не будет поддерживаться, так как сопротивление
вода продолжала бы действовать на нее, и без контакта между ее ногами
и стена бассейна, единственной силой, действующей на нее, будет это сопротивление;
следовательно, ее скорость уменьшится.
Давайте теперь обобщим то, что мы узнали из этих примеров.
Ключевые моменты
- Ускорение объекта, на который действует сила, прямо пропорциональна силе, действующей на тело, и его массе. Эту связь можно выразить формулой 𝐹=𝑚𝑎, где 𝐹 — сила, действующая на объект, 𝑚 – масса объекта, а 𝑎 — ускорение объекта.
- Формула 𝐹=𝑚𝑎 можно переставить, чтобы определить массу или ускорение объекта.
- Когда на объект действует несколько сил, ускорение объекта равно прямо пропорциональна равнодействующей этих сил.
Второй закон движения Ньютона: определение, формулы
Первый закон движения Ньютона познакомил вас с концепцией инерции и с тем, почему тело в состоянии покоя или в движении продолжает оставаться в этом состоянии. Это означает, что у объектов, находящихся в равновесии, все силы уравновешены. Первый закон заставляет задуматься, что произойдет, если к телу приложить внешнюю силу? Как изменение уравновешенных сил повлияет на состояние равновесия? Решение вашего вопроса лежит во втором законе движения Ньютона.
Первый закон движения предполагал, что когда силы, действующие на тело, уравновешены, ускорение равно 0 м/с, т. е. тела, находящиеся в равновесии, не ускоряются. Итак, по Ньютону, неуравновешенная сила ускоряет объект.
Второй закон Ньютона определение движения : Сила равна скорости изменения импульса. Когда масса постоянна, сила, действующая на тело, равна массе, умноженной на ускорение.
Второй закон движения Ньютона можно записать в следующей математической форме.
F = ma
Понимание второго закона НьютонаВторой закон Ньютона предполагает, что ускорение тела зависит от двух переменных:
- Суммарная сила, действующая на объект
- Масса объекта
Поскольку F = ma, ускорение в теле будет прямо пропорционально действующей на него чистой силе, но обратно пропорционально массе тела.
Итак, при увеличении силы, приложенной к объекту, будет увеличиваться и ускорение. Однако, когда масса объекта увеличивается, ускорение уменьшается.
Ниже приведены некоторые распространенные применения второго закона Ньютона:
- Толкание или тяга пустой тележки можно сравнить с нагруженной тележкой, которая имеет большую массу.
- При приложении одной и той же силы для перемещения автомобиля и велосипеда ускорение автомобиля будет меньше, чем ускорение велосипеда, потому что автомобиль имеет большую массу.
- При ударе по мячу вы прикладываете к нему силу в определенном направлении. Он движется в направлении, соответствующем величине приложенной силы. Если вы приложите больше силы, расстояние, пройденное мячом, будет больше.
| Подумайте об этом: Что произойдет с ускорением, если удвоить приложенную силу и удвоить массу тела? |
Если предположить, что масса движущегося точечного объекта равна m, тела будет p = масса × скорость
Итак, начальный импульс будет записан следующим образом:
P i =mu
Конечный импульс будет записан как:
P f =mv
Изменение импульса может быть представлено следующим математическим выражением:
⇒⇒△2p =P − P i
⇒△p = mv− mu
Теперь, если взять временной интервал для этого изменения импульса равным t. Тогда скорость изменения импульса записывается следующим образом:
Тогда скорость изменения импульса записывается следующим образом:
⇒ Скорость изменения импульса =△p/t
⇒△p/t =mv – mu/t
Выражение можно также записать следующим образом:
⇒△p/t =m (v-u)/t
Поскольку известно, что (v-u)/t есть выражение для ускорения тела, при подстановке значение, получаем
⇒△p/t =ma
Второй закон Ньютона утверждает, что F ∝ △p/t
Итак, F∝ma
Удалив знак пропорциональности,
⇒F=kma
2 Здесь k — константа пропорциональности.
Расчет единицы силы,
1 единица силы = k×(1кг)×(1м/ s 2 )
Следовательно, k=1/1×1=1
Итак, когда значение k принимается равным 1, уравнение принимает следующий вид:
⇒F = ma
Сила изменения массыПредположим, что тело в точке (0), определяемой положением X o и временем t o , имеет массу m0 и движется со скоростью v o .
При приложении силы F она перемещается в точку 1, определяемую местоположением X 1 и временем t 1 . Кроме того, скорость и масса тела претерпевают изменения во время движения. Масса изменяется до значений m 1 , а скорость становится v 1 .
Кроме того, скорость и масса тела претерпевают изменения во время движения. Масса изменяется до значений m 1 , а скорость становится v 1 .
Согласно второму закону Ньютона, вы можете определить новые значения m1 и v1 при заданном значении силы, действующей на тело, по следующей формуле: Примеры
Ниже приведены некоторые решенные примеры, основанные на втором законе движения Ньютона.
| Пример 1: Какая сила необходима для ускорения автомобиля массой 100 кг со скоростью 5 м/с 2 ? Ответ: Второй закон Ньютона устанавливает связь между массой объекта, результирующей силой и его ускорением: Таким образом, по следующей формуле можно рассчитать силу: F = мАПри подстановке значений 100 кг × 5 м/ с 2 = 500 Н Следовательно, сила, необходимая для ускорения автомобиля массой 100 кг на 5 м/ с 2 , равна 500 Н |
Пример 2: Поезд отправляется в путь от железнодорожной станции и за 80 секунд набирает скорость 40 м/с. Если общая масса поезда вместе с пассажирами составляет 10 000 кг, какова общая сила, приложенная двигателем поезда, чтобы тянуть поезд? Если общая масса поезда вместе с пассажирами составляет 10 000 кг, какова общая сила, приложенная двигателем поезда, чтобы тянуть поезд? Ответ: Дано: начальная скорость = u = 0 м/ с 2 Конечная скорость = v= 40 м/с Время= t= 80 секунд Масса= m= 10 000 кг F = мАа = (v-u)/t а = (40-0)/80 а = 1/2 м/ с 2 а = 0,5 м/ с 2 F= мАПодстановка значения a в приведенное выше уравнение F= 10 000 (0,5) F= 5000 Н Таким образом, сила, приложенная двигателем поезда, равна 5000 Н. |
| Проверьте свои знания : Q1. Какое ускорение возникнет, если к телу массой 5 кг приложить результирующую силу 12 Н? Q2. Если к телу приложена результирующая сила 25 Н, которая заставляет его ускоряться со скоростью 10 м/ с 2 , какова будет масса тела? Q3. | 1. Запуск ракеты в космос. Второй закон Ньютона объясняет концепцию ракет с точки зрения их массы, ускорения и силы.

 Сани разгоняются со скоростью 7 м/ с 2 . Если масса останется неизменной, а результирующая сила увеличится втрое, каково будет новое ускорение саней?
Сани разгоняются со скоростью 7 м/ с 2 . Если масса останется неизменной, а результирующая сила увеличится втрое, каково будет новое ускорение саней?
 Почему автомобиль имеет большее ускорение, чем грузовик, если его толкают с одинаковой силой?
Почему автомобиль имеет большее ускорение, чем грузовик, если его толкают с одинаковой силой? 
 Он математически дает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона является количественным и широко используется для расчета того, что происходит в ситуациях, связанных с силой. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, которое дает точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые идеи, о которых мы упоминали ранее.
Он математически дает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона является количественным и широко используется для расчета того, что происходит в ситуациях, связанных с силой. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, которое дает точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые идеи, о которых мы упоминали ранее. Интуитивное представление о внешнее верно — оно находится вне интересующей нас системы. Например, на рисунке \(\PageIndex{1a}\) система, представляющая интерес, представляет собой автомобиль и человека внутри него. Две силы, приложенные двумя студентами, являются внешними силами. Напротив, между элементами системы действует внутренняя сила. Таким образом, сила, с которой человек в машине держится за руль, является внутренней силой между элементами рассматриваемой системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы уравновешивают друг друга, как объясняется в следующем разделе.) Следовательно, мы должны определить границы системы, прежде чем мы сможем определить, какие силы являются внешними. Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. Эта концепция неоднократно пересматривалась при изучении физики.
Интуитивное представление о внешнее верно — оно находится вне интересующей нас системы. Например, на рисунке \(\PageIndex{1a}\) система, представляющая интерес, представляет собой автомобиль и человека внутри него. Две силы, приложенные двумя студентами, являются внешними силами. Напротив, между элементами системы действует внутренняя сила. Таким образом, сила, с которой человек в машине держится за руль, является внутренней силой между элементами рассматриваемой системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы уравновешивают друг друга, как объясняется в следующем разделе.) Следовательно, мы должны определить границы системы, прежде чем мы сможем определить, какие силы являются внешними. Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. Эта концепция неоднократно пересматривалась при изучении физики.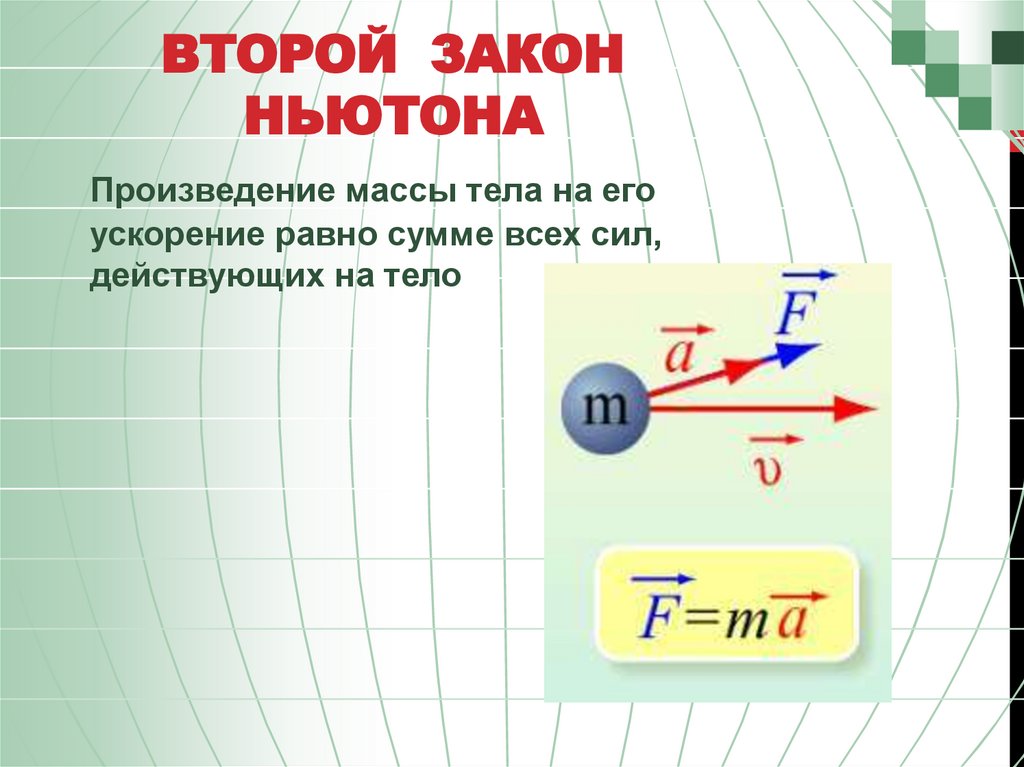
 (Более подробно мы обсудим трение в следующей главе.) На рисунке \(\PageIndex{1b}\) все внешние силы, действующие на систему, складываются вместе, чтобы создать результирующую силу \(\vec{F}_{net} \). Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, векторы показаны коллинеарно. Наконец, на рисунке \(\PageIndex{1c}\) большая результирующая внешняя сила создает большее ускорение (\(\vec{a}’ > \vec{a}\)), когда эвакуатор тянет машину.
(Более подробно мы обсудим трение в следующей главе.) На рисунке \(\PageIndex{1b}\) все внешние силы, действующие на систему, складываются вместе, чтобы создать результирующую силу \(\vec{F}_{net} \). Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, векторы показаны коллинеарно. Наконец, на рисунке \(\PageIndex{1c}\) большая результирующая внешняя сила создает большее ускорение (\(\vec{a}’ > \vec{a}\)), когда эвакуатор тянет машину. (Вспомним из «Сил», что чистая внешняя сила представляет собой векторную сумму всех внешних сил и иногда обозначается как \(\sum \vec{F}\).) Эта пропорциональность показывает то, что мы сказали словами: ускорение прямо пропорционально чистая внешняя сила. Как только интересующая система выбрана, определите внешние силы и проигнорируйте внутренние. Пренебрежение многочисленными внутренними силами, действующими между объектами внутри системы, такими как мышечные силы в телах учащихся, не говоря уже о бесчисленных силах между атомами в объектах, является огромным упрощением. Тем не менее, это упрощение помогает нам решать некоторые сложные проблемы.
(Вспомним из «Сил», что чистая внешняя сила представляет собой векторную сумму всех внешних сил и иногда обозначается как \(\sum \vec{F}\).) Эта пропорциональность показывает то, что мы сказали словами: ускорение прямо пропорционально чистая внешняя сила. Как только интересующая система выбрана, определите внешние силы и проигнорируйте внутренние. Пренебрежение многочисленными внутренними силами, действующими между объектами внутри системы, такими как мышечные силы в телах учащихся, не говоря уже о бесчисленных силах между атомами в объектах, является огромным упрощением. Тем не менее, это упрощение помогает нам решать некоторые сложные проблемы. Пропорциональность записывается как
Пропорциональность записывается как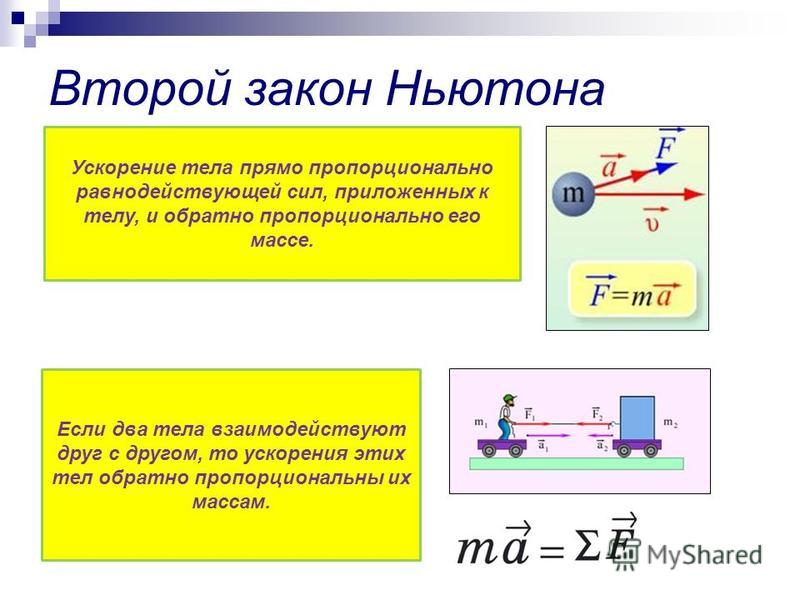

 Это результат векторного соотношения, выраженного во втором законе Ньютона, то есть вектор, представляющий результирующую силу, является скалярным множителем вектора ускорения. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны компенсироваться, поскольку в вертикальном направлении не возникает никакого ускорения (косилка движется). только по горизонтали). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.
Это результат векторного соотношения, выраженного во втором законе Ньютона, то есть вектор, представляющий результирующую силу, является скалярным множителем вектора ускорения. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны компенсироваться, поскольку в вертикальном направлении не возникает никакого ускорения (косилка движется). только по горизонтали). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости. Если к кораблю приложить силу 6 МН (6 х 10 6 Н), какое ускорение он испытает?
Если к кораблю приложить силу 6 МН (6 х 10 6 Н), какое ускорение он испытает? Какая сила больше, \(\vec{F}_{двигатель}\) или \(\vec{F}_{трение}\)? Объяснять.
Какая сила больше, \(\vec{F}_{двигатель}\) или \(\vec{F}_{трение}\)? Объяснять. Согласно второму закону Ньютона, чтобы вызвать ускорение, необходима результирующая сила.
Согласно второму закону Ньютона, чтобы вызвать ускорение, необходима результирующая сила. Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами.
Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. См. диаграмму свободного тела на рисунке \(\PageIndex{5}\).
См. диаграмму свободного тела на рисунке \(\PageIndex{5}\). (Вспомним, что g, ускорение свободного падения, равно 9,80 м/с 2 . Когда мы говорим, что ускорение равно 45 g, это 45 x 90,8 м/с 2 , что примерно равно 440 м/с 2 .) Хотя живые объекты больше не используются, с ракетными салазками была получена наземная скорость 10 000 км/ч.
(Вспомним, что g, ускорение свободного падения, равно 9,80 м/с 2 . Когда мы говорим, что ускорение равно 45 g, это 45 x 90,8 м/с 2 , что примерно равно 440 м/с 2 .) Хотя живые объекты больше не используются, с ракетными салазками была получена наземная скорость 10 000 км/ч. Если величина ускорения грузовика равна 10 м/с 2 , какова величина ускорения спортивного автомобиля?
Если величина ускорения грузовика равна 10 м/с 2 , какова величина ускорения спортивного автомобиля? Найдите: а) результирующую силу, действующую на мяч; б) модуль и направление результирующей силы.
Найдите: а) результирующую силу, действующую на мяч; б) модуль и направление результирующей силы.

 Масса автомобиля 1000,0 кг. Дорога скользкая, поэтому трением можно пренебречь. а) Чему равна результирующая сила, действующая на автомобиль? б) Чему равно ускорение автомобиля?
Масса автомобиля 1000,0 кг. Дорога скользкая, поэтому трением можно пренебречь. а) Чему равна результирующая сила, действующая на автомобиль? б) Чему равно ускорение автомобиля? 7}\]
7}\]