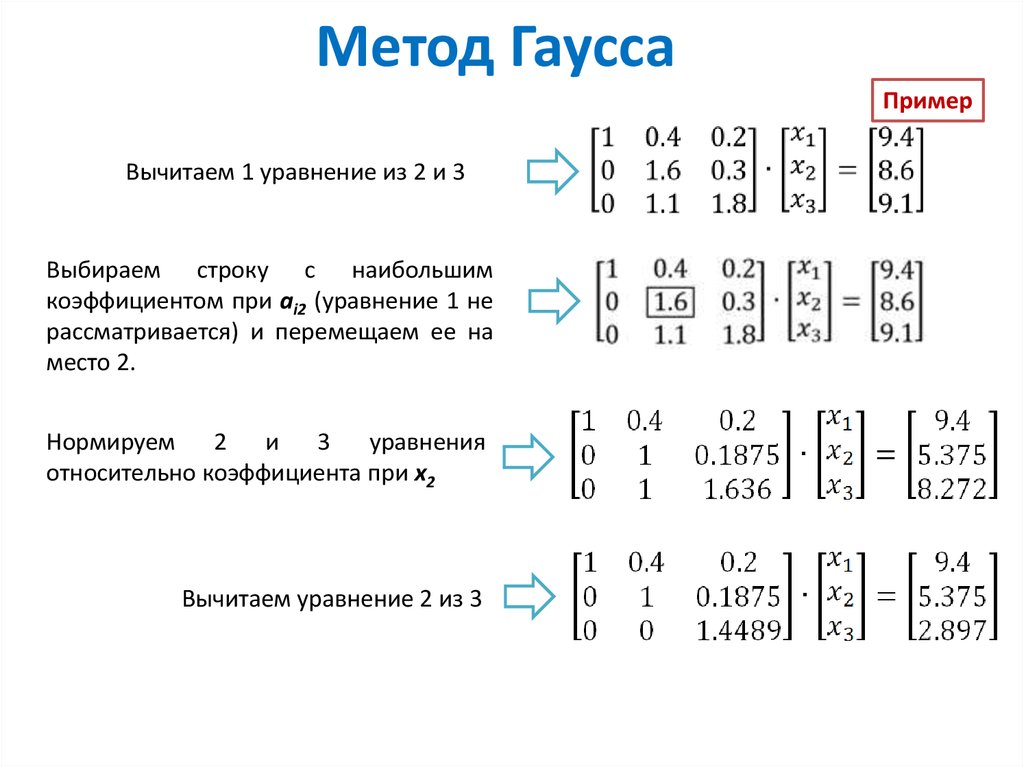
Нормальное распределение
Одномерное нормальное распределение
Графики плотности нормального распределения
Вычисления процентных точек нормального распределения
Двумерное нормальное распределение
Графики плотности двумерного распределения
Нормальное распределение (normal distribution) – играет важную роль в анализе данных.
Иногда вместо термина нормальное распределение употребляют термин гауссовское распределение в честь К. Гаусса (более старые термины, практически не употребляемые в настоящее время: закон Гаусса, Гаусса-Лапласа распределение).
Одномерное нормальное распределение
Нормальное распределение имеет плотность::
(*)
В этой формуле , фиксированные параметры, – среднее

Графики плотности при различных параметрах приведены ниже.
Характеристическая функция нормального распределения имеет вид:
Дифференцируя характеристическую функцию и полагая t = 0, получаем моменты любого порядка.
Кривая плотности нормального распределения симметрична относительно и имеет в этой точке единственный максимум, равный
Параметр стандартного отклонения меняется в пределах от 0 до ∞.
Среднее меняется в пределах от -∞ до +∞.
При увеличении параметра кривая растекается вдоль оси х, при стремлении к 0 сжимается вокруг среднего значения (параметр характеризует разброс, рассеяние).
При изменении кривая сдвигается вдоль оси х (см. графики).
Варьируя параметры и , мы получаем разнообразные модели случайных величин, возникающие в телефонии.
Типичное применение нормального закона в анализе, например, телекоммуникационных данных – моделирование сигналов, описание шумов, помех, ошибок, трафика.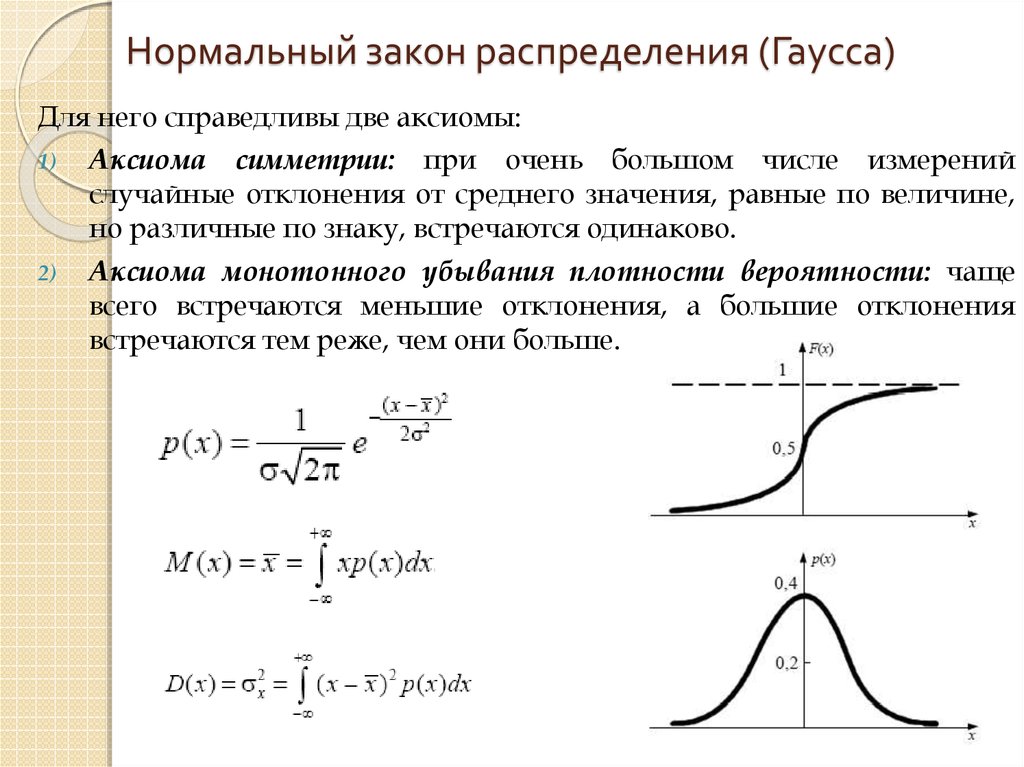
Графики одномерного нормального распределения
Рисунок 1. График плотности нормального распределения: среднее равно 0, стандартное отклонение 1
Рисунок 2. График плотности стандартного нормального распределения с областями, содержащими 68% и 95% всех наблюдений
Рисунок 3. Графики плотностей нормальных распределений c нулевым средним и разными отклонениями (=0.5, =1, =2)
Рисунок 4 Графики двух нормальных распределений N(-2,2) и N(3,2).
Заметьте, центр распределения сдвинулся при изменении параметра .
Замечание
В программе STATISTICA под обозначением N(3,2) понимается нормальный или гауссов закон с параметрами: среднее = 3 и стандартное отклонение =2.
В литературе иногда второй параметр трактуется как дисперсия, т.е. квадрат стандартного отклонения.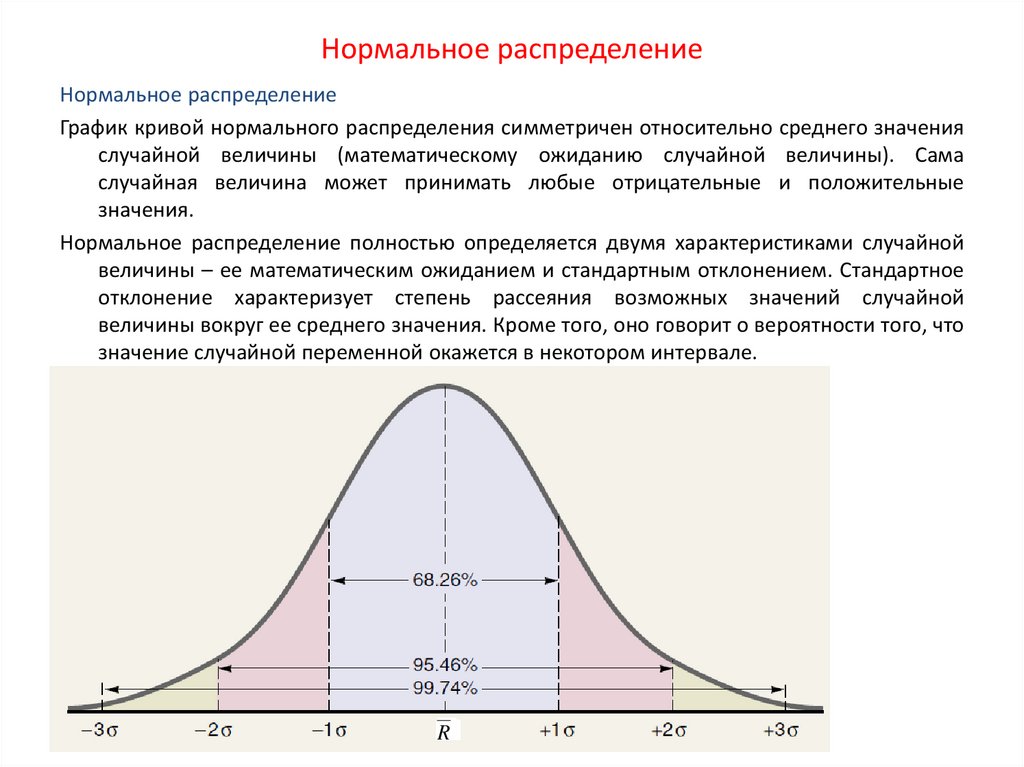
Вычисления процентных точек нормального распределения с помощью вероятностного калькулятора
STATISTICAС помощью вероятностного калькулятора STATISTICA можно вычислить различные характеристики распределений, не прибегая к громоздким таблицам, используемым в старых книгах.
Шаг 1. Запускаем Анализ / Вероятностный калькулятор / Распределения.
Рисунок 5. Запуск калькулятора вероятностных распределений
Шаг 2. Указываем интересующие нас параметры.
Например, мы хотим вычислить 95% квантиль нормального распределения со средним 0 и стандартным отклонением 1.
Укажем эти параметры в полях калькулятора (см. поля калькулятора среднее и стандартное отклонение).
Введем параметр p=0,95.
Галочка «Обратная ф.р». отобразится автоматически. Поставим галочку «График».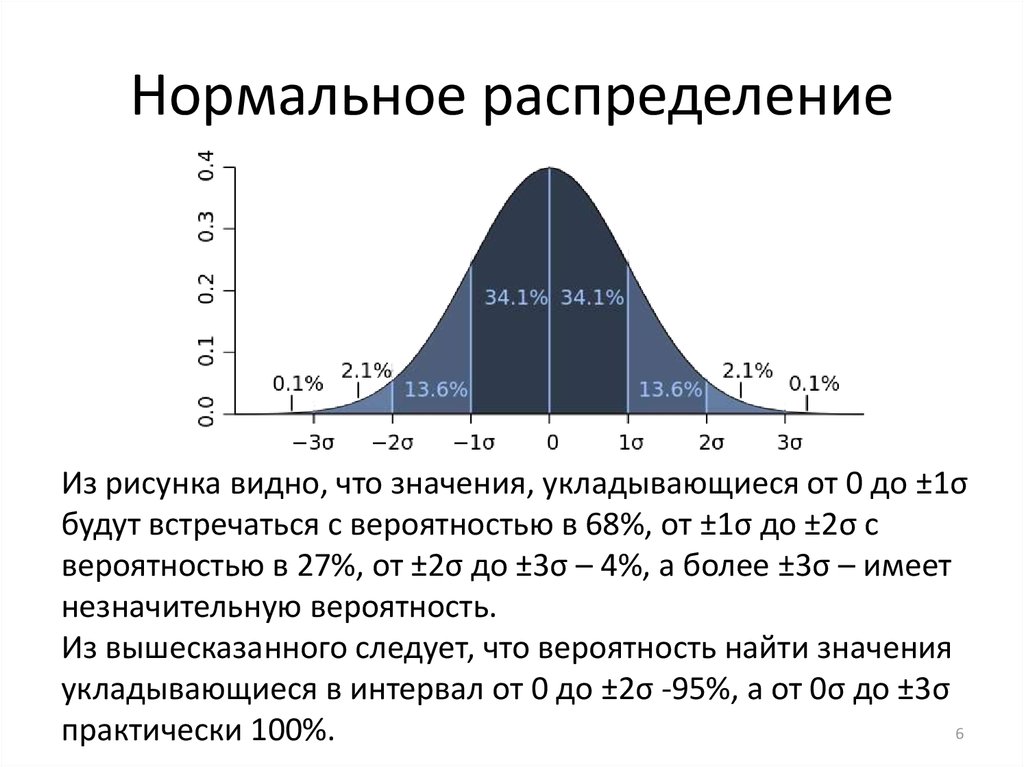
Нажмем кнопку «Вычислить» в правом верхнем углу.
Рисунок 6. Настройка параметров
Шаг 3. В поле Z получаем результат: значение квантиля равно 1,64 (см. следующее окно).
Рисунок 7. Просмотр результата работы калькулятора
Далее автоматически появится окно с графиками плотности и функции распределения нормального закона:
Рисунок 8. Графики плотности и функции распределения. Прямая x=1,644485
Рисунок 9. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=-1.5, x=-1, x=-0.5, x=0
Оценка параметров нормального распределения
Значения нормального распределения можно вычислить с помощью интерактивного калькулятора.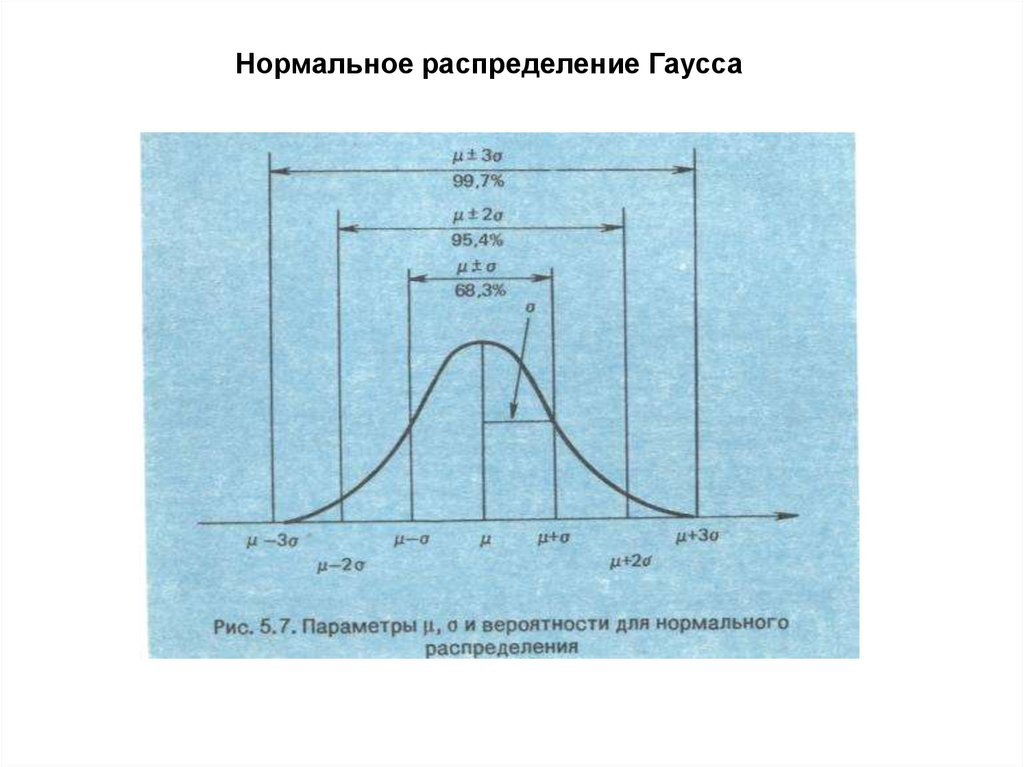
Двумерное нормальное распределение
Одномерное нормальное распределение естественно обобщается на двумерное нормальное распределение.
Например, если вы рассматриваете сигнал только в одной точке, то вам достаточно одномерного распределения, в двух точках – двумерного, в трех точках – трехмерного и т.д.
Общая формула для двумерного нормального распределения имеет вид:
Где – парная корреляция между X1 и X2;
– среднее и стандартное отклонение переменной X1соответственно;
– среднее и стандартное отклонение переменной X2соответственно.
Если случайные величины Х1 и Х2 независимы, то корреляция равна 0, = 0, соответственно средний член в экспоненте зануляется, и мы имеем:
f(x1,x2) = f(x1)*f(x2)
Для независимых величин двумерная плотность распадается в произведение двух одномерных плотностей.
Графики плотности двумерного нормального распределения
Рисунок 11. График плотности двумерного нормального распределения (нулевой вектор средних, единичная ковариационная матрица)
Рисунок 12. Сечение графика плотности двумерного нормального распределения плоскостью z=0.05
Рисунок 13. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной)
Рисунок 14. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной) плоскостью z= 0.05
Рисунок 15. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0. 5 на побочной)
5 на побочной)
Рисунок 16. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной) плоскостью z=0.05
Рисунок 17. Сечения графиков плотностей двумерного нормального распределения плоскостью z=0.05
Для лучшего понимания двумерного нормального распределения попробуйте решить следующую задачу.
Задача. Посмотрите на график двумерного нормального распределения. Подумайте, можно ли его представить, как вращение графика одномерного нормального распределения? Когда нужно применить прием деформации?
Читайте далее – многомерное нормальное распределение
Связанные определения:
Cтандартное нормальное распределение
Нормальное распределение
Шапиро-Уилка W критерий
В начало
Содержание портала
| Распределение ГауссаGaussian distribution Распределение Гаусса (нормальное распределение)
− плотность распределения вероятностей случайной величины n. Функция GXσ называется функцией Гаусса.
Говорят, что результаты измерений имеют нормальное распределение, если они
описываются функцией Гаусса. Распределение Гаусса, в отличие от распределения
Пуассона, характеризуется двумя независимыми параметрами X и σ. X − среднее
число отсчетов, которое мы ожидаем получить в случае многократного повторения
измерений. σ − среднее стандартное отклонение. На рис. Сравним распределения Гаусса GXσ(n) и Пуассона .
Pμ(n) ≈ GXσ(n), при X = μ, σ = √μ.
|
Интерпретация распределения Гаусса – Вечная загадка
~ Пратик Джоши
Когда мы имеем дело с большим объемом данных, у нас не может быть конкретных правил для каждого экземпляра. Мы должны придумать модель, которая определяет все данные. Затем эту модель можно использовать для анализа неизвестных входных данных. Чаще всего данные имеют некоторый базовый шаблон. Когда мы думаем о модели, мы извлекаем определенные характеристики из данных и придумываем формулировку, которая лучше всего объясняет поведение данных. Одним из наиболее часто встречающихся паттернов является распределение Гаусса. Он используется практически повсеместно в науке и технике. Но что именно? Зачем нам это нужно?
Статистика
Проще говоря, статистика — это наука об анализе и интерпретации данных. Весь предмет статистики основан на идее, что у вас есть большой набор данных, и вы хотите проанализировать его с точки зрения отношений между отдельными точками в этом наборе данных. Мы используем определенные меры для анализа данных, а именно среднее значение и стандартное отклонение. Давайте посмотрим, что это такое.
Весь предмет статистики основан на идее, что у вас есть большой набор данных, и вы хотите проанализировать его с точки зрения отношений между отдельными точками в этом наборе данных. Мы используем определенные меры для анализа данных, а именно среднее значение и стандартное отклонение. Давайте посмотрим, что это такое.
Среднее
Среднее имеет разные значения в разных контекстах. В общем, среднее относится к среднему значению набора значений. Почему мы должны заботиться о среднем? Среднее значение распределения дает нам общее представление о значении, вокруг которого сосредоточены точки данных. После экзамена мы спрашиваем средний балл класса. Это среднее значение дает нам представление о том, как студенты выступили на этом экзамене.
Стандартное отклонение
Чтобы понять стандартное отклонение, нам нужен набор данных. Статистики обычно занимаются выборкой населения. Это означает, что нам не нужно заботиться о каждой точке данных.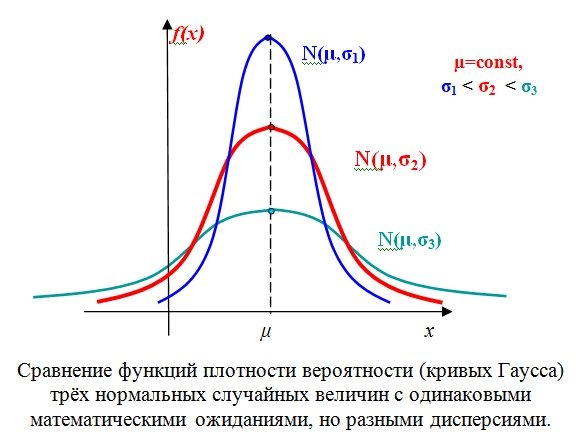 Если использовать в качестве примера предвыборные опросы, население — это все люди в стране, тогда как выборка — это подмножество населения, которое измеряют статистики. Самое замечательное в статистике то, что, измеряя только выборку населения, вы можете определить, что, скорее всего, будет измерением, если вы использовали все население. Нам нужно знать, сколько людей согласны друг с другом или имеют близкое друг к другу мнение. Вот здесь и появляется стандартное отклонение.
Если использовать в качестве примера предвыборные опросы, население — это все люди в стране, тогда как выборка — это подмножество населения, которое измеряют статистики. Самое замечательное в статистике то, что, измеряя только выборку населения, вы можете определить, что, скорее всего, будет измерением, если вы использовали все население. Нам нужно знать, сколько людей согласны друг с другом или имеют близкое друг к другу мнение. Вот здесь и появляется стандартное отклонение.
Стандартное отклонение (SD) набора данных — это мера того, насколько разбросаны данные. Это скажет нам, насколько уверенно модель прогнозирует и анализирует любые новые данные. Он говорит нам, насколько близки точки данных к среднему значению распределения. Если стандартное отклонение мало, это говорит нам о том, что большинство точек данных близки к среднему значению распределения. Термин «дисперсия» относится к квадрату стандартного отклонения.
Распределение Гаусса
Распределение Гаусса также называют нормальным распределением.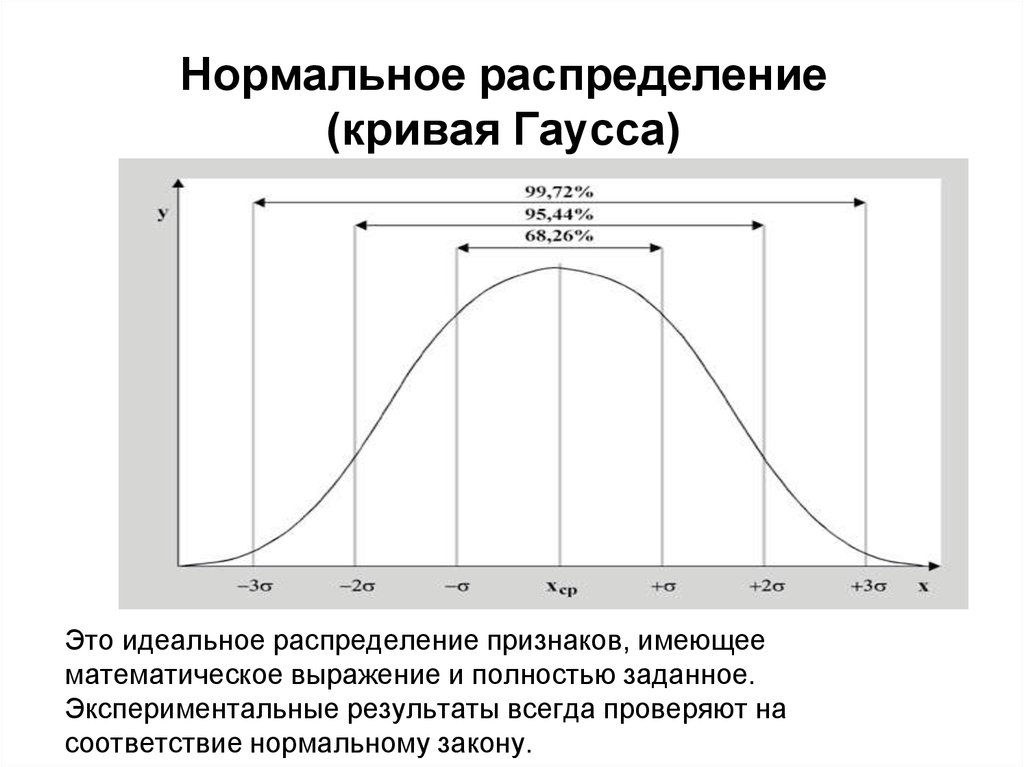 Распределение Гаусса относится к семейству непрерывных распределений вероятностей, описываемых уравнением Гаусса. Уравнение Гаусса представляет собой экспоненциально затухающую кривую, центрированную вокруг среднего значения распределения, масштабированного с помощью коэффициента. Коэффициент масштабирования обратно пропорционален стандартному отклонению распределения. Если это было запутанно, я постараюсь прояснить это в ближайшее время.
Распределение Гаусса относится к семейству непрерывных распределений вероятностей, описываемых уравнением Гаусса. Уравнение Гаусса представляет собой экспоненциально затухающую кривую, центрированную вокруг среднего значения распределения, масштабированного с помощью коэффициента. Коэффициент масштабирования обратно пропорционален стандартному отклонению распределения. Если это было запутанно, я постараюсь прояснить это в ближайшее время.
График распределения Гаусса зависит от двух факторов – среднего значения и стандартного отклонения. Среднее значение распределения определяет положение центра графика, а стандартное отклонение определяет высоту и ширину графика. Высота определяется коэффициентом масштабирования, а ширина определяется коэффициентом степени экспоненты. Когда стандартное отклонение велико, кривая короткая и широкая; когда стандартное отклонение мало, кривая высокая и узкая. Все распределения Гаусса выглядят как симметричные колоколообразные кривые. Если вы посмотрите на изображение здесь, кривая справа — это кривая с меньшим стандартным отклонением, чем кривая слева.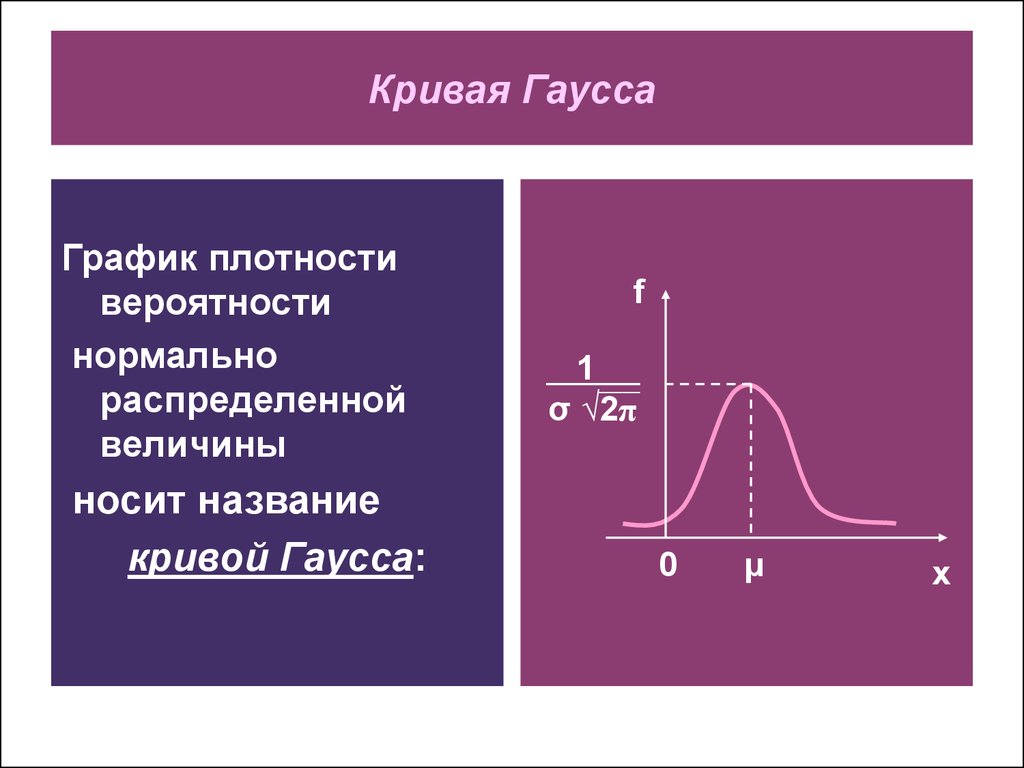
Многие данные реального мира имеют характеристики Гаусса. Это позволяет ученым и исследователям легко анализировать неизвестные данные с помощью этой модели. Он используется в биологии для изучения характеристик нервных тканей. Он используется в финансах для анализа и прогнозирования обменных курсов, курсов акций, общего анализа данных и т. д. Он часто встречается в квантовой физике, обработке сигналов, производстве микросхем, биологии и т. д. Когда мы собираем большие объемы данных и изучаем лежащий в основе паттерн, он обычно имеет гауссовский характер. Нет необходимости, чтобы данные всегда имели гауссовский характер. Есть много других типов дистрибутивов. Но мы сохраним это обсуждение для другого поста в блоге.
Многомерное распределение Гаусса
Распределение Гаусса, которое изменяется более чем в одном измерении, называется многомерным распределением Гаусса. Например, если у вас есть набор чисел и вы нарисуете простую кривую, поместив эти числа на числовую прямую, вы получите одномерное распределение Гаусса.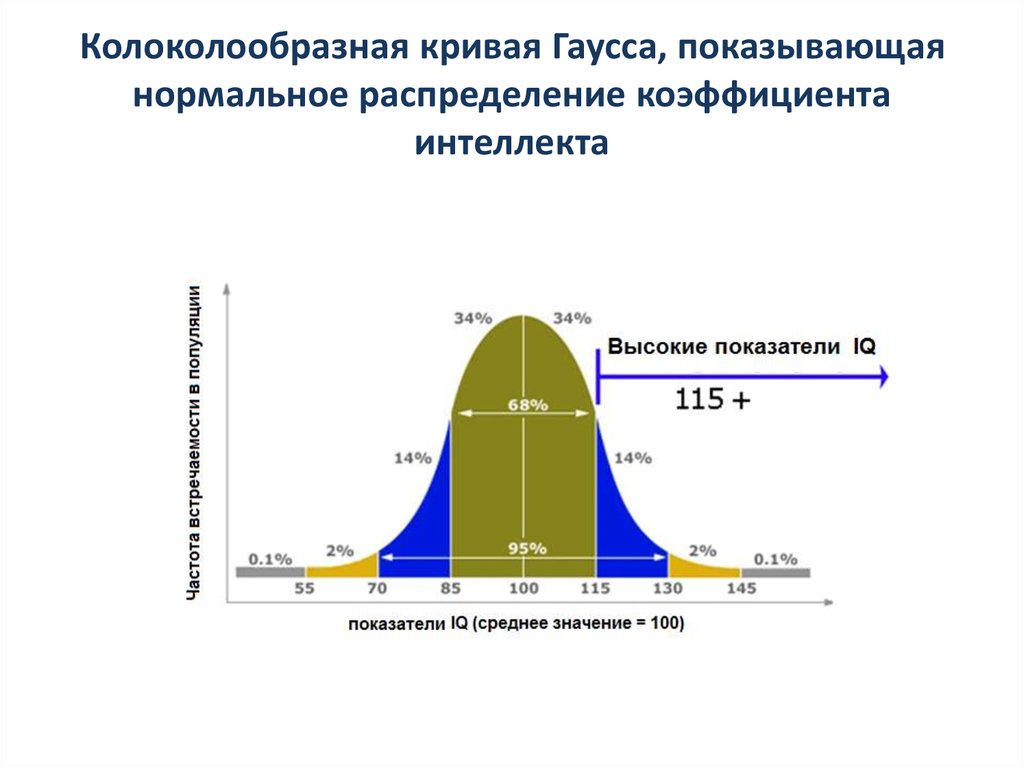 Но что, если бы у вас были пары чисел, такие как точки на плоскости или высота и ширина объекта и т. д.? Здесь первое число во всех парах будет иметь распределение Гаусса, а второе число будет иметь другое распределение Гаусса. Когда вы посмотрите на них вместе, вы получите распределение Гаусса, которое может выглядеть как кривая, показанная на изображении здесь.
Но что, если бы у вас были пары чисел, такие как точки на плоскости или высота и ширина объекта и т. д.? Здесь первое число во всех парах будет иметь распределение Гаусса, а второе число будет иметь другое распределение Гаусса. Когда вы посмотрите на них вместе, вы получите распределение Гаусса, которое может выглядеть как кривая, показанная на изображении здесь.
Мультимодальное распределение Гаусса
Гауссово распределение, имеющее более одной моды, называется мультимодальным распределением. Конкретный режим соответствует конкретному значению среднего и стандартного отклонения. Эти кривые имеют два или более пика с разной дисперсией. Эти распределения полезны, когда одни и те же величины группируются вокруг двух или более средних значений. Если вы попытаетесь обобщить его с помощью одного среднего значения, мы можем потерять важную информацию. На рисунке, показанном здесь, распределение имеет два режима. Как мы видим, они отличаются своими средними значениями и стандартными отклонениями.
Анализ данных является неотъемлемой частью почти каждой отрасли науки. Распределение Гаусса встречается во многих формах и в разных местах. Название Gaussian происходит от имени математика Карла Фридриха Гаусса. Он придумал эту формулу около 200 лет назад. Его называют «принцем математики», и это правильно! Он был вундеркиндом и одним из самых влиятельных математиков всех времен. Его теории и формулировки глубоко укоренились во многих различных областях.
Нравится Загрузка…
Опубликовано в Машинное обучение, Математика РаспределениеСреднее по Гауссумультимодальноемногомерноестандартное отклонение Основатель Плутошифта. Автор 13 книг по машинному обучению. Представлено в Forbes, NBC, Bloomberg, CNBC, TechCrunch, Silicon Valley Business Journal и других изданиях. Спикер на таких конференциях, как TEDx, Global Big Data Conference, Machine Learning Developers Conference и Sensors Expo. Вы можете узнать больше обо мне здесь: www.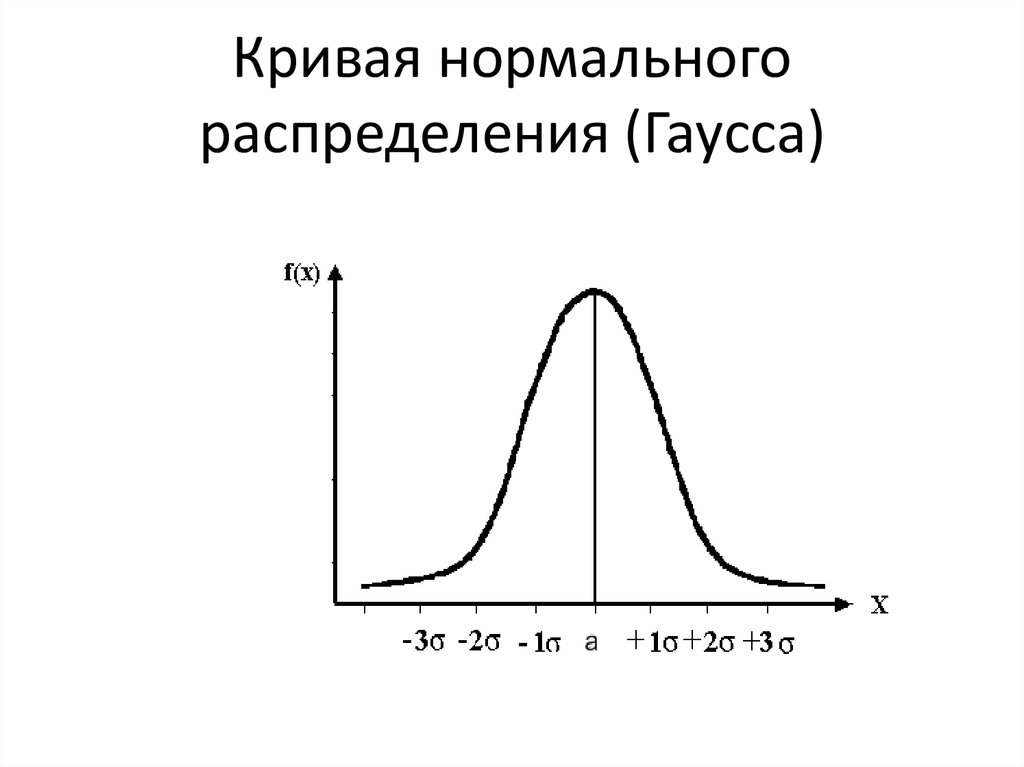 prateekj.com
Просмотреть все сообщения Пратика Джоши
prateekj.com
Просмотреть все сообщения Пратика Джоши
Объяснение распределения Гаусса | Марио Эммануэль
При определенных условиях игра в кости может быть смоделирована как распределение Гаусса. Фото Edge2Edge Media на UnsplashРаспределение Гаусса — это одно из многих статистических распределений, которые могут описывать наборы данных, и оно очень важно, поскольку многие реальные процессы следуют этому распределению. Примеры гауссовых распределений включают финансовую отдачу и рост населения.
В этом примере мы искусственно сгенерируем выборку данных из распределения Гаусса, нанесем ее на теоретическую кривую распределения Гаусса, а затем применим критерий Колмогорова-Смирнова, если набор данных является частью распределения Гаусса или нет, что в этот случай явно таков, поскольку он был сгенерирован из нормального распределения — .
В этом примере мы будем использовать MATLAB, но, конечно, есть эквиваленты один к одному с использованием numpy и Matplotlib.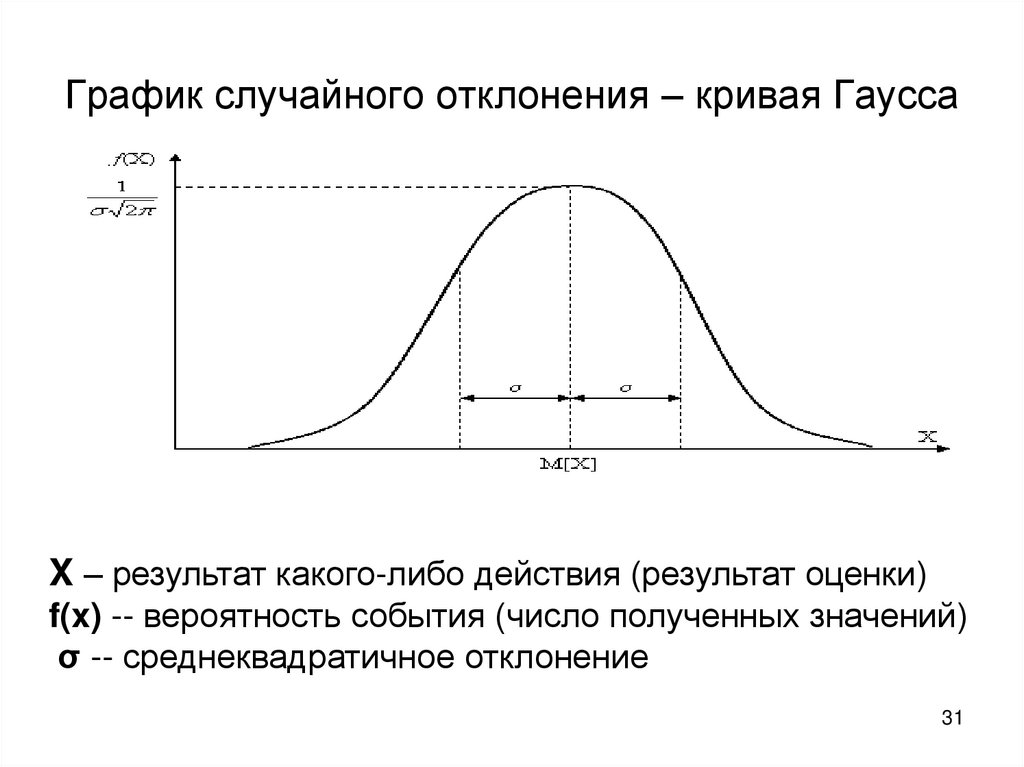 Функция плотности вероятности модели Гаусса показывает, насколько вероятность имеет определенные значения по сравнению с другими.
Функция плотности вероятности модели Гаусса показывает, насколько вероятность имеет определенные значения по сравнению с другими.
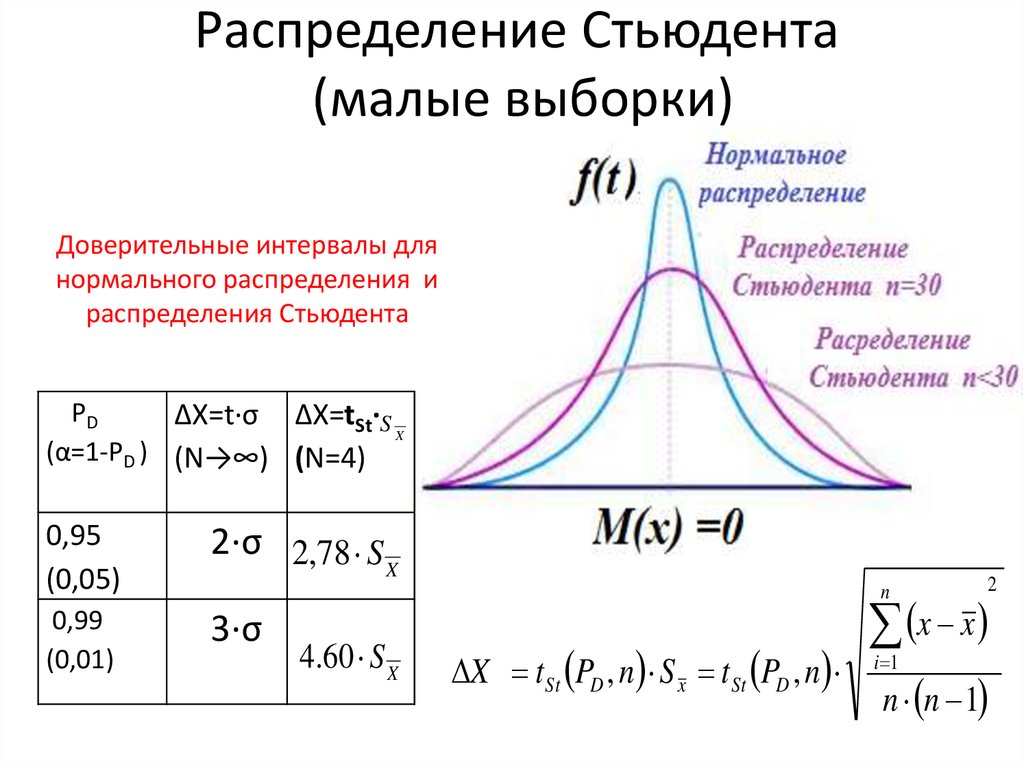
Первым шагом является создание модели распределения по Гауссу. В этом случае мы будем использовать мю (μ), равное 2, и сигма (σ), равное 1. μ представляет собой среднее значение, а σ представляет место, где находится 68% данных. Использование 2 σ даст где 95% данных находится. Сигма (σ) измеряется от среднего (μ) и показывает, насколько данные близки или далеки от среднего значения.
В качестве второго шага мы создадим два графика: один график выборочных данных, а другой — гистограмму выборочных данных и теоретическую кривую Гаусса.
Создаются оба графика:
Рис. 1. Примеры наборов данных. Изображение создано с помощью Matlab онлайн. Рисунок 2. Пример гистограммы набора данных. Изображение создано с помощью Matlab онлайн.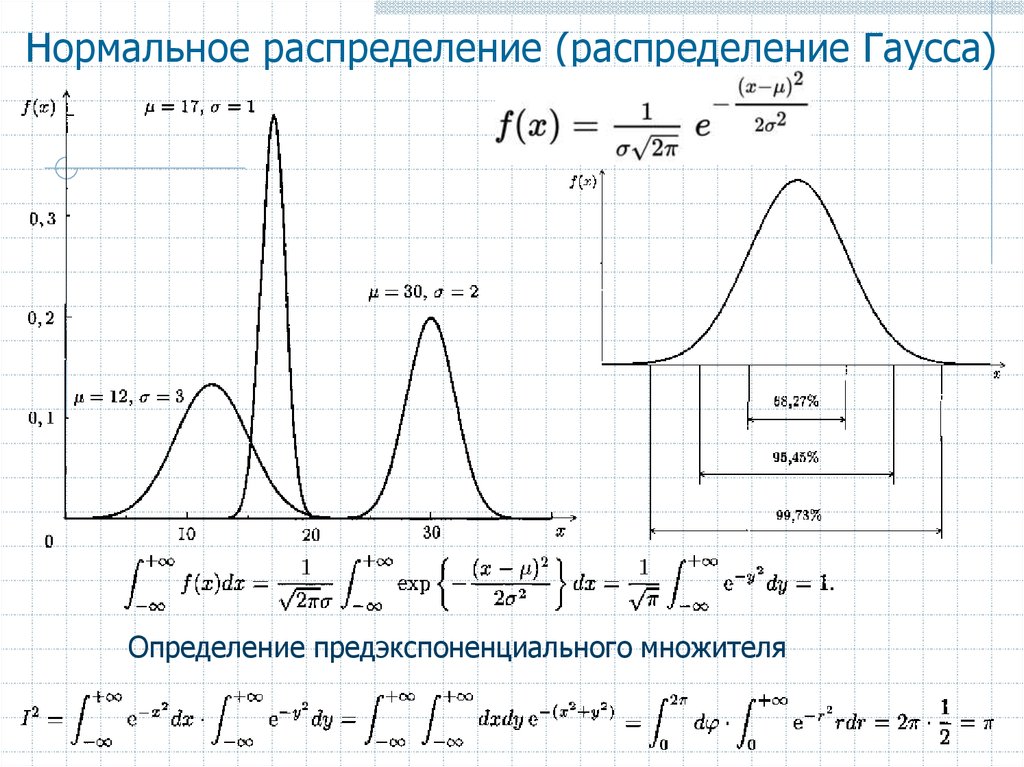
При построении точек данных видно, что они сосредоточены вокруг μ и что большая часть данных (68%) содержится в пределах μ-σ и μ+σ.
На втором графике мы видим, что теоретическая кривая Гаусса имеет намного меньший масштаб, чем наш набор данных, это связано с тем, что мы должны масштабировать область нашего набора данных до 1. Matlab может сделать это автоматически через параметр нормализации:
Рис. 3. Пример гистограммы набора данных с теоретической эквивалентной кривой Гаусса. Изображение создано с помощью Matlab онлайн.В этом примере мы искусственно сгенерировали данные из модели распределения по Гауссу. Это, очевидно, подразумевает, что данные являются гауссовыми. Хотя иногда это и предполагается (нам может понадобиться набор данных, который поступает прямо из нормального распределения), в большинстве случаев мы просто сталкиваемся с данными, которые кажутся гауссовыми по своей природе, и мы хотим проверить это предположение.
Существует несколько способов проверить, является ли набор данных гауссовым или нет. Одним из них является тест Колмогорова-Смирнова, который оценивает нулевую гипотезу о том, что данные являются гауссовыми.
Одним из них является тест Колмогорова-Смирнова, который оценивает нулевую гипотезу о том, что данные являются гауссовыми.
Критерий Колмогорова-Смирнова по умолчанию основан на выборке данных со средним значением 0 и сигмой 1. Поэтому, если мы применим тест к нашему набору данных, мы вернем, что набор данных не является гауссовым. На самом деле речь идет об указании среднего и сигмы.
Если мы вычтем ожидаемое среднее значение и разделим его на дисперсию, мы сможем нормально применить тест.
График Q-Q — это визуальный способ проверить, является ли набор данных гауссовым или нет. В MATLAB есть возможность указать распределение или нет, хотя оба графика кажутся одинаковыми, правильный — второй (тот, который использует созданное нами распределение), поскольку он генерирует точную ось (среднее значение и сигма).
Рис. 4. График QQ с использованием стандартного нормального распределения. Рисунок создан с помощью Matlab онлайн.Обратите внимание, что вторая диаграмма сосредоточена вокруг нашего среднего распределения:
Рис. 5. График QQ с использованием нашего гауссовского распределения. Рисунок создан с помощью Matlab онлайн.
5. График QQ с использованием нашего гауссовского распределения. Рисунок создан с помощью Matlab онлайн.Графики «квантиль-к-квантилю» — это простой и наглядный способ показать, как набор данных вписывается в гауссову модель.
Асимметрия и эксцесс — две хорошо известные меры, которые можно применять к распределениям Гаусса.
Асимметрия измеряет асимметрию вокруг среднего значения, числовое значение, которое говорит вам, есть ли другие значения справа от среднего или слева. Совершенная симметричная гауссиана приведет к асимметрии со значением 0. Значения асимметрии менее 0,5 более или менее симметричны, значения от 0,5 до 1 умеренно асимметричны, а значения выше 1 в значительной степени асимметричны. Конкретные пороги будут зависеть от вашей конкретной модели.
Эксцесс — это мера того, насколько экстремальным является хвост распределения, и его иногда называют мерой формы пика распределения, хотя эта интерпретация дискредитирована. Следовательно, его можно использовать в качестве признака для определения того, насколько далеко заходят выбросы в конкретном распределении.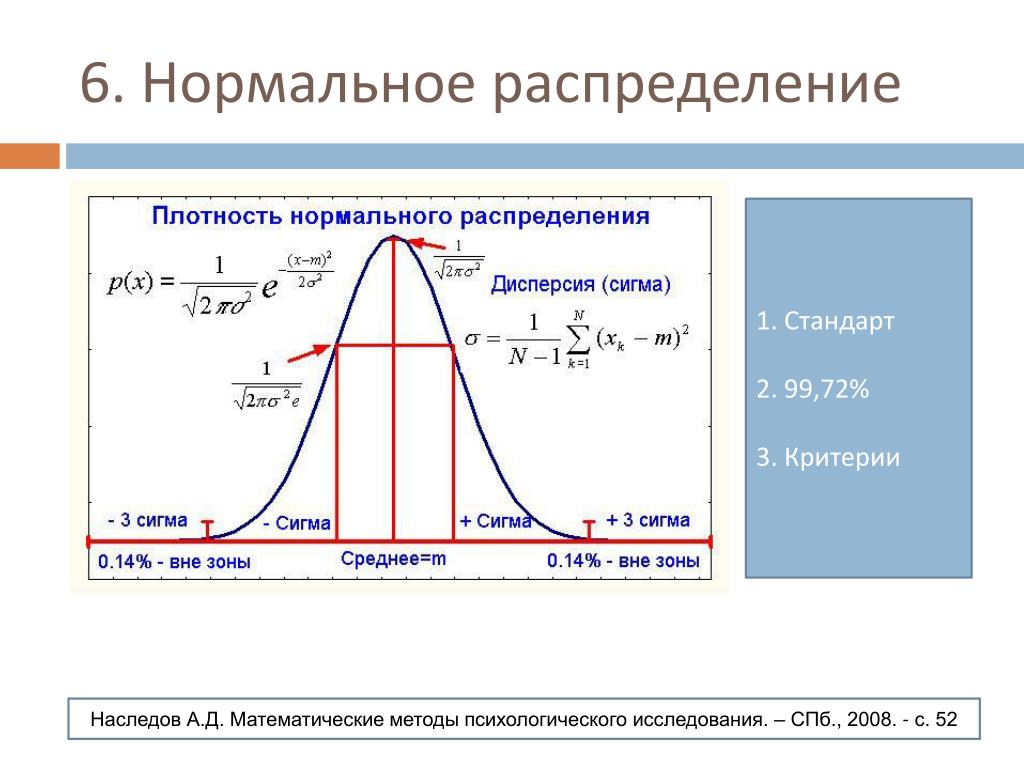

 Боттомоний
Боттомоний Чармоний
Чармоний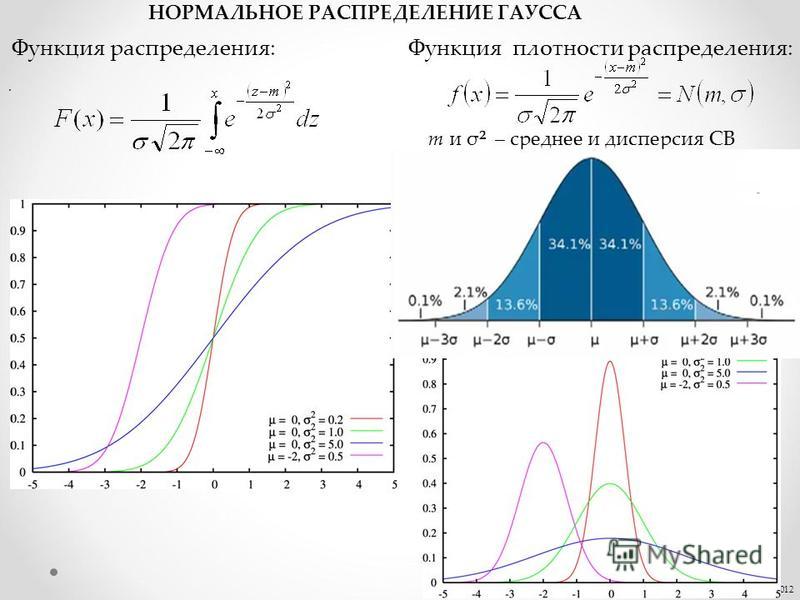
 1 показано два нормальных или
гауссовых распределения, соответствующие различным измерениям с одинаковыми
значениями X и разными σ. В первом случае X = 50, σ = 0.5, во втором случае
− X = 50, σ = 1. Величина σ в знаменателе экспоненты обеспечивает для более
узкого распределения большую высоту в максимуме.
1 показано два нормальных или
гауссовых распределения, соответствующие различным измерениям с одинаковыми
значениями X и разными σ. В первом случае X = 50, σ = 0.5, во втором случае
− X = 50, σ = 1. Величина σ в знаменателе экспоненты обеспечивает для более
узкого распределения большую высоту в максимуме. к. ширина распределения Пуассона σ автоматически определяется величиной
μ (σ = √μ).
к. ширина распределения Пуассона σ автоматически определяется величиной
μ (σ = √μ).