Как легко решать матрицы: умножение, сложение, вычитание. Как решать, с чего начать

От действий над матрицами к пониманию их сути… / Хабр

Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья “Математика на пальцах”, и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.

Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя).

Сдаётесь? — тогда читаем дальше…

Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.

Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что “площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма”.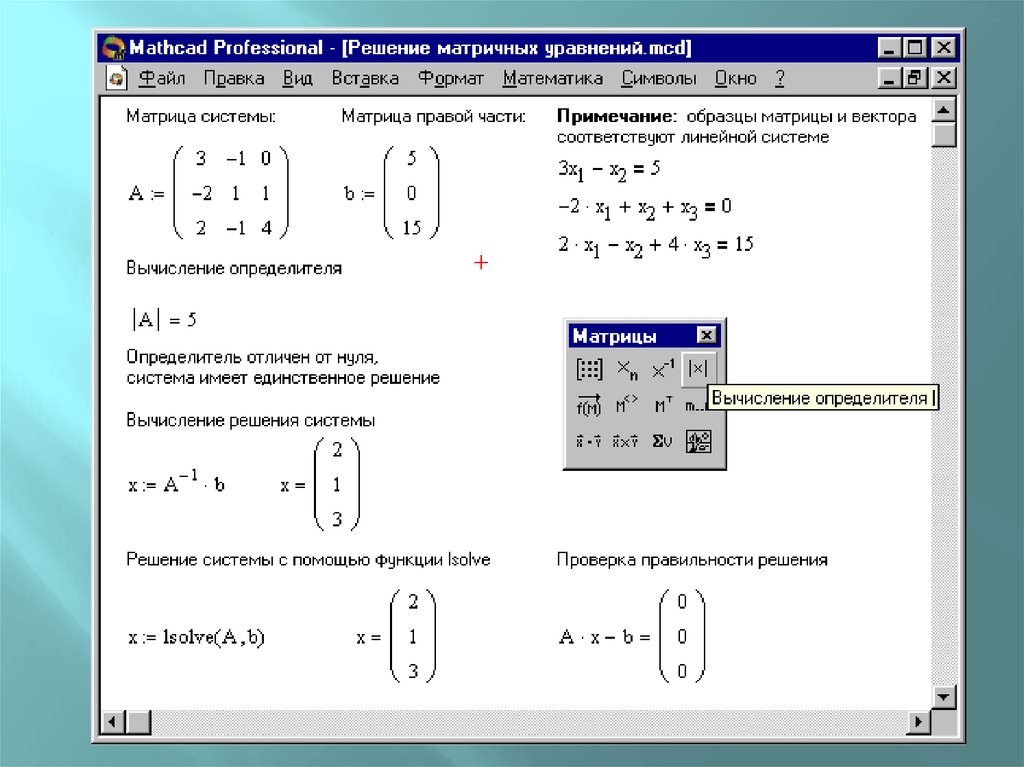 Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.

Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.

Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…

Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.

Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?

Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…

Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.

В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1).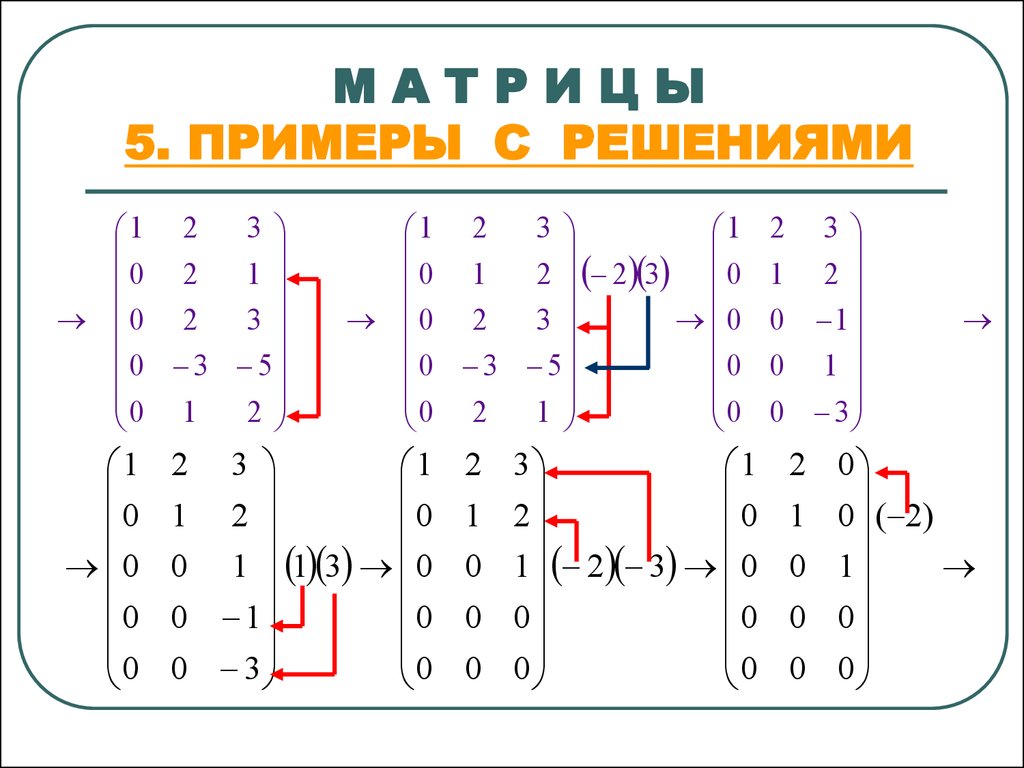

Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.

Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках».

Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».

Решение матричных уравнений — Журнал «Код»

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях». 

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано. 

Краткое содержание прошлых частей: 

• Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности. 
• Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел. 
• Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше). 
• Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
• Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми. 
• Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный. 

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

9 простых задач на математику

Шаг 1. Упрощаем уравнение 

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

Приводим матричное уравнение к упрощённому виду

Шаг 2. Вводим единичную

матрицу 

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу. 

Можно представить, что есть число 100 — это «сто в первой степени», 100¹

И есть число 0,01 — это «сто в минус первой степени», 100^-1

При перемножении этих двух чисел получится единица:
100¹ × 100^-1 = 100 × 0,01 = 1. 

Вот такое, только в мире матриц. 

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А^-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение: 

А-1 × А × Х = А-1 × В  

Добавляем единичную матрицу и упрощаем запись: 

А-1 × А = E — единичная матрица 

E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А-1 × В — новая запись уравнения 

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.  

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A^-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто. 

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы: 

1. Делим единицу на определитель матрицы A. 
2. Считаем транспонированную матрицу алгебраических дополнений. 
3. Перемножаем значения и получаем нужную матрицу.

Формула вычисления обратной матрицыПервое действие. Мы посчитали определитель и убедились, что он не равен нулю, — это значит, что у матричного уравнения есть вариант решения и можно продолжатьВторое действие, часть 1: получаем матрицу миноровВторое действие, часть 2: переводим матрицу миноров в транспонированную матрицу алгебраических дополнений

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Третье действие: получаем обратную матрицу

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А^-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново. 

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Проверяем ответ и получаем матрицу B — наши расчёты верны

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Этого котика не существует, а матрицы — существуют. 

Текст:

Александр Бабаскин

Редактура:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Мария Дронова

Соцсети:

Олег Вешкурцев

5 лучших советов по решению матричных уравнений

Математика не сложный предмет, но некоторые темы трудно понять. Итак, студенты всегда боятся арифметики и всех ее критических понятий. Матрица — одна из них. Студенты часто спрашивают, как решать матричные уравнения и понятия.

Но это становится проще, если вы понимаете обоснование и логику математических понятий, а не задаете каждый математический вопрос.

Кроме того, Matrix представляет числа или линейные уравнения в блочном формате для их решения. Вы также можете складывать или вычитать или умножать две матрицы друг на друга. Вот почему многие студенты борются с матрицами и спрашивают, как их решить.

Здесь мы познакомим вас со всеми методами простого решения матрицы с подходящим пошаговым руководством и лучшими примерами матричных уравнений.

Что такое Матрица?

Содержание

Матрица — основное понятие математики. Смысл матрицы в том, что это прямоугольный массив чисел, символов или выражений, расположенных в строках и столбцах. Матрицы обычно используются в различных областях, таких как математика, физика, инженерия, информатика и т. д.

Матрица представлена ​​тем, что все ее компоненты заключены в квадратные или круглые скобки. Более того, размеры матрицы описываются количеством содержащихся в ней строк и столбцов. Например, матрица с двумя строками и тремя столбцами называется матрицей 2×3.

Давайте узнаем, почему используется матрица. Матрицы описывают широкий спектр математических объектов и процессов, таких как системы линейных уравнений, модификации геометрии и многое другое. Они также играют важную роль в линейной алгебре, разделе математики, который имеет дело с векторными пространствами и линейными модификациями.

10 лучших типов матриц

Вы можете вычислить матрицу с помощью различных типов. Это следующие типы матриц.

1. Квадратная матрица

В математике квадратная матрица — это матрица с одинаковым количеством строк и столбцов. Матрица размера n на n известна как квадратная матрица порядка n. Можно складывать и перемножать любые две квадратные матрицы одного порядка. Квадратные матрицы часто представляют собой простые линейные преобразования, такие как сдвиг или вращение.

2. Прямоугольная матрица

Матрица называется прямоугольной, если количество строк не равно количеству столбцов.

3. Единичная матрица

Квадратная матрица, в которой все диагональные элементы равны 1, а все остальные элементы равны 0, называется единичной матрицей.

4. Нулевая матрица

Матрица, в которой все элементы равны 0, называется нулевой матрицей.

5. Диагональная матрица

Квадратная матрица, в которой все недиагональные элементы равны 0, называется диагональной матрицей.

6. Верхняя треугольная матрица

Квадратная матрица, в которой все элементы ниже главной диагонали равны 0, называется верхней треугольной матрицей.

7. Нижняя треугольная матрица

Квадратная матрица, в которой все элементы выше главной диагонали равны 0, называется нижней треугольной матрицей.

8.

Симметричная матрица

Квадратная матрица, элементы которой симметричны относительно главной диагонали, называется симметричной матрицей.

9. Кососимметричная матрица

Квадратная матрица, в которой элементы кососимметричны относительно главной диагонали, называется кососимметричной матрицей.

10. Эрмитова матрица

Комплексная квадратная матрица, в которой элементы симметричны относительно главной диагонали и сопряжены симметричны относительно сопряженной диагонали, называется эрмитовой матрицей.

5 лучших советов по решению матричных уравнений с примерами

Следующие шаги помогут решить матричные уравнения

1. Решение матрицы

Первый шаг к решению матрицы — проверить, достаточно ли у вас данных, чтобы найти каждую переменную линейного уравнения с помощью матрицы.

Матрица используется для решения линейного уравнения, но для использования матричного метода должно быть более одного линейного уравнения. Таким образом, если у вас есть только два уравнения, вы также можете использовать матричный метод для определения переменных.

https://www.calltutors.com/AskAssignment

Каждое линейное уравнение имеет определенные переменные, которые нам нужно найти, и такие переменные имеют определенные коэффициенты. Давайте разберемся на примере –

2x + 3y – 5z = 2

Здесь x, y и z – переменные уравнения, которые нам нужно узнать, а +2, +3 и -5 – коэффициенты в уравнении.

2. Запишите ваши уравнения

Второй шаг в Как решить Матрицу, чтобы записать ваши уравнения в калькуляторе стандартной формы. Следующий вопрос – какова стандартная форма записи линейного уравнения, тогда ответ Ax + By + Cz = D.

Итак, вам нужно написать все уравнения в такой форме, чтобы узнать значения переменных с помощью матрицы.

Нет необходимости иметь только 3 переменные; может быть меньше 3 переменных и точно так же может быть больше 3 переменных. Если у вас более 3 переменных, вы добавите их слева после переменной z, например: Ax + By + Cz + Dw = E.

Здесь A, B, C и D — коэффициенты, а x, y , z, мы переменные.

3. передача данных уравнения

Следующим шагом в разделе «Как решить матрицу» является передача данных уравнения в матричной форме. Итак, следующее, чему нужно научиться, — это записывать уравнения в матричной форме. Давайте разберемся на примерах, предположим, что у нас есть следующие 3 уравнения –

x + 2y – 3z = 5

x + y + z = 6

2x + y – z = 1

Теперь нам нужно узнать формат матрицы. Как мы видим, уравнения уже имеют стандартную форму, поэтому мы можем приступить к переводу таких уравнений в матричный вид.

Запишем коэффициенты каждого уравнения в строчках один за другим. Итак, здесь мы сначала запишем 1, 2 и -3 в первой строке матрицы, после этого мы запишем коэффициенты второго уравнения, а затем третьего уравнения. Посмотрите на ниже, чтобы понять лучше –

Здесь строки и столбцы также именуются. Таким образом, мы можем назвать строку 1 как R1, в которой есть 1, 2 и -3, строку 2 как R2, в которой есть 1, 1 и 1, и аналогично, строку 3 как R3, в которой есть 2, 1 и -1.

Точно так же мы можем назвать столбцы как C1, C2 и C3. C1 имеет 1, 1 и 2, C2 имеет 2, 1 и 1, и, наконец, C3 имеет -3, 1 и -1.

4. заключить в большие скобки первый и последний столбцы

Следующий шаг в решении матрицы – заключить в большие скобки первый и последний столбцы, чтобы получилась матрица. Таким образом, вы поместите квадратные скобки [] вокруг всего блока. Это просто символ матриц и больше ничего, о чем можно не волноваться и не пугаться.

5. Решить матрицу

Следующее, чему нужно научиться при решении матриц, это сложение двух матриц. Вы можете добавить или вычесть две матрицы.

Предположим, две матрицы равны

А вторая

Теперь вы можете сложить матрицы, добавив R1 к R1 второй матрицы и аналогичным образом все числа блока.

Таким образом, вы получите

Точно так же вы будете выполнять другие функции, такие как вычитание или умножение и т.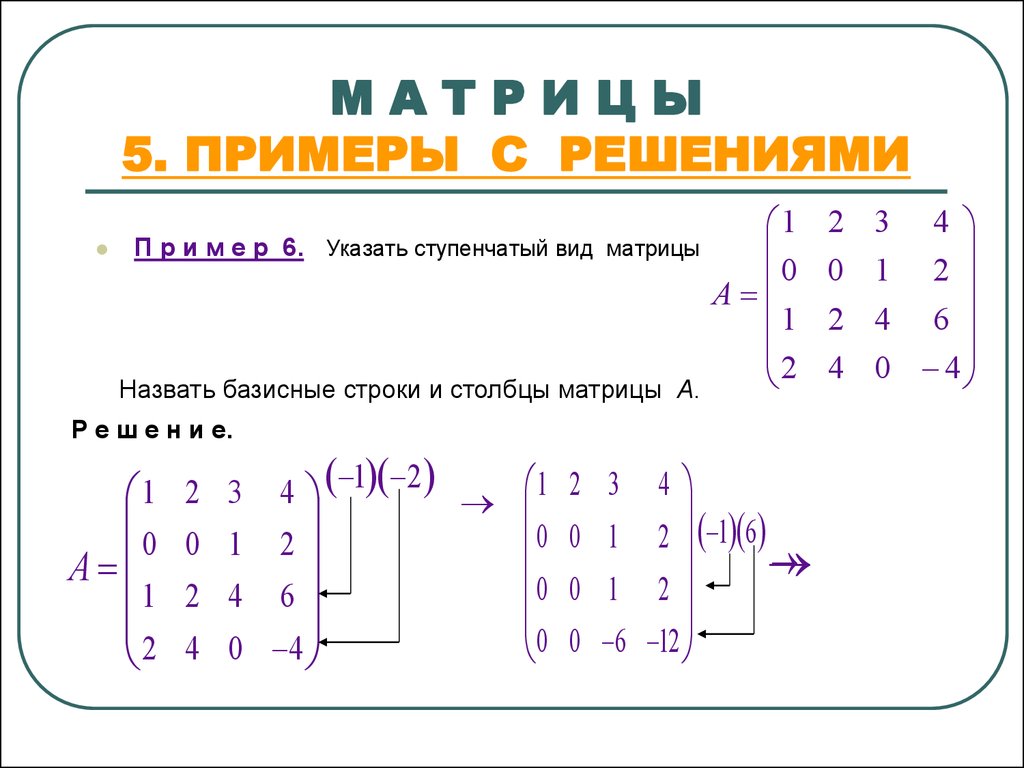 д.

Вывод

Всех нас пугает даже название математики. Мы изо всех сил пытаемся решить большинство понятий и впадаем в панику при упоминании математики. Тем не менее, если мы понимаем логику решения математических задач, мы можем легко решить все задачи независимо от их сложности. Многие студенты сталкиваются с проблемами при решении матриц. Они также следуют шагам и руководствам о том, как легко решать матрицы. Получите лучшую помощь с домашним заданием по математике от экспертов.

Часто задаваемые вопросы

Какова формула матрицы?

Для любой единичной матрицы A×I _n×n  = A, где A — любая квадратная матрица порядка n×n.

Как работают матричные вычисления?

Для умножения матриц количество столбцов в первой матрице должно равняться количеству строк во второй матрице.

Что такое матричный метод в алгебре?

Матричная алгебра — это математическая запись, упрощающая представление и решение одновременных уравнений

Решение систем линейных уравнений с использованием матриц

Привет! Эта страница будет иметь смысл только тогда, когда вы немного знакомы с системами линейных уравнений и матриц, поэтому, пожалуйста, идите и изучите их, если вы еще не знакомы с ними.

Пример

Одним из последних примеров по системам линейных уравнений был этот:

Пример: решить

• x + y + z = 6
• 2г + 5г = -4
• 2x + 5y – z = 27

Мы решили ее с помощью «исключения», но мы также можем решить ее с помощью матриц!

Использование матриц облегчает жизнь, потому что мы можем использовать компьютерную программу (такую ​​как Калькулятор матриц), чтобы выполнить всю «обработку чисел».

Но сначала нам нужно написать вопрос в матричной форме.

В форме матрицы?

ОК. Матрица — это массив чисел:

.

Матрица

Ну, подумай над уравнениями:

х	+	и	+	г	=	6
		2 года	+	5з	=	−4
2x	+	5 лет	−	г	=	27

Их можно превратить в таблицу чисел, например:

1		1		1	=	6
0		2		5	=	−4
2		5		−1	=	27

Мы могли бы даже разделить числа до и после “=” на:

1	1	1		6
0	2	5	и	−4
2	5	−1		27

Теперь у нас есть 2 матрицы.

На самом деле у нас есть третий, который равен [x y z]:

 

Почему [x y z] идет туда? Потому что, когда мы умножаем матрицы, мы используем «точечный продукт» следующим образом:

Это первое из наших исходных уравнений выше (вы можете это проверить). Вот она для второй строки.

 Попробуйте сами.

Матричное решение

Мы можем сократить это:

на это:

АХ = В

где

• A — матрица 3×3 из x, y и z коэффициентов
• X равно x, y и z и
• B — это 6, −4 и 27

Тогда (как показано на странице, обращенной к матрице) решение таково:

Х = А ^-1 В

Что это значит?

Это означает, что мы можем найти матрицу X (значения x, y и z) путем умножения , обратной матрицы A , на матрицу B .

Итак, давайте сделаем это.

Во-первых, нам нужно найти , обратную матрице A (при условии, что она существует!)

С помощью Калькулятора матриц получаем:

(я оставил 1/определитель вне матрицы, чтобы упростить числа)

Затем умножьте A ^-1 на B (мы можем снова использовать матричный калькулятор):

Готово! Решение:

х = 5
у = 3
z = −2

Как на странице “Системы линейных уравнений”.

Довольно аккуратно и элегантно, и человек думает, а компьютер делает расчеты.

Просто для удовольствия … Сделай это снова!

Для развлечения (и чтобы помочь вам научиться) давайте проделаем все это снова, но сначала поставьте матрицу «X».

Я хочу показать вам этот способ, потому что многие люди думают, что приведенное выше решение настолько изящно, что должно быть единственным способом.

Итак, мы решим это так:

ХА = В

И из-за того, как перемножаются матрицы, нам нужно настроить матрицы по-другому. Ряды и столбцы должны быть переключены («транспонированы»):

И XA = B выглядит так:

Матричное решение

Затем (также показано на странице, обращенной к матрице) решение таково:

Х = БА ^-1

Вот что мы получаем для A ^-1 :

На самом деле это то же самое, что инверсия, которую мы получили раньше, но с транспонированием (строки и столбцы меняются местами).