Урок 5. Неопределённый интеграл | Уроки математики и физики для школьников и родителей
ВИДЕО УРОК
Нахождение производных и нахождение неопределённых интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия. Как, например, сложение и вычитание или умножение и деление.
В чём сложность изучения неопределённых интегралов ? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно чёткий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приёмов интегрирования. И, если способ интегрирования изначально подобран неверно, то интеграл нельзя решить.
В первую очередь следует хорошо разобраться в простейших интегралах.
Посмотрим на таблицу интегралов.
Таблица интегралов. Метод интегрирования частями. Как и в производных, видно несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций.
Любой табличный интеграл (и вообще любой неопределённый интеграл) имеет вид:
∫f(x)dx = F(x) + C,
где C = const
Обозначения и термины.
∫ – значок интеграла.
f(x) – подынтегральная функция.
dx – значок дифференциала.
f(x)dx – подынтегральное выражение.
F(x) – первообразная функция.
F(x) + С – множество первообразных функций.
Самое важное, что в любом неопределённом интеграле к ответу приплюсовывается константа С.
– это значит превратить его в определённую функцию
F(x) + С,
пользуясь некоторыми правилами, приёмами и таблицей.
Например, табличный интеграл
превратился в функцию
–cos x + C
Как и
в случае с производными, для того, чтобы научиться находить интегралы, не
обязательно быть в курсе, что такое интеграл, первообразная функция с
теоретической точки зрения.
совсем не обязательно понимать, почему интеграл
превращается именно в
–cos x + C.
Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.
Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно, справедливо следующее:
(F(x) + С)‘ = F‘ (x) + 0 = f(x).
Другими словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.
ПРИМЕР:
Возьмём табличный интеграл:
Убедимся в справедливости
данной формулы.
Для этого возьмём производную от правой части
(–cos x + C)‘ = –(cos x)‘ + (C)‘ = –(– sin x) + 0 = sin x.
Получилась исходная подынтегральная функция.
Теперь стало понятнее, почему к функции F(x) всегда приписывается константа С. При дифференцировании константа всегда превращается в ноль.
Решить неопределённый интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию.
ПРИМЕР:
∫ sin xdx = –cos x + C.
Получается бесконечно много решений, например
–cos x + 5,
–cos x – 4/7,
–cos x + sin 2,
–cos x + е3.
Поэтому записывают коротко
∫ sin xdx = –cos x + C.
где С – const.
Таким образом, любой неопределённый интеграл можно легко проверить в отличии от производных.
ПРИМЕР:
Найти неопределённый интеграл. РЕШЕНИЕ: ПРИМЕР:
Найти неопределённый интеграл:
РЕШЕНИЕ: ПРИМЕР:
Найти неопределённый интеграл:
Анализируя интеграл, видно, что имеется
произведение двух функций и возведения в степень целого выражения. Так как нет
хороших и удобных формул для интегрирования произведения и частного надо
попытаться преобразовать подынтегральную функцию в сумму.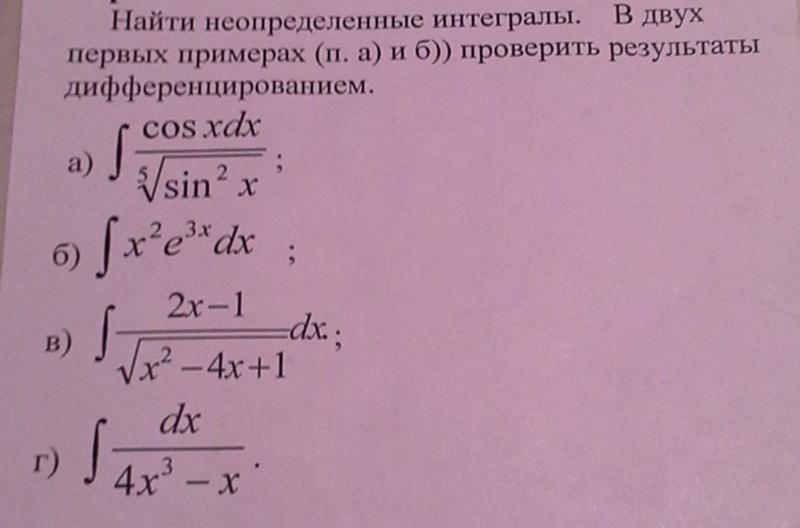
ПРИМЕР:
Найти неопределённый интеграл. РЕШЕНИЕ:
Используем формулу сокращённого умножения.
Найти неопределённый интеграл:
РЕШЕНИЕ:
В данном примере подынтегральная функция
представляет собой дробь. Когда в подынтегральном выражении дробь, то сначала
необходимо попытаться избавиться от этой дроби или упростить её. Сначала делим
числитель на знаменатель. ПРИМЕР:
Найти неопределённый интеграл:
РЕШЕНИЕ:
§ 2 Методы интегрирования
Рассмотрим три
основных метода интегрирования: метод
непосредственного интегрирования;
метод замены переменной, метод
интегрирования по частям.
1) Метод непосредственного интегрирования.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием, а также на свойстве 4, 5 неопределенного интеграла. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Пример 2.1. Требуется найти значение интеграла . На основе известной формулы дифференцирования можно сделать вывод, что искомый интеграл равен , где – некоторое постоянное число. Однако, с другой стороны . Таким образом, окончательно можно сделать вывод:
.
Пример 2.2. Требуется найти интеграл .
Решение.
При вычислении данного интеграла были использованы 1 и 2 формулы табличных интегралов.
Пример 2.3. Требуется найти интеграл .
Решение.
Пример 2.4. Требуется найти интеграл .
Решение. Подынтегральная функция представляет собой неправильную рациональную дробь. Необходимо числитель разделить на знаменатель по правилу деления многочленов (это правило подробным образом рассматривается далее в разделе «Интегрирование рациональных дробей»).
.
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец, определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода
непосредственного интегрирования, то
он применим только для некоторых весьма
ограниченных классов функций. Функций,
для которых можно с ходу найти первообразную
очень мало. Поэтому в большинстве случаев
применяются способы, описанные ниже.
2) Метод замены переменных или метод подстановки. Данный метод основан на следующей теореме.
Теорема 2.1. Если первообразная функции , а – дифференцируемая функция, то функция также имеет первообразную, причем .
Доказательство.
По правилу дифференцирования сложной функции
, т.е. функция имеет в качестве одной из своих первообразных функцию . Следовательно, , что и требовалось доказать.
Поскольку , то
. (2.1)
По формуле (1.2.1) осуществляется замена переменной в неопределенном интеграле.
Пример 2.5. Найти неопределенный интеграл .
Решение.
Сделаем замену . Тогда данный интеграл сводится к интегралу .
Пример 2.6. Найти неопределенный интеграл .
Решение.
Замена Получаем:
.
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.
3) Метод интегрирования по частям.
Метод основан на следующей формуле:
(2.
2)
Поскольку или . Проинтегрировав обе части последнего равенства и применив свойства неопределенного интеграла, получим требуемую формулу .
Формула интегрирования по частям позволяет находить интегралы многих элементарных функций. Она применяется к интегрированию выражений, которые можно так представить в виде произведения двух сомножителей и , чтобы отыскание функции по ее дифференциалу и вычисление интеграла составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла . Умение разбивать разумным образом данное подынтегральное выражение на множители и вырабатывается в процессе решения задач. Мы покажем на ряде примеров как применяется данный метод.
Пример 2.7. Найти неопределенный интеграл .
Решение.
.
Замечание 2.1. При определении функции
по дифференциалу
мы можем брать любую произвольную
постоянную, так как в конечный результат
она не входит (что легко проверить,
подставив в равенство (2.
2) вместо
выражение ).
Поэтому удобно считать эту постоянную
равной нулю.
Метод интегрирования по частям применяется, как правило, при нахождении интегралов следующего вида:
, ,
, .
Также этот метод применяется к интегралам, содержащим некоторые обратные тригонометрические функции такие как .
Пример 2.8. Вычислим следующие неопределенные интегралы:
1)
.
2)
.
3)
= .
4)
.
5)
.
6) Рассмотрим так называемые «круговые интегралы», которые находятся дважды интегрированием по частям.
.
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства. В результате имеем:
.
.
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным интегралам. Среди них рассмотрим применение частного случая метода подстановки – «внесение функции под знак дифференциала».
Пример 2.9. Вычислим следующие неопределенные интегралы:
1)
.
2)
.
3)
.
4)
.
5)
.
Метод внесения функции под знак дифференциала был применен в первом, третьем и четвертом случаях примера 9.
Неопределенные интегралы – Photomath
Исследуйте Интегралы
Производные? Был там. Поиск производных? Сделано это.
А как же интегралы? Как насчет нахождения неопределенных интегралов?
Не волнуйтесь — вы у нас есть.
Что такое неопределенный интеграл?
Пусть $$f(x)$$ — функция.
Первообразной $$f(x)$$ является любая функция $$F(x)$$ такая, что:
$$F'(x) = f(x)$$
Так как первообразных много одной функции, неопределенный интеграл от f дает нам все свои первообразные:
$${\int f(x) dx = F(x) + C}$$
где $$C$$ — любая константа, называемая константой интегрирования.
Хммм, ладно, но как нам найти этот интеграл?
Используем свойства и правила интегралов!
Свойства интегралов используются для упрощения процесса интегрирования путем разделения процедуры на несколько шагов. Вот список всех свойств и правил, которые вы захотите держать под рукой:
| Постоянное кратное интегралов | $$\int{(c\times f(x))}dx=c\times \int{f(x)}dx$$ |
| Правило сумм для интегралов | $$\int{(f(x) + g(x))}dx=\int{f(x)}dx + \int{g(x)}dx$$ |
| Правило сумм для интегралов | {\ простое число} (t) dt = \ int {f (x)} dx $ $|
| Интеграция по частям | $$\int{u}dv=uv-\int{v}du$$ |
Почему неопределенный интеграл так полезен?
Нахождение неопределенного интеграла — своего рода «первый шаг» во многих математических вычислениях, например, при решении дифференциальных уравнений или даже при нахождении определенного интеграла! 92}+C, C\in \mathbb{R}$$
Отличная работа!
Вы можете применить этот процесс к любой проблеме, которую выберете.
Просто помните об этих шагах:
Резюме исследования
- Упростите выражение, если это возможно.
- Используйте свойства интеграла.
- Оцените интеграл. 9{4x}}{4}+C, C \in \mathbb{R}$$
- Антипроизводная равна
- Антипроизводная от равна
Нужна помощь? Были здесь! Просто отсканируйте проблему с помощью приложения Photomath, и мы поможем вам выполнить каждый шаг.
Вот краткий обзор того, что вы увидите:
/
Есть домашнее задание по математике?
Зайдите в приложение Photomath, чтобы быстро найти пошаговые решения всех ваших математических задач.
Неопределенные интегралы — исчисление 2
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 … 25 26 Следующая →
Исчисление 2 Помощь » Интегралы » Нахождение интегралов » Неопределенные интегралы
Решите:
Возможные ответы:
Правильный ответ:
Пояснение:
Неопределенный интеграл можно разбить на два отдельных интеграла.
Вычислите каждый интеграл.
Ответ на первый интеграл:
Будьте осторожны, так как ответ на не так как это производная от . Чтобы решить этот интеграл, нам нужно будет использовать интегрирование по частям.
Если мы позволим, то получим путем дифференцирования, а если позволим, то получим путем интегрирования. Константу можно добавить в конце задачи.
Напишите формулу интегрирования по частям.
Подставьте члены в формулу.
Упростите члены внутри интеграла и оцените.
Ответ на второй интеграл:
Объедините два ответа. Константы могут быть объединены в один постоянный термин в конце.
Ответ:
Сообщить об ошибке
Оценка:
Возможные ответы:
Правильный ответ:
Объяснение:
В этом интеграле необходимо заменить оба термина и .
Если допустим , то .
Дифференциация относительно .
Подставим все члены обратно в интеграл.
Термин также совпадает с , который может быть умножен в скобках. Упростите интеграл.
Вычислите этот интеграл.
Замена .
Ответ:
Сообщить об ошибке Объяснение:
Знаменатель неприводим, а это значит, что мы не можем использовать частичные дроби для определения коэффициентов разделимых дробей. Единственный метод, который мы можем использовать, — это завершить квадрат и использовать тождество обратной тригонометрии.
Заполните квадрат знаменателя. Это делается путем возведения в квадрат половины среднего члена, а затем вычитания этой цифры в конце.
Разложите параболическую функцию в скобках и упростите.
Перепишите интеграл и вытащите шестерку перед интегралом.
Запишите интегральное свойство арктангенса.
По этому правилу подставляем термины и упрощаем, чтобы получить термины и .
Подставьте члены и в правило арктангенса.
Рационализируйте знаменатель коэффициента.
Если подставить это обратно в исходный интеграл, это означает, что:
Не забудьте умножить шесть, которая находится вне интеграла.
Ответ:
Сообщить об ошибке
Найти интеграл от
Возможные ответы:
Правильный ответ:
Объяснение:
Упрощение:
Интеграция:
Отчет о ошибке
Возможные ответы:
Правильный ответ:
.
Объяснение:
Использование Интеграция по частям:
=
Сообщить об ошибке. Объяснение:
Чтобы найти неопределенный интеграл, мы используем правило обратной степени, которое гласит:
Для задачи в этом вопросе:0003
Найдите неопределенный интеграл. Объяснение:
Поскольку интегрирование является линейной операцией, мы можем антидифференцировать функцию почленно.
Мы используем свойства, которые
решить неопределенный интеграл
Сообщить об ошибке
Вычислить следующий интеграл:
Возможные ответы:
Правильный ответ:
2 9 Пояснение:Чтобы проинтегрировать, мы должны проинтегрировать по частям, по формуле
Теперь выбираем наши u (из которых получаем du) и dv (из которых получаем v):
Правила вывода и интегрирования:
,
(Обратите внимание, что мы не включаем константу интегрирования.
)
Используйте приведенную выше формулу и проинтегрируйте:
Интегрирование было выполнено по тому же правилу, что и выше.
Сообщить об ошибке
Вычислить неопределенный интеграл.
Возможные ответы:
Ни один из других ответов
Правильный ответ:
Объяснение:
Этот интеграл можно вычислить с помощью разложения на неполные дроби следующим образом.
. Старт
. Полностью факторизовать знаменатель.
Теперь используйте метод разложения на неполные дроби
Умножьте обе части на и упростите.
Распределить .
Приравняв подобные коэффициенты, мы можем переписать приведенное выше в виде системы уравнений
Решая эту систему уравнений любым способом, получаем .