Как находится мгновенная скорость: Мгновенная и средняя скорость

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Определение 1

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

Определение 2

Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ=∆r∆t; υ↑↑∆r.

Рисунок 1. Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется υ=S∆t.

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Определение 3

Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:

υ=lim∆t∆r∆t=drdt=r˙.

Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.

Рисунок 2. Вектор мгновенной скорости υ

Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:

υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.

Слишком сложно?

Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ=υ=υx2+υy2+υz2=x2+y2+z2.

Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:

υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.

Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:

υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.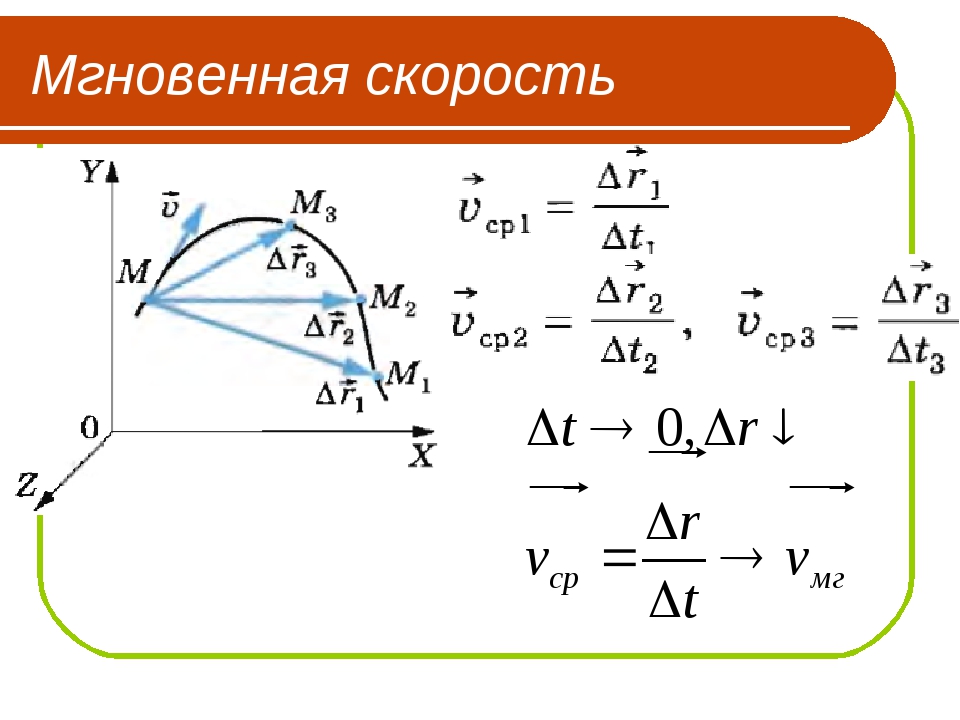

Определение 4

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt

Пример 1

Дан закон прямолинейного движения точки x(t)=0,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ(t)=x˙(t)=0.3t-2; υ(10)=0.3×10-2=1 м/с.

Ответ: 1 м/с.

Пример 2

Движение материальной точки задается уравнением x=4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ(t)=x˙(t)=4-0,1t.

4-0,1t=0;tост=40 с;υ0=υ(0)=4;υ=∆υ∆t=0-440-0=0,1 м/с.

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м/с.

Мгновенная и средняя скорость | Физика

1. Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.

Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).

Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.

Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координаты от времени

На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.

Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).

Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела.

(Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих задачах используют среднюю скорость, связанную с пройденным путем:

v_ср = l/t.     (1)

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

v_ср = (l₁ + l₂)/(t₁ + t₂),     (2)

где l₁ и t₁ – путь и время для первого участка, а l₂ и t₂ – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?

? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂.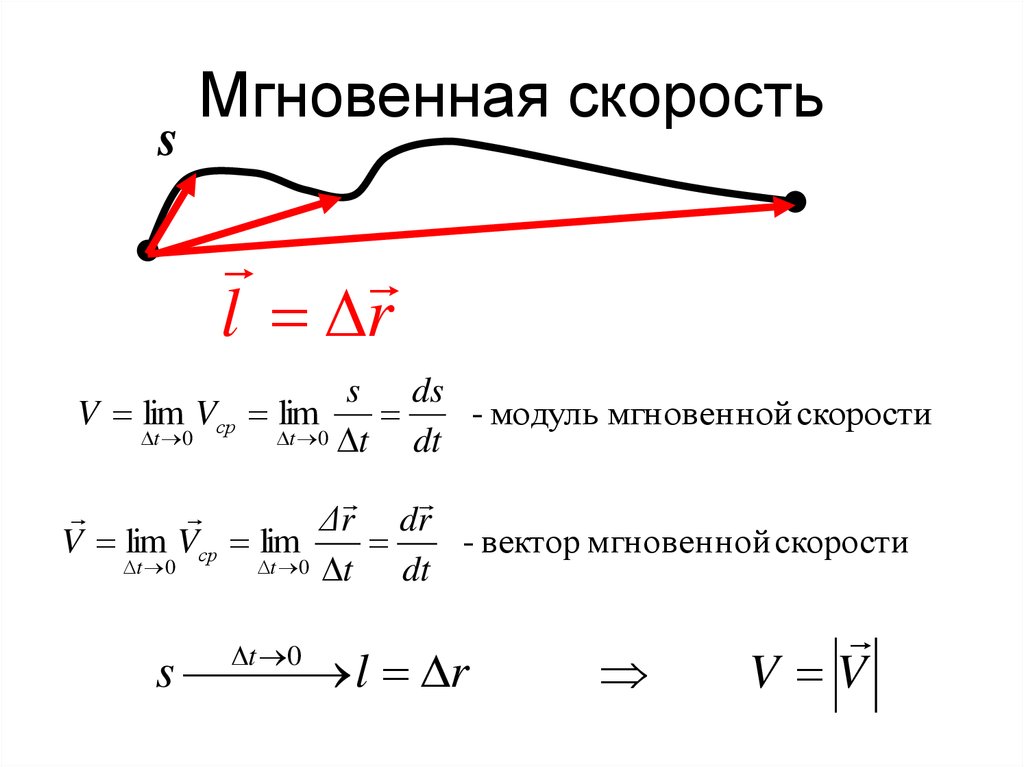 Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l₁ и l₂.

? 8. Выразите через v₁, v₂ и t:
a) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

? 9. Выразите через v₁, v₂ и l:
а) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.

? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

? 11. На первом участке пути тело двигалось со скоростью v₁, а на втором – со скоростью v₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v₁ и v₂?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v₁, а оставшееся время – со скоростью v₂.
а) Выразите пройденный поездом путь через v₁, v₂ и все время движения t.
б) Выразите среднюю скорость поезда через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 60 км/ч, v₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью v₁, а оставшийся участок пути – со скоростью v₂.
а) Выразите все время движения автомобиля через v₁, v₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 80 км/ч, v₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t².
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.

Мгновенная скорость

Средняя скорость

Если тело перемещается неравномерно, то описывая его движение в качестве одного из параметров можно воспользоваться средней скоростью движения на отдельных отрезках пути. Но такое описание дает очень приближенную, грубую характеристику перемещения. Поскольку находя средние скорости, мы проводим замену неравномерного движения на движение с постоянной скоростью на избранных отрезках пути, думая, что скорость изменяется скачкообразно при переходе от одного отрезка времени к другому. Графиком пути, отражающем перемещение тела, с постоянной скоростью, отличающейся на разных временных отрезках, станет ломаная линия, имеющая звенья с различным наклоном.

Допустим, что материальная точка перемещается вдоль прямой линии, которая не совпадает с осями координат. При этом ее положение определяет радиус- вектор $\vec r_1$, соответствующий моменту времени $t_1$. В момент времени $t_2$ положение материальной точки в пространстве определяет вектор $\vec r_2$.

Вектор перемещения нашей материальной точки определим как:

$\Delta \vec r=\vec r_2-\vec r_1(1).$

Определение 1

Средняя скорость материальной точки будет определена выражением:

$ \vec v_{sr}=\frac{\Delta \vec r}{\Delta t}=\frac{\vec r_2-\vec r_1}{t_2-t_1}(2).$

Из формулы (2) видно, что в ней происходит деление вектора на скаляр, в результате мы имеем вектор, направление которого совпадает с направлением вектора перемещения.

Векторы скорости и перемещения обладают одинаковыми направлениями.

Переход от средней скорости к мгновенной скорости

В выражении (2) средняя скорость найдена для отрезка времени, равного $\Delta t$. Разделим данный временной отрезок на более мелкие. Если материальная точка перемещается неравномерно, то вновь найденные средние скорости будут отличаться, от средней скорости для всего отрезка $\Delta t$. Уменьшим временной отрезок $\Delta t$, станут меньше и отрезки времени внутри него. Средние скорости в уменьшенных промежутках времени будут отличаться от средней скорости на всем отрезке времени, но величина различия станет меньше.

Устремим рассматриваемый промежуток времени к нулю (∆t→0), средняя скорость при этом устремится к предельному значению, которое называют мгновенной скоростью.

Определение 2

Мгновенной скоростью или скоростью в данный момент времени называют векторную величину, равную:

$\vec v(t)= \frac {d\vec r}{dt}(3).$

Если тело перемещается равномерно, то мгновенная скорость его движения в каждый момент времени совпадает со скоростью этого движения. Говорят, что мгновенная скорость равномерного движения является постоянной.

Мгновенная скорость неравномерного перемещения – это переменный параметр, который принимает разные значения для разных моментов времени. При этом мгновенную скорость можно считать изменяющейся непрерывно на всем отрезке времени, на котором рассматривается движение.

Мгновенную скорость в каждый момент времени можно определить как тангенс угла наклона касательной к кривой – траектории движения в рассматриваемой точке.

Компоненты вектора мгновенной скорости в декартовой системе координат

В декартовой системе координат радиус-вектор запишем как:

$\vec r(t)=x(t)\vec i+y(t)\vec j+z(t)\vec k (4)$,

принимая во внимание, что единичные орты ($\vec i ; \vec j; \vec k$) не изменяются во времени, и используя определение мгновенной скорости (3), получаем:

$\vec v(t)=\frac{dx}{dt}\vec i+\frac{dy}{dt}\vec j+\frac{dz}{dt}\vec k (5). 2 (9).$

Направление мгновенной скорости

Будем описывать движение материальной точки через параметры траектории. При этом нам известны траектория движения точки и связь пути ($s$) и времени $t$. Путь отмеряется по траектории, от точки траектории, которую мы принимаем за начальную. При этом любая точка траектории характеризуется собственной величиной $s$. Из сказанного выше следует, что радиус-вектор – это функция от $s$, траекторию зададим уравнением:

$\vec r = \vec r(s)(10)$.

Получаем, что в определении мгновенной скорости (3) мы можем считать радиус – вектор как сложную функцию ($\vec r(s(t))$). При этом ее производную найдем, применяя правило дифференцирования сложной функции:

$\vec v=\frac{d\vec r}{dt}=\frac{d\vec r}{ds}\frac{ds}{dt}(11)$,

где по определению мгновенной скорости ее величина равна: $v=\frac{ds}{dt}$.

Обозначим $\Delta s$ – расстояние между парой точек по траектории; $|\Delta \vec r|$– расстояние между рассматриваемыми точками по кратчайшему расстоянию (прямой). При сближении наших точек разница между $\Delta s$ и $|\Delta \vec r|$ уменьшается, запишем:

$\frac{d\vec r}{ds}=\lim_{\Delta s\to 0} (\frac {\Delta \vec r}{\Delta s})=\lim_{\Delta s\to 0}(\frac{\Delta \vec r}{|\Delta r|}\frac {|\Delta r|}{\Delta s})=\vec \tau (12).$

где $\vec \tau$ – единичный вектор, являющийся касательным к траектории движения точки.

Принимая во внимание сказанное выше выражение (12) для мгновенной скорости можно записать как:

$\vec v=v\vec \tau$(13).

Из формулы (13) становится очевидно, что мгновенная скорость направлена по касательной к траектории движения материальной точки.

Рассматривая направления мгновенной скорости движения материальной точки подчеркнем, что:

1. Мгновенная скорость материальной точки перемещающейся по прямой – это вектор, который направлен по траектории ее движения.
2. При перемещении материальной точки по криволинейной траектории вектор мгновенной скорости имеет направление по касательной к траектории движения точки.

Скорость при равнопеременном движении

Самым простым способом неравномерного движения является равнопеременное перемещение тела, движение с постоянным ускорением. Это движение бывает:

• равноускоренным, если скорость и ускорение имеют одинаковые направления, при этом величина скорости увеличивается;
• равнозамедленное, при противоположном направлении скорости и ускорения, в этом случае скорость по модулю уменьшается.

При равнопеременном движении скорость в любой момент времени можно вычислить, если использовать выражение:

$\vec v(t)=\vec v_0+\vec a \bullet t (14),$

где $\vec v_0$ – начальная скорость движения точки; $\vec a$ – постоянное ускорения точки.

1. Мгновенная скорость.

Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:

Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.

2. Средняя скорость.

Средней скоростью на некотором участке называется величина равная отношению перемещения к промежутку времени, за который это перемещение произошло.

3. Угловая скорость. Формула. СИ.

Угловой скоростью называется векторная физическая величина равная первой производной угла поворота тела по времени. [рад/с]

4. Связь угловой скорости с периодом вращения.

Равномерное вращение характеризуется периодом вращения и частотой вращения.

5. Угловое ускорение. Формула. СИ.

Это физическая величина равная первой производной угловой скорости или второй производной угла поворота тела по времени. [рад/с²]

6. Как направлен вектор угловой скорости/углового ускорения.

Вектор угловой скорости направлен по оси вращения причем так чтобы вращение рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки(правило правой руки).

При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.

7/8. Связь между нормальным ускорением и угловой скоростью/Связь между тангенциальным и угловым ускорением.

9. Что определяет и как направлена нормальная составляющая полного ускорения? Нормальное ускорение СИ.Нормальное ускорение определяет быстроту изменения скоро-сти по направлению и направлено к центру кривизны траектории.

В СИ нормальное ускорение [м/с²]

10. Что определяет и как направлена тангенциальная составляющая полного ускорения.

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

11. Тангенциальное ускорение в СИ.

м/с²

12. Полное ускорение тела. Модуль этого ускорения.

13. Масса. Сила. Законы Ньютона.

Масса − это физическая величина, являющаяся мерой инерционных и гравитационных свойств тела. Единицей массы в СИ [m] = кг.

Сила − это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение. Единица измерения силы в СИ – Ньютон; кг*м/с²

Первый закон Ньютона (или закон инерции): если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.

Второй закон Ньютона: ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе. Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основным уравнением динамики поступательного движения.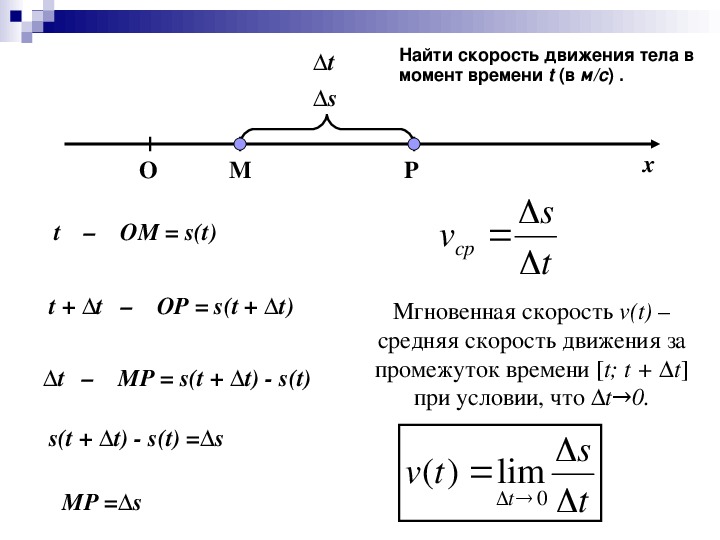

Третий закон Ньютона: сила, с которой одно тело действует на другое, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

Новые камеры – за среднюю скорость, но вне закона :: Autonews

Национальная любовь к быстрой езде может остаться в прошлом. ГИБДД собирается бороться с пробками новыми радикальными методами. В декабре на трассах Подмосковья появится 50 новых комплексов видеофиксации «Автодория». В отличие от уже использующихся камер, измеряющих мгновенную скорость автомобиля, «Автодория» будет фиксировать среднюю. И если она окажется выше разрешенной на данном участке, водителя ждет штраф.

До сих пор человеку за рулем с переменным успехом удавалось обходить запреты и ограничения. Раньше моргали фарами встречные машины предупреждая засадах «гаишников». Затем в салонах автомобилей запищали антирадары. Еще через несколько лет, в эпоху первого поколения навигаторов, у водителей появилась возможность самостоятельно «забивать» все опасные места в память электронного штурмана. Сегодня навигационное приложение в смартфоне буквально сжирает батарейку, ежеминутно оповещая сообщениями от других автолюбителей о стационарных и мобильных комплексах мгновенного измерения скорости, только успевай жать на тормоз. Новые камеры, возможно, лишат автомобилистов шанса уйти от наказания, вот только пока что они находятся вне правового поля.

Полевые испытания «Автодория» проходила в Татарстане. На участках дорог протяженностью от 500 метров до 10 километров устанавливались две камеры, фиксирующие координаты, время проезда автомобиля и его госномер. Принцип работы новой системы «Автодория» примитивен, но так же действенен. Проехал, к примеру, по федеральной трассе 90 километров из точки «А» в точку «Б» быстрее, чем за час – жди «письма счастья».

Разработчики системы уверены, с ее появлением аварийность на дорогах страны резко снизится. Меньше станет и опасных ситуаций в зоне «ответственности» обычных камер, где водители для снижения скорости нередко применяют экстренное торможение.

Внедрение системы «косвенной» фиксации нарушений активно обсуждается в интернете. У «Автодории» есть как и свои сторонники, так и ярые противники. Координатор «Синих Ведерок» Петр Шкуматов, к примеру, считает, что установка таких систем в местах, где происходят самые тяжелые аварии: тоннелях, мостах и эстакадах резко снизит количество пострадавших и погибших в ДТП. И опыт многих европейских стран, где аналоги «Автодории» действуют, подтверждает это.

В самой же ГИБДД, как ни парадоксально, к появлению новой системы относятся с меньшим энтузиазмом, напоминая, что комплексы фиксации средней скорости в той же Франции, Италии и Великобритании обычно дублируются традиционными камерами, измеряющими мгновенную скорость автомобиля. Кроме того, наказывают за превышение средней скорости далеко не во всех странах Европы. В частности, в Германии камеры «средней скорости» хоть и выпускаются (на экспорт), но законодательно запрещены. Здесь считается, что по направлению движения автомобиля на определенном участке можно понять, куда направляется его водитель, а это уже вмешательство в личную жизнь.

Впрочем, и в России «средняя скорость» пока вне законодательных норм. Такого понятия попросту не существует. А чтобы его ввести, необходимо подготовить целый комплекс поправок в ПДД и КоАП, утверждает председатель «Движения автомобилистов России» Виктор Похмелкин. По его мнению, в рамках действующего законодательства, чтобы оштрафовать человека, необходимо точно указать: где, когда и какое конкретно он совершил административное правонарушение. Иначе, если дело дойдет до суда, штрафные квитанции такого рода можно будет просто выбросить.

Сергей Канаев, директор Национального общественного центра безопасности движения, видит в установках систем фиксации средней скорости нерациональное использование бюджетных средств. По его мнению, даже на участках, где эти системы установлены, лихачи найдут возможность и превысить скорость, и создать аварийную ситуацию. «Что такое «средняя скорость»? Значит, можно гнать и сайгачить между рядами, а потом банально остановиться на обочине – и вот гонщика уже не накажут, время будет «средним». А на участках, где стоят обычные камеры – просто приятно ехать: никто не гоняет», – отметил Сергей Канаев.

Впрочем, помимо юридической казуистики, повсеместному законному внедрению «Автодории» мешают и технические проблемы. Свое местоположение система определяет посредством навигационного оборудования ГЛОНАСС, а значит, рассчитывает расстояние по кратчайшей траектории. Использовать «Автодорию» на участках дороги с поворотами нельзя.

Алексей Матвеев

КИНЕМАТИКА • Большая российская энциклопедия

КИНЕМА́ТИКА (от греч. ϰίνημα, род. п. ϰινήματος – дви­же­ние), раз­дел ме­ха­ни­ки, в ко­то­ром опи­сы­ва­ют­ся гео­мет­рич. ха­рак­те­ри­сти­ки дви­же­ния ме­ха­ни­че­ско­го – дви­же­ния ма­те­ри­аль­ных то­чек и их сис­тем, аб­со­лют­но твёр­дых тел и т. д. Со­от­вет­ст­вен­но вы­де­ля­ют раз­де­лы К.: К. ма­те­ри­аль­ной точ­ки, К. сис­те­мы то­чек, К. твёр­до­го те­ла и т. д.

Осн. по­ня­тия К. (мгно­вен­ная ско­рость и мгно­вен­ное ус­ко­ре­ние ма­те­ри­аль­ной точ­ки) бы­ли вве­де­ны Г.  Га­ли­ле­ем в фун­дам. тру­де «Бе­се­ды и ма­те­ма­тич. до­ка­за­тель­ст­ва, ка­саю­щие­ся двух но­вых от­рас­лей нау­ки, от­но­ся­щих­ся к ме­ха­ни­ке и ме­ст­но­му дви­же­нию» (1638). Га­ли­лей по­лу­чил стро­гие ма­те­ма­тич. за­ко­ны К. на ос­но­ве обоб­ще­ния экс­пе­рим. дан­ных, ус­та­но­вил прин­цип от­но­си­тель­но­сти (см. Га­ли­лея прин­цип от­но­си­тель­но­сти). Х. Гюй­генс (1672) кон­кре­ти­зи­ро­вал прин­ци­пы и по­ня­тия К., вве­дён­ные Га­ли­ле­ем. Ра­бо­ты Гюй­ген­са по­слу­жи­ли ба­зой для соз­да­ния ме­ха­ни­ки И. Нью­то­на (1687). В 1765 Л. Эй­лер за­ло­жил ос­но­вы К. твёр­до­го те­ла. В нач. 19 в. Г. Ко­рио­лис дал окон­ча­тель­ную фор­му­ли­ров­ку тео­рии от­но­си­тель­но­го дви­же­ния. С сер. 19 в. К. на­ча­ла ак­тив­но ис­поль­зо­вать­ся для опи­са­ния пре­об­ра­зо­ва­ния дви­же­ния в ме­ха­низ­мах и вы­де­ли­лась в са­мо­стоя­тель­ный раз­дел тео­ре­тич. ме­ха­ни­ки.

Кинематика материальной точки

Дви­же­ние ма­те­ри­аль­ной точ­ки опи­сы­ва­ет­ся по от­но­ше­нию к вы­бран­ной сис­те­ме ко­ор­ди­нат $Oxyz$. 2\}$. Кро­ме пря­мо­уголь­ных ко­ор­ди­нат ($x,y,z$) в К. для опи­са­ния дви­же­ния точ­ки ис­поль­зу­ют­ся так­же и кри­во­ли­ней­ные ко­ор­ди­на­ты (ци­лин­д­ри­че­ские, по­ляр­ные, сфе­ри­че­ские и т. п.).

Гео­мет­рич. ме­сто по­сле­до­ва­тель­ных по­ло­же­ний точ­ки в про­цес­се её дви­же­ния на­зы­ва­ет­ся тра­ек­то­ри­ей. Со­от­но­ше­ние $\boldsymbol r=\boldsymbol r(t)$ пред­став­ля­ет со­бой па­ра­мет­рич. фор­му урав­не­ния тра­ек­то­рии как не­ко­то­рой кри­вой в про­стран­ст­ве. За­кон дви­же­ния ма­те­ри­аль­ной точ­ки мо­жет быть так­же оп­ре­де­лён фор­мой тра­ек­то­рии, её по­ло­же­ни­ем в про­стран­ст­ве, по­ло­же­ни­ем на­чаль­ной точ­ки $O$ на тра­ек­то­рии и по­ло­жи­тель­ным на­прав­ле­ни­ем от­счё­та ду­го­вой ко­ор­ди­на­ты $s$ от на­чаль­ной точ­ки до её те­ку­ще­го зна­че­ния.

Урав­не­ние $s=s(t)$ оп­ре­де­ля­ет за­кон дви­же­ния точ­ки по тра­ек­то­рии. Ско­рость ма­те­ри­аль­ной точ­ки рав­на $\boldsymbol v=\boldsymbol \tau ds/dt$, где $\boldsymbol \tau$  – еди­нич­ный век­тор ка­са­тель­ной к тра­ек­то­рии в не­ко­то­рой точ­ке $M$.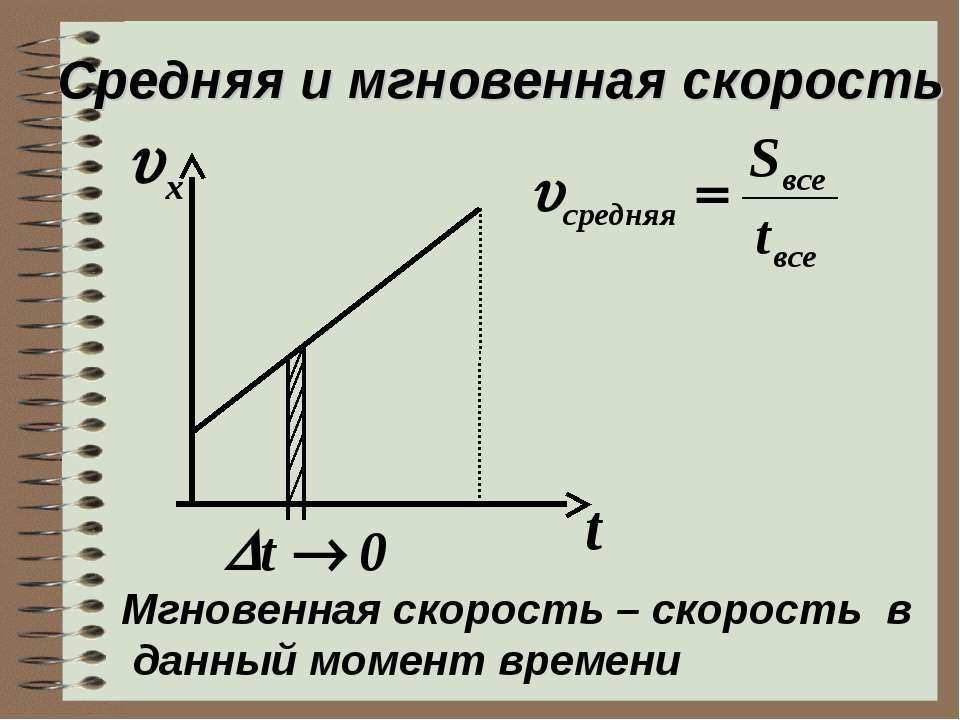 2/R$. Здесь пол­ное ус­ко­ре­ние точ­ки пред­став­ле­но в ви­де сум­мы двух вза­им­но ор­то­го­наль­ных век­то­ров – ка­са­тель­но­го ус­ко­ре­ния $\boldsymbol w_\tau$ (пер­вое сла­гае­мое) и цен­тро­ст­ре­ми­тель­но­го ус­ко­ре­ния $\boldsymbol w_n$ (вто­рое сла­гае­мое), на­прав­лен­но­го вдоль глав­ной нор­ма­ли к тра­ек­то­рии в сто­ро­ну цен­тра кри­виз­ны, от­стоя­ще­го от точ­ки $M$ на рас­стоя­ние $R$. Про­ек­ция век­то­ра ус­ко­ре­ния на би­нор­маль все­гда рав­на ну­лю.

Для тра­ек­то­рии, пред­став­ляю­щей со­бой пря­мую, в лю­бой её точ­ке рас­стоя­ние $R= \infty$; та­кое дви­же­ние ма­те­ри­аль­ной точ­ки на­зы­ва­ет­ся пря­мо­ли­ней­ным. Ес­ли ве­ли­чи­на ско­ро­сти ма­те­ри­аль­ной точ­ки ос­та­ёт­ся по­сто­ян­ной $[v(t)=\text {const} \neq0]$, то та­кое её дви­же­ние на­зы­ва­ет­ся рав­но­мер­ным. Ес­ли ка­са­тель­ное ус­ко­ре­ние точ­ки по­сто­ян­но $(dv(dt)=\text {const} \neq0)$, то та­кое дви­же­ние на­зы­ва­ет­ся рав­но­ус­ко­рен­ным.

Путь, прой­ден­ный точ­кой в её дви­же­нии вдоль тра­ек­то­рии, оп­ре­де­ля­ет­ся как ин­те­грал по вре­ме­ни от мо­ду­ля ско­ро­сти. Ве­ли­чи­на пу­ти мо­но­тон­но воз­рас­та­ет, в то вре­мя как ко­ор­ди­на­та точ­ки мо­жет то воз­рас­тать, то умень­шать­ся. Напр., при не­за­ту­хаю­щих ко­ле­ба­ни­ях ма­те­ма­тич. ма­ят­ни­ка путь ко­леб­лю­щей­ся ма­те­ри­аль­ной точ­ки не­пре­рыв­но воз­рас­та­ет, а её ду­го­вая ко­ор­ди­на­та при­ни­ма­ет зна­че­ния, ог­ра­ни­чен­ные ам­пли­ту­дой $A$ ко­ле­ба­ний (от $-A$ до $+A$).

Кинематика относительного движения

Сис­те­ма ко­ор­ди­нат $Oxyz$, от­но­си­тель­но ко­то­рой рас­смат­ри­ва­ет­ся дви­же­ние ма­те­ри­аль­ной точ­ки $M$, мо­жет быть свя­за­на с не­ко­то­рым те­лом, ко­то­рое са­мо дви­жет­ся от­но­си­тель­но не­под­виж­ной сис­те­мы $Ox_1y_1z_1$. В этом слу­чае ско­рость и ус­ко­ре­ние точ­ки $M$ от­но­си­тель­но сис­те­мы $Oxyz$ на­зы­ва­ют от­но­си­тель­ны­ми и обо­зна­ча­ют со­от­вет­ст­вен­но $\boldsymbol v_{отн}$ и $\boldsymbol w_{отн}$. Дви­же­ние той же ма­те­ри­аль­ной точ­ки от­но­си­тель­но сис­те­мы $Ox_1y_1z_1$ на­зы­ва­ют аб­со­лют­ным, его ско­рость и ус­ко­ре­ние обо­зна­ча­ют $\boldsymbol v_{абс}$ и $\boldsymbol w_{абс}$. При от­сут­ст­вии от­но­си­тель­но­го дви­же­ния $(v_{отн}=0)$ точ­ка $M$ пе­ре­но­сит­ся дви­жу­щим­ся те­лом, с ко­то­рым свя­за­на сис­те­ма $Oxyz$, и её ско­рость сов­па­да­ет со ско­ро­стью $\boldsymbol v_{пер}$ той точ­ки $N$ те­ла, в ко­то­рой в дан­ный мо­мент на­хо­дит­ся точ­ка $M$: $\boldsymbol r_N(t)=\boldsymbol r_M(t)$, но не то­ж­де­ст­вен­но (т. к. речь идёт о не­за­ви­си­мых точ­ках). Век­тор $\boldsymbol v_{пер}=d \boldsymbol r_N/dt$ на­зы­ва­ет­ся пе­ре­нос­ной ско­ро­стью или ско­ро­стью пе­ре­нос­но­го дви­же­ния. Фор­му­ла $\boldsymbol v_{абс}=\boldsymbol v_{отн}+ \boldsymbol v_{пер}$ вы­ра­жа­ет т. н. тео­ре­му сло­же­ния ско­ро­стей. Ус­ко­ре­ние точ­ки $N$ на­зы­ва­ют пе­ре­нос­ным и обо­зна­ча­ют $\boldsymbol w_{пер}$. Сло­же­ние ус­ко­ре­ний опи­сы­ва­ет­ся тео­ре­мой Ко­рио­ли­са: $\boldsymbol w_{абс}=\boldsymbol w_{отн}+ \boldsymbol w_{пер}+ \boldsymbol w_{Кор}$. Здесь до­пол­ни­тель­ное сла­гае­мое $\boldsymbol w_{Кор}$ (Ко­рио­ли­са ус­ко­ре­ние) воз­ни­ка­ет в том слу­чае, ес­ли сис­те­ма $Oxyz$ вра­щает­ся от­но­си­тель­но сис­те­мы $O_1x_1y_1z_1$: $\boldsymbol w_{Кор}=2[\boldsymbol \omega, \boldsymbol v_{отн}]$, где $\boldsymbol \omega$  – век­тор уг­ло­вой ско­ро­сти под­виж­ной сис­те­мы ко­ор­ди­нат.

Кинематика систем связанных точек и тел

Ма­ши­ны, ме­ха­низ­мы и др. объ­ек­ты тех­ни­ки час­то мо­де­ли­ру­ют сис­те­мой свя­зан­ных ма­те­ри­аль­ных то­чек и тел (см. Свя­зи ме­ха­ни­че­ские). В сис­те­ме со свя­зя­ми по­ло­же­ния и ско­ро­сти разл. то­чек сис­те­мы не мо­гут быть за­да­ны про­из­воль­но. Пер­вой за­да­чей К. та­ких сис­тем яв­ля­ет­ся фор­ма­ли­за­ция свя­зей, ко­то­рые за­пи­сы­ва­ют в ви­де урав­не­ний свя­зей – пол­но­го на­бо­ра не­за­ви­си­мых со­от­но­ше­ний ме­ж­ду ко­ор­ди­на­та­ми то­чек сис­те­мы. Вто­рая за­да­ча К. сис­тем свя­зан­ных то­чек и тел сво­дит­ся к со­кра­ще­нию чис­ла ве­ли­чин, не­об­хо­ди­мых для пол­но­го опи­са­ния дви­же­ния объ­ек­та. Для это­го из об­ще­го чис­ла ве­ли­чин ис­клю­ча­ют те, ко­то­рые вы­ра­жа­ют­ся че­рез дру­гие ве­ли­чи­ны при по­мо­щи урав­не­ний свя­зей. По­след­няя за­да­ча не­ред­ко ре­ша­ет­ся с по­мо­щью под­хо­дя­ще­го вы­бо­ра обоб­щён­ных ко­ор­ди­нат.

Обе за­да­чи К. до­пус­ка­ют не­од­но­знач­ные ре­ше­ния. Из всех ре­ше­ний вы­би­ра­ют­ся та­кие, ко­то­рые по­зво­ля­ют при­дать сис­те­ме диф­фе­рен­ци­аль­ных урав­не­ний дви­же­ния объ­ек­та наи­бо­лее удоб­ную фор­му. В тео­рии ма­шин и ме­ха­низ­мов, кро­ме то­го, не­об­хо­ди­мо свя­зать вход­ные и вы­ход­ные ха­рак­те­ри­сти­ки дви­же­ния (cм. Ки­не­ма­ти­ка ме­ха­низ­мов).

Кинематика твёрдого тела

В этом раз­де­ле К. рас­смат­ри­ва­ют­ся разл. ти­пы дви­же­ний аб­со­лют­но твёр­до­го те­ла. Под аб­со­лют­но твёр­дым те­лом по­ни­ма­ют сис­те­му ма­те­ри­аль­ных то­чек, вза­им­ное по­ло­же­ние ко­то­рых не из­ме­ня­ет­ся. Осн. за­да­ча К. твёр­до­го те­ла – оп­ре­де­ле­ние ско­ро­стей и ус­ко­ре­ний всех его то­чек. 

С гео­мет­рич. точ­ки зре­ния дви­же­ние аб­со­лют­но твёр­до­го те­ла от­но­си­тель­но не­под­виж­ной сис­те­мы ко­ор­ди­нат $O_1x_1y_1z_1$ с на­ча­лом в точ­ке $O_1$ эк­ви­ва­лент­но дви­же­нию свя­зан­ной с этим те­лом сис­те­мы $Oxyz$ с на­ча­лом в про­из­воль­но вы­бран­ной точ­ке $O$ те­ла. По­ло­же­ние те­ла од­но­знач­но оп­ре­де­ля­ет­ся по­ло­же­ни­ем трёх его то­чек, не ле­жа­щих на од­ной пря­мой. По­ло­же­ние трёх то­чек в сис­те­ме $O_1x_1y_1z_1$ за­да­ёт­ся с по­мо­щью де­вя­ти ко­ор­ди­нат, на ко­то­рые на­ло­же­ны три ус­ло­вия по­сто­ян­ст­ва вза­им­ных рас­стоя­ний ме­ж­ду точ­ка­ми. Это со­кра­ща­ет чис­ло не­за­ви­си­мых ве­ли­чин (оп­ре­де­ляю­щих макс. чис­ло сте­пе­ней сво­бо­ды те­ла) до шес­ти. До­пол­нит. ог­ра­ни­че­ния на дви­же­ние те­ла умень­ша­ют чис­ло сте­пе­ней сво­бо­ды и оп­ре­де­ля­ют тип дви­же­ния те­ла. Так, при фик­си­ро­ван­ных ко­ор­ди­на­тах ука­зан­ных то­чек те­ло на­хо­дит­ся в со­стоя­нии по­коя от­но­си­тель­но сис­те­мы $O_1x_1y_1z_1$.

По­сту­па­тель­ное дви­же­ние те­ла. Дви­же­ние твёр­до­го те­ла на­зы­ва­ют по­сту­па­тель­ным, ес­ли ка­ж­дый пря­мо­ли­ней­ный от­ре­зок, со­стоя­щий из то­чек те­ла, пе­ре­ме­ща­ет­ся па­рал­лель­но са­мо­му се­бе. В этом слу­чае оси сис­те­мы ко­ор­ди­нат, свя­зан­ной с те­лом, мож­но рас­по­ло­жить со­на­прав­лен­но осям не­под­виж­ной сис­те­мы. Ско­рость и ус­ко­ре­ние лю­бой точ­ки те­ла рав­ны со­от­вет­ст­вен­но ско­ро­сти и ус­ко­ре­нию точ­ки $O$ (на­ча­ла сис­те­мы ко­ор­ди­нат, свя­зан­ной с те­лом). Точ­ка $O$ мо­жет дви­гать­ся как по пря­мой, так и по пло­ской или про­стран­ст­вен­ной кри­вой. Напр., ва­гон по­ез­да на пря­мом уча­ст­ке пу­ти дви­жет­ся по­сту­па­тель­но и пря­мо­ли­ней­но. Ка­би­на ко­ле­са обо­зре­ния то­же дви­жет­ся по­сту­па­тель­но, но её точ­ки опи­сы­ва­ют ок­руж­но­сти.

Те­ло, дви­жу­щее­ся по­сту­па­тель­но, име­ет три сте­пе­ни сво­бо­ды (столь­ко же, сколь­ко у ма­те­ри­аль­ной точ­ки), для опи­са­ния его дви­же­ния дос­та­точ­но за­дать три не­за­ви­си­мые ко­ор­ди­на­ты.

Вра­ще­ние те­ла во­круг оси. При вра­ща­тель­ном дви­же­нии те­ла свя­зан­ная с ним сис­те­ма ко­ор­ди­нат из­ме­ня­ет свою ори­ен­та­цию от­но­си­тель­но не­под­виж­ной сис­те­мы, т. е. со­вер­ша­ет по­во­рот. Наи­бо­лее про­стой слу­чай вра­ща­тель­но­го дви­же­ния – вра­ще­ния те­ла во­круг не­по­движ­ной оси. 2_N/R_N$.

Дан­ный раз­дел К. твёр­до­го те­ла ис­поль­зу­ют для опи­са­ния разл. ме­ха­низ­мов, со­дер­жа­щих вра­щаю­щие­ся эле­мен­ты (ро­то­ры, тур­би­ны, ко­лё­са).

При бо­лее слож­ных вра­ща­тель­ных дви­же­ни­ях учи­ты­ва­ет­ся пре­цес­сия оси вра­ще­ния. В этом слу­чае вра­ща­тель­ное дви­же­ние те­ла мо­жет быть пред­став­ле­но су­пер­по­зи­ци­ей двух про­стых вра­ще­ний: те­ло вра­ща­ет­ся во­круг сво­ей оси $Oz$, ко­то­рая в свою оче­редь вра­ща­ет­ся во­круг не­под­виж­ной оси $Oz_1$. То­гда ори­ен­та­ция те­ла в про­стран­ст­ве оп­ре­де­ля­ет­ся тре­мя ко­ор­ди­на­та­ми – т. н. Эй­ле­ра уг­ла­ми [$\psi(t)$ – угол пре­цес­сии, $\phi(t)$ – угол соб­ст­вен­но­го вра­ще­ния, $\theta$ – по­сто­ян­ный угол ну­та­ции].

Вра­ще­ние те­ла во­круг не­по­движ­ной точ­ки. При про­из­воль­ном вра­ще­нии те­ла во­круг не­под­виж­ной точ­ки $O$ все три уг­ла Эй­ле­ра за­ви­сят от вре­ме­ни, при­чём дви­же­ние те­ла нель­зя све­сти к двум про­стым вра­ще­ни­ям. Как по­ка­зал Л.  Эй­лер, для опи­са­ния дан­но­го дви­же­ния мож­но най­ти та­кой век­тор $\omega$ (на­зы­вае­мый мгно­вен­ной уг­ло­вой ско­ро­стью те­ла), что ско­рость $\boldsymbol v_N$ точ­ки $N$ те­ла оп­ре­де­ля­ет­ся фор­му­лой $\boldsymbol v_N=\boldsymbol [\omega, \boldsymbol r_N]$. Те точ­ки те­ла, для ко­то­рых век­то­ры $\boldsymbol r_N$ и $\boldsymbol \omega$ кол­ли­не­ар­ны, об­ра­зу­ют мгно­вен­ную ось вра­ще­ния те­ла (мгно­вен­ная ско­рость этих то­чек рав­на ну­лю). Век­тор $\boldsymbol \omega=\{\omega_x, \omega_y, \omega_z \}$ пред­став­ля­ет со­бой гео­мет­рич. сум­му трёх век­то­ров: $\boldsymbol e_1d\psi/dt$ – уг­ло­вая ско­рость пре­цес­сии (орт $\boldsymbol e_1$ не­из­ме­нен в не­под­виж­ной сис­те­ме ко­ор­ди­нат), $\boldsymbol e_2d\phi/dt$ – уг­ло­вая ско­рость соб­ст­вен­но­го вра­ще­ния (орт $\boldsymbol e_2$ не­из­ме­нен от­но­си­тель­но те­ла), $\boldsymbol e_3d\theta/dt$ – уг­ло­вая ско­рость ну­та­ции (орт $\boldsymbol e_3$ вра­ща­ет­ся во­круг $\boldsymbol e_1$). Дви­же­ние твёр­до­го те­ла от­но­си­тель­но не­под­виж­ной точ­ки опи­сы­ва­ет­ся сле­дую­щи­ми ки­не­ма­ти­чес­ки­ми Эй­ле­ра урав­не­ния­ми: $$\omega_x=(d\theta/dt)\cos \phi – (d \psi /dt)\sin \theta \sin \phi;\\ \omega_y=(d\theta/dt)\sin \phi – (d \psi /dt)\sin \theta \cos \phi;\\ \omega_z=d\phi/dt+(d\psi/dt)\cos \theta. $$

Кро­ме уг­лов Эй­ле­ра для опи­са­ния вра­ща­тель­но­го дви­же­ния те­ла мо­гут быть ис­поль­зо­ва­ны и др. па­ра­мет­ры: уг­лы Кры­ло­ва, па­ра­мет­ры Род­ри­га – Га­миль­то­на и т. п. Ус­ко­ре­ние $\boldsymbol w_N$ точ­ки $N$ те­ла вы­чис­ля­ет­ся по фор­му­ле Ри­валь­са: $\boldsymbol w_N=[d\boldsymbol\omega/dt, \boldsymbol r_N]+[\boldsymbol\omega,[\boldsymbol\omega,\boldsymbol r_N]]$.

Про­из­воль­ное дви­же­ние те­ла. Про­из­воль­ное дви­же­ние твёр­до­го те­ла мож­но раз­ло­жить на две со­став­ляю­щие: по­сту­па­тель­ное дви­же­ние со ско­ро­стью $\boldsymbol v_O$ не­ко­то­рой точ­ки $O$ те­ла и вра­ще­ние во­круг этой точ­ки с уг­ло­вой ско­ро­стью $\boldsymbol \omega$. За­ме­на точ­ки $O$ на др. точ­ку, напр. точ­ку $N$, вно­сит из­ме­не­ние в опи­са­ние это­го же дви­же­ния. Во­об­ще го­во­ря, из­ме­ня­ет­ся на­прав­ле­ние и ве­ли­чи­на ско­ро­сти $\boldsymbol v_N$ по­сту­па­тель­но­го дви­же­ния, но не из­ме­ня­ет­ся уг­ло­вая ско­рость $\boldsymbol \omega$ вра­ще­ния, со­вер­шае­мо­го те­перь во­круг точ­ки $N$.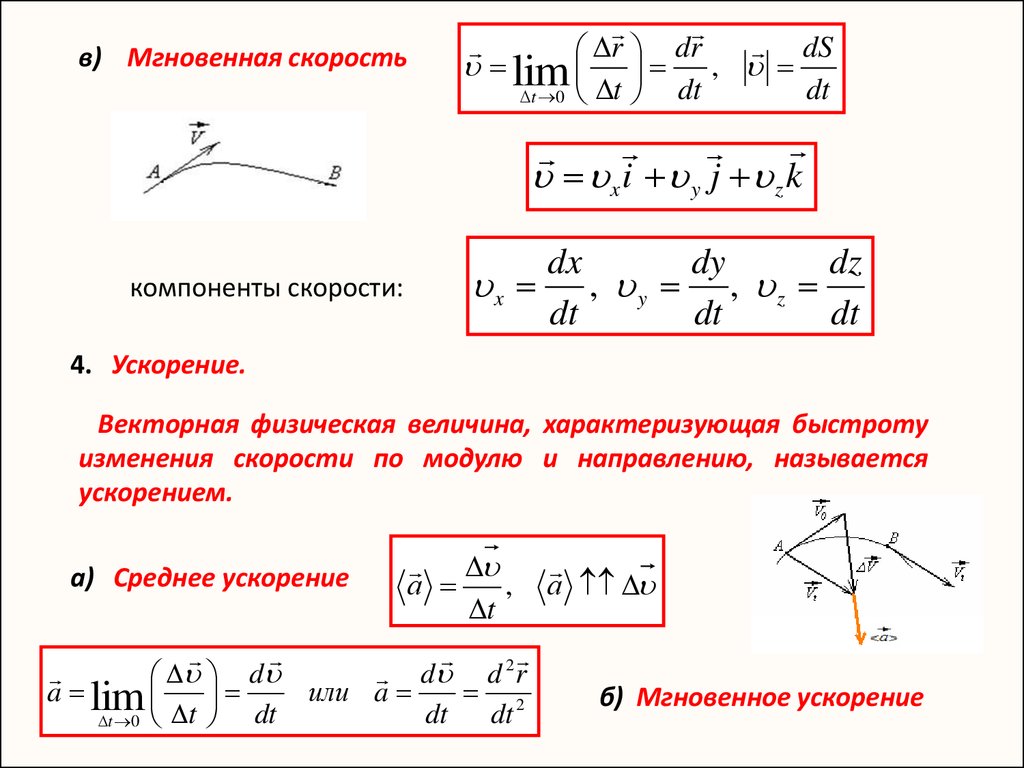 Ес­ли $\omega \neq 0$ и $(\boldsymbol v_O, \boldsymbol \omega) \neq 0$, в те­ле су­ще­ст­ву­ет мно­же­ст­во то­чек, для ко­то­рых век­то­ры $\boldsymbol v$ и $\boldsymbol \omega$ кол­ли­не­ар­ны. Эти точ­ки об­ра­зу­ют мгно­вен­ную вин­то­вую ось дви­же­ния те­ла (см. Вин­то­вое дви­же­ние).

Плос­ко­па­рал­лель­ное дви­же­ние те­ла. Те­ло со­вер­ша­ет плос­ко­па­рал­лель­ное дви­же­ние, ес­ли ско­ро­сти всех его то­чек в лю­бой мо­мент вре­ме­ни па­рал­лель­ны не­ко­то­рой не­под­виж­ной плос­ко­сти. Спро­ек­ти­ро­вав те­ло на эту плос­кость, по­лу­чим пло­скую фи­гу­ру, дви­же­ние ко­то­рой по плос­ко­сти эк­ви­ва­лент­но дви­же­нию те­ла. Ес­ли в этом дви­же­нии $w(t) \neq0$, то век­тор $\boldsymbol \omega$ ор­то­го­на­лен ука­зан­ной плос­ко­сти, $(\boldsymbol v_O, \boldsymbol \omega) \neq 0$ и ось мгно­вен­но­го вин­та пе­ре­се­ка­ет фи­гу­ру в мгно­вен­ном цен­тре вра­ще­ния. Ес­ли $\omega=0$, но $v_O \neq 0$, то те­ло на­хо­дит­ся в со­стоя­нии мгно­вен­но по­сту­па­тель­но­го дви­же­ния.

К. сплош­ных сред (де­фор­ми­руе­мо­го те­ла, не­сжи­мае­мой и сжи­мае­мой жид­ко­сти) тре­бу­ет бо­лее слож­ных про­це­дур опи­са­ния: рас­смат­ри­ва­ет­ся об­щая тео­рия де­фор­ма­ций, оп­ре­де­ля­ют­ся т. н. урав­не­ния не­раз­рыв­но­сти и т. д. (см. Ме­ха­ни­ка сплош­ной сре­ды, Ме­ха­ни­ка жид­ко­сти и га­за).

Мгновенная скорость – физика, уроки

Лекционный материал по теме: мгновенная скорость, а также решение задач по данной теме, примеры решения данных задач.

Просмотр содержимого документа
«Мгновенная скорость»

МОБУ СОШ с.Малиново

Конспект урока по теме:

Мгновенная скорость

Учитель математики и физики:

Бойко Тамара

Владимировна

2016год

Мгновенная скорость движения

ОПРЕДЕЛЕНИЕ

Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории.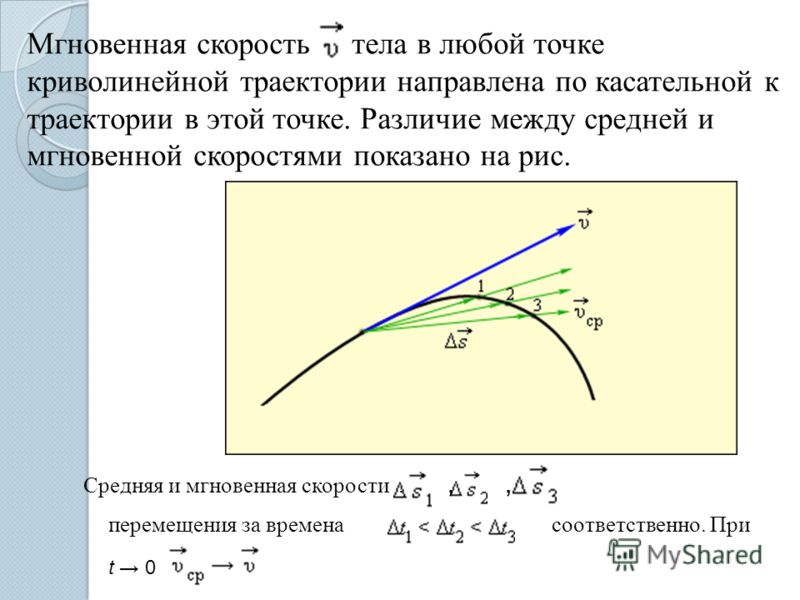 Это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени.

Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.

Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.

Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.

Имеет ли понятие «мгновенной скорости» физический смысл? Скорость – это характеристика изменения перемещения тела в пространстве.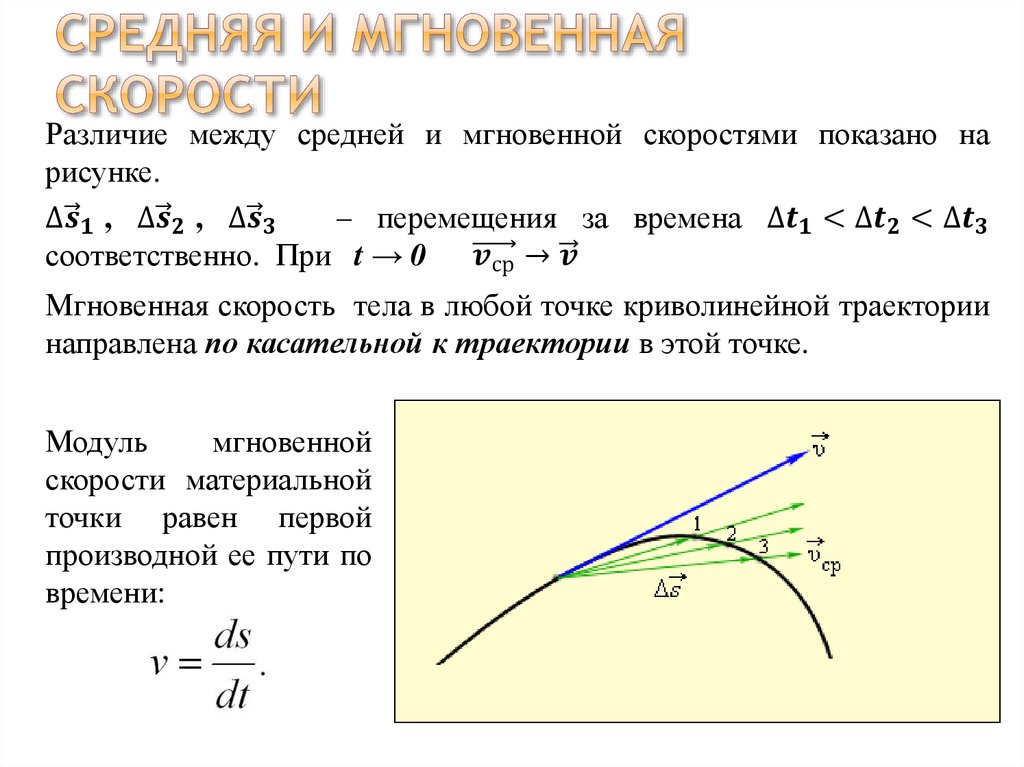 Однако, для того, чтобы определить, как изменилось перемещение, необходимо наблюдать за движением в течение некоторого времени. Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть достаточно малый , однако это все-таки конечный временной интервал, а не момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако, понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно пользуются.

Примеры решения задач по теме «Мгновенная скорость»

ПРИМЕР 1

Задание	О какой скорости – средней или мгновенной – идет речь в следующих случаях: 1) самолет летит из Санкт-Петербурга в Москву со скоростью 800 км/ч; 2) пуля вылетает из винтовки со скоростью 800 м/с; 3) велосипедист едет по шоссе со скоростью 12 км/ч; 4) прибор показывает скорость тепловоза 75 км/ч?
Ответ	1) и 3) – речь идет о средней скорости; 2) и 4) – речь идет о мгновенной скорости.

ПРИМЕР 2

Задание	Закон движения точки по прямой задается уравнением  . Найти мгновенную скорость точки через 10 секунд после начала движения.
Решение	Мгновенная скорость точки – это первая производная радиус-вектора по времени. Поэтому для мгновенной скорости можно записать:    Через 10 секунд после начала движения мгновенная скорость будет иметь значение:  м/с
Ответ	Через 10 секунд после начала движения мгновенная скорость точки  м/с.

ПРИМЕР 3

Задание	Тело движется по прямой так, что его координата  (в метрах) изменяется по закону  . Через сколько секунд после начала движения тело остановится?
Решение	Найдем мгновенную скорость тела В момент остановки мгновенная скорость тела будет равна нулю: откуда время остановки:
Ответ	Тело остановится через 5 секунд после начала движения.

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Определение 1

Величина, которая описывает быстроту изменения положения координаты, называется скоростью .

Определение 2

Средняя скорость – это величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ = ∆r∆t; υ ↑↑ ∆r.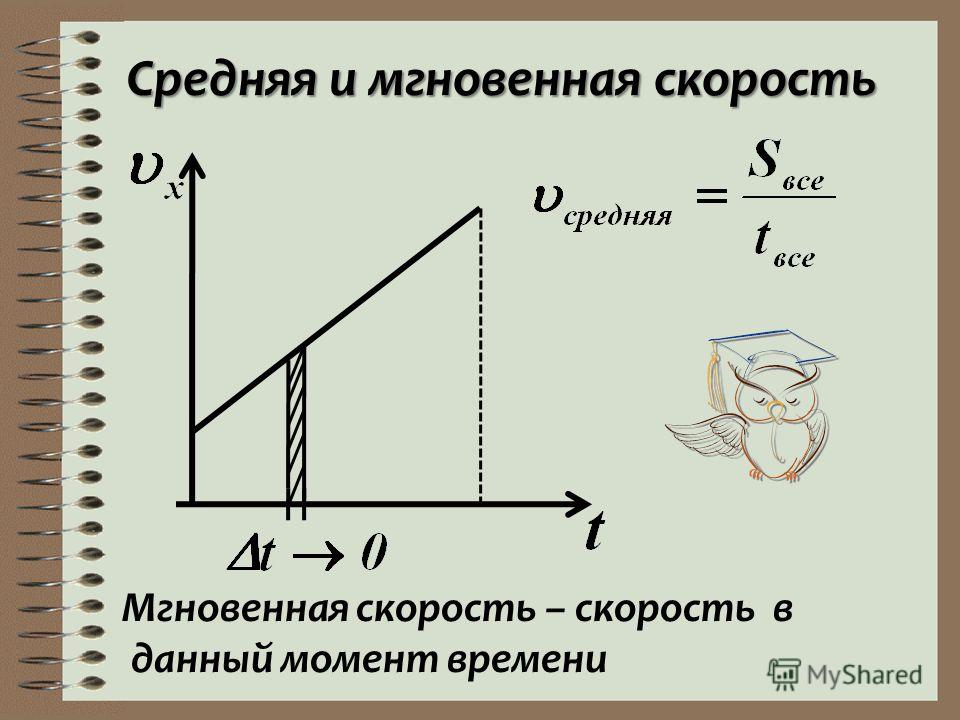

Рисунок 1. Средняя скорость сонаправлена ​​перемещению

Модуль средней скорости по пути равняется υ = S∆t.

Мгновенная скорость точки. Формулы

Мгновенная скорость соответствует движению в момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Определение 3

Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:

υ = lim∆t∆r∆t = drdt = r˙.

Направление вектора υ идет по касательной к криволинейной траектории, потому что как бесконечно малое перемещение доктор совпадает с бесконечно малым траектории ds.

Рисунок 2. Вектор мгновенной скорости υ

Имеющееся ниже выражение υ = lim∆t∆r∆t = drdt = r˙ в декартовых координатах идентично предложенным устройствам:

υx = dxdt = x˙υy = dydt = y˙υz = dzdt = z˙.

Слишком сложно?

Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ = υ = υx2 + υy2 + υz2 = x2 + y2 + z2.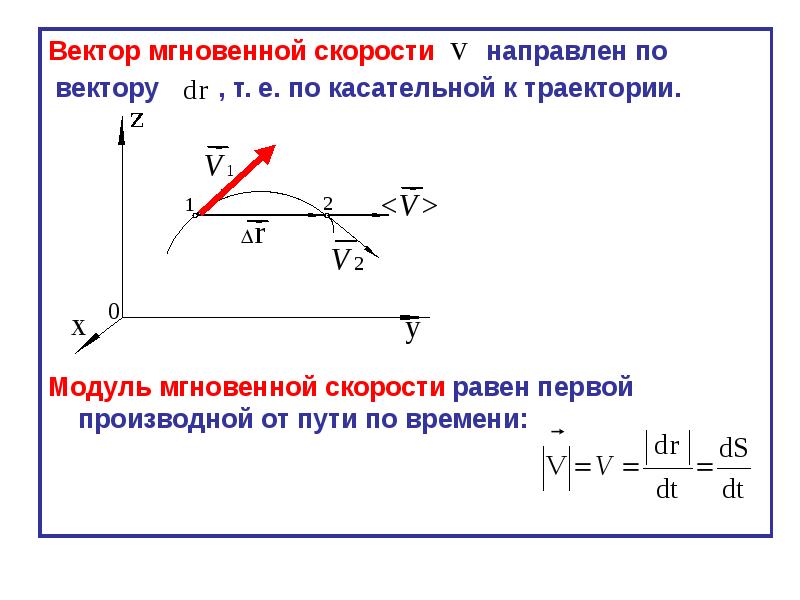

перейдите от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = rq1, q2, q3, тогда значение скорости запишется как:

υ = drdt = ∑i = 13∂r∂qi∂qi∂r = ∑i = 13∂r∂qiq˙i.

Рисунок 3. Перемещение и мгновенная скорость в системе криволинейных координат

При сферических координатах предположим, что q1 = r; q2 = φ; q3 = θ, то получим υ, представленную в такой форме:

υ = υrer + υφeφ + υθφθ, где υr = r˙; υφ = rφ˙sin θ; υθ = rθ˙; r˙ = drdt; φ˙ = dφdt; θ˙ = dθdt; υ = r1 + φ2sin2θ + θ2.

Определение 4

Мгновенной скоростью называют значение производной функции перемещения по времени в заданный момент, используемым с помощью элементов перемещением dr = υ (t) dt

Пример 1

Дан закон прямолинейного движения точки x (t) = 0,15t2-2t + 8. Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектор-вектор по времени.Тогда ее запись примет вид:

υ (t) = x˙ (t) = 0,3т-2; υ (10) = 0,3 × 10-2 = 1 м / с.

Ответ : 1 м / с.

Пример 2

Движение материальной точки задается уравнением x = 4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ (t) = x˙ (t) = 4-0,1т.

4-0,1t = 0; tост = 40 с; υ0 = υ (0) = 4; υ = ∆υ∆t = 0-440-0 = 0,1 м / с.

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м / с.

Мгновенная и средняя скорость | Физика

1. Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

На рисунке 4.1 показано положение разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с.Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим подробнее.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно .

Теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).

Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, когда эти промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы.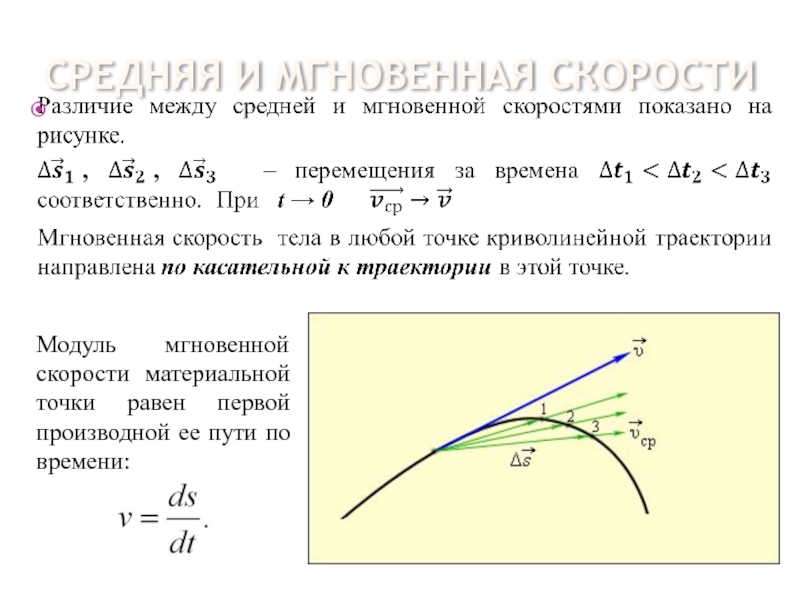 Это означает, что движение автомобиля в течение коротких промежутков времени можно с хорошей точностью прямолинейным равномерным.

Оказывается, этим замечательным криволинейное движение: если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый данный момент времени называют его скоростью в момент времени t, если этот момент времени находится в промежутке времени t. А более точное ее название – мгновенная скорость .

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движения тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) предполагмевать обычно мгновенную скорость.

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координат от времени

На рисунке 4.4 изображен график зависимости координат от времени для автомобиля, который движется по прямолинейному шоссе.

Мы видим, что он движется неравномерно, потому что график зависит от его координат от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малое промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., Например, шкалу времени).

Мы видим, что этот участок практически неотличим от отрезка прямого (красный отрезок).За последовательные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

Возвращаясь к текущему масштабу чертежа, мы увидим, что прямая красная диаграмма, с которой практически совпадение малый участок графика, – касательная к графику зависимости координат от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела .(Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени с понятием производной функции.) Это понятие вы будете изучать в курсе «Алгебра и начала касательной аиализа».) А в тех точках графика, где угол наклона касательной равенства нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите самую большую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих случаях используют среднюю скорость, связанную с использованием:

в _ср = л / т. (1)

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км / ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих движениях движение на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

v _ср = (l ₁ + l ₂ ) / (t ₁ + t ₂ ), (2)

где l ₁ и t ₁ – путь и время для первого участка, а l ₂ и t ₂ – для второго.Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км / ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км / ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростному, с помощью которого Саша ехал и шелел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км / ч, а потом прошел такое же расстояние пешком со скоростью 5 км / ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этой средней скорости не равна среднему арифметическому скоростям езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом.Почему?

? 7. Между двумя промежутками времени, в течение которых Саша ехал в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим случай, когда тело двигалось сначала с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v ₁ , а вторую половину – со скоростью v ₂ . Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l ₁ и l ₂ .

? 8. Выразите через v ₁ , v ₂ и t:
a) l ₁ и l ₂ ; б) л; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростям движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v ₁ , а вторую половину – со скоростью v ₂ . Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых двигалось на первом и втором участке, обозначим соответственно t ₁ и t ₂ .

? 9. Выразите через v ₁ , v ₂ и l:
а) t ₁ и t ₂ ; б) т; в) среднюю скорость.

Ответ на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этим скоростям.

? 10. Докажите, что оно двигалось на двух участках равной длины с разными скоростями, чем если бы оно двигалось на двух участках с теми же скоростями в равных промежутках времени.
Подсказка.Выразите для каждого из двух случаев среднюю скорость через скорость на первом и втором участках.

? 11. На первом участке пути тело двигалось со скоростью v ₁ , а на втором – со скоростью v ₂ . Чему равно отношению длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v ₁ и v ₂ ?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v ₁ , оставшееся время – со скоростью v ₂ .
а) Выразите пройденный поездом путь через v ₁ , v ₂ и все время движения t.
б) Выразите среднюю скорость поезда через v ₁ и v ₂ .
в) Найдите числовое значение средней скорости при v ₁ = 60 км / ч, v ₂ = 90 км / ч.

13. Автомобиль ехал три четверти всего пути со скоростью v ₁ , а оставшийся участок пути – со скоростью v ₂ .
а) Выразите все время движения автомобиля через v ₁ , v ₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v ₁ и v ₂ .
в) Найдите числовое значение средней скорости при v ₁ = 80 км / ч, v ₂ = 100 км / ч.

14. Автомобиль ехал 2 ч со скоростью 60 км / ч. Сколько времени после этого он должен ехать со скоростью 80 км / ч, чтобы его средняя скорость на всем пути стала равной 66,7 км / ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t ² .
а) Выберите удобный масштаб и изобразите график зависимости x (t) в течение первых 6 с.
б) Соответствует средней скорости за все время движения.

Мгновенная скорость

Средняя скорость

Если перемещается неравномерно, то описывая его движение в качестве одного из параметров можно использовать средней скоростью движения на отдельных отрезках пути. Такое описание дает очень приближенную, грубую характеристику перемещения. Время находя средние скорости, мы проводим замену неравномерного движения на движение с постоянной скоростью на избранных отрезках пути, думая, что скорость изменяется скачкообразно при переходе от одного отрезка времени к другому. Графиком пути, отражающем перемещение тела, со скоростью, отличающейся на разных отрезках, становится ломаная линия, имеющая звенья с различными наклоном.

Допустим, что материальная точка перемещается вдоль прямой линии, которая не совпадает с осями координат. При этом ее положение определяет радиус- вектор $ \ vec r_1 $, соответствующий моменту времени $ t_1 $. В момент времени $ t_2 $ положение материальной точки в изображении определяет вектор $ \ vec r_2 $.

Перемещение нашей материальной точки определенным как:

$ \ Delta \ vec r = \ vec r_2- \ vec r_1 (1).$

Определение 1

Средняя скорость материальной точки будет определена выражением:

$ \ vec v_ {sr} = \ frac {\ Delta \ vec r} {\ Delta t} = \ frac {\ vec r_2- \ vec r_1} {t_2-t_1} (2). $

Из формулы (2) видно, что в ней происходит деление вектора на скаляр, в результате которого мы имеем вектор, направление которого совпадает с направленным перемещением.

Векторы скорости и перемещения обладают одинаковыми направлениями.

Переход от средней скорости к мгновенной скорости

В выражении (2) средняя скорость найдена для отрезка времени, равного $ \ Delta t $.Разделим данный временной отрезок на более мелкие. Если материальная точка перемещается неравномерно, то вновь найденные средние скорости будут отличаться, от средней скорости для всего отрезка $ \ Delta t $. Уменьшим временный отрезок $ \ Delta t $, станут меньше и отрезки времени внутри него. Средние скорости в уменьшенных промежутках времени будут отличаться от средней скорости на всем промежутке времени, но разница станет меньше.

Устремим рассматриваемый промежуток времени к нулю (∆t → 0), средняя скорость при этом устремится к предельному значению, которое представляет собой мгновенную скорость.

Определение 2

Мгновенной скоростью или скоростью в данный момент времени называют вектор равную:

$ \ vec v (t) = \ frac {d \ vec r} {dt} (3). $

Если перемещается равномерно, то мгновенная скорость его движения в каждый момент времени совпадает со скоростью этого движения. Говорят, что мгновенная скорость равномерного движения является постоянной.

Мгновенная скорость неравномерного перемещения – это переменный параметр, который принимает разные значения для разных моментов времени.При этом мгновенную скорость можно считать изменяющейся непрерывно на всем отрезке времени.

Мгновенную скорость в каждый момент времени можно определить как тангенс угла наклона касательной к кривой – траектории движения в рассматриваемой точке.

Компоненты вектора мгновенной скорости в декартовой системе координат

В декартовой системе координат-вектор запишем как:

$ \ vec r (t) = x (t) \ vec i + y (t) \ vec j + z ( t) \ vec k (4) $,

во внимание, что единичные орты ($ \ vec i; \ vec j; \ vec k $) не изменяются во времени, и используя определение мгновенной скорости (3), получаем:

$ \ vec v (t) = \ frac {dx} {dt} \ vec i + \ frac {dy} {dt} \ vec j + \ frac {dz} {dt} \ vec k (5).2 (9). $

Направление мгновенной скорости

Будемывать движение материальной точки через параметры траектории. При этом нам известны траектория движения точки и связь пути ($ s $) и времени $ t $. Путь отмеряется по траектории, от точки траектории, которую мы принимаем за начальную. При этой любой точке траектории проявляется собственная величиной $ s $. Из сказанного выше следует, что радиус-вектор – это функция от $ s $, траекторию зададим уравнением:

$ \ vec r = \ vec r (s) (10) $.

Получаем, что в мгновенной оценке скорости (3) мы можем считать радиус – вектор как сложную функцию ($ \ vec r (s (t)) $). При этом ее производную найдем, применяя правило дифференцирования сложной функции:

$ \ vec v = \ frac {d \ vec r} {dt} = \ frac {d \ vec r} {ds} \ frac {ds} {dt} (11) $,

где по определению мгновенной скорости ее величина равна: $ v = \ frac {ds} {dt} $.

Обозначим $ \ Delta s $ – расстояние между парой точек по траектории; $ | \ Delta \ vec r | $ – расстояние между рассматриваемыми точками по прямому кратчайшему расстоянию ().При сближении наших точек разница между $ \ Delta s $ и $ | \ Delta \ vec r | $ уменьшается, запишем:

$ \ frac {d \ vec r} {ds} = \ lim _ {\ Delta s \ to 0} (\ frac {\ Delta \ vec r} {\ Delta s}) = \ lim _ {\ Delta s \ to 0} (\ frac {\ Delta \ vec r} {| \ Delta r |} \ frac {| \ Delta r |} {\ Delta s}) = \ vec \ tau (12). $

где $ \ vec \ tau $ – единичный вектор, являющийся касательным к траектории движения точки.

Принимая во внимание сказанное выше выражение (12) для мгновенной скорости можно записать как:

$ \ vec v = v \ vec \ tau $ (13).

Из формулы (13) становится очевидно, что мгновенная скорость направлена ​​по касательной к траектории движения материальной точки.

Рассматривая направления мгновенной скорости движения материальной точки подчеркнем, что:

1. Мгновенная скорость материальной точки перемещающейся по прямой – это вектор, который направлен по траектории ее движения.
2. При перемещении материальной точки по криволинейной траектории векторной скорости имеет направление по касательной к траектории движения точки.

Скорость при равнопеременном движении

Самым простым неравным движением является равнопеременное перемещение тела, движение с постоянным ускорением. Это движение бывает:

• равноускоренным, если скорость и ускорение имеют одинаковые направления, при этом величина скорости увеличивается;
• равнозамедленное, при противоположном направлении скорости и ускорения, в этом случае скорость по модулю уменьшается.

При равнопеременном движении в любой момент времени можно вычислить, если использовать выражение:

$ \ vec v (t) = \ vec v_0 + \ vec a \ bullet t (14), $

где $ \ vec v_0 $ – начальная скорость движения точки; $ \ vec a $ – постоянное ускорение точки.

1. Мгновенная скорость.

Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Это первая физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:

Другими словами, мгновенная скорость – это первая производная радиус-вектор по времени.

2. Средняя скорость.

Средней скорость на некотором участке называется величина равная перемещение к промежутку времени, который за это перемещение произошло.

3. Угловая скорость. Формула. СИ.

Угловой скорость называется нашей физическая величина равная первая производной угла поворота тела по времени. [рад / с]

4.Связь угловой скорости с периодом вращения.

Равномерное вращение характеризуется периодом вращения и вращения.

5. Угловое ускорение. Формула. СИ.

Это физическая величина равная первая производной угловой скорости или второй производной угла поворота тела по времени. [рад / с ² ]

6. Как направлен вектор угловой скорости / углового ускорения.

Вектор угловой скорости направлен по оси вращения причем так чтобы вращение рассматриваемое с конца конца угловой скорости, происходило против хода правые стрелки (правило правой руки).

При ускоренном вращении вектора углового ускорения сонаправлен с вектором угловой скорости, а замедленном – противоположен ему.

7/8. Связь между нормальным ускорением и угловой скоростью / Связь между тангенциальным и угловым ускорением.

9. Что определяют и как направлена нормальная составляющая полного ускорения? Нормальное ускорение СИ. Нормальное ускорение определяет быстроту изменения скоро-сти по направлению и направлено к центру кривизны траектории.

В СИ нормальное ускорение [м / с ² ]

10. Что определяют и как направлена тангенциальная составляющая полного ускорения.

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

11. Тангенциальное ускорение в СИ.

м / с ²

12. Полное ускорение тела.Модуль этого ускорения.

13.Масса. Сила. Законы Ньютона.

Масса – это физическая величина, являющаяся мерой инерционных и гравитационных свойств тела. Единицей массы в СИ [ м ] = кг.

Сила – это первая физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело деформируется или приобретает ускорение. Единица измерения силы в СИ – Ньютон; кг * м / с ²

Первый закон Ньютона (или закон инерции ): если на тело не силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.

Второй закон Ньютона : ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе.Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основной уравнением динамики поступательного движения .

Третий закон Ньютона : сила, с которой одно действует на другое, равно по величине и противоположна по направлению силе, с которой второе тело действует на первое.

Физические основы механики

Скорость – величина, характеризующая не только быстроту передвижения частиц по траектории, но и направление, в котором движется частица в каждый момент времени.

Средняя скорость за время от т ₁ до т ₂ перемещение перемещения за это время к промежутку времени, за которое это перемещение имело место:

Тот факт, что это именно средняя скорость, мы будем отмечать, заключая среднюю оценку в угловые скобки: <...>, как это сделано выше.

Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения < f (x) > произвольной функции f (x) на промежутке [ a, b ]:

Действительно

Средняя скорость может оказаться слишком грубой характеристикой движения.Например, средняя скорость за период периода колебаний всегда равна нулю, в зависимости от характера этих колебаний, из-за того, что простой случай колеблется, колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю.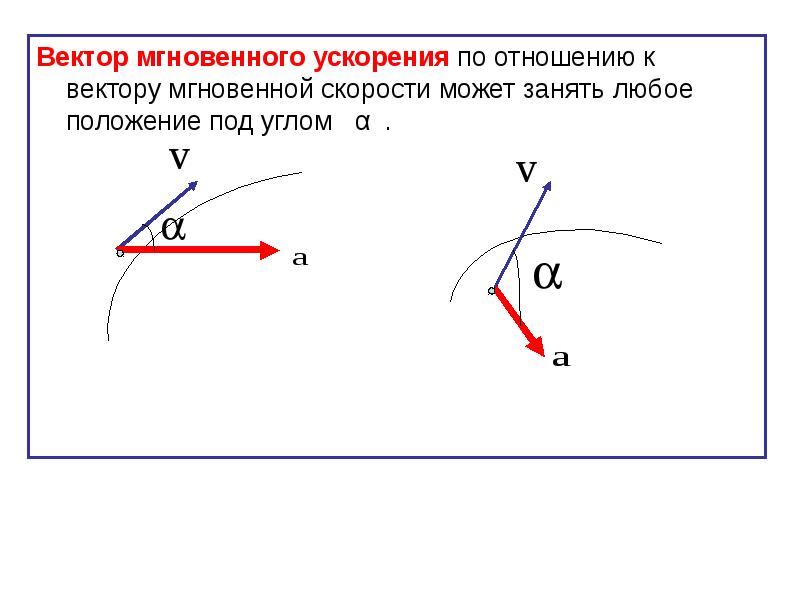 По этой и ряду других причин, вводится мгновенная скорость – скорость в данный момент времени. В подразумеваемой подразумевая мгновенную скорость, просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумению.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения при стремлении промежутка времени t ₂ – t ₁ к нулю. Сделаем переобозначения: t ₁ = t и t ₂ = t + и перепишем верхнее соотношение в виде:

Скорость в момент времени t предел отношения перемещения за время промежутка времени, когда это перемещение имело место, стремление последнего к нулю

Рис.2.5. К определению мгновенной скорости.

В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметьте, что если и есть конечное перемещение и конечное промежуток времени, то и – их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости

есть ничто, как дробь – часто используется в виде

.

Здесь и далее мы будем использовать восходящее движение к Ньютону обозначения производной по времени в виде точки над величиной:

По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в точке в ее стороне движения.

Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.

Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX , OY , OZ использовать обозначения,, или, соответственно). Факторами такого разложения являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно.Разложим по базису радиус-векторной точкой движущейся материальной

Учитывая постоянство декартовых единичных векторов, продифференцируем это выражение по времени

С другой стороны, разложение по базису вектор скорости имеет вид

– Поставление двух последних выражений, с учетом единства представления любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть

Модуль движения скорости равен

Получим ещё одно, важное, выражение для модуля вектора скорости.

Уже отмечалось, что при величине || все меньше и меньше отличается от соответствующего пути (см. рис. 2). Поэтому

и в пределе (> 0)

Иными словами, модуль скорости – это производная пройденного пути по времени.

Окончательно имеем:

Средний модуль вектора скорости , определяется следующим образом:

Среднее значение модуля скорости равно пройденного ко времени, в течение которого этот путь был пройден:

Здесь с (t ₁ , t ₂ ) – путь за время от t ₁ до t ₂ и, соответственно, с (t ₀ , t ₂ ) – путь за время от t ₀ до t ₂ и s (t ₀ , t ₂ ) – путь за время от t ₀ до t ₁ .

Вектор скорости или просто средняя скорость, как указано выше, равенство

Модуль среднего скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектор не равен среднему модулю этого вектора. Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.

Рассмотрим пример.Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени (за время от 0 до t ). Используя физический смысл скорости, в который мгновенная скорость равна средней путевой скорости за первые секунды движения точки.

Рис. 2.6. Определение мгновенной и средней скорости тела

Модуль скорости в данный момент времени

будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости торца момента времени t * .Средний модуль скорости за промежуток времени от 0 до t * есть угловой коэффициент секущей, проходящей через точку той же графики, соответствующей началу t = 0 и концу t = t * временного интервала. Нам надо найти такой момент времени t * , когда оба угловых совпадают. Для этого через начало проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s (t) и дает t * .В нашем примере получается

Как найти мгновенную скорость

Чтобы найти мгновенную скорость при равномерном движении, поделите расстояние, пройденное телом, на время, которое оно преодолевалось. При неравномерном движении, узнавайте значение ускорения и размещайте скорость в каждый момент времени. При свободном падении мгновенная скорость зависит от ускорения свободного падения и времени. Измерьте с помощью рулетки или дальномера отрезка пути в метрах, после чего поделите полученное пройденное значение на промежуток времени в секундах, за который этот отрезок был .Время измерьте секундомером. После этого найдите среднюю скорость, поделив длину на время его прохождения (v = S / t). А как движение равномерное, то средняя скорость будет равной мгновенной скорости.

Определение мгновенной скорости при неравномерном движенииОсновным видом неравномерного движения является равноускоренное движение. С помощью акселерометра или другим способом измерьте значение ускорения. После этого, зная начальная скорость движения, прибавьте к ней произведение ускорения и времени, на протяжении которого находится в движении.Результатом будет значение мгновенной скорости в данный момент времени. (v = v0 + a • t). При расчетах учтите, что если тело уменьшает свою скорость (тормозит), то уменьшает значение ускорения будет отрицательным. В случае если движение начинается из состояния покоя, начальная скорость равна нулю.

Определение мгновенной скорости при свободном паденииДля определения мгновенной скорости свободно падающего тела нужно время падения умножить на ускорение свободного падения (9,81 м / с²), расчет по формуле v = g • t.Учтите, что при свободном падении начальная скорость тела равна нулю. В момент падения с высоты этого числа 19,62, а из полученного числа извлеките квадратный корень.

Определение мгновенной скорости спидометром или радаром Если движущееся тело оборудовано спидометром (автомобиль), то на его шкале или электронном табло будет непрерывно непрерывно скорость в данный момент времени.При наблюдении за телом с неподвижной точки (земля) направьте на него сигнал радара, на его табло отображается мгновенная скорость тела в данный момент времени.

Мгновенная скорость – физика, уроки

Лекционный материал по теме: мгновенная скорость, а также решение задач по данной теме, примеры решения данных задач.

Просмотр содержимого документа
«Мгновенная скорость»

МОБУ СОШ с.Малиново

Конспект урока по теме:

Мгновенная скорость

Учитель математики и физики:

Бойко Тамара

Владимировна

2016год

Мгновенная скорость движения это

Мгновенная скорость этого движения

73

тела в данный момент времени или в данной точке траектории. Это физическая величина, численно равная пределу, к которой стремится средняя скорость за бесконечно малое промежуток времени.

Другими словами, мгновенная скорость – это первая производная радиус-момент по времени.

Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.

Мгновенная скорость дает точную информацию о в данный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км / ч. Через некоторое время стрелка спидометра указывает на значение 90 км / ч, а еще спустя несколько минут – на 110 км / ч.Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.

Имеет ли понятие «мгновенной скорости» физический? Скорость – это характеристика изменения перемещения тела в простран. Однако, для того, чтобы определить, как изменить перемещение, необходимо наблюдать за движением в течение некоторого времени.Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть малый, однако это все-таки конечный временной интервал, а не момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако, понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно.

Примеры решения задач по теме «Мгновенная скорость»

ПРИМЕР 1

Задание	О какой скорости – средней или мгновенной – идет речь в следующих случаях: ) самолет летит из Санкт-Петербурга в Москву со скоростью 800 км / ч; 2) пуля вылетает из винтовки со скоростью 800 м / с; 3) велосипедист едет по шоссе со скоростью 12 км / ч; 4) прибор показывает скорость тепловоза 75 км / ч?
Ответ	1) и 3) – речь идет о средней скорости; 2) и 4) – речь идет о мгновенной скорости.

ПРИМЕР 2

Задание	Закон движения точки по прямому задается уравнением. Найти мгновенную скорость точки через 10 секунд после начала движения.
Решение	Мгновенная скорость точки – это первая производная радиус-события по времени. Поэтому для мгновенной скорости можно записать: Через 10 секунд после начала движения мгновенная скорость будет иметь значение: м / с
Ответ	Через 10 секунд после начала движения мгновенная скорость точки м / с.

ПРИМЕР 3

Задание

Тело движется по прямому так, что его координата (в месте) действует по закону. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: