Как найти f физика: Физика: Как найти F(силу), зная массу 12т? ПОЖАЛУЙСТА

Физика: Как найти F(силу), зная массу 12т? ПОЖАЛУЙСТА

E) 2 дптрТест тапсырмалары1 Линзаның фокус аралығы 20 см. Денеден линзаға дейінгі қашықтык 40 см. Кескін қандайболады?A) f-40 см В) f=20 см C) =36,2 с … м D) f=6,4 см Е) =13,2 см2 Фокус аралығы 20 см жинағыш линзаның оптикалық күшінің абсолют мәні неге тең болады?А) 0,2 дптрВ) 20 дптр C) 5 дптрD) 0.05 дптр3 Егер дене екі еселенген фокус аралығындай кашыктықта орналасқан болса, онда жұкажинағыш линза көмегімен алынған кескін:A) Биіктігі өзгермеген, тура, жалғанB) Биіктігі өзгермеген, төңкерілген, шыңC) Үлкейтілген, төңкерілген, шың D) Кішірейтілген , төңкерілген, шыңE) Кішірейтілген, тура, жалғанЕгер дене екі еселенген фокус аралығындай тысқары орналасқан болса, онда жұқа жинагышГинза көмегімен алынған кескін:D) Биіктігі өзгермеген, тура, жалған B) Биіктігі өзгермеген, төңкерілген, шың) Үлкейтілген, төңкерілген, Шың D) Кішірейтілген , төңкерілген, шыңКішірейтілген, тура, жалғанЕгер дене бас фокуста орналасқан болса, онда жұқа шашыратқыш линза көмегіменынған кескін:Үлкейтілген, тура, жалғанВ) Кішірейтілген, тура, ШыңКескін мүлдем болмайды D) Кішірейтілген , төңкерілген, шыңКішірейтілген, тура, жалғанашыратқыш линза беретін кескін қандай?.

СРОЧНООО ПОЖАЛУЙСТА​

в тканях организма при поглощении ядром атома 23 11Na нейтрона образуется радиоактивный изотоп натрия. Написать ядерную реакцию. Какое излучение будет … сопровождать эту реакцию​

Два человека, Самуил и Имангали несут трубу весом P = 160 Н. Один человек поддерживает трубу на расстоянии l1 = 1 м от её конца, а второй держит проти … воположный конец трубы. Определить нагрузку, приходящуюся на каждого человека, если длина трубы l = 5 м. ​

Найдите момент силы величиной 6 Н, плечо которой равно 50 см. ​

Допишите ядерные реакции

срочно ……………

2. На рычаг действует сила F1 равная 350 Н, и F2 равная 50 Н. Плечо l1 =5см. Чему равно плечо l2 ? ​

помогите,пожалуйста, даю звезду и оценку 2 балла​

До наших дней в некоторых арабских странах существует верблюжья кавалерия. Кавалерист скачет на верблюде со скоростью 15 км/ч от города до оазиса, нах … одящегося на расстоянии 30 км. Там он останавливается на время, равное 1/2 времени движения от города до оазиса. Затем кавалерист на уставшем верблюде отправляется обратно в город со скоростью 10 км/ч. 1) Какое время кавалерист отсутствовал в городе? 2) Определите среднюю путевую скорость кавалериста за всё время его отсутствия в городе. Ответ: 1) ч; 2) км/ч.

Ю25 0 в лаборатории завода в запаянной колбе из толстого стекла хранилась ртуть. Перед отправкой ртути в производственный цех завода лаборанту было по … ручено, не вскрывая колбу, измерить массу ртути. Лаборант определил массу колбы с ртутью и внешний объём колбы. Измерения дали результат: m = 1,610 кг и V= 200 см”. Используя справочные данные, лаборант правильно вычислил массу ртути. Плотность ртути pp = 13,6 г/см”, плотность стекла Рc = 2,5 г/см. 1) Чему равна масса колбы с ртутью, если её выразить в граммах? 2) Определите массу ртути в колбе, если ртуть заполняла внутреннее пространство колбы практически полностью. 3) Во сколько раз масса ртути больше массы пустой колбы? Округлите до сотых.

Напишите полное решение этой задачи. Ответы на вопросы обоснуйте соответствующими рассуждениями или решением задачи. Решение:

Физическая работа — урок. Физика, 8 класс.

Совершённая работа равна изменению энергии, потраченной на совершение работы.

Величину работы можно определить, вычитая из конечного значения энергии начальное значение энергии.

 

A=Eконеч.−Eнач.,или A=ΔE, где A — работа (Дж); E — энергия (Дж).

 

Работу, как и энергию, измеряют в джоулях (Дж).

 

Если энергия тела увеличивается, тогда общая совершённая работа является положительной.

Пример:

Когда автомобиль начинает двигаться, его кинетическая энергия увеличивается. Значит, двигатель автомобиля совершает положительную работу.

Если энергия тела уменьшается, тогда общая совершённая работа является отрицательной.

Пример:

Когда автомобиль свободно катится по горизонтальной поверхности, его скорость и кинетическая энергия уменьшаются. Значит, сила сопротивления совершает отрицательную работу.

 

В физике рассматривают физическую работу, которая связана с перемещением тел.

Если при прямолинейном движении на тело действует неизменная сила, направленная в сторону движения тела, тогда работа, произведённая приложенной силой, равна произведению величины силы на величину проделанного перемещения.

Если к телу приложена сила под вертикальным углом к направлению движения тела, как это показано на рисунке, тогда величина совершённой работы зависит от:

1) величины приложенной силы (F), которая совершает работу;

2) расстояния (l), на которое перемещается тело;

3) угла \(α\) между направлением действия силы и направлением движения тела.

Работа определяется по формуле: A=F⋅l⋅cosα.

  

  

Обрати внимание!

Если сила направлена параллельно направлению перемещения, тогда угол \(α = 0\), а \(косинус\) угла \(α\) равен \(1\). В этом случае формула упрощается: A=F⋅l.

Если проделанный путь является прямолинейным, тогда вместо пути \(l\) можно использовать перемещение (s). 

В этом случае формула для расчёта работы приобретает такой вид: A=F⋅s.

На трёх рисунках изображены случаи, когда направление силы и направление движения тела совпадают.

1) Действие силы и направление движения тела направлены горизонтально. Например, автомобиль едет по прямому пути, и сила тяги автомобиля приложена в том же направлении.

 

 

2) Действие силы и направление движения тела направлены под одинаковым углом наклона по отношению к горизонту. Например, автомобиль едет в гору.

  

  

3) Действие силы и направление движения тела направлены вертикально. Например, груз поднимается вверх, и сила упругости троса тоже направлена вверх. В этом случае величину совершённой работы можно рассчитать также по формуле A=m⋅g⋅h, где

(m) — масса тела, (g) — ускорение свободного падения,

(h) — высота подъёма тела над поверхностью земли.

 

 

Обрати внимание!

Если направление действия силы противоположно направлению движения, тогда совершаемая этой силой работа отрицательна.

Работа отрицательна, так как функция \(косинус\) в интервале значений угла \(90° — 180°\) является отрицательной.

Таким образом, любая работа, совершённая силой трения или сопротивления, является отрицательной.

Пример:

Когда автомобиль едет с равномерной скоростью по прямой дороге, как это показано на рисунке, работа силы тяги автомобиля является положительной, а работа силы сопротивления равна по величине, но является отрицательной. В результате этого кинетическая и потенциальная энергия автомобиля остаются неизменными. 

Если сила направлена прямо противоположно направлению движения, тогда работу вычисляют по формуле: A=−F⋅l.

  

Источники:

 

E. Šilters, V. Regusts, A. Cābelis. «Fizika 10 klasei», Lielvārds, 2004, 256 lpp.

(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)

Давление и сила давления | Физика

Проделаем опыт. Возьмем небольшую доску, в углы которой вбиты четыре гвоздя, и поместим ее остриями вверх на песок. Сверху на нее положим гирю (рис. 81). Мы увидим, что шляпки гвоздей лишь незначительно вдавятся в песок. Если же мы перевернем доску и снова поставим ее (вместе с гирей) на песок, то теперь гвозди войдут в него значительно глубже (рис. 82). В обоих случаях вес доски был одним и тем же, однако эффект оказался разным. Почему?Вся разница в рассматриваемых случаях заключалась в том, что площадь поверхности, на которую опирались гвозди, в одном случае была больше, а в другом меньше. Ведь сначала песка касались шляпки гвоздей, а затем их острия.

Мы видим, что результат воздействия зависит не только от силы, с которой тело давит на поверхность, но и от площади этой поверхности. Именно по этой причине человек, способный скользить по рыхлому снегу на лыжах, сразу же проваливается в него, как только их снимет (рис.

83).Но дело не только в площади. Важную роль играет и величина прикладываемой силы. Если, например, на ту же. доску (см. рис. 81) положить еще одну гирю, то гвозди (при той же площади опоры) погрузятся в песок еще глубже.

Силу, прикладываемую перпендикулярно поверхности, называют силой давления на эту поверхность.

Силу давления не следует путать с давлением. Давление — это физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности:

,(32.1)

где

р — давление, F — сила давления, S — площадь.

Итак, чтобы определить давление, надо силу давления разделить на площадь поверхности, на которую оказывается давление.

При одной и той же силе давление больше в том случае, когда площадь опоры меньше, и, наоборот, чем больше площадь опоры, тем давление меньше.

В тех случаях, когда силой давления является вес находящегося на поверхности тела (F = P = mg), давление, оказываемое телом, можно найти по формуле

Если давление р и площадь S известны, то можно определить силу давления F; для этого надо давление умножить на площадь:

    F = pS    (32. 2)

Сила давления (как и любая другая сила) измеряется в ньютонах. Давление же измеряется в паскалях.

Паскаль (1 Па) — это такое давление, которое производит сила давления в 1 Н, будучи приложенной к поверхности площадью 1 м²:

1 Па = 1 Н/м².

Используются также другие единицы давления — гектопаскаль (гПа) и килопаскаль (кПа):

1 гПа = 100 Па, 1 кПа = 1000 Па.

1. Приведите примеры, показывающие, что результат действия силы зависит от площади опоры, на которую действует эта сила. 2. Почему человек, идущий на лыжах, не проваливается в снег? 3. Почему острая кнопка легче входит в дерево, чем тупая? 4. Что называют давлением? 5. Какие вы знаете единицы давления? 6. Чем отличается давление от силы давления? 7. Как можно найти силу давления, зная давление и площадь поверхности, к которой приложена сила?

Открытая Физика. Импульс тела

Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила F→. Под действием этой силы скорость тела изменилась на Δυ→=υ→2-υ→1. Следовательно, в течение времени Δt тело двигалось с ускорением a→=Δυ→Δt=υ→2-υ→1Δt.

Из основного закона динамики (второго закона Ньютона) следует: F→=ma→=m(υ→2-υ→1)Δt  или  F→Δt=mυ→2-mυ→1=mΔυ→=Δ(mυ→).

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или

количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кгċм/с).

Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.

В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.

Обозначив импульс тела буквой p→, второй закон Ньютона можно записать в виде F→Δt=Δp→.

Именно в таком общем виде сформулировал второй закон сам Ньютон.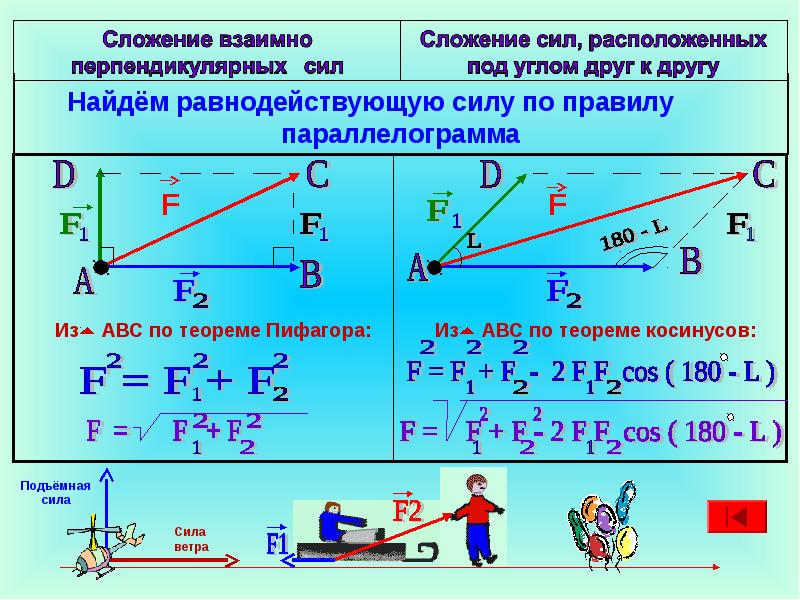

Сила F→ в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси: F_x Δt = Δp_x; F_y Δt = Δp_y; F_z Δt = Δp_z.

Импульс тела

Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, т. е. движение тела по одной из координатных осей (например, оси OY). Пусть тело свободно падает с начальной скоростью

υ₀ под действием силы тяжести; время падения равно t. Направим ось OY вертикально вниз. Импульс силы тяжести F_т = mg за время t равен mgt. Этот импульс равен изменению импульса тела F_тt = mgt = Δp = m (υ – υ₀), откуда υ = υ₀ + gt.

Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения. В этом примере сила оставалась неизменной по модулю на всем интервале времени t. Если сила изменяется по величине, то в выражение для импульса силы нужно подставлять среднее значение силы

F_ср на промежутке времени ее действия. Рис. 1.16.1 иллюстрирует метод определения импульса силы, зависящей от времени.

Вычисление импульса силы по графику зависимости F(t)

Выберем на оси времени малый интервал Δt, в течение которого сила F (t) остается практически неизменной. Импульс силы F (t) Δt за время Δt будет равен площади заштрихованного столбика. Если всю ось времени на интервале от 0 до t разбить на малые интервалы Δt_i, а затем просуммировать импульсы силы на всех интервалах Δt_i, то суммарный импульс силы окажется равным площади, которую образует ступенчатая кривая с осью времени. В пределе (Δt_i → 0) эта площадь равна площади, ограниченной графиком F (t) и осью t. Этот метод определения импульса силы по графику F (t) является общим и применим для любых законов изменения силы со временем. Математически задача сводится к интегрированию функции F (t) на интервале [0; t].

Импульс силы, график которой представлен на рис. 1.16.1, на интервале от t₁ = 0 с до t₂ = 10 с равен: Fср (t2-t1)=12Fmax (t2-t1)=100 Нċс=100 кгċм/с.

В этом простом примере Fср=12Fmax=10 Н.

В некоторых случаях среднюю силу F_ср можно определить, если известно время ее действия и сообщенный телу импульс. Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить ему скорость υ = 30 м/с. Время удара приблизительно равно 8ċ10^–3 с.

Импульс p, приобретенный мячом в результате удара есть: p = mυ = 12,5 кгċм/с.

Следовательно, средняя сила F_ср, с которой нога футболиста действовала на мяч во время удара, есть: Fср=pΔt=1,56ċ103 Н.

Это очень большая сила. Она приблизительно равна весу тела массой 160 кг.

Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный p→1 и конечный p→2 импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса Δp→ удобно использовать диаграмму импульсов, на которой изображаются вектора p→1 и p→2, а также вектор Δp→=p→2-p→1, построенный по правилу параллелограмма. В качестве примера на рис. 1.16.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m налетел на стенку со скоростью υ→1 под углом α к нормали (ось OX) и отскочил от нее со скоростью υ→2 под углом β. Во время контакта со стеной на мяч действовала некоторая сила F→, направление которой совпадает с направлением вектора Δp→.

Отскок мяча от шероховатой стенки и диаграмма импульсов

При нормальном падении мяча массой m на упругую стенку со скоростью υ→1=υ→ после отскока мяч будет иметь скорость υ→2=- υ→. Следовательно, изменение импульса мяча за время отскока равно Δp→=-2mυ→. В проекциях на ось OX этот результат можно записать в скалярной форме Δp_x = –2mυ_x. Ось OX направлена от стенки (как на рис. 1.16.2), поэтому υ_x < 0 и Δp_x > 0. Следовательно, модуль Δp изменения импульса связан с модулем υ скорости мяча соотношением Δp = 2mυ.

Сила тяги

Сила тяги: определение

Определение 1

Силой тяги называют силу, прикладываемую к телу для поддержании его в постоянном движении.

Прекращение действия силы тяги приводит к остановке вследствие трения, вязкости окружающей среды и других противодействующих движению сил.

Тело, на которое не действуют силы, движется с постоянной скоростью $v = const$ (первый закон Ньютона). Частным случаем такого движения является состояние покоя ($v = 0$). Движение с постоянной скоростью называют состоянием инерции. Чтобы вывести тело из такого состояния, нужно приложить к нему силу. Скорость тела в этом случае изменится, т.е. оно получит ускорение (либо замедление, которое можно считать отрицательным ускорением).

Величина ускорения обратнопропорциональна массе тела (чем оно массивнее, тем труднее его вывести из состояния инерции) и прямопропорциональна интенсивности приложенной силы. Таким образом:

$F = m \cdot a$,

где:

• $F$ – сила,
• $m$ – масса,
• $a$ – ускорение.

Замечание 1

Эта формула отражает Второй закон Ньютона.

Формулы для расчета

В качестве примера силы тяги, выводящей тело из состояния покоя, можно рассмотреть спортсмена, поднимающего штангу. В исходном состоянии штанга находится в состоянии инерции (остается неподвижной). Когда спортсмен отрывает ее от земли, его мышцы должны сокращаться с такой силой, чтобы она превысила вес штанги, т.е. силу, с которой ее притягивает гравитационное поле Земли. Если штангисту удастся оторвать штангу от пола – значит она переместится вверх на некоторое расстояние, т.е. получит ускорение. Т.е. силой тяги, двигающей данный снаряд, является сила сокращающихся мышц спортсмена. При этом должно соблюдаться условие:

$F_м$ > $F_т$, т.е. $F_м$ >$ m \cdot g$,

где $F_м$ – сила мышц (в данном случае сила тяги), $F_т$ – сила тяжести (гравитация), $m$ – масса, $g$ – ускорение свободного падения.

Состояние движения по инерции следует отличать от равномерного движения, когда сила тяги уравновешивается противодействующими силами. Например, при движении автомобиля работающий двигатель через систему трансмиссии передает на колеса силу, преодолевающую силы трения внутри механизмов автомобиля, трения колес о поверхность дороги, сопротивления воздуха и т.д. Силу тяги можно в этом случае вычислить зная время разгона $t$ до нужной скорости $v$ и массу автомобиля $m$:

$F = m \cdot \frac{v}{t}$

Здесь ускорение выражено как частное от деления скорости на время разгона. 2$, если его масса составляет 1,5 тонны, а сила трения – 10% от силы тяжести.

Рассмотрим силу тяги как сумму двух сил:

1. разгоняющей автомобиль с заданным ускорением: $F_1 = m \cdot a$, где $m$ – масса, $a$ – ускорение;
2. преодолевающей силу трения: $F_2 = \mu \cdot m \cdot g$, где $\mu$ – коэффициент силы трения, $g$ – ускорение свободного падения.

Подставив числовые значения в формулу

$F = F_1 + F_2 = m \cdot a + \mu \cdot m \cdot g$

получим, попутно переведя тонны в единицы СИ килограммы,

$F = 1500 \cdot 3 + 0,1 \cdot 9,8 \cdot 1500 = 1500 \cdot (3 + 0,98) = 5970$

Ответ: 5970 ньютонов.

Определение работы силы с помощью интеграла

Известную формулу из физики A = Fs для определения работы силы можно использовать лишь тогда, когда на тело воздействует постоянная сила, направленная по направлению движения. Однако часто требуется определить работу тогда, когда сила изменяется с пройденным путём. Например, чтобы растянуть пружину, нужно приложить силу, которая пропорциональна пройденному пути – удлиннению пружины.

Пусть тело перемещается по отрезку [a, b] оси Ox, при этом проекция вектора силы на ось Ox является функцией F(x) аргумента x. Чтобы определить работу, совершённую силой, разделим отрезок [a, b] на n частей точками a = x0 < x1 < x2 < …xn = b. Таким образом, всё перемещение тела из a в b состоит из n участков пути.

Приложенная сила A будет равна сумме элементарных работ, совершённых при перемещении тела по каждому из участков пути.

Поэтому вся приложенная сила для перемещения тела по прямой будет равна пределу интегральной суммы или определённому интегралу

. (1)

Это и есть формула для определения работы силы.

Пример 1. Сжатие S винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 5 см, если для сжатия её на 1 см нужна сила в 1 кг.

Решение. Сила F и перемещение S связаны по условию зависимостью F=kS, где k – постоянная. Будем выражать S в метрах, F – в килограммах. При S=0,01 F=1, то есть 1=k*0,01, откуда k=100, F=100S.

По формуле (1) определяем работу силы:

.

Пример 2. Сила F, с которой электрический заряд e1 отталкивает заряд e2 (того же знака), находящийся от него на расстоянии r, выражается формулой

,

где k – постоянная.

Вычислить работу силы F при перемещении заряда e2 из точки A1, отстоящей от e1 на расстоянии r1, в точку A2, отстоящую от e1 на расстоянии r2, полагая, что заряд e1 помещён в точке A0, принятой за начала отсчёта.

Решение. По формуле (1) вычисляем работу силы:

.

При получим

.

При получим . Последняя величина называется потенциалом поля, создаваемого зарядом e1.

Пример 3. Вычислить работу, которую нужно совершить, чтобы вытащить шарик массой 9 г из бочки, высота которой 3 м.

Решение. Из физики известно, что F=Ph, то есть . Вес шарика будет равен произведению массы на ускорение свободного падения, то есть P=gm, где g=9,8. Теперь можем вычислить работу силы:

Начало темы “Интеграл”

Оптика – Основные формулы

1. Фотометрия и светотехника

1.1 Поток излучения

Φ — поток излучения,
W — энергия излучения,
t — время прохождения энергии излучения.

1.2 Сила света

I — сила света,
Φ — поток излучения,
Ω — телесный угол, через который проходит поток излучения.

1.3 Освещенность

E — освещенность,
Φ — поток излучения,
σ — площадь, через которую проходит поток излучения.

1.4 Яркость источника света

L — яркость источника света,
I — сила света,
σ — площадь видимой светящейся поверхности.

1.5 Коэффициент поглощения

α — коэффициент поглощения,
Φ_α — световой поток, поглощенный телом,
Φ_i — световой поток, падающий на тело.

1.6 Коэффициент отражения

ρ — коэффициент отражения,
Φ_ρ — световой поток, отраженный телом,
Φ_i — световой поток, падающий на тело.

1.7 Коэффициент пропускания

τ — коэффициент пропускания,
Φ_τ — световой поток, пропущенный телом,
Φ_i — световой поток, падающий на тело.

2. Геометрическая оптика

2.1 Относительный показатель преломления

n — относительный показатель преломления для граничащих сред
n₂ — абсолютный показатель преломления для второй среды,
n₁ — абсолютный показатель преломления для первой среды.

2.2 Закон преломления света

i — угол отражения,
r — угол преломления,
n — относительный показатель преломления для граничащих сред.

2.3 Предельный угол полного внутреннего отражения

i_пр — предельный угол полного внутреннего отражения,
n — относительный показатель преломления для граничащих сред.

2.4 Основная формула тонкой линзы

a — расстояние от источника света до линзы,
a’ — расстояние от линзы до изображения источника света,
f — фокусное расстояние линзы.

2.5 Основная формула сферического зеркала

a — расстояние от источника света до зеркала,
a’ — расстояние от зеркала до изображения источника света,
R — радиус кривизны зеркала,
f — фокусное расстояние зеркала.

2.6 Линейное увеличение

β — линейное увеличение линзы или зеркала,
h — высота источника света,
h’ — высота изображения источника света,
a — расстояние от источника света до линзы или зеркала,
a’ — расстояние от линзы или зеркала до изображения источника света.

2.7 Угловое увеличение

γ — угловое увеличение линзы или зеркала,
β — линейное увеличение линзы или зеркала.

2.8 Оптическая сила линзы

D — оптическая сила линзы,
f — фокусное расстояние.

2.9 Светосила линзы

E — светосила линзы,
d — диаметр линзы или диафрагмы, закрывающей линзу,
f — фокусное расстояние.

3. Оптические приборы

3.1 Увеличение лупы

N — увеличение лупы,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние лупы.

3.2 Увеличение микроскопа

N — увеличение микроскопа,
N₁ — увеличение окуляра микроскопа,
N₂ — увеличение объектива микроскопа,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние системы линз микроскопа: окуляра и объектива.

3.3 Увеличение зрительной (подзорной) трубы

N — увеличение зрительной (подзорной) трубы,
f₁ — фокусное расстояние объектива,
f₂ — фокусное расстояние окуляра.

Определение индивидуальных значений силы

Как было сказано ранее в Уроке 3 (а также в Уроке 2), результирующая сила – это векторная сумма всех индивидуальных сил. В Уроке 2 мы узнали, как определить чистую силу, если известны величины всех отдельных сил. В этом уроке мы узнаем, как определять величины всех отдельных сил, если известны масса и ускорение объекта. Три основных уравнения, которые будут полезны: уравнение для чистой силы (F _net = m • a), уравнение для гравитационной силы (F _grav = m • g) и уравнение для силы трения (F _frict = μ • F _norm ).

Процесс определения значения отдельных сил, действующих на объект, включает применение второго закона Ньютона (F _net = m • a) и применение значения чистой силы. Если масса (м) и ускорение (а) известны, то чистая сила (F _net ) может быть определена с использованием уравнения.

F _net = m • a

Если числовое значение чистой силы и направление чистой силы известны, то можно определить значение всех индивидуальных сил.Таким образом, задача включает использование приведенных выше уравнений, данной информации и вашего понимания чистой силы для определения значения отдельных сил.

Ваша очередь практиковаться

Чтобы понять, как применяется этот метод, попробуйте выполнить следующие практические задачи. Проблемы прогрессируют от простых к более сложным. Решив проблему, нажмите кнопку, чтобы проверить свои ответы.

Практика №1

Диаграммы свободного тела для четырех ситуаций показаны ниже.Чистая сила известна для каждой ситуации. Однако величина некоторых отдельных сил неизвестна. Проанализируйте каждую ситуацию индивидуально и определите величину неизвестных сил.

Практика №2

К объекту весом 6 кг прикладывают направленную вправо силу, чтобы перемещать его по шероховатой поверхности с постоянной скоростью.На объект действует сила трения 15 Н. Используйте диаграмму, чтобы определить гравитационную силу, нормальную силу, чистую силу и приложенную силу. (Пренебрегая сопротивлением воздуха.)

Практика № 3

К объекту весом 10 кг прикладывают направленную вправо силу, чтобы перемещать его по шероховатой поверхности с постоянной скоростью.Коэффициент трения между предметом и поверхностью 0,2. Используйте диаграмму, чтобы определить гравитационную силу, нормальную силу, приложенную силу, силу трения и чистую силу. (Пренебрегая сопротивлением воздуха.)

Практика № 4

К объекту весом 5 кг прикладывают направленную вправо силу для перемещения его по шероховатой поверхности с ускорением вправо 2 м / с / с.Коэффициент трения между объектом и поверхностью 0,1. Используйте диаграмму, чтобы определить гравитационную силу, нормальную силу, приложенную силу, силу трения и чистую силу. (Пренебрегая сопротивлением воздуха.)

Практика №5

К объекту массой 4 кг прикладывают направленную вправо силу 25 Н, чтобы переместить его по шероховатой поверхности с правым ускорением 2.5 м / с / с. Используйте диаграмму, чтобы определить гравитационную силу, нормальную силу, силу трения, чистую силу и коэффициент трения между объектом и поверхностью. (Пренебрегая сопротивлением воздуха.)

Еще пара практических задач представлена ​​ниже. Вы должны постараться решить как можно больше проблем без помощи заметок, решений, учителей и других учеников.Примите решение индивидуально решать проблемы. А пока стоит упомянуть важное предостережение:

Избегайте принуждения проблемы к форме ранее решенной проблемы. Проблемы в физике редко выглядят одинаково. Вместо того чтобы решать проблемы наизусть или путем имитации ранее решенной проблемы, используйте свое концептуальное понимание законов Ньютона для поиска решений проблем. Используйте свое понимание веса и массы, чтобы найти m или Fgrav в проблеме.Используйте свое концептуальное понимание чистой силы (векторная сумма всех сил ), чтобы найти значение Fnet или значение отдельной силы. Не отделяйте решение физических задач от вашего понимания концепций физики. Если вы не можете решать физические задачи, подобные приведенным выше, это не обязательно означает, что у вас есть математические трудности. Вполне вероятно, что у вас проблемы с физическими концепциями.

Мы хотели бы предложить… Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащемуся исследовать влияние изменений приложенной силы, чистой силы, массы и трения на ускорение объекта.

Проверьте свое понимание

1. Ли Милон катается на санях со своими друзьями, когда его раздражает один из комментариев друга.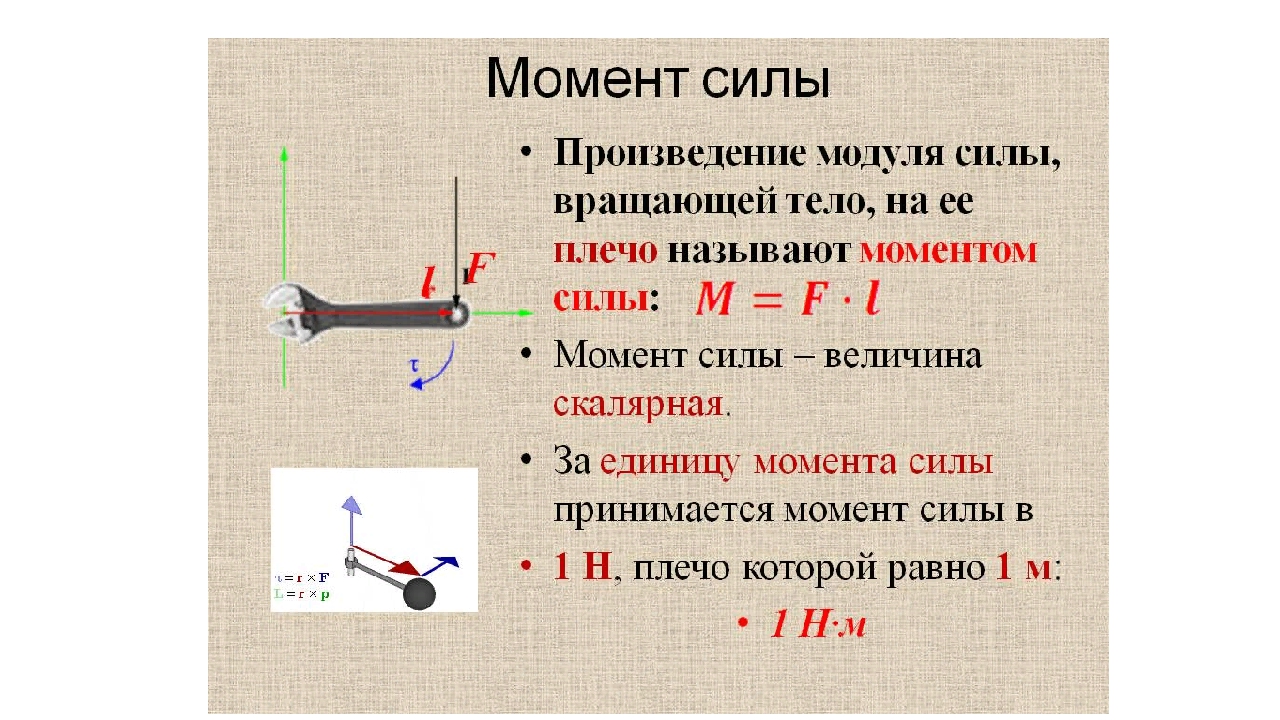 Он прилагает к своим 4,68 кг сани с силой 9,13 Н, направленной вправо, чтобы разогнать их по снегу. Если ускорение саней составляет 0,815 м / с / с, то каков коэффициент трения саней по снегу?

2.В лаборатории физики Эрнесто и Аманда прикладывают направленную вправо силу 34,5 Н к тележке массой 4,52 кг, чтобы разогнать ее по горизонтальной поверхности со скоростью 1,28 м / с / с. Определите силу трения, действующую на тележку.

Вычислительная сила – Физика средней школы

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Формула кинетического трения

Кинетическое трение – это сила, действующая между движущимися поверхностями. Объект, который перемещается по поверхности, будет испытывать силу, противоположную его движению. Величина силы зависит от коэффициента кинетического трения между двумя видами материала. Каждая комбинация индивидуальна. Коэффициент кинетического трения обозначается греческой буквой «мю» ( μ ) с нижним индексом « k ». Сила кинетического трения в μ _k раз больше нормальной силы, действующей на объект, и выражается в единицах ньютонов (Н).

сила кинетического трения = (коэффициент кинетического трения) (нормальная сила)

F _k = μ _k η

F _k = сила кинетического трения

μ _k = коэффициент кинетического трения

η = нормальная сила (греческая буква «эта»)

Формула кинетического трения Вопросы:

1) Рабочий в складском помещении толкает по полу большую картонную коробку.Коэффициент кинетического трения составляет μ _k = 0,520. Коробка имеет массу 75,0 кг, кг, и рабочий прикладывает вперед усилие в 400,0 Н . Какова величина силы трения и какая результирующая сила перемещает коробку?

Ответ: На плоской поверхности нормальная сила, действующая на объект, составляет η = mg . Используя эту формулу, можно найти силу трения:

F _k = μ _k η

F _k = μ _k мг

F _k = (0.520) (75,0 кг) (9,80 м / с ² )

F _k = 382,2 кг ∙ м / с ²

F _к = 382,2 N

Сила кинетического трения, действующая в направлении, противоположном движению коробки, составляет 382,2 Н. Итоговая сила, действующая на коробку, представляет собой сумму сил. Две силы, которые следует учитывать, – это сила кинетического трения, действующая в направлении, противоположном движению коробки, и сила, действующая со стороны рабочего, которая составляет 400 Н вперед.Если мы определим «вперед» как положительное направление, результирующая сила составит:

F _net = F _{Рабочий} -F _k

F _нетто = 400,0 N -382,2 N

F _нетто = 17,8 N

Чистая сила, действующая на коробку, составляет 17,8 Н вперед.

2) Женщина катается на лыжах прямо с заснеженного холма. Коэффициент кинетического трения между лыжами и снегом составляет μ _k = 0.0800. Холм расположен под углом 60,0 ° к горизонтали. Масса лыжника 55,00 кг . Какова величина силы кинетического трения и какова суммарная сила в направлении движения лыжника?

Ответ: На плоской поверхности нормальная сила, действующая на объект, составляет η = mg . На поверхности, расположенной под углом к ​​горизонтальной оси, общая сила тяжести, F = mg , должна быть разбита на компоненты. Нормальная сила – это составляющая, которая перпендикулярна наклонной поверхности, а оставшаяся сила параллельна наклонной поверхности.Нормальная сила составляет η = mg cosθ , а оставшаяся составляющая силы составляет F = mg sinθ . Используя эту формулу, можно найти величину силы кинетического трения:

F _k = μ _k η

F _k = μ _k мг cosθ

F _k = (0,0800) (55,00 кг ) (9,80 м / с ² ) cos (60 °)

F _k = 21. 6 кг ∙ м / с ²

F _k = 21,6 N

Сила кинетического трения препятствует движению лыжника. Сила, которая перемещает лыжника вниз по склону, является оставшимся компонентом силы тяжести, F _θ = mg sinθ. Эта сила:

F = мг sinθ

F = (55,0 кг ) (9,80 м / с ² ) sin (60 °)

Факс = 466.8 кг ∙ м / с ²

F = 466,8 N

Чистая сила, действующая на лыжника, представляет собой сумму сил. Две силы, которые следует учитывать, – это сила, направленная вниз по склону, и сила кинетического трения, направленная вверх по склону. Если мы определим положительное направление как спуск по склону, то есть направление движения лыжника, результирующая сила составит:

F _net = F-F _k

F _net = 466. 8 N -21,6 N

F _нетто = 445,2 N

Чистая сила, действующая на лыжника в направлении ее движения на бокс, составляет 445,2 Н .

3.6: Сила и потенциальная энергия

Сила и функция потенциальной энергии

Теперь у нас есть альтернатива использованию теоремы о работе-энергии, когда задействованы консервативные силы – она ​​заключается в вычислении потенциальной энергии и применении механического сохранения энергии.B \ overrightarrow F \ cdot \ overrightarrow {dl} \]

Как мы видели в разделе 3.4, мы можем выразить потенциальную энергию системы как функцию положения, поэтому возникает вопрос: «Есть ли способ« перевернуть »уравнение 3.6.1, чтобы мы могли получить функциональную форму консервативная сила из функции потенциальной энергии? ” Мы знаем, что производные являются «противоположностью» интегралов, поэтому не должно быть слишком удивительным, что обратное уравнению 3. 6.1 принимает форму производной.Чтобы увидеть, как это работает, давайте рассмотрим только очень крошечное изменение потенциальной энергии из-за очень небольшого смещения. Это изменяет левую часть уравнения 3.6.1 на бесконечно малую, а правая часть больше не является суммой многих частей, а представляет собой только одну часть:

\ [dU = – \ overrightarrow F \ cdot \ overrightarrow {dl} \]

В трех измерениях крошечное смещение можно записать как:

\ [\ overrightarrow {dl} = dx \; \ widehat i + dy \; \ widehat j + dz \; \ widehat k \]

Это означает, что скалярное произведение на вектор силы равно:

\ [\ overrightarrow F \ cdot \ overrightarrow {dl} = F_x dx + F_y dy + F_z dz \]

Предположим, что мы делаем крошечное смещение только вдоль оси \ (x \), так что \ (dy \) и \ (dz \) равны нулю.Тогда ясно, что вся работа, выполняемая силой, определяется первым членом выше, и мы получаем, что небольшое изменение потенциальной энергии, которое происходит при небольшом изменении положения в направлении \ (x \), составляет:

\ [dU \ left (x \ rightarrow x + dx \ right) = -F_xdx \; \; \; \ Rightarrow \; \; \; F_x = – \ dfrac {dU} {dx} \]

Это нормально для потенциала, который изменяется только в направлении \ (x \), но что произойдет, если потенциальная энергия также является функцией \ (y \) и \ (z \)? Ответ заключается в том, что мы, , относимся к \ (y \) и \ (z \) как к константам , что означает, что \ (dy = dz = 0 \), и наш результат выше работает. Когда мы рассматриваем \ (y \) и \ (z \) как константы, мы должны сделать что-то немного другое с нашей производной. Например, если мы возьмем производную функции \ (U \ left (x, y \ right) = xy \) по \ (x \), мы получим из правила произведения:

\ [\ dfrac {dU} {dx} = \ dfrac {d} {dx} \ left (xy \ right) = \ left (1 \ right) \ left (y \ right) + \ left (x \ right) \ left (\ dfrac {dy} {dx} \ right) \]

Но если мы будем рассматривать \ (y \) и \ (z \) как константы, производная этих переменных равна нулю, в результате чего второй член выше обращается в нуль.Мы называем эту производную “удержания других переменных постоянными” частной производной , и мы даже используем немного другой символ для ее представления:

\ (частичная \; производная \; от \; функции \; f \; с \; уважением \; к \; x = \ dfrac {\ partial f} {\ partial x} \)

Итак, следуя приведенному выше обсуждению, мы обнаруживаем, что, удерживая две переменные постоянными одновременно (так, чтобы смещение для работы происходило только вдоль одной оси), мы можем получить все компоненты силы из потенциальной функции \ ( U \ влево (х, у, г \ вправо) \):

\ [F_x = – \ dfrac {\ partial} {\ partial x} U, \; \; \; F_y = – \ dfrac {\ partial} {\ partial y} U, \; \; \; F_z = – \ dfrac {\ partial} {\ partial z} U \]

Пример \ (\ PageIndex {1} \)

Объект массой 2. 3} \ nonumber \]

Найдите величину ускорения объекта, когда он достигает положения \ (\ left (x, y, z \ right) = \ left (1,50 м, 3,00 м, 4,00 м \ вправо) \).

Решение

Мы знаем массу объекта, поэтому, если мы можем определить действующую на него действующую силу, мы можем получить его ускорение из второго закона Ньютона. Единственная сила, действующая на этот объект, – это консервативная сила с заданной функцией потенциальной энергии, так что это чистая сила.2}} \ nonumber \]

Мы можем проверить, чтобы убедиться, что этот метод получения силы из потенциальной энергии согласуется со случаями, которые мы уже видели:

Гравитация: \ (U \ left (x, y, z \ right) = mgy + U_o \)

\ [\ left. \ begin {array} {l} F_x = – \ dfrac {\ partial} {\ partial x} U = – \ dfrac {\ partial} {\ partial x} \ left (mgy + U_o \ right) = 0 \\ F_y = – \ dfrac {\ partial} {\ partial y} U = – \ dfrac {\ partial} {\ partial y} \ left (mgy + U_o \ right) = -mg \\ F_z = – \ dfrac {\ partial} {\ partial z} U = – \ dfrac {\ partial} {\ partial z} \ left (mgy + U_o \ right) = 0 \ end {array} \ right \} \; \; \; \Правая стрелка \;\;\; \ overrightarrow F_ {gravity} = – мг \; \ widehat j \]

Сила упругости: \ (U \ left (x, y, z \ right) = \ frac {1} {2} kx ^ 2 + U_o \)

\ [\ left. 2 + U_o \ right) = 0 \ end {array} \ right \} \; \; \; \Правая стрелка \;\;\; \ overrightarrow F_ {elastic} = – kx \; \ widehat i \]

Определение консерваторов или неконсерваторов

Мы знаем, что потенциальную энергию можно определить только для консервативной силы, и до сих пор, чтобы показать, что сила неконсервативна, нам приходилось проводить два линейных интеграла между одними и теми же двумя точками и показывать, что они дают разные результаты, но это Программа нахождения силы из функции потенциальной энергии дает нам еще один менее обременительный метод для этого.Это выглядит примерно так:

• Начните с силы, о которой мы хотим знать, и проинтегрируйте компонент \ (x \) относительно \ (x \), чтобы «отменить» отрицательную частную производную функции потенциальной энергии относительно \ (x \ ). Не забудьте добавить к интегрированию произвольную константу (это неопределенный интеграл):

\ [U \ left (x, y, z \ right) = – \ int F_x dx + constant \]

• Поскольку мы отменили частную производную (которая предполагает, что другие переменные являются постоянными), даже переменные \ (y \) и \ (z \) являются хорошей игрой для произвольной постоянной интегрирования, поэтому запишите константу как неизвестную функция этих переменных:

\ [U \ left (x, y, z \ right) = – \ int F_x dx + h \ left (y, z \ right) \]

Нетрудно показать, что это правильно, взяв отрицательную частную производную по \ (x \) с обеих сторон.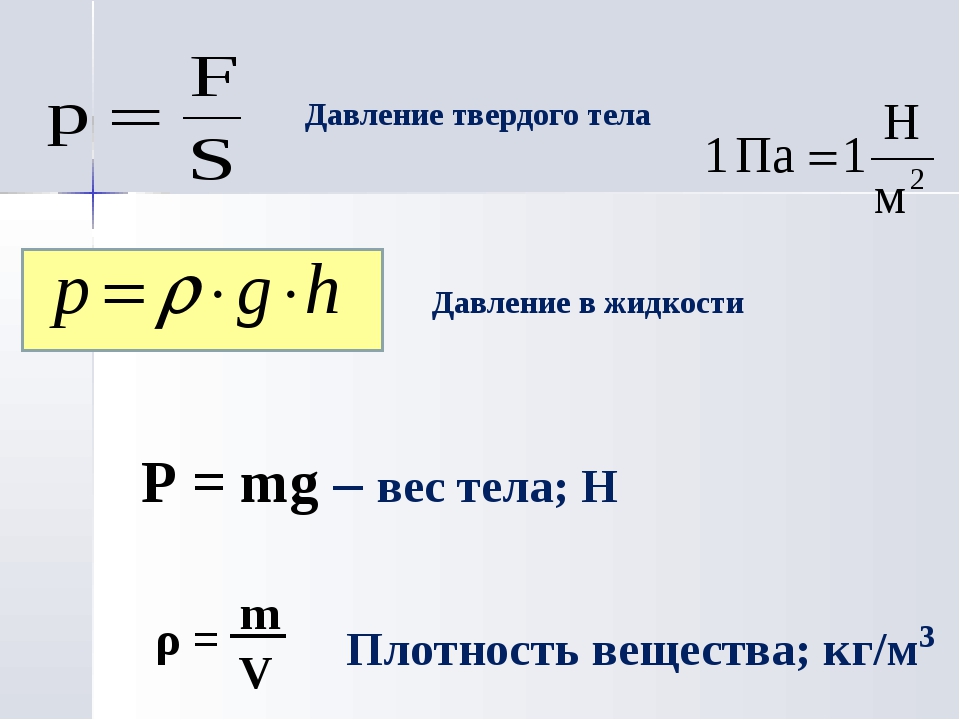

• Используйте эту функцию потенциальной энергии “кандидата”, чтобы получить два других компонента вектора силы. Если это возможно, то функция \ (h \ left (y, z \ right) \) может быть найдена (с точностью до числовой константы). Если нет возможности добраться до компонентов \ (y \) и \ (z \) вектора силы, то это неконсервативно.

Пример \ (\ PageIndex {2} \)

Покажите, что сила, указанная в Примере 3.2.1 (снова приведенном ниже), неконсервативна, используя метод попытки интегрирования силы.

\ [\ overrightarrow F \ left (y \ right) = \ alpha y \ widehat i \ nonumber \]

Решение

Имеется только \ (x \) – составляющая силы, поэтому проинтегрируйте это по отношению к \ (x \):

\ [U \ left (x, y, z \ right) = – \ int F_x dx = – \ alpha xy + h \ left (y, z \ right) \ nonumber \]

Если мы выберем функцию \ (h \ left (y, z \ right) \) равной нулю, не так ли? Разве мы не показали, что сила консервативна? В конце концов, его производная по \ (x \) дает нам \ (x \) – составляющую силы, и это единственная составляющая. Не так быстро! Остальные компоненты равны нулю, и мы также должны иметь возможность получить эти компоненты из частных производных. Вот где у нас возникают проблемы. Взяв частную производную по \ (y \) и положив ее равной нулю, получим:

\ [F_y = – \ dfrac {\ partial} {\ partial y} U = – \ dfrac {\ partial} {\ partial y} \ left (- \ alpha xy + h \ left (y, z \ right) \ right) = \ alpha x – \ dfrac {\ partial h} {\ partial y} \ nonumber \]

Это может быть равно нулю (и дать правильную составляющую \ (y \) силы), если \ (\ dfrac {\ partial h} {\ partial y} \) равно \ (\ alpha x \).Но как это может быть правдой, если функция \ (h \) зависит от \ (y \) и \ (z \)? Это невозможно математически, а это значит, что эта сила неконсервативна.

Хотя маловероятно, что вы столкнулись с этим на данном этапе, если вы не прошли больше курсов математики, чем обычно, вам следует знать о сокращенной записи, которая существует для этого процесса получения вектора силы из функции потенциальной энергии. Вместо того, чтобы писать три уравнения – по одному для каждой составляющей силы – это соотношение часто записывается как векторное уравнение, которое выглядит так:

\ [\ overrightarrow F = – \ overrightarrow \ nabla U \]

Забавный на вид треугольник вектор называется градиентным оператором , или «дель», и может быть записан так:

\ [\ overrightarrow \ nabla \ Equiv \ widehat i \; \ dfrac {\ partial} {\ partial x} + \ widehat j \; \ dfrac {\ partial} {\ partial y} + \ widehat k \; \ dfrac {\ partial} {\ partial z}, \]

Обратите внимание, что \ (\ overrightarrow \ nabla \) сам по себе не является вектором – он должен «воздействовать» на функцию для создания вектора.2 \ вправо) \]

Обратите внимание, что каждая точка, находящаяся на одинаковом расстоянии от начала координат, дает одинаковую потенциальную энергию, поскольку функция потенциальной энергии пропорциональна квадрату радиуса сферы с центром в начале координат. Это означает, что если объект движется между двумя точками в пространстве, где обе точки находятся на одинаковом расстоянии от начала координат, то (при условии, что это единственная действующая сила) объект движется с одинаковой скоростью в обеих точках. Это потому, что механическая энергия сохраняется, а потенциальная энергия не изменилась, поэтому кинетическая энергия также не изменилась.

Каждое значение, доступное для \ (U \ left (x, y, z \ right) \) выше, определяет поверхность сферы с центром в начале координат, на которой каждая точка соответствует одной и той же потенциальной энергии. Но приведенная выше функция потенциальной энергии не уникальна. Каждая такая функция определяет поверхности с одинаковой потенциальной энергией. Мы называем эти эквипотенциальные поверхности . Хороший пример этого – пунктирные линии, которые вы видите на топографических картах, используемых туристами – каждая пунктирная линия представляет фиксированную высоту и, следовательно, равный гравитационный потенциал.

Давайте вычислим вектор силы для потенциала, указанного выше:

\ [\ overrightarrow F = \ widehat i \; \ left (- \ dfrac {\ partial U} {\ partial x} \ right) + \ widehat j \; \ left (- \ dfrac {\ partial U} {\ partial y} \ right) + \ widehat k \; \ left (- \ dfrac {\ partial U} {\ partial z} \ right) = 2 \ alpha \ left (x \ widehat i + y \ widehat j + z \ widehat k \ right) \]

Надеюсь, вы узнали часть этого вектора в скобках. Это вектор положения относительно начала координат, уравнение 1.6.1. Этот вектор указывает прямо на точку \ (\ left (x, y, z \ right) \) от начала координат, что означает, что он находится на перпендикулярно сфере с центром в начале координат, содержащей эту точку . Оказывается, общим свойством является то, что консервативная сила, связанная с потенциалом, перпендикулярна эквипотенциальным поверхностям во всем пространстве .

Обратите внимание, что для функции \ (U \ left (x, y, z \ right) \) выше, если \ (\ alpha> 0 \), потенциальная энергия становится на меньше по мере удаления от начала координат, и вектор силы от этого потенциала направлен от начала координат.Это также общая черта – консервативная сила, связанная с потенциалом, указывает в направлении от большего потенциала к более низкому потенциалу . По многим причинам должно быть ясно, почему это так. Если объект перемещается из области с более высоким потенциалом в область с более низким потенциалом, это уменьшение PE должно быть уравновешено увеличением KE , что означает, что объект ускоряется. Объекты ускоряются, когда результирующая сила, действующая на них, направлена ​​в том же направлении, что и они движутся, поэтому сила должна указывать от места, где PE выше, к месту ниже.

Второй закон Ньютона – Законы Ньютона – WJEC – GCSE Physics (Single Science) Revision – WJEC

Несбалансированные силы

Когда силы, действующие на объект, не уравновешиваются, результирующая сила заставит объект ускоряться в направлении равнодействующей силы.

Другими словами, результирующая сила, действующая на тело, заставит его изменить свое скорость. Это просто означает, что неуравновешенные силы вызовут:

• ускорение
• $3.$1″> замедление
• изменение направления

Результирующая сила – это остаточная или чистая сила, когда все силы, действующие на объект, были объединены.{2}} {\ text {)}} \]

\ [\ text {F} = \ text {m} \ times \ text {a} \]

Вы должны будете иметь возможность сформулировать это уравнение в экспертиза.

Вопрос

Автомобиль весит 1000 кг. Результирующая сила равна 5000 Н. Используйте треугольник Fma, чтобы найти ускорение автомобиля.

Показать ответ

1.0.$0.$1.$9.3″>

Ускорение = результирующая сила ÷ масса

a = 5000 Н ÷ 1000 кг = 5 м / с ²

Результирующая сила и расчет ускорения

Для расчета ускорения необходимо найти равнодействующую силу, так что вы можете разделить ее на массу автомобиля.

Результирующая сила = 4000 Н – 1000 Н = 3000 Н

\ [\ text {ускорение} = \ frac {\ text {результирующая сила}} {\ text {mass}} \]

= 3000 Н ÷ 1000 кг

= 3 м / с ^{0.0.0.1:0.1.0.$0.$2.$6.$1″> 2}

Первая машина ускоряется, потому что она движется в том же направлении, что и результирующая сила. Теперь посмотрим на вторую машину.

Результирующая сила = -7000 Н

\ [\ text {ускорение} = \ frac {\ text {результирующая сила}} {\ text {mass}} \]

= -7000 Н ÷ 1000 кг

= – 7 м / с ²

Вторая машина замедляется.Он движется в направлении, противоположном результирующей силе.

Ускорение и масса обратно пропорциональны. Это означает, что если масса автомобиля удваивается, ускорение уменьшается вдвое, если результирующая сила не меняется.

Результирующая сила и ускорение прямо пропорциональны. Если результирующая сила удваивается, ускорение транспортного средства также удваивается, если масса транспортного средства такая же.

Вопрос

Автомобиль имеет массу 1200 кг и двигатель, развивающий силу 6000 Н.Найдите ускорение автомобиля.

Показать ответ

a = F ÷ m

= 6000 Н ÷ 1200 кг

= 5 м / с ^{11ryh83bg18.0.0.0.1:0.1.0.$0.$2.$16.3.$2.$1″> 2}

Вопрос

Найдите силу, развиваемую двигателем скоростного катера, если лодка имеет массу 300 кг и может ускоряться со скоростью 1,5 м / с ² .

Показать ответ

F = m × a

= 300 кг × 1,5 м / с ²

= 450 N

11ryh83bg18.0.0.0.1:0.1.0.$0.$2.$18″>

Вопрос

В тематическом парке на одной из аттракционов двигатель, который может передавать пустому легковому автомобилю усилие в 3600 Н, заставляя его ускоряться со скоростью 4.5 м / с ² .

Найдите массу автомобиля.

Показать ответ

m = F ÷ a

= 3600 Н ÷ 4,5 м / с ²

1.0.$0.$2.$18.3.$2″> = 800 кг

Урок 19: Net Force

До этого момента мы фокусировались на ситуациях, в которых на объект действует только одна сила.

• В реальном мире редко можно встретить подобные ситуации.
• Обычно на объект действует как минимум пара сил.
• Что нам нужно сделать, так это выяснить, как все эти отдельные силы действуют на объект в целом.

Это то, что мы делаем, когда смотрим на чистую силу.

• Что они имеют в виду, когда говорят о своей заработной плате брутто и нетто?
  • Валовая заработная плата – это сумма, которую вам платят до любых удержаний.
  • Чистая зарплата – это сумма, которую вы фактически получаете на свой чек после всех удержаний.
• То же самое, когда мы исследуем чистую силу.
• После того, как вы сложите и вычтете все силы, у вас останется чистая сила, действующая на объект.

Есть несколько общих сил, действующих на объекты, которые вам необходимо запомнить:

F _г = сила тяжести

F _a = приложенная сила

F _Н = нормальная сила

F _NET = полезная сила

F _f = сила трения

Чтобы отслеживать, как все эти силы действуют на один объект, рекомендуется нарисовать диаграмму свободного тела.

• Схема свободного тела – это просто эскиз объекта, показывающий все силы, действующие на него.
  1. Нарисуйте быстрый набросок объекта.
  2. Нарисуйте стрелку, показывающую каждые силы, действующие на объект.
  3. Чтобы вычислить чистую силу, сложите любые векторы, действующие на одной оси (x и y), обращая внимание на направления.

Довольно часто мы можем игнорировать многие силы, которые нейтрализуют друг друга.

• Мы сосредотачиваемся на силах, которые на самом деле участвуют в движении объекта.
• В большинстве случаев мы можем сосредоточить внимание на двух силах: F _, и F _{, f} .
• При расчете чистой силы, действующей на объект в этих ситуациях, мы используем формулу…

F _NET = F _a + F _f

• Обратите внимание, что мы не говорим, что вычитаем две силы.
• Вместо этого вы должны помнить, что если одна из сил указывает в одном направлении (например, вправо), а другая сила указывает в другом направлении (например, влево), вам нужно будет сделать одну из них. положительный и другой отрицательный.

Пример 1. Я хочу протолкнуть клетку моего тарантула 8,7 кг через стол. Я толкаю с силой 29 Н, а сила трения между столом и клеткой составляет 8 Н. Определите , насколько клетка будет ускоряться.

Сначала нарисуйте диаграмму свободного тела.

Поскольку по оси Y ничего не происходит, мы можем игнорировать силы F _g и F _N .

F _NET = F _a + F _f

= 29N + -8N

F _NET = 21N

Мне пришлось сделать трение отрицательной силой, потому что оно направлено в направлении, противоположном приложенной силе.

Если вы хотите рассчитать ускорение объекта, всегда используйте действующую на него чистую силу.

F _NET = ma

a = F _NET / м

= (21N) / (8,7 кг)

a = 2,4 м / с ²

Вопрос лифта

Понятие чистой силы становится немного сложнее, если вы исследуете сложную систему, такую ​​как лифт, поднимающийся и опускающийся.

• Назвать лифт комплексом может показаться странным, но это действительно серьезная проблема.
• Как вы думаете, вы бы ответили на вопрос о вашем весе, когда лифт ускоряется вверх или вниз?

Что произойдет с вашим весом, когда лифт набирает скорость?

• Вы когда-нибудь замечали, что когда лифт впервые начинает подниматься, вы чувствуете, что вас немного толкают вниз?
• Это потому, что вы чувствуете ускорение лифта . .. это на мгновение заставляет вас чувствовать себя немного тяжелее.
• Весы покажут это как увеличение вашего веса (временно).

Что произойдет с вашим кажущимся весом, если лифт начнет ускоряться вниз?

• Вы почувствуете, как под вами выпадает лифт.
• Если бы он действительно выпал из-под вас, это было бы похоже на то, как будто он падает на «Космический выстрел» в Galaxyland… вы бы чувствовали себя невесомым!
• Весы покажут уменьшение вашего веса.

Давайте посмотрим, как мы на самом деле вычислим некоторые числа для этого типа вопросов, посмотрев на пример.

• Держите одну вещь в глубине души. Обычная шкала предназначена для измерения вещей в килограммах и рассчитана на нормальную гравитацию Земли 9,81 м / с ² . Позже вы поймете, почему это важно.

Пример 2: Вы стоите на весах лифта. У вас масса 75 кг. Определите, что на шкале будет отображаться как ваша «кажущаяся» масса (в килограммах), если…

a) лифт начинает ускоряться вверх со скоростью 3,0 м / с ² .

Нам нужно думать о чистой силе как о силе, давящей на весы, заставляющей их давать показания.

• Лифт, толкающий меня вверх , заставит меня толкнуть вниз на полу (3-й закон Ньютона).
  • Мы покажем это, сделав ускорение (3,0 м / с ² ) отрицательным значением.
• Формула для этого будет выглядеть так…

F _NET = F _g + F _a

• Мы будем рассматривать силу тяжести (F _g ) как обычную силу моего тела, толкающего вниз пол лифта.
• Приложенная сила (F _a ) – это то, насколько ускорение лифта увеличивает или уменьшает мою силу на полу лифта.

F _NET = F _g + F _a

= мг + ма <- так как масса обычная, я вычту ее

= м (г + а)

= 75 кг (-9,81 м / с ² + -3,0 м / с ² ) <- оба отрицательны

= 75 кг (-12. 81 м / с ² )

F _NET = -9,6e2 N

• Ой! Когда вы в последний раз видели, как шкала показывает значение в ньютонах?
  • Я могу преобразовать это значение в килограммы, вспомнив, что весы, которые мы используем, понятия не имеют, что происходит … они все еще думают, что находятся в чьей-то ванной, где сила тяжести – хорошая постоянная 9,81 м / с ² .

F _NET = мг

m = F _NET / г

= (-9.6e2 Н) / (-9,81 м / с ² )

м = 98 кг

Значит, на обычных весах вы весите 98 кг!

б) лифт начинает ускоряться вниз со скоростью 4,0 м / с ² .

Мы рассмотрим эту часть вопроса точно так же.

• Единственная разница в том, что из-за того, что лифт вылетает из-под меня, я буду меньше прижиматься к полу.
• Ускорение лифта будет положительным.

F _NET = F _g + F _a

= мг + ма

= м (г + а)

= 75 кг (-9,81 м / с ² + 4,0 м / с ² ) <- оба отрицательны

= 75 кг (-5,81 м / с ² )

F _NET = -4,4e2 N

На шкале будет …

F _NET = мг

m = F _NET / г

= (-4.4e2 Н) / (-9,81 м / с ² )

м = 44 кг

Значит, на обычных весах вы весите 44 кг!

Задачи динамики (сила или 2-й закон Ньютона) – Физика

Задачи динамики (сила или 2-й закон Ньютона)

Задачи динамики (силы) просят вас связать движение с вызывающими его силами. Обратите внимание, что слово «сила» не всегда используется явно в формулировке проблемы. Вы знаете, что многие силы, такие как гравитация, натяжение и нормальная сила, присутствуют, даже если они не указаны в задаче.

Примеры проблем

• 1D

• 2D

• Многократный объект

• Циркуляр

• Buoyant Force

• Составной

• Электричество и магнетизм

Как решить проблемы с силой

• 1.Определите проблему

  Любая проблема, которая просит вас связать силу и движение, является проблемой Второго закона Ньютона, , независимо от того, что было дано или запрошено в задаче . В некоторых случаях второй закон Ньютона легко идентифицировать – например, проблема может спросить вас о значении определенной силы.

  В других случаях труднее распознать проблемы второго закона. Вы можете знать силы, которые присутствуют, но о силе никогда не упоминалось в задаче, и вас могут спросить, как быстро объект движется по кругу или какая часть объекта находится под водой.Понимание того, как подойти к этим проблемам, приходит на основе опыта – уделение времени тому, чтобы ответить на вопрос «откуда я узнал, что это проблема второго закона» для каждого отдельного примера силы, с которым вы работаете, поможет развить ту интуицию, которая вам понадобится на заключительном экзамене. .

• 2. Нарисуйте картинку

  Когда вы подходите к задачам силы, диаграмма свободного тела позволит вам как представить себе, что происходит, так и напрямую отобразить картинку в уравнении. Вся физика делается в процессе рисования диаграммы – после этого шага остается только алгебра.

  Первое, что вам нужно сделать, это определить , какие объекты будут в центре внимания диаграммы – другими словами, какую систему вам нужно рассмотреть, чтобы ответить на вопрос. В некоторых случаях вам нужно будет рассматривать несколько объектов как отдельные системы. В таких случаях вы будете рисовать диаграммы свободного тела и составлять уравнения для каждого объекта отдельно. Вы, скорее всего, воспользуетесь третьим законом Ньютона, чтобы связать силы, действующие на два объекта.

  После того, как вы определили свою систему, подумайте обо всех силах в этой системе, отбросьте все, что слишком мало, чтобы иметь значение.Только вынуждает воздействовать на , объект должен быть показан, поскольку вы пытаетесь понять, что вызывает движение объекта. Диаграмма свободного тела отображается непосредственно в левую часть ∑F ​​= ma. Ускорение – это результат, а не причина – если вы хотите изобразить ускорение, убедитесь, что вы делаете это в стороне, а не в зарисовке сил.

  Поскольку Второй закон Ньютона является векторным уравнением, вам нужно разделить все силы на их x- и y-компоненты, чтобы работать с уравнением.Математика всегда будет проще, если вы выберете одну ось в направлении , ускорение . Таким образом, один компонент a будет равен нулю, и у вас будет меньше связанных уравнений.

• 3. Выберите родство

  Все силовые задачи начинаются с соотношения ∑F = ma. Это правда, независимо от того, что вас просят найти. Если потребуется дополнительная информация, она станет очевидной по мере того, как вы решите проблему.

• 4.Решить проблему

  ∑F = ma – векторное уравнение, поэтому оно задается отдельно в направлениях x и y. Тщательно продумайте направление каждой силы и поставьте соответствующий знак. После того, как вы вложите свои силы в эти уравнения, у вас останется только алгебра, и вы сможете решать уравнения любым удобным способом. В общем, проще всего сначала решить уравнение, в котором a = 0, так как иногда вам понадобятся эти значения в другом выражении.

• 5.Поймите результаты

  Решив проблему, взгляните на нее еще раз. Ваш ответ имеет смысл? Было ли это поведение, которое вы интуитивно ожидали найти? Можете ли вы сейчас выполнить действия, которые раньше вызывали у вас проблемы? Вы можете словами объяснить, что происходит? Если вы определили это как проблему второго закона только из-за заголовка раздела в вашем учебнике, укажите информацию, которую вы бы использовали, чтобы распознать подобную проблему на выпускном экзамене.

Помогите! Я не могу найти пример, который мне нужен для работы!

• Вы уверены, что ваша проблема – проблема Второго закона Ньютона?

  Одна из самых распространенных ошибок – слишком много думать. Если вам сообщают чистую силу и запрашивают ускорение или наоборот, вам не нужно проходить все этапы задачи Второго закона Ньютона. Проверьте задачи определения и соотношения, чтобы увидеть, сможете ли вы найти полезный пример.

  Также возможно, что вашу задачу лучше решить с помощью кинематики (описания движения) или энергии и импульса. Можете ли вы четко объяснить себе, что ваша проблема требует, чтобы вы связали причину движения (силы) с действием этих сил (ускорение или изменение скорости?)

• Да, моя проблема определенно является проблемой Второго закона Ньютона.

  В таком случае подумайте шире о том, что является полезным примером. Помните, вы получили задание практиковать подход к решению проблем не потому, что отвечает на на ваши проблемы особенно интересными. Пример, в котором вы просто заменяете числами числа в задаче, даст вам возможность попрактиковаться в вводе чисел на калькуляторе, но ничего не научит вас физике, а когда вы сдадите экзамен, каждая задача будет казаться вам новой и непохожей. Так что думайте о своем примере как о поддержке, которая поможет вам практиковать подход к решению проблем.

  и Каждая проблема в этом разделе использует один и тот же подход, поэтому любая проблема является подходящим примером, который поможет вам подойти к вашей проблеме. То, как вы ее решаете, определяет не то, как выглядит проблема , а тип взаимодействия (в данном случае сила), который вам нужно учитывать. Тем не менее, разные ситуации требуют от вас решения разных побочных задач.Круговое движение требует, чтобы вы знали о центростремительном ускорении, подъемная сила требует, чтобы вы знали о плотности, наклонная плоскость требует, чтобы вы знали, как делить векторы на компоненты, а задачи с множеством объектов требуют от вас понимания Третьего закона Ньютона. Так что, если ваша проблема имеет какие-либо из этих функций, вам может быть полезно выбрать пример, который также имеет. Но не волнуйтесь, вам не нужен (и не нужен) пример, который точно соответствовал бы вашей задаче!

.