Как найти х0 в физике: Подскажите формула х0 по физике — Знания.site

Определение координаты движущегося тела (9 класс)

Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.

Механическое движение

При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.

Равномерное движение

При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).

Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо

Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:

Рис. 1. Формула координаты тела при прямолинейном равномерном движении

Где:

• Xо – начальная координата тела;
• X – координата в момент времени t;
• Vx – проекция скорости на ось X.

Неравномерное движение

Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.

Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)

Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.

Рис. 2. Формула ускорения

Следовательно, скорость в любой момент времени можно найти следующим образом:

V=Vо+at

Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.

Как найти путь при равноускоренном движении?

Рис. 3. Прямолинейное равноускоренное движение

Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2

Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2

Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или

X=Xo+Voxt+axt2/2

Движение тела по вертикали

Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения.

Оно всегда одинаковое: g=9,8 м/кв.с.

При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.

Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2

Движение тела по окружности

При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.

Что мы узнали?

Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.

Оценка доклада

А какая ваша оценка?

Уравнение координаты при равноускоренном прямолинейном движении

Определение и формулы

Уравнение координаты — зависимость координаты тела от времени:

x = x(t)

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени

t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с². Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел.

Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с² без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с.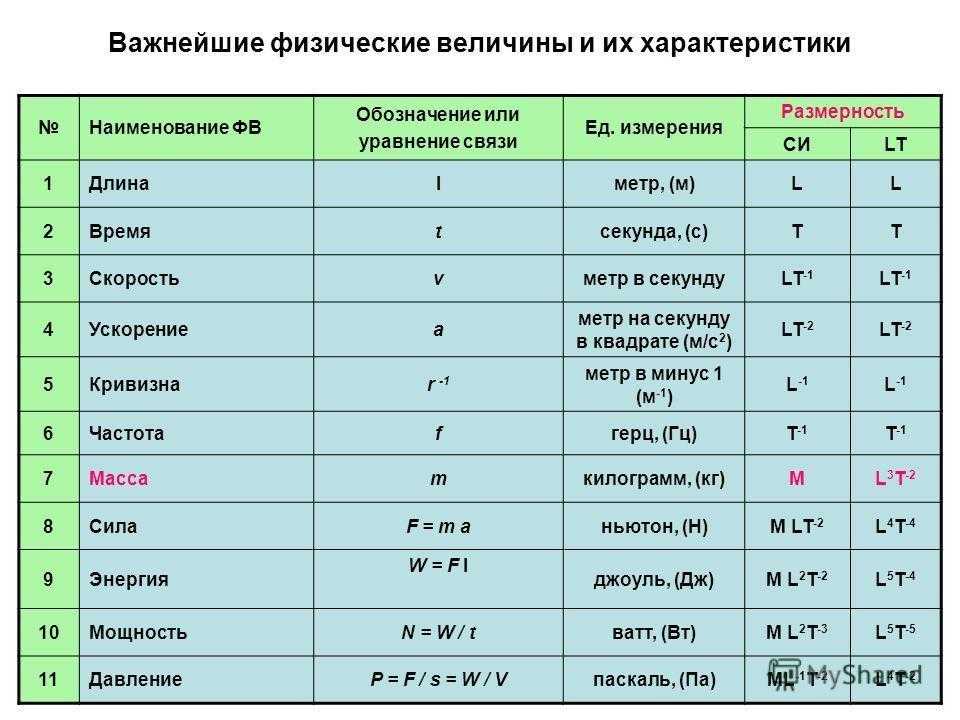

Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Пример №3.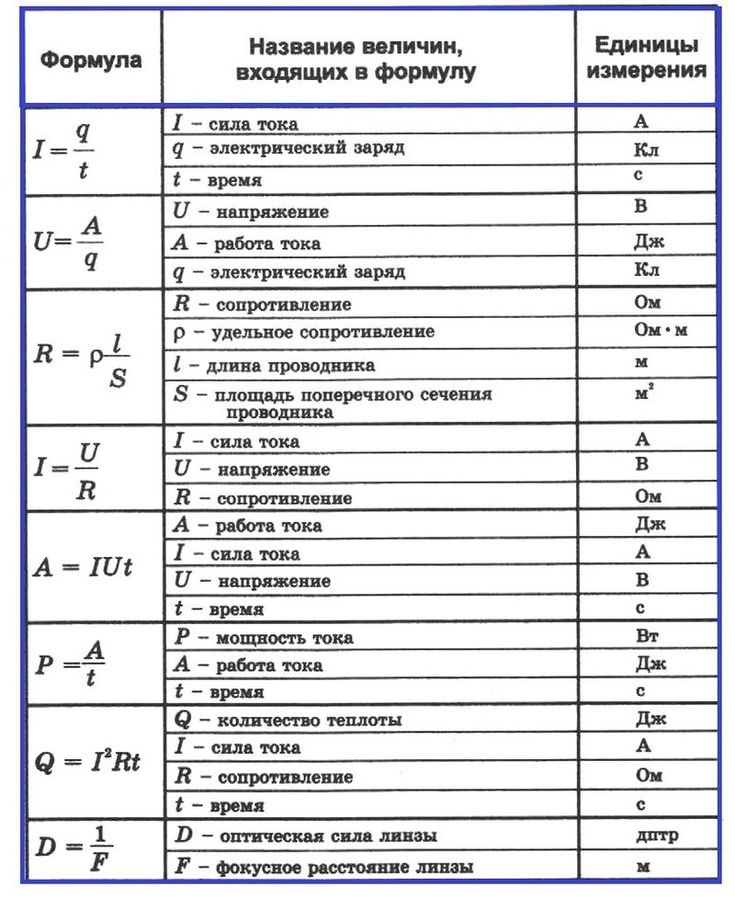 Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с² и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с

2, достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t

:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение.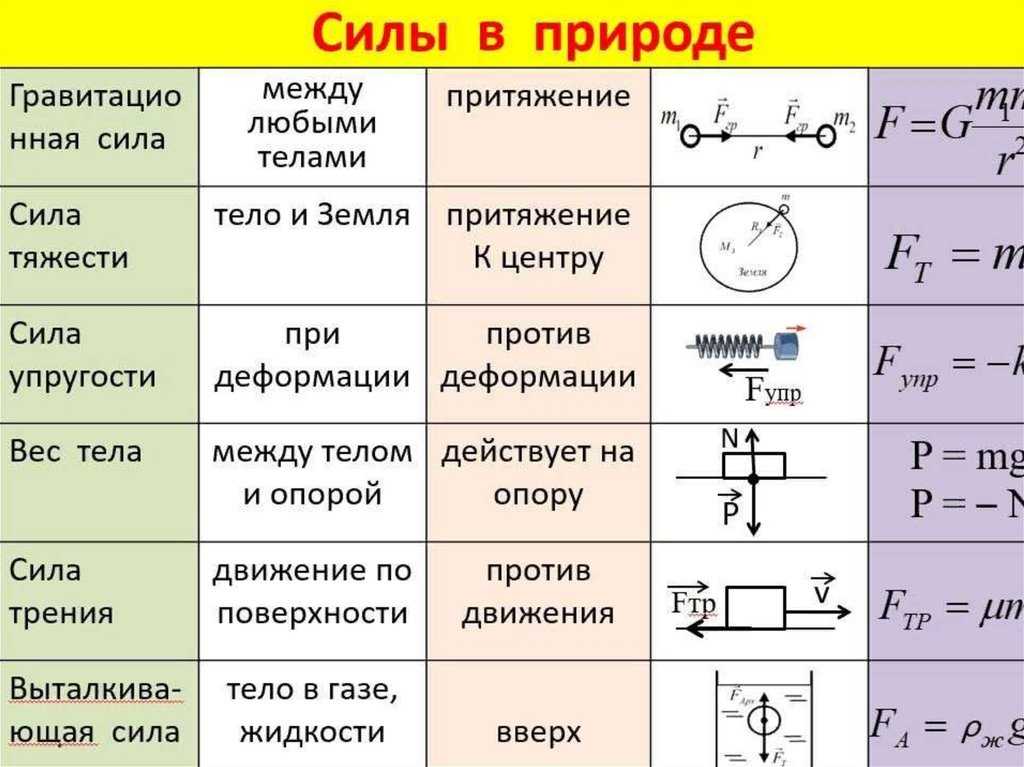 Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Задание EF18609

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x

и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

---

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17682 Мимо остановки по прямой улице с постоянной  скоростью проезжает грузовик. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с², и догоняет грузовик на расстоянии 150 м от остановки. Чему равна скорость грузовика?

---

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

Исходные данные:

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с².

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет вид:

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 14.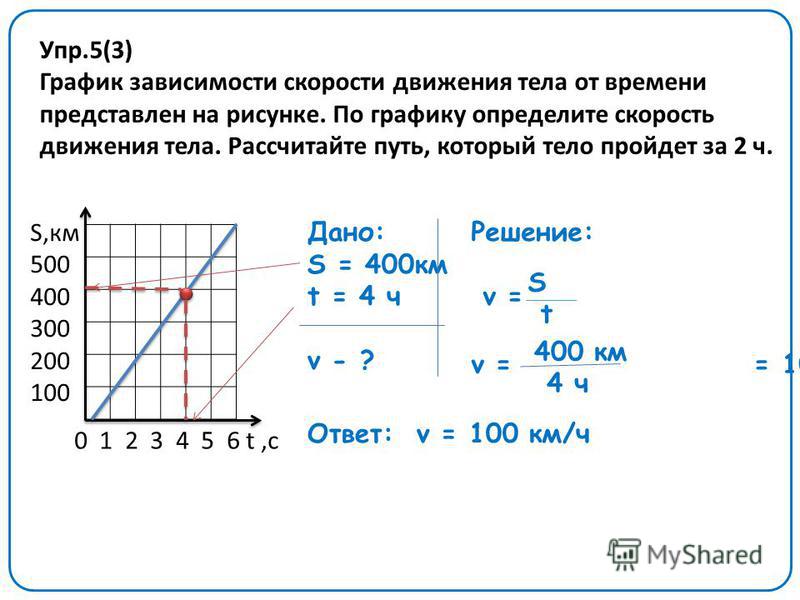 3k

Гармоническое движение

Гармоническое движение

Говорят, что объект, движущийся вдоль оси X, демонстрирует простое гармоническое движение , если его положение как функция времени изменяется как

x(t) = x ₀ + A cos(ωt + φ).

Объект колеблется вокруг положения равновесия x ₀ . Если мы выбираем начало нашей системы координат так, что x ₀ = 0, тогда смещение x от положения равновесия как функция времени определяется выражением

x(t) = A cos(ωt + φ).

А – амплитуда колебаний, т. е. максимальное смещение объекта из положения равновесия либо в положительное или отрицательное направление x. Простое гармоническое движение повторяется. период T – время, за которое объект совершить одно колебание и вернуться в исходное положение. угловая частота ω определяется как ω = 2π/T. Угловая частота измеряется в радианах в секунду. Обратная сторона период частота f = 1/T. частота f = 1/T = ω/2π движения дает число полных колебаний в единицу времени. Измеряется в герцах (1 Гц = 1/с).

Скорость объекта как функция времени определяется как

v(t) = dx(t)/dt = -ω A sin(ωt + φ),

а ускорение дается

a(t) = dv(t)/dt = -ω ² A cos(ωt + φ) = -ω ² x.

Величина φ называется фазовой постоянной . Он определяется начальными условиями движения. Если при t = 0 объект имеет максимальное смещение в положительном направлении x, тогда φ = 0, если он имеет максимальное смещение в отрицательном направлении x, тогда φ = π. Я толстый t = 0 частица движется через положение равновесия с максимальным скорость в отрицательном направлении x, тогда φ = π/2. Величина ωt + φ равна называется фаза .

На рисунке ниже положение и скорость представлены как функция времени. для колебательного движения с периодом 5 с. Амплитуда и максимальная скорость имеют условные единицы. Положение и скорость вне фазы . Скорость равна нулю при максимальном смещении, и смещение равно нулю на максимальной скорости.

Для простого гармонического движения ускорение a = -ω ² x равно пропорционально смещению, но в обратном направлении. Простой гармоническое движение – ускоренное движение . Если объект демонстрирует простое гармоническое движение, на него должна действовать сила. объект. Сила

F = ma = -mω ² х.

Он подчиняется закону Гука , F = -kx, при k = mω ² .

Ссылка: простая гармоническое движение (Youtube)

---

F = ma = md ² x/dt ² с F = -kx ведет к второго порядка дифференциальное уравнение

d ² х/dt ² = -(к/м)х.

Теперь мы знаем, как решить это уравнение. Решение

x(t) = Acos(ωt + φ), где ω ² = k/m.

Решение дифференциального уравнения второго порядка включает две константы интеграция. Здесь этими константами являются A и φ. Они определяются начальными условиями задачи.

Одни и те же уравнения имеют одни и те же решения. Всякий раз, когда вы сталкиваетесь с дифференциальное уравнение вида d ² x/dt ² = -b ² x, вы знаете что решение x(t) = Acos(ωt + φ), при ω = b.

---

Сила пружины подчиняется закону Гука. Предположим, что объект прикреплен к пружине, которая растягивается или сжимается. Тогда пружина давит сила на объект. Эта сила пропорциональна смещению х тела. пружинит из положения равновесия и движется в направлении, противоположном смещение.

Ф = -кх

Предположим, что пружина растянута на расстояние A от положения равновесия, а затем отпущена. Объект прикрепленный к пружине, ускоряется, возвращаясь к положению равновесия.

a = -(к/м)х

Он набирает скорость по мере продвижения к положению равновесия, потому что его ускорение направлено в сторону его скорости. Когда он находится в равновесии положение, ускорение равно нулю, но объект имеет максимальная скорость. Он выходит за пределы положения равновесия и начинает замедляться. вниз, потому что ускорение теперь в направлении, противоположном направлению от его скорости. Пренебрегая трением, он останавливается, когда пружина сжимается на расстояние А, а затем ускоряется обратно к равновесию позиция. Он снова промахивается и останавливается в исходном положении, когда пружина растягивается на расстояние A. Движение повторяется. Объект колеблется взад и вперед. Он выполняет простое гармоническое движение. Угловой частота движения

ω = √(к/м),

период

Т = 2π√(м/к),

и частота

f = (1/(2π))√(к/м).

Резюме: Если единственная сила, действующая на тело массой m, является силой закона Гука, 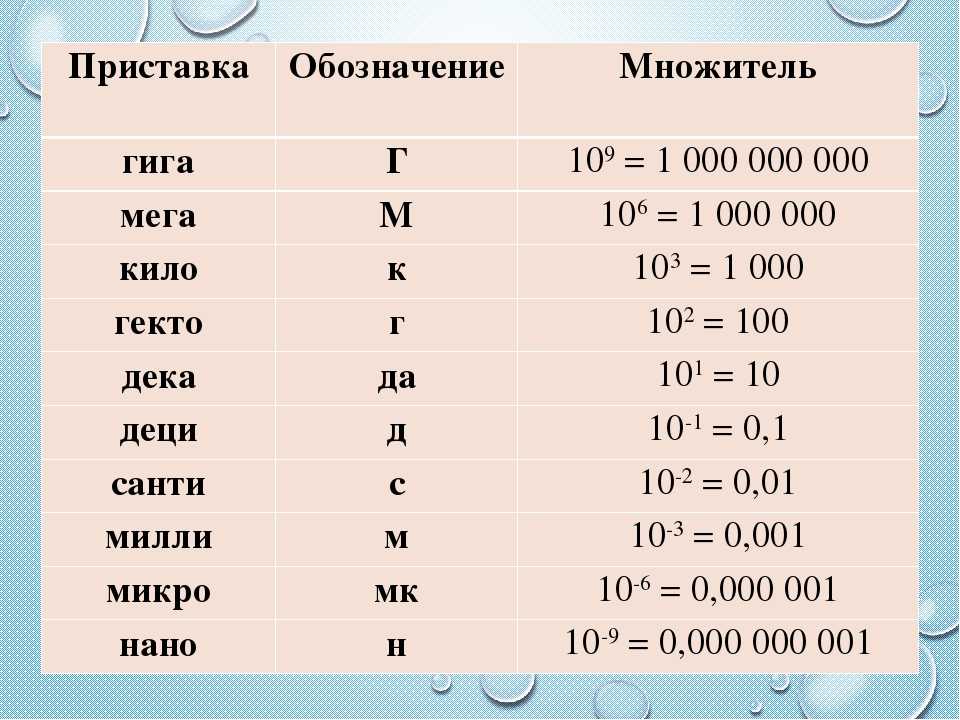F = -kx тогда движение объекта представляет собой простое гармоническое движение. Если x — смещение от равновесия, мы имеем . x(t) = Acos(ωt + φ), v(t) = -ωAsin(ωt + φ), a(t) = -ω2Acos(ωt + φ) = -ω2x. ω = (к/м) ½ = 2πf = 2π/T. А = амплитуда ω = угловая частота f = частота Т = период φ = фазовая постоянная

Проблема:

Частица совершает простые гармонические колебания, так что ее перемещение изменяется согласно выражению x = (5 cm)cos(2t + π/6) где x в сантиметрах, t в секундах. При t = 0 найти
(а) смещение частицы,
(б) его скорость и
(c) его ускорение.
(г) Найдите период и амплитуду движения.

Решение:

• Рассуждение:
  Анализ простого гармонического движения.
  x(t) = A cos(ωt + φ). A = амплитуда, ω = угловая частота, φ = фазовая постоянная.
  v(t) = -ω A sin(ωt + φ), a(t) = -ω ² A cos(ωt + φ) = -ω ² x.
• Детали расчета:
  (a) Смещение как функция времени: x(t) = Acos(ωt + ф). Здесь ω = 2/s, φ = π/6, A = 5 см.
  Перемещение при t = 0 равно x(0) = (5 см)cos(π/6) = 4,33 см.
  (b) Скорость при t = 0 равна v(0) = -ω(5 см)sin(π/6) = -5 см/с.
  (c) Ускорение при t = 0 равно a(0) = -ω ² (5 см)cos(π/6) = -17,3 см/с ² .
  (г) Период движения T = 2π/ω = π с, а амплитуда равна 5 см.

Проблема:

Частица массой 20 г движется в простом гармоническом движении с частотой 3 колебаний в секунду и амплитудой 5 см.
(а) Какое общее расстояние проходит частица за один цикл его движение?
(b)  Какова его максимальная скорость? Где это происходит?
(с) Найдите максимальное ускорение частицы. Где в движении делает происходит максимальное ускорение?

Решение:

• Рассуждение:
  Проанализируйте простое гармоническое движение, x(t) = A cos(ωt + φ).
• Детали расчета:
  (a) Общее расстояние d, которое проходит частица за один цикл, равно от x = -A до x = +A и обратно к x = -A, поэтому d = 4A = 20 см.
  (б) Максимальная скорость частицы
  v _макс. = ωA = 2πfA = 2π 15 см/с = 0,94 м/с.
  Частица имеет максимальную скорость при прохождении через положение равновесия.
  (c) Максимальное ускорение частицы равно 9от 0050 до _макс. = ω ² А = (2πf) ² А = 17,8 м/с ² .
  Частица имеет максимальное ускорение в точках поворота, где имеет максимальное водоизмещение.

Проблема:

Груз массой 1 кг, прикрепленный к пружине с постоянной силой 25 Н/м, совершает колебания на горизонтальная дорожка без трения. При t = 0 масса выходит из состояния покоя при x = -3 см, то есть пружина сжата на 3 см. Пренебречь массой весны. Найти
(а) период его движения,
(б) максимальное значение его скорости и ускорения и
(в) перемещение, скорость и ускорение как функция времени.

Решение:

• Рассуждение:
  Для простого гармонического движения
  x(t) = Acos(ωt + φ),
  v(t) = -ωAsin(ωt + φ),
  a(t) = -ω2Acos(ωt + φ) = -ω2x.
  ω = (к/м) ^½ = 2πf = 2π/T.
• Детали расчета:
  (a) Период равен T = 2π(m/k) ^½ = 2π(1 с ² /25) ^½ = 1,26 с.
  (b)  Угловая скорость ω = (к/м) ^½ = 5/с.
  Максимальная скорость v _max = ωА = 15 см/с.
  Максимальное ускорение частицы составляет _макс. = ω ² А = 0,75 м/с ² .
  (в) x(t) = Acos(ωt + φ) = (3 см)cos((5/с)t + π) = -(3 см)cos((5/с)t),
  v(t) = -ωAsin(ωt + φ) = (15 см/с)sin((5/с)t),
  a(t) = -ω ² Acos(ωt + φ) = (0,75 м/с ² )cos((5/с)t).

Предположим, что масса подвешена к вертикальной пружине с жесткостью k. В равновесия пружина растянута на расстояние x ₀ = мг/к. Если масса смещается из положения равновесия вниз, а пружина растягивается дополнительное расстояние x, то полная сила, действующая на массу, равна mg – k(x ₀ + x) = -kx, направленный в сторону положения равновесия. Если масса смещен вверх на расстояние x, то полная сила, действующая на массу, равна mg – k(x ₀ – х) = kx, направленный к положению равновесия. Масса будет выполнять простые гармонические движения. Угловая частота ω = (к/м) ^½ то же для массы, колеблющейся на пружине в вертикальном или горизонтальном положении. Но равновесная длина пружины, вокруг которой она колеблется, различна для вертикальное положение и горизонтальное положение.

---

Предположим, что объект, прикрепленный к пружине, совершает простое гармоническое движение. Позволять один конец пружины прикрепите к стене и дайте предмету двигаться горизонтально на столе без трения.

Какова полная энергия объекта?

Кинетическая энергия объекта

K = ½mv ² = ½mω ² A ² sin ² (ωt + ф).

Его потенциальная энергия является упругой потенциальной энергией. Упругий потенциал энергия, накопленная в пружине, смещенной на расстояние x от положения равновесия U = ½kx ² . Таким образом, потенциальная энергия объекта равна

.

U = ½kx ² = ½mω ² x ² = ½mω ² A ² cos ² (ωt + φ).

Полная механическая энергия объекта

E = K + U = ½mω ² A ² (sin ² (ωt + φ) + cos ² (ωt + φ)) = ½mω ² A ² .

Энергия E в системе пропорциональна квадрату амплитуды .

Е = ½ кА ² .

Это постоянно меняющаяся смесь кинетической и потенциальной энергии.

Для любого объекта, совершающего простое гармоническое движение с угловой частотой ω, восстанавливающая сила F = -mω ² x подчиняется закону Гука и, следовательно, является консервативная сила . Мы можем определить потенциальную энергию U = ½mω ² x ² , а полная энергия объекта определяется выражением E = ½mω ² А ² .

Проблема:

Частица, подвешенная на пружине, совершает колебания с угловой частотой 2 рад/с. Пружина подвешена к потолку кабины лифта и висит неподвижно (относительно автомобиля) по мере снижения автомобиля с постоянной скоростью 1,5 РС. Затем машина внезапно останавливается. Массой пружины пренебречь.
С какой амплитудой колеблется частица?

Решение:

• Рассуждение:
  При движении в лифте с постоянной скоростью общая сила, действующая на масса равна нулю. Сила, действующая на пружину, по величине равна силе силы тяжести, действующей на массу, пружина имеет равновесную длину вертикальная пружина. Когда лифт внезапно останавливается, конец пружины крепятся к потолочным упорам. Однако масса имеет импульс, p = mv, и поэтому начинает растягивать пружину. Он движется через положение равновесия вертикальной пружины с ее максимальной скоростью v _макс. = 1,5 м/с.
  Его скорость как функция времени равна v(t) = -ωAsin(ωt + φ).
• Детали расчета:
  Поскольку v _max = ωA и ω = 2/с, амплитуда амплитуды колебания А = 0,75 м.

Проблема:

Система масса-пружина совершает колебания с амплитудой 3,5 см. Если сила постоянная пружины 250 Н/м и масса 0,5 кг, определить
(а) механическая энергия системы,
(b) максимальная скорость массы и
в) максимальное ускорение.

Решение:

• Рассуждение:
  Механическая энергия системы, совершающей простое гармоническое движение, равна E = ½kA ² = ½mω ² А ² .
• Детали расчета:
  (а) Имеем m = 0,5 кг, A = 0,035 м, k = 250 Н/м, ω ² = к/м = 500/с ² , ω = 22,36/с.
  Механическая энергия системы E = ½kA ² = 0,153 Дж.
  (б) Максимальная скорость массы v _макс. = ωA = 0,78 м/с.
  (c) Максимальное ускорение составляет _макс. = ω ² А = 17,5 м/с ² .

Уравнение скорости (формула): как найти скорость

Уравнение скорости — одна из фундаментальных формул в физике. Хотя многие понятия в физике имеют научные определения, отличные от их использования в разговорной речи, ваше интуитивное восприятие скорости, вероятно, довольно похоже на ее определение в физике. Уравнение скорости:

v _avg = xf-x0/tf-t0

Скорость — это просто скорость изменения положения объекта относительно выбранной точки отсчета, поэтому изменение положения, деленное на время. «Xf» — конечное положение объекта, а «X0» — начальное положение. Точно так же «Tf» — это конечный период времени, а «T0» — начальный период времени.

«Мне нравится физика. Я думаю, что это лучшая наука из всех трех, потому что в целом она более полезна. Вы узнаете о скорости, скорости и времени, и это все умные вещи». — Том Фелтон

Большое изменение положения за достаточно короткий промежуток времени означает, что объект имеет высокую скорость, в то время как небольшое изменение положения за больший промежуток времени означает, что объект имеет более низкую скорость.

Уравнение для скорости

Фото: My Own

Единицы расстояния скорости делятся на время. Подумайте, как скорость автомобиля часто выражается в километрах в час или милях в час. Средняя скорость объекта может быть определена как изменение положения объекта, деленное на время, затраченное на перемещение.

В записи формулы скорости V(avg) — это средняя скорость объекта, а Δx — величина изменения положения объекта, называемая смещением. X0 — начальное положение объекта в момент времени t0, а Xf — конечное положение объекта в момент времени tf. Обратите внимание, что когда начальное время задано равным нулю, уравнение для средней скорости дается следующим образом:

Vavg = Δx/t

В этом уравнении скорость задается как вектор. Векторы — это геометрические объекты, имеющие как направление, так и величину, и поэтому их можно использовать для отслеживания движения чего-либо в пространстве. По отношению к скорости объекта скорость считается вектором, потому что перемещение считается вектором (обладающим как направлением, так и величиной). Скорость обычно указывается в метрах в секунду, так как метры — это международная система единиц. Однако вы часто будете видеть скорость, указанную в других единицах, таких как мили в час, километры в час и даже сантиметры в секунду.

Примеры

Давайте заполним формулу для скорости практическим примером:

Если кто-то идет по тротуару, начиная с дальнего конца тротуара, со скоростью -4 метра каждые пять секунд (отрицательно, потому что они движутся влево от своего начального положения), скорость смещения может быть выражена следующим образом: не предоставляют нам информацию о том, как человек действовал между их конечной точкой и их отправной точкой. Имея только среднюю скорость, мы не можем сказать, споткнулся ли человек и, следовательно, ему потребовалось больше времени, чтобы преодолеть расстояние, чем обычно. Вы можете разбить расстояние поездки на более мелкие участки и рассчитать эти отдельные скорости, чтобы получить больше информации о поездке. Например, общую скорость поездки, или Δxtot, можно представить в виде четырех различных сегментов — Δxa, Δxb, Δxc, Δxd.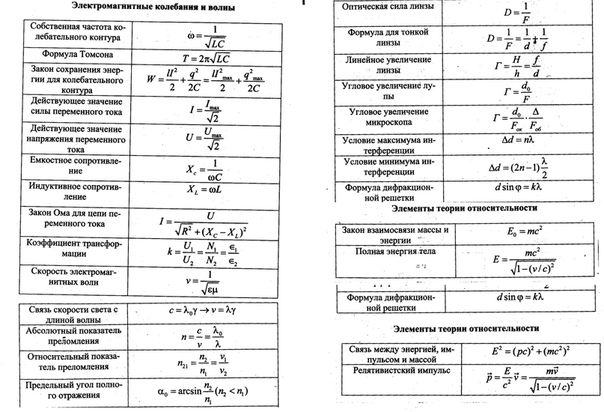

«Все, что я делаю, так или иначе связано со скоростью». — Hansulrich Obrist

Чем меньшие фрагменты вы разбиваете на расчет скорости, тем больше информации вы можете получить о событиях во время полного движения объекта, или тем более подробной становится доступная информация. Для кусков интервалов измеренная скорость называется «мгновенной скоростью». Мгновенная скорость — это, по сути, скорость объекта в конкретный момент времени или средняя скорость в конкретный момент. Спидометр автомобиля показывает величину автомобиля, скорость изменения (а не направление изменения). Чтобы сделать эту разницу более явной: когда полицейский останавливает машину, он будет использовать мгновенную скорость машины, чтобы выписать штраф, но когда вы пытаетесь рассчитать, сколько времени вам потребуется, чтобы пересечь два разных города, вы хотите использовать среднюю скорость.

Давайте рассмотрим еще один пример:

Если автомобиль проезжает 1000 метров и достигает конечной точки, двигаясь с максимальной скоростью за 1 минуту и ​​20 секунд (80 секунд), какова будет скорость транспортного средства? Скорость транспортного средства можно рассчитать следующим образом:

Vavg = (Xf – Xi)/t = Δx/t
или…
Vavg = 1000 м – 0,00 м/80,0 с (где конечная точка пути – 1000 м).
Vср = 1000 м/80 с
Vср = 12,5 м/с

Следовательно, скорость автомобиля равна 12,5 м/с.

Разница между скоростью и скоростью

Фото: LoggaWiggler через Pixabay, CC0

Большинство людей используют термин «скорость» так, как будто он эквивалентен термину «скорость», поэтому в разговорной речи эти термины взаимозаменяемы. Тем не менее, вы должны знать, что в области физики скорость и скорость — это две разные вещи со своими собственными значениями. Одно из основных различий между скоростью и скоростью состоит в том, что скорость имеет направление, а скорость — нет. Скорость — это всего лишь скалярная величина, переменная, имеющая только одно значение в каждый момент времени.

Подобно разнице между средней и мгновенной скоростью, существует также разница между средней и мгновенной скоростью. Мгновенную скорость можно рассматривать как эквивалент величины мгновенной скорости. Таким образом, в то время как скорость может быть отрицательной относительно начальной точки объекта, как в приведенном выше примере -4,0 м/5 с, мгновенная скорость будет положительной 4,0 м/5 с.