Как найти момент инерции: Как определить момент инерции тела. Формула момента инерции - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Момент инерции – формулировка, свойства и методы решения

Одним из фундаментальных свойств физических тел является момент инерции. Люди с ним сталкиваются в повседневной жизни при езде на велосипеде или автомобиле, запуске различных механизмов, игре с мячом, катании на карусели и т. д. Изучают характеристику на уроках физики и сопромата. Знание этого параметра важно и в механике, особенно при нахождении силы, которая может привести тело к вращению.

Содержание

Основные понятия и суть
Вычисление параметра
- Методика решения
- Моменты простейших объектов
Теорема Гюйгенса — Штейнера
Пример задачи

Основные понятия и суть

Инерция — это способность тела сохранять приданную ей скорость движения при отсутствии какого-либо внешнего воздействия. Например, во время езды на общественном транспорте всем приходится держаться за поручни. Если этого не сделать, то при изменении скорости движения транспортного средства существует большая вероятность упасть вперёд или назад. Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.

Это свойство и описывается понятием инертность. Раньше изучали это явление известные учёные Галилей, Ньютон, Мах. В соответствии с их исследованиями было установлено классическое правило момента вращения, физический смысл которого заключается в распределении массы в теле, определяемой суммой произведения простейшей массы на расстояние до начального множества в квадрате. Классическая формула, описывающая характеристику, выглядит следующим образом: Ja = Σmi*r²j. В ней:

mi — масса в точке;
rj — расстояние от точки до координаты.

То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²). Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.

М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.

Вычисление параметра

Характеристика инерции тел зависит от их количественных показателей и формы. Для того чтобы найти характеристику, можно рассмотреть вращение материальной точки, находящейся на невесомой штанге, имеющей длину r и массу m. Для такой ситуации формулу момента инерции можно записать: I = m*r². Длина r представляет собой радиус кольца, по которому происходит вращение объекта по оси. Таким образом, рассматриваемый момент зависит не только от массы тела, но и геометрических характеристик.

Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc. На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой. Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.

Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.

Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2.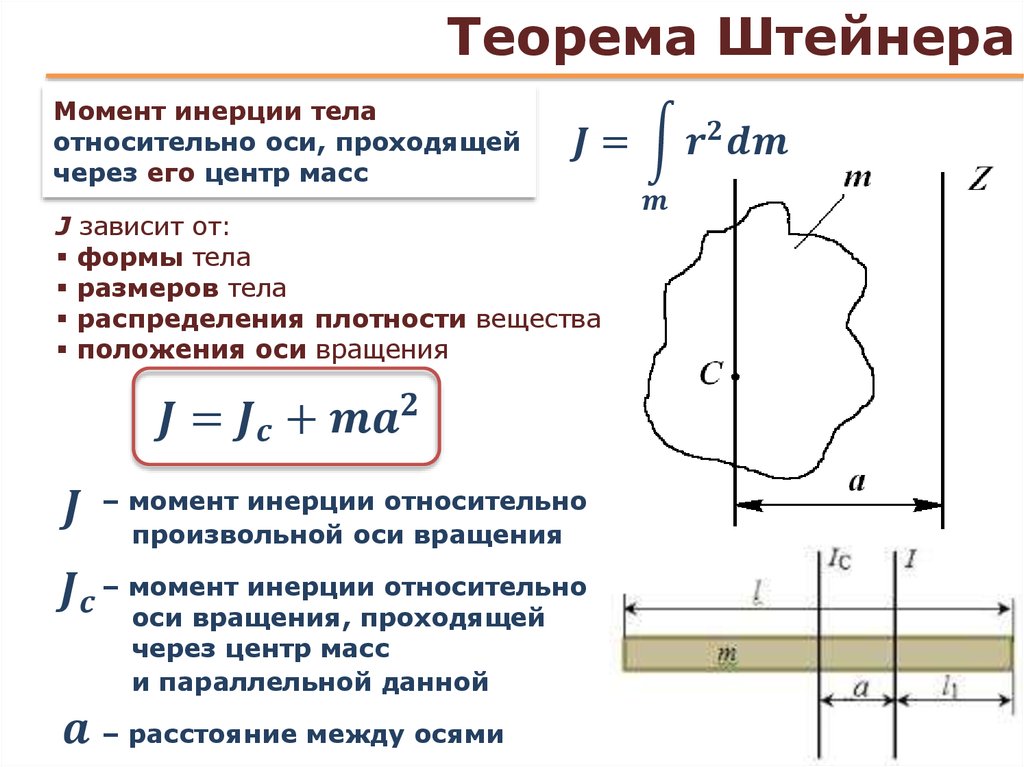 Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.

Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей. Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.

Методика решения

Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения. Для того чтобы решить поставленную задачу, используются два принципа:

Аддитивность — свойство, обозначающее, что величина целого значения определяется суммой соответствующих ему частей.
Формула нахождения момента для материальной точки I = m*r².

Всё тело можно разделить на мельчайшие частички, которые представляют собой материальные точки. Номера этих кусков обозначают в виде i. Масса произвольной части будет определяться как дельта mi. Пусть этот кусок находится на расстоянии ri от оси вращения O. Для этой части момент вращения находится с помощью выражения Ii = Δ mi*ri². Учитывая аддитивность, общий момент будет равен I = Σ Δ mi*ri², где i принимает значение от 1 до n.

Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя. Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования. Понимая физический смысл момента инерции, можно отметить следующие зависимости:

прямая пропорциональность массе;
соответствие квадрату размера;
изменение с учетом оси вращения.

Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.

Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8). После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000. Получается, если спицу будут закручивать с одинаковым моментом вокруг вертикальной оси и горизонтальной, то в первом случае она станет крутиться в 15 тыс. раз быстрее.

Моменты простейших объектов

Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур. При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта. Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:

Кольцо. Предположив, что точка имеет симметричное значение с противоположной стороны оси, можно утверждать, что формула не изменится. Если же точку распределить по плоскости перпендикулярной оси, то получится кольцо. Оно будет иметь такую же массу с кусками, находящимися на одинаковом расстоянии от центра r. Вычисление момента относительно оси вращения выполняют по той же формуле, что и для материальной точки: I = m * r².

Тонкостенный цилиндр. Нарисовав такую фигуру и указав на ней ось вращения, массу и радиус, несложно будет увидеть, что формула для нахождения момента будет аналогична кольцу.

Диск. Вращение его происходит относительно оси, проходящей через его центр. Учитывая, что масса однородного диска распределена по всей его площади, то момент его будет меньше, чем у кольца.

Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r² / 2.

Сплошной цилиндр. Получают такую фигуру простым распределением массы сплошного диска вдоль оси. По аналогии с кольцом расчёт его характеристики инерции будет совпадать с однородным диском.

Шар. Момент проходящей оси через центр тяжести равен удвоенному произведению m*r2, разделенному на 5: I = (m*r2) * 2/5.

Сфера. Такой объект отличается от шара лишь тем, что внутри он полый. Направление вращения оси происходит через центр. Значение параметра для неё будет больше, чем шара, так как масса собрана не статически в одном месте, а размещена по всей поверхности. Расчёты показывают, что найти момент можно по формуле I =2*m*r2 /3.

Стержень. Момент вращения проходит через центр вдоль оси, перпендикулярной стержню: I = (1/12) * m*L2. L — длина стержня.

При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.

Теорема Гюйгенса — Штейнера

Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:

Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri ²)/ m.

Универсального расчёта инерции любого тела: I = Σ Δ mi*ri ².

Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.

Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).

В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.

Находится ri’² по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri’ совпадает с длиной гипотенузы. Таким образом, ri’² = (xi — Oц)² + yi². Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц)² + yi²). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i² — 2*m*xi² = I — m*xi².

Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d². Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d².

Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.

Пример задачи

Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.

Для этого нужно знать характеристику прямой, пересекающей центр монеты Io. Решение будет определяться суммой Io и расстоянием от центра до касательной, которая равняется диаметру монеты: I = Io + md². Фактически задача состоит в нахождении Io. Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.

Момент вращения относительно диска определяется с помощью выражения I1 = m* d² / 2. Для решения задачи она будет выглядеть Io = m* d² / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.

ФизикаБроуновское движение в физике

ФизикаУсловия плавания тел – формулы, основные принципы и положения закона Архимеда

Как считать момент инерции. Расчёт моментов инерции некоторых тел

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции» .

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела . Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm , то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m , вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r , а масса – dm . Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и .

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе . Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Тела относительно какой-либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции его сводится к вычислению интеграла

в котором r – расстояние от элемента массы dm до оси вращения.

Момент инерции тонкого однородного стержня относительно перпендикулярной оси. Пусть ось проходит через конец стержня А (рис. 4.4).

Для момента инерции можно написать I A = kml 2 , где l – длина стержня, k – коэффициент пропорциональности. Центр стержня С является его центром масс. По теореме Штейнера I A = I C + m (l /2) 2 . Величину I C можно представить как сумму моментов инерции двух стержней, СА и СВ , длина каждого из которых равна

l /2, масса m /2, а следовательно, момент инерции равен Таким образом, I C = km (l/ 2) 2 . Подставляя эти выражения в формулу для теоремы Штейнера, получим

откуда k = 1/3. В результате находим

(4.16)

Момент инерции бесконечно тонкого круглого кольца (окружности). Момент инерции относительно оси Z (рис. 4.5) равен

I Z = mR 2 , (4.17)

где R – радиус кольца. Ввиду симметрии I X = I У .

Формула (4.17) очевидно, дает также момент инерции полого однородного цилиндра с бесконечно тонкими стенками относительно его геометрической оси.

Рис. 4.5 Рис. 4.6

Момент инерции бесконечно тонкого диска и сплошного цилиндра. Предполагается, что диск и цилиндр однородны, т. е. вещество распределено в них с постоянной плотностью. Пусть ось Z проходит через центр диска С перпендикулярно к его плоскости (рис. 4.6). Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным радиусом r + dr . Площадь такого кольца dS = 2 prdr . Его момент инерции найдется по формуле (4.17), он равен dI z = r 2 dm. Момент инерции всего диска определяется интегралом Ввиду однородности диска

dm = , где S = pR 2 – площадь всего диска. Вводя это выражение под знак интеграла, получим

(4.18)

Формула (4.18) дает также момент инерции однородного сплошного цилиндра относительно его продольной геометрической оси.

Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции его относительно точки . Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений.

Моментом инерции тела относительно точки О называется сумма произведений масс материальных точек, из которых тело состоит, на квадраты их расстояний R до точки О : q = ΣmR 2 . В случае непрерывного распределения масс эта сумма сводится к интегралу q = ∫R 2 dm . Само собой понятно, что момент θ не следует смешивать с моментом инерции I относительно оси. В случае момента I массы dm умножаются на квадраты расстояний до этой оси, а в случае момента θ – до неподвижной точки.

Рассмотрим сначала одну материальную точку с массой m и с координатами x , у , z относительно прямоугольной системы координат (рис. 4.7). Квадраты расстояний ее до координатных осей

Х , Y , Z равны соответственно у 2 + z 2 , z 2 + x 2 , x 2 + у 2 , а моменты инерции относительно тех же осей

I X = m (y 2 + z 2), I У = m (z 2 + x 2),

I Z = m (x 2 + y 2).

Сложим эти три равенства, получим I X + I У + I Z = 2m (x 2 + у 2 + z 2).

Но х 2 + у 2 + z 2 = R 2 , где R – расстояние точки m от начала координат О. Поэтому

I X + I У + I Z = 2θ. (4.19)

Это соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке О, равна удвоенному моменту инерции того же тела относительно этой точки.

Момент инерции полого шара с бесконечно тонкими стенками .

Сначала найдем момент инерции θ относительно центра шара. Очевидно, он равен θ = mR 2 . Затем применяем формулу (4.19). Полагая в ней ввиду симметрии I X = I Y = I Z = I. В результате находим момент инерции полого шара относительно его диаметра

Наименование параметра	Значение
Тема статьи:	Момент инерции
Рубрика (тематическая категория)	Механика

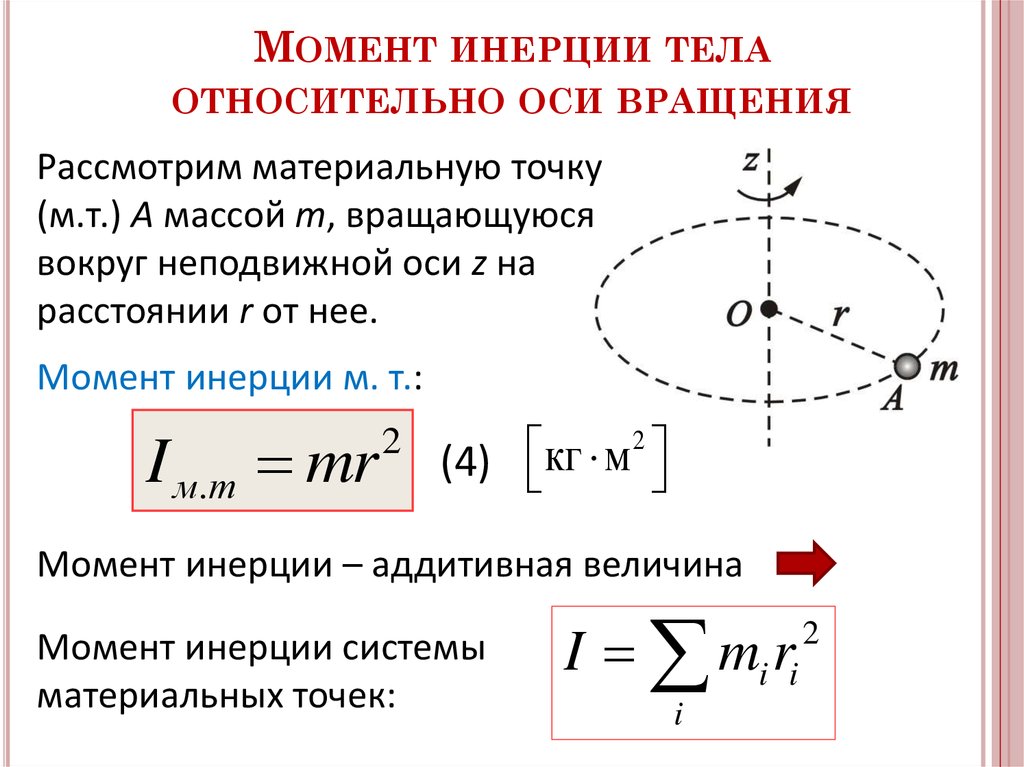
Рассмотрим материальную точку массой m , которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси принято называть скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:

J = mr 2 (75)

Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек

(76)

К определению момента инерции точки

В случае если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объёмы dv, каждый из которых обладает массой dm. В результате получается следующее выражение:

(77)

Для однородного по объёму тела плотность ρ постоянна, и записав элементарную массу в виде

dm = ρdv, преобразуем формулу (70) следующим образом:

(78)

Размерность момента инерции – кг*м 2 .

Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.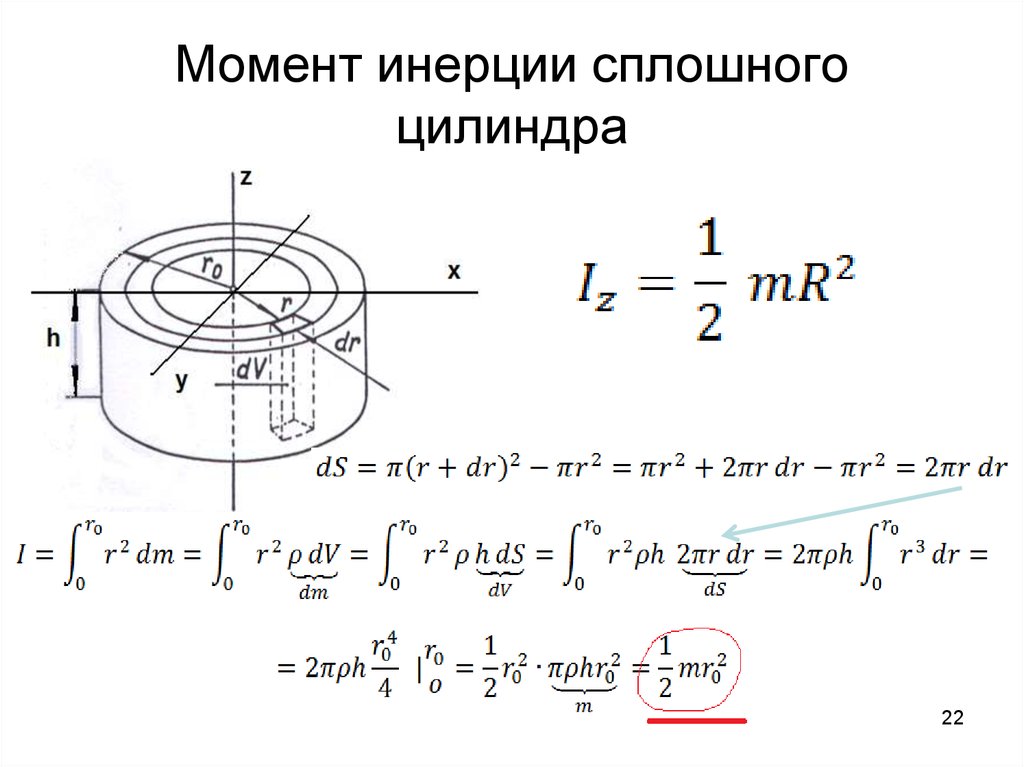

Момент инерции – это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения . Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.

Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.

В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.

Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:

Момент инерции шара радиуса R :

Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:

Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:

Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:

Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.

Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).

К расчету момента инерции стержня

Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инерции относительно оси OO плюс md 2 . Отсюда получаем:

Очевидно: момент инерции неодинаков относительно разных осей, и в связи с этим, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, к примеру, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.

Момент силы F относительно точки O

Момент инерции – понятие и виды. Классификация и особенности категории “Момент инерции” 2017, 2018.

– Момент инерции тела относительно произвольной оси.

Рис.35 Проведем через центр масс С тела произвольные оси Cx”y”z”, а через любую точку О на оси Сх” – оси Oxyz, такие, что Оy½½Сy”, Oz½½Cz” (рис. 35). Расстояние между осями Cz” и Оz обозначим через d. Тогда но, как видно из рисунка, для любой точки тела или, а. Подставляя… .

– Момент инерции тела

Момент инерции тела – величина, определяющая его инертность во вращательном движении. В динамике поступательного движения инерцию тела полностью характеризует его масса. Влияние собственных свойств тела на динамику вращательного движения оказывается более сложным,… .

– Лекция 4-5. Момент силы относительно неподвижной точки и оси. Момент инерции, момент импульса материальной точки и механической системы относительно неподвижной точки и оси.

Лекция 3. Силы. Масса, импульс материальной точки и механической системы. Динамика поступательного движения в инерциальных системах отсчета. Закон изменения импульса механической системы. Закон сохранения импульса. Динамика изучает движение тел с учетом причин,… .

– Момент инерции твердого тела.

Проанализируем формулу для момента инерции твердого тела. Момент инерции зависит от 1) массы тела, 2) формы и размеров тела, 3) положения оси вращения относительно тела (рис 2) Рис. 2а Рис.2б Итак, момент инерции есть мера инертности тела при вращательном движении,… .

– Момент инерции относительно центральной оси называется центральным моментом инерции.

Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Из формулы видно, что момент инерции относительно центральной оси меньше, чем момент…

Момент инерции
Для вычисления момента инерции мы должны мысленно расчленить тело на достаточно малые элементы, точки которых можно считать лежащими на одинаковом расстоянии от оси вращения, затем найти произведение массы каждого элемента на квадрат его расстояния от оси и, наконец, просуммировать все полученные произведения. Очевидно, это весьма трудоемкая задача. Для подсчета
моментов инерции тел правильной геометрической формы можно воспользоваться в ряде случаев приемами интегрального исчисления.
Нахождение конечной суммы моментов инерции элементов тела заменим суммированием бесконечно большого числа моментов инерции, вычисленных для бесконечно малых элементов:
lim i = 1 ∞ ΣΔm i r i 2 = ∫r 2 dm . (при Δm → 0) .
Вычислим момент инерции однородного диска или сплошного цилиндра высотой h относительно его оси симметрии

Расчленим диск на элементы в виде тонких концентрических колец с центрами на оси его симметрии. Полученные кольца имеют внутренний диаметр r и внешний r + dr , а высоту h . Так как dr , то можем считать, что расстояние всех точек кольца от оси равно r .
Для каждого отдельно взятого кольца момент инерции
i = ΣΔmr 2 = r 2 ΣΔm ,
где ΣΔm − масса всего кольца.
Объем кольца 2πrhdr . Если плотность материала диска ρ , то масса кольца
ρ2πrhdr .
Момент инерции кольца
i = 2πρhr 3 dr .
Чтобы подсчитать момент инерции всего диска, надо просуммировать моменты инерции колец от центра диска (r = 0 ) до края его (r = R ), т. е. вычислить интеграл:
I = 2πρh 0 R ∫r 3 dr ,
или
I = (1/2)πρhR 4 .
Но масса диска m = ρπhR 2 , следовательно,
I = (1/2)mR 2 .
Приведем (без вычисления) моменты инерции для некоторых тел правильной геометрической формы, выполненных из однородных материалов

1. Момент инерции тонкого кольца относительно оси, проходящей через его центр перпендикулярно его плоскости (или тонкостенного полого цилиндра относительно его оси симметрии):
I = mR 2 .
2. Момент инерции толстостенного цилиндра относительно оси симметрии:
I = (1/2)m(R 1 2 − R 2 2)
где R 1 − внутренний и R 2 − внешний радиусы.
3. Момент инерции диска относительно оси, совпадающей с одним из его диаметров:
I = (1/4)mR 2 .
4. Момент инерции сплошного цилиндра относительно оси, перпендикулярной к образующей и проходящей через ее середину:
I = m(R 2 /4 + h 2 /12)
где R − радиус основания цилиндра, h − высота цилиндра.
5. Момент инерции тонкого стержня относительно оси, проходящей через его середину:
I = (1/12)ml 2 ,
где l − длина стержня.
6. Момент инерции тонкого стержня относительно оси, проходящей через один из его концов:
I = (1/3)ml 2
7. Момент инерции шара относительно оси, совпадающей с одним из его диаметров:
I = (2/5)mR 2 .

Если известен момент инерции какого-либо тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой оси, параллельной первой, может быть найден на основании так называемой теоремы Гюйгенса-Штейнера.
Момент инерции тела I относительно любой оси равен моменту инерции тела I с относительно оси, параллельной данной и проходящей через центр масс тела, плюс масса тела m , умноженная на квадрат расстояния l между осями:
I = I c + ml 2 .
В качестве примера подсчитаем момент инерции шара радиуса R и массой m , подвешенного на нити длиной l, относительно оси, проходящей через точку подвеса О . Масса нити мала по сравнению с массой шара. Так как момент инерции шара относительно оси, проходящей через центр масс I c = (2/5)mR 2 , а расстояние
между осями (l + R ), то момент инерции относительно оси, проходящей через точку подвеса:
I = (2/5)mR 2 + m(l + R) 2 .
Размерность момента инерции:
[I] = [m] × = ML 2 .

Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси.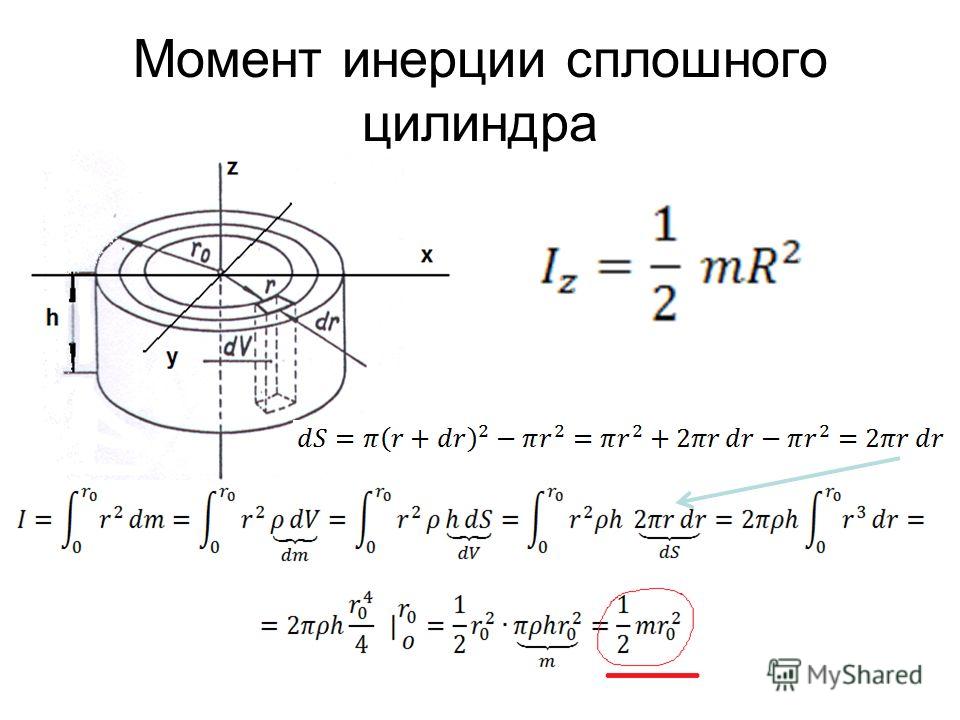 Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массыdm =  dV . Тогда момент инерции тела относительно оси равен интегралу по объёму тела:

где r – расстояние элементаdm до оси.

Вычисление момента инерции тела относительно оси часто упрощается, если предварительно вычислить его момент инерции относительно точки  . Он вычисляется по формуле, аналогичной (1):

(2)

где r – расстояние элементаdm до выбранной точки (относительно которой вычисляется ). Пусть эта точка является началом системы координатX , Y , Z (рис. 1). Квадраты расстояний элементаdm до координатных осейX , Y , Z и до начала координат равны соответственноy 2 + z 2 , z 2 + x 2 , x 2 + y 2 , x 2 + y 2 + z 2 . Моменты инерции тела относительно осейX , Y , Z и относительно начала координат

Из этих соотношений следует, что

Таким образом, сумма моментов инерции тела относительно трёх любых взаимно перпендикулярных осей, проходящих через одну точку, равна удвоенному моменту инерции тела относительно этой точки.

Момент инерции тонкого кольца. Все элементы кольцаdm (рис. 2) находятся на одинаковом расстоянии, равном радиусу кольцаR , от его оси симметрии (осьY) и от его центра. Момент инерции кольца относительно осиY

(4)

Момент инерции тонкого диска. Пусть тонкий однородный диск массыm с концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусыR 1 иR 2 . Мысленно разобьём диск на тонкие кольца радиусаr , толщиныdr . Момент инерции такого кольца относительно осиY (рис. 3, она перпендикулярна рисунку и не показана), в соответствии с (4):

Момент инерции диска:

(6)

В частности, полагая в (6) R 1 = 0, R 2 = R , получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси:

Момент инерции диска относительно его оси симметрии не зависит от толщины диска . Поэтому по формулам (6) и (7) можно вычислять моменты инерции соответствующих цилиндров относительно их осей симметрии.

Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6),  = J y , а моменты инерции относительно осейX иZ равны между собой,J x = J z . Поэтому, в соответствии с (3): 2 J x + J y = 2 J y , J x = J y /2, или

(8)

Момент инерции цилиндра. Пусть имеется полый симметричный цилиндр массыm , длины h , внутренний и внешний радиусы которого равныR 1 и R 2 . Найдём его момент инерции относительно осиZ , проведенной через центр масс перпендикулярно оси цилиндра (рис. 4). Для этого мысленно разобьём его на диски бесконечно малой толщиныdy . Один из таких дисков, массойdm = mdy / h , расположенный на расстоянииy от начала координат, показан на рис. 4. Его момент инерции относительно осиZ , в соответствии с (8) и теоремой Гюйгенса – Штейнера

Момент инерции всего цилиндра

Момент инерции цилиндра относительно оси Z  (оси вращения маятника) найдём по теореме Гюйгенса – Штейнера

где d – расстояние от центра масс цилиндра до осиZ  . В работе 16 этот момент инерции обозначен какJ ц

(11)

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Нанесение экспериментальных точек и проведение по ним графика «на глаз», а также определение по графику абсцисс и ординат точек, не отличаются высокой точностью. Её можно повысить, если использовать аналитический метод. Математическое правило построения графика заключается в подборе таких значений параметров «а» и «в» в линейной зависимости вида у = ах + b , чтобы сумма квадратов отклонений  у i (рис. 5) всех экспериментальных точек от линии графика была наименьшей (метод «наименьших квадратов» ), т.е. чтобы величина

(1)

Момент инерции однородного тела

Лабораторная работа №1

Определение момента инерции различных тел.

Теорема Штейнера.

Цель работы: определение момента инерции различных тел, проверка справедливости теоремы Гюйгенса–Штейнера.

Оборудование

Вращающийся вал Диск с диаметральными отверстиями Динамометр, 2 Н Световой барьер со счетчиком Источник питания, 5 В/2,4 А Треножник «PASS» Цилиндрическая опора «PASS» Линейка, пластмассовая,

Ключевые слова

Твердое тело, момент инерции, центр тяжести, ось вращения, крутильное колебание, жесткость пружины, возвращающая сила.

ТЕОРИЯ

Поступательное и вращательное движения являются частными проявлениями общего процесса механического движения материи. Физическое единство отражается в аналогии математической формы записи законов, описывающих эти виды движения. Основной закон динамики поступательного движения описывается выражением

или (1)

Величина m – масса тела – выражает численно меру инертности тела, т.е. его способность изменять состояние поступательного движения под действием силы F. Основной закон динамики вращательного движения твердого тела, вращающегося вокруг оси симметрии тела, записывается в виде

или (1а)

L- момент импульса тела;

j – вектор углового перемещения;

e- угловое ускорение;

Коэффициент пропорциональности Jносит название момента инерции. Момент инерции является мерой инерции тела во вращательном движении и определяет способность тела изменять состояние вращательного движения под действием момента силы M. Размерность момента инерции в системе СИ – [кг×м 2 ]. Исходя из размерности момента инерции, можно дать определение момента инерции материальной точки относительно оси вращения в виде

(2)

r_i – радиус вращения материальной точки,

Масса реального тела представляется в виде суммы масс материальных точек, его составляющих. Аналогично этому, момент инерции тела есть совокупность моментов инерции его частей, рассматриваемых как материальные точки:

(3)

Для тел правильной геометрической формы суммирование (а в пределе – интегрирование) по (3) дает следующие результаты для моментов инерции, вычисленных относительно оси, проходящей через центр симметрии этих тел:

Моменты инерции некоторых однородных тел

Диск или цилиндр вращающийся вокруг центральной оси
Момент инерции стержня при вращении относительно оси, проходящей через его конец
Момент инерции стержня при вращении относительно оси, проходящей через его центр
Момент инерции шара при вращении относительно оси, проходящей через его центр

r – радиус соответствующих тел,

Рис.

Если необходимо рассчитать момент инерции тела относительно осиА, не проходящей через центр симметрии, но параллельной ей (рис. 1), можно воспользоваться теоремой Гюйгенса–Штейнера: «Момент инерции тела J_А относительно любой осиА параллельной оси О, проходящей через центр симметрии тела, равен моменту инерции J_о этого тела относительно оси О, сложенному с величиной ml 2 ; l=r- расстояние между осями А и О; m – масса тела

(4)

Используя формулы (3) и (4), можно аналитически рассчитать момент инерции любого тела, условно разделяя его на составные части правильной геометрической формы и определяя расстояния, на которых они находятся от общей оси вращения тела. В случаях, когда аналитическое определение момента инерции затруднено сложностью формы тела или неоднородностью распределения массы, его определяют опытным путем, что является одной из целей настоящей работы.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10615 – | 7994 – или читать все.

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Материальная точка массы m

На расстоянии r от точки, неподвижная

Полый тонкостенный цилиндр или кольцо радиуса r и массы m

Сплошной цилиндр или диск радиуса r и массы m

Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁

Сплошной цилиндр длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

Прямой тонкий стержень длины l и массы m

Ось перпендикулярна к стержню и проходит через его центр масс

Тонкостенная сфера радиуса r и массы m

Ось проходит через центр сферы

Шар радиуса r и массы m

Ось проходит через центр шара

Конус радиуса r и массы m

Равнобедренный треугольник с высотой h, основанием a и массой m

Ось перпендикулярна плоскости треугольника и проходит через вершину

Правильный треугольник со стороной a и массой m

Ось перпендикулярна плоскости треугольника и проходит через центр масс

Квадрат со стороной a и массой m

Ось перпендикулярна плоскости квадрата и проходит через центр масс

Тонкостенный цилиндр (кольцо, обруч)

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

Толстостенный цилиндр (кольцо, обруч)

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

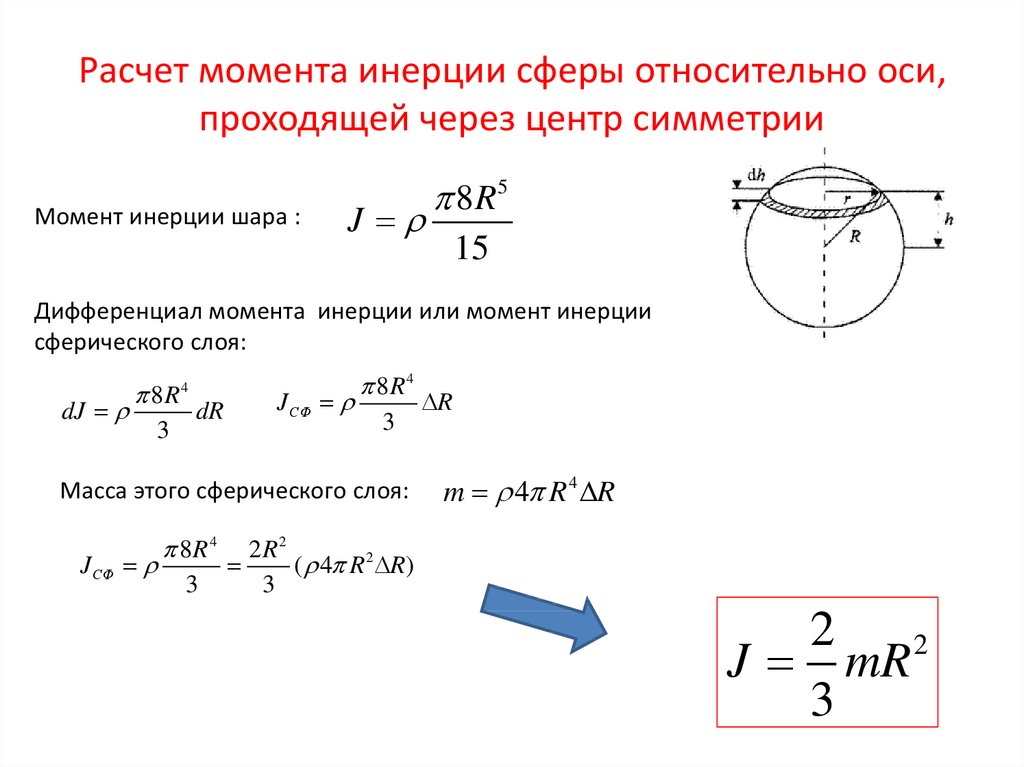
Сплошной однородный шар

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

Тонкий стержень (ось проходит через центр)

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

Тонкий стержень (ось проходит через конец)

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Пример решения задачи на нахождение момента инерции

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Крутящий момент
– Как найти момент инерции сложных объектов?
Спросил 3 года, 2 месяца назад
Изменено 2 года, 4 месяца назад
Просмотрено 1к раз
$\begingroup$
Допустим, у нас есть зубчатый венец, к которому прикреплена некоторая масса и которая должна вращать эту массу. Эта шестерня приводится в движение другой шестерней. Как найти момент инерции ведомой шестерни, чтобы рассчитать крутящий момент, необходимый для вращения этой зубчатой передачи? Это просто общая присоединенная масса, умноженная на квадрат радиуса шестерни, или что-то более продвинутое? 92 дВ},$$ где $\rho$ — плотность массы, а $r$ — расстояние от оси, относительно которой вы хотите рассчитать момент инерции (часто это ось симметрии). 2 $ по-прежнему будет действительным, а $R$ будет иметь значение где-то между этими двумя радиусами. 9{2}$$
, где $m_{i}$ — масса $i$-го объекта, а $r_{i}$ — расстояние объекта $i$-й массы от оси вращения. Теперь для непрерывного объекта суммирование становится интегральным, как в ответе Пака.
Теперь в простейшем случае зубчатый венец можно рассматривать как кольцо массы $M$, радиуса $R$ с равномерной плотностью (пусть масса на единицу длины = $\lambda$). Тогда момент инерции относительно оси, проходящей через центр масс и перпендикулярной к зубчатому венцу, равен: 92$$
При этом мы исходили из того, что $R >>>>$ толщина обода.
Если к шестерне прикреплены массы, вам необходимо добавить моменты инерции, связанные с массами, но брать МИ от той же оси.
$\endgroup$
$\begingroup$
Используйте теорему о параллельных осях для перемещения MMOI из одной точки в другую. 2$$ 92 \end{vmatrix} $$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Момент инерции: определение, формула и уравнения
момент инерции или массовый момент инерции — это скалярная величина , которая измеряет сопротивление вращающегося тела вращению. Чем выше момент инерции, тем более устойчиво тело к угловому вращению. Тело обычно состоит из нескольких мелких частиц, образующих всю массу. Массовый момент инерции зависит от распределения каждой отдельной массы относительно перпендикулярного расстояния к оси вращения. Однако в физике мы обычно предполагаем, что масса объекта сосредоточена в одной точке, называемой центр масс .
Уравнение момента инерции
Математически момент инерции может быть выражен через его отдельные массы как сумма произведения каждой отдельной массы и квадрата перпендикулярного расстояния до оси вращения. Вы можете увидеть это в уравнении ниже. I — момент инерции, измеренный в килограммах на квадратный метр (кг·м ² ), m — масса, измеренная в килограммах (кг), и r — расстояние по перпендикуляру к оси вращения, измеренное в метрах (м).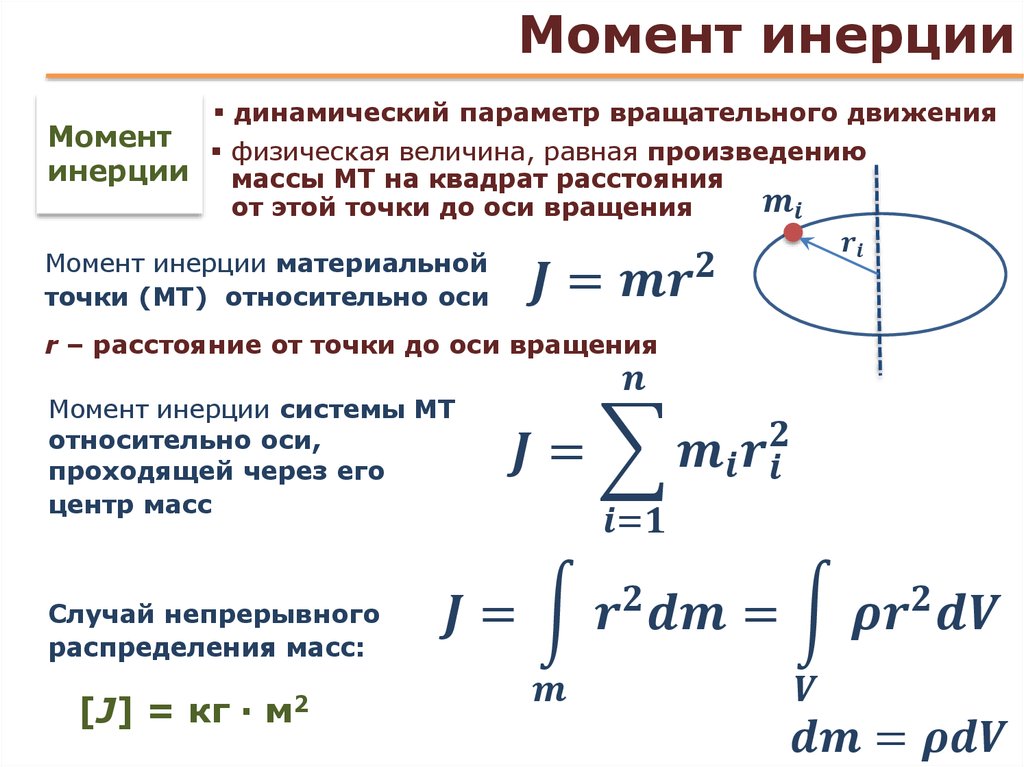
Мы также можем использовать приведенное ниже уравнение для объекта , масса которого предполагается сосредоточенной в одной точке . На изображении показано расстояние оси вращения r.
Рис. 1 – Диаграмма, показывающая расстояние оси вращения r
Откуда взялся момент инерции?
Закон Ньютона гласит, что линейное ускорение объекта линейно пропорционально суммарной силе, действующей на него, когда масса постоянна. Мы можем сформулировать это с помощью приведенного ниже уравнения, где F _t — результирующая сила, m — масса объекта, а _t — поступательное ускорение .
Аналогично мы используем крутящий момент для вращательного движения , который равен произведению вращательной силы и перпендикулярного расстояния к оси вращения. Однако поступательное ускорение при вращательном движении равно произведению углового ускорения α на радиус r.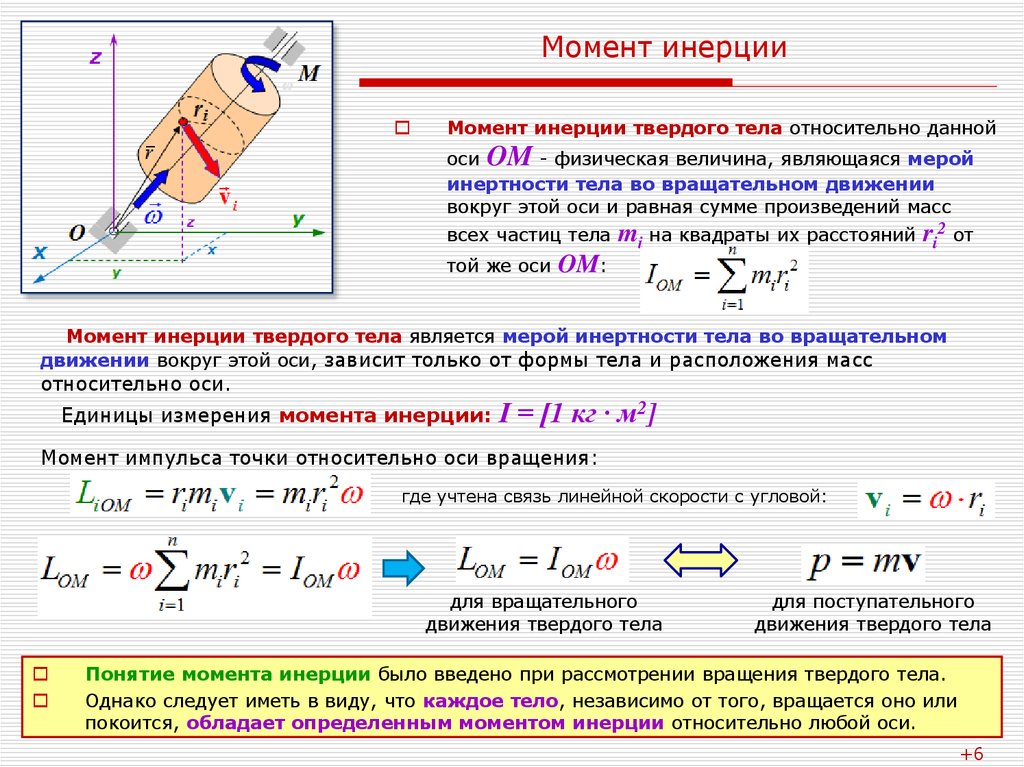
Момент инерции равен обратной величине массы во втором законе Ньютона для линейного ускорения, но применяется к угловому ускорению. Второй закон Ньютона описывает момент силы, действующий на тело, который прямо пропорционален моменту инерции массы тела и его угловому ускорению. Как видно из приведенного выше вывода, крутящий момент T равен произведению момента инерции I и углового ускорения α.
Моменты инерции для различных форм
Момент инерции индивидуален для формы и оси каждого объекта . Из-за различий в геометрических формах момент инерции дан для различных часто используемых форм, которые вы можете увидеть на изображении ниже.
Рис. 2 – Момент инерции для различных форм
Мы можем рассчитать момент инерции для любой формы путем интегрирования (по оси x) произведения уравнения, которое описывает ширину или толщину d, скорость изменения y и A, умноженное на квадрат расстояния до оси.
Чем больше толщина, тем больше момент инерции.
Примеры расчета момента инерции
Тонкий диск диаметром 0,3 м и суммарным моментом инерции 0,45 кг·м ² вращается вокруг своего центра масс. На внешней части диска находятся три камня массой 0,2 кг. Найдите полный момент инерции системы.
Решение
Радиус диска 0,15м. Мы можем рассчитать момент инерции каждого камня как
Следовательно, суммарный момент инерции будет равен
Спортсмен сидит на вращающемся стуле, держа в каждой руке тренировочный вес по 10 кг. Когда спортсмен будет чаще вращаться: когда он вытягивает руки далеко от тела или когда он отводит руки близко к телу?
Решение
Когда спортсмен вытягивает руки, момент инерции увеличивается по мере увеличения расстояния между весом и его осью вращения.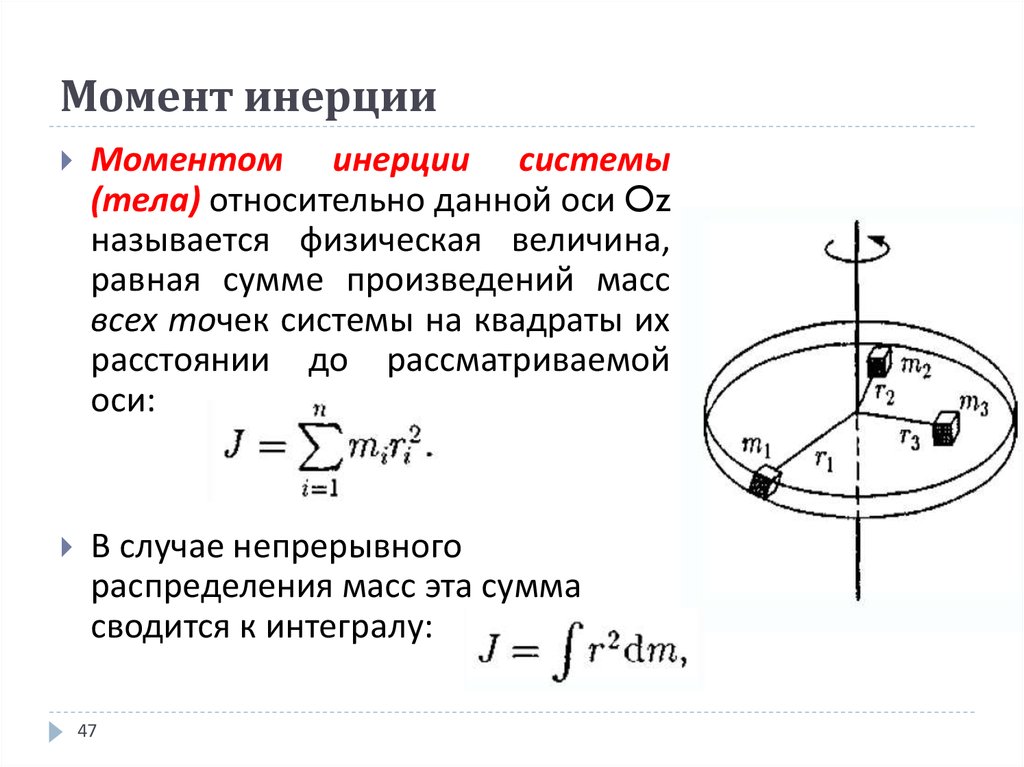 Когда спортсмен отводит руки назад, расстояние между отягощением и осью вращения уменьшается, а вместе с ним и момент инерции.
Следовательно, спортсмен с большей вероятностью будет вращаться, когда отводит руки назад, так как момент инерции будет меньше, а тело будет меньше сопротивляться вращению.
Очень тонкий диск диаметром 5 см вращается вокруг своего центра масс, а другой более толстый диск диаметром 2 см вращается вокруг своего центра масс. Какой из двух дисков имеет больший момент инерции?
Решение
Диск большего диаметра будет иметь больший момент инерции . Как следует из формулы, момент инерции пропорционален квадрату расстояния до оси вращения, следовательно, чем больше радиус, тем больше момент инерции.
Момент инерции — основные выводы
Момент инерции — это мера сопротивления вращающегося объекта вращению. Это зависит от массы и распределения ее массы вокруг оси вращения.
Момент инерции — это величина, обратная массе во втором законе Ньютона, примененном к вращению.
Момент инерции различен и зависит от формы и оси каждого объекта.
Изображения
Инерция вращения. https://web2.ph.utexas.edu/~coker2/index.files/RI.htm
Часто задаваемые вопросы о моменте инерции
Момент инерции можно рассчитать как сумму произведений отдельных масс объект и их соответствующее квадратное расстояние по перпендикуляру к оси вращения.
Момент инерции или момент инерции массы — это скалярная величина, которая измеряет сопротивление вращающегося тела вращению. Чем выше момент инерции, тем труднее телу вращаться и наоборот.
Момент инерции является величиной, обратной массе во втором законе Ньютона для линейного ускорения, но применяется для углового ускорения.
org/Thing” data-name=”flashcards-dot”> Викторина «Последний момент инерции»
Вопрос
Каков момент инерции?
Показать ответ
Ответ
Момент инерции — это мера сложности вращения объекта вокруг своей оси вращения.
Показать вопрос
Вопрос
Как определяется момент инерции?
Показать ответ
Ответ
Момент инерции – это произведение массы объекта на расстояние от его распределенной массы до оси вращения.
Показать вопрос
Вопрос
Какое уравнение мы используем для расчета момента инерции?
Показать ответ
Ответ
I=m·r ²
Показать вопрос
Вопрос
Что представляет r в уравнении момента инерции?
Показать ответ
Ответ
Расстояние распределенной массы объекта до его оси вращения.
Показать вопрос
Вопрос
Какова единица момента инерции?
Показать ответ
Ответ
Единицей момента инерции является кг·м ² .
Показать вопрос
Вопрос
Как момент инерции связан со вторым законом Ньютона?
Показать ответ
Ответ
Момент инерции есть величина, обратная массе во втором законе Ньютона.
Показать вопрос
Вопрос
Какая связь между вторым законом Ньютона и законом вращения Ньютона?
Показать ответ
Ответ
F=m·a и T=I·a. Они имеют одинаковую форму, следовательно, момент инерции есть величина, обратная массе во втором законе Ньютона для линейного ускорения.
Показать вопрос
Вопрос
Означает ли более высокий момент инерции, что тело с большей вероятностью будет вращаться?
Показать ответ
Ответ
Нет, более высокий момент инерции не означает, что тело будет вращаться с большей вероятностью.
Показать вопрос
Вопрос
Означает ли высокий момент инерции, что тело с меньшей вероятностью будет вращаться?
Показать ответ
Ответ
Показать вопрос
Вопрос
Фигуристка пытается выполнять аэробику во время катания на коньках. Как он может гарантировать, что он останется стабильным после выполнения своих вращений?
Показать ответ
Ответ
Он может вытягивать руки и ноги как можно дальше от центра масс.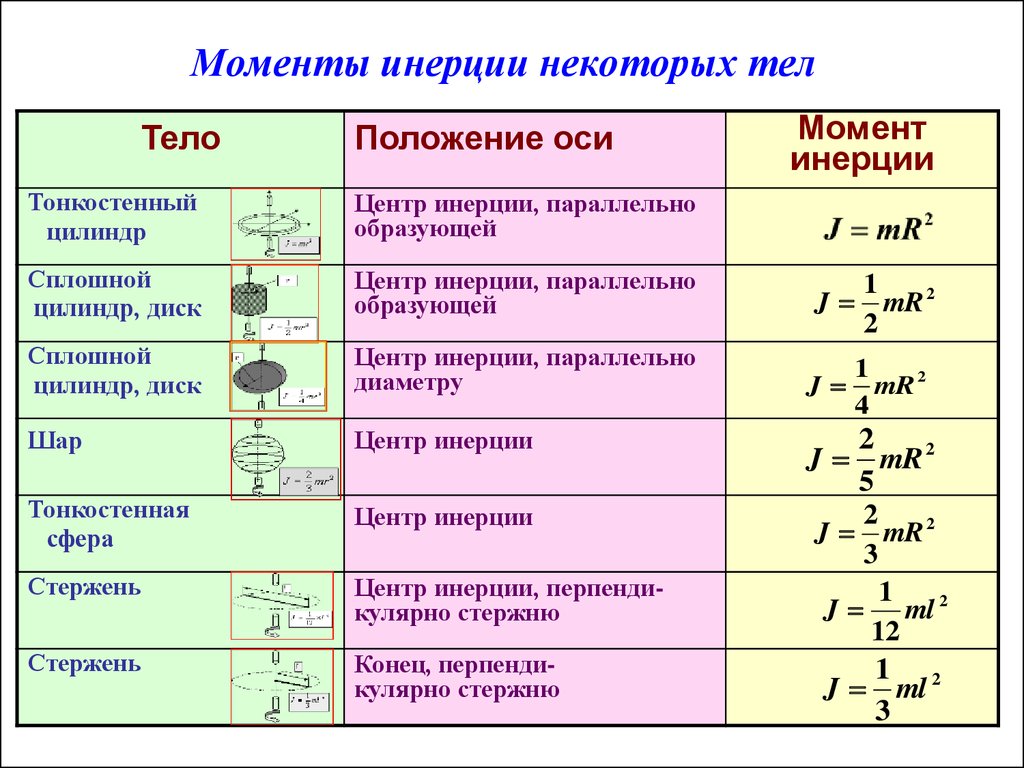
Показать вопрос
Вопрос
Когда кто-то вращается и внезапно вытягивает руки из своего тела, как изменяется момент инерции?
Показать ответ
Ответ
Момент инерции увеличивается по мере увеличения расстояния между распределением массы и осью вращения.
Показать вопрос
Вопрос
Тренировочный вес состоит из двух дисков, соединенных стержнем. Когда будет легче вращать тренировочный вес?
Показать ответ
Ответ
Когда два утяжеляющих диска помещаются в середину штанги.
Показать вопрос
Вопрос
Два человека сидят в маленькой лодке Как они должны сидеть, чтобы сопротивляться вращению лодки?
Показать ответ
Ответ
Они могут сидеть на двух концах лодки.
Показать вопрос
Вопрос
Объект имеет момент инерции 60 кг·м ² . Как изменится момент инерции, если расстояние по перпендикуляру к оси вращения или его распределенной массе удвоится?
Показать ответ
Ответ
Суммарный момент инерции увеличится в четыре раза.
Момент инерции прямоугольника0005
-Повернутые оси
-Основные оси
-Размеры
-Массовый момент инерции
-Применение
Поделиться этим
См. Также
Момент инерции прямоугольника
-доктором MINAS E. Lemonis, PhD – Обновлено: 12 ноября 2019 г.
Главная > Момент инерции > Прямоугольная площадь
Этот инструмент вычисляет момент инерции I (второй момент площади) прямоугольника. Введите размеры формы «b» и «h» ниже.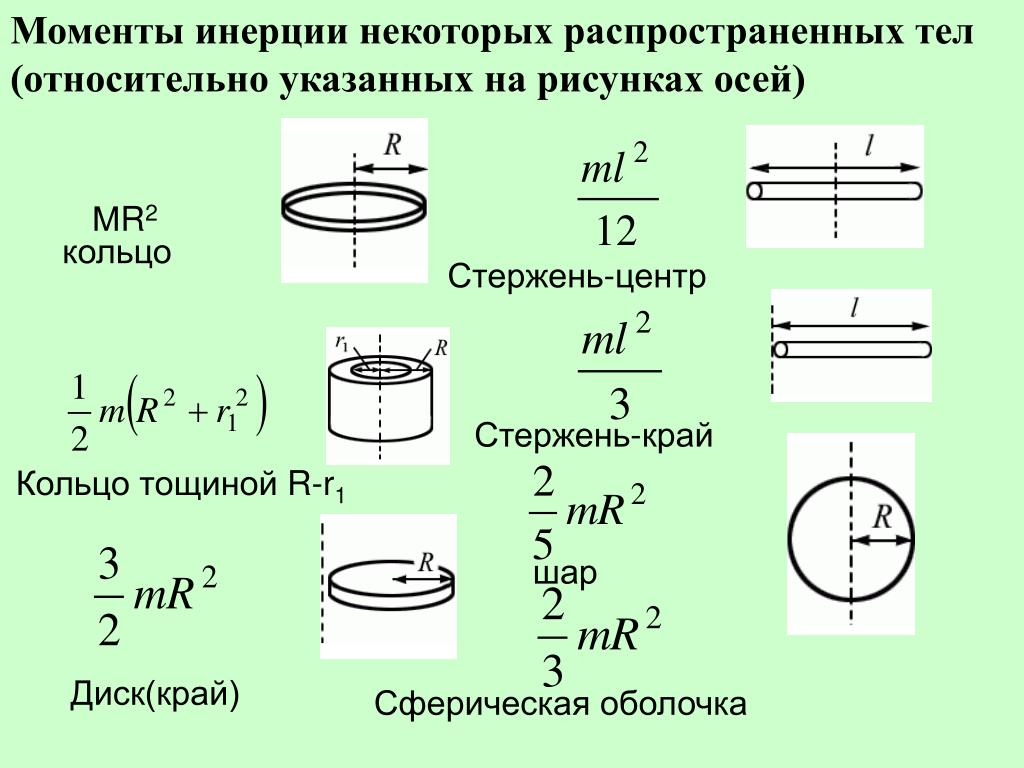 Вычисленные результаты будут иметь те же единицы измерения, что и введенные вами. Пожалуйста, используйте согласованные единицы для любых входных данных.
h =
b =
Results:
Looking for another axis?
Реклама
Реклама
СОДЕРЖАНИЕ
-Калькулятор
-Определения
-Парикола.2
где I’ — момент инерции относительно произвольной оси, I — момент инерции относительно центральной оси, параллельной первой, d — расстояние между двумя параллельными осями и A — площадь форма (=bh в случае прямоугольника).
Для произведения инерции Ixy теорема о параллельных осях принимает аналогичную форму:
I_{xy’} = I_{xy} + A d_{x}d_{y}
относительно центроидальных осей x,y и Ixy’ есть произведение инерции относительно осей, параллельных центроидальным x,y, имеющих смещения от них d_{x} и d_{y} соответственно.
Повернутые оси
Для преобразования моментов инерции от одной системы осей x,y к другой u,v, повернутой на угол φ, используются следующие уравнения:
\begin{split} I_u & = \frac{I_x+I_y}{2} + \frac{I_x-I_y}{2} \cos{2\varphi} -I_{xy} \sin{2\varphi} \\ I_v & = \frac{I_x +I_y}{2} – \frac{I_x-I_y}{2} \cos{2\varphi} +I_{xy} \sin{2\varphi} \\ I_{uv} & = \frac{I_x-I_y }{2} \sin{2\varphi} +I_{xy} \cos{2\varphi} \end{split}
где Ix, Iy – моменты инерции относительно начальных осей, а Ixy – произведение инерции. Iu, Iv и Iuv – соответствующие величины для вращающихся осей u,v. Произведение инерции Ixy прямоугольника равно нулю, потому что x и y являются осями симметрии.
Главные оси
В главных осях, повернутых на угол θ относительно исходных центроидальных осей x,y, произведение инерции становится равным нулю. Из-за этого любая ось симметрии формы также является главной осью. Моменты инерции относительно главных осей I_I, I_{II} называются главными моментами инерции и являются максимальным и минимальным для любого угла поворота системы координат. Для прямоугольника оси x и y являются осями симметрии, и поэтому они определяют главные оси формы. В результате Ix и Iy являются главными моментами инерции прямоугольника. 94 .
Массовый момент инерции
В физике термин момент инерции имеет другое значение. Это связано с распределением массы объекта (или нескольких объектов) вокруг оси. Это отличается от определения, которое обычно дается в инженерных дисциплинах (также на этой странице) как свойство площади формы, обычно поперечного сечения, вокруг оси. Термин 90 529 секунды момента площади 90 530 кажется более точным в этом отношении.
Приложения
Момент инерции (секундный момент или площадь) используется в теории балок для описания жесткости балки по отношению к изгибу (см. теорию изгиба балки). Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:
M = E\times I \times \kappa
где E – модуль Юнга, свойство материала, и κ искривление балки из-за приложенной нагрузки.