Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5.  СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1.  § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ  СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4.  СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2.  ПРЕДЕЛ ФУНКЦИИ ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
| |||||||||||||||||||
| Специальный поиск | |||||||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
||||||||||||||||||
ускорения точек момент Задача 40658 Точка вращается по кругу радиусом R = 1,2 м.
Задача 40765 Уравнение колебаний материальной точки описывается уравнением x = sin20πt см. Найти ускорение точки в тот момент, когда ее смещение равно 0,5 см.
Задача 40797 Определить модуль ускорения точки в момент времени 1 с, если уравнение движения точки x = cos πt см, y = sin πt см.
Задача 25894 Две материальные точки движутся по одной прямой, совпадающей с осью Ох декартовой системы координат. В начальный момент времени первая точка имела координату х10 = 4 м, а вторая х20 = 8 м. Скорости точек изменяются по законам v1 = bt + ct2 и v2 = –bt + ct2, где b = 1 м/с2, с = 2 м/с3.
Задача 26579 Положение точки на плоскости определяется ее радиусом-вектором r = 0,3t2i + 0,1 t3j. Определить модуль ускорения точки в момент времени t = 2 с.
Задача 12213 Определить скорость ν и полное ускорение а точки в момент времени t = 2 с, если она движется по окружности радиусом R = 1 м согласно уравнению ξ = At+Bt3, где А = 8 м/с, В = –1 м/с3, ξ — криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности.
Задача 12239 Движение точки описывается уравнением s = 4t4 + 2t2 + 7. Найти скорость и ускорение точки в момент времени 2с и среднюю скорость за первые 2с движения.
Задача 12263 Прямолинейное движение точки описывается уравнением s(t) = 4t4 + 2t2 + 7 м.
Задача 13938 Материальная точка движется в плоскости ху согласно уравнениям х = 5 + 7t – 2t2 и у = 3 + t + 0,2t2. Найти модули скорости и ускорения точки в момент времени t = 5 с.
Задача 15009 Определить скорость ν и полное ускорение а точки в момент времени t = 1,38 с, если она движется по окружности радиусом R = 1,76 м согласно уравнению φ = At + Bt3, где А = 6,47 рад/с, В = –1,84 рад/с3.
Задача 20080 Материальная точка совершает колебательное движение вдоль оси ОХ по закону X = 8cos(πt+π/2), см. Найти период колебаний и ускорение точки в момент t = T/2, построить график зависимости x(t).
Задача 20113 Уравнение движения точки по прямой имеет вид: х = 2 + 6t – t2 (м). Найти: 1) путь и перемещение точки за промежуток времени от t1 = 2 с до t2 = 4 с; 2) среднюю скорость и среднее ускорение точки за этот промежуток; 3) скорость и ускорение точки в момент времени t = 2 с.
Задача 20123 Уравнение движения точки по прямой имеет вид: х = –1–3t2+2t3 (м). Найти: 1) путь и перемещение точки за промежуток времени от t1 = 0 с до t2 = 2 с; 2) среднюю скорость и среднее ускорение точки за этот промежуток; 3) скорость и ускорение точки в момент времени t = 1 с.
Задача 19823 Материальная точка движется по закону: Y(t) = At+Ct2+Bt4, где A = 6 м/с, C = 0,2 м/с2, B = –0,125 м/с4 .
Задача 19826 Материальная точка движется по закону: Y(t) = At2–Ct4, где A = 4,5 м/с2, C = 0,25 м/с4. Найти скорость и ускорение точки в моменты времени t1 = 2 c и t2 = 4 с. Каковы средняя скорость перемещения и средняя путевая скорость для промежутка времени от 2 до 4 с ?
Задача 20135 Материальная точка имеет массу m = 9 кг и движется по криволинейной траектории под действием силы, проекция которой на касательную Fτ = 5,7 Н, на нормаль Fn = 2·t2 Н. Определите модуль ускорения точки в момент времени t = 19,8 с.
Задача 20876 Уравнение движения точки по прямой имеет вид: х = –1 + 2t2 – t4 (м).
Задача 21342 Скорость колеблющейся материальной точки меняется по закону v = vmaxcos(ωt). Максимальная скорость vmax = 5 см/с, период равен 0,1 с. Найти ускорение точки в момент времени t = 0,25 с.
Задача 22933 Движение точки описывается уравнением S = 5t3–4t2+40 (в единицах СИ). Найдите скорость и ускорение точки в момент времени t1 = 2 c. Найдите путь, пройденный телом к моменту времени t2 = 3 c.
| |||||||||||||||||||
геометрия – Найти координаты точки на окружности
спросил
Изменено 9 месяцев назад
Просмотрено 192к раз
$\begingroup$
У меня вот такой круг
Учитывая поворот θ и радиус r , как мне найти координату (x, y)? Имейте в виду, что это вращение может быть где угодно между 0 и 360 градусами.
Например, у меня есть радиус 12 и поворот θ на 115 градусов. Как бы вы нашли точку (x, y)?
- геометрия
- тригонометрия
- круги
- вращения
$\endgroup$
2
$\begingroup$
Судя по картинке, ваша окружность имеет центр начала координат и радиус $r$. Вращение, кажется, по часовой стрелке. И вопрос, похоже, в том, где заканчивается точка $(0,r)$ в верхней части круга.
Точка $(0,r)$ заканчивается в $x=r\sin\theta$, $y=r\cos\theta$.
В общем, предположим, что вы вращаетесь вокруг начала координат по часовой стрелке на угол $\theta$. Тогда точка $(s,t)$ оказывается в точке $(u,v)$, где $$u=s\cos\theta+t\sin\theta\qquad\text{and} \qquad v=-s\sin\theta+t\cos\theta.$$
$\endgroup$
3
$\begingroup$
При угле 115° по часовой стрелке вы можете найти точку (x,y), как показано на диаграмме, с помощью следующей математики:
Любая точка $(x,y)$ на пути окружности $x = r*sin(θ), y = r*cos(θ)$
таким образом: $(x,y) = (12*sin(115), 12*cos(115))$
Итак, ваша точка будет примерно будет $(10,876, -5,071)$ (при условии, что верхний правый квадрант равен x+, y+)
$\endgroup$
$\begingroup$
Стандартный круг рисуется с начальной точкой 0 градусов на пересечении круга и оси x с положительным углом, направленным против часовой стрелки.
Таким образом, стандартная параметризация учебника: х=cos т y=sin t
На вашем рисунке показан другой сценарий. Как это нарисовано, начальная точка находится вверху, а градусы увеличиваются по часовой стрелке. Таким образом, стандартная параметризация должна быть изменена в соответствии с вашей ситуацией.
Посмотрите, каково значение x на вашей картинке в начальной точке, а затем, что происходит, когда t увеличивается. x начинается с 0, затем увеличивается до максимума 1, а затем возвращается к 0, когда t = Pi.
Теперь вы хотите сравнить это поведение со стандартным графиком sin и cos, чтобы решить, какой из них соответствует вашим потребностям. X=sin t ведет себя именно так, так что теперь у вас есть параметризация x. Обратите внимание, что это не x = cos t, как учит стандартный учебник по математике, потому что в классе тригонометрии они обычно имеют 0 градусов на пересечении оси x и единичной окружности.
Теперь y на вашем чертеже начинается с 1, а затем уменьшается, пока вы не достигнете 0, а затем -1 в PI.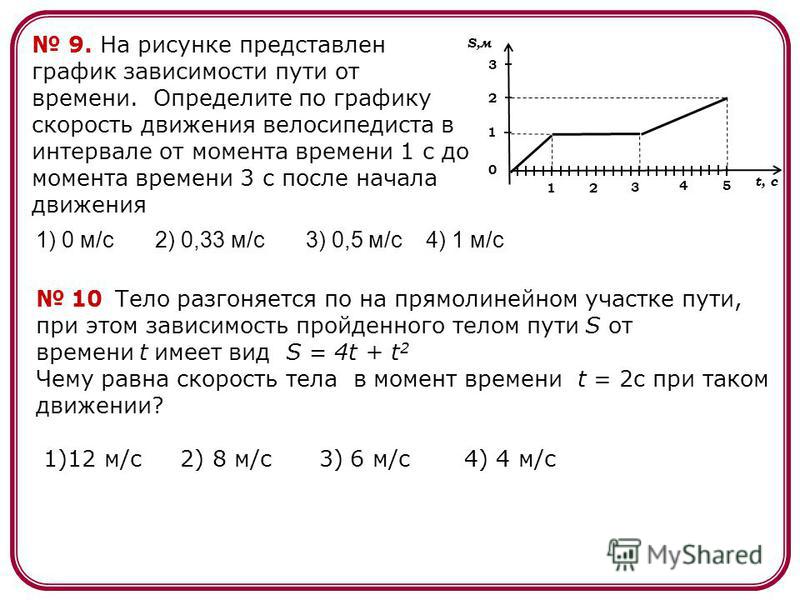 Глядя на график sin или cos, можно увидеть, что cos ведет себя именно так.
Глядя на график sin или cos, можно увидеть, что cos ведет себя именно так.
Итак… Y=cos t.
Я публикую это, потому что это может помочь тому, кто знает о sin и cos, но имеет проблему, в которой начальная точка 0 градусов находится в нестандартном положении, а направление положительных градусов находится в направлении по часовой стрелке, а не направление против часовой стрелки.
$\endgroup$
1
геометрия – Как найти координаты отраженной точки?
спросил
Изменено 1 год, 4 месяца назад
Просмотрено 124 тыс. раз
$\begingroup$
Как я могу найти координаты точки, отраженной от линии, которая не обязательно может быть какой-либо из осей?
Пример вопроса:
Если P является отражением (образом) точки (3, -3) в прямой $2y = x+1$, найти координаты точки P.
Я знаю, что ответ $(-1,5)$, нарисовав график, но кроме этого я не могу предоставить какие-либо предварительные расчеты, потому что я не знаю, с чего начать…
- геометрия
- аналитика- геометрия 92}$$
Изображение точки находится на том же расстоянии от прямой, что и сама точка от прямой. Итак, мы должны умножить это на 2. Вот что я думаю.
Вот доказательство из моей книги:
Извините за размер изображения.. 😛
$\endgroup$
3
$\begingroup$
Найти прямую, перпендикулярную $ 2y=x+1$, которая проходит через $(3, -3)$
$$2x+y=3$$
Найти точку пересечения этих двух линий (фут перпендикуляра)
$$(1,1)$$
Используйте формулу средней точки (частный случай формулы сечения), чтобы получить требуемую точку (основание перпендикуляра — это середина точки отражения и исходной точки)
$$(-1,5)$$
$\endgroup$
0
$\begingroup$ 9{2}}\right)$$
Доказательство здесь (комплексные числа не нужны!).
$$\\$$
Итак, в этом случае ваша точка равна $(p,q)=(3,-3)$, а ваша линия равна $2y-x-1=0$ (переписана в виде $ay +bx+c=0$). Так что просто подставьте числа, чтобы получить $(-1,5)$ по желанию.
Или вы можете использовать электронную таблицу под названием «Отражение точки в линии» здесь.
(Я искал общее решение, но не смог найти его в Интернете, поэтому решил поделиться своей работой здесь.)
$\endgroup$
$\begingroup$
Мне нравится использовать для этого комплексные числа. Сначала сделаем это, когда ось симметрии проходит через начало координат. Пусть $\alpha$ будет углом, который он образует с осью $x$, и обозначим $u=\cos\alpha+i\sin\alpha$; тогда вы получите симметричную точку $z\in\mathbb{C}$, сначала повернув на $-\alpha$, затем сопрягая, а затем снова вращая на $\alpha$: при первом повороте ось симметрии совпадает с осью симметрии. Ось $x$, поэтому отражение — это просто сопряжение.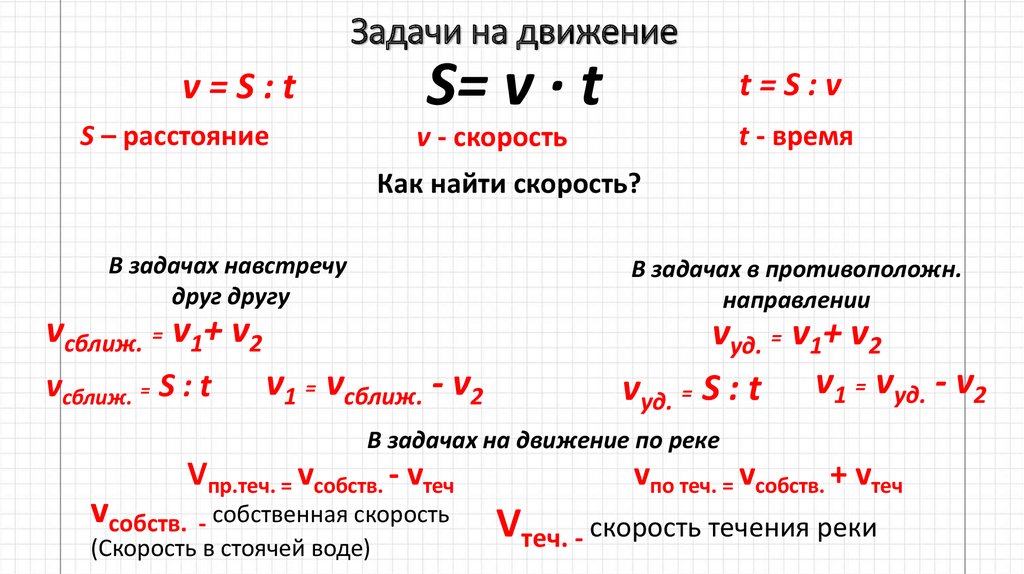 92}
\правильно)
$$
В данном случае $m=1/2$ и $q=1/2$, поэтому, просто подставив,
$$
(3,-3)\mapsto (-1,5)
$$
92}
\правильно)
$$
В данном случае $m=1/2$ и $q=1/2$, поэтому, просто подставив,
$$
(3,-3)\mapsto (-1,5)
$$
Конечно, это излишество, если вы просто хотите узнать образ в одной точке , но я считаю, что этот метод хорошо иллюстрирует мощь комплексных чисел.
$\endgroup$
2
$\begingroup$
Вот один способ: есть много других.
Пусть искомая точка изображения будет $(a,b)$. Тогда вам нужны два условия:
1) Середина отрезка между данной точкой и точкой изображения находится на данной прямой. Это дает нам $$2\frac{-3+b}2= \frac{3+a}2+1$$ 2) Прямая, содержащая данную точку и точку изображения, перпендикулярна данной прямой. Это означает, что их наклоны являются отрицательными обратными величинами, что дает нам $$\frac{-3-b}{3-a}=-\frac{1}{1/2}$$
Это два уравнения с двумя неизвестными, позволяющие найти $a$ и $b$.

 Уравнение движения точки φ = Аt + Вt3, где А = 0,5 рад/с; В = 0,2 рад/с3. Определить тангенциально аτ, нормальное an и полное а ускорения точки в момент времени t = 4 с.
Уравнение движения точки φ = Аt + Вt3, где А = 0,5 рад/с; В = 0,2 рад/с3. Определить тангенциально аτ, нормальное an и полное а ускорения точки в момент времени t = 4 с. Определить ускорения точек в момент их встречи.
Определить ускорения точек в момент их встречи. Найти скорость и ускорение точки в момент времени 2 с, а также среднюю скорость и среднее ускорение за первые две секунды движения и за вторые две секунды движения.
Найти скорость и ускорение точки в момент времени 2 с, а также среднюю скорость и среднее ускорение за первые две секунды движения и за вторые две секунды движения.
 Найти скорость и ускорение точки в моменты времени t1 = 0 c и t2 = 2 с, а также среднюю скорость перемещения и среднее ускорение за первые 2 с движения.
Найти скорость и ускорение точки в моменты времени t1 = 0 c и t2 = 2 с, а также среднюю скорость перемещения и среднее ускорение за первые 2 с движения.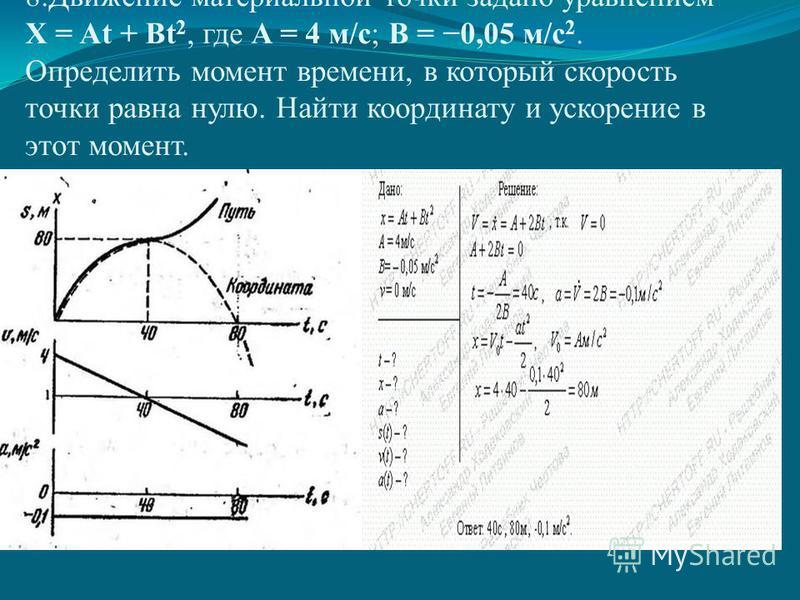 Найти: 1) путь и перемещение точки за промежуток времени от t1 = 0 с до t2 = 2 с; 2) среднюю скорость и среднее ускорение точки за этот промежуток; 3) скорость и ускорение точки в момент времени t = 2 с.
Найти: 1) путь и перемещение точки за промежуток времени от t1 = 0 с до t2 = 2 с; 2) среднюю скорость и среднее ускорение точки за этот промежуток; 3) скорость и ускорение точки в момент времени t = 2 с.