100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
Единое национальное тестирование
История Казахстана
Онлайн тесты и шпаргалки по истории Казахстана
Далее
Всемирная история
Онлайн тесты и шпаргалки по Всемирной истории.
Далее
Математика
Онлайн тесты и шпаргалки по математике.
Далее
Химия
Онлайн тесты и шпаргалки по химии.
Далее
Физика
Онлайн тесты и шпаргалки по физике.
Далее
Биология
Онлайн тесты и шпаргалки по биологии.
Далее
География
Онлайн тесты и шпаргалки по географии.
Далее
Русский язык
Онлайн тесты и шпаргалки по русскому языку.
Далее
Готовые работы
ДИПЛОМНЫЕ РАБОТЫ
Многое уже позади и теперь ты – выпускник, если, конечно, вовремя напишешь дипломную работу. Но жизнь – такая штука, что только сейчас тебе становится понятно, что, перестав быть студентом, ты потеряешь все студенческие
радости, многие из которых, ты так и не попробовал, всё откладывая и откладывая на потом. И теперь, вместо того, чтобы навёрстывать упущенное, ты корпишь над дипломной работой? Есть отличный выход: скачать нужную тебе дипломную
работу с нашего сайта – и у тебя мигом появится масса свободного времени!
Но жизнь – такая штука, что только сейчас тебе становится понятно, что, перестав быть студентом, ты потеряешь все студенческие
радости, многие из которых, ты так и не попробовал, всё откладывая и откладывая на потом. И теперь, вместо того, чтобы навёрстывать упущенное, ты корпишь над дипломной работой? Есть отличный выход: скачать нужную тебе дипломную
работу с нашего сайта – и у тебя мигом появится масса свободного времени!
Дипломные работы успешно защищены в ведущих Университетах РК.
Стоимость работы от 20 000 тенге
Перейти
КУРСОВЫЕ РАБОТЫ
Курсовой проект – это первая серьезная практическая работа. Именно с написания курсовой начинается подготовка к разработке дипломных проектов. Если студент научиться правильно излагать содержание темы в курсовом проекте
и грамотно его оформлять, то в последующем у него не возникнет проблем ни с написанием отчетов, ни с составлением дипломных работ, ни с выполнением других практических заданий.
Перейти
МАГИСТЕРСКИЕ ДИССЕРТАЦИИ
В настоящее время в высших учебных заведениях Казахстана и стран СНГ очень распространена ступень высшего профессионального образования, которая следует после бакалавриата – магистратура. В магистратуре обучаются с
целью получения диплома магистра, признаваемого в большинстве стран мира больше, чем диплом бакалавра, а также признаётся зарубежными работодателями. Итогом обучения в магистратуре является защита магистерской диссертации.
Мы предоставим Вам актуальный аналитический и текстовый материал, в стоимость включены 2 научные статьи и автореферат.
Перейти
ОТЧЕТЫ ПО ПРАКТИКЕ
После прохождения любого типа студенческой практики (учебной, производственной, преддипломной) требуется составить отчёт. Этот документ будет подтверждением практической работы студента и основой формирования оценки
за практику. Обычно, чтобы составить отчёт по практике, требуется собрать и проанализировать информацию о предприятии, рассмотреть структуру и распорядок работы организации, в которой проходится практика, составить календарный
план и описать свою практическую деятельность.
Этот документ будет подтверждением практической работы студента и основой формирования оценки
за практику. Обычно, чтобы составить отчёт по практике, требуется собрать и проанализировать информацию о предприятии, рассмотреть структуру и распорядок работы организации, в которой проходится практика, составить календарный
план и описать свою практическую деятельность.
Перейти
Пропустить новости сайта
Новости сайта
Пропустить Навигация Пропустить Меню блога
- Просмотр всех записей
Назад
Вы не вошли в систему (Вход)
Расстояние в равноускоренном движении. Перемещение при равноускоренном движении. Уравнение координаты
Прямолинейное равномерное движение – это такое движение, при котором за одинаковые промежутки времени, тело проходит одинаковое расстояние.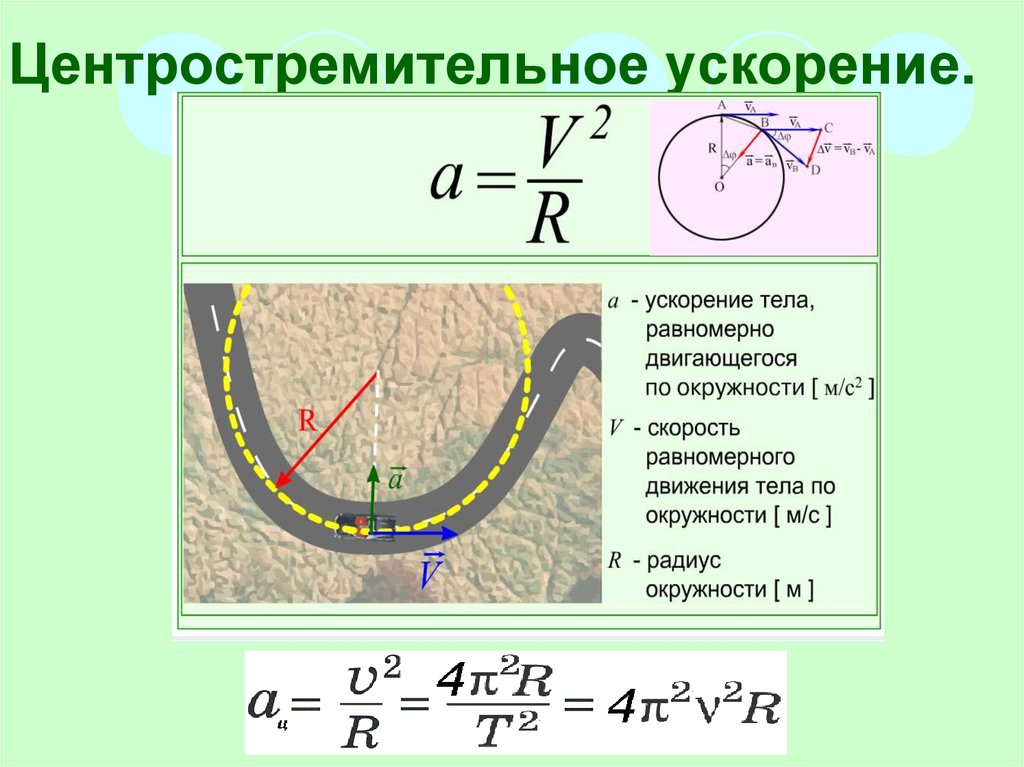
Равномерное движение – это такое движение тела, при котором его скорость остается постоянной (),то есть все время движется с одной скоростью, а ускорение или замедление не происходит ().
Прямолинейное движение – это движение тела по прямой линии, то есть траектория у нас получается – прямая.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор скорости совпадает с вектором перемещения. При всем этом средняя скорость в любой промежуток времени равна начальной и мгновенной скорости:
Скорость равномерного прямолинейного движения
Из данной формулы. мы легко можем выразить перемещение тела при равномерном движении:
Рассмотрим зависимость скорости и перемещения от времени
Так как тело у нас движется прямолинейно и равноускоренно (), то график с зависимостью скорости от времени будет выгладить, как параллельная прямая оси времени.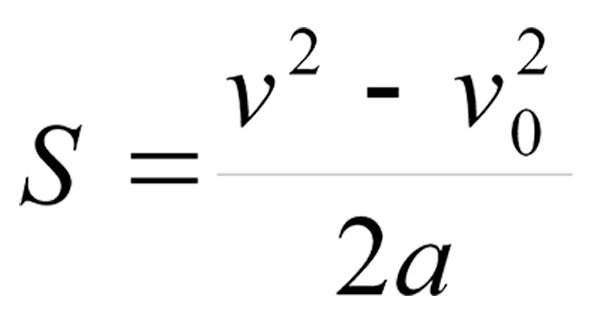
В зависимости проекции скорости тела от времени ничего сложного нет. Проекция перемещения тела численно равна площади прямоугольника АОВС, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
На графике мы видим зависимость перемещения от времени .
Из графика видно, что проекция скорости равна:
Рассмотрев эту формулу. мы можем сказать, чем больше угол, тем быстрей движется наше тело и оно проходит больший путь за меньшее время
График зависимости V(t) для этого случая показан на рис.1.2.1. Промежуток времени Δt в формуле (1.4) можно брать любой. Отношение ΔV/Δt от этого не зависит. Тогда ΔV=аΔt . Применяя эту формулу к промежутку от t о
V(t)=V 0 + at. (1.5)
Здесь V 0 – значение скорости при t о = 0. Если направления скорости и ускорения противоположны, то говорят о равнозамедленном движении (рис. 1.2.2).
Если направления скорости и ускорения противоположны, то говорят о равнозамедленном движении (рис. 1.2.2).
При равнозамедленном движении аналогично получаем
V(t) = V 0 – at.
Разберём вывод формулы перемещения тела при равноускоренном движении. Заметим, что в этом случае перемещение и пройденный путь – одно и тоже число.
Рассмотрим малый промежуток времени
S= ½·(V 0 + V)t
подставляя (1. 5), получим для равноускоренного движения:
5), получим для равноускоренного движения:
S = V 0 t + (at 2 /2) (1.6)
Для равнозамедленного движения перемещение L вычисляется так:
L= V 0 t–(at 2 /2).
Разберем задачу 1.3.
Пусть график скорости имеет вид, изображенный на рис. 1.2.4. Нарисуйте качественно синхронные графики пути и ускорения от времени.
Студент: – Мне не приходилось встречаться с понятием «синхронные графики», я также не очень представляю, что значит «нарисовать качественно».
– Синхронные графики имеют одинаковые масштабы по оси абсцисс, на которой отложено время. Расположены графики один под другим. Удобны синхронные графики для сопоставления сразу нескольких параметров в один момент времени. В этой задаче мы будем изображать движение качественно, т. е. без учета конкретных числовых значений. Для нас вполне достаточно установить: убывает функция или возрастает, какой вид она имеет, есть ли у нее разрывы или изломы и т. д. Думаю, для начала нам следует рассуждать вместе.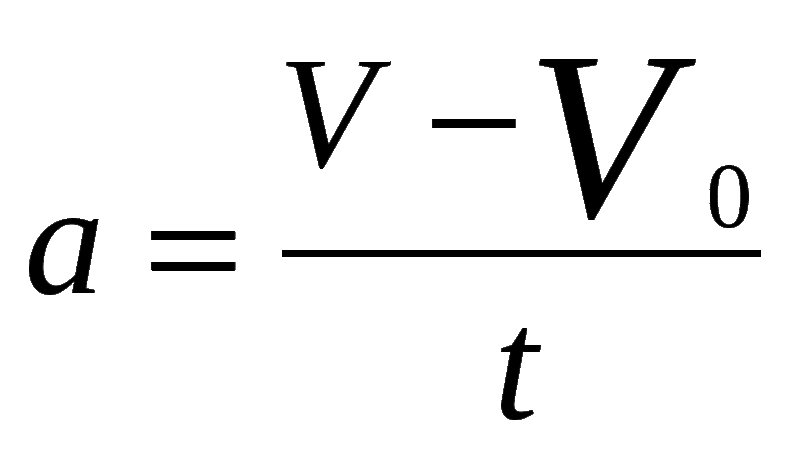
Разделим все время движения на три промежутка ОВ , BD , DE . Скажите, какой характер носит движение на каждом из них и по какой формуле будем вычислять пройденный путь?
Студент: – На участке ОВ тело двигалось равноускоренно с нулевой начальной скоростью, поэтому формула для пути имеет вид:
S 1 (t) = at 2 /2.
Ускорение можно найти, разделив изменение скорости, т.е. длину АВ , на промежуток времени ОВ .
Студент: – На участке ВD тело движется равномерно со скоростью V 0 , приобретенной к концу участка ОВ . Формула пути – S = Vt . Ускорения нет.
S 2 (t) = at 1 2 /2 + V 0 (t– t 1).
Учитывая это пояснение, напишите формулу для пути на участке DE .
Студент: – На последнем участке движение равнозамедленное. Буду рассуждать так. До момента времени

К нему надо добавить выражение для равнозамедленного случая, учитывая, что время отсчитывается от значения t 2 получаем пройденный путь, за время t – t 2:
S 3 =V 0 (t–t 2)–/2.
Предвижу вопрос о том, как найти ускорение a 1 . Оно равно СD/DE . В итоге получаем путь, пройденный за время t>t 2
S (t)= at 1 2 /2+V 0 (t–t 1)– /2.
Студент: – На первом участке имеем параболу с ветвями, направленными вверх. На втором – прямую, на последнем – тоже параболу, но с ветвями вниз.
– Ваш рисунок имеет неточности. График пути не имеет изломов, т. е. параболы следует плавно сопрягать с прямой. Мы уже говорили, что скорость определяется тангенсом угла наклона касательной. По Вашему чертежу получается, что в момент t 1 скорость имеет сразу два значения. Если строить касательную слева, то скорость будет численно равна tg α, а если подходить к точке справа, то скорость равна tg β.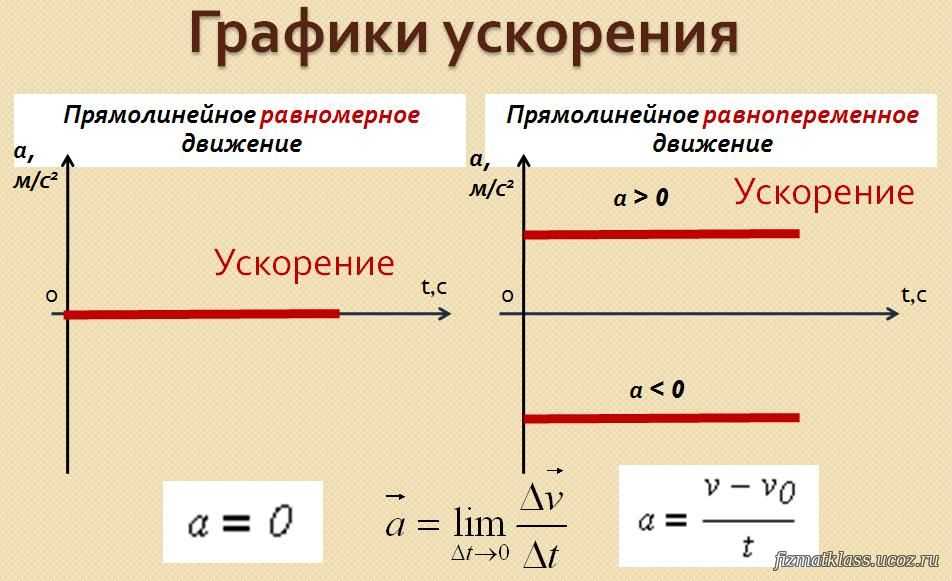 Но в нашем случае скорость – непрерывная функция. Противоречие снимается, если график построить так.
Но в нашем случае скорость – непрерывная функция. Противоречие снимается, если график построить так.
Есть еще одно полезное соотношение между S , a, V и V 0 . Будем предполагать, что движение происходит в одну сторону. В этом случае перемещение тела от начальной точки совпадает с пройденным путём. Используя (1.5), выразите время t и исключите его из равенства (1.6). Так Вы получите эту формулу.
Студент: – V(t) = V 0 + at , значит,
t = (V– V 0)/a,
S = V 0 t + at 2 /2 = V 0 (V– V 0)/a + a[(V– V 0)/a] 2 = .
Окончательно имеем:
S = . (1.6а)
История .
Однажды во время обучения в Геттингене Нильс Бор плохо подготовился к коллоквиуму, и его выступление оказалось слабым. Бор, однако, не пал духом и в заключение с улыбкой сказал:
– Я выслушал здесь столько плохих выступлений, что прошу рассматривать моё как месть.
Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить перемещение автомобиля? Ответы мы получим после того, как познакомимся с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координаты от времени при равноускоренном движении»
При равноускоренном движении график имеет вид прямой линии, уходящей вверх, так как его проекция ускорения больше нуля.
При равномерном прямолинейном движении площадь численно будет равна модулю проекции перемещения тела. Оказывается, этот факт можно обобщить для случая не только равномерного движения, но и для любого движения, то есть показать, что площадь под графиком численно равна модулю проекции перемещения. Это делается строго математически, но мы воспользуемся графическим способом.
Рис. 2. График зависимости скорости от времени при равноускоренном движении ()
Разобьем график проекции скорости от времени для равноускоренного движения на небольшие промежутки времени Δt. Предположим, что они так малы, что на их протяжении скорость практически не менялась, то есть график линейной зависимости на рисунке мы условно превратим в лесенку. На каждой ее ступеньке мы считаем, что скорость практически не поменялась. Представим, что промежутки времени Δt мы сделаем бесконечно малыми. В математике говорят: совершаем предельный переход. В этом случае площадь такой лесенки будет неограниченно близко совпадать с площадью трапеции, которую ограничивает график V x (t). А это значит, что и для случая равноускоренного движения можно сказать, что модуль проекции перемещения численно равен площади, ограниченной графиком V x (t): осями абсцисс и ординат и перпендикуляром, опущенным на ось абсцисс, то есть площади трапеции ОАВС, которую мы видим на рисунке 2.
А это значит, что и для случая равноускоренного движения можно сказать, что модуль проекции перемещения численно равен площади, ограниченной графиком V x (t): осями абсцисс и ординат и перпендикуляром, опущенным на ось абсцисс, то есть площади трапеции ОАВС, которую мы видим на рисунке 2.
Задача из физической превращается в математическую задачу – поиск площади трапеции. Это стандартная ситуация, когда ученые физики составляют модель, которая описывает то или иное явление, а затем в дело вступает математика, которая обогащает эту модель уравнениями, законами – тем, что превращает модель в теорию.
Находим площадь трапеции: трапеция является прямоугольной, так как угол между осями – 90 0 , разобьем трапецию на две фигуры – прямоугольник и треугольник. Очевидно, что общая площадь будет равна сумме площадей этих фигур (рис. 3). Найдем их площади: площадь прямоугольника равна произведению сторон, то есть V 0x · t, площадь прямоугольного треугольника будет равна половине произведения катетов – 1/2АD·BD, подставив значения проекций, получим: 1/2t·(V x – V 0x), а, вспомнив закон изменения скорости от времени при равноускоренном движении: V x (t) = V 0x + а х t, совершенно очевидно, что разность проекций скоростей равна произведению проекции ускорения а х на время t, то есть V x – V 0x = а х t.
Рис. 3. Определение площади трапеции (Источник)
Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, получим:
S х(t) = V 0 x t + а х t 2 /2
Мы с вами получили закон зависимости проекции перемещения от времени при равноускоренном движении в скалярной форме, в векторной форме он будет выглядеть так:
(t) = t + t 2 / 2
Выведем еще одну формулу для проекции перемещения, в которую не будет входить в качестве переменной время. Решим систему уравнений, исключив из нее время:
S x (t) = V 0 x + а х t 2 /2
V x (t) = V 0 x + а х t
Представим, что время нам неизвестно, тогда выразим время из второго уравнения:
t = V x – V 0x / а х
Подставим полученное значение в первое уравнение:
Получим такое громоздкое выражение, возведем в квадрат и приведем подобные:
Мы получили очень удобное выражение проекции перемещения для случая, когда нам неизвестно время движения.
Пусть у нас начальная скорость автомобиля, когда началось торможение, составляет V 0 = 72 км/ч, конечная скорость V = 0, ускорение а = 4 м/с 2 . Узнаем длину тормозного пути. Переведя километры в метры и подставив значения в формулу, получим, что тормозной путь составит:
Узнаем длину тормозного пути. Переведя километры в метры и подставив значения в формулу, получим, что тормозной путь составит:
S x = 0 – 400(м/с) 2 / -2 · 4 м/с 2 = 50 м
Проанализируем следующую формулу:
S x = (V 0 x + V x) / 2 · t
Проекция перемещения- это полусумма проекций начальной и конечной скоростей, умноженная на время движения. Вспомним формулу перемещения для средней скорости
S x = V ср · t
В случае равноускоренного движения средняя скорость будет:
V ср = (V 0 + V к) / 2
Мы вплотную подошли к решению главной задачи механики равноускоренного движения, то есть получению закона, по которому меняется координата со временем:
х(t) = х 0 + V 0 x t + а х t 2 /2
Для того чтобы научиться пользоваться этим законом, разберем типичную задачу.
Автомобиль, двигаясь из состояния покоя, приобретает ускорение 2 м/с 2 . Найти путь, который прошел автомобиль за 3 секунды и за третью секунду.
Дано: V 0 x = 0
Запишем закон, по которому меняется перемещение со временем при
равноускоренном движении: S х = V 0 x t + а х t 2 /2. 2 c
2 c
Мы можем ответить на первый вопрос задачи, подставив данные:
t 1 = 3 c S 1х = а х t 2 /2 = 2· 3 2 / 2 = 9 (м) – это путь, который прошел
c автомобиль за 3 секунды.
Узнаем сколько он проехал за 2 секунды:
S х (2 с) = а х t 2 /2 = 2· 2 2 / 2 = 4 (м)
Итак, мы с вами знаем, что за две секунды автомобиль проехал 4 метра.
Теперь, зная два эти расстояния, мы можем найти путь, который он прошел за третью секунду:
S 2х = S 1х + S х (2 с) = 9 – 4 = 5 (м)
Страница 8 из 12
§ 7. Перемещение при равноускоренном
прямолинейном движении
1. Используя график зависимости скорости от времени, можно получить формулу перемещения тела при равномерном прямолинейном движении.
На рисунке 30 приведен график зависимости проекции скорости равномерного движения на ось X от времени. Если восставить перпендикуляр к оси времени в некоторой точке C , то получим прямоугольник OABC . Площадь этого прямоугольника равна произведению сторон OA и OC . Но длина стороны OA равна v x , а длина стороны OC – t , отсюда S = v x t . Произведение проекции скорости на ось X и времени равно проекции перемещения, т. е. s x = v x t .
Но длина стороны OA равна v x , а длина стороны OC – t , отсюда S = v x t . Произведение проекции скорости на ось X и времени равно проекции перемещения, т. е. s x = v x t .
Таким образом, проекция перемещения при равномерном прямолинейном движении численно равна площади прямоугольника, ограниченного осями координат, графиком скорости и перпендикуляром, восставленным к оси времени.
2. Получим аналогичным образом формулу проекции перемещения при прямолинейном равноускоренном движении. Для этого воспользуемся графиком зависимости проекции скорости на ось X от времени (рис. 31). Выделим на графике малый участок ab и опустим перпендикуляры из точек a и b на ось времени. Если промежуток времени Dt , соответствующий участку cd на оси времени, мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура cabd мало отличается от прямоугольника и ее площадь численно равна проекции перемещения тела за время, соответствующее отрезку cd .
В этом случае фигура cabd мало отличается от прямоугольника и ее площадь численно равна проекции перемещения тела за время, соответствующее отрезку cd .
На такие полоски можно разбить всю фигуру OABC , и ее площадь будет равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время t численно равна площади трапеции OABC . Из курса геометрии вы знаете, что площадь трапеции равна произведению полусуммы ее оснований и высоты:S = (OA + BC )OC .
Как видно из рисунка 31, OA = v 0x , BC = v x , OC = t . Отсюда следует, что проекция перемещения выражается формулой: s x = (v x + v 0x )t .
При равноускоренном прямолинейном движении скорость тела в любой момент времени равна v x = v 0x + a x t , следовательно,s x = (2v 0x + a x t )t .
Отсюда:
Чтобы получить уравнение движения тела, подставим в формулу проекции перемещения ее выражение через разность координат s x = x – x 0 .
Получим: x – x 0 = v 0x t + , или
x = x 0 + v 0x t + . |
По уравнению движения можно определить координату тела в любой момент времени, если известны начальная координата, начальная скорость и ускорение тела.
3. На практике часто встречаются задачи, в которых нужно найти перемещение тела при равноускоренном прямолинейном движении, но время движения при этом неизвестно. В этих случаях используют другую формулу проекции перемещения. Получим ее.
Из формулы проекции скорости равноускоренного прямолинейного движения v x = v 0x + a x t выразим время:
t = .
Подставив это выражение в формулу проекции перемещения, получим:
s x = v 0x + .
Отсюда:
s x = , или
–= 2a x s x .
Если начальная скорость тела равно нулю, то:
2a x s x .
4. Пример решения задачи
Лыжник съезжает со склона горы из состояния покоя с ускорением 0,5 м/с 2 за 20 с и дальше движется по горизонтальному участку, проехав до остановки 40 м. С каким ускорением двигался лыжник по горизонтальной поверхности? Какова длина склона горы?
Дано : | Решение |
v 01 = 0 a 1 = 0,5 м/с 2 t 1 = 20 с s 2 = 40 м v 2 = 0 | Движение лыжника состоит из двух этапов: на первом этапе, спускаясь со склона горы, лыжник движется с возрастающей по модулю скоростью; на втором этапе при движении по горизонтальной поверхности его скорость уменьшается. |
a 2? s 1? |
Систему отсчета свяжем с Землей, ось X направим по направлению скорости лыжника на каждом этапе его движения (рис. 32).
Запишем уравнение для скорости лыжника в конце спуска с горы:
v 1 = v 01 + a 1 t 1 .
В проекциях на ось X получим: v 1x = a 1x t . Поскольку проекции скоростии ускорения на ось X положительны, модуль скорости лыжника равен: v 1 = a 1 t 1 .
Запишем уравнение, связывающее проекции скорости, ускорения и перемещения лыжника на втором этапе движения:
–= 2a 2x s 2x .
Учитывая, что начальная скорость лыжника на этом этапе движения равна его конечной скорости на первом этапе
v 02 = v 1 , v 2x = 0 получим
– = –2a 2 s 2 ; (a 1 t 1) 2 = 2a 2 s 2 .
Отсюда a 2 = ;
a 2 == 0,125 м/с 2 .
Модуль перемещения лыжника на первом этапе движения равен длине склона горы. Запишем уравнение для перемещения:
s 1x = v 01x t + .
Отсюда длина склона горы равна s 1 = ;
s 1 == 100 м.
Ответ: a 2 = 0,125 м/с 2 ; s 1 = 100 м.
Вопросы для самопроверки
1. Как по графику зависимости проекции скорости равномерного прямолинейного движения на ось X
2. Как по графику зависимости проекции скорости равноускоренного прямолинейного движения на ось X от времени определить проекцию перемещения тела?
3. По какой формуле рассчитывается проекция перемещения тела при равноускоренном прямолинейном движении?
4. По какой формуле рассчитывается проекция перемещения тела, движущегося равноускоренно и прямолинейно, если начальная скорость тела равна нулю?
Задание 7
1. Чему равен модуль перемещения автомобиля за 2 мин, если за это время его скорость изменилась от 0 до 72 км/ч? Какова координата автомобиля в момент времени t = 2 мин? Начальную координату считать равной нулю.
Чему равен модуль перемещения автомобиля за 2 мин, если за это время его скорость изменилась от 0 до 72 км/ч? Какова координата автомобиля в момент времени t = 2 мин? Начальную координату считать равной нулю.
2. Поезд движется с начальной скоростью 36 км/ч и ускорением0,5 м/с 2 . Чему равны перемещение поезда за 20 с и его координата в момент времени t = 20 с, если начальная координата поезда 20 м?
3. Каково перемещение велосипедиста за 5 с после начала торможения, если его начальная скорость при торможении равна 10 м/с,а ускорение составляет 1,2 м/с 2 ? Чему равна координата велосипедиста в момент времени t = 5 с, если в начальный момент времени он находился в начале координат?
4. Автомобиль, движущийся со скоростью 54 км/ч, останавливается при торможении в течение 15 с. Чему равен модуль перемещения автомобиля при торможении?
5. Два автомобиля движутся навстречу друг другу из двух населенных пунктов, находящихся на расстоянии 2 км друг от друга. Начальная скорость одного автомобиля 10 м/с и ускорение 0,2 м/с 2 , начальная скорость другого – 15 м/с и ускорение 0,2 м/с 2 . Определите время и координату места встречи автомобилей.
Начальная скорость одного автомобиля 10 м/с и ускорение 0,2 м/с 2 , начальная скорость другого – 15 м/с и ускорение 0,2 м/с 2 . Определите время и координату места встречи автомобилей.
Лабораторная работа № 1
Исследование равноускоренного
прямолинейного движения
Цель работы:
научиться измерять ускорение при равноускоренном прямолинейном движении; экспериментально установить отношение путей, проходимых телом при равноускоренном прямолинейном движении за последовательные равные промежутки времени.
Приборы и материалы:
желоб, штатив, металлический шарик, секундомер, измерительная лента, цилиндр металлический.
Порядок выполнения работы
1. Укрепите в лапке штатива один конец желоба так, чтобы он составлял небольшой угол с поверхностью стола.У другого конца желоба положите в него цилиндр металлический.
2. Измерьте пути, проходимые шариком за 3 последовательных промежутка времени, равных 1 с каждый. Это можно сделать по‑разному. Можно поставить мелом на желобе метки, фиксирующие положения шарика в моменты времени, равные 1 с, 2 с, 3 с, и измерить расстояния s_ между этими метками. Можно, отпуская каждый раз шарик с одной и той же высоты, измерить путь s , пройденный им сначала за 1 с, затем за 2 с и за 3 с, а затем рассчитать путь, пройденный шариком за вторую и третью секунды. Результаты измерений запишите в таблицу 1.
Это можно сделать по‑разному. Можно поставить мелом на желобе метки, фиксирующие положения шарика в моменты времени, равные 1 с, 2 с, 3 с, и измерить расстояния s_ между этими метками. Можно, отпуская каждый раз шарик с одной и той же высоты, измерить путь s , пройденный им сначала за 1 с, затем за 2 с и за 3 с, а затем рассчитать путь, пройденный шариком за вторую и третью секунды. Результаты измерений запишите в таблицу 1.
3. Найдите отношения пути, пройденного за вторую секунду, к пути, пройденному за первую секунду, и пути, пройденного за третью секунду, к пути, пройденному за первую секунду. Сделайте вывод.
4. Измерьте время движения шарика по желобу и пройденныйим путь. Вычислите ускорение его движения, используя формулуs = .
5. Используя экспериментально полученное значение ускорения, вычислите пути, которые должен пройти шарик за первую, вторую и третью секунды своего движения. Сделайте вывод.
Таблица 1
№ опыта | Экспериментальные данные | Теоретические результаты | |||||
Время t, с | Путь s, см | Время t, с | Путь s, см | Ускорение a, см/с2 | Время t , с | Путь s, см | |
1 | 1 | 1 | |||||
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY , была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).
Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY , была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.
Рисунок 1. Проекции векторов скорости и ускорения на координатные оси. a x = 0, a y = –g |
При равноускоренном прямолинейном движении скорость тела определяется формулой
(*)
В этой формуле υ 0 – скорость тела при t = 0 (начальная скорость ), a = const – ускорение. На графике скорости υ (t ) эта зависимость имеет вид прямой линии (рис. 1.4.2).
Рисунок 1.4.2. Графики скорости равноускоренного движения |
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC :
Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна ), тем больше ускорение тела.
Для графика I: υ 0 = -2 м/с, a = 1/2 м/с 2 .
Для графика II: υ 0 = 3 м/с, a = -1/3 м/с 2
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t . Выделим на оси времени некоторый малый промежуток времени Δt . Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt . Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt . Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt , получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF . Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.
1.4.2. Время t принято равным 5,5 с.
Так как υ – υ 0 = at , окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
(**)
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y 0 прибавить перемещение за время t :
(***)
Это выражение называют законом равноускоренного движения .
При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ 0 и конечной υ скоростей и ускорения a . Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t . Результат записывается в виде
Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ 0 , ускорение a и перемещение s :
Если начальная скорость υ 0 равна нулю, эти формулы принимают вид
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ 0 , υ, s , a , y 0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
кинематика – Расчет перемещения под действием силы, действующей на тело в течение некоторого времени
спросил
Изменено 8 месяцев назад
Просмотрено 237 раз
$\begingroup$
По определению 1 Ньютон – это сила, которая, действуя на тело массой 1 кг в течение 1 секунды, переместит его на 1 метр. Это понятно. 92}$$ $$s = \frac{1}{2}m=0,5\пространственных метров$$
Верна ли эта формула?
Везде в инете вижу именно первую формулу с $\frac{1}{2}$, но она бессмысленна. Даже если оперировать не силой и массой, а ускорением, то нет смысла, потому что ускорение ОДИН метр на ОДНУ секунду в течение ОДНА секунда дает ПОЛ метра перемещения. 2$, которую практически все согласны называть $N$ для Ньютона. 92$ и $S=.5 м$.
2$, которую практически все согласны называть $N$ для Ньютона. 92$ и $S=.5 м$.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
3.6 Определение скорости и смещения по ускорению — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Выведите кинематические уравнения для постоянного ускорения с помощью интегрального исчисления.
- Использовать интегральную формулировку кинематических уравнений при анализе движения.
- Найдите функциональную форму зависимости скорости от времени по заданной функции ускорения.
- Найдите функциональную форму зависимости положения от времени по заданной функции скорости.
В этом разделе предполагается, что у вас достаточно знаний в области исчисления, чтобы быть знакомым с интеграцией. В разделах «Мгновенная скорость и скорость» и «Среднее и мгновенное ускорение» мы ввели кинематические функции скорости и ускорения с помощью производной. Взяв производную от функции положения, мы нашли функцию скорости, и точно так же, взяв производную от функции скорости, мы нашли функцию ускорения. Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения, а функцию положения из функции скорости.
Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения, а функцию положения из функции скорости.
Кинематические уравнения интегрального исчисления
Начнем с частицы с ускорением a (t), которое является известной функцией времени. Поскольку производная по времени от функции скорости есть ускорение,
ddtv(t)=a(t),ddtv(t)=a(t),
мы можем взять неопределенный интеграл от обеих частей, найдя
∫ddtv(t)dt=∫a(t)dt+C1,∫ddtv(t)dt=∫a(t)dt+C1,
где C 1 — постоянная интегрирования. Поскольку ∫ddtv(t)dt=v(t)∫ddtv(t)dt=v(t), скорость определяется выражением
v(t)=∫a(t)dt+C1.v(t)=∫a(t)dt+C1.
3.18
Точно так же производная по времени от функции положения является функцией скорости,
ddtx(t)=v(t).ddtx(t)=v(t).
Таким образом, мы можем использовать те же математические манипуляции, которые мы только что использовали, и найти
x(t)=∫v(t)dt+C2,x(t)=∫v(t)dt+C2,
3,19
, где C 2 — вторая постоянная интегрирования.
Мы можем вывести кинематические уравнения для постоянного ускорения, используя эти интегралы. С a ( t ) = a константа, и, выполняя интегрирование в уравнении 3.18, мы находим
v(t)=∫adt+C1=at+C1.v(t)=∫adt+C1=at+C1.
Если начальная скорость v (0) = v 0 , то
v0=0+C1.v0=0+C1.
Тогда С 1 = v 0 и
v(t)=v0+at,v(t)=v0+at,
, что соответствует уравнению 3.12. Подставив это выражение в уравнение 3.19дает
x(t)=∫(v0+at)dt+C2.x(t)=∫(v0+at)dt+C2.
Делаем интегрирование, находим
х(t)=v0t+12at2+C2.x(t)=v0t+12at2+C2.
Если х (0) = х 0 , мы имеем
х0=0+0+С2;х0=0+0+С2;
так, С 2 = х 0 . Подставляя обратно в уравнение для x ( t ), мы, наконец, имеем
Подставляя обратно в уравнение для x ( t ), мы, наконец, имеем
х(t)=x0+v0t+12at2,x(t)=x0+v0t+12at2,
, что соответствует уравнению 3.13.
Пример 3.17
Движение моторной лодки
Моторная лодка движется с постоянной скоростью 5,0 м/с, когда она начинает ускоряться, противоположное движению, чтобы достичь причала. Его ускорение равно a(t)=−14tm/s3a(t)=−14tm/s3. а) Какова функция скорости моторной лодки? б) В какой момент времени скорость достигает нуля? в) Какова функция положения моторной лодки? г) Каково водоизмещение моторной лодки с момента, когда она начала ускоряться против движения, до момента, когда скорость равна нулю? (e) Нарисуйте график функций скорости и положения.
Стратегия
(a) Чтобы получить функцию скорости, мы должны проинтегрировать и использовать начальные условия, чтобы найти постоянную интегрирования. (b) Мы устанавливаем функцию скорости равной нулю и находим t . (c) Точно так же мы должны проинтегрировать, чтобы найти функцию положения, и использовать начальные условия, чтобы найти константу интегрирования. (d) Поскольку начальное положение принимается равным нулю, нам нужно только оценить функцию положения в момент времени, когда скорость равна нулю.
(b) Мы устанавливаем функцию скорости равной нулю и находим t . (c) Точно так же мы должны проинтегрировать, чтобы найти функцию положения, и использовать начальные условия, чтобы найти константу интегрирования. (d) Поскольку начальное положение принимается равным нулю, нам нужно только оценить функцию положения в момент времени, когда скорость равна нулю.
Решение
Примем t = 0 за время, когда лодка начинает ускоряться против движения.
- Из функциональной формы ускорения мы можем решить уравнение 3.18, чтобы получить v ( t ):
v(t)=∫a(t)dt+C1=∫−14tdt+C1=−18t2+C1.v(t)=∫a(t)dt+C1=∫−14tdt+C1=−18t2+C1 .
При t = 0 имеем v (0) = 5,0 м/с = 0 + C 1 , поэтому C 1 = 5,0 м/с или v(t)=5,0 м/ с-18t2v(t)=5,0 м/с-18t2.
- v(t)=0=5,0 м/с−18t2 м/с3⇒t=6,3sv(t)=0=5,0 м/с−18t2 м/с3⇒t=6,3 с
- Решите уравнение 3.19:
x(t)=∫v(t)dt+C2=∫(5,0−18t2)dt+C2=5,0tm/s−124t3m/s3+C2.x(t)=∫v(t)dt+C2= ∫(5,0−18t2)dt+C2=5,0tм/с−124t3м/с3+C2.
При t = 0 мы устанавливаем x (0) = 0 = x 0 , поскольку нас интересует только смещение с момента, когда лодка начинает ускоряться, противоположное движению. У нас естьх(0)=0=С2.х(0)=0=С2.
Следовательно, уравнение положенияx(t)=5,0t−124t3.x(t)=5,0t−124t3.
- Поскольку начальное положение принимается равным нулю, нам нужно оценить функцию положения только в момент времени, когда скорость равна нулю. Это происходит при t = 6,3 с. Следовательно, смещение равно
x (6,3) = 5,0 (6,3 с) − 124 (6,3 с) 3 = 21,1 м. x (6,3) = 5,0 (6,3 с) − 124 (6,3 с) 3 = 21,1 м.
Рисунок
3. 30
а) Зависимость скорости моторной лодки от времени. Моторная лодка уменьшает скорость до нуля за 6,3 с. В моменты времени, превышающие это значение, скорость становится отрицательной, то есть лодка меняет направление. (b) Положение моторной лодки в зависимости от времени. В t = 6,3 с, скорость равна нулю и лодка остановилась. В моменты времени, превышающие это, скорость становится отрицательной — это означает, что если лодка продолжает двигаться с тем же ускорением, она меняет направление и направляется обратно к тому месту, где она возникла.
30
а) Зависимость скорости моторной лодки от времени. Моторная лодка уменьшает скорость до нуля за 6,3 с. В моменты времени, превышающие это значение, скорость становится отрицательной, то есть лодка меняет направление. (b) Положение моторной лодки в зависимости от времени. В t = 6,3 с, скорость равна нулю и лодка остановилась. В моменты времени, превышающие это, скорость становится отрицательной — это означает, что если лодка продолжает двигаться с тем же ускорением, она меняет направление и направляется обратно к тому месту, где она возникла.
Значение
Функция ускорения линейна во времени, поэтому при интегрировании используются простые полиномы. На рис. 3.30 мы видим, что если мы расширим решение за точку, где скорость равна нулю, скорость станет отрицательной, и лодка изменит направление. Это говорит нам о том, что решения могут дать нам информацию, выходящую за рамки нашего непосредственного интереса, и мы должны быть осторожны при их интерпретации.

 Величины, относящиеся к первому этапу движения, запишем с индексом 1, а ко второму этапус индексом 2.
Величины, относящиеся к первому этапу движения, запишем с индексом 1, а ко второму этапус индексом 2.  4.1.
4.1.