Как найти перемещение физика формула: Перемещение при прямолинейном равномерном движении — урок. Физика, 9 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Перемещение тела при прямолинейном равноускоренном движении без начальной скорости 9 класс онлайн-подготовка на

Прямолинейное равноускоренное движение

Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в XVI веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении без изменения направления скорости модуль перемещения совпадает по своему значению с пройденным путем. Формула выглядит следующим образом:

где – это ускорение.

Примеры равноускоренного движения без начальной скорости

Равноускоренное движение без начальной скорости – важный особый случай равноускоренного движения. Рассмотрим примеры:

1. Свободное падение без начальной скорости. Примером такого движения может быть падение сосульки в конце зимы (рис. 1).

Рис. 1. Падение сосульки

В тот момент, когда сосулька отрывается от крыши, ее начальная скорость равна нулю, после чего она движется равноускоренно, ведь свободное падение – это равноускоренное движение.

2. Старт любого движения. Например, автомобиль трогается с места и разгоняется (рис. 2).

Рис. 2. Старт движения

Когда мы говорим, что время набора скорости 100 км/ч у автомобиля той или иной марки, например, 6 с., чаще всего мы говорим о движении равноускоренном без начальной скорости. Аналогично когда мы говорим о старте ракеты и т. д.

3. Особую актуальность равноускоренное движение имеет для разработчиков оружия. Ведь вылет любого снаряда или пули

– это движение без начальной скорости, а во время движения в стволе пуля (снаряд) движется равноускоренно. Рассмотрим пример.

Длина автомата Калашникова – . Пуля в стволе автомата движется с ускорением . С какой скоростью пуля будет вылетать из ствола?

Рис. 3. Иллюстрация к задаче

Для нахождения скорости вылета пули из ствола автомата воспользуемся выражением для перемещения при прямолинейном равноускоренном движении, если неизвестно время:

Движение осуществляется без начальной скорости, а значит, , тогда .

Получим следующее выражение для нахождения скорости вылета пули из ствола:

Решение задачи записываем следующим образом с учетом единиц измерения в СИ:

Дано:

СИ:

Решение:

Ответ: .

Равноускоренное движение без начальной скорости часто встречается и в природе, и в технике. Более того, умение работать с таким движением позволяет решать обратные задачи, когда начальная скорость существует, а конечная равна нулю.

Случай равномерного движения

Если , то уравнение, приведенное выше, превратится в уравнение:

Это уравнение дает возможность найти пройденный путь равномерного движения. в данном случае является проекцией вектора перемещения. Ее можно определить как разность координат: . Если подставить это выражение в формулу, то получим зависимость координаты от времени:

Случай движения без начальной скорости

Рассмотрим ситуацию, когда – начальная скорость равна нулю. Это значит, что движение начинается из состояния покоя. Тело покоилось, затем начинает приобретать и увеличивать скорость. Движение из состояния покоя будет записываться без начальной скорости:

Если S (проекцию перемещения) обозначить как разность начальной и конечной координаты (), то получится уравнение движения, которое дает возможность определить координату тела для любого момента времени:

Проекция ускорения может быть, как отрицательной, так и положительной, поэтому можно говорить о координате тела, которая может как увеличиваться, так и уменьшаться.

График зависимости скорости от времени

Так как равноускоренное движение без начальной скорости является особым случаем равноускоренного движения, рассмотрим график зависимости проекции скорости от времени для такого движения.

На рис. 4 представлен график зависимости проекции скорости от времени для равноускоренного движения без начальной скорости (график начинается в начале координат).

График устремлен вверх. Это говорит о том, что проекция ускорения положительна

Рис. 4. График зависимости проекции скорости от времени при равноускоренном движении без начальной скорости

Используя график, можно определить проекцию перемещения тела или пройденный путь. Для этого необходимо посчитать площадь фигуры, ограниченной графиком, координатными осями и перпендикуляром, опущенным на ось времени. То есть необходимо найти площадь прямоугольного треугольника (половина произведения катетов)

где – конечная скорость при равноускоренном движении без начальной скорости:

тогда:

На рис.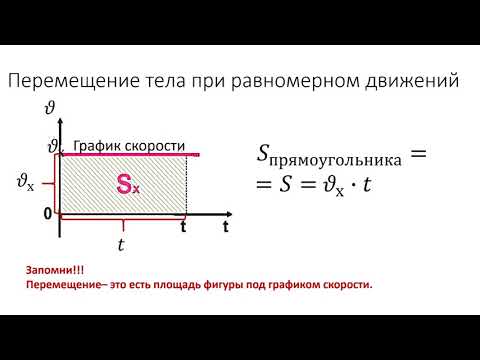 5 представлен график зависимости проекции перемещения от времени двух тел для равноускоренного движения без начальной скорости.

Рис. 5. График зависимости проекции перемещения от времени двух тел для равноускоренного движения без начальной скорости

Начальная скорость обоих тел равна нулю, так как вершина параболы совпадает с началом координат:

У первого тела проекция ускорения положительна , у второго – отрицательна . Причем у первого тела проекция ускорения тела больше, так как перемещение у него осуществляется быстрее.

Пропорциональность пути квадрату времени

– пройденный путь (с точностью до знака), он пропорционален , т. е. квадрату времени. Если рассматривать равные промежутки времени – , , , то можно заметить следующие соотношения:

Если продолжить вычисления, закономерность сохранится. Пройденные расстояния увеличиваются пропорционально квадрату увеличения промежутков времени.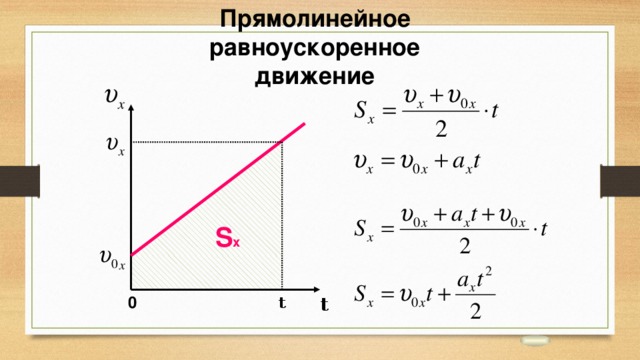

Например, если , то пройденный путь будет пропорционален . Если , пройденный путь будет пропорционален и т. д. Расстояние будет расти пропорционально квадрату этих промежутков времени (рис. 6).

Рис. 6. Пропорциональность пути квадрату времени

Перемещения за последовательные (равные) промежутки времени

Если за единицу времени выбираем некий промежуток, то полные расстояния, пройденные телом за последующие равные промежутки времени, будут относиться как квадраты целых чисел.

Иными словами, перемещения, совершенные телом за каждую последующую секунду, будут относиться как нечетные числа:

Рис. 7. Перемещения за каждую секунду относятся как нечетные числа

Исследованные два очень важных заключения свойственны только прямолинейному равноускоренному движению без начальной скорости.

Рассмотренные закономерности на примере задачи

Задача. Автомобиль начинает двигаться от остановки, т. е. из состояния покоя, и за четвертую секунду своего движения проходит 7 м. Определите ускорение тела и мгновенную скорость через 6 с после начала движения (рис. 8).

Рис. 8. Иллюстрация к задаче

Дано:

Решение:

Ответ:; .

Решение: автомобиль начинает движение из состояния покоя, следовательно, путь, который проходит автомобиль, рассчитывается по формуле: . Мгновенная скорость определяется как .

– расстояние, которое автомобиль прошел за четвертую секунду своего движения.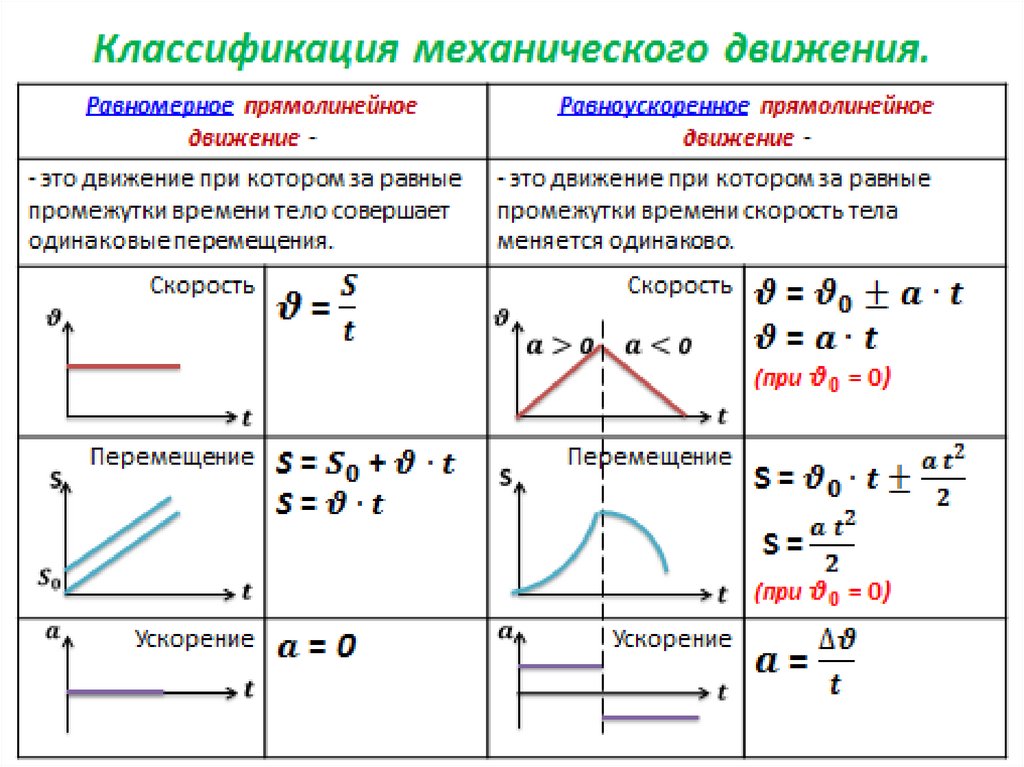 Его можно выразить как разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с (рис. 9).

Рис. 9. Разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с

Решив уравнение, получаем ускорение .

Чтобы определить мгновенную скорость, т. е. скорость в конце шестой секунды, следует ускорение умножить на время, т. е. на 6 с, во время которых тело которое продолжало двигаться.

Заключение

Уравнения, которые сегодня мы использовали в уроке, впервые были исследованы Галилео Галилеем. На следующем уроке мы рассмотрим, как именно были проведены эти опыты.

Список литературы

Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
Соколович Ю.А., Богданова Г.

С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал «phscs.ru» (Источник)
Интернет-портал «fizikaklass.ru» (Источник)
Интернет-портал «sernam.ru» (Источник)

Домашнее задание

Запишите формулу, которая используется для определения перемещения тела при его равноускоренном движении из состояния покоя.
Если увеличить время движения тела из состояния покоя в 5 раз, во сколько увеличится модуль вектора перемещения тела?

Автобус начинает свое движение от остановки и за 5 с своего движения проходит 15 м. Определите ускорение автобуса через 8 с после начала движения.

Перемещение тела при РУД

Урок 7. Физика 9 класс (ФГОС)

Посмотрев данный видеоурок, вы вспомните, как определяется скорость и ускорение тела при прямолинейном равноускоренном движении. Также мы выведем формулу, по которой можно рассчитать проекцию вектора перемещения тела при равноускоренном движении. Узнаем, как зависит от времени координата тела при таком движении. Сравним зависимости основных кинематических величин для двух видов прямолинейного движения. И научимся строить графики зависимости от времени координаты тела и проекции его перемещения.

Конспект урока “Перемещение тела при РУД”

На прошлых уроках мы с вами начали изучать прямолинейное равноускоренное движение, то есть движение с постоянным по модулю ускорением. Напомним, что ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости:

Также мы с вами выяснили, что при равноускоренном движении, скорость тела линейно зависит от времени:

Теперь мы должны выяснить самое главное — как изменяется со временем координата тела при его прямолинейном равноускоренном движении. Для этого, как мы знаем, необходимо знать перемещение тела, так как проекция вектора перемещения как раз и равна изменению координаты тела.

При изучении графического представления равномерного движения мы говорили о том, что проекция перемещения при равномерном движении численно равна площади прямоугольника, ограниченного графиком скорости, осью времени и перпендикулярами к этой оси, восставленными из точек, соответствующих моментам начала и конца наблюдения.

Это же правило применимо и для неравномерного движения. Покажем это. Для чего воспользуемся графиком зависимости проекции скорости от времени. Выберем на графике достаточно малый участок

АВ и проведём перпендикуляры из точек А и В» на ось времени:

Длина полученного на оси времени отрезка равна тому малому промежутку времени, в течение которого произошло изменение скорости от её значения в точке А, до её значения в точке В. Если этот промежуток времени достаточно мал, то изменением скорости за это время можно пренебречь, то есть движение тела можно считать равномерным. Следовательно, полученная полоска ABCD мало отличается от прямоугольника.

А его площадь численно равна проекции перемещения тела за время, соответствующее отрезку CD.

Очевидно, что на такие узкие полоски мы можем разбить всю площадь фигуры под графиком скорости.

Тогда, согласно рисунку, проекция перемещения при равноускоренном движении определяется площадью трапеции. Площадь же трапеции, как известно из геометрии, равна произведению полусуммы её оснований на высоту. В нашем случае длина одного из оснований численно равна проекции начальной скорости тела, другого — проекции скорости через время t, высота же трапеции численно равна времени:

Обратите внимание на первый множитель в уравнении. Мы знаем, что среднее значение проекции скорости равно отношению проекции перемещения тела к промежутку времени, в течение которого это перемещение произошло. Тогда из формулы следует,

что средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей:

При равноускоренном движении эта формула выполняется не только для проекций, но и для векторов скорости.

Теперь подставим в полученную формулу для проекции перемещения уравнение скорости и, проведя простые математические преобразования, получим формулу, выражающую зависимость проекции перемещения от времени при равноускоренном движении:

При использовании формулы нужно помнить, что входящие в неё величины могут иметь разные знаки, так как это проекции векторов перемещения, начальной скорости и ускорения.

Учитывая, что проекция перемещения равна разности конечной и начальной координат тела, получим формулу, выражающую кинематический закон равноускоренного движения:

Из полученных формул видим, что при равноускоренном движении проекция перемещения тела и его координата квадратично зависят от времени. В математике квадратичную зависимость записывают в виде

Её график представляет собой параболу, направление ветвей которой зависят от знака коэффициента с. Следовательно, для равноускоренного движения графиком проекций перемещений при равноускоренном движении являются участки парабол, положение вершин которых зависят от направлений начальной скорости и ускорения тела.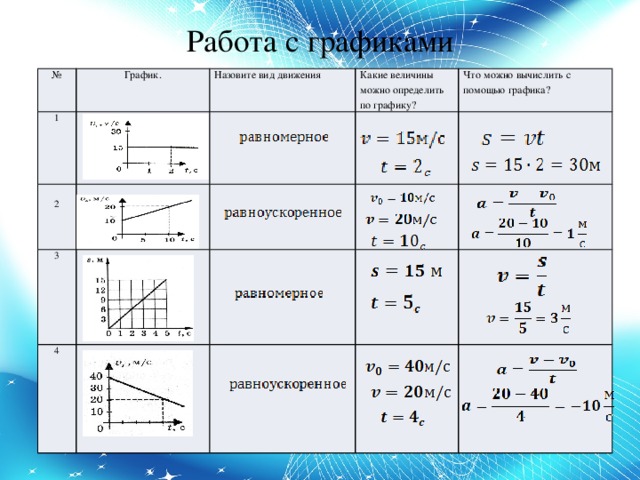

На первом графике проекция перемещения всё время растёт, что соответствует движению с положительным ускорением, а на втором графике — растёт до некоторого момента времени, а затем уменьшается. Так происходит потому, что в этот момент времени скорость тела становится равной нулю и направление движения тела изменяется на противоположное. Поэтому второй график соответствует движению тела с отрицательной проекцией ускорения.

— А каким будет график пути?

Для движения, при котором направление скорости не изменяется, график пути совпадает с графиком проекции перемещения. Если же скорость меняет своё направление, то эти графики совпадают лишь до момента поворота. После поворота проекция перемещения начинает уменьшаться, а путь продолжает расти. Причём он увеличивается ровно на столько, на сколько за то же время уменьшается проекция перемещения.

Что касается графика зависимости координаты тела от времени, то он получается из графика проекции перемещения смещением вверх, если начальная координата тела положительна, или вниз, если начальная координата тела отрицательна.

Теперь давайте сравним зависимости основных кинематических величин для двух видов прямолинейного движения:

Как видно из таблицы, если проекция ускорения равна нулю, то формулы равноускоренного движения переходят в формулы равномерного.

Закрепления материала.

Локомотив двигался со скоростью 5 м/с. Увидев зелёный свет светофора, машинист увеличил скорость, причём ускорение при разгоне составило 0,6 м/с². Рассчитайте путь, на котором скорость локомотива увеличилась до 20 м/с.

Предыдущий урок 6 Скорость РУД. График скорости

Следующий урок 8 Перемещение при РУД без начальной скорости

Получите полный комплект видеоуроков, тестов и презентаций Физика 9 класс (ФГОС)

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Как рассчитать смещение в физической задаче

: Стивен Холцнер и

Обновлен: 05-01-2017

Из книги: Physics I для Dummies

Physics I For Dummies

. Купить книгу на Amazon

Смещение — это расстояние между начальным положением объекта и его конечным положением, которое обычно измеряется или определяется вдоль прямой линии. Поскольку это расчет, который измеряет расстояние, стандартной единицей измерения является метр (м).

Как найти рабочий объем

В физике вы находите смещение, вычисляя расстояние между начальным положением объекта и его конечным положением.

В терминах физики вы часто видите, что смещение называют переменной s.

Официальная формула смещения выглядит следующим образом:

с = с f – с i

с = смещение
с i = исходное положение
с f = конечная позиция

Пример расчета смещения

Скажем, например, что у вас есть прекрасный новый мяч для гольфа, который может катиться. Этот конкретный мяч для гольфа любит кататься по большой измерительной палке, и вы хотите знать , как рассчитать перемещение при движении мяча.

Вы помещаете мяч для гольфа в положение 0 на измерительной палке, как показано на рисунке ниже, диаграмма А.

Проверка смещения с помощью мяча для гольфа.

Мяч для гольфа перекатывается в новую точку, на 3 метра правее, как вы видите на рисунке, диаграмма B. Мяч для гольфа переместился, поэтому произошло смещение. При этом смещение составляет всего 3 метра вправо. Его начальное положение было 0 метров, а его конечное положение +3 метра. Водоизмещение 3 метра.

Ученые, будучи теми, кто они есть, любят вдаваться в подробности. Вы часто видите термин s _i , который описывает начальную позицию , ( i означает начальное ). И вы можете увидеть термин s _f , используемый для описания конечной позиции .

В этих терминах, переходя от диаграммы A к диаграмме B на рисунке, s _i находится на отметке 0 метров и s _f находится на +3 метра. Смещение, с, равно конечной позиции минус начальная позиция:

Смещения не обязательно должны быть положительными; они также могут быть нулевыми или отрицательными. Если положительное направление вправо, то отрицательное смещение означает, что объект сместился влево.

На диаграмме C беспокойный мяч для гольфа переместился в новое место, которое измеряется как -4 метра на измерительной рейке. Перемещение определяется разницей между начальным и конечным положением. Если вы хотите узнать смещение мяча от его положения на диаграмме B, примите начальное положение мяча равным 9.0053 с _i = 3 метра; тогда смещение будет равно

. При работе над физическими задачами вы можете разместить начало координат вашей системы измерения положения там, где это удобно. Измерение положения объекта зависит от того, где вы решили разместить свое происхождение; однако смещение из начального положения s _i в конечное положение s _f не зависит от положения начала координат, потому что смещение зависит только от разница между позициями, а не сами позиции.

Об этой статье

Эта статья из книги:

Физика I для чайников,

Об авторе книги:

Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был редактором журнала PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором титулов для чайников, в том числе Физика для чайников и Основы физики для чайников. Доктор Хольцнер получил докторскую степень в Корнелле.

Эту статью можно найти в категории:

Физика,

Как найти смещение в физике

Содержание

Что такое смещение в физике

В этом посте я помогу вам понять, как найти перемещение в физике.

Как рассчитать смещение с помощью подшипника

Определение смещения в физике: Смещение — это мера расстояния между двумя точками в заданном направлении. Перемещение является векторной величиной и измеряется в метрах.

Описание автомобиля, движущегося в заданном направлении

Когда человек движется из одной точки в другую (меняет свое положение) в прямом, заданном направлении. Мы измеряем его расстояние как смещение. Перемещение прямое, прямое и в форме поступательного движения. В отличие от расстояния, линия движения смещения не является случайной или зигзагообразной.

Для точного описания перемещения предположим, что человек присоединился к поезду, и поезд движется из города Y в город Z по прямой, преодолевая расстояние в 300 километров. Доехав до города Z, поезд следовал по тому же маршруту и остановился на 80-м километре, не доезжая до пункта назначения.

Чтобы найти смещение пути человека, вычтем 80 км из 300 км, так как маршрут такой же и прямой. Следовательно, перемещение человека составляет (300 км – 80 км = 220 км) 220 км.

Смещение имеет сходство с расстоянием, поскольку они оба измеряются в метрах и являются мерой расстояния между двумя точками. Однако смещение — это полная противоположность расстоянию, потому что смещение находится в определенном направлении, а расстояние — нет.

Перемещение связано со скоростью, а расстояние связано со скоростью. Оба они связаны со временем.

Формула для расчета смещения в физике

Формула смещения может быть:

Поскольку скорость = расстояние/время, мы также можем сказать, что скорость (v) = перемещение (с)/время (t). Сделав смещение предметом формулы, мы теперь имеем Смещение = скорость x время. Следовательно, теперь мы можем написать s = v x t
Мы также можем применить уравнения движения, чтобы найти перемещение объекта, которое равно S = ut + 1/2 при ² или

S = (v ² -u ² )/2a
Мы также можем применить S = √[ (x ₂ -x ₁ ) ² + (у ₂ -у ₁ ) ² + (z ₂ -z ₁ ) ² ]
Кроме того, мы можем рассчитать водоизмещение, применив формулу, которая говорит: x _общее = x _{конечное} – x _{начальное} (где x _общее = общее водоизмещение, x _{начальное} = начальное смещение, и x _{конечное} = окончательный рабочий объем)

Вы также можете прочитать:

Позиция по физике

Примеры того, как найти смещение в физике

Вот несколько примеров, которые помогут вам понять, как найти смещение в физике.

Пример 1

Мяч переместили из точки О в точку А по прямой на расстояние 5 метров. Позже он был возвращен в О по тому же пути. Каково результирующее смещение?

Решение

Данные:

Перемещение от О до А равно 5 м

Возвращение от А к О по тому же пути означает, что АО также равно 5 м

Таким образом,

Водоизмещение OA = 5 м

Водоизмещение AO = 5 м

Полное перемещение от O до A, а затем обратно до O является суммой OA и -AO

AO отрицательно, поскольку возвращается к в том же направлении и исключая начальное перемещение

Таким образом,

Чтобы найти результирующее смещение, мы говорим:

Результирующее смещение = OA + (-AO) = 5м + (-5м) = 5м – 5м = 0

Следовательно, полное перемещение от О к А и обратно к О равно нулю. Это показывает, что никакого смещения шара нет.