Движение под углом к горизонту
(Данное движение состоит из двух движений: Вертикальное равноускоренное движение и Равномерное горизонтальное).
Какие отличия можно отметить между данным движением и ранее рассматривающимися РуВД и РмГД?
1 отличие: в том, что скорость при вертикальном движении, равна вертикальной составляющей – Vу (вертикальной проекции), а горизонтальное движение происходит с горизонтальной составляющей скорости-Vх. (Эти проекции скоростей выражаются через тригонометрические функции Sin и Cos).
2 отличие: в том, что свободное движение по вертикали протекает с ускорением свободного падения g, а при движении под углом к горизонту по оси ОУ движение может быть как свободным ( с ускорением g), так и любым равноускоренным движением с ускорением ат .
3 отличие:в том, что перемещение тела происходит вверх-вниз (h) – высота подъёма и вперёд (S) – дальность полёта
OY: Определим проекции скоростей в точках О, С, А и сравним их по величине.
На рисунке хорошо видно, что проекции этих скоростей отличаются по величине:
VOY > VCY >VAY , при этом проекция скорости в точке А на ось OY равна нулю (VAY = 0), а проекции остальных скоростей соответственно:
VOY = V0 sin α, VCY = Vc sin β .
По определению основных характеристик вертикального движения можно записать их формулы:
2.Конечная скорость подъёма в т.А: VAY = VOY – gtпод, но т.к. VAY = 0, то эту формулу можно записать в виде: 0 = V0 sin α – gtпод => gtпод = V0 sin α
3. Высоту подъёма можно вычислить по четырём формулам:
При этом надо помнить, что при свободном движении время подъёма равно времени падения
tпод = tпад , а все время движения можно найти по формуле tвсё= 2tпад
Рассмотрим теперь это движение в проекции на ось OX (движение вдоль оси Oх).
Это движение соответствует равномерному горизонтальному движению (при условии, что нет никаких помех со стороны других тел по горизонтальному направлению):
OX: По определению путь тела или его горизонтальное перемещение равны произведению горизонтальной проекции скорости на время горизонтального движения:S = VOXtвсё = V0
Если учесть что tвсё= 2tпад и , тогда формула дальности полёта примет вид:
Тогда, зная значение высоты подъёма и дальности полёта, можно сравнить эти две характеристики между собой:
, т. е. дальность полёта S в 4ctg α больше высоты подъёма h:
!!! S > h в 4ctg α
Т.к. движение вдоль оси OX равномерное то скорость в любой точке на этой оси одинакова, т.
VOX = VСX=VАX= VВX =VДX , где VOX=V0cos α ,VСX=VСcos β ,VАX=VА,
VВX=VВcos β ,VДХ = VДcos α
На рисунке видно, что проекции скоростей( на обе оси соответственно) в симметричных точках равны, но отличаются направлением.
V0cosα = VСcosβ = VA (проекция скорости на ось OX в т. А равна сама себе)
т.к. это РМДв, то
VOX = V0cosα = VДХ = VДcosα (но начальная скорость подъёма, равна конечной скорости падения ). Угол между направлениями начальной и конечной скорости этого движения равен 2α.
Рассмотрим первый частный случай этого движения, когда тело бросают горизонтально с некоторой высоты:
Особенность этого случая в том что здесь всё время движения равно времени падения тела: tвсё = tпад
Рассмотрим второй частный случай этого движения, когда тело бросают под углом к горизонту или вниз или вверх с некоторой высоты:
Такое движение аналогично первому частному случаю, но при этом | Такое движение делится на два случая на движение под углом к горизонту |
При рассмотрении движения под углом необходимо помнить ещё одну ОСОБЕННОСТЬ этого движения – это движение является симметричным относительно оси, проходящей через высоту подъёма, а это позволяет сделать следующий вывод:
Если на пути тела «стоит» стена, от которой тело при упругом ударе отскочит, то расстояние, на которое оно отлетит, будет равно расстоянию «непройденному» телом по причине «помехи»:
|
| |
АМ (S) – дальность возможного полёта, если бы не было стены. | ||
При решении такого типа задач следут найти значение возможной дальности полёта S (для случая без препятствия ). Зная, на каком расстоянии находилось тело от стены, можно определить где оно окажется после удара.
Как вычислить скорость движения. Как найти скорость, зная время и расстояние
Интернет
Скорость является функцией времени и определяется как абсолютной величиной, так и направлением. Часто в задачах по физике требуется найти начальную скорость (ее величину и направление), которой изучаемый объект обладал в нулевой момент времени. Для вычисления начальной скорости можно использовать различные уравнения. Основываясь на данных, приведенных в условии задачи, вы можете выбрать наиболее подходящую формулу, которая позволит легко получить искомый ответ.
Шаги
Нахождение начальной скорости по конечной скорости, ускорению и времени
При решении физической задачи необходимо знать, какая формула вам понадобится.
Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, ускорение и время, для определения начальной скорости удобно использовать следующее соотношение:- V i = V f – (a * t)
- V i – начальная скорость
- V f – конечная скорость
- a – ускорение
- t – время
- Обратите внимание, что это стандартная формула, используемая для вычисления начальной скорости.
Выписав все исходные данные и записав необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Если вы где-либо допустили ошибку, то легко сможете найти ее, просмотрев свои записи.
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для получения искомого результата.
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
- Запишем исходные данные:
- V i = ?, V f = 200 м/с, a = 10 м/с 2 , t = 12 с
- Умножим ускорение на время: a * t = 10 * 12 =120
- Вычтем полученное значение из конечной скорости: V i = V f – (a * t) = 200 – 120 = 80 V i = 80 м/с на восток
- м/с
Нахождение начальной скорости по пройденному пути, времени и ускорению
Используйте подходящую формулу. При решении какой-либо физической задачи необходимо выбрать соответствующее уравнение. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:
- В эту формулу входят следующие величины:
- V i – начальная скорость
- d – пройденное расстояние
- a – ускорение
- t – время
- В эту формулу входят следующие величины:
Подставьте в формулу известные величины.
- Допустив ошибку в решении, вы сможете без труда найти ее, просмотрев свои записи.
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для нахождения ответа. Если возможно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
- Запишем исходные данные:
- V i = ?, d = 150 м, a = 7 м/с 2 , t = 30 с
- Умножим ускорение на время: a * t = 7 * 30 = 210
- Поделим произведение на два: (a * t) / 2 = 210 / 2 = 105
- Поделим расстояние на время: d / t = 150 / 30 = 5
- Вычтем первую величину из второй: V i = (d / t) – [(a * t) / 2] = 5 – 105 = -100 V i = -100 м/с в западном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с , а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
Нахождение начальной скорости по конечной скорости, ускорению и пройденному пути
Используйте подходящее уравнение. Для решения физической задачи необходимо выбрать соответствующую формулу. Первым делом следует записать все начальные данные, указанные в условии задачи. Если известны конечная скорость, ускорение и пройденное расстояние, для определения начальной скорости удобно использовать следующее соотношение:
- V i = √
- Эта формула содержит следующие величины:
- V i – начальная скорость
- V f – конечная скорость
- a – ускорение
- d – пройденное расстояние
Подставьте в формулу известные величины.
После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.- Допустив где-либо ошибку, вы сможете без труда найти ее, просмотрев ход решения.
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. По возможности используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
- Запишем исходные данные:
- V i = ?, V f = 12 м/с, a = 5 м/с 2 , d = 10 м
- Возведем в квадрат конечную скорость: V f 2 = 12 2 = 144
- Умножим ускорение на пройденное расстояние и на 2: 2 * a * d = 2 * 5 * 10 = 100
- Вычтем результат умножения из квадрата конечной скорости: V f 2 – (2 * a * d) = 144 – 100 = 44
- Извлечем квадратный корень из полученного значения: = √ = √44 = 6,633 V i = 6,633 м/с в северном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с , а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, ускорение и время, для определения начальной скорости удобно использовать следующее соотношение:
Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с , а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
Необходимо указать единицы измерения, то есть метры в секунду, или м/с , а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.Скорость – это величина, которая описывает быстроту перемещения объекта из точки А в точку Б. Обозначается латинской буквой V – сокращение от латинского velocitas – скорость. Скорость можно узнать, если известно время (t), в течение которого перемещался объект, и расстояние (S), которое объект преодолел.
Чтобы расчитать скорость, используйте формулу пути: V=S/t. Например, за 12 секунд объект продвинулся на 60 метров, значит его скорость равнялась 5 м/с (V=60/12=5).
Используйте одинаковые единицы измерения, если сравниваете скорость двух разных объектов. Основной единицей измерения скорости в международной системе единиц являются метры в секунду или сокращенно м/с.
Также распространены километры в часы, километры в секунду, метры в минуту и метры в секунду. В англоязычных странах используются мили в секунду, мили в час, футы в секунду и футы в минуту.
Помните, точность определения скорости зависит от характера движения. Точнее всего формула пути помогает найти скорость при равномерном движении – объект преодолевает одинаковое расстояние за равные промежутки времени. Однако равномерное движение очень редко встречается в реальном мире. Это, к примеру, движение секундной стрелки в часах или вращение Земли вокруг Солнца. В случае неравномерного движения, например, прогулка по городу, формула пути помогает найти среднюю скорость.
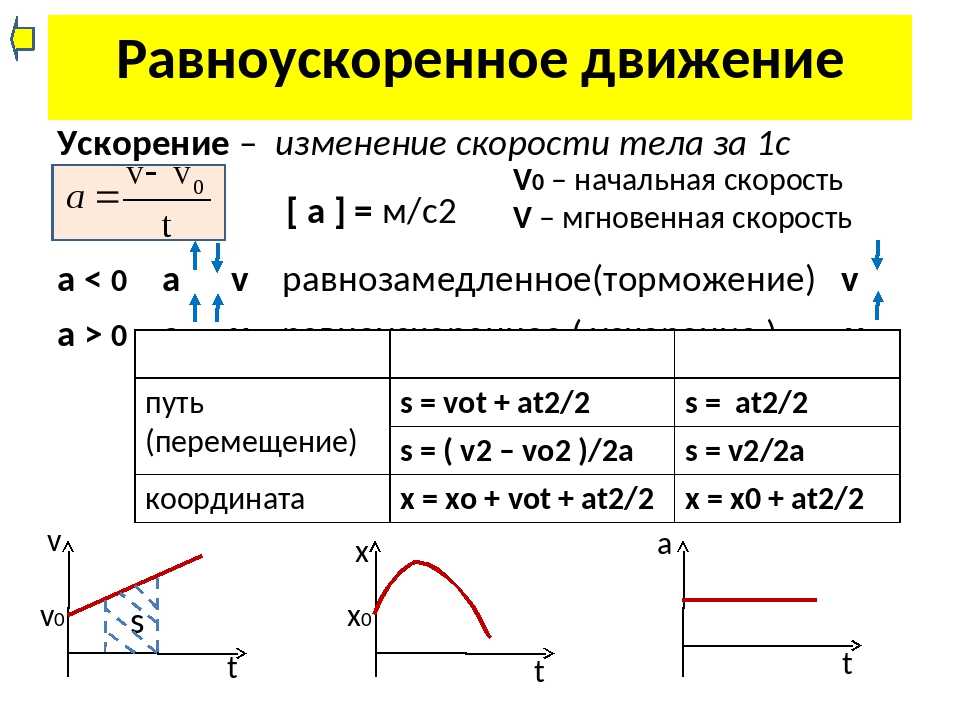
При прямолинейном равноускоренном движении тело
- двигается вдоль условной прямой линии,
- его скорость постепенно увеличивается или уменьшается,
- за равные промежутки времени скорость меняется на равную величину.
Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно.
Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с 2 .
Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.
Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:
При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:
Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т.
е. как быстро менялась скорость), разделив скорость на время:
Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с 2 . Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:
Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:
Получим из этих формул формулы ускорения. В случае ускорения:
at = v – v 0
a = (v – v 0)/t
В случае торможения:
at = v 0 – v
a = (v 0 – v)/t
В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0.
Тогда формула сокращается до такого вида:
Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:
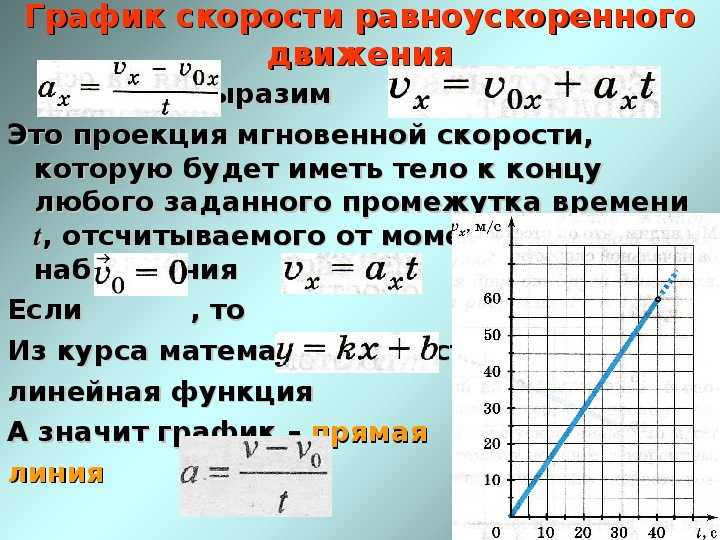
Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении . Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.
При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени).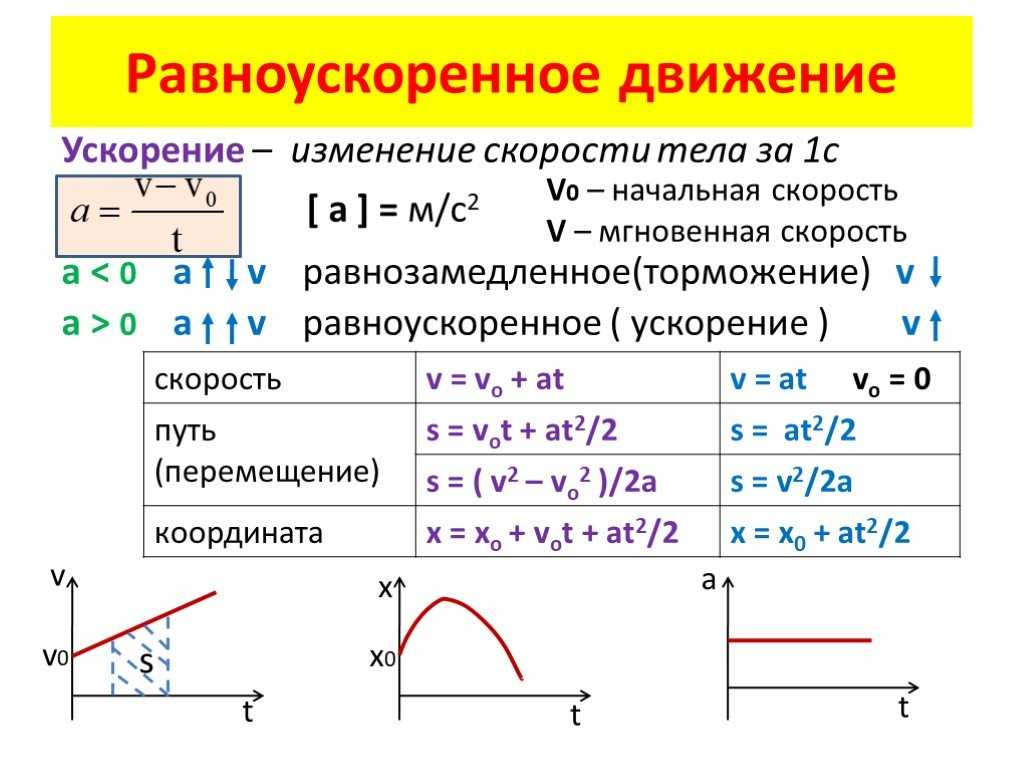
Проекция на ось x – это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.
Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:
s = ½ * (v 0 + v) * t
Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:
s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2
Итак, пройденный путь определяется по формуле:
s = v 0 t + at 2 /2
(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)
Если тело начало двигаться равноускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2 /2.
Если вектор ускорения был противоположен скорости, то произведение at 2 /2 надо вычитать.
Понятно, что при этом разность v 0 t и at 2 /2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v 0 /a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле.
Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время {\displaystyle {\text{Скорость}}={\frac {\text{Пройденный путь}}{\text{Время}}}} . Но в некоторых задачах даются два значения скорости – на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.
Шаги
По одному значению пути и одному значению времени
- длина пути, пройденного телом;
- время, за которое тело прошло этот путь.
- Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.
Формула: , где v {\displaystyle v} – средняя скорость, s {\displaystyle s} – пройденный путь, t {\displaystyle t} – время, за которое пройден путь.
В формулу подставьте пройденный путь. Значение пути подставьте вместо s {\displaystyle s} .
- В нашем примере автомобиль проехал 150 км. Формула запишется так: v = 150 t {\displaystyle v={\frac {150}{t}}} .
В формулу подставьте время. Значение времени подставьте вместо t {\displaystyle t} .
- В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: .
Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).
Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s}
).
- В нашем примере автомобиль проехал 150 км, 120 км и 70 км. Общий пройденный путь: .
T {\displaystyle t} ).
- . Таким образом, формула запишется так: .
- В нашем примере:
v = 340 6 {\displaystyle v={\frac {340}{6}}}Таким образом, если автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).
По нескольким значениям скоростей и нескольким значениям времени
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
Запишите формулу для вычисления средней скорости. Формула: v = s t {\displaystyle v={\frac {s}{t}}} , где v {\displaystyle v} – средняя скорость, s {\displaystyle s} – общий пройденный путь, t {\displaystyle t} – общее время, за которое пройден путь.
Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время.
Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s}
).- Например:
50 км/ч в течение 3 ч = 50 × 3 = 150 {\displaystyle 50\times 3=150} км
60 км/ч в течение 2 ч = 60 × 2 = 120 {\displaystyle 60\times 2=120} км
70 км/ч в течение 1 ч = 70 × 1 = 70 {\displaystyle 70\times 1=70} км
Общий пройденный путь: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} км. Таким образом, формула запишется так: v = 340 t {\displaystyle v={\frac {340}{t}}} .
- Например:
Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо t {\displaystyle t} ).
- В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч. Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6}
. Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}}
.
- В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч. Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6}
. Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}}
.
Разделите общий путь на общее время. Вы найдете среднюю скорость.
- В нашем примере:
v = 340 6 {\displaystyle v={\frac {340}{6}}}
v = 56 , 67 {\displaystyle v=56,67}
Таким образом, если автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).
- В нашем примере:
Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s}
).
По двум значениям скоростей и двум одинаковым значениям времени
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:
- два или несколько значений скоростей, с которыми двигалось тело;
- тело двигалось с определенными скоростями в течение равных промежутков времени.
- Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
Запишите формулу для вычисления средней скорости, если даны две скорости, с которыми тело движется в течение равных промежутков времени.
Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}}
, где v {\displaystyle v}
– средняя скорость, a {\displaystyle a}
– скорость тела в течение первого промежутка времени, b {\displaystyle b}
– скорость тела в течение второго (такого же, как первый) промежутка времени.- В таких задачах значения промежутков времени не важны – главное, чтобы они были равны.
- Если дано несколько значений скоростей и равные промежутки времени, перепишите формулу так: v = a + b + c 3 {\displaystyle v={\frac {a+b+c}{3}}} или v = a + b + c + d 4 {\displaystyle v={\frac {a+b+c+d}{4}}} . Если промежутки времени равны, сложите все значения скоростей и разделите их на количество таких значений.
В формулу подставьте значения скоростей. Неважно, какое значение подставить вместо a {\displaystyle a} , а какое – вместо b {\displaystyle b} .
- Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .
- Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .
Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.
- Например:
v = 40 + 60 2 {\displaystyle v={\frac {40+60}{2}}}
v = 100 2 {\displaystyle v={\frac {100}{2}}}
v = 50 {\displaystyle v=50}
Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.
- Например:
Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}}
, где v {\displaystyle v}
– средняя скорость, a {\displaystyle a}
– скорость тела в течение первого промежутка времени, b {\displaystyle b}
– скорость тела в течение второго (такого же, как первый) промежутка времени.
Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.
Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.
Как найти скорость – равномерное движение
Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.
Тогда V=S/t, где:
- V – искомая скорость,
- S – пройденное расстояние (общий путь),
- t – общее время движения.
Как найти скорость – ускорение постоянно
Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:
V=V (нач) + at, где:
- V (нач) – первоначальная скорость движения объекта,
- a – ускорение тела,
- t – общее время пути.
Как найти скорость – неравномерное движение
В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.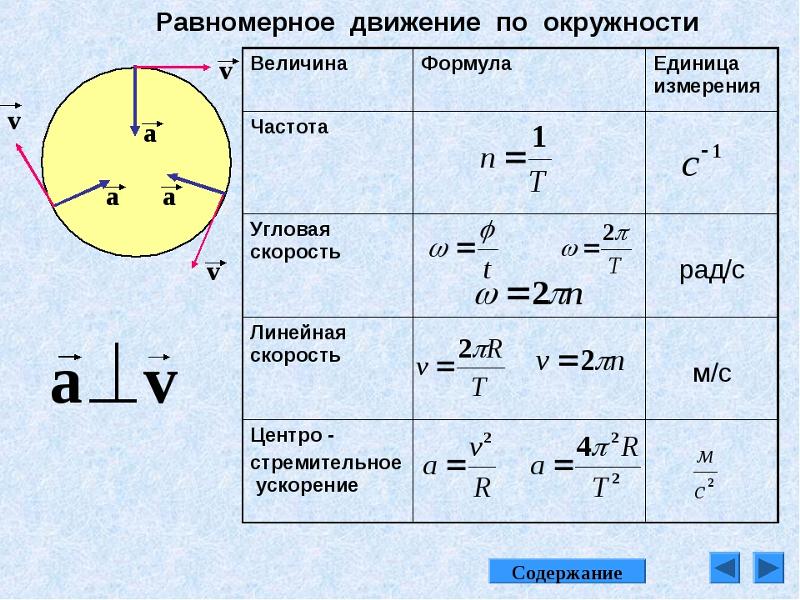
д.
На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.
Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:
Как найти скорость – вращение объекта
В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).
- ω = Δφ/Δt, где:
Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).
- В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:
ω = 2π/T, где:
π – константа ≈3,14,
T – период.
Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.
- При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:
ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.
Как найти скорость – сближение и отдаление точек
В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.
Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.
Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).
Как найти скорость – движение по водоему
Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?
В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).
| Начальная и конечная скорость
В этом калькуляторе смещения мы покажем вам, как найти перемещение за считанные секунды. Мы также поможем вам понять определение смещения и формулу смещения.
Что такое смещение ? В чем разница между смещениями и расстоянием ? Как рассчитать перемещение в физике? Найдите все ответы здесь!
Предпочитаю смотреть перечитал? Узнайте все, что вам нужно, за 90 секунд с этим видео , которое мы сделали для вас :
Определение смещения: что такое смещение?
Начнем с самого начала с определения смещения. Смещение означает разные вещи в разных контекстах, так что же такое смещение в физике? В физике (и геометрии) смещение — это величина, на которую объект переместился независимо от выбранного пути .
Мы лучше это увидим, когда посмотрим на формулу смещения, но смещение можно рассматривать как расстояние между начальной и конечной точками. Он не учитывает путь, пройденный от одной точки до другой, поэтому не измеряет пройденное расстояние.
Расстояние между городами, например, от Нью-Йорка до Вашингтона, которое вам предстоит преодолеть, зависит от выбранного вами маршрута. Однако какую бы дорогу вы ни выбрали, конечное перемещение всегда будет одним и тем же: расстоянием по прямой от одного города до другого.
Знаете ли вы, что еще один тип смещения известен как угловое смещение! Если вы хотите узнать об этом больше, воспользуйтесь нашим калькулятором углового смещения.
Как рассчитать водоизмещение: формула водоизмещения
Итак, как рассчитать перемещение, если оно не совпадает с пройденным расстоянием? Первое, что нужно сделать, это взглянуть на формулу смещения и забыть о дебатах о смещении и расстоянии. Существует много формулировок формулы смещения, но нас интересует следующая:
d=vtd = vtd=vt
где
- ddd — это смещение;
- ttt — время от начала до конца; и
- vvv — средняя скорость между точками.
Решающим моментом здесь является скорость; мы не говорим о скорости.
Скорость учитывает направление движения.
Поскольку мы говорим о перемещении в физике, мы также можем рассчитать среднюю скорость, используя калькулятор ускорения или формулу ускорения (если ускорение постоянно):
a=12(v1−v0)a = \frac{1 {2}(v_1 – v_0)a=21(v1−v0)
где
- aaa – ускорение;
- v0v_0v0 — начальная скорость; и 92 + v_0 td=21at2+v0t
В качестве альтернативы, мы могли бы вычислить среднюю скорость из набора скоростей, выполнив их взвешенное среднее, где вес каждой скорости – это время, проведенное на этой скорости. Сделать это удобно с помощью калькулятора средневзвешенных значений.
Если вы хотите узнать, как найти среднюю скорость изменения расстояния со временем (т. е. среднюю скорость), воспользуйтесь калькулятором средней скорости изменения.
Как найти водоизмещение с помощью калькулятора водоизмещения?
В калькуляторе смещения, который вы видите слева, мы реализовали три режима.
Стандартный и самый простой способ найти смещение — использовать постоянную скорость . По мере увеличения сложности (и количества необходимых входных данных) у нас есть метод, который позволяет вам вычислять перемещение, используя начальную и конечную скорости или ускорение .В третьем режиме калькулятора перемещений вы можете ввести до 10 различных скоростей (и соответствующие им времена), и он рассчитает для вас общее водоизмещение. Когда вы заполните одну скорость, появится новая.
Вот пример того, как найти перемещение по ускорению и времени:
- Введите время, в течение которого объект находится в движении.
- Введите ускорение.
- Введите начальную или конечную скорость.
- Смотрите, как результирующее смещение рассчитывается для вас.
В качестве бонуса мы также найдем для вас конечную/начальную скорость.
Теперь, когда вы научились вычислять смещение, вам может быть интересно, как оно отличается от расстояния; мы вас прикрыли!
Перемещение в зависимости от расстояния; различия и сходства
Перемещение и расстояние часто путают, главным образом потому, что в нашей повседневной жизни мы всегда называем оба расстоянием .
Смещение в физике (и геометрии) немного отличается, очень похоже на то, как скорость отличается от скорости.Логический способ думать о дилемме смещения и расстояния состоит в том, что перемещение относится к скорости так же, как расстояние к скорости. Когда вы используете ненаправленную скорость, вы получаете расстояние, то есть длину пройденного пути. С другой стороны, используя векторная скорость дает вам разницу в положении между началом и концом: смещение.
Несмотря на то, что расстояние является наиболее практичной величиной в нашей обычной жизни, в физике перемещение занимает центральное место. Такие величины, как работа, зависят от силы и перемещения, но не от расстояния.
3 факта о времени с учетом ускорения и расстояния
Объект приобретает скорость, когда меняет свое положение со временем, и ускоряется, когда его скорость меняется со временем. Если мы знаем значение смещения и времени, мы можем найти скорость; аналогично можно найти ускорение.
Теперь возникает вопрос, как найти время с ускорением и расстоянием? В основном, это зависит от вопроса и количества, указанного в вопросе. Мы можем узнать время линейного движения, если у нас есть следующие три типа комбинаций данных, заданных в вопросе, - Ускорение, а также начальная и конечная скорость объекта
- скорость и пройденный путь
- скорость и ускорение
Предположим, вопрос предоставляет величину ускорения, начальную скорость и конечную скорость объекта. В этом случае лучший способ вычислить время, необходимое для завершения движения, — это решить первое кинематическое уравнение движения.
Предположим, что автомобиль начинает движение с начальной скоростью (u) и конечной скоростью (v), которая в процессе движения ускоряется. Величина ускорения (а) в положительном направлении х. Теперь, чтобы узнать время, необходимое для совершения движения, воспользуемся первым уравнением кинематики.
Автомобиль, движущийся в направлении x Первое кинематическое уравнение движения:
Изображение предоставлено: Videoplasty.com, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, через Wikimedia CommonsСледовательно,
U – начальная скорость автомобиля
В – окончательная скорость автомобиля
T – время, необходимое для завершения движения
A – Ускорение автомобиля
, когда скорость и расстояние, охваченное объектом, дано
Когда вопрос дает величину скорости и расстояние, которое преодолевает объект, мы можем быстро определить время, необходимое для этого движения. Мы знаем, что скорость — это скорость изменения смещения во времени. Математически записывается как
Следовательно,
Используя приведенные выше формулы, мы можем рассчитать время, необходимое для завершения его движения.
Когда заданы скорость и ускорениеКогда объект движется с непрерывно изменяющейся скоростью, это означает, что объект ускоряется в движении с некоторой величиной (a).
Мы знаем, что ускорение — это скорость изменения скорости во времени. Итак, если вопрос дает величину средней скорости и ускорения объекта, мы можем легко узнать время, необходимое для этого движения. Как известно,Следовательно,
–
Некоторые примеры и FAQ Велосипед начинает двигаться с начальной скоростью 30 м/с и ускорение 30 м/с 2 . его скорость 90 м/сек. Сколько времени требуется велосипеду, чтобы набрать конечную скорость?Дано,
начальная скорость (u) – 30 м/с
конечная скорость (v) – 9{2}[/latex]
Здесь мы задали начальную скорость, конечную скорость, а также ускорение велосипеда, затем используем первое кинематическое уравнение, чтобы узнать время,
уравнение движения:
V = u + at
0003
Следовательно, велосипеду требуется 2 секунды, чтобы развить скорость 90 м/с.
Автомобиль движется со скоростью 50 м/с. Сколько времени потребуется, чтобы преодолеть расстояние 500 км?Дано, скорость автомобиля – 50 м/с
Пройденное расстояние – 500 км время
т. е. скорость = расстояние/время
Время = расстояние/скорость
t = 10000 с
т.е. t = 2,7 часа
Автомобиль движется из положения А в положение со скоростью 30 м/с и ускорением 3 м/ 900 за одно движение . Сколько времени нужно, чтобы добраться из пункта А в пункт Б?Мы знаем, что ускорение — это изменение скорости во времени.
Ускорение = скорость/время
Из приведенного выше уравнения мы можем найти время, необходимое для перемещения автомобиля из точки A в точку B.
Время = скорость /ускорение
, поместив заданные значения,
T = 30/3
Следовательно, T = 10 с
Следовательно, автомобиль требует 10 секунд для перемещения от A к B
FAQ Что такое прямолинейное движение объекта?когда объект совершает прямолинейное движение из точки А в точку В, то такое линейное движение называется прямолинейным движением.
В чем разница между скоростью и скоростью? Скорость — это скалярная величина, а скорость — векторная величина. Скорость определяет величину, с которой движется объект, а скорость определяет величину и направление движения объектов. можно сказать, что скорость есть величина скорости.
Какие три кинематических уравнения движения?три кинематических уравнения выглядят следующим образом:
- v =u + at
- s = ut + 1/2 at 2
- v 2 = u 2 + 2as
where, s, a, t, u, v представляют перемещение, ускорение, начальную скорость, конечную скорость и время движения соответственно.
Что такое Средняя скорость объекта?средняя скорость – это отношение общего расстояния, пройденного при движении, к общему времени, необходимому для совершения движения.
Стандартный и самый простой способ найти смещение — использовать постоянную скорость . По мере увеличения сложности (и количества необходимых входных данных) у нас есть метод, который позволяет вам вычислять перемещение, используя начальную и конечную скорости или ускорение .
Смещение в физике (и геометрии) немного отличается, очень похоже на то, как скорость отличается от скорости.
Теперь возникает вопрос, как найти время с ускорением и расстоянием? В основном, это зависит от вопроса и количества, указанного в вопросе. Мы можем узнать время линейного движения, если у нас есть следующие три типа комбинаций данных, заданных в вопросе, 
Мы знаем, что ускорение — это скорость изменения скорости во времени. Итак, если вопрос дает величину средней скорости и ускорения объекта, мы можем легко узнать время, необходимое для этого движения. Как известно,
