Как найти постоянное ускорение: Прямолинейное равноускоренное движение. Ускорение — урок. Физика, 9 класс.

Как найти постоянное ускорение по скорости и времени: задачи и примеры

Когда мы говорим о постоянных сущностях, должно быть постоянное изменение терминов, вовлеченных в процесс. Мы знаем, как построить график постоянного ускорения из предыдущего поста, но как найти постоянное ускорение со скоростью и временем?

Чтобы найти постоянное ускорение со скоростью и временем, движение частицы должно быть линейным. Равномерное увеличение или уменьшение скорости во времени дает полезный материал для нахождения постоянное ускорение. Этот пост в основном посвящен тому, как найти постоянное ускорение со скоростью и временем в различных аспектах и ​​​​подходах.

Чтобы рассчитать постоянное ускорение, нам нужно предположить, что некоторые вещи, такие как изменение скорости, должны быть постоянными, а движение должно быть одномерным. Эти предположения помогают нам найти постоянное ускорение.

Как найти постоянное ускорение через скорость и время?

Устойчивое изменение скорости с постоянным интервалом времени дает постоянное ускорение. Когда частица однородна линейное движение, изменение скорости во времени неизменно; тогда мы можем найти постоянное ускорение.Кредиты изображения: Изображение предоставлено B Нюффлеупагус от Pixabay 

Чтобы найти постоянное ускорение со скоростью и временем, мы должны взять производную скорости по времени, потому что можно легко доказать, что функция постоянна, используя метод дифференциального исчисления. Таким образом, мы берем скорость как функцию времени, чтобы найти производную для достижения постоянное ускорение быстро.

Ускорение частицы определяется выражением

а = v/t

Случай (i) Поскольку мы имеем дело с постоянным ускорением, то мы должны рассматривать устойчивое изменение скорости.

Изменение скорости определяется выражением

а = Δv / Δt

Изменение скорости означает, что частица должна достичь более одной скорости. Итак, предположим, что в начальный момент частица движется со скоростью v₀ в момент времени t=0, а в следующем случае скорость увеличилась до v в момент времени t. При этом скорость частицы увеличивается в v раз за каждый последующий интервал времени, так что ускорение будет постоянным на протяжении всего движения.Как найти постоянное ускорение со скоростью и временем с нулевой начальной скоростью

Теперь изменение скорости можно переписать как

а = v – v₀/t₀

Из вышеприведенного уравнения получаем уравнение движения в виде

v = v.₀ + в

Мы взяли Начальная скорость равен нулю, поэтому уравнение будет

v = 0 + при

v = в

Переставляя их для нашего удобства, чтобы найти постоянная скорость as

а = v/t

Теперь мы снова получили общее выражение ускорения. Продифференцируем приведенное выше уравнение.

а = дв/дт

Говорят, что ускорение постоянно, когда мы получаем производную приведенного выше уравнения как ненулевое число. т.е.,

Если dv/dt = константа, то a = константа.

Это также можно интерпретировать на графике; узнать больше о графическое представление постоянного ускорения со скоростью и временем. Поскольку наклон графика скорость-время дает ускорение.

Вы можете легко понять приведенное выше выражение, решив пример. Давайте решим пример. Если мы рассматриваем движение объекта на плоскости и его скорость определяется выражением v(t) = 4t-4, ускорение постоянно или не может быть решено производным уравнением. Уравнение ускорения имеет вид

а = дв/дт

Мы знаем v(t) = 4t-4,

Дифференцируя приведенное выше уравнение по t,

дв/дт =4(1)-0

дв/дт =4

Таким образом, производная скорости по времени является постоянным числом; следовательно, ускорение постоянно в заданной функции скорости.

Случай (ii) Предположим, что начальная скорость не равна нулю, тогда постоянное ускорение может быть задано как

v = v.₀ + в

Дифференциация вышеуказанного термина

дв/дт = дв₀/ дт + а

а=дв/дт-=дв₀/дт = постоянная

Таким образом, разница между первой производной начального и конечная скорость по времени не должно быть равно нулю и должно быть постоянным числом.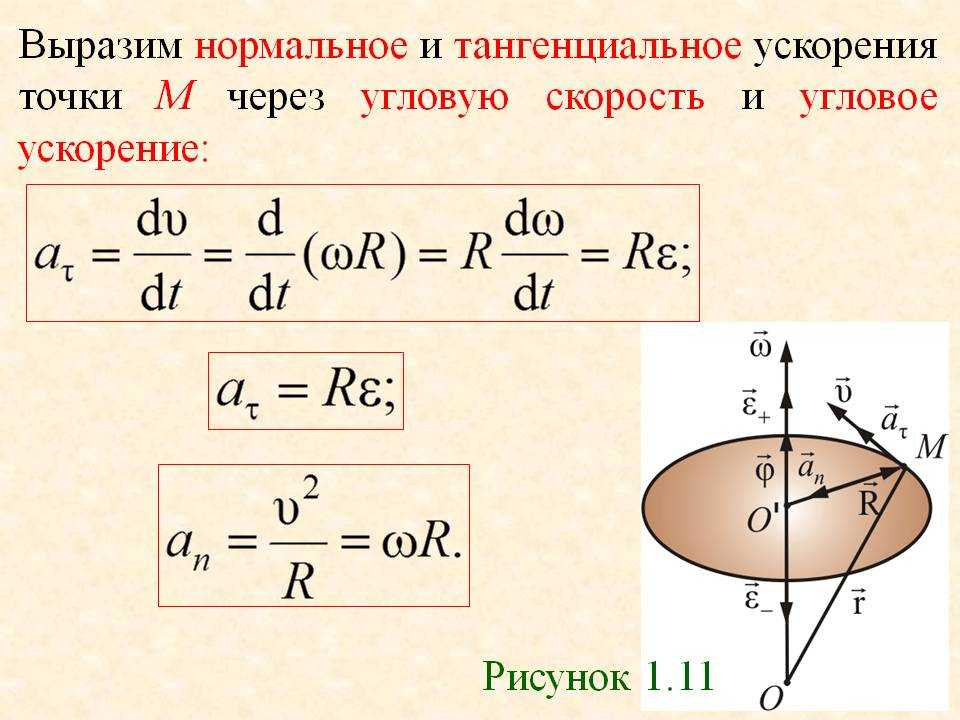

Это может быть представлено графиком, как показано нижеКак найти постоянное ускорение со скоростью и временем, используя начальную и конечную скорость на графике

Примеры задач о том, как найти постоянное ускорение по скорости и времени

Задача 1) Самолет движется по взлетно-посадочной полосе с начальной скоростью 76 м/с. Через 28 секунд его скорость равна 82 м/с. после этого скорость самолета постоянно меняется каждые 28 секунд, прежде чем он сможет взлететь. Рассчитайте изменение скорости и постоянного ускорения самолета.

Решение:

Данные для расчета – начальная скорость самолета v0 = 76 м/с.

Конечная скорость самолета v = 82 м/с.

Время, за которое самолет достигает конечной скорости t = 28 секунд.

Изменение скорости

∆v = vv₀

∆v = 82 – 76

∆v = 6 м / с.

Это означает, что каждые 28 секунд скорость самолета увеличивается на 6 м/с.

Постоянная скорость определяется выражением

а = ∆v/∆t

Подставляя значение ∆v, получаем

а=6/28

а=0. 21 м/с².

Задача 2) является ли ускорение постоянным или нет, если начальная скорость движущегося объекта определяется как v0(t)= 5t-6, а конечная скорость определяется как v(t) = 7t+5.

Решение:

Задана начальная скорость, а конечная скорость дана как функция времени t. Таким образом, нам нужно найти ускорение следующим образом.

Начальная скорость движущегося объекта определяется выражением

v₀(т) = 5т-6

Теперь продифференцируй по ‘t’

dv₀/дт=5(1)-0

dv₀/дт =5

Конечная скорость объекта определяется выражением

V(t) = 7t+5

Продифференцируем указанную выше функцию по t

дв/дт =7(1)+0

дв/дт =7

Постоянное ускорение определяется выражением

а=дв/дт – дв₀/ дт

Подставляя начальное и конечное значение функции скорости, получаем

а = 7-5

a = 2 м / с².

Таким образом, производная функции скорости постоянна, а постоянное ускорение данной функции скорости равно 2 м/с2.

Задача 3) Бегун бежит по парку с определенной скоростью. Каждые 12 секунд его скорость бега увеличивается на 2 м/с; найти постоянное ускорение бегуна.

Решение:

Данные, предоставленные для расчета – изменение скорости бегуна v= 2 м/с.

Бегуну требуется время, чтобы увеличить скорость бега трусцой t = 12 с.

Постоянное ускорение определяется выражением

а=Δv/Δt

а = 2 / 12

a = 0.166 м / с².

Задача 4) Как найти постоянное ускорение со скоростью и временем, если начальная скорость движущегося тела задана функцией времени как v0(t) = t²-6т+5

Решение:

Начальная скорость определяется выражением

v₀(т) = т²-6т+5

Дифференцируя приведенное выше уравнение, мы получаем

dv₀/dt=2t-6+0

dv₀/дт=2т-6

Из приведенного выше уравнения ускорение непостоянно. Есть колебания скорости во времени. Отсюда получаем значение ускорения как функцию времени.

а = 2t-6 м/с².

Задача 5) Лодка движется со скоростью 45 м/с в момент времени t=23 секунды, а та же лодка имеет скорость 64 м/с в момент времени t=56 секунд. Вычислите изменение скорости и времени и, следовательно, найдите постоянное ускорение.

Решение:

Данные, приведенные для расчета – скорость лодки в v₁ = 45 м / с

Скорость этой же лодки v₂ = 64 м / с.

Время, затраченное лодкой t₁ для достижения скорости v₁= 23 с.

Время, пройденное той же лодкой t₂ для достижения скорости v₂ = 56 с.

Изменение скорости

∆v = v₂ – v₁

∆v = 64 – 45

∆v = 19 м / с.

Изменение во времени

∆t = т₂-t₁

∆t = 56-23

∆t = 33 с.

Лодка увеличивает свою скорость каждые 33 секунды на 19 м/с.

So ускорение заданной скорости и время

а = Δv/Δt = 19/33

a = 0. 575 м / с².

Ускорение. Уравнение движения точки с постоянным ускорением

Мы с вами изучили равномерное прямолинейное движение, то есть движение, при котором точка за любые равные промежутки времени совершает одинаковые перемещения. Но, как мы уже отмечали, при реальном движении тел их скорости обычно меняются или по модулю, или по направлению, или же одновременно и по модулю, и по направлению. Например, когда автомобиль трогается с места, его скорость постепенно возрастает. А при торможении на перекрёстке, наоборот, — уменьшается.

При вращательном движении скорость любой точки дисков электрофорной машины изменяется лишь по направлению (конечно же, при условии, что число оборотов в единицу времени не изменяется).

Наконец, при выстреле из пушки под некоторым углом к горизонту скорость ядра будет изменяться как по модулю, так и по направлению.

При этом очевидно, что в рассмотренных нами примерах изменение скорости может происходит как очень быстро, так и достаточно медленно.

Физическая векторная величина, характеризующая быстроту изменения скорости, называется ускорением.

Давайте вспомним, как определяется ускорение точки. Для этого рассмотрим её неравномерное движение вдоль некоторой криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М и имеет скорость υ. А спустя некоторый промежуток времени Δt₁ — положение М₁ и скорость υ₁.

Найдём изменение скорости точки за это время как геометрическую разность векторов конечной и начальной скоростей и укажем эту разность на рисунке:

Если теперь мы с вами разделим вектор изменения скорости на промежуток времени, в течение которого это изменение произошло, то тем самым получим так называемый вектор среднего ускорения точки:

Он направлен точно так же, как и вектор изменения скорости.

Но как же нам определить ускорение точки в положении М? Для этого будем уменьшать рассматриваемые промежутки времени и находить вектор изменения скорости для каждого случая. Из полученного рисунка видим, что вектор изменения скорости, а следовательно, и вектор среднего ускорения, уменьшается по модулю и при этом меняется его направление. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости точки за это время. Следовательно, при стремлении промежутка времени к нулю отношение  будет стремиться к своему некоторому предельному значению.

Физическая векторная величина, равная пределу отношения изменения скорости к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенным ускорением (или просто ускорением):

Важно запомнить, что вектор ускорения направлен так же, как и вектор изменения скорости при стремлении промежутка времени к нулю. И в общем случае вектор ускорения не совпадает с направлением вектора скорости, а составляет с ним некоторый угол.

Как мы уже видели, при неравномерном движении по криволинейной траектории скорость точки непрерывно меняется по модулю и направлению.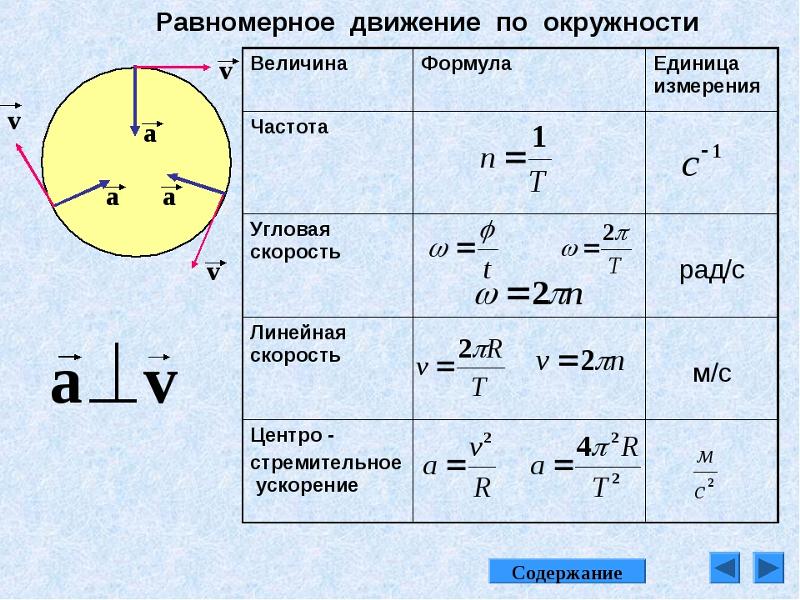 Поэтому вектор ускорения часто называют полным ускорением и представляют в виде суммы двух ускорений:

Первое ускорение называется тангенциальным (или касательным)

, так как направлено оно по касательной к траектории движения. Его модуль характеризует изменение модуля скорости:

Второе ускорение всегда направлено перпендикулярно вектору мгновенной скорости и поэтому называется нормальным (нормаль — это перпендикуляр) или центростремительным. Его модуль характеризует изменение скорости по направлению:

А вектор центростремительного ускорения в любой момент времени направлен к центру кривизны траектории.

Конечно же движение точки может происходить как с постоянным, так и с переменным ускорением. Так, если отношение изменения скорости к промежутку времени в течение которого это изменение произошло одинаково для любого интервала времени, то говорят, что точка движется с постоянным ускорением.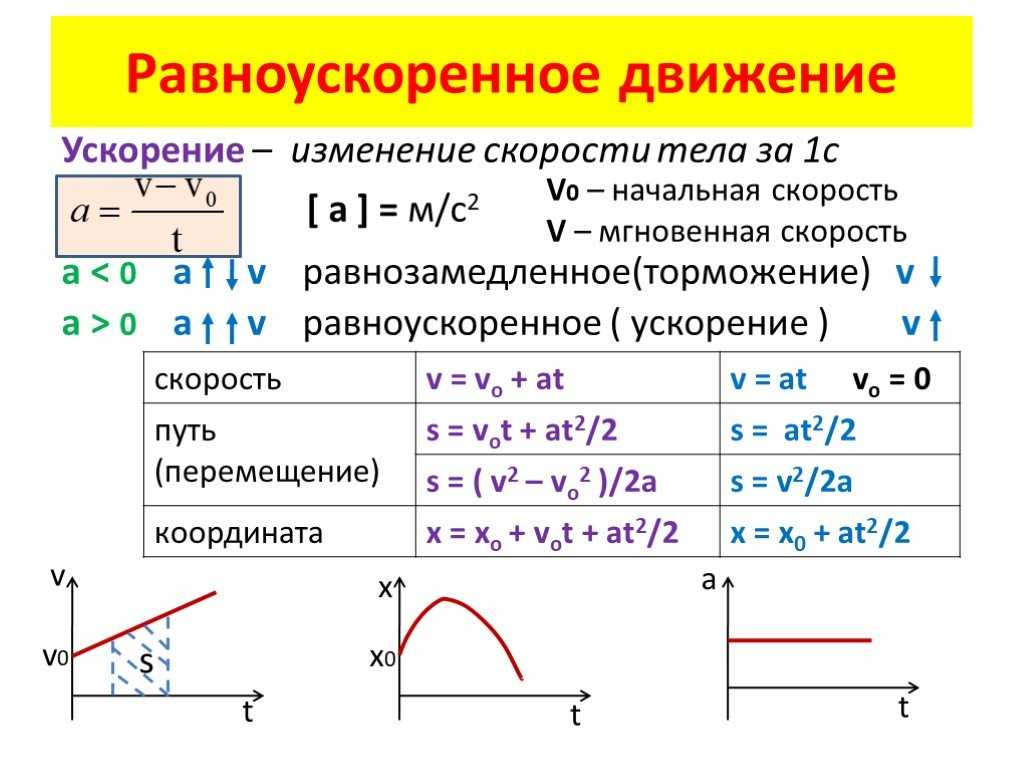

А движение точки называют равноускоренным движением:

Из формулы видно, что если скорость и промежуток времени выражены в единицах СИ, то единицей измерения ускорения является метр на секунду в квадрате (м/с²).

Также из формулы следует, что за единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1 с скорость точки изменяется на 1 м/с.

Теперь давайте выясним, как зависит скорость точки от времени при её равноускоренном движении. Итак, пусть в начальный момент времени

t₀ скорость точки равнялась , а в момент времени t — .

Тогда ускорение точки равно изменению вектора скорости к промежутку времени, за который это изменение произошло:

Если начальный момент времени принять равным нулю, то из этого уравнения легко получить формулу для определения скорости точки в любой момент времени при её равноускоренном движении — уравнение скорости:

Таким образом, чтобы определить скорость точки в произвольный момент времени, необходимо знать её начальную скорость и ускорение.

На практике при вычислениях скорости мы будем пользоваться формулами, в которые входят не векторы, а их проекции на соответствующие координатные оси:

Из записанных формул видно, что при равноускоренном движении скорость точки линейно зависит от времени. Значит, график скорости представляет собой прямую линию, наклонённую к оси времени под некоторым углом. При этом чем больше ускорение точки, тем больший угол с осью времени составляет график проекции скорости.

Теперь посмотрим на прямую 3. Что можно сказать о движении тела в этом случае?

Во-первых, очевидно, что за промежуток времени от нуля до t₁ проекция скорости была положительна.

Во-вторых, скорость точки уменьшалась и в момент времени, равный t₁ она стала равной нулю. Точка пересечения графика скорости с осью времени называется точкой поворота. В ней направление скорости меняется на противоположное, после чего тело начинает двигаться равноускоренно.

Теперь давайте вспомним, что основной задачей механики является определение положения точки в любой момент времени. Получим уравнения, которые позволяют это сделать для равноускоренного движения. Для примера рассмотрим случай, когда проекция начальной скорости и ускорения положительны.  По аналогии со случаем равномерного прямолинейного движения логично предположить, что проекция перемещения, совершённого телом за время

t, будет равна площади фигуры, ограниченной графиком, осью времени и перпендикуляром, восставленным к графику из точки t. В данном случае эта фигура — трапеция.

Для доказательства этого предположения рассмотрим очень малый промежуток времени Δt внутри выбранного интервала времени. По аналогии с мгновенной скоростью, если выбранный промежуток времени достаточно мал, то изменением скорости за это время можно пренебречь. То есть движение точки можно считать равномерным.

Значит, проекция перемещения за это время будет равна площади этого маленького прямоугольника. При этом очевидно, что на такие узкие полоски мы можем разбить всю площадь фигуры под графиком скорости

Тогда, согласно рисунку, проекция перемещения при равноускоренном движении определяется площадью трапеции. Площадь же трапеции, как известно из геометрии, равна произведению полусуммы её оснований на высоту. В нашем случае длина одного из оснований численно равна проекции начальной скорости точки, второго — проекции скорости через время

t. Высота же трапеции численно равна времени.

Теперь вспомним, что по определению проекция перемещения численно равна разности конечной и начальной координат точки:

Тогда после небольших математических преобразований получим формулу для определения координаты точки при её равноускоренном движении:

Важно помнить, что в формулу входят проекции начальной скорости и ускорения точки. А они могут быть как положительными, так и отрицательными. Координата начального положения точки также может быть больше или меньше нуля,

Если движение точки происходит в пространстве, то для определения оставшихся двух координат используют уравнения, имеющие аналогичной вид:

Записанные нами формулы называются кинематическими уравнениями движения точки в координатной форме. Они применимы для описания как прямолинейного, так и криволинейного движения.

В общем виде кинематические уравнения движения можно записать с помощью одного векторного уравнения:

Теперь для закрепления материала решим с вами одну небольшую задачку. Итак, на рисунке представлен график зависимости скорости точки от времени. Определите, в какой момент времени координата точки станет равной 30 м, если в момент начала наблюдения её координата равнялась –6 м. Определите скорость точки в этот момент времени.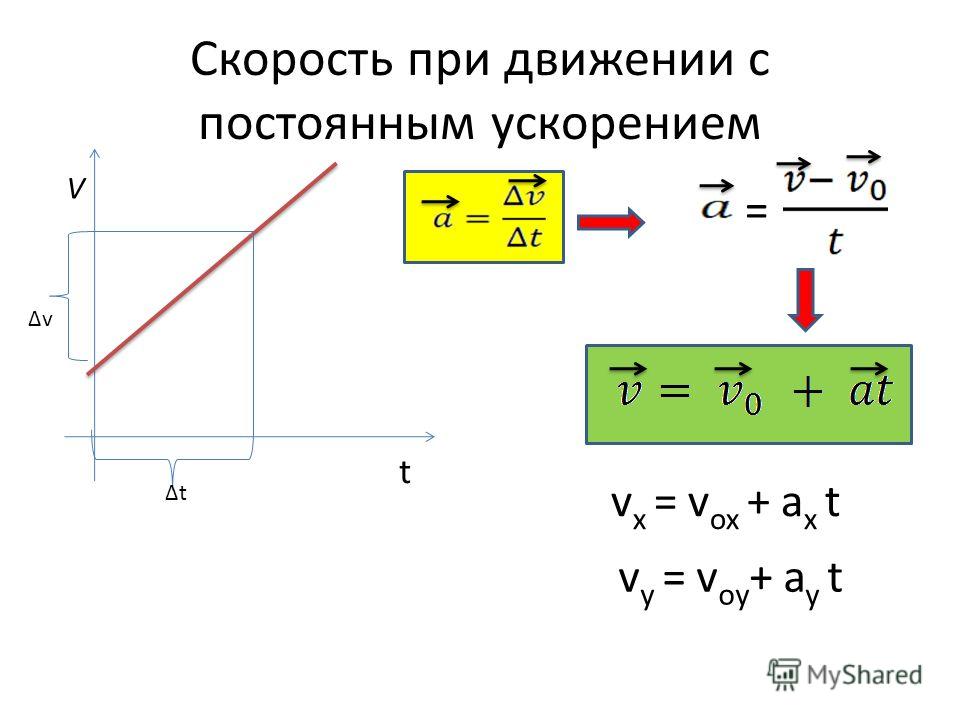

Уравнения движения с постоянным ускорением

Прямолинейное движение с равномерным ускорением (u.a.r.m.) , также известное как движение с постоянным ускорением , представляет собой прямолинейное движение с постоянным ускорением, отличным от нуля. В этом разделе мы будем изучать:

• Понятие и свойства движения с постоянным ускорением
• Уравнения движения с постоянным ускорением
• Как вывести уравнения
• Теорема Мертона

Концепция движения с постоянным ускорением

Движение с постоянным ускорением довольно часто встречается в вашей повседневной жизни. Объект, которому разрешено падать и который не встречает препятствий на своем пути (свободное падение), или лыжник, который спускается со склона непосредственно перед тем, как прибыть в зону прыжка, являются хорошими примерами этого. Движение с постоянным ускорением или равноускоренное прямолинейное движение (u.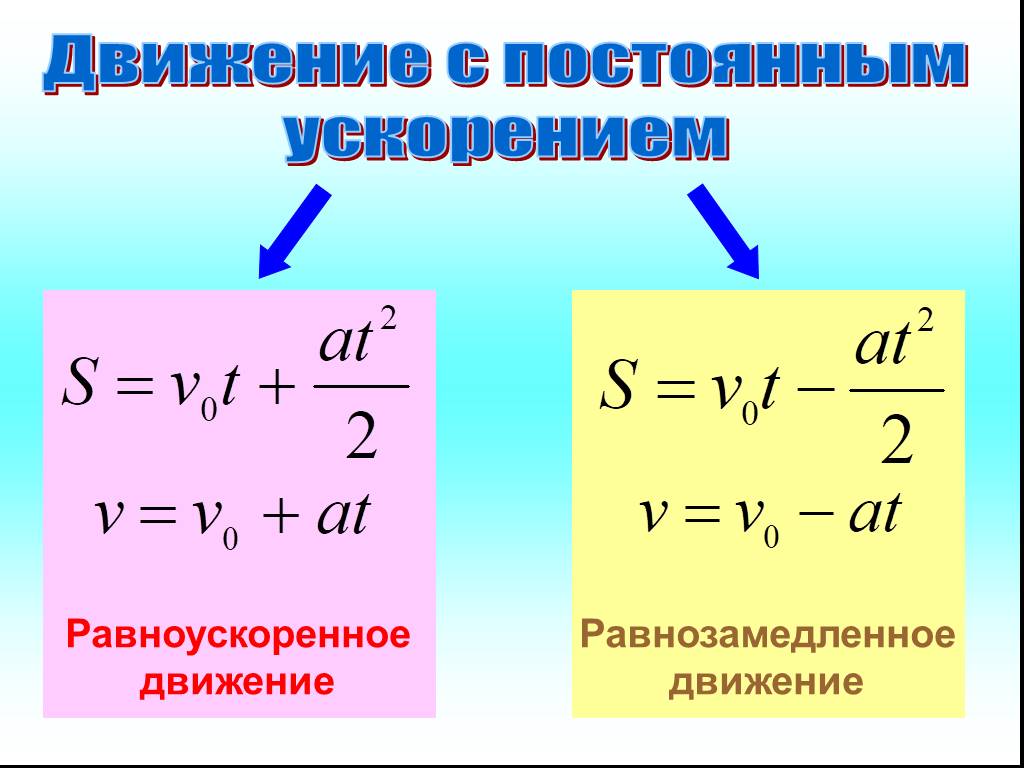 a.r.m.) имеет следующие свойства :

• Траектория представляет собой прямую линию, поэтому нормальное или центростремительное ускорение равно нулю
• Мгновенная скорость изменяет свою величину (скорость) равномерно: она увеличивается или уменьшается на одну и ту же величину в каждую единицу времени. Это подразумевает следующий пункт
• Тангенциальное ускорение постоянно. Следовательно, среднее ускорение равно мгновенному ускорению для любого изучаемого периода (a=am)

Тело движется с движение с постоянным ускорением или равномерно ускоренное прямолинейное движение (u.a.r.m.) , когда его траектория представляет собой прямую линию и его ускорение постоянно и отличается от 0 . Это означает, что скорость увеличивает или уменьшает свою величину равномерно .

Равноускоренное прямолинейное движение

В нашем примере автомобиль описывает н. а.м., поскольку он движется прямолинейно с постоянным ускорением, эквивалентным 2 м/с ² . [Обратите внимание, что в каждую секунду скорость и расстояние, проходимое телом, увеличиваются в зависимости от значения ускорения в предыдущую секунду.]

Обратите внимание, что, хотя в разговорной речи мы проводим различие между ускоряющимся и тормозящим телом, от с точки зрения физики, оба являются равноускоренными прямолинейными движениями . Разница в том, что в то время как один имеет положительное ускорение, другой имеет отрицательное ускорение.

Уравнения движения с постоянным ускорением

Уравнения движения постоянного ускорения или равномерно ускоренного прямолинейного движения (U.A.R.M.) :

V = V0+A>

x = x0+V0T+12AT2

, где:

9009 41T+12AT2

, где:

9009 41T+12AT2

, где:

9009 41T+12AT2

, где:

9009 41T+12AT2

, где:

9009 41T+12AT2

, где:

9009 41T+12AT2

, где:

9009 . , x ₀ : Положение тела в данный момент времени ( x ) и в начальный момент времени ( x ₀ ). Его единицей в Международной системе (СИ) является метр (м)

.

v , v ₀ : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v ₀ ). Его единицей в Международной системе является метр в секунду (м/с)

.

: Ускорение кузова. Остается постоянным со значением, отличным от 0. Его единицей в Международной системе является метр в секунду (м/с ² )

t : Время изучается. Его единицей в Международной системе является секунда ( с )

Хотя первые являются основными уравнениями u.a.r.m. и единственные необходимые для решения упражнений, иногда полезно знать следующее выражение:

v2=v02+2·a·∆x

Приведенная выше формула позволяет связать скорость и пройденный путь, если известно ускорение, и может быть выведен из предыдущих, как вы можете видеть ниже.

v=v0+a·tx=x0+v0·t+12·a·t2⇒t=v-v0a∆x=v0·t+12·a·t2⇒∆x=v0v-v0a+12·a ·в-в0а2;

2·a·∆x=v2-v02

Вывод уравнений движения с постоянным ускорением

Чтобы вывести уравнений движения с постоянным ускорением или равноускоренного прямолинейного движения (u.a.r.m.) , необходимо принять во внимание, что:

• Значение нормального или центростремительного ускорения равно ноль: an=0
• Среднее ускорение, мгновенное ускорение и тангенциальное ускорение имеют одно и то же значение: a=aa=at=cst

С учетом этих ограничений получаем:

aa=aaa=ΔvΔt=v-v0t-t0=⏟t0=0x-x0t→v-v0=a⋅t→v=v0+a⋅t

Это первое уравнение связывает скорость тела с его ускорением при в любой момент времени и представляет собой прямую линию ( v ), наклон которой равен величине ускорения, а его координата y в начале координат является начальной скоростью ( v ₀ ). Нам нужно получить уравнение, которое позволит нам получить позицию. Существуют разные методы его вывода. Мы будем использовать теорема о средней скорости или правило равномерного ускорения Мертона :

«Тело, движущееся с равноускоренным ускорением, за любой момент времени проходит такое же расстояние, какое прошло бы тело, движущееся с постоянной скоростью, равной средней скорости первого тела».

Это означает, что

∆x=va⋅t

Значение средней скорости при постоянном ускорении можно ясно увидеть на следующем рисунке:

va=v+v02

Если мы разовьем уравнения, которые мы видели до сих пор, мы получим уравнение положения в равноускоренном прямолинейном движении (u.a.r.m.) :

∆x=x-x0=va ⋅t=⏞1v+v02t=⏞2v0+at+v02t=2v0+at2t=22v0t+at22⇒x=x0+v0t+12at2

Куда мы обращались:

1. va=v+v02

2. v=v0+a⋅t

Наконец, обратите внимание, что в предыдущих уравнениях движение рассматривалось в ось х . Если мы движемся по оси y , например, в свободном падении или вертикальном старте, просто замените x на y для положения, в результате чего получится следующее уравнение:

y=y0+v0t+12at2

Пример

Велосипедист начал утреннюю поездку и через 10 секунд его скорость составила 7,2 км/ч. В этот момент он видит приближающуюся собаку и тормозит на 6 секунд, пока велосипед не остановится. Рассчитайте:

а) Ускорение до тех пор, пока он не начнет замедляться.
b) Тормозное ускорение велосипеда.
в) Общее пройденное расстояние.

Решение

Постоянное ускорение — алгебраическое

Постоянное ускорение — алгебраическое

---

[Глава 2 цели]

БХС -> Персонал -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница

---

Во многих ситуациях, которые мы будем изучать в механике, ускорение интересующего объекта будет не менее приблизительно постоянный. Это оказывается удачей, потому что постоянный ускорение позволяет анализировать движение, используя только простые алгебра.

---

Как решить проблемы кинематики

Хочу сказать, что решать задачи численной кинематики творческое решение проблем в лучшем виде, но это было бы ложь. Хотя начинающие физики часто сталкиваются с проблемами кинематики поначалу довольно сложно, как только вы поймете, они, как правило, довольно рутина.

Для того, чтобы войти в ритм решения задач по кинематике как как можно быстрее и проще, используйте следующие шаги, чтобы усилия по решению проблем. Этот метод иллюстрируется несколькими примеры на следующих страницах.

Помните, что в физике будет много ситуаций, в которых ваше решение проблемы будет оцениваться, а не только ответ. На самом деле, во многих случаях решением будет весит гораздо больше, чем правильный ответ . Поэтому важно развивать профессиональный подход к решению проблем. стиль. Вот хороший способ:

1. Понимание проблемы:
   1. Внимательно прочитайте задачу . Что вы нужно найти? Вы были бы поражены тем, как много людей паникуют и попытаться начать решать проблему, не зная, что они должны делать!
   2. Сделайте набросок, показывающий проблемную ситуацию. В В частности, большинство задач кинематики имеют дело с движущимся объектом. из некоторой исходной ситуации в какую-то другую конечную ситуацию – машина стартует с места и едет по дороге, или мяч упал и падает на Землю, например. Будьте уверены что ваша диаграмма представляет собой как начальный, так и конечный ситуации . Не тратьте время на то, чтобы сделать свой эскиз художественным – сосредоточиться на физике.
   3. В своем эскизе укажите, что вы знаете об обоих Начальная и конечная ситуации. Укажите направление каждой количество кинематики – перемещение, скорость и ускорение.
2. Переведите проблему на «Физический язык» : Составьте список каждого количество кинематики в задаче. Определите каждый с помощью правильная кинематическая переменная. Не забывайте единицы!
3. Поиск кинематики Отношения, которые решат проблему : Сделайте «мысленное сканирование» вашего списка уравнений кинематики, чтобы найти уравнение, содержащее кинематические величины в вашей задаче. Запишите это уравнение. Конечно, вам нужно уравнение, которое решит проблему максимально эффективно, но, как вы увидите из примеров, существует более одного способа решения большинство проблем с кинематикой.
4. Решить: Решить математическое уравнение для количество кинематики, которое вам нужно знать.
5. Замена известных значений: Замена известных значений кинематические величины в ваше уравнение. Рассматривайте единицы как вы бы любую другую алгебраическую величину. Не копируйте каждый цифра на дисплее вашего калькулятора! Округлите свой ответ до того же количество значащих цифр как наименее точное значение в проблема. Не забывайте единицы!
   
   1. Примечание: Профессиональный физики и инженеры алгебраически решат количество, которое они хотят сначала узнать, а затем подставить известное значений, как показано в шагах 4 и 5. Если бы вы хотели больше удобно сначала подставить известные значения, а затем решая уравнение с одной переменной, это будет отлично. Вы можете использовать любой удобный для вас способ с.
6. Сообщите о своем ответе: Не ждите, что кто-то найдет ответ на проблему в вашем решении и интерпретировать его правильно. Напишите предложение, которое дает полный ответ на задачу. Быть обязательно упомяните направление, если это уместно, и никогда не забывайте о правильном единицы измерения.
7. Чек: Потратьте минуту, чтобы убедиться, что вы действительно ответил на исходный вопрос, и что ваш ответ разумный. Если проблема состоит из нескольких частей, убедитесь, что ваш ответ на эту часть согласуется с остальной частью вашего решение.

---

Перевод вербальной кинематики Задачи по “Физике”

Чтобы применить мощь математики к задачам кинематики, нужно уметь переводить словесное описание кинематики задачу на символическом языке математики.

Проблема кинематики обычно состоит из трех ситуаций. В исходной (или исходной) ситуации некоторый объект находится в положение “х _o ” и имеет скорость “v _o ” в момент, когда часы показывают «t _o ». Тогда объект имеет постоянное ускорение “а” в течение некоторого времени “” пока он перемещается на расстояние “”. В финальной ситуации объект находится в позиции «х» и имеет скорость “v” в тот момент, когда часы показывают “t”. Данные значения для некоторых из этих величин ваша задача состоит в том, чтобы найти значения для некоторых из другие.

В таблице ниже показаны переменные, которые мы будем использовать для представления каждое количество кинематики.

Общепринятые обозначения кинематических величин
Кинематика Количество	Математический символ
Должность:
конечная позиция – где находится объект момент, когда часы показывают “т”	х
исходное (или начальное) положение – где объект был в тот момент, когда часы показывали “t o ”	х или
смещение (знаковое, чистое) расстояние до объекта переехал
Скорость:
final speed – спидометр объекта чтение в тот момент, когда часы показывают “t”	против
исходная (или начальная) скорость – скорость объекта показания спидометра в тот момент, когда часы показывают “т или ”	v или
изменение скорости
средняя скорость
Ускорение:
(постоянное) ускорение	и
Время:
окончательное чтение часов	т
исходное (или начальное) чтение часов	т или
временной интервал (изменение времени)

---

Уравнения кинематики:

В приведенной ниже таблице вы найдете 7 уравнений, которые вам нужно решить. уметь решать задачи по кинематике. Не паникуйте! Первые 3 уравнения определения, которые вы уже видели! Обратите внимание, что уравнения в таблице были разделены на две группы. «Зеленая группа» – это в основном определения кинематики. Использование этих уравнений часто приводит к многошаговые решения задач кинематики – но каждый шаг хорош просто. «Синяя группа» — это более сложные уравнения, которые могут часто решают задачи кинематики за один шаг, но алгебра в их использовании часто немного сложнее. Следующие страницы покажет вам, откуда берутся эти уравнения, и покажет, как уравнения могут быть использованы для решения задач кинематики.

Уравнения Вам нужно Знать для решения кинематики Проблемы ( Запомнить Эти уравнения)
Уравнение кинематики	Комментарий
	Определение водоизмещения в алгебраических символах- Обратите внимание, что “” всегда означает «изменить», и что угодно всегда означает “конечное значение – исходное значение”. Следовательно, определяет «изменение скорости» и определяет «изменение во времени».
	Это определение среднего скорость в математических символах. (Полоса над количеством означает «среднее».) Скорость — это скорость изменения положения. Средняя скорость равна смещению, деленному на время. Это уравнение часто встречается в форме , что, по сути, говорит: «расстояние равно средней скорости раз время”
	Это определение ускорения в математических символах. На самом деле, мы сказали, что в среднем ускорение есть изменение скорости, деленное на время, но поскольку ускорение постоянно, среднее ускорение и мгновенное ускорение одинаково. Вот некоторые примеры его использования при решении задач кинематики.
	Это уравнение говорит, что если ускорение равно константа , средняя скорость в любой интервал времени равна просто среднее значение исходной и конечной скоростей. Это очень прост в использовании и удобен для упрощения многих расчеты. Однако его вывод требует вычислений.
	Это уравнение является старым добрым “расстояние равно среднему скорость умножить на время” вы узнали еще в 5-м классе – одетый немного вверх! Это может быть очень полезно, особенно в сочетании с предыдущим уравнением.
	Это уравнение очень тесно связано с , и часто любой из них может быть использован для решения проблемы. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: