Как найти производную функции примеры решения: Как найти производную функции, примеры решения

алгоритм и примеры решений. Производные высших порядков показательной функции

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций.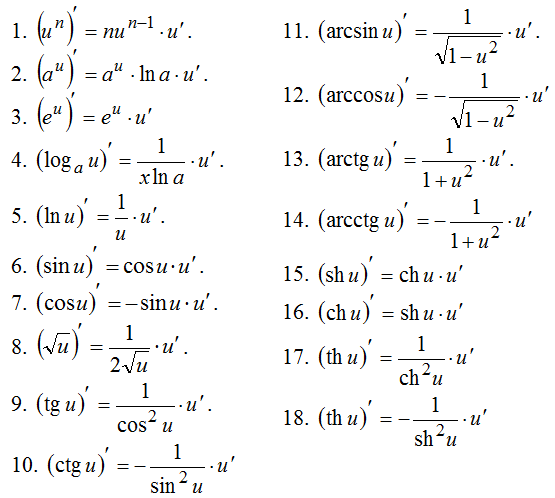 То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.

Как найти?

Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования :

1. Вынос константы за знак производной: $$ (Cu)” = C(u)” $$
2. Производная суммы /разности функций: $$ (u \pm v)” = (u)” \pm (v)” $$
3. Производная произведения двух функций: $$ (u \cdot v)” = u”v + uv” $$
4. Производная дроби : $$ \bigg (\frac{u}{v} \bigg)” = \frac{u”v – uv”}{v^2} $$
5. Производная сложной функции : $$ (f(g(x)))” = f”(g(x)) \cdot g”(x) $$

Примеры решения

Пример 1

Найти производную функции $ y = x^3 – 2x^2 + 7x – 1 $

Решение

Производная суммы/разности функций равна сумме/разности производных: $$ y” = (x^3 – 2x^2 + 7x – 1)” = (x^3)” – (2x^2)” + (7x)” – (1)” = $$ Используя правило производной степенной функции $ (x^p)” = px^{p-1} $ имеем: $$ y” = 3x^{3-1} – 2 \cdot 2 x^{2-1} + 7 – 0 = 3x^2 – 4x + 7 $$ Так же было учтено, что производная от константы равна нулю. 2 – 4x + 7 $$

Калькулятор вычисляет производные всех элементарных функций, приводя подробное решение. Переменная дифференцирования определяется автоматически.

Производная функции — одно из важнейших понятий в математическом анализе. К появлению производной привели такие задачи, как, например, вычисление мгновенной скорости точки в момент времени , если известен путь в зависимоти от времени , задача о нахождении касательной к функции в точке.

Чаще всего производная функции определяется как предел отношения приращения функции к приращению аргумента, если он существует.

Определение. Пусть функция определена в некоторой окрестности точки . Тогда производной функции в точке называется предел, если он существует

Как вычислить производную функции?

Для того, чтобы научиться дифференцировать функции, нужно выучить и понять правила дифференцирования и научиться пользоваться таблицей производных .

Правила дифференцирования

Пусть и — произвольные дифференцируемые функции от вещественной переменной, — некоторая вещественная постоянная. Тогда

— правило дифференцирования произведения функций

— правило дифференцирования частного функций

0″> — дифференцирование функции с переменным показателем степени

— правило дифференцирования сложной функции

— правило дифференцирования степенной функции

Производная функции онлайн

Наш калькулятор быстро и точно вычислит производную любой функции онлайн. Программа не допустит ошибки при вычислениях производной и поможет избежать долгих и нудных расчётов. Онлайн калькулятор будет полезен и в том случае, когда есть необходимость проверить на правильность своё решение, и если оно неверно, быстро найти ошибку.

Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.

Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.

Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.

Для их обозначения будем использовать латинские буквы f, g и др.

Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g” означает, что мы будем находить производную функции g.

Таблица производных

Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.

1. (sin x)”=cos x
2. (cos x)”= –sin x
3. (x n)”=n x n-1
4. (e x)”=e x
5. (ln x)”=1/x
6. (a x)”=a x ln a
7. (log a x)”=1/x ln a
8. (tg x)”=1/cos 2 x
9. (ctg x)”= – 1/sin 2 x
10. (arcsin x)”= 1/√(1-x 2)
11. (arccos x)”= – 1/√(1-x 2)
12. (arctg x)”= 1/(1+x 2)
13. (arcctg x)”= – 1/(1+x 2)

Пример 1. Найдите производную функции y=500.

Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).

Пример 2. Найдите производную функции y=x 100 .

Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).

(x 100)”=100 x 99

Пример 3. Найдите производную функции y=5 x

Это показательная функция, вычислим ее производную по формуле 4.

Пример 4. Найдите производную функции y= log 4 x

Производную логарифма найдем по формуле 7.

(log 4 x)”=1/x ln 4

Правила дифференцирования

Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С – константа.

1. Постоянный коэффициент можно выносить за знак производной

Пример 5. Найдите производную функции y= 6*x 8

Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.

(6*x 8)” = 6*(x 8)”=6*8*x 7 =48* x 7

2. Производная суммы равна сумме производных

(f + g)”=f” + g”

Пример 6. Найдите производную функции y= x 100 +sin x

Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)”=100 x 99 и (sin x)”=cos x. Производная суммы будет равна сумме данных производных:

(x 100 +sin x)”= 100 x 99 +cos x

3. Производная разности равна разности производных

(f – g)”=f” – g”

Пример 7. Найдите производную функции y= x 100 – cos x

Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)”= – sin x.

(x 100 – cos x)”= 100 x 99 + sin x

Пример 8. Найдите производную функции y=e x +tg x– x 2 .

В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:

(e x)”=e x , (tg x)”=1/cos 2 x, (x 2)”=2 x. Тогда производная исходной функции равна:

(e x +tg x– x 2)”= e x +1/cos 2 x –2 x

4. Производная произведения

(f * g)”=f” * g + f * g”

Пример 9. Найдите производную функции y= cos x *e x

Для этого сначала найдем производного каждого множителя (cos x)”=–sin x и (e x)”=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.

(cos x* e x)”= e x cos x – e x *sin x

5. Производная частного

(f / g)”= f” * g – f * g”/ g 2

Пример 10. Найдите производную функции y= x 50 /sin x

Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)”=50 x 49 и (sin x)”= cos x. Подставив в формулу производной частного получим:

(x 50 /sin x)”= 50x 49 *sin x – x 50 *cos x/sin 2 x

Производная сложной функции

Сложная функция – это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:

(u (v))”=u”(v)*v”

Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) – сложная функция. Функцию u назовем внешней, а v – внутренней.

Например:

y=sin (x 3) – сложная функция.

Тогда y=sin(t) – внешняя функция

t=x 3 – внутренняя.

Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.

(sin t)”=cos (t) – производная внешней функции (где t=x 3)

(x 3)”=3x 2 – производная внутренней функции

Тогда (sin (x 3))”= cos (x 3)* 3x 2 – производная сложной функции.

Навигация по странице.

Производная постоянной.

При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :

Следует заметить, что под знаком предела получается выражение , которое не является , так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.

Таким образом, производная постоянной функции равна нулю на всей области определения .

Пример.

Найти производные следующих постоянных функций

Решение.

В первом случае мы имеем производную натурального числа 3 , во втором случае нам приходится брать производную от параметра а , который может быть любым действительным числом, в третьем – производную иррационального числа , в четвертом случае имеем производную нуля (ноль является целым числом), в пятом – производную рациональной дроби .

Ответ:

Производные всех этих функций равны нулю для любого действительного x (на всей области определения)

Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле :

Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.

Следует рассмотреть два случая: при положительных x и отрицательных x .

Сначала будем полагать . В этом случае . Выполним логарифмирование равенства по основанию e и применим свойство логарифма:

Пришли к неявно заданной функции. Находим ее производную:

Осталось провести доказательство для отрицательных x .

Когда показатель p представляет собой четное число, то степенная функция определена и при , причем является четной (смотрите раздел ). То есть, . В этом случае и также можно использовать доказательство через логарифмическую производную.

Когда показатель p представляет собой нечетное число, то степенная функция определена и при , причем является нечетной. То есть, . В этом случае и логарифмическую производную использовать нельзя. Для доказательства формулы в этом случае можно воспользоваться правилами дифференцирования и правилом нахождения производной сложной функции:

Последний переход возможен в силу того, что если p – нечетное число, то p-1 либо четное число, либо нуль (при p=1 ), поэтому, для отрицательных x справедливо равенство .

Таким образом, формула производной степенной функции доказана для любого действительного p .

Пример.

Найти производные функций .

Решение.

Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции:

Производная показательной функции.

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

По определению производной для функции синуса имеем .

Воспользуемся формулой разности синусов:

Осталось обратиться к первому замечательному пределу:

Таким образом, производная функции sin x есть cos x .

Абсолютно аналогично доказывается формула производной косинуса.

При решении задач дифференцирования мы будем постоянно обращаться к таблице производных основных функций, иначе зачем мы ее составляли и доказывали каждую формулу. Рекомендуем запомнить все эти формулы, в дальнейшем это сэкономит Вам массу времени.

Copyright by cleverstudents

Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.

3.1 Производная функция

О чем вы узнаете: -Definition производной -NOTATION -RELATION Определение: Производной функции f по переменной x является функция f’, значение которой в точке x равно: Если f'(x) существует, мы говорим, что f имеет производную и дифференцируемый. 93. Решение: Применение определения, мы имеем: Производная функция F в точке x = A – предел: Пример 2 . Определение Дифференцировать f(x) = x². используя альтернативное определение. Решение: В точке x = a,                                  Обозначение: График f’ из f: Пример 3  ГРАФИК f. от f   График производная функции f, график которой показан на рисунке ниже. Обсудите поведение f с точки зрения знаков и значений f ‘. Решение: ① Проводим пару координатных осей, маркировка горизонтальной оси в единицах x и вертикальной оси в единицах наклона. ② Мы оцениваем наклон графика f в различных точках, строя соответствующие значения наклона с использованием нового оси. В точке A(0, f(0)) график функции f имеет наклон 4, поэтому f'(0)=4. В точке B график функции f имеет наклон 1, поэтому f ‘= 1 в точке B’ и так далее.                 Путем соединения нанесенных точек гладкой кривой, мы завершаем наш график. По графику мы можем найти, что f равно уменьшается, когда f ‘отрицательно, и увеличивается, когда f ‘положительно. Где ж ‘ равен нулю, график функции f имеет касательную по горизонтали, изменяющуюся от возрастающей к убывающей (точка С) или от убывающей к возрастающей (точка F). Односторонние производные: Функция y = f(x) дифференцируема на отрезке [a,b], если она имеет производную во всех внутренних точках отрезка и пределы существуют на конечных точках. Пример 4   Односторонние производные могут отличаться в точке Покажите, что следующая функция имеет левые и правые производные в точке x . 0, но нет производной на рисунке ниже. Решение: Проверяем существование левой производной:    Проверяем существование правой производной:   Так как левая производная равна 0, а правая равна 2 , производные не равны в x . 0. Функция не имеет производной в точке 0. Практические задачи: Используйте предельное определение производной для вычисления f ‘(x) от 1 до 6. 1. F (x) = 5 (решение) A. 5 B. 10 C. 0 D. 0,5 2. F (x) = 9 – 3x (решение) A. -3 B. 9 C. 6 D. 0 3. F (x) = X² + 2 (решение) A. 2 B. 2x C. 4 D. 0 4. F (x) = 5x² + 3x – 7 (решение) A. 1 B. 10x + 3 C. 10 + 3x D. 5x + 3 5. F (x) = 7x³ – – 3 (решение) A. 21 B. 7x² C. 21x² D. 4x 6. F (x) = 1 / (x + 3) (решение) A. -1 B. 1 C. ( x + 3)²         D. -1 / (x + 3)² 7. Выберите правильный график f ‘(x) для функции f (x), показанной ниже. (Решение) A. B. C. 8. Пусть F (x) = 2x² + 1 (a) Экспресс f ‘(3) в качестве предела коэффициента дифференциации, как в определении производная. (b) Оцените предел в части (a).                                               (Решение) 9. Нарисуйте приближенный график производной функции, показанной ниже. (решение) 10. Рассмотрим функцию f (x) = x² – 2x. (a) Выразите f ‘(3) как предел разностного отношения, как в альтернативном определении производной. (b) Оцените предел в части (a). (решение) 11. Производная функция: (решение) A. Уравнение B. Функция C. Рисунок 12. Производная функция в Точка: (решение) A. Уравнение B. Число C. Функция 13. Производная тесно связана со следующим понятием: (Решение) A. множество решений уравнения B. наклон прямой C. ноль функции A. Повседневное ноль B. Constant C. Линейный 15. Понятие производной функции x � F ( x ) Предоставляет ответ на следующий вопрос: ( x ). 0008 A. Каково содержимое области под графиком? B. Как ведет себя значение функции, когда x немного изменяется? C. Где график пересекает ось x ? D. Как функцию можно представить графически? (Решение) Дополнительные примеры см. на странице видеоуроков.

Производные алгебраических функций: формула, доказательство и примеры

Производные алгебраических функций — это ряд формул, которые можно использовать для быстрого дифференцирования алгебраических функций. В этой статье мы изучим производные алгебраических функций и их формулы с доказательствами и решенными примерами, графическое представление производных и как найти производную.

Алгебраическая функция — это функция, которую можно определить как корень полиномиального уравнения. Алгебраическая функция использует только алгебраические операции, такие как сложение, вычитание, умножение и деление, а также дробные или рациональные показатели. Производные алгебраических функций — это стандартные функции, которые дают производные различных алгебраических функций. Производные алгебраических функций используются для нахождения решений дифференциальных уравнений.

​᠎​Правило суммы

Правило суммы гласит, что производная суммы функций равна сумме их производных. Правило разности гласит, что производная разности функций есть разность их производных.

\({d\over{dx}} [f(x) + g(x)] = {d\over{dx}}f(x) + {d\over{dx}}g(x)\ )

Правило разности

Правило разности гласит, что производная разности функций есть разность их производных.

\({d\over{dx}} [f(x) – g(x)] = {d\over{dx}}f(x) – {d\over{dx}}g(x)\ )

Product Rule

Иногда нам даются функции, которые на самом деле являются продуктами других функций. Это означает, что две функции перемножаются. Специальное правило, правило произведения, существует для дифференциации произведений двух (или более) функций.

Если y = uv, то 

\({dy\over{dx}} = u{dv\over{dx}} + v{du\over{dx}}\)

Частное правило

Специальное правило , правило отношения, существует для дифференцирования частных двух функций. Функции часто приходят в виде частных, под которыми мы подразумеваем одну функцию, деленную на другую функцию. Есть формула, которую мы можем использовать, чтобы дифференцировать частное — она называется правилом частного. 9b\), где «b» обозначает переменную, а «x» обозначает константу, которая также называется основанием функции. Логарифмическая функция является обратной экспоненциальной функцией. Логарифмические функции в математике — это оператор, который поможет вам точно вычислить показатель степени, удовлетворяющий показательному уравнению. Уравнение логарифмической функции выглядит следующим образом: \(c=\log_{b}a\) для a>0, таких что b>0 и \(b\ne1\).

Производные экспоненциальных функций

Давайте посмотрим, как мы можем вычислить производные экспоненциальных функций. 9x.\ln{a}\)

Производные экспоненциальных функций e по степенному правилу

Производная экспоненциального члена, который содержит переменную в качестве основания и константу в качестве степени, называется производной постоянной степени правило. x\)

Производная логарифмической функции

Производная логарифмической функции переменной относительно самой себя равна ее обратной величине.

\({d\over{dx}}{logx}={1\over{x}}\).

Производные логарифмических функций используются для нахождения решений дифференциальных уравнений.

Производная квадратного корня

Производная квадратного корня из x может быть найдена с помощью степенной формулы. Здесь мощность х равна ½. Производная x, возведенная в степень n, записывается в математической форме следующим образом. 9{-\frac{3}{2}} \end{matrix}\)

Надеюсь, что эта статья о производных алгебраических функций была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!

Часто задаваемые вопросы о производных алгебраических функций

В.1 Что такое производная в алгебре?

Ответ 1 Производная функции действительной переменной измеряет чувствительность к изменению значения функции (выходное значение) по отношению к изменению ее аргумента (входное значение). Производная функции одной переменной при выбранном входном значении, если она существует, представляет собой наклон касательной к графику функции в этой точке.
Производная функции, представленная \({dy\over{dx}}\) или f′(x), представляет собой предел наклона секущей, когда h приближается к нулю.
Пример. Производная функции смещения — это скорость.

Q.2 Что такое алгебраические функции?

Ответ 2 Алгебраическая функция — это функция, которую можно определить как корень полиномиального уравнения. Пример:

Q.3 Каковы свойства алгебраических функций?

Ответ 3 Пусть f(x) и g(x) — две алгебраические функции от x. Эти две функции будут иметь следующие свойства.
(f + g)(x) = f(x) + g(x)
(f + g)(x) = f(x) – g(x)
(f x g)(x) = f(x) x g(x)
(f \ g)(x) = f(x) \ g(x), где g(x) не равно нулю.
Вот список производных алгебраических функций.

Q.