Как найти производную функции в точке x0
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача.
На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).

- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.
 е. f’(x) ≥ 0.
е. f’(x) ≥ 0. - Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x).
В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−3; 3), B (5; 5), C (5; 3). Угол наклона касательной к оси абсцисс будет равен углу BAC. Поэтому
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.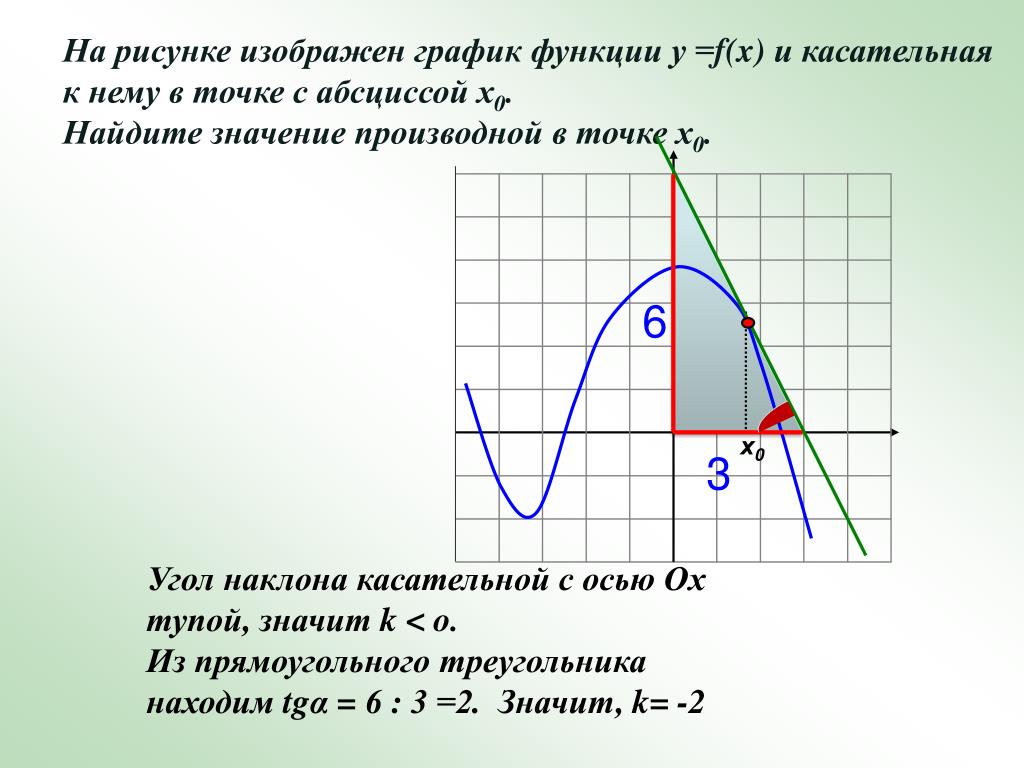
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции в точке
Справка: Следующие способы обозначения функции эквивалентны: В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке :
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции в точке
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции в точке . Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение . Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
Ну вот, совсем другое дело. Вычислим значение производной в точке :
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции в точке .
Это пример для самостоятельного решения.
Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной кграфику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
Составить уравнение касательной к графику функции в точке с абсциссой . Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):
Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственнойточке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.
Применительно к нашему случаю: при касательная (стандартное обозначение) касается графика функции в единственной точке .
И наша задача состоит в том, чтобы найти уравнение прямой .
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции в точке
Справка: Следующие способы обозначения функции эквивалентны:
В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке :
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции в точке
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции в точке .
Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение . Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
Ну вот, совсем другое дело. Вычислим значение производной в точке :
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции в точке .
Это пример для самостоятельного решения.
Как найти значение производной функции F(x) в точке Хо? Как вообще это решать?
Sfash
Если формула задана, то найти производную и вместо Х подставить Х-нулевое. Посчитать
Если речь идет о б-8 ЕГЭ, график, то надо найти тангенс угла (острый или тупой) , который образует касательная с осью Х (с помощью мысленного построения прямоугольного треугольника и определения тангенса угла)
Тимур адильходжаев
Во-первых, надо определиться со знаком. Если точка х0 находится в нижней части координатной плоскости, то знак в ответе будет минус, а если выше, то +.
Во-вторых, надо знать что такое тангес в прямоугольном прямоугольнике. А это соотношение противолежащей стороны (катета) к прилежащей стороне (тоже катета) . На картине обычно есть несколько черных отметок. Из эти отметок составляешь прямоугольный треугольник и находишь тангес.
Как найти значение производной функции f x в точке x0?
Bk.Ru
В общем случае, что бы найти значение производной какой-либо функции по некоторой переменной в какой-либо точке, нужно продифференцировать заданную функцию по этой переменной. В вашем случае по переменной Х. В полученное выражение вместо Х поставить значение икса в той точке, для которой надо найти значение производной, т.е. в Вашем случае подставить нулевой Х и вычислить полученное выражение.
Ну а ваше стремление разобраться в этом вопросе, на мой взгляд, бесспорно заслуживает +, который ставлю с чистой совестью.
Lady v
Такая постановка задачи на нахождение производной часто ставится для закрепления материала на геометрический смысл производной. Предлагается график некоей функции, совершенно произвольной и не заданной уравнением и требуется найти значение производной (не саму производную заметьте!) в указанной точке Х0. Для этого строится касательная к заданной функции и находится точки ее пересечения с осями координат. Потом составляется уравнение этой касательной в виде y=кx+b.
Потом составляется уравнение этой касательной в виде y=кx+b.
В этом уравнении коэффициент к и будет являться значением производной. остается лишь найти значение коэффициента b. Для этого находим значение у при х=о, пусть оно равно 3 — это и есть значение коэффициента b. Подставляем в исходное уравнение значения Х0 и У0 и находим к — нашу значение производной в этой точке.
Определение производной функции в точке
Определение производной
- Производная функции в точке
- Пусть функция f(x) определена в некоторой окрестности точки x.
Производной f′(x) функции f(x) в точке x называется конечный предел отношения приращения функции к приращению ее аргумента, когда последний стремится к нулю:
(1) . - Приращение аргумента функции
- в точке x – это разность значений аргумента в некоторой точке и точке x:
.
Приращение аргумента является независимой переменной. - Приращение функции
- в точке x – это разность значений функции в некоторой точке и точке x: .

Приращение функции является зависимой переменной. Оно зависит от и , или от и . - Дифференцирование
- – это процесс вычисления производной.
В определении (1), приращение аргумента является одной переменной, хотя ее обозначение состоит из двух букв: и . Обычно переменную принято обозначать одной буквой или буквой с одним или несколькими индексами. Но приращение в математическом анализе настолько часто встречается, что его обозначают с небольшим нарушением правил. Приращение функции также является одной переменной.
В приведенных выше определениях, является независимой переменной, а – зависимой. зависит от двух переменных. Если использовать выражение , то приращение функции зависит от переменных x и . Если использовать , то зависит от x и . Но когда мы вычисляем производную в заданной точке x, то считаем, что x является постоянной. Тогда является функцией, зависящей только от одной переменной . Таким образом задача о нахождении производной в точке x сводится к задаче о вычислении предела от функции , зависящей от одной переменной при , или от функции , зависящей от одной переменной при .
В правой части (1) мы сделали замену, и перешли от переменной к переменной . Тогда . При ,
.
После того, как мы нашли производную в заданной точке, то x уже можно считать не фиксированным числом, а переменной. То есть предел (1) можно рассматривать как функцию от x.
Еще раз подчеркнем, что выражение является функцией от двух переменных: x и . А выражение , полученное после вычисления предела, зависит только от одной переменной x.
Ниже приводятся примеры вычислений производных ⇓, используя определение ⇑.
Обозначение производной
Обозначение Лагранжа
Наиболее популярным является обозначение Лагранжа. Производную функции обозначают как и саму функцию, добавляя штрих после ее характеристики: . Если функция задана алгебраическим выражением, то это выражение заключают в скобки, и ставят знак штриха справа за закрывающей скобкой: . При этом производная также является функцией от той же переменной x, что и . Правда область определения производной может не совпадать с областью определения функции, а является ее подмножеством.
Напомним, что в обозначении функции фигурируют три символа: независимая переменная, характеристика функции и зависимая переменная (см. «Определение функции»). Так, в выражении
(2) ,
x является независимой переменной, или аргументом функции; f – характеристикой функции; y – зависимой переменной, или значением функции. Обозначение зависимой переменной может совпадать или не совпадать с обозначением характеристики. Производную функции (2) обозначают так:
.
Независимую переменную производной обозначают так же, как и независимую переменную функции. В нашем случае это x.
Характеристику производной обозначают тем же символом, что и характеристику функции, добавляя штрих справа: .
Зависимую переменную производной обозначают аналогично характеристике, добавляя штрих к обозначению зависимой переменной функции. Так, для примера (2), это будет : .
Если функция зависит от нескольких переменных, например
(3) ,
но все кроме одной считают постоянными, то к характеристике производной добавляют нижний индекс, обозначающий ту переменную, по которой вычисляют производную. При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда в данном контексте, является функцией от одной переменной . К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование:
При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда в данном контексте, является функцией от одной переменной . К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование:
.
Подобные производные функций от нескольких переменных называются частными производными. Детально они будут рассмотрены позже.
Нижний индекс добавляют и при вычислениях, связанных со сложными функциями. Пусть, например, функцию можно представить как сложную: , составленную из двух функций: и . При этом множества значений функций и совпадают. Поэтому их удобно обозначить одной переменной y. Тогда производную от y, выраженную через переменную x, обозначают как :
.
А производную от y, выраженную через переменную , обозначают как :
.
Обозначение производной по времени в физике
В механике и физике, производную по времени обозначают не штрихом, а точкой над зависимой переменной. Обычно время обозначают буквой t. Тогда
Обычно время обозначают буквой t. Тогда
.
Обозначение Лейбница
В способе Лейбница, зависимую переменную обозначают в форме отношения дифференциалов:
.
Этот способ удобен, поскольку указывает, по какой переменной ведется дифференцирование. Такой способ применяется только для функций от одной переменной. Для функций от многих переменных используют обозначение частной производной: .
Иногда в форме дифференциалов обозначают характеристику производной, добавляя справа аргумент:
.
Однако этот способ скорее неудачен, и может привести к путанице.
Обозначение Коши
Также, для обозначения производной, используют обозначение Коши:
.
Но мы не будем им пользоваться.
Существование производной
Рассмотрим вопрос о существовании предела, который используется при вычислении производной, при заданном значении x:
(4) .
Здесь могут возникнуть три случая:
1) в точке x существует конечный предел (4);
2) существует бесконечный предел или ;
3) предела (4) не существует.
1) Если существует конечный предел (4), то говорят, что функция имеет производную в точке x.
2) Если в некоторой точке x существует бесконечный предел (4), то говорят, что производной в этой точке не существует. Это согласуется с определением, ⇑ в котором указано, что производной называется конечный предел. Однако при этом говорят, что функция f имеет в точке x бесконечную производную, равную или . Здесь стоит обратить внимание на различие в определении предела и производной. Возможна ситуация, когда предел (4) существует (равный бесконечности), но при этом производная не существует (хотя существует ее значение, равное бесконечности).
См. пример ⇓.
3) Если предела (4) не существует, то функция не имеет производной в точке x.
Производные справа и слева
Определение
- Правая (левая) производная функции f в точке x
- Пусть функция f(x) определена в правой окрестности точки x. Тогда правой производной функции f в точке x называется правый предел
.
Соответственно, если функция определена в левой окрестности x, то левой производной функции f в точке x называется левый предел
.
Правую (левую) производную также называют производной справа (слева) в точке x, или правосторонней (левосторонней) производной в точке x.
Лемма об односторонних производных
Функция имеет в точке x производную тогда и только тогда, когдаона имеет в этой точке производные справа и слева, и они равны:
.
При этом
.
Доказательство
Для доказательства применим теорему об односторонних пределах.
Пусть существует производная функции в точке x. Это означает, что она определена в некоторой окрестности точки x, и существует конечный предел функции при :
.
Но тогда существуют правая и левая окрестности точки x, на которых определена. По теореме об односторонних пределах, существуют равные правый и левый пределы:
.
Отсюда следует, что в точке x существуют односторонние производные
.
Пусть теперь, в точке x, существуют равные односторонние производные:
.
Это означает, что существуют правая и левая окрестности точки x, в которой определена . И существуют односторонние равные пределы:
.
Отсюда следует, что существует двусторонняя окрестность точки x, на которой определена . И по теореме об односторонних пределах, существует двусторонний предел:
.
Это означает, что в точке x существует производная
.
Лемма доказана.
Следствие о неравных односторонних производных
Если функция имеет в точке x не равные односторонние производные:,
то она не имеет производной в этой точке.
Действительно, допустим противное. Пусть функция имеет в точке x не равные односторонние производные, но при этом имеет производную в этой точке. Тогда, согласно лемме об односторонних производных, она имеет в этой точке равные производные слева и справа, что противоречит предположению.
См. пример ⇓.
Примеры вычисления производной, используя определение
Все примеры Здесь и далее мы приводим подробные решения примеров, в которых нужно вычислить производную функции , используя определение производной ⇑.
решение ⇓ ; ⇓ ; ⇓ .
Пример
Все примеры ⇑ Найти производную функции , используя определение производной.
Решение
Функция определена для всех x. Поэтому она определена в любой окрестности любой точки x. Используем определение (1). Считаем, что x – фиксированное число, то есть что его значение задано. Найдем приращение функции в точке x:
.
Находим отношение приращения функции к приращению ее аргумента:
.
Находим предел функции , зависящей от переменной . При этом считаем, что x является фиксированным, заданным числом:
.
Итак, мы нашли производную:
.
Поскольку вычисленный нами предел существует, и является конечным числом для всех x, то функция имеет производную для всех значений аргумента x.
Ответ
.
Пример бесконечной производной +∞
Все примеры ⇑ Найдем производную функции .
Решение
Производная функции в точке x = 0 равна плюс бесконечности.
Функция определена для всех x. Найдем отношение приращения функции к приращению ее аргумента в точке x:
Найдем отношение приращения функции к приращению ее аргумента в точке x:
.
Применим формулу . Тогда
;
(5) .
Считаем, что x является фиксированным числом. Тогда отношение является функцией от одной переменной : . При она определена для всех . При она определена для всех .
Пусть . Тогда:
.
Пусть . Подставим в (5) :
.
Поскольку , то
.
Ответ
Таким образом мы нашли, что функция имеет производную для всех . При функция не имеет производной, она равна .
Пример
Все примеры ⇑ Найдем производную функции . Покажем, что несмотря на то, что функция определена для всех x, ее производная в точке не существует.
Решение
Функция y = |x| не имеет производной в точке x = 0.
Функция определена для всех значений аргумента x. Поэтому она определена в любой окрестности произвольной точки x.
1. Пусть . Тогда ,
.
2. Пусть . Тогда ,
.
3. Рассмотрим точку . В ней
.
Найдем производную справа в точке . При этом ,
.
Теперь найдем производную слева в точке . В этом случае ,
.
Итак, мы нашли, что односторонние производные в точке существуют, но они не равны друг другу:
.
Согласно следствию леммы об односторонних производных, производной функции в точке не существует.
Ответ
;
;
.
В точке производная не существует.
Использованная литература:
Г.Е. Иванов. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2018.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
определения, формулы и примеры решения задач
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Приращение аргумента и функции
- Определение производной
- Дифференцирование функции
Пусть задана некоторая функция $y=f(x)$. Возьмем какое-нибудь
значение $x_{0}$ из области определения этой функции:
$x_{0} \in D[f]$ . Соответствующее значение функции в этой точке
будет равно $y_{0}=f\left(x_{0}\right)$ .
Возьмем какое-нибудь
значение $x_{0}$ из области определения этой функции:
$x_{0} \in D[f]$ . Соответствующее значение функции в этой точке
будет равно $y_{0}=f\left(x_{0}\right)$ .
Приращение аргумента и функции
Определение
Приращением аргумента называется разность между двумя значениями аргумента: “новым” и “старым”.
Обычно обозначается как $\Delta x=x_{1}-x_{0}$ .
Пример
Задание. Найти приращение аргумента $x$, если он переходит от значения 3 к значению 3,2.
Решение. Искомое приращение: $\Delta x=3,2-3=0,2$ .
Ответ. $\Delta x=0,2$
Больше примеров решений Решение производных онлайн
Зададим аргументу $x_{0}$ приращение $\Delta x$. А тогда значение функции в новой точке $f\left(x_{0}+\Delta x\right)$.
Определение
Приращением функции $y=f(x)$ в точке $x_{0}$, соответствующее приращению аргумента $\Delta x=x-x_{0}$, называется величина:
$\Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. {\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\infty$ .
{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\infty$ .
Теорема
(О непрерывности функции в точке)
Если функция $y=f(x)$ имеет конечную производную в точке $x_{0}$ , то она непрерывна в этой точке.
Замечание. Обратное заключение не всегда верно: если функция $y=f(x)$ непрерывна в некоторой точке $x_{0}$ , то она может и не иметь производной в этой точке.
Определение
Функция $y=f(x)$ называется дифференцируемой в точке $x$, если приращение функции, соответствующее приращению аргумента, можно представить в виде:
$\Delta y=A \cdot \Delta x+\alpha(\Delta x) \cdot \Delta x$
где $A$ – число, не зависящее от $\Delta x$, $\alpha(\Delta x)$ – б.м. функция при $\Delta x \rightarrow 0$.
Теорема
(О необходимом и достаточном условии дифференцируемости)
Для того чтобы функция $y=f(x)$ была дифференцируемой
в точке $x$, необходимо и достаточно,
чтобы $y=f(x)$ имела в этой точке конечную производную.
Теорема устанавливает, что для функции $y=f(x)$ дифференцируемость в данной точке $x$ и существование конечной производной в этой точке – понятия равносильные.
Читать дальше: односторонние производные.
Производная функции
Исторически математический анализ произошёл из задач механики, из необходимости описывать движение физических тел, их скорости и ускорения. Со временем оказалось, что в тех же терминах можно говорить о множестве разных процессов и объектов. В этой лекции мы введём понятие производной, формализующее идею о скорости какого-либо изменения.
15.1Определение производной
15.1.1Функции как динамические процессы
Рассмотрим функцию y=f(x) и пусть x — это время, а y — результат измерения
какой-то величины в момент времени x. Это может быть артериальное давление у
пациента, или популяция некоторого вида, или количество людей, зараженных вирусом
— что угодно. Но проще всего про это думать так: есть точка, которая может
двигаться вверх и вниз, f(x) — это вертикальная координата (то есть просто
высота) этой точки в момент времени x. Тогда про эту функцию можно думать в
динамических терминах. Например, рассмотрим функцию, заданную графиком на
рис. 15.1.
Тогда про эту функцию можно думать в
динамических терминах. Например, рассмотрим функцию, заданную графиком на
рис. 15.1.
Рис. 15.1: График функции
Этот график можно интерпретировать следующим образом. В момент времени x=−4 точка находилась на высоте y=−1. Она сразу стала двигаться вверх, и спустя две единицы времени, в момент x=−2 достигла высоты y=3. Тут она на мгновение остановилась (перестала двигаться вверх) и изменила направление движения. Далее она двигалась вниз на протяжении четырёх единиц времени, до момента x=2. Тут она снова на мгновение остановилась, и стала двигаться вверх, вплоть до момента времени x=4 (точка достигла высоты y=3). Дальнейшая её судьба неизвестна.
Рис. 15.2: График функции и движение точки
Именно такую интерпретацию функций мы будем использовать в дальнейшем в этой лекции.
15.1.2Производная как мгновенная скорость
Рассмотрим функцию, заданную графиком на рис. 15.3. Пусть нас
интересует скорость движения точки в какой-то момент времени x0.
15.3. Пусть нас
интересует скорость движения точки в какой-то момент времени x0.
Рис. 15.3: Вычисление средней скорости движения на интервале времени от x0 до x0+Δx.
В школе нас учат, что чтобы найти скорость, нужно поделить расстояние на время. Рассмотрим период от момента x0 до момента x0+Δx, где Δx — какое-то небольшое число. (Выражение Δx нужно воспринимать как неделимый символ, читается «дельта-икс».) В начале периода точка имела высоту f(x0), а в конце — f(x0+Δx). Пройденное расстояние между двумя моментами равно разности этих двух значений:
расстояние=f(x0+Δx)−f(x0)
Тут нужно иметь в виду, что нас интересует «чистое расстояние», вычисляемое с
учётом знака — не «сколько мы проехали», а «на сколько поднялись». Например,
если в течение этого промежутка точка в какой-то момент двигалась вниз, в это
время «пройденное расстояние» уменьшалось, а не увеличивалось. Также
«расстояние» может быть отрицательным, если новое значение высоты f(x0+Δx) окажется меньше исходного (то есть в итоге точка опустилась ниже, чем
была).
Вернёмся к вычислению скорости. Время движения равно просто Δx. Значит, скорость движения — вернее, средняя скорость движения на интервале от x0 до x0+Δx находится по формуле:
средняя скорость=f(x0+Δx)−f(x0)Δx
Однако, нужно иметь в виду, что на промежутке от x0 до x0+Δx движение не обязано быть равномерным — в какие-то моменты точка могла двигаться быстрее, в какие-то медленнее. Нас же интересует, что происходит в сам момент времени x0, интересует мгновенная скорость в этот момент. Чтобы изменение скорости на промежутке длиной Δx не влияло на оценку скорости в момент x0, нужно сделать длину этого промежутка как можно меньше. Иными словами, перейти к пределу при Δx→0. Так мы и получим производную.
Определение 1.Производная функции f в точке x0 равна мгновенной скорости изменения функции в этой точке. Она обозначается через f′(x0) и определяется следующим образом:
f′(x0)=limΔx→0f(x0+Δx)−f(x0)Δx. (15.1)
(15.1)
f′(x0)==limΔx→0f(x0+Δx)−f(x0)Δx.(15.1)
Также можно обозначить x:=x0+Δx и записать тот же предел следующим образом:
f′(x0)=limx→x0f(x)−f(x0)x−x0.(15.2)
15.2Интерпретация производной
15.2.1Линейная функция и равномерное движение
Рассмотрим функцию f(x)=kx+b. Это хорошо известная линейная функция (по крайней мере, в матанализе её называют именно так, хотя специалисты по линейной алгебре с этим могли бы и поспорить). Возьмём произвольный начальный момент x0, произвольный промежуток длины Δx и посчитаем среднюю скорость за этот промежуток:
ср. скорость=f(x0+Δx)−f(x0)Δx=k(x0+Δx)+b−(kx0+b)Δx==kx0+kΔx+b−kx0−bΔx=kΔxΔx=k.
ср. скорость=f(x0+Δx)−f(x0)Δx==k(x0+Δx)+b−(kx0+b)Δx==kx0+kΔx+b−kx0−bΔx==kΔxΔx=k.
Итак, каким бы ни был начальный момент и какой бы промежуток мы ни взяли,
средняя скорость будет всегда одинаковой и равной k. Таким образом, линейная
функция задаёт движение с постоянной скоростью. Производная линейной функции,
как следует из определения, во всех точках одинакова и равна k.
Таким образом, линейная
функция задаёт движение с постоянной скоростью. Производная линейной функции,
как следует из определения, во всех точках одинакова и равна k.
Коэффициент k называется угловым коэффициентом линейной функции f(x)=kx+b (или угловым коэффициентом прямой, которая является графиком этой функции). Он показывает, на сколько позиций мы сдвинемся вверх, если подождём одну единицу времени (то есть сдвинемся на одну единицу по горизонтали), см. рис. 15.4.
Рис. 15.4: Линейная функция y=kx+b, её график и смысл коэффициентов. Коэффициент b задаёт смещение по вертикали, а k — наклон прямой.
Геометрически, угловой коэффициент — это тангенс угла наклона прямой, заданной как график линейной функции, к горизонтальной оси.
15.2.2Секущие и касательные
Рассмотрим теперь какую-нибудь нелинейную функцию, например, такую, график
которой изображён на рис. 15.5. Пусть нас интересует производная в
точке x0. Рассмотрим выражение под знаком предела в определении производной
(15.1) и возьмём какое-то конкретное значение Δx.
Проведём прямую через точки (x0,f(x0)) и (x+Δx,f(x+Δx)). Она
называется секущей для графика функции y=f(x). Поскольку секущая — это
прямая, она является графиком линейной функции. Угловой коэффициент этой прямой
как раз и равен средней скорости. Иными словами, если мы хотим двигаться
равномерно (с постоянной скоростью) на промежутке времени от x0 до x0+Δx и при этом пройти именно то расстояние, которое мы прошли: от f(x0) до
f(x0+Δx), то нужно двигаться как раз со средней скоростью на этом
промежутке.
Рассмотрим выражение под знаком предела в определении производной
(15.1) и возьмём какое-то конкретное значение Δx.
Проведём прямую через точки (x0,f(x0)) и (x+Δx,f(x+Δx)). Она
называется секущей для графика функции y=f(x). Поскольку секущая — это
прямая, она является графиком линейной функции. Угловой коэффициент этой прямой
как раз и равен средней скорости. Иными словами, если мы хотим двигаться
равномерно (с постоянной скоростью) на промежутке времени от x0 до x0+Δx и при этом пройти именно то расстояние, которое мы прошли: от f(x0) до
f(x0+Δx), то нужно двигаться как раз со средней скоростью на этом
промежутке.
Рис. 15.5: Секущая к графику функции
Будем теперь уменьшать Δx. В этом случае одна точка на графике
будет неподвижной, а другая будет к ней приближаться, см. анимацию на
рис. 15.6. Секущая при этом может
поворачиваться вокруг точки (x0,f(x0)). Однако если существует
предел в определении производной, то у секущей будет существовать предельный
угловой коэффициент, и значит предельное положение — она будет «стремиться» (в
кавычках — потому что мы не определяли, что может значить «стремиться» для
прямых) к прямой, проходящей через точку (x0,f(x0)) с угловым коэффициентом
k=f′(x0). У этой прямой есть специальное название: касательная.
У этой прямой есть специальное название: касательная.
Определение 2. Касательная к графику функции y=f(x) в точке x0 — это прямая, проходящая через точку (x0,f(x0)) и имеющая угловой коэффициент k=f′(x0).
Рис. 15.6: Секущая стремится к касательной
Про касательную можно думать так. Представьте себе, что график на рис. 15.5 вблизи точки (x0,f(x0)) вырезан из фанеры — вернее, то, что находится над графиком — это кусок фанеры, а то, что под графиком, мы отрезали лобзиком (ровно по графику). Теперь можно взять недлинную линейку и приложить её к графику в точке (x0,f(x0)) как можно плотнее. Тогда линейка пройдёт ровно вдоль касательной, см. рис. 15.7.
Рис. 15.7: Нахождение касательной с помощью линейки.
Рис. 15.8: В отличие от касательной к окружности, касательная к графику функции может иметь больше одной точки пересечения с графиком
15.2.3Производная как функция
Выбирая разные точки в качестве x0 в определении
производной, мы будем получать разное значение предела
(15. 1). Таким образом, производная функции — это новая функция.
1). Таким образом, производная функции — это новая функция.
Полезно представлять себе визуально, как связан график функции и график её производной. По определению, производная — это мгновенная скорость возрастания функции в точке. Таким образом, если по графику видно, что где-то функция возрастает, то её производная там положительна. Если возрастает быстро, производная большая. Если убывает, производная отрицательна, и так далее. (Аккуратные формулировки для этих утверждений мы приведём позже, а потом их докажем.) Можно мысленно прикладывать касательные в разных точках, прикидывать их угловые коэффициенты и находить таким образом точки на графике производной.
Рассмотрим, например, график, изображенный на рис. 15.9 сверху, и прикинем, чему равна производная в отмеченных точках.
Рис. 15.9: Связь графика функции с графиком касательной.
В точке x1 функция убывает, равно как и в точке x2. Но если посмотреть на
касательные в этих точках, видно, что в x1 функция убывает быстрее, чем в
x2 (в x1 касательная ближе к вертикальной, график более крутой, чем в
x2), то есть f′(x1)<f′(x2)<0. Можно отметить на графике касательной
две точки: они обе должны быть ниже горизонтальной оси, и точка, соответствующая
x1, ниже, чем та, которая соответствует x2. Теперь посмотрим на точку
x3=0. В ней касательная горизонтальна. Выражаясь динамическим языком, это
момент разворта: левее мы двигались вниз (функция убывала), в момент времени 0
на мгновение остановились и потом стали двигаться вверх. Мгновенная скорость в
точке 0 равна нулю. Это значит, что соответствующая точка на графике
касательной будет лежать на горизонтальной оси. Наконец, можно посмотреть на
точки x4 и x5. Мы видим, что в обоих точках функция возрастает, но в x5
возрастает быстрее, чем в x4 — график со временем становится начинает расти
круче. Это означает, что производная в точке x5 больше производной в x4, и
это также нужно отразить на графике производной. Получается кривая, похожая на
изображенную на рисунке 15.9 внизу.
Можно отметить на графике касательной
две точки: они обе должны быть ниже горизонтальной оси, и точка, соответствующая
x1, ниже, чем та, которая соответствует x2. Теперь посмотрим на точку
x3=0. В ней касательная горизонтальна. Выражаясь динамическим языком, это
момент разворта: левее мы двигались вниз (функция убывала), в момент времени 0
на мгновение остановились и потом стали двигаться вверх. Мгновенная скорость в
точке 0 равна нулю. Это значит, что соответствующая точка на графике
касательной будет лежать на горизонтальной оси. Наконец, можно посмотреть на
точки x4 и x5. Мы видим, что в обоих точках функция возрастает, но в x5
возрастает быстрее, чем в x4 — график со временем становится начинает расти
круче. Это означает, что производная в точке x5 больше производной в x4, и
это также нужно отразить на графике производной. Получается кривая, похожая на
изображенную на рисунке 15.9 внизу.
Весь этот анализ мы провели, исходя просто из формы графика, не обращаясь к
формулам. Конечно, наш результат носит качественный характер — чисто глазомерно
нельзя найти точных значений производной функции, которая задана графиком,
нарисованным от руки. Тем интереснее сравнить эти «глазомерные» результаты с
точно посчитанными.
Тем интереснее сравнить эти «глазомерные» результаты с
точно посчитанными.
График, который мы нарисовали, похож на параболу, график функции f(x)=x2. Давайте найдём её производную, пользуясь опредлением:
f′(x0)=limΔx→0(x0+Δx)2−x20Δx=limΔx→0x20+2×0Δx+Δx20−x20Δx=limΔx→0(2×0+Δx)=2×0.
f′(x0)=limΔx→0(x0+Δx)2−x20Δx==limΔx→0x20+2×0Δx+Δx20−x20Δx==limΔx→0(2×0+Δx)=2×0.
Точка x0 произвольная, можно заменить её просто на x и записать f′(x)=2x. Скорее всего, вы помните эту формулу из школьного курса. Таким образом, график производной — это прямая линия. И она ведёт себя именно так, как мы нарисовали!
15.3Существование производной
15.3.1Дифференцируемость и непрерывность
Всякий раз, когда мы видим определение, заданное с помощью предела, мы должны задать вопрос: а всегда ли существует этот предел? Как правило, ответ: «не всегда». Это относится и к производной.
Определение 3. Если у функции f существует производная в точке x0, функция назыается дифференцируемой в этой точке.
Если у функции f существует производная в точке x0, функция назыается дифференцируемой в этой точке.
Что может помешать функции быть дифференцируемой? Много что.
Во-первых, чтобы предел (15.1) в принципе имел бы смысл, функция f должна быть определена в точке x0 (иначе нельзя посчитать f(x0)) и некоторой её окрестности (иначе нельзя посчитать f(x0+Δx)). Но этого, конечно, мало.
Необходимым условием дифференцируемости является непрерывность. Если функция не является непрерывной в точке, то она точно не является дифференцируемой в этой точке. Это можно сформулировать в виде следующей теоремы.
Теорема 1. Если функция f дифференцируема в точке x0, то она непрерывна в этой точке.
Доказательство. Пусть мы знаем, что производная существует, то есть существует предел
limΔx→0f(x0+Δx)−f(x0)Δx=f′(x0).
Чтобы доказать непрерывность функции f в точке x0, нужно изучить предел limx→x0f(x), или, что то же самое,
limΔx→0f(x0+Δx).
Преобразуем выражение под знаком предела. Во-первых, вычтем и добавим f(x0):
limΔx→0f(x0+Δx)=limΔx→0(f(x0+Δx)−f(x0)+f(x0))=….
limΔx→0f(x0+Δx)==limΔx→0(f(x0+Δx)−f(x0)+f(x0))=….
Теперь возьмём первые два слагаемые и умножим и поделим их на Δx (под знаком предела Δx не может обращаться в ноль, поэтому операция корректна):
…=limΔx→0(f(x0+Δx)−f(x0)Δx⋅Δx+f(x0)).
Теперь заметим, что выражение f(x0+Δx)−f(x0)Δx стремится к f′(x0) при Δx→0, Δx стремится к нулю, значит, их произведение стремится к f′(x0)⋅0=0. Предел второго слагаемого, числа f(x0), равен ему самому (это константа, не зависящая от Δx). Значит, предел всего выражения равен 0+f(x0), то есть f(x0). Значит
limx→x0f(x)=limΔx→0f(x0+Δx)=f(x0)
и функция f непрерывна в точке x0.∎
15.3.2Точки изломов
Итак, чтобы быть дифференцируемой в некоторой точке, функция должна быть по
меньшей мере непрерывной в этой точке. Но достаточно ли этого? Оказывается, нет.
Но достаточно ли этого? Оказывается, нет.
Пример 1. Рассмотрим функцию f(x)=|x|, см. рис. 15.10.
Рис. 15.10: График функции y=|x|.
Есть ли у неё производная в точке x0=0? Давайте найдём предел:
limΔx→0|0+Δx|−|0|Δx=limΔx→0|Δx|Δx.
Модуль раскрывается по-разному в зависимости от знака Δx. Как мы обсуждали выше (см. замечание 1), Δx не обязана быть положительной, и нужно рассмотреть два случая. Если Δx>0, выражение под знаком предела превращается в 1, то есть
limΔx→0+|Δx|Δx=limΔx→0+1=1.
Для отрицательных Δx модуль раскрывается со знаком минус, и дробь равна −1. Значит,
limΔx→0−|Δx|Δx=limΔx→0−(−1)=−1.
Таким образом, при приближении к нулю с разных сторон, функция стремится к разным значениям, и общего предела нет. Функция не дифференцируема в точке x=0.
Графически, это соответствует тому, что у неё в точке x=0 наблюдается
излом. Если проводить секущие, то при Δx>0 они будут совпадать с
прямой y=x, а при Δx<0 — с прямой y=−x. Никакого общего
предельного положения секущей не будет, и касательной в точке x=0 тоже не
будет.
Если проводить секущие, то при Δx>0 они будут совпадать с
прямой y=x, а при Δx<0 — с прямой y=−x. Никакого общего
предельного положения секущей не будет, и касательной в точке x=0 тоже не
будет.
15.3.3Вертикальные касательные
Точки изломов, как у функции f(x)=|x| — один из механизмов, как непрерывная функция может быть не дифференцируемой. Но он не единственный.
Пример 2. Рассмотрим функцию f(x)=3√x−1. Попробуем построить касательную в
точке x0=1. На анимации на рис. 15.11 видно, что по
мере приближения второй точке пересечения к точке (1,0), секущая
становится всё вертикальнее и вертикальнее. Можно аккуратно доказать (вы
сделаете это на семинаре), что предел в определении производной в этом
случае равен бесконечности, то есть не существует. Касательная тоже не
существует — по крайней мере, в соответствии с нашим определением. Можно
было бы сказать, что касательная вертикальна, но вертикальная прямая не
является графиком функции y=kx+b, и это потребовало бы расширения нашего
определения касательной — чего мы делать не будем, поскольку в этом сейчас
нет никакой непосредственной необходимости.
Рис. 15.11: Вертикальная касательная
Вертикальные касательные и изломы — не единственные причины, по которым функция может не будет дифференцируемой — но, пожалуй, самые важные с практической точки зрения. С некоторыми другими способами вы встретитесь на семинаре.
15.4Касательные и линейные приближения
15.4.1Формулировка и иллюстрация
По своему смыслу, касательная — это такая прямая, которая проходит вблизи графика функции (что, собственно, и означает «касается»). Чтобы придать этому аккуратный смысл, сформулируем такое утверждение.
Утверждение 1. Функция f дифференцируема в точке x0 тогда и только тогда, когда существует такое число k∈R и такая функция α(Δx), определенная в проколотой окрестности нуля, и стремящаяся к нулю при Δx→0, что справедливо равенство
f(x0+Δx)=f(x0)+kΔx+α(Δx)⋅Δx.(15.3)
f(x0+Δx)==f(x0)+kΔx+α(Δx)⋅Δx.(15.3)
В этом случае k=f′(x0).
Прежде, чем приступить к доказательству, давайте обсудим, что всё это значит. Что означает условие (15.3)? С помощью замены x=x0+Δx, его можно переписать в таком виде:
f(x)=f(x0)+k(x−x0)+α(x−x0)⋅(x−x0).(15.4)
f(x)==f(x0)+k(x−x0)++α(x−x0)⋅(x−x0).(15.4)
Пусть f дифференцируема в точке x0 и k=f′(x0). Рассмотрим функцию l, заданную следующим образом:
l(x)=f(x0)+f′(x0)⋅(x−x0).
Это линейная функция, графиком которой является касательная к графику y=f(x) в точке x0. Действительно, во-первых, она проходит через точку (x0,f(x0)) (подставьте x=x0 и убедитесь в этом). А во-вторых, её угловой коэффициент равен значению производной в точке x0.
Таким образом, равенство (15.4) записывается в виде:
f(x)=l(x)+α(x−x0)⋅(x−x0).(15.5)
f(x)==l(x)+α(x−x0)⋅(x−x0).(15.5)
Если бы в нём не было второго слагаемого, это бы просто означало, что функция
линейна и её график совпадает с касательной. Второе слагаемое, α(x−x0)⋅(x−x0) показывает, на сколько сильно график функции отклоняется от
касательной, см. рис. 15.12.
Второе слагаемое, α(x−x0)⋅(x−x0) показывает, на сколько сильно график функции отклоняется от
касательной, см. рис. 15.12.
Рис. 15.12: Отклонение графика функции от касательной
Утверждение, которое мы сейчас рассматриваем, говорит, что это отклонение становится маленьким, если Δx маленькое — но не просто маленьким, а «маленьким по сравнению с Δx». Действительно, если вернуться к выражению (15.3), в правой части мы видим три слагаемых: f(x0), kΔx и α(Δx)Δx. Второе и третье слагаемые оба становятся маленькими при маленьких Δx. Но при этом второе слагаемое пропорционально Δx, а третье — уменьшается быстрее, чем Δx. Например, если k=1/10, выражение kΔx всегда ровно в десять раз меньше Δx, а выражение α(Δx)Δx при уменьшении Δx становится в десять, потом в сто, потом в тысячу раз меньше Δx — и так во сколько угодно раз меньше.
Почему это важно? Давайте посмотрим на график какой-нибудь функции вблизи фиксированной точки, см. рис. 15.13.
Рис. 15.13: Увеличение графика функции и касательной вблизи фиксированной точки.
На каждом графике мы выбираем область вблизи точки (x0,f(x0)) (она
нарисована зелёным) и растягиваем её на всю картинку — так получается
следующий график.
15.13: Увеличение графика функции и касательной вблизи фиксированной точки.
На каждом графике мы выбираем область вблизи точки (x0,f(x0)) (она
нарисована зелёным) и растягиваем её на всю картинку — так получается
следующий график.
На первом графике различие между графиком нашей функции и её касательной было хорошо заметно, при каждом увеличении это различие становилось всё меньше и меньше, и на последней картинке настоящий график практически не виден — его полностью загораживает касательная, то есть две кривые почти совпадают. Почему так происходит?
Чтобы посмотреть на график под большим увеличением вблизи точки (x0,f(x0)),
нужно выбрать на исходной картинке небольшой прямоугольник вблизи этой точки и
растянуть его на всю картинку. Пусть в качестве этого прямоугольника мы взяли
квадрат со стороной 2h (то есть отступили от точки x0 вправо и влево на
h, и аналогично по вертикали отступили от f(x0) вверх и вниз на h). Если
мы теперь растянем этот квадратик на всю картинку (допустим, размера 1 на 1), то
все расстояния умножатся на 1/h. (Когда h маленькое, 1/h
большое и произойдёт сильное увеличение.)
(Когда h маленькое, 1/h
большое и произойдёт сильное увеличение.)
Посмотрим теперь на формулу (15.5). Она говорит, что разница между графиком функции и касательной равна α(Δx)Δx. Поскольку мы рисуем только часть картинки в нашем квадратике, |Δx|≤h. В новом масштабе, с учётом растяжения в 1/h раз, соответствующее расстояние между графиками окажется равно
|α(Δx)||Δx|h≤|α(Δx)|.
Но если h маленькое, то |Δx| маленький и эта величина стремится к нулю! Таким образом, результат, который мы видим на рис. 15.13, не является чем-то удивительным — в нём вся суть понятия касательной, и на самом деле вся суть идеи дифференцируемости: вблизи фиксированной точки дифференцируемая функция очень близка к линейной функции, задающей касательную в этой точке.
15.4.2Доказательство утверждения о линейном приближении
Доказательство утверждения 1. Нам нужно доказать эквивалентность двух утверждений:
- функция f дифференцируема в точке x0;
- существует представление (15.
 3), которое говорит о
том, что функция f хорошо приближается некоторой линейной
функцией в окрестности точки x0.
3), которое говорит о
том, что функция f хорошо приближается некоторой линейной
функцией в окрестности точки x0.
Из дифференцируемости следует линейное приближение. Пусть функция f дифференцируема в точке x0. Положим k=f′(x0) и
α(Δx):=f(x0+Δx)−f(x0)Δx−k.
В этом случае представление (15.3) соблюдается (я просто выразил α(Δx) из него), и содержательным является утверждение, что α(Δx)→0 при Δx→0. Докажем его:
limΔx→0α(Δx)=limΔx→0(f(x0+Δx)−f(x0)Δx−k)=f′(x0)−k=0.
limΔx→0α(Δx)==limΔx→0(f(x0+Δx)−f(x0)Δx−k)==f′(x0)−k=0.
Мы воспользовались определением производной, теоремой о пределе суммы и тем фактом, что мы сами выбрали k=f′(x0).
Из линейного приближения следует дифференцируемость. Наборот, пусть теперь известно, что представление (15.3) верно для какого-то k и α(Δx), причём α(Δx)→0. Докажем, что функция f дифференцируема в точке x0 и f′(x0)=k. Из (15.3) следует, что
α(Δx)=f(x0+Δx)−f(x0)Δx−k.
Перенесём k в левую часть и перейдём к пределу при Δx→0. Имеем:
limΔx→0f(x0+Δx)−f(x0)Δx=limx→Δxα(Δx)+k=k.
limΔx→0f(x0+Δx)−f(x0)Δx==limx→Δxα(Δx)+k=k.
Мы воспользовались тем фактом, что α(Δx)→0 при Δx→0 и пределом суммы. Теперь в левой части стоит определение производной функции f в точке x0, а справа k. Значит, производная существует и равна k.∎
15.5Заключение
Производная — мощный инструмент анализа функций. Мы аккуратно ввели это понятие и обсудили механическую и геометрическую интуицию, которая за ним стоит. На следующей лекции мы обсудим, как находить производные, а затем — как их применять.
← Предыдущая глава Следующая глава →
определение, как найти, примеры решений
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое –4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) – f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) – f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f “(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f “(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)” = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо – в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ – раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности – включая административные, технические и физические – для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
{\large\bf Производная функции}
Рассмотрим функцию y=f(x) , заданную на интервале (a, b) . Пусть x – любое фиксированная точка интервала (a, b) , а Δx – произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b) . Это число Δx называют приращением аргумента.
Это число Δx называют приращением аргумента.
Определение . Приращением функции y=f(x) в точке x , соответствующим приращению аргумента Δx , назовем число
Δy = f(x+Δx) – f(x) .
Считаем, что Δx ≠ 0 . Рассмотрим в данной фиксированной точке x отношение приращения функции в этой точке к соответствующему приращению аргумента Δx
Это отношение будем называть разностным отношением. Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx . Эта функция определена для всех значений аргумента Δx , принадлежащих некоторой достаточно малой окрестности точки Δx=0 , за исключением самой точки Δx=0 . Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .
Определение . Производной функции y=f(x) в данной фиксированной точке x называется предел при Δx → 0 разностного отношения, то есть
При условии, что этот предел существует.
Обозначение . y′(x) или f′(x) .
Геометрический смысл производной : Производная от функции f(x) в данной точке x равна тангенсу угла между осью Ox и касательной к графику этой функции в соответствующей точке:
f′(x 0) = \tgα .
Механический смысл производной : Производная от пути по времени равна скорости прямолинейного движения точки:
Уравнение касательной к линии y=f(x) в точке M 0 (x 0 ,y 0) принимает вид
y-y 0 = f′(x 0) (x-x 0) .
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f′(x 0)≠ 0 , то уравнение нормали к линии y=f(x) в точке M 0 (x 0 ,y 0) записывается так:
Понятие дифференцируемости функции
Пусть функция y=f(x) определена на некотором интервале (a, b) , x – некоторое фиксированное значение аргумента из этого интервала, Δx – любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b) .
Определение . Функция y=f(x) называется дифференцируемой в данной точке x , если приращение Δy этой функции в точке x , соответствующее приращению аргумента Δx , может быть представимо в виде
Δy = A Δx +αΔx ,
где A – некоторое число, не зависящее от Δx , а α – функция аргумента Δx , являющая бесконечно малой при Δx→ 0 .
Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:
Δy = A Δx +o(Δx) .
Теорема . Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x , необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x) , то есть
Δy = f′(x) Δx +o(Δx) .
Операцию нахождения производной обычно называют дифференцированием.
Теорема . Если функция y=f(x) x , то она непрерывна в этой точке.
Если функция y=f(x) x , то она непрерывна в этой точке.
Замечание . Из непрерывности функции y=f(x) в данной точке x , вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| – непрерывна в точке x=0 , но не имеет производной.
Понятие дифференциала функции
Определение . Дифференциалом функции y=f(x) называется произведение производной этой функции на приращение независимой переменной x :
dy = y′ Δx, df(x) = f′(x) Δx .
Для функции y=x получаем dy=dx=x′Δx = 1· Δx= Δx , то есть dx=Δx – дифференциал независимой переменной равен приращению этой переменной.
Таким образом, можем записать
dy = y′ dx, df(x) = f′(x) dx
Дифференциал dy и приращение Δy функции y=f(x) в данной точке x , оба отвечающие одному и тому же приращению аргумента Δx , вообще говоря, не равны друг другу.
Геометрический смысл дифференциала : Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение Δx .
Правила дифференцирования
Теорема . Если каждая из функций u(x) и v(x) дифференцируема в данной точке x , то сумма, разность, произведение и частное этих функций (частное при условии, что v(x)≠ 0 ) также дифференцируемы в этой точке, причем имеют место формулы:
Рассмотрим сложную функцию y=f(φ(x))≡ F(x) , где y=f(u) , u=φ(x) . В этом случае u называют промежуточным аргументом , x – независимой переменной .
Теорема . Если y=f(u) и u=φ(x) – дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
е.
Замечание . Для сложной функции, являющейся суперпозицией трех функций y=F(f(φ(x))) , правило дифференцирования имеет вид
y′ x = y′ u u′ v v′ x ,
где функции v=φ(x) , u=f(v) и y=F(u) – дифференцируемые функции своих аргументов.
Теорема . Пусть функция y=f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x 0 . Пусть, кроме того, эта функция дифференцируема в указанной точке x 0 и ее производная в этой точке f′(x 0) ≠ 0 . Тогда в некоторой окрестности соответствующей точки y 0 =f(x 0) определена обратная для y=f(x) функция x=f -1 (y) , причем указанная обратная функция дифференцируема в соответствующей точке y 0 =f(x 0) и для ее производной в этой точке y справедлива формула
Таблица производных
Инвариантность формы первого дифференциала
Рассмотрим дифференциал сложной функции. Если y=f(x) , x=φ(t) – дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой
y′ t = y′ x x′ t .
По определению dy=y′ t dt , тогда получим
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx ,
dy = y′ x dx .
Итак, доказали,
Свойство инвариантности формы первого дифференциала функции : как в случае, когда аргумент x является независимой переменной, так и в случае, когда аргумент x сам является дифференцируемой функцией новой переменной, дифференциал dy функции y=f(x) равен производной этой функции, умноженной на дифференциал аргумента dx .
Применение дифференциала в приближенных вычислениях
Мы показали, что дифференциал dy функции y=f(x) , вообще говоря, не равен приращению Δy этой функции. Тем не менее с точностью до бесконечно малой функции более высокого порядка малости, чем Δx , справедливо приближенное равенство
Δy ≈ dy .
Отношение называют относительной погрешностью равенства этого равенства. Так как Δy-dy=o(Δx) , то относительная погрешность данного равенства становится как угодно малой при уменьшении |Δх| .
Учитывая, что Δy=f(x+δ x)-f(x) , dy=f′(x)Δx , получим f(x+δ x)-f(x) ≈ f′(x)Δx или
f(x+δ x) ≈ f(x) + f′(x)Δx .
Это приближенное равенство позволяет с ошибкой o(Δx) заменить функцию f(x) в малой окрестности точки x (т.е. для малых значений Δx ) линейной функцией аргумента Δx , стоящей в правой части.
Производные высших порядков
Определение . Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.
Обозначение второй производной функции y=f(x) :
Механический смысл второй производной . Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная f″(x) равна ускорению движущейся точки в момент времени x .
Аналогично определяется третья, четвертая производная.
Определение . n -й производной (или производной n -го порядка) функции y=f(x) называется производная от ее n-1 -й производной:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′ .
Обозначения: y″′ , y IV , y V и т.д.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного – в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного – в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
12. Производная арктангенса Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на .
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
В данной функции видим произведение, один из сомножителей которых – квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн .
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Производная функции, заданной таблично — Студопедия.Нет
Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«ФИНАН
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Департамент анализа данных, принятия решений и финансовых технологий
Р. М.Магомедов, Е.В.Маевский
М.Магомедов, Е.В.Маевский
Приближенное вычисление производной функции в заданной точке (Excel)
Учебно-методические рекомендации для проведения
семинара №5 по компьютерному практикуму
Для бакалавров направления 38.03.01 «Экономика»
Электронное издание
Москва 2017
Приближенное вычисление производной
Функции в заданной точке (Excel)
Введение
Пусть функция определена в окрестности точки . Тогда производной функции в точке называется .
Простейшими формулами для приближенного численного вычисления производной являются так называемые двухточечные формулы, которые можно получить непосредственно из определения производной: , . Такое название связано с тем, что указанные формулы позволяют оценить значение производной в точке по значениям функции в двух точках.
Если зафиксировать функцию и точку и исследовать зависимость погрешности двухточечной оценки производной от малого шага , то можно доказать, что погрешность будет пропорциональна величине .
Более точная оценка получится, если использовать значения функции в трех точках: , , . Первая из этих формул используется при оценке производной на левой границе промежутка, вторая – во всех внутренних точках промежутка, а третья – на правой границе. Погрешности трехточечных формул пропорциональны .
Еще более точными являютсяформулы, оценивающие производную по большему количеству точек (4 и более). Однако следует иметь в виду, что увеличение количества участвующих в формуле точек усложняет вычисление по формуле и увеличивает ошибку округления, возникающую при этом вычислении. Потому, хотя и возможно теоретически использовать для оценки производной в данной точке весь массив известных значений функции, но на практике этого никогда не делают.
Другой способ уточнения значения производной – уменьшение шага . Такой подход представляется более рациональным для функций, заданных аналитическим выражением, но неприменим к функции, заданной таблицей значений. 2+2*(-B4)+2))/(2*B4)
2+2*(-B4)+2))/(2*B4)
9.2. ВыделяемдиапазонячеекA3:A103, C3:D103.
9.3. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками.В результате должна получиться диаграмма как показано на рисунке:
Задание 2.Найти первую производную функции в точке . Заметим, что производная приведенной функции в точке , вычисленная аналитическим методом, равна 12 – это значение нам понадобится для проверки результата, полученного путем вычисления численным методом в электронной таблице.
Из вышесказанного известно, что выражение для вычисления производной функции одной переменной в точке x, имеет вид:
где – очень малая конечная величина. То есть вместо выражения можно взять достаточно маленькое число, например, 0,00001.
Примечание. Количество точек после запятой для выражения hзависить от того с какой заданной точностью нужно вычислить производную, если, например, производную нужно вычислить с точностью до 2 знаков после запятой, то достаточно взять h равной 0,0001. 2 -4*B3+6.
2 -4*B3+6.
3. Копируем эту формулу в ячейку C4.
4. В ячейку E3 вводим формулу вычисления производной(рис.):
=(C4-C3)/(B4-B3).
В результате вычисления в ячейке E3 будет выведено приближенное значение производной заданной функции в точке , величина которой равна 12, что соответствует результату, полученному аналитически.
Задание 3.Найти первую производную функции в точке .
Из вышесказанного известно, что выражение для вычисления первой производной функции одной переменной в точке x, имеет вид:
где – очень малая конечная величина. То есть вместо выражения h можно взять достаточно маленькое число, например, 0,00001.
Решение
1. Вводим в ячейку B2 рабочего листа заданное значение аргумента, равное =3*пи()/14, в другой ячейке – B3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке В3 вычисляем сумму В3=В1+В2.
2. В ячейку E3 вводим формулу для вычисления производной:
=((SIN(1+1/C4))^2-(SIN(1+1/C2))^2)????????????? /h
3. 2).
2).
3. После нажатия клавиши Enter получаем результат вычисления 44,00003917 (см. рис.).
Производная функции, заданной таблично
В случае таблично заданной функции имеем: дискретному множеству значений аргумента ( ) поставлено в соответствие множество значений функции ( ), Шаг – разность между соседними значениями аргумента, , постоянный.
Производную функции в узле можно найти с помощью конечных разностей несколькими способами:
ü левые разности:
ü правые разности:
ü центральные разности:
Заметим, что вторая производная будет вычисляться по формуле:
Задание 5.Найти производную функции, заданной таблично.Функция , где . Найти производную функции в точке
Производную функции заданной таблично, найдем по формуле:
Решение
1. Вводим в ячейку С3 рабочего листа значение аргумента , равное 1,5, в ячейке –С4значение аргумента , равное 2,5,в ячейке –С5значение аргумента , равное 3,5, в ячейке С6 найдем по формуле С6=С5-С3. 2.
2.
3. Копируем эту формулу до ячейкиD5.
4. В ячейку D3 вводим формулу для вычисления производной функции в точке
=(D5-D3)/C6
5. После нажатия клавиши Enter получаем результат вычисления 415,00 (см. рис.).
Производная в точке — исчисление 2
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 Следующая →
Исчисление 2 Помощь » Производные » Производный обзор » Производная в точке
По заданной функции найдите наклон точки.
Возможные ответы:
Наклон не может быть определен.
Правильный ответ:
Объяснение:
Чтобы найти наклон в точке функции, возьмите производную функции.
Производная от это .
Следовательно, производная становится
с .
Теперь подставим заданную точку, чтобы найти наклон в этой точке.
Отчет о ошибке
Найдите значение следующего производного в точке:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, сначала нам нужно взять производную функции. Будет проще переписать уравнение, так как отсюда мы можем взять производную и упростить, чтобы получить
Отсюда нам нужно произвести оценку в данной точке. В этом случае важно только значение x, поэтому мы оцениваем нашу производную при x=2, чтобы получить.
Сообщить об ошибке
Оценить значение производной данной функции в точке:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, сначала нам нужно взять производную функции.
Отсюда нам нужно произвести оценку в данной точке. В этом случае важно только значение x, поэтому мы оцениваем нашу производную при x=1, чтобы получить
.
Сообщить об ошибке
Найти значение производной данной функции в точке:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, сначала нам нужно взять производную функции. Для этого нам нужно использовать частное правило и упростить следующим образом:
Отсюда нам нужно произвести оценку в данной точке. В этом случае важно только значение x, поэтому мы оцениваем нашу производную при x=2, чтобы получить
.
Сообщить об ошибке
Найти наклон в для функции .
Возможные ответы:
Правильный ответ:
Объяснение:
Производная от равна:
Замените точку на .
Сообщить об ошибке
Каков наклон в ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти наклон функции в определенной точке, подставьте эту точку в первую производную функции. Наш первый шаг здесь состоит в том, чтобы взять первую производную.
Поскольку мы видим, что f(x) состоит из двух разных функций, мы должны использовать правило произведения. Помните, что правило произведения выглядит следующим образом:
Следуя этой процедуре, мы устанавливаем равно и равно .
,
который можно упростить до
.
Теперь подставьте 1, чтобы найти наклон при x=1.
Помните об этом .
Сообщить об ошибке
Рассмотрим функцию: . Что такое производная в ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти производную от , используйте неявное дифференцирование, что означает получение производной каждого члена по переменной в этом члене.
Подставляем точку в производную.
Сообщить об ошибке
Используйте неявное дифференцирование, чтобы найти наклон касательной к в точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Мы должны взять производную, потому что это даст нам наклон. С левой стороны мы получим
, а с правой стороны получим .
Мы включили слева, потому что является функцией , поэтому ее производная неизвестна (поэтому мы пытаемся найти ее!).
Теперь мы можем вынести на множитель слева, чтобы получить
, и разделить на , чтобы найти.
Это даст вам
.
Мы хотим найти уклон в , поэтому мы можем заменить для и .
.
Сообщить об ошибке
Найдите производную следующей функции в точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Здесь мы должны использовать правило произведения.
Предположим, что и наше выражение принимает вид
.
Вопрос требует, чтобы мы оценили это в .
Сообщить об ошибке
Учитывая функцию, каков наклон в точке?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку наклон определяется как производная данной функции в данной точке, нам нужно будет взять производную и подставить в -значение точки .
Использование мощного правила для всех , . Подписка в , .
Сообщить об ошибке
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 Следующая →
Уведомление об авторских правах
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Обучение по концепции
2.
 4 Производная функция
4 Производная функцияМы видели, как создать или вывести новую функцию $f'(x)$ из функция $f(x)$, резюмированная в абзаце, содержащем уравнение 2.1.1. Теперь, когда у нас есть концепция пределов, мы можем сделать это более точным.
Определение 2.4.1 Производная функции $f$, обозначаемой $f’$, есть $$f'(x)=\lim_{\Delta x\to 0} {f(x+\Delta x)-f(x)\over \Delta x}.$$ $\квадрат$
Мы знаем, что $f’$ несет важную информацию об исходном
функция $f$. В одном примере мы видели, что $f'(x)$ говорит нам, насколько крутой
график $f(x)$ есть; в другом мы видели, что $f'(x)$ сообщает нам
скорость объекта, если $f(x)$ сообщает нам положение объекта в
время $х$. Как мы уже говорили ранее, эта же математическая идея полезна
всякий раз, когда $f(x)$ представляет некоторую изменяющуюся величину, и мы хотим знать
что-то о том, как оно меняется, или, грубо говоря, о «скорости», с которой оно
изменения. Большинство функций, встречающихся на практике, строятся из
небольшой набор “примитивных” функций несколькими простыми способами, для
например, добавляя или перемножая функции вместе, чтобы получить новые, более
сложные функции. Чтобы эффективно использовать информацию, предоставленную
$f'(x)$ нам нужно уметь вычислять его для множества таких
функции.
92} – 24\над\Дельта х}.
$$
Знаменатель здесь измеряет расстояние в направлении $x$,
иногда называемый «бегом», а числитель измеряет расстояние в
направление $y$, иногда называемое “подъем” и “подъем над
run» — это наклон линии. Напомним, что иногда такой числитель
сокращенно $\Delta y$, заменив краткость более подробным
выражение. Таким образом, в общем случае производная определяется выражением
$$
y’=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$
Чтобы напомнить форму предела, мы иногда говорим вместо этого, что
$$
{dy\over dx}=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$ Другими словами, $dy/dx$ — это другое обозначение производной, и
это напоминает нам, что это связано с фактическим уклоном между двумя
точки. Это обозначение называется
92)$.
$\квадрат$
Чтобы эффективно использовать информацию, предоставленную
$f'(x)$ нам нужно уметь вычислять его для множества таких
функции.
92} – 24\над\Дельта х}.
$$
Знаменатель здесь измеряет расстояние в направлении $x$,
иногда называемый «бегом», а числитель измеряет расстояние в
направление $y$, иногда называемое “подъем” и “подъем над
run» — это наклон линии. Напомним, что иногда такой числитель
сокращенно $\Delta y$, заменив краткость более подробным
выражение. Таким образом, в общем случае производная определяется выражением
$$
y’=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$
Чтобы напомнить форму предела, мы иногда говорим вместо этого, что
$$
{dy\over dx}=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$ Другими словами, $dy/dx$ — это другое обозначение производной, и
это напоминает нам, что это связано с фактическим уклоном между двумя
точки. Это обозначение называется
92)$.
$\квадрат$
Пример 2.4.3 Найдите производную $y=f(x)=1/x$.
Расчет: $$ \выравнивание{ y’ = \lim_{\Delta x\to0}{\Delta y\over\Delta x}&= \lim_{\Delta x\to0}{{1\over x+\Delta x} – {1\over x}\over \Delta х}\кр &=\lim_{\Delta x\to0}{{x\over x(x+\Delta x)} – {x+\Delta x\over x(x+\Delta x)}\over \Delta x}\cr &=\lim_{\Delta x\to0}{{x-(x+\Delta x)\over x(x+\Delta x)}\over \Delta x}\cr &=\lim_{\Delta x\to0} {x-x-\Delta x\over x(x+\Delta x)\Delta x}\cr &=\lim_{\Delta x\to0} {-\Delta x\over x(x+\Delta x)\Delta x}\cr &=\lim_{\Delta x\to0} {-1\over x(x+\Delta x)}={-1\over x^2}\cr } $$
$\квадрат$
Примечание. Если вы знаете некоторые “производные формулы” из
более ранний курс, на данный момент вы должны делать вид, что вы делаете
не знать их.
В примерах, подобных приведенным выше и приведенным ниже упражнениям, от вас требуется
знать, как найти производную формулу, исходя из основных принципов.
Позже мы разработаем некоторые формулы, чтобы нам не всегда нужно было
делать такие вычисления, но нам по-прежнему нужно знать, как делать
более сложные вычисления.
Если вы знаете некоторые “производные формулы” из
более ранний курс, на данный момент вы должны делать вид, что вы делаете
не знать их.
В примерах, подобных приведенным выше и приведенным ниже упражнениям, от вас требуется
знать, как найти производную формулу, исходя из основных принципов.
Позже мы разработаем некоторые формулы, чтобы нам не всегда нужно было
делать такие вычисления, но нам по-прежнему нужно знать, как делать
более сложные вычисления.
Иногда встречается точка в области определения функции $y=f(x)$, где
у нет производной , потому что нет касательной. В целях
чтобы понятие касательной в точке имело смысл, кривая должна
быть “гладкой” в этой точке. Это означает, что если вы представляете себе частицу
движущейся с некоторой постоянной скоростью вдоль кривой, то частица не
испытать резкое изменение направления. Есть два типа
ситуации, о которых вы должны знать — углы и выступы — где есть
внезапная смена направления и, следовательно, отсутствие производной.
Пример 2.4.4 Обсудите производную функции абсолютного значения $y=f(x)=|x|$.
Если $x$ положительна, то это функция $y=x$, производная которой равна константа 1. (Напомним, что когда $y=f(x)=mx+b$, производная есть наклон $m$.) Если $x$ отрицательно, то мы имеем дело с функцией $y=-x$, производная которой есть константа $-1$. Если $x=0$, то функция имеет угол, т. е. касательной нет. Касательная линия должны указывать в направлении кривой, но есть 93$. (отвечать)
Пример 2.4.6 Показан график функции $f(x)$. Нарисуйте график $f'(x)$ оценивая производную в ряде точек интервала: оценивайте производную через равные промежутки времени с одного конца интервале от другого, а также в «особых» точках, например, когда производная равна нулю. Убедитесь, что вы указали все места, где производной не существует.
Пример 2.4.7 Показан график функции $f(x)$. Нарисуйте график $f'(x)$
оценивая производную в ряде точек интервала:
оценивайте производную через равные промежутки времени с одного конца
интервале от другого, а также в «особых» точках, например, когда
производная равна нулю. Убедитесь, что вы указали все места, где
производной не существует.
92+ax-3$ имеет горизонтальную касательную в точке $x=4$.
(отвечать)
Убедитесь, что вы указали все места, где
производной не существует.
92+ax-3$ имеет горизонтальную касательную в точке $x=4$.
(отвечать)
| 1 | Найдите производную — d/dx | бревно натуральное х | |
| 2 | Оценка интеграла | интеграл натурального логарифма x относительно x | |
| 3 | 92)|||
| 21 | Оценка интеграла | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найдите производную — d/dx | грех(2x) | |
| 23 | Найдите производную — d/dx | (3x) по отношению к x||
| 41 | Оценка интеграла | интеграл от cos(2x) по x | |
| 42 | Найдите производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найдите производную — d/dx | х/2 | |
| 46 | Найдите производную — d/dx | -cos(x) | |
| 47 | Найдите производную — d/dx | грех(3x) | 92+1|
| 68 | Оценка интеграла | интеграл от sin(x) по x | |
| 69 | Найдите производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найдите производную — d/dx | лог х | |
| 86 | Найдите производную — d/dx | арктан(х) | |
| 87 | Найдите производную — d/dx | бревно натуральное 5х92 |
Является ли производная функции касательной? – Блог Магуш
Шон Олт, , 20 января 2017 г. , ОБНОВЛЕНО 14 июня 2022 г., в AP
, ОБНОВЛЕНО 14 июня 2022 г., в AP
В исчислении мы узнаем, что касательная для функции может быть найдена путем вычисления производной. Таким образом, существует тесная связь между производными и касательными. Однако это не одно и то же. Для начала производная f ‘( x ) — это функция, а касательная — это линия.
Вместо этого правильное утверждение таково: «Производная измеряет наклон касательных линий».
Подумайте об этом: часы — это не то же самое, что время . Но если вы хотите узнать время суток, вы можете посмотреть на часы, чтобы узнать. Часы измеряют время в любой момент дня .
Давайте подробнее рассмотрим касательные линии.
Что такое касательная?
Касательная линия для функции f ( x ) в заданной точке x = a – это линия (линейная функция), которая соответствует графику функции при x =
7 a
8 и имеет тот же наклон , что и кривая в этой точке.
Иногда мы можем сказать, что касательная « только что касается » кривой или « пересекает кривую только один раз », но иногда эти идеи могут ввести нас в заблуждение.
На приведенном ниже графике показаны касательные линии (выделены красным, фиолетовым и пурпурным) в трех разных точках кривой y = f ( x ) (черным цветом) .
Наклон и производные
Как же узнать, каким должен быть наклон касательной? Узнав о производных , вы можете использовать простую формулу
. м = f ‘( a ).
В этой формуле заданы функции f и x – значения a . Ваша задача — найти м , что представляет собой наклон касательной. Если у вас есть наклон, написать уравнение касательной линии довольно просто.
Нахождение касательной
Предположим, вас попросили найти касательную для функции f ( x ) в заданной точке x = a . Вот пошаговый подход:
Вот пошаговый подход:
- Найдите производную, f ‘( x ).
- Подставьте x = к , чтобы получить наклон. То есть вычислите м = f ‘( a ).
- Если еще не задано в задаче, найти и -координату точки. Как всегда, вы подставляете значение x в функцию, чтобы получить значение y . Пусть b = f ( a ).
- Используйте точка-наклон формы и решить для y , чтобы найти уравнение касательной линии. Другими словами, подставьте ваши значения m , a и b в уравнение,
у = м ( х – а ) + б .
Наклон производных мер
Давайте еще раз посмотрим на первый шаг: « Найдите производную ». Помните, что производная — это функция (входной переменной x ). Подставляя различные входные значения, x = a , выходные значения f ‘( x ) дают вам наклоны касательных линий в каждой точке x = a .
Вот что мы имеем в виду, когда говорим, что «производная измеряет наклон касательных линий».
Если я хочу узнать наклон f при x = 1, то я вычисляю f ‘(1). И если я хочу узнать наклон при x = -352/13, то я вычисляю f ‘(-352/13). Просто как тот!
Пример: Многочлен
Теперь давайте рассмотрим пример функции: f ( x ) = x 3 + 3 x 2 + 1. Мы найдем касательные линии в нескольких разных точках.
Прежде всего, найдите производную: f ‘( x ) = 3 x 2 + 6 х . (чтобы попрактиковаться в поиске деривативов, ознакомьтесь с этой статьей Magoosh о деривативах).
Значение функции и значение производной в нескольких точках показаны в таблице ниже:
x -3 -2 -1 0 1 ф ( x ) = x 3 + 3 x 2 + 1 1 5 3 1 5 3 1 5 5 5 3 1 5 3 1 5 3 1 5 f ‘( x ) = 3 x 2 + 6 x 9 0 -3 0 9
Для перечисленных точек мы легко можем найти уравнение касательной. Обратите внимание, что на экзамене AP по математическому анализу ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам как форму точка-наклон, так и упрощенную, или наклон-пересечение , форма касательной.
Обратите внимание, что на экзамене AP по математическому анализу ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам как форму точка-наклон, так и упрощенную, или наклон-пересечение , форма касательной.
x Касательная, форма точка-наклон Касательная, упрощенная -3 у = 9( х + 3) + 1 у = 9 х 4 + 09 -2 у = 0( х + 2) + 5 у = 5 -1 y = -3( x + 1) + 3 y = -3 x 0 y = 0( x – 0) + 1 y = 1 1 y = 9( x – 1) + 5 y = 9 x – 4
Теперь давайте посмотрим на график y = f ( x ) вместе с касательными, которые мы только что нашли.
Резюме
Итак, теперь вы знаете. Производная – это не то же самое, что касательная. Вместо этого производная является инструментом для измерения наклона касательной в любой конкретной точке, точно так же, как часы измеряют время в течение дня. Имея это в виду, у вас не возникнет проблем с решением задач касательной линии на экзамене AP Calculus!
Чтобы узнать больше о наклоне, касательных и производных, ознакомьтесь со следующими статьями Magoosh: Is the Derivative of a Function the Slope? и Как найти наклон линии, касательной к кривой.
Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!
Автор
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
Расчет AP
← Предыдущий
Следующий →
Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно!
Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели инструментов Magoosh. Спасибо!
Спасибо!
Производная
Производная функции — это скорость изменения выходного значения функции относительно ее входного значения. При y = f(x) производная f(x), обозначаемая f'(x) (или df(x)/dx), определяется следующим пределом:
Определение производной выводится по формуле наклона прямой. Напомним, что наклон линии — это скорость изменения линии, которая вычисляется как отношение изменения у к изменению х. Геометрически производная представляет собой наклон линии, касательной к кривой в интересующей точке. Иногда его называют мгновенной скоростью изменения. Обычно мы вычисляем наклон линии, используя две точки на линии. Для кривой это невозможно, поскольку наклон кривой меняется от точки к точке. Рассмотрим рисунок ниже.
На рисунке показана кривая (синяя) с двумя точками: (x, f(x)) и (x + h, f(x + h)). Серая секущая линия представляет собой наклон между этими двумя точками и рассчитывается как:
Обратите внимание, что это начинает выглядеть как определение производной. Однако эта формула дает нам наклон между двумя точками, который является средним значением наклона кривой. Производная в точке x представлена красной линией на рисунке. Чтобы вычислить наклон этой линии, нам нужно изменить формулу наклона, чтобы ее можно было использовать для одной точки. Мы делаем это, вычисляя предел формулы наклона по мере того, как изменение x (Δx), обозначаемое h, приближается к 0. Делая это, мы находим наклон между двумя точками, разделенными настолько малой разницей, что она обеспечивает приближение для наклон в одной точке, что приводит нас к приведенному выше определению производной.
Однако эта формула дает нам наклон между двумя точками, который является средним значением наклона кривой. Производная в точке x представлена красной линией на рисунке. Чтобы вычислить наклон этой линии, нам нужно изменить формулу наклона, чтобы ее можно было использовать для одной точки. Мы делаем это, вычисляя предел формулы наклона по мере того, как изменение x (Δx), обозначаемое h, приближается к 0. Делая это, мы находим наклон между двумя точками, разделенными настолько малой разницей, что она обеспечивает приближение для наклон в одной точке, что приводит нас к приведенному выше определению производной.
Примеры
Используйте предельное определение производной для дифференцирования (нахождения производной) следующих функций.
1. f(x) = x 2 :
Таким образом, производная x 2 равна 2x. Чтобы найти производную в данной точке, мы просто подставляем значение x. Например, если мы хотим узнать производную при x = 1, мы должны подставить 1 в производную, чтобы найти, что:
f'(x) = f'(1) = 2(1) = 2
2. f(x) = sin(x):
f(x) = sin(x):
Для решения этой задачи воспользуемся следующими тригонометрическими тождествами и пределами:
(1) (2) (3)
Точки, в которых применяются вышеуказанные тождества и ограничения, будут обозначаться с использованием соответствующих идентификаторов: (1), (2) и (3).
(1) (2) (3)
Таким образом, производная от sin(x) равна cos(x), или:
Таблица правил производных
Обратите внимание на приведенные выше примеры, что вычисление производных с использованием определения предела может быть довольно громоздким. К счастью, правила вычисления производных для различных типов функций четко определены, поэтому простое знание этих правил (или возможность сослаться на них) позволяет нам различать большинство функций.
Функция: f(x) Производная: f'(x)
(силовое правило)
для некоторой константы a > 0 и a ≠ 1
для некоторой константы а > 0
для любой константы c и функции f
для любых функций f и g
правило продукта
правило частных
обозначает композицию, а не умножение
Цепная линейка
Неопределенные производные
Не всегда возможно найти производную функции. В некоторых случаях производная функции может не существовать в определенных точках ее области определения или даже во всей ее области определения. Как правило, производная функции не существует, если наклон ее графика не определен четко. Ниже приведены некоторые из этих случаев.
В некоторых случаях производная функции может не существовать в определенных точках ее области определения или даже во всей ее области определения. Как правило, производная функции не существует, если наклон ее графика не определен четко. Ниже приведены некоторые из этих случаев.
Разрывные функции
Чтобы функция имела производную в данной точке, она должна быть непрерывной в этой точке. Функция, которая имеет разрыв в точке, не имеет наклона в этой точке и, следовательно, не имеет производной. Вкратце, функция f(x) непрерывна в точке a, если выполняются следующие условия:
- f(a) определена.
- .
- .
На рисунке ниже показан один тип разрыва, называемый разрывом скачка, в точке x = 3.
Поскольку в этой точке функция разрывна, она не имеет производной при x = 3.
Изгибы/углы
не имеют производных в этих точках. Это связано с тем, что наклон слева и справа от этих точек неодинаков.
Куспид Угол
Обе функции имеют либо острие, либо угол при x = 2, где наклон функции различается в зависимости от того, подходим ли мы к точке слева или справа. Таким образом, производная не определена при x = 2.
Вертикальные касательные или бесконечный наклон
Функция, имеющая вертикальную касательную, имеет бесконечный наклон и, следовательно, не определена.
Функция имеет вертикальную касательную при x = 0. По обе стороны от вертикальной касательной наклон функции стремится к бесконечности. 92\\
\pdiff{f}{x}(3,2) & = 12 &
\pdiff{f}{y}(3,2) & = 9
\конец{выравнивание*}
Следовательно, градиент равен
\начать{выравнивать*}
\nabla f (3,2) = 12 \vc{i} + 9 \vc{j} = (12,9).
\конец{выравнивание*}
(b) Пусть $\vc{u}=u_1\vc{i} + u_2 \vc{j}$ — единичный вектор.
производная по направлению в точке (3,2) в направлении $\vc{u}$ равна
\начать{выравнивать}
D_{\vc{u}}f(3,2) &= \nabla f(3,2) \cdot \vc{u}\notag\\
&= (12 \vc{i} + 9 \vc{j}) \cdot (u_1\vc{i} + u_2 \vc{j})\notag\\
&= 12 и_1 + 9 и_2. \label{Дублировать}
\end{выравнивание}
92}} = \frac{(1,2)}{\sqrt{5}} =
(1/\sqrt{5},2/\sqrt{5}).
\конец{выравнивание*}
Подставив это выражение для $\vc{u} = (u_1, u_2)$ в
уравнение \eqref{Dub}
для производной по направлению, и мы находим, что
производная по направлению в точке $(3,2)$ в направлении
$(1,2)$ это
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{12}{\sqrt{5}} + \frac{18}{\sqrt{5}}
= \frac{30}{\sqrt{5}}.
\конец{выравнивание*}
\label{Дублировать}
\end{выравнивание}
92}} = \frac{(1,2)}{\sqrt{5}} =
(1/\sqrt{5},2/\sqrt{5}).
\конец{выравнивание*}
Подставив это выражение для $\vc{u} = (u_1, u_2)$ в
уравнение \eqref{Dub}
для производной по направлению, и мы находим, что
производная по направлению в точке $(3,2)$ в направлении
$(1,2)$ это
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{12}{\sqrt{5}} + \frac{18}{\sqrt{5}}
= \frac{30}{\sqrt{5}}.
\конец{выравнивание*}
Пример 2
Для $f$ Примера 1,
найти производную по направлению от $f$ в точке
точку (3,2) в направлении $(2,1)$.
Решение : Единичный вектор в направлении $(2,1)$ равен
\начать{выравнивать*}
\vc{u} = \frac{(2,1)}{\sqrt{5}} = (2/\sqrt{5},1/\sqrt{5}).
\конец{выравнивание*}
Поскольку мы все еще находимся в точке (3,2),
уравнение \eqref{Dub}
все еще
действительный. Мы подключаем наш новый $\vc{u}$, чтобы получить
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{24}{\sqrt{5}} + \frac{9}{\sqrt{5}}
= \frac{33}{\sqrt{5}}
\конец{выравнивание*}
Пример 3
Для $f$ Примера 1 в точке (3,2), (a), в каком направлении
производная по направлению максимальна, (b) какова направленность
производная в этом направлении? 92} = 15$. Следовательно
производная по направлению в точке (3,2) в направлении (12,9)
равно 15.
Следовательно
производная по направлению в точке (3,2) в направлении (12,9)
равно 15.
Мы могли бы перепроверить, вычислив результат, используя
уравнение \eqref{Dub}
и единичный вектор $\vc{u} = (4/5,3/5)$. Затем мы находим
что
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{48}{5} + \frac{27}{5}
= \фрак{75}{5}=15,
\конец{выравнивание*}
что согласуется с нашим результатом.
Пример 4
Для $f$ Примера 1 в точке (3,2), (a) каково направление
производная по направлению (-3,4) (которое перпендикулярно $\nabla
f(3,2)$), и (b) какова производная по направлению в направлении
(-4,-3) (что противоположно направлению $\nabla
f(3,2)$)? 92-5}$. Вычислить градиент $f$ в точке $(1,3,-2)$ и вычислить производную по направлению $D_{\vc{u}}f$ в точке $(1,3,-2)$ в направление вектора $\vc{v}=(3,-1,4)$.
Решение : Вектор градиента в трех измерениях подобен двумерному случаю. Чтобы вычислить градиент $f$ в точке $(1,3,-2)$, нам достаточно вычислить три частные производные от $f$.
 Вот пошаговый подход:
Вот пошаговый подход:у = м ( х – а ) + б .

 Обратите внимание, что на экзамене AP по математическому анализу ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам как форму точка-наклон, так и упрощенную, или наклон-пересечение , форма касательной.
Обратите внимание, что на экзамене AP по математическому анализу ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам как форму точка-наклон, так и упрощенную, или наклон-пересечение , форма касательной.
 Спасибо!
Спасибо! Однако эта формула дает нам наклон между двумя точками, который является средним значением наклона кривой. Производная в точке x представлена красной линией на рисунке. Чтобы вычислить наклон этой линии, нам нужно изменить формулу наклона, чтобы ее можно было использовать для одной точки. Мы делаем это, вычисляя предел формулы наклона по мере того, как изменение x (Δx), обозначаемое h, приближается к 0. Делая это, мы находим наклон между двумя точками, разделенными настолько малой разницей, что она обеспечивает приближение для наклон в одной точке, что приводит нас к приведенному выше определению производной.
Однако эта формула дает нам наклон между двумя точками, который является средним значением наклона кривой. Производная в точке x представлена красной линией на рисунке. Чтобы вычислить наклон этой линии, нам нужно изменить формулу наклона, чтобы ее можно было использовать для одной точки. Мы делаем это, вычисляя предел формулы наклона по мере того, как изменение x (Δx), обозначаемое h, приближается к 0. Делая это, мы находим наклон между двумя точками, разделенными настолько малой разницей, что она обеспечивает приближение для наклон в одной точке, что приводит нас к приведенному выше определению производной. f(x) = sin(x):
f(x) = sin(x):
(силовое правило)
для некоторой константы a > 0 и a ≠ 1
для некоторой константы а > 0
для любой константы c и функции f
для любых функций f и g
правило продукта
правило частных
обозначает композицию, а не умножение
Цепная линейка
 В некоторых случаях производная функции может не существовать в определенных точках ее области определения или даже во всей ее области определения. Как правило, производная функции не существует, если наклон ее графика не определен четко. Ниже приведены некоторые из этих случаев.
В некоторых случаях производная функции может не существовать в определенных точках ее области определения или даже во всей ее области определения. Как правило, производная функции не существует, если наклон ее графика не определен четко. Ниже приведены некоторые из этих случаев.
 \label{Дублировать}
\end{выравнивание}
92}} = \frac{(1,2)}{\sqrt{5}} =
(1/\sqrt{5},2/\sqrt{5}).
\конец{выравнивание*}
Подставив это выражение для $\vc{u} = (u_1, u_2)$ в
уравнение \eqref{Dub}
для производной по направлению, и мы находим, что
производная по направлению в точке $(3,2)$ в направлении
$(1,2)$ это
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{12}{\sqrt{5}} + \frac{18}{\sqrt{5}}
= \frac{30}{\sqrt{5}}.
\конец{выравнивание*}
\label{Дублировать}
\end{выравнивание}
92}} = \frac{(1,2)}{\sqrt{5}} =
(1/\sqrt{5},2/\sqrt{5}).
\конец{выравнивание*}
Подставив это выражение для $\vc{u} = (u_1, u_2)$ в
уравнение \eqref{Dub}
для производной по направлению, и мы находим, что
производная по направлению в точке $(3,2)$ в направлении
$(1,2)$ это
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{12}{\sqrt{5}} + \frac{18}{\sqrt{5}}
= \frac{30}{\sqrt{5}}.
\конец{выравнивание*} Следовательно
производная по направлению в точке (3,2) в направлении (12,9)
равно 15.
Следовательно
производная по направлению в точке (3,2) в направлении (12,9)
равно 15.




 е. f’(x) ≥ 0.
е. f’(x) ≥ 0. В ответе укажите сумму целых чисел, входящих в эти промежутки.
В ответе укажите сумму целых чисел, входящих в эти промежутки.

 3), которое говорит о
том, что функция f хорошо приближается некоторой линейной
функцией в окрестности точки x0.
3), которое говорит о
том, что функция f хорошо приближается некоторой линейной
функцией в окрестности точки x0.