какой буквой обозначается, как найти, формула с примерами задач
Что такое путь в физике
ОпределениеПутем называется длина траектории, пройденной телом за определенный промежуток времени. Путь не является векторной величиной, хоть тело и движется в определенном направлении. Это величина скалярная и равняется модулю разницы координат тела в момент окончания и начала движения.
ПримечаниеОтличие пути от перемещения состоит именно в том, что перемещение — величина векторная. Оно имеет значение, которое равно длине вектора.
Источник: fizmat.by
В решении задач на нахождении пути используются специальные символы. Так, при одномерном перемещении часто используется обозначение Δx (дельта х). Знак Δ обозначает разницу конечной и начальной координат тела.
Кроме этого обозначения можно встретить буквы латинского алфавита: S, l, h. В отличие от S, значение которой всегда «расстояние» либо «длина пути», l и h могут обозначать длину и высоту.
В задачах часто сразу оговаривается, что тело движется в трехмерном пространстве. Тогда в обозначении его координат участвуют три координатные прямые: x, y, z. Соответственно, изменения его координат будут обозначаться Δx, Δy, Δz.
Перемещаясь в пространстве, тело (материальная точка) проходит определенные точки пространства. Эти точки можно соединить линией, получив траекторию. В жизни она бывает как видимой, ток и не заметной простым глазом. Например, за лыжником сзади тянется длинный след (траектория) от лыж. В то же время пролетевшая птица не оставляет заметной человеческому глазу траектории.
ПримечаниеТраекторию часто нельзя охарактеризовать однозначно. Ее форма определяется используемой системой отсчета. Например, движущееся колесо относительно планеты совершает винтовые движения, а относительно точки на земной поверхности — прямая линия.
Зная вид траектории, а также координаты начальной и конечной точки положения тела, легко определить пройденный путь. Однако всегда необходимо понимать, относительно чего он рассматривается. Если пассажир, находящийся в конце автобуса, проходя к переднему выходу, совершает путь, равный длине этого автобуса, то относительно системы отсчета — планета Земля — его путь будет состоять из двух расстояний: длины автобуса и длины траектории движения самого автобуса (относительно планеты).
Однако всегда необходимо понимать, относительно чего он рассматривается. Если пассажир, находящийся в конце автобуса, проходя к переднему выходу, совершает путь, равный длине этого автобуса, то относительно системы отсчета — планета Земля — его путь будет состоять из двух расстояний: длины автобуса и длины траектории движения самого автобуса (относительно планеты).
Формула нахождения пути
Чтобы выразить путь в принятых единицах измерения применяют физические формулы, которые также могут содержать различные показатели:
- Для кинематики характерной формулой при равномерном прямолинейном движении является выражение пути через скорость движения и время, за которое оно совершается: S=Vt, где V — скорость, t — время.
- Если совершается равноускоренное перемещение, то используются формулы:
Источник: formulki.ru
Обозначения V0 и V применяются для начальной и конечной скорости соответственно. При этом, если движение равноускоренное, то разница скоростей со знаком плюс, если равнозамедленное — то со знаком минус.
Графики зависимости пути от времени для разных типов движения
Кроме того, что можно вычислить значение пути, пройденного телом, с помощью специальных формул, его можно увидеть на графике. Физические задачи опираются на несколько графиков, характеристики которых продиктованы особенностями конкретного движения.
ПримерГрафик, который отражает равномерное движение материальной точки (тела):
Источник: repetitor.org.ua
Формулой, определяющей путь, отраженный на этом графике, является S=V*t.
Бывает, что подобные разновидности графиков отличаются друг от друга из-за того, что тело проходит разные отрезки пути с различной скоростью.
ПримерНапример, если на одном участке в течение часа оно преодолело 20 км, далее в течение двух часов — не двигалось, а затем четыре часа преодолевало еще 20 км, график не будет выглядеть в виде прямой линии. Он будет иметь следующий вид:
Источник: repetitor.org.ua
На одном рисунке может быть отражено два и больше графиков движения тел:
Источник: repetitor. org.ua
org.ua
Чем быстрее движется тело, тем больший угол образуют прямые оси времени и графика движения.
Схематические характеристики движения могут выражаться и в графиках, отражающих скорость. В таком случае в прямоугольной системе координат по горизонтали откладывают время, а по вертикали — модуль скорости.
Источник: repetitor.org.ua
Анализ графика показывает, что, согласно выбранным единицам измерения, первое тело двигалось со скоростью 25 м/с, второе — 10 м/с.
Примеры задач
3 Задача 1
ЗадачаОт выбранной точки отсчета отъехал человек на велосипеде. Его начальная скорость составляла 20 км/ч. Спустя 4 часа из этой же точки выехала машина. Ее скорость была 60 км/ч. Произвести расчет и изобразить графически, через сколько часов машина догонит велосипедиста.
Графики движений велосипедиста и машины выглядят так:
Источник: repetitor.org.ua
Из рисунка следует, что время, когда состоится встреча велосипедиста и машины-6 часов с момента выезда велосипеда.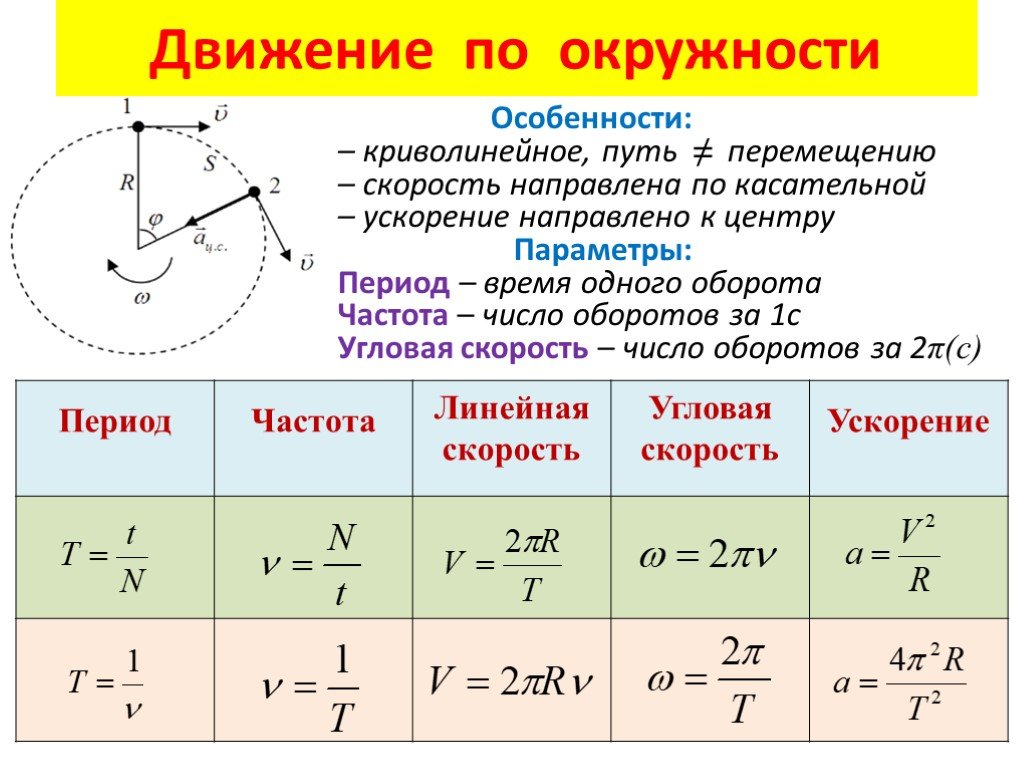 Это произойдет по истечении 2х часов с момента выезда машины.
Это произойдет по истечении 2х часов с момента выезда машины.
Из двух разных поселков выехали навстречу один другому мотоциклисты: первый со скоростью 10 км/ч, второй — 12 км/ч. Их встреча произошла через 2 часа. Необходимо высчитать расстояние между поселками.
Краткий путь решения следующий:
- Определяем скорость сближения мотоциклистов: 10+12=22 км/ч.
- Для определения расстояния между поселками производим умножение скорости сближения и времени: 22*2=44 (км).
Схематически решение задачи выглядит так:
Источник: spacemath.xyz
ЗадачаРасстояние между городами 60 км. Из них в одно время выехали друг навстречу другу велосипедисты: первый со скоростью 14 км/ч, второй — 16 км/ч. Сколько нужно часов, чтобы они встретились?
Решение
Суммируем скорости их движения, находя скорость сближения:
14+16=30 км/ч
Следовательно, каждый час расстояние между велосипедистами сокращается на 30 км.
Зная, что расстояние между городами 60 км, легко высчитать время встречи: 60:30=2 (ч).
Схема задачи следующая:
Источник: spacemath.xyz
ЗадачаТри машины с промежутком в один час выехали из города A в город B. Первая имела скорость 50 км/ч, вторая — на 10 км/ч больше. Какова скорость третьей машины, если указывается, что она смогла поравняться с первыми двумя.
Решение
Введем дополнительные обозначения:
- Точка A — город, из которого машины отправились — точка отправления.
- Точка B — город, в который машины направлялись — точка назначения.
- Точка C — точка, в которой произошла встреча всех трех машин.
Если первая машина доехала до точки C за время t (ч), то вторая — за t-1 (ч). Для третьей машины справедливо выражение времени t-2 (ч).
Определяем скорость второй машины: 50+10=60 (км/ч).
Поскольку пройденные всеми тремя машинами расстояния одинаковые, приравняем выражения:
AC=50t=60(t-1)=v(t-2)
В равенстве v — скорость третьей машины.
Произведя вычисления, находим, что 50t=60(t-1), откуда t=6.
Находим, что AC=300 (км), после чего получаем, что 60(t-1)= v(t-2)
Из данного равенства находим, что v=75 км/ч.
Среднее значение свободного пробега, столкновения молекул
Среднее значение свободного пробега, столкновения молекулДлина свободного пробега или среднее расстояние между столкновениями для молекулы газа может быть оценено с помощью кинетической теории. Подход Серуэя является хорошей визуализацией: если молекулы имеют диаметр d, то эффективное сечение столкновения можно смоделировать с помощью , используя круг диаметром 2d для представления эффективной площади столкновения молекул, рассматривая «целевые» молекулы как точечные массы. За время t круг охватит показанный объем, и количество столкновений можно оценить по количеству молекул газа, находившихся в этом объеме. Средняя длина свободного пробега может быть принята как длина пути, деленная на количество столкновений. Проблема с этим выражением заключается в том, что используется средняя молекулярная скорость, но молекулы-мишени также движутся. Частота столкновений зависит от средней относительной скорости беспорядочно движущихся молекул.
| Индекс Концепции газового права Концепции кинетической теории Ссылка: Rohlf | |||
| Назад |
Интуитивное построение выражения для длины свободного пробега страдает существенным недостатком — оно предполагает, что «целевые» молекулы находятся в состоянии покоя, тогда как на самом деле они имеют высокую среднюю скорость.
, который пересматривает выражение для эффективного объема, выметаемого за время t В результате длина свободного пробега равна Число молекул в единице объема может быть определено из числа Авогадро и закона идеального газа, что приводит к Следует отметить, что это выражение для длины свободного пробега молекул рассматривает их как твердые сферы, тогда как настоящие молекулы таковыми не являются. Для благородных газов столкновения, вероятно, близки к абсолютно упругим, поэтому приближение твердых сфер, вероятно, является хорошим. Но реальные молекулы могут иметь дипольный момент и иметь значительное электрическое взаимодействие, когда они приближаются друг к другу.
Артикул: Вики: средний свободный путь Wiki: вязкость Вязкость газа Расчет | Индекс Концепции кинетической теории | |||||
| 11 Вернуться 9м. Значения давления, температуры и молекулярного диаметра можно изменить выше, чтобы пересчитать длину свободного пробега. Номинальный молекулярный диаметр 0,3 нм = 3 x 10 90 146 -10 90 147 м даст вам разумное приближение.
Давление, необходимое для заданной длины свободного пробега, можно рассчитать, изменив указанное выше значение длины свободного пробега λ. Из длины свободного пробега и средней скорости можно рассчитать среднее время между столкновениями и частоту столкновений.
| Индекс Концепции кинетической теории | ||||
| Назад |
Вас может удивить длина длины свободного пробега по сравнению со средним расстоянием между молекулами в идеальном газе.
| Индекс Концепции газового закона Концепции кинетической теории | ||||||||||||
В этом случае необходимо знать конечную скорость v_f объекта. Затем вы можете решить уравнение для расстояния d. Как найти время для объекта в свободном падении Количество времени, в течение которого объект находится в свободном падении, зависит от его скорости и расстояния, на которое он падает. Если известны начальная и конечная скорости объекта, то проще всего вычислить время с помощью кинематического уравнения:
Это уравнение можно решить для времени. Затем вам нужно будет только подставить значения скоростей и ускорений под действием силы тяжести. Другой способ найти время, если вы не знаете конечную скорость объекта, состоит в использовании уравнения:
Обратите внимание, что в этом уравнении есть два члена, которые включают время t. Если начальная скорость не равна нулю, это может затруднить решение этого уравнения для времени. Как найти конечную скорость объекта в свободном паденииКонечная скорость объекта в свободном падении зависит от количества времени, в течение которого он падает. Из-за ускорения свободного падения скорость будет увеличиваться каждую секунду на 92 + 2ad |
Это уравнение требует, чтобы вместо этого вы знали расстояние, на которое падает объект. Если вы используете это уравнение для нахождения конечной скорости, помните, что в этом уравнении конечная скорость возводится в квадрат. Это означает, что вам нужно будет извлечь квадратный корень в качестве последнего шага для определения конечной скорости.
Примеры свободного паденияВ следующем разделе мы применим методы, которые вы только что изучили, для решения некоторых задач, связанных со свободным падением. 92
д=122,625\текст{м}
Следовательно, высота здания составляет около 123\text{ м}.
Пример 2. Как найти конечную скорость объекта с начальной скоростью
В другом примере объект в свободном падении имеет начальную скорость вниз 2\text{ м/с} и падает с расстояния 45 \текст{ м}. Какова конечная скорость объекта?
В этом сценарии нам дана начальная скорость объекта v_i и расстояние d. Мы также знаем, что ускорение равно 92}
v_f=29,78\text{ м/с}
Следовательно, конечная скорость объекта составляет около 30\text{ м/с}.
Графики движения объектов в свободном паденииПомимо использования физических уравнений, мы также можем представить движение свободного падения с помощью графиков движения. Графики положение-время, графики скорость-время и графики ускорения-время могут многое рассказать нам о движении объекта во времени. Хотите более подробный обзор графиков движения? Посмотрите этот пост в блоге!
График положение-время для объекта в свободном падении
С точки зрения положения, многие объекты в свободном падении начинаются в высоком положении или на высоте над землей и движутся вниз.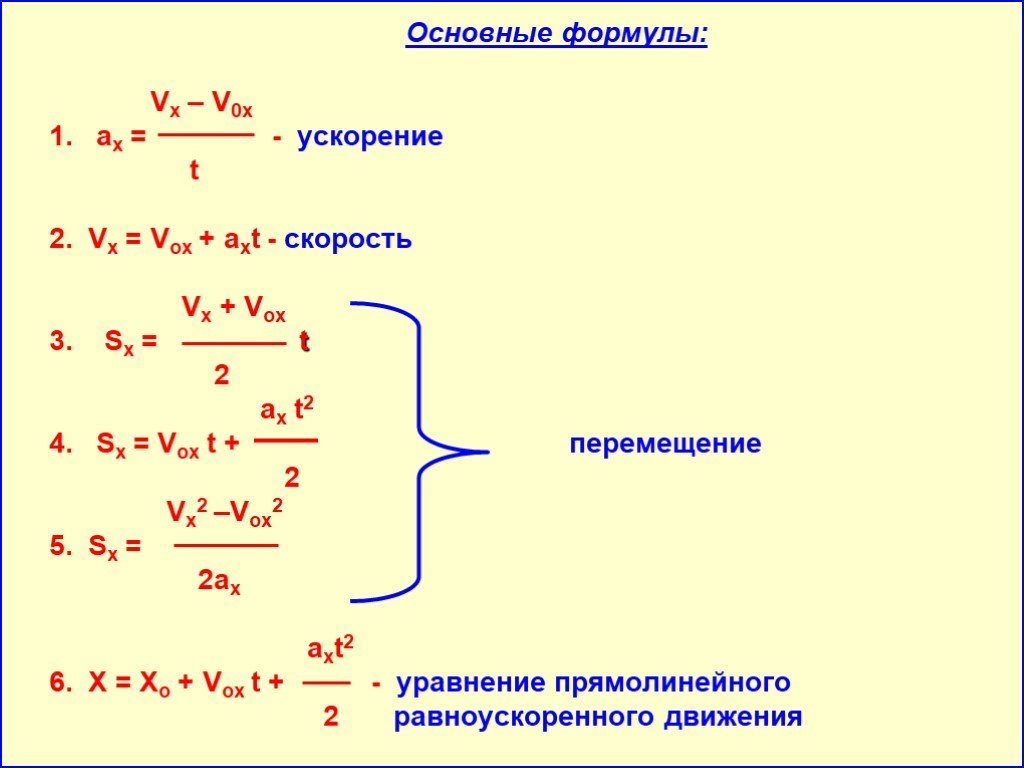 Объекты в свободном падении ускоряются под действием силы тяжести. Следовательно, график зависимости положения от времени при свободном падении должен быть кривым. Это означает, что объекты в свободном падении начинают с низкой скорости и постепенно ускоряются, что представлено крутой нисходящей кривой на графике.
Объекты в свободном падении ускоряются под действием силы тяжести. Следовательно, график зависимости положения от времени при свободном падении должен быть кривым. Это означает, что объекты в свободном падении начинают с низкой скорости и постепенно ускоряются, что представлено крутой нисходящей кривой на графике.
График скорости и времени для объекта в свободном падении 92. Как показано на графике ниже, график зависимости ускорения от времени представляет собой постоянную отрицательную линию.
Движение снарядаСнаряд — это объект, запускаемый или подбрасываемый в воздух, на который затем действует только сила тяжести. Движение снаряда во многом похоже на движение свободного падения, однако снаряды могут также перемещаться по горизонтали в дополнение к падению вертикально вниз.
Примеры движения снарядаТочная траектория или путь снаряда зависит от того, как он будет запущен. Однако все снаряды следуют по кривой траектории, как на изображении ниже:
Если вы играете или смотрите спортивные состязания, вы, вероятно, уже наблюдали движение снаряда. Движение снаряда описывает дугу баскетбольного мяча при штрафном броске, летящего мяча в бейсболе или волейбольного мяча, переброшенного через сетку.
Движение снаряда описывает дугу баскетбольного мяча при штрафном броске, летящего мяча в бейсболе или волейбольного мяча, переброшенного через сетку.
Для анализа движения снаряда мы должны разделить движение на горизонтальную и вертикальную составляющие. Горизонтальная составляющая скорости снаряда не зависит от вертикальной составляющей скорости. Поскольку гравитация действует вертикально, на снаряды не действуют горизонтальные силы. Это означает, что горизонтальная составляющая скорости снаряда остается постоянной на протяжении всего полета. 9{\circ} угол. Чему равна горизонтальная составляющая скорости снаряда?
Нам нужно будет использовать триггерные тождества для определения компонентов скорости. Мы можем визуализировать компоненты в виде треугольника, где гипотенуза — начальная скорость, а стороны — горизонтальная, v_{ix}, и вертикальная, v_{iy}, составляющие скорости.
Косинус определяется как прилежащая сторона треугольника, деленная на гипотенузу. Поскольку горизонтальная составляющая примыкает к углу, мы можем использовать косинус, чтобы найти горизонтальную составляющую скорости: 9{\ круг})
Поскольку горизонтальная составляющая примыкает к углу, мы можем использовать косинус, чтобы найти горизонтальную составляющую скорости: 9{\ круг})
v_{ix}=4\text{ м/с}
Следовательно, горизонтальная составляющая начальной скорости равна 4\text{ м/с}.
Нужно проверить свои триггерные идентификаторы? Попробуйте этот ресурс от Академии Хана.
Вертикальная составляющая скоростиНа вертикальную составляющую скорости снаряда будет влиять гравитация, которая действует вертикально на объект, заставляя его ускоряться вниз. Поэтому вертикальная составляющая скорости будет изменяться на протяжении всего полета снаряда. Мы можем вычислить вертикальную составляющую скорости в определенный момент времени методом, аналогичным вычислению горизонтальной составляющей. 9{\ круг})
v_{iy}=6.9\text{ м/с}
Решение вопросов о движении снарядовДавайте применим то, что мы узнали, к некоторым примерам движения снарядов!
Пример 1.
 Определение дальности полета снаряда
Определение дальности полета снарядаВ этом примере снаряд вылетает горизонтально со скоростью 5\text{ м/с} со скалы высотой 60\text{ м}. На каком расстоянии от основания скалы приземлится снаряд?
В этом сценарии нам задана начальная горизонтальная скорость v_{ix}=5\text{ м/с} и вертикальное изменение положения d_y=-60\text{ м}. Поскольку снаряд запускается горизонтально, начальная вертикальная скорость v_{iy} равна нулю. Мы также всегда знаем, что при движении снаряда вертикальное ускорение равно a_y=-9.2}}
т=3,5\текст{с}
Теперь мы можем использовать это время для расчета горизонтального смещения снаряда:
d_x=v_{ix} t
d_x=(5\текст{м/с})(3,5\текст{с})=17,5\текст{м}
Следовательно, снаряд приземлится примерно в 17.5\text{ м} от основания скалы.
Пример 2. Определение максимальной высоты снаряда
В качестве другого примера: снаряд стартует с земли с начальной скоростью 25\text{ м/с} под углом 50^{\circ}. Какова максимальная высота снаряда? 92)}
Какова максимальная высота снаряда? 92)}
d_y=18.7\text{м}
Следовательно, снаряд достигнет максимальной высоты около 18,7\text{ м} .
Для получения дополнительных примеров и объяснения решения этих типов задач движения снаряда посмотрите это видео на YouTube от профессора Дэйва.
Заключение Понимание свободного падения и движения снаряда позволит вам решить некоторые из самых сложных задач, с которыми вы столкнетесь в начальной физике. На все снаряды действует только сила тяжести, а вертикальная и горизонтальная составляющие движения не зависят друг от друга. Это позволяет нам применить наши кинематические уравнения для определения времени полета, скорости и смещения снаряда в каждом направлении.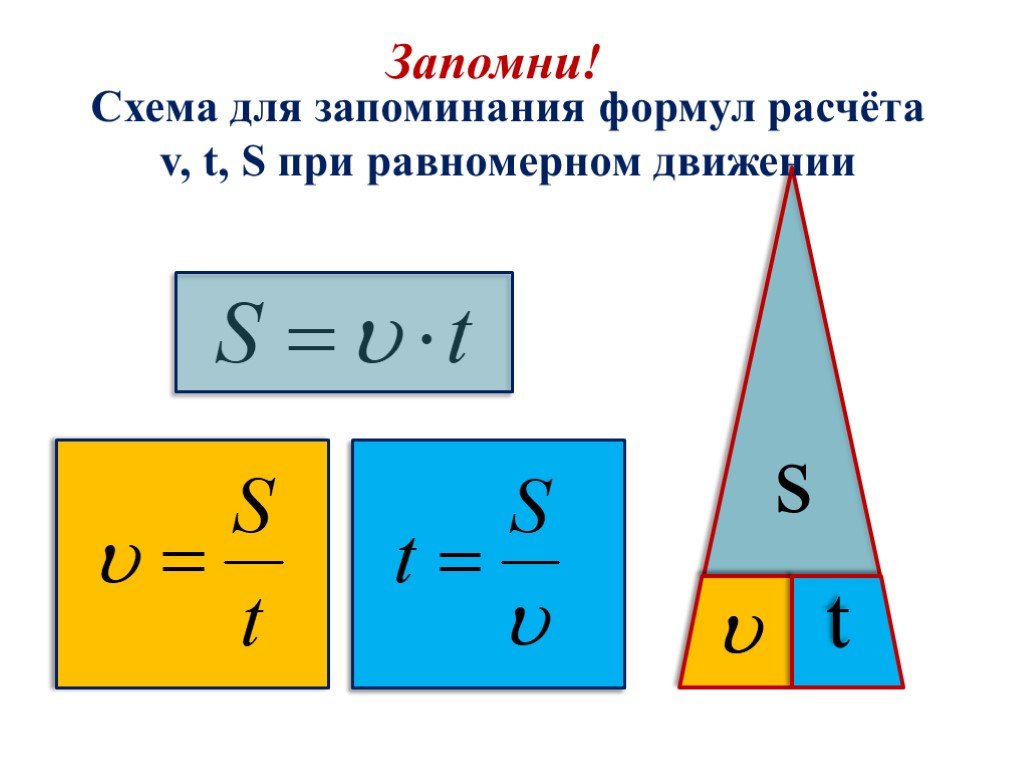


 Что необходимо, так это средняя относительная скорость, и вычисление этой скорости по распределению молекулярных скоростей дает результат
Что необходимо, так это средняя относительная скорость, и вычисление этой скорости по распределению молекулярных скоростей дает результат
 Расчет не допускает каких-либо других изменений (их значения будут заменены без изменений при расчете).
Расчет не допускает каких-либо других изменений (их значения будут заменены без изменений при расчете). Для расчета других расстояний был принят атомный размер 0,3 нм.
Для расчета других расстояний был принят атомный размер 0,3 нм.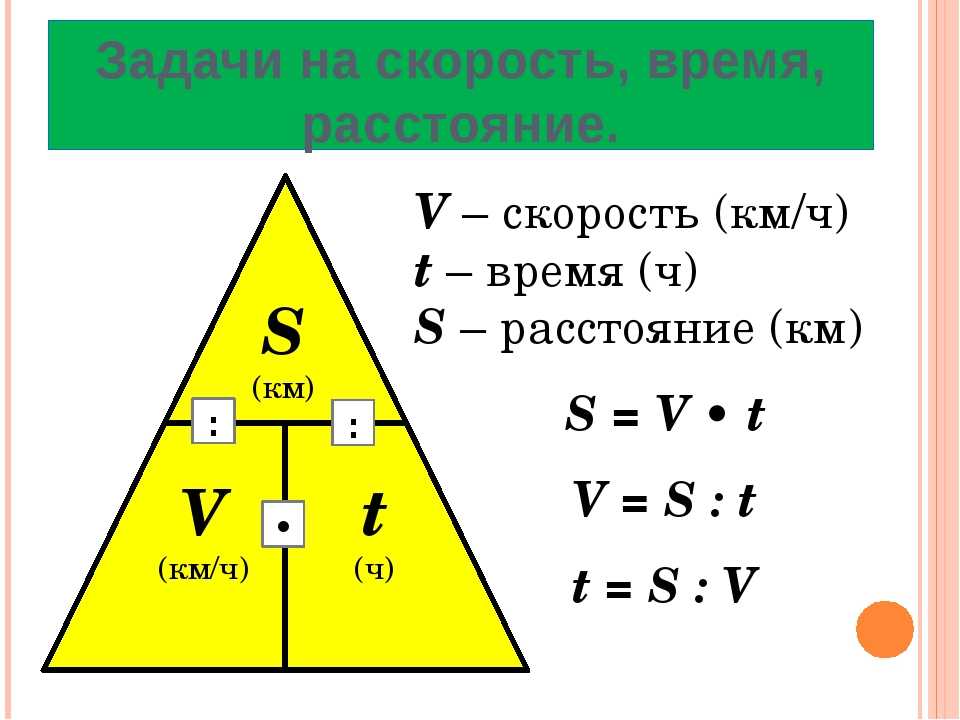
 92.
92. Как и в случае с расстоянием, есть два уравнения, которые вы можете использовать, чтобы найти время, в зависимости от того, что вы знаете.
Как и в случае с расстоянием, есть два уравнения, которые вы можете использовать, чтобы найти время, в зависимости от того, что вы знаете. Если вы используете это уравнение, вам может понадобиться использовать квадратную формулу для определения времени.
Если вы используете это уравнение, вам может понадобиться использовать квадратную формулу для определения времени.