Как найти путь зная ускорение время и скорость: Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Как найти Равнозамедленное движение

Статьи › Чем отличается › Чем отличается равномерное и неравномерное движение

В физике, чтобы определить тип движения (равноускоренное или равнозамедленное), достаточно найти ускорение тела. Если ускорение тела получилось меньше нуля, значит оно направлено против движения тела, следовательно, движение является равнозамедленным, то есть тело снижает скорость.

1. Как найти путь в Равнозамедленном движении
2. Чему равно Равнозамедленное движение
3. Какая формула равномерного движения
4. Что такое Равноускоренное и Равнозамедленное движение
5. Как найти путь по формуле
6. Как найти Равноускоренное движение
7. Как найти время равномерного движения
8. Как определить Равноускоренное и Равнозамедленное
9. Чему равна скорость равномерного движения
10. Чем отличается равномерное движение от Равнозамедленного
11. Как найти ускорение физика 9 класс
12. Как определяется движение
13. Как найти путь при равномерном движении
14. Что значит Равнопеременное движение
15. Что такое равномерное движение 7 класс
16. Какой вид имеет формула пути для равномерного движения
17. Как называется равномерное движение
18. Как вычислить скорость тела при равномерном движении

Как найти путь в Равнозамедленном движении

При движении тела с постоянным ускорением а, путь тела S определяется формулой: S = V0 * t + a * t2 / 2, где V0 — начальная скорость движения тела, t — время движения тела. Так как тело начинает своё движение из состояния покоя V0 = 0 м/с, то формула примет вид: S = a * t2 / 2.

Чему равно Равнозамедленное движение

Ответы1. Равнозамедленное движение — движение, при котором модуль (величина) скорости равномерно меняется, а вектор ускорения остаётся постоянным и по модулю, и по направлению.

Какая формула равномерного движения

Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения. v → = s → t. Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s → = v → ⋅ t.

Что такое Равноускоренное и Равнозамедленное движение

Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину. При этом, если скорость увеличивается — движение называют равноускоренным, а если скорость уменьшается — равнозамедленным.

Как найти путь по формуле

Путь — это расстояние, которое преодолело тело. Путь обозначается — S. Единица измерения — метры. Формула S=v*t, где v- скорость тела, t — время, за которое тело прошло путь.

Как найти Равноускоренное движение

Скорость прямолинейного равноускоренного движения: v x = v 0 x + a x t, где v 0 x — проекция начальной скорости, a x — проекция ускорения, t — время. Если в начальный момент тело покоилось, то v 0 → = 0. Для этого случая формула принимает следующий вид: v x = a x t.

Как найти время равномерного движения

Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.

Как определить Равноускоренное и Равнозамедленное

В физике, чтобы определить тип движения (равноускоренное или равнозамедленное), достаточно найти ускорение тела. Если ускорение тела получилось меньше нуля, значит оно направлено против движения тела, следовательно, движение является равнозамедленным, то есть тело снижает скорость.

Чему равна скорость равномерного движения

Скорость равномерного прямолинейного движения точки — величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. 2). Равноускоренное движение- это движение с постоянным ускорением. Равномерное — это когда два тела идут с одинаковой скоростью. Равноускоренное — это, когда в задаче еще добавляется ускорение.

Как найти ускорение физика 9 класс

Пусть в начальный момент времени t0 = 0 скорость тела равна v0. В некоторый момент времени t она стала равной v. Тогда изменение скорости за промежуток времени t — t0 = t равно v– v0, а за единицу времени —. Это отношение называется ускорением.

Как определяется движение

Движение материальной точки полностью определяется изменением её координат во времени (например, для плоскости — изменением абсциссы и ординаты). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.

Как найти путь при равномерном движении

Чтобы определить путь, пройденный телом при равномерном движении, надо скорость тела умножить на время его движения: S=Vt Если тело движется неравномерно, то, зная его среднюю скорость движения и время, за которое происходит это движения, находят путь: S=Vсрt.

Что значит Равнопеременное движение

Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением. изменение скорости, а Δt — промежуток времени.

Что такое равномерное движение 7 класс

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным.

Какой вид имеет формула пути для равномерного движения

Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением: x (t) = x0 + υt. В этом уравнении υ = const — скорость движения тела, x0 — координата точки, в которой тело находилось в момент времени t = 0.

Как называется равномерное движение

Если тело движется с постоянной скоростью и за любые равные промежутки времени проходит равные расстояния, то такое движение называется равномерным.

Как вычислить скорость тела при равномерном движении

Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени, разделить на этот промежуток времени: скорость = путь/время.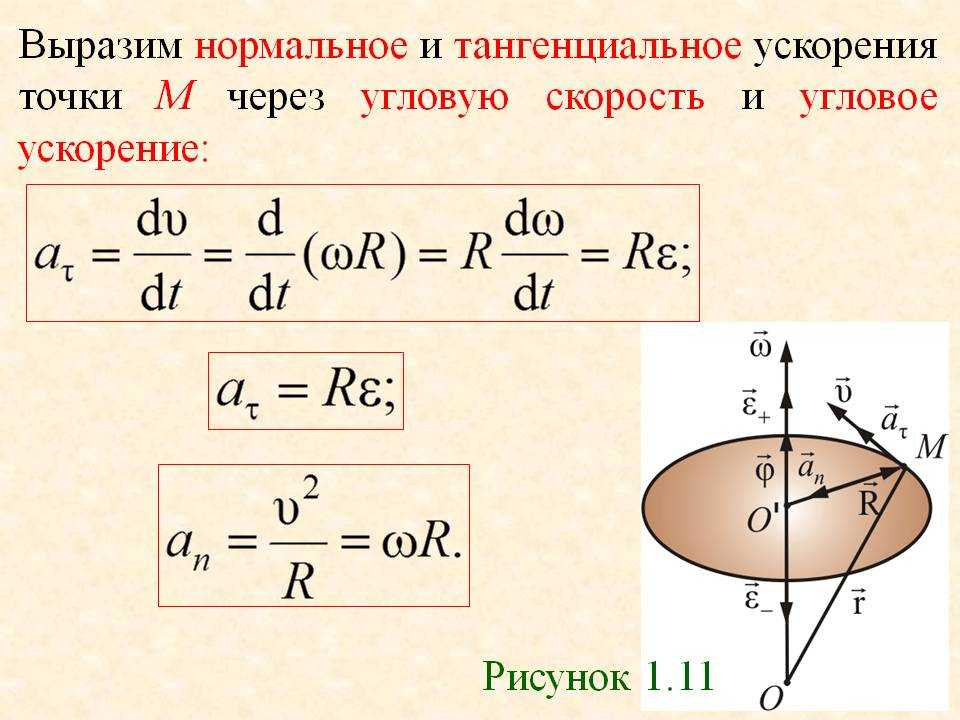 Скорость обозначают буквой v, путь — s, время — t.

Формулы для расчета ускорения при равноускоренном движении. Равноускоренное прямолинейное движение

На данном уроке мы с вами рассмотрим важную характеристику неравномерного движения – ускорение. Кроме того, мы рассмотрим неравномерное движение с постоянным ускорением. Такое движение еще называется равноускоренным или равнозамедленным. Наконец, мы поговорим о том, как графически изображать зависимости скорости тела от времени при равноускоренном движении.

Домашнее задание

Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.

1. Задачи 48, 50, 52, 54 сб. задач А.П. Рымкевич, изд. 10.

2. Запишите зависимости скорости от времени и нарисуйте графики зависимости скорости тела от времени для случаев, изображенных на рис. 1, случаи б) и г). Отметьте на графиках точки поворота, если такие есть.

3. Рассмотрите следующие вопросы и ответы на них:

Вопрос. Является ли ускорение свободного падения ускорением, согласно данному выше определению?

Ответ. Конечно, является. Ускорение свободного падения – это ускорение тела, которое свободно падает с некоторой высоты (сопротивлением воздуха нужно пренебречь).

Вопрос. Что произойдет, если ускорение тела будет направлено перпендикулярно скорости движения тела?

Ответ. Тело будет двигаться равномерно по окружности.

Вопрос. Можно ли вычислять тангенс угла наклона, воспользовавшись транспортиром и калькулятором?

Ответ. Нет! Потому что полученное таким образом ускорение будет безразмерным, а размерность ускорения, как мы показали ранее, должно иметь размерность м/с 2 .

Вопрос. Что можно сказать о движении, если график зависимости скорости от времени не является прямой?

Ответ. Можно сказать, что ускорение этого тела меняется со временем. Такое движение не будет являться равноускоренным.

Важнейшей характеристикой при движении тела является его скорость. Зная ее, а также некоторые другие параметры, мы всегда можем определить время движения, пройденное расстояние, начальную, конечную скорость и ускорение. Равноускоренное движение же является только одним из типов движения. Обычно оно встречается в задачах по физике из раздела кинематики. В подобных задачах тело принимают за материальную точку, что существенно упрощает все расчеты.

Скорость. Ускорение

Прежде всего, хотелось бы обратить внимание читателя на то, что эти две физических величины являются не скалярными, а векторными. А это значит, что при решении определенного рода задач необходимо обращать внимание на то, какое ускорение имеет тело в плане знака, а также каков вектор самой скорости тела. Вообще в задачах исключительно математического плана подобные моменты опускают, но в задачах по физике это достаточно важно, поскольку в кинематике из-за одного неверно поставленного знака ответ может получиться ошибочным.

Примеры

В качестве примера можно привести равноускоренное и равнозамедленное движение. Равноускоренное движение характеризуется, как известно, разгоном тела. Ускорение остается постоянным, но скорость непрерывно увеличивается в каждый отдельный момент времени. А при равнозамедленном движении ускорение имеет отрицательное значение, скорость тела непрерывно снижается. Эти два вида ускорения заложены в основу многих физических задач и достаточно часто встречаются в задачах первой части тестов по физике.

Пример равноускоренного движения

Равноускоренное движение мы встречаем ежедневно повсеместно. Ни один автомобиль не движется в реальной жизни равномерно. Даже если стрелка спидометра показывает ровно 6 километров в час, следует понимать, что это на самом деле не совсем так. Во-первых, если разбирать данный вопрос с технической точки зрения, то первым параметром, который будет давать неточность, станет прибор. Вернее, его погрешность.

Их мы встречаем во всех контрольно-измерительных приборах. Те же самые линейки. Возьмите штук десять хоть одинаковых (по 15 сантиметров, например) линеек, хоть разных (15, 30, 45, 50 сантиметров). Приложите их друг к другу, и вы заметите, что есть небольшие неточности, а их шкалы не совсем совпадают. Это и есть погрешность. В данном случае она будет равна половине цены деления, как и у других приборов, выдающих определенные значения.

Вторым фактором, который будет давать неточность, является масштаб прибора. Спидометр не учитывает такие величины, как половина километра, одна вторая километра и так далее. Заметить на приборе это глазом достаточно тяжело. Практически невозможно. Но ведь изменение скорости есть. Пускай на такую маленькую величину, но все же. Таким образом, это будет равноускоренное движение, а не равномерное. То же самое можно сказать и про обычный шаг. Идем, допустим, мы пешком, и кто-то говорит: наша скорость – 5 километров в час. Но это не совсем так, а почему, было рассказано немного выше.

Ускорение тела

Ускорение может быть положительным и отрицательным. Об этом говорилось ранее. Добавим, что ускорение – это векторная величина, которая числено равна изменению скорости за определенный промежуток времени. То есть через формулу его можно обозначить следующим образом: a = dV/dt, где dV – изменение скорости, dt – промежуток времени (изменение времени).

Нюансы

Сразу может возникнуть вопрос о том, как ускорение при таком раскладе может быть отрицательным. Те люди, которые задают подобный вопрос, мотивируют это тем, что даже скорость не может быть отрицательной, не то что время. На самом деле время отрицательным быть действительно не может. Но очень часто забывают о том, что скорость принимать отрицательные значения вполне может. Это же векторная величина, не следует забывать об этом! Все дело, наверное, в стереотипах и некорректном мышлении.

Так вот, для решения задач достаточно уяснить одну вещь: ускорение будет положительным в том случае, если тело разгоняется. И оно будет отрицательным в том случае, если тело тормозит. Вот и все, достаточно просто. Простейшее логическое мышление или способность видеть между строк уже будет, по сути дела, частью решения физической задачи, связанной со скоростью и ускорением. Частный случай – это ускорение свободного падения, и оно не может быть отрицательным.

Формулы. Решение задач

Следует понимать, что задачи, связанные со скоростью и ускорением, бывают не только практического, но и теоретического характера. Поэтому мы будем разбирать их и по возможности постараемся объяснить, почему тот или иной ответ правильный или, наоборот, неправильный.

Теоретическая задача

Очень часто на экзаменах по физике в 9 и 11 классах можно встретить подобные вопросы: “Как будет вести себя тело, если сумма всех действующих на него сил равна нулю?”. На самом деле формулировка вопроса может быть самой разной, но ответ все равно один. Здесь первым делом в ход нужно пускать поверхностные здания и обыкновенное логическое мышление.

На выбор ученика предоставляется 4 ответа. Первый: “скорость будет равна нулю”. Второй: “скорость тела убывает в течение некоторого периода времени”. Третий: “скорость тела постоянна, но она точно не равна нулю”. Четвертый: “скорость может иметь любое значение, но в каждый момент времени она будет постоянной”.

Правильным ответом здесь будет, конечно же, четвертый. Сейчас разберемся, почему именно так. Давайте попробуем рассмотреть все варианты по очереди. Как известно, сумма всех сил, действующих на тело, есть произведение массы на ускорение. Но масса у нас остается величиной постоянной, ее мы отбросим. То есть если сумма всех сил равна нулю, ускорение тоже будет равно нулю.

Итак, предположим, что скорость будет равна нулю. Но этого не может быть, поскольку нулю у нас равно ускорение. Чисто физически это допустимо, но только не в данном случае, поскольку сейчас речь идет о другом. Пускай скорость тела убывает в течение некоторого периода времени. Но как она может убывать, если ускорение постоянно, и оно равно нулю? Никаких причин и предпосылок для убывания или возрастания скорости нет. Поэтому второй вариант мы отметаем.

Предположим, что скорость тела постоянна, но она точно не равна нулю. Она действительно будет постоянной в силу того, что ускорение просто-напросто отсутствует. Но нельзя однозначно сказать, что скорость будет отлична от нулевой. А вот четвертый вариант – прямо в яблочко. Скорость может быть любой, но, поскольку ускорение отсутствует, она будет постоянной во времени.

Практическая задача

Определите, какой путь был пройден телом в определенный период времени t1-t2 (t1 = 0 секунд, t2 = 2 секунды), если имеются следующие данные. Начальная скорость тела на отрезке от 0 до 1 секунды равна 0 метров в секунду, конечная – 2 метра в секунду. Скорость тела по состоянию на время 2 секунды равна также 2 метрам в секунду.

Решить подобную задачу достаточно просто, нужно лишь уловить ее суть. Итак, требуется найти путь. Ну что же, начнем искать его, предварительно выделив два участка. Как легко заметить, первый участок пути (от 0 до 1 секунды) тело проходит равноускоренно, о чем свидетельствует увеличение его скорости. Тогда найдем это ускорение. Его можно выразить как разность скоростей, разделенную на время движения.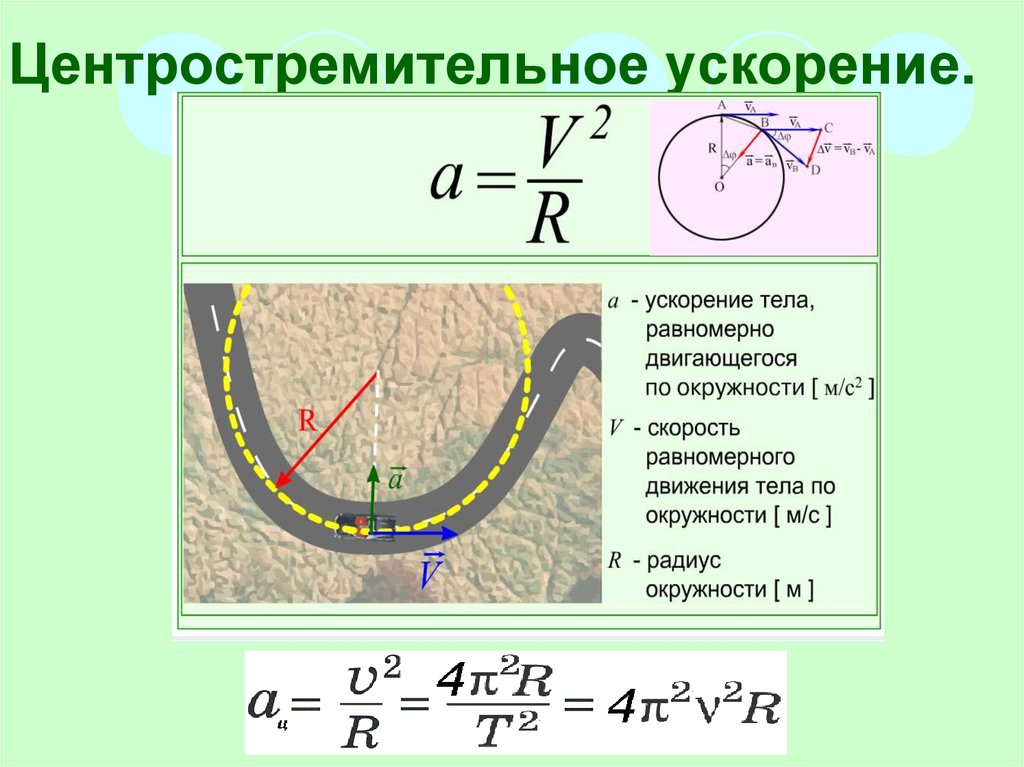

2/2 = 0 + 1 = 1 метр. На втором же участке пути в период от 1 секунды до 2 секунд тело движется равномерно. Значит, расстояние будет равно V*t = 2*1 = 2 метра. Теперь суммируем расстояния, получаем 3 метра. Это и есть ответ.

Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить перемещение автомобиля? Ответы мы получим после того, как познакомимся с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координаты от времени при равноускоренном движении»

При равноускоренном движении график имеет вид прямой линии, уходящей вверх, так как его проекция ускорения больше нуля.

При равномерном прямолинейном движении площадь численно будет равна модулю проекции перемещения тела. Оказывается, этот факт можно обобщить для случая не только равномерного движения, но и для любого движения, то есть показать, что площадь под графиком численно равна модулю проекции перемещения. Это делается строго математически, но мы воспользуемся графическим способом.

Рис. 2. График зависимости скорости от времени при равноускоренном движении ()

Разобьем график проекции скорости от времени для равноускоренного движения на небольшие промежутки времени Δt. Предположим, что они так малы, что на их протяжении скорость практически не менялась, то есть график линейной зависимости на рисунке мы условно превратим в лесенку. На каждой ее ступеньке мы считаем, что скорость практически не поменялась. Представим, что промежутки времени Δt мы сделаем бесконечно малыми. В математике говорят: совершаем предельный переход. В этом случае площадь такой лесенки будет неограниченно близко совпадать с площадью трапеции, которую ограничивает график V x (t). А это значит, что и для случая равноускоренного движения можно сказать, что модуль проекции перемещения численно равен площади, ограниченной графиком V x (t): осями абсцисс и ординат и перпендикуляром, опущенным на ось абсцисс, то есть площади трапеции ОАВС, которую мы видим на рисунке 2.

Задача из физической превращается в математическую задачу – поиск площади трапеции. Это стандартная ситуация, когда ученые физики составляют модель, которая описывает то или иное явление, а затем в дело вступает математика, которая обогащает эту модель уравнениями, законами – тем, что превращает модель в теорию.

Находим площадь трапеции: трапеция является прямоугольной, так как угол между осями – 90 0 , разобьем трапецию на две фигуры – прямоугольник и треугольник. Очевидно, что общая площадь будет равна сумме площадей этих фигур (рис. 3). Найдем их площади: площадь прямоугольника равна произведению сторон, то есть V 0x · t, площадь прямоугольного треугольника будет равна половине произведения катетов – 1/2АD·BD, подставив значения проекций, получим: 1/2t·(V x – V 0x), а, вспомнив закон изменения скорости от времени при равноускоренном движении: V x (t) = V 0x + а х t, совершенно очевидно, что разность проекций скоростей равна произведению проекции ускорения а х на время t, то есть V x – V 0x = а х t.

Рис. 3. Определение площади трапеции (Источник)

Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, получим:

S х(t) = V 0 x t + а х t 2 /2

Мы с вами получили закон зависимости проекции перемещения от времени при равноускоренном движении в скалярной форме, в векторной форме он будет выглядеть так:

(t) = t + t 2 / 2

Выведем еще одну формулу для проекции перемещения, в которую не будет входить в качестве переменной время. Решим систему уравнений, исключив из нее время:

S x (t) = V 0 x + а х t 2 /2

V x (t) = V 0 x + а х t

Представим, что время нам неизвестно, тогда выразим время из второго уравнения:

t = V x – V 0x / а х

Подставим полученное значение в первое уравнение:

Получим такое громоздкое выражение, возведем в квадрат и приведем подобные:

Мы получили очень удобное выражение проекции перемещения для случая, когда нам неизвестно время движения.

Пусть у нас начальная скорость автомобиля, когда началось торможение, составляет V 0 = 72 км/ч, конечная скорость V = 0, ускорение а = 4 м/с 2 . Узнаем длину тормозного пути. Переведя километры в метры и подставив значения в формулу, получим, что тормозной путь составит:

S x = 0 – 400(м/с) 2 / -2 · 4 м/с 2 = 50 м

Проанализируем следующую формулу:

S x = (V 0 x + V x) / 2 · t

Проекция перемещения- это полусумма проекций начальной и конечной скоростей, умноженная на время движения. Вспомним формулу перемещения для средней скорости

S x = V ср · t

В случае равноускоренного движения средняя скорость будет:

V ср = (V 0 + V к) / 2

Мы вплотную подошли к решению главной задачи механики равноускоренного движения, то есть получению закона, по которому меняется координата со временем:

х(t) = х 0 + V 0 x t + а х t 2 /2

Для того чтобы научиться пользоваться этим законом, разберем типичную задачу.

Автомобиль, двигаясь из состояния покоя, приобретает ускорение 2 м/с 2 . Найти путь, который прошел автомобиль за 3 секунды и за третью секунду.

Дано: V 0 x = 0

Запишем закон, по которому меняется перемещение со временем при

равноускоренном движении: S х = V 0 x t + а х t 2 /2. 2 c

Мы можем ответить на первый вопрос задачи, подставив данные:

t 1 = 3 c S 1х = а х t 2 /2 = 2· 3 2 / 2 = 9 (м) – это путь, который прошел

c автомобиль за 3 секунды.

Узнаем сколько он проехал за 2 секунды:

S х (2 с) = а х t 2 /2 = 2· 2 2 / 2 = 4 (м)

Итак, мы с вами знаем, что за две секунды автомобиль проехал 4 метра.

Теперь, зная два эти расстояния, мы можем найти путь, который он прошел за третью секунду:

S 2х = S 1х + S х (2 с) = 9 – 4 = 5 (м)

И время движения, можно найти пройденный путь:

Подставляя в эту формулу выражение V ср =V /2, мы найдем путь, пройденный при равноускоренном движении из состояния покоя:

Если же мы подставим в формулу (4.1) выражение V ср =V 0 /2, то получим путь, пройденный при торможении:

В последние две формулы входят скорости V 0 и V . Подставляя выражение V =at в формулу (4.2), а выражение V 0 =at – в формулу (4.3), получим

Полученная формула справедлива как для равноускоренного движения из состояния покоя, так и для движения с уменьшающейся скоростью, когда тело в конце пути останавливается. В обоих этих случаях пройденный путь пропорционален квадрату времени движения (а не просто времени, как это было в случае равномерного движения). Первым, кто установил эту закономерность, был Г. Галилей.

В таблице 2 даны основные формулы, описывающие равноускоренное прямолинейное движение.

Своей книги, в которой излагалась теория равноускоренного движения (наряду со многими другими его открытиями), Галилею увидеть не довелось. Когда она была издана. 74-летний ученый был уже слепым. Галилей очень тяжело переживал потерю зрения . “Вы можете себе представить,- писал он,- как я горюю, когда я сознаю, что это небо, этот мир и Вселенная, которые моими наблюдениями и ясными доказательствами расширены в сто и в тысячу раз по сравнению с тем, какими их считали люди науки во все минувшие столетия, теперь для меня так уменьшились и сократились”.

За пять лет до этого Галилей был подвергнут суду инквизиции. Его взгляды на устройство мира (а он придерживался системы Коперника, в которой центральное место занимало Солнце, а не Земля) уже давно не нравились служителям церкви. Еще в 1614 г. доминиканский священник Каччини объявил Галилея еретиком, а математику – изобретением дьявола. А в 1616 г. инквизиция официально заявила, что “учение, приписываемое Копернику, что Земля движется вокруг Солнца, Солнце же стоит в центре Вселенной, не двигаясь с востока на запад, противно Священному писанию, а потому его не можно ни защищать, ни принимать за истину”. Книга Коперника с изложением его системы мира была запрещена, а Галилея предупредили, что если “он не успокоится, то его подвергнут заключению в тюрьму”.

Но Галилей “не успокоился”. “В мире нет большей ненависти,- писал ученый,- чем у невежества к знанию”. И в 1632 г. выходит его знаменитая книга “Диалог о двух главнейших системах мира – птолемеевой и коперниковой”, в которой он привел многочисленные аргументы в пользу системы Коперника. Однако продать удалось всего лишь 500 экземпляров этого сочинения, так как уже через несколько месяцев по распоряжению Папы
Римского издатель книги получил приказ приостановить про дажу этого труда.

Осенью того же года Галилей получает предписание инквизиции явиться в Рим, и через некоторое время больного 69-летнего ученого на носилках доставляют в столицу Здесь, в тюрьме инквизиции, Галилея заставляют отречься от своих взглядов на устройство мира, и 22 июня 1633 г в римском монастыре Минервы Галилей зачитывает и подписывает заранее приготовленный текст отречения

“Я, Галилео Галилей, сын покойного Винченцо Галилея из Флоренции, 70 лет от роду, доставленный лично на суд и колено- приклоненный перед Вашими Преосвященствами, высокопреподобными господами кардиналами, генеральными инквизиторами против ереси во всем христианском мире, имея перед собой священное Евангелие и возлагая на него руки, клянусь, что я всегда верил, верую ныне и с Божией помощью буду веровать впредь во все то, что святая католическая и апостольская римская церковь признает, определяет и проповедует”

Согласно решению суда, книга Галилея была запрещена, а сам он был приговорен к тюремному заключению на неопределенный срок Однако Папа Римский помиловал Галилея и заменил заключение в тюрьме изгнанием Галилей переезжает в Арчетри и здесь, находясь под домашним арестом, пишет книгу “Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению” В 1636 г рукопись книги была переправлена в Голландию, где и была издана в 1638 г Этой книгой Галилей подводил итог своим многолетним физическим исследованиям В том же году Галилей полностью ослеп Рассказывая о постигшем великого ученого несчастье, Вивиани (ученик Галилея) писал “Случились у него тяжкие истечения из глаз, так что спустя несколько месяцев совсем остался он без глаз – да, говорю я, без своих глаз, которые за краткое время увидели в этом мире более, чем все человеческие глаза за все ушедшие столетия смогли увидеть и наблюсти”

Посетивший Галилея флорентийский инквизитор в своем письме в Рим сообщил, что нашел его в очень тяжелом состоянии На основании этого письма Папа Римский разрешил Галилею вернуться в родной дом во Флоренции Здесь ему сразу же вручили предписание “Под страхом пожизненного заключения в истинную тюрьму и отлучения от церкви не выходить в город и ни с кем, кто бы это ни был, не говорить о проклятом мнении насчет двоякого движения Земли”

У себя дома Галилей пробыл недолго Через несколько месяцев ему снова было приказано приехать в Арчетри Жить ему оставалось около четырех лет 8 января 1642 г в четыре часа ночи Галилей умер.

1. Чем отличается равноускоренное движение от равномерного? 2. Чем отличается формула пути при равноускоренном движении от формулы пути при равномерном движении? 3. Что вы знаете о жизни и творчестве Г. Галилея? В каком году он родился?

Отослано читателями из интернет-сайтов

Материалы с физики 8 класс, задание и ответы с физики по классам, конспекты для подготовке к урокам физики, планы конспектов уроков по физике 8 класс

Содержание урока

конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации

аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения

рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие

Совершенствование учебников и уроков

исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей

идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

Счет, математика и статистика — Комплект академических навыков

Графики скорость-время и расстояние-время (механика)

Главное меню ContentsToggle 1 Графики скорость-время 2 Рабочий пример: Графики скорость-время и графики ускорение-время 3 Проверьте себя

Графики скорость-время

На графике скорость-время скорость всегда откладывается по вертикальной оси, а время всегда откладывается по горизонтальной. Это представляет собой движение частицы, ускоряющейся от скорости в момент времени $0$, $u$, до скорости $v$ в момент времени $t$.

Градиент линии графика скорость-время есть ускорение частицы (для прямых ускорение постоянно). \begin{align} \text{Градиент линии} & = \frac{\text{изменение скорости} }{\text{время}}, \\ & = \frac{v – u}{t}, \\ &= а. \end{align} Площадь под графиком скорость-время – это расстояние, которое проходит частица. \begin{align} \text{Заштрихованная область} & = \left( \frac{u + v}{2} \right)t, \\ & = s. \end{выравнивание}

Графики “расстояние-время” и Графики “ускорение-время” также могут быть построены для движения частицы, где время всегда откладывается по горизонтальной оси.

Прямая линия на графике расстояние-время показывает, что частица имеет постоянную скорость . Кривизна предполагает, что частица ускоряется или замедляется .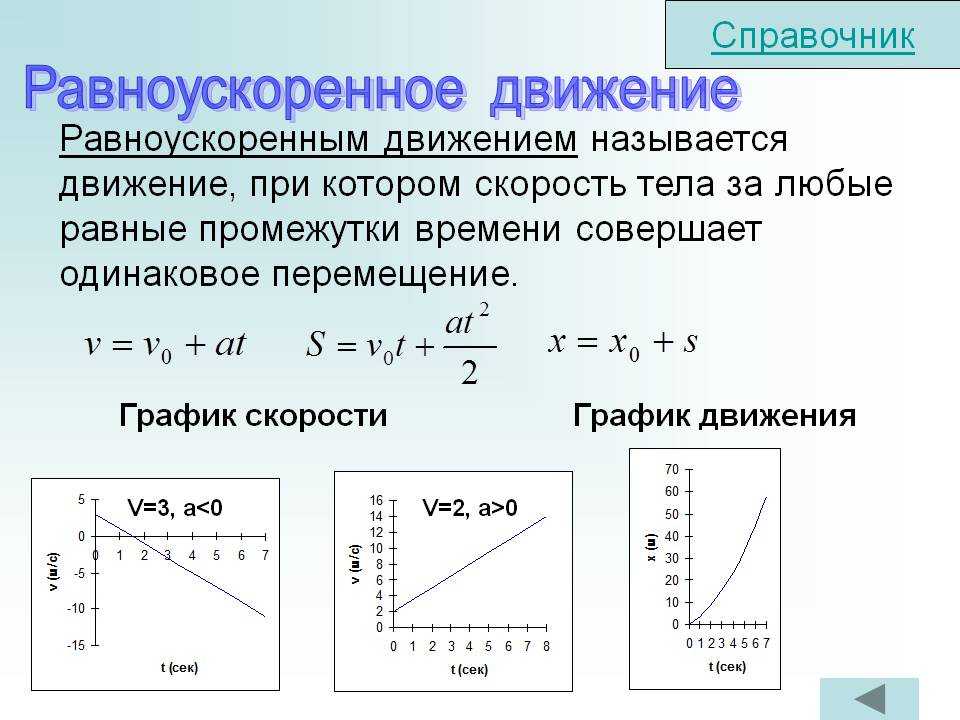

Рабочий пример: графики скорость-время и ускорение-время

Пример с автомобилем на прямой дороге 9{-1} }$ за $2T \mathrm{seconds}$. Затем он движется с постоянной скоростью в течение $1 \mathrm{минуты}$. Затем автомобиль равномерно замедляется до состояния покоя еще за $8T \mathrm{seconds}$. Нарисуйте график зависимости скорости от времени, иллюстрирующий движение автомобиля. Если общее расстояние, пройденное автомобилем, равно $800\mathrm{м}$, найдите значение $T$ и нарисуйте график ускорения и времени, иллюстрирующий движение автомобиля.

Решение

Нарисуем следующий график зависимости скорости от времени.

Площадь трапеции равна \begin{align} s & = \frac{1}{2} (a+b) h, \\ & = \frac{1}{2} (60 + 2T + 60 + 8T) \times 10, \\ & = 5 (10T + 120) \mathrm{m}. \end{align} Где $a$ представляет собой более короткую из двух параллельных сторон трапеции, а $b$ представляет другую. Нам дано, что $s=800 \mathrm{m}$, поэтому мы приравниваем это к приведенному выше выражению и находим $T$. {-2} }. \end{align} Здесь за последние 32 секунды координата $v$ уменьшается на 10, а координата $t$ увеличивается на 32. Это дает отрицательный ответ.

Проверь себя

Попробуйте наш тест Numbas на Линейное измерение – расстояние и длина.

Попробуйте наш тест Numbas на скорость.

Определение наклона (и ускорения)

Ранее в уроке 4 мы узнали, что наклон линии на графике зависимости скорости от времени равен ускорению объекта. Если объект движется с ускорением +4 м/с/с (т. е. меняет свою скорость на 4 м/с в секунду), то наклон линии будет +4 м/с/с. Если объект движется с ускорением -8 м/с/с, то наклон линии будет -8 м/с/с. Если объект имеет скорость 0 м/с, то наклон линии будет 0 м/с. Из-за его важности изучающий физику должен хорошо понимать, как вычислить наклон линии. В этой части урока будет обсуждаться метод определения наклона линии на графике скорость-время.

Давайте начнем с рассмотрения приведенного ниже графика зависимости скорости от времени.

Линия идет вверх вправо. Но математически, насколько он наклоняется вверх за каждую 1 секунду по горизонтальной (временной) оси? Чтобы ответить на этот вопрос, мы должны использовать уравнение наклона.

Использование уравнения наклона

Уравнение наклона гласит, что наклон линии находится путем определения величины подъема линии между любыми двумя точками, деленной на число запустить линии между теми же двумя точками. Способ выполнения расчета:

1. Выберите две точки на прямой и определите их координаты.
2. Определить разницу координат y для этих двух точек ( рост ).
3. Определить разницу координат x для этих двух точек ( запустить ).
4. Разделите разницу в координатах y на разницу в координатах x (подъем/спуск или уклон).

Приведенные ниже расчеты показывают, как можно применить этот метод для определения наклона линии. Обратите внимание, что три разных вычисления выполняются для трех разных наборов из двух точек на линии.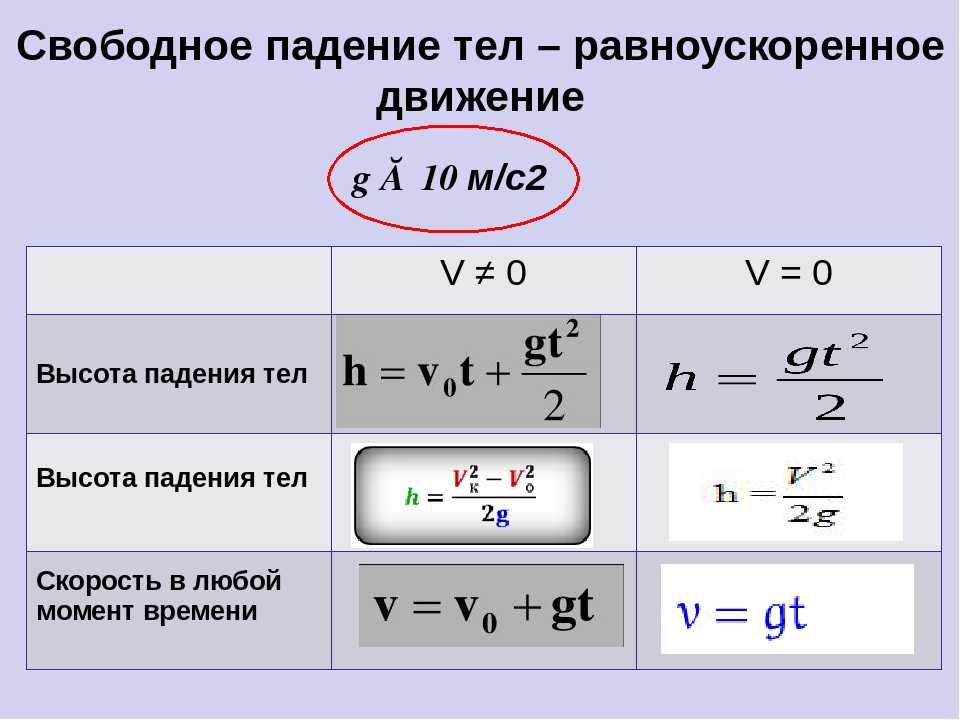 В каждом случае результат один и тот же: уклон равен 10 м/с/с.

 

Для точек (5 с, 50 ​​м/с) и (0 с, 0 м/с):

Наклон = (50 м/с – 0 м/с) / (5 с – 0 с) = 10 м/с/с

 

Для точек (5 с, 50 ​​м/с) и (2 с, 20 м/с):

Уклон = (50 м/с – 20 м/с) / (5 с – 2 с) = 10 м/с/с

 

Для точек (4 с, 40 м/с) и (3 с, 30 м/с):

Уклон = (40 м/с – 30 м/с) / (4 с – 3 с) = 10 м/с. серийный номер

Обратите внимание, что независимо от того, какие две точки на линии выбраны для расчета уклона, результат остается тем же — 10 м/с/с.

 

 

Проверьте свое понимание

Рассмотрим приведенный ниже график зависимости скорости от времени. Определите ускорение (т. е. наклон) объекта, как показано на графике. Используйте кнопку, чтобы просмотреть ответ.

 

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом.