Урок физики в 7 классе по теме “Сила Архимеда”
Тема: Архимедова сила
Урок – изучение новой темы по ФГОС в 7 классе
Оборудование: проектор, компьютер, установка с «Ведерком Архимеда», лабораторное оборудование на столах: стакан с водой, динамометр, набор цилиндров одинакового объема, мензурка.
Цели урока:
1. Дать понятие выталкивающей силы, действующей на тело, погруженное в жидкость или газ;
2. Экспериментально найти способы нахождения выталкивающей силы;
3. Развивать логическое мышление, формировать интерес к наблюдаемым
физическим явлениям;
4. Научить делать выводы из наблюдаемых явлений и формировать научное
мышление.
Ход урока
1. Организационный момент. – Сегодня, ребята, мы проведем урок-исследование, в котором познакомимся с новым видом сил, действующих на тела, погруженных в жидкость или газ.
Создание проблемной ситуации:
«Егорушка разбежался и полетел с полуторасаженной высоты, описав в воздухе дугу, он упал в воду, глубоко погрузился, но дна не достал.
Какая – то сила, холодная и приятная на ощупь, подхватила его и понесла обратно на верх. Он прыгнул и … опять нырнул… Опять та же сила, не давая ему коснуться дна и побыть в прохладе, понесла его на верх.»
отрывок из рассказа А.П.Чехова «Степь»
2. Проблемный вопрос: – Вспомните купание летом или в бассейне. Вам приходилось нырять за предметами, лежащими на дне? Это может быть камень или игрушка на дне бассейна. Какие необычные ощущения вам приходилось испытывать?
Ответ: Чтобы нырнуть, надо набрать воздуха в легкие и задержать дыхание. В воду надо входить вертикально вниз. Чтобы нырнуть глубже, надо взять с собой груз – камень. Затем, достав дно – вода выталкивает тело наверх.
Учитель: – Кто такого не ощущал? Давайте продемонстрируем это явление на резиновом мячике – опыт с мячиком, погруженным в жидкость.
Учитель: – Ребята, как вы думаете, почему мячик всплывает?
Ответ: Он наполнен воздухом, у него малая сила тяжести, на него действует сила, направленная вверх, эта сила называется выталкивающей силой.
Учитель: – Теперь пришло время рассказать вам одну древнюю легенду о древнегреческом ученом – механике и математике. «Однажды царь Гиерон (250 лет до н.э.) поручил ученому проверить честность мастера, изготовившего золотую корону. Хотя корона весила столько, сколько было отпущено на нее золота, царь заподозрил, что она изготовлена из сплава золота с другими, более дешевыми металлами. Ученому было поручено узнать, не ломая короны, есть ли в ней примесь. Много дней мучила ученого эта задача. Взвесить корону было легко, но как найти ее объем, ведь корона была очень сложной формы… И вот однажды, находясь в бане, он погрузился в наполненную водой ванну, и его внезапно осенила мысль, давшая решение задачи. Ликующий и возбужденный своим открытием, ученый воскликнул: «Эврика! Эврика!», что значит «Нашел! Нашел!»
– Смоделируем ситуацию: У нас есть корона – позолоченная и есть ванна.
– Ребята, как найти объем короны или любого тела неправильной формы?
Ответ: Надо погрузить корону в ванну, измерить высоту подъема уровня жидкости, найти площадь основания ванны, затем вычислить объем вытесненной воды.
Этот объем равен объему короны V=S·Δh. Вывод: Любое тело, погруженное в жидкость, вытесняет объем воды, равный объему тела.
– Ребята, как звали этого знаменитого ученого? Кто знает? Подумайте, как теперь называется выталкивающая сила?
Ответ: Учёного звали Архимед, поэтому сила называется «сила Архимеда» или «Архимедова сила».
Учитель: – Мы подошли к самому главному. Сформулируйте тему нашего урока. Открываем тетради, записываем число и тему урока «Сила Архимеда». Какие мы сегодня поставим задачи урока? Далее нам предстоит найти способ нахождения Архимедовой силы экспериментальным путем, найти формулу для расчета Архимедовой силы и сформулировать закон Архимеда.
Учитель: – Мы уже выяснили, что выталкивающая сила направлена вверх. Теперь нам предстоит найти формулы, по которым можно найти силу Архимеда и сформулировать закон Архимеда. Посмотрим, какие приборы есть у вас на столах.
Задача 1. Вам предстоит выяснить, как найти выталкивающую силу, действующую на цилиндр, погруженный в воду.
Какие есть идеи? Как вы думаете, вес цилиндра в воздухе и в воде будет одинаковым? Давайте проверим.
Р1= 1,6 Н Р2= 1,4 Н
– Почему в жидкости вес стал меньше?
Ответ: На тело действует выталкивающая сила, направленная вверх.
Учитель: – Как найти выталкивающую силу?
Fвыт =P1 – P2 = Fарх
– Как мы ее назвали по-другому?
– Обводим формулу в рамочку.
Fарх = 1,6 Н – 1,4 Н = 0,2 Н
Учитель: – Теперь возьмите цилиндр из другого вещества (алюминиевый). Найдите силу Архимеда? Какой получился результат? Почему оказалось, что выталкивающие силы одинаковые?
Ответ: У тел разная плотность, масса, но одинаковые объемы.
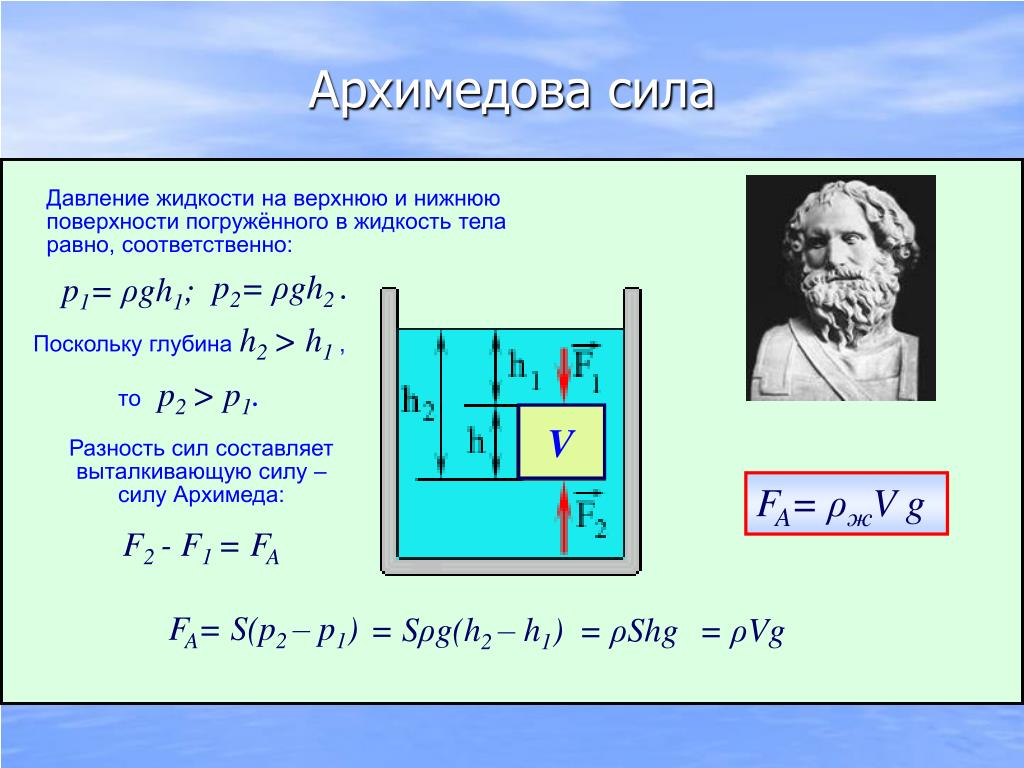
Учитель: – Значит, существует другой способ нахождения выталкивающей силы, этот способ связан с объёмом тела? Обратимся к рисунку 148. Открываем учебник.
Вывод формулы Fвыт =F2 – F1
– что означают силыF1 и F2 на рис.
?
Ответ: Это силы гидростатического давления. F1 – сила, действующая на верхнюю грань, F2 – сила, действующая на нижнюю грань, S – площадь поверхности тела на которую действует жидкость.
F1 = Р1·ρж S = ρжgh1s
Fарх = ρжg Vт
F2 = Р2· S = ρжgh2s
Подставим Fвыт =F2 – F1 = ρжgh2s – ρжgh1s = ρжgs( h2 – h1) = ρжghs = ρжg Vт
Vт– объем тела, если ρж· Vт = mж
Fвыт = Fарх = mжg =Рж
Вывод: – Выталкивающая сила равна весу жидкости, заключенной в объеме этого тела.
Попробуем подтвердить теоретические расчеты экспериментом
Фронтальный эксперимент с ведерком Архимеда
Демонстрация с «Ведёрком Архимеда» подробное объяснение всех действий.
Очень важно:
«Вода уравновесила выталкивающую силу» – говорят ученики.
Учитель: «Но силу может уравновесить только сила»!
Какая сила воды уравновесила выталкивающую силу?
Вес воды.
Но вес, какой воды? Вода, вытесненная телом!
Наблюдают и учатся делать выводы из наблюдений:
Растяжение пружины динамометра уменьшилось – значит, уменьшился вес тела в воде.
Объём вытесненной воды равен объёму тела.
Вода уравновесила выталкивающую силу.
Вес воды, вытесненной телом, уравновесил выталкивающую силу.
Задача 2. Как найти силу Архимеда другим способом? Например, зная плотность жидкости и объем тела?
Ответ: 1) измерим Vтс помощью мензурки
Vт = V2 – V1 = 20 см3; ρж = 1г/см3
2) найдем массу жидкости mж = ρж· Vт = 1г/см3·20 см3 = 20 г = 0,02 кг.
3) найдем силу Архимеда Fарх = mжg = 0,02 кг·10 Н/кг = 0,2 Н.
Ответ: Fарх = 0,2 Н.
Учитель: — Молодцы! Вы замечательно поработали, и пришла пора немножко отдохнуть
Физ. минутка
Учитель: — Отдохнули?
Итак, первая цель достигнута, далее начинается работа в шести группах.
От чего зависит, архимедова сила? А сейчас вы – исследователи, вы выясните, от чего зависит, архимедова сила. У каждой группы своя задача. Приступаем к работе, соблюдая технику безопасности, так как вы работаете со стеклом.
Задание первой группе.
Оборудование: сосуд с водой, динамометр, алюминиевый и медный цилиндры одинакового объема, нить.
Определить архимедову силу, действующие на первое и вторе тела.
Сравнить плотность тел и архимедовы силы, действующие на тела.
Сделайте вывод зависимости (независимости) архимедовой силы от плотности тела.
Вывод: архимедова сила не зависит от плотности вещества, из которого изготовлено тело.
Задание второй группе.
Оборудование: сосуд с водой, тела разного объема из пластилина, динамометр, нить.
Вывод: архимедова сила зависит от объема тела, чем больше объем тела, погруженного в жидкость, тем больше архимедова сила.
Задание третьей группе.
Оборудование: динамометр, нить, сосуды с водой, с соленой водой и маслом, алюминиевый цилиндр.
Определить архимедову силу, действующую на тело в воде, соленой воде и масле.
Чем отличаются эти жидкости?
Что можно сказать об архимедовых силах, действующих на тело в различных жидкостях?
Установите зависимости архимедовой силы от плотности жидкости.
Вывод: архимедова сила зависит от плотности жидкости, чем больше плотность жидкости, тем больше архимедова сила.
Задание четвертой группе.
Оборудование: тела разной формы, одинакового объема, сделанные из пластилина, сосуд с водой, нить, динамометр,
Поочередно опуская каждое тело в воду (кусок пластилина в форме шара, куба и цилиндра), с помощью динамометра определить архимедову силу.
Сравним эти силы и сделаем вывод о зависимости и независимости архимедовой силы от формы тела.
Вывод: архимедова сила не зависит от формы тела, погруженного в жидкость или газ.
Задание пятой группе.
Оборудование: мензурка с водой, алюминиевый цилиндр, нить динамометра.
Определю архимедову силу, действующую на тело, погруженное на 1/4 объема, 1/2 объема, 3/4 объема.
Сделаем вывод зависимости архимедовой силы от объёма погруженной части тела.
Вывод: архимедова сила зависит от объема погруженной части, чем больше объем погруженной части тела, тем больше архимедова сила.
Задание шестой группе.
Оборудование: мензурка с водой, алюминиевый цилиндр, нить динамометра.
1. Определю силу Архимеда, действующую на целиком погруженное в воду тело, на различной глубине h1 = , h2 =
2. Сделаем вывод о зависимости Архимедовой силы от глубины погружения данного тела.
Вывод: Архимедова сила не зависит от глубины погружения тела.
Поле получения результатов каждая группа отчитывается устно о своей проделанной работе. Затем учащиеся записывают выводы в виде таблицы, а учитель на доске.
Архимедова сила | |
Не зависит | Зависит |
От формы тела | От объема тела |
От плотности тела | От плотности жидкости |
От глубины погружения | От объема погруженной части |
Учитель: – Подведем итоги:
1) Какая сила действует на тело, погруженное в жидкость?
2) Как направлена выталкивающая сила?
3) По каким формулам можно вычислить выталкивающую силу?
Учитель: – Ребята, нам осталось сделать последний шаг, сформулировать закон Архимеда.
Если тело погружено в жидкость (или газ), то оно теряет в своем весе столько, сколько весит вытесненная им жидкость или газ.
Сила, действующая на тело, погруженное в жидкость или газ равна весу жидкости или газа в объеме данного тела.
Учитель: – Закон Архимеда, открытый более 2250 лет назад, имеет важное значение. Как вы думаете, где его можно использовать?
Ответ: В воздухоплавании (воздушный шар, зонды), плавании судов (лодки, катера, лайнеры).
Учитель: ― Ребята, вы все отлично поработали на уроке! Проверим свои знания. Тестирование с последующей взаимопроверкой.
Давайте подведем итоги сегодняшнего урока. Ответьте на следующие три вопроса:
1) что вы узнали нового на уроке?
2) где могут пригодиться знания, которые вы получили на уроке?
3) оцените свою работу и работу соседа по парте с помощью фигур
На следующем уроке мы углубим знания по теме Архимедова сила и узнаем много нового! Спасибо за урок, ребята! Урок закончен!
Домашнее задание: § 50, 51, упр 26 (1-4).
Простая физика – EASY-PHYSIC
В этой статье представляю задачи, связанные с плаванием тел и силой Архимеда. Как обычно, сначала пытаемся решить задачи простые, а затем перейдем к более сложным, которые вы найдете в следующей статье.
Задача 1. В воду погружен стеклянный кубик с ребром 10 см. Нижняя его грань находится на глубине 30 см. Рассчитайте силу давления жидкости, действующую: а) на верхнюю грань кубика; б) на нижнюю грань кубика; в) на правую грань; г) на левую грань; д) на переднюю и заднюю грани. Найдите равнодействующую всех этих сил.
Давление на грани кубика
Давление столба жидкости может быть вычислено по формуле , а сила давления может быть найдена из формулы , из которой находим: .
Не забываем, что очень важно помнить про перевод всех данных задачи в систему СИ, поэтому все расстояния и глубины из сантиметров переводим в метры.
Тогда сила давления на грань: , где – длина ребра кубика в метрах, – глубина, причем для боковых граней возьмем среднее значение () так как давление у верхнего края боковых граней и у нижнего – разное.
Сила давления на верхнюю грань, Н:
Сила давления на нижнюю грань, Н:
Сила давления на боковые грани, заднюю и переднюю, Н:
Понятно, что все силы, действующие на боковые, заднюю и переднюю грани друг друга компенсируют, а равнодействующая всех сил будет в итоге суммой сил давления на нижнюю и верхнюю грани:
Так как сила давления на нижнюю грань больше, чем на верхнюю, то равнодействующая направлена вверх.
Задача 2. Определите объем куска алюминия, на который в керосине действует архимедова сила величиной 120 Н.
Сила Архимеда может быть вычислена как , где – плотность жидкости, а – объем самого тела. То есть сила Архимеда не зависит от того, из чего сделано тело, а только от его объема. Вы спросите: почему тогда одинаковые по объему тела, например, шарики равных радиусов, сделанные из дерева и какого-либо металла, по-разному себя ведут в воде: один плавает, второй – тонет? Да просто есть ведь и сила тяжести, которая зависит как раз от массы тела, и в случае деревянного шарика сила Архимеда достаточна, чтобы компенсировать силу тяжести, а в случае с металлическим шариком – нет.
Рассчитаем объем: м
Задача 3. Плавающий деревянный брусок вытесняет 0,5 л воды. Сколько весит брусок?
Так как брусок плавает, то сила Архимеда равна силе тяжести. Нас спрашивают в задаче про вес бруска. Так как система в покое и ускорения нет, то вес бруска равен силе тяжести:
Можно эту задачу решить иначе: вес тела равен весу воды, вытесняемой им. Брусок вытеснил 0,5 литра воды. Воспользовавшись формулой плотности вещества, определяем, что масса такого количества воды равна 0,5 кг, а вес, значит, 5Н.
Задача 4. Тела изготовлены из дерева, пробки и стали. Они имеют объем 100 см каждое. Найдите архимедову силу, действующую на каждое тело, если его погрузить в воду.
Как было показано в одной из предыдущих задач, неважно, из чего изготовлено тело, а важен его объем, поэтому, раз тела обладают одним и тем же объемом, то и сила Архимеда на них действует одинаковая:
Ответ: 1 Н
Задача 5.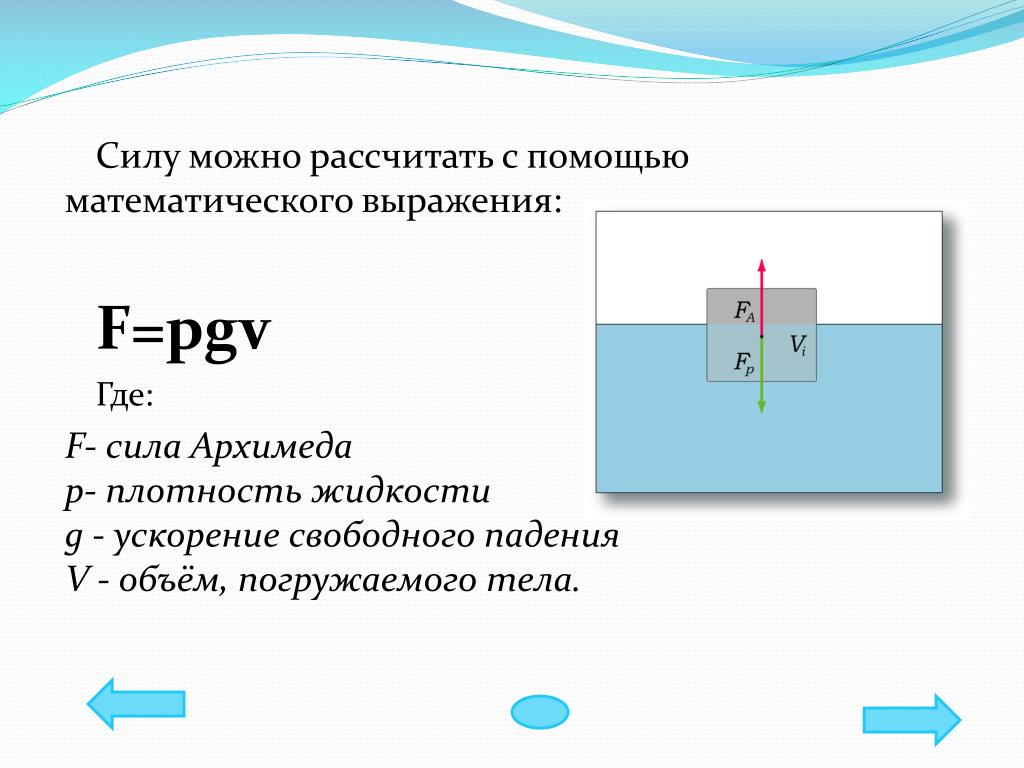
Тело при погружении в воду становится легче в 5 раз, чем в воздухе. Определите плотность этого тела.
Мы с вами помним, конечно, что на всякое тело, погруженное как в жидкость, так и в газ, действует сила Архимеда. Поэтому в воздухе она также будет действовать на тело. Однако плотность воздуха так мала по сравнению с плотностью воды, что, я думаю, мы этой силой пренебрежем, и примем вес тела в воздухе равным силе тяжести.
Тогда вес тела – на воздухе, а вес тела в воде . А уменьшился вес этого тела в воде благодаря силе Архимеда: , откуда получаем, что
Масса тела равна произведению его плотности на объем:
Подставим:
Откуда и найдем плотность тела:
Ответ: плотность тела 1250 кг/м
Задача 6. На предмет, целиком погруженный в керосин, действует выталкивающая сила величиной 2 кН. Какой будет архимедова сила, действующая на него в воде? А в спирте?
Чтобы узнать, какой будет Архимедова сила, нужно знать объем предмета.
Определим его, зная Архимедову силу в керосине: , откуда получаем, что .
Зная объем, определяем Архимедову силу в воде, Н:
Так как плотность спирта равна плотности керосина, то и Архимедовы силы в этих жидкостях будут одинаковы.
Задача 7.Цинковый шар имеет массу 360 г. При погружении в воду его вес становится равным 2,8 Н. Сплошной этот шар или полый?
Определим объем шара в предположении, что полости в нем нет, по формуле плотности (то есть найдем объем куска цинка массой 360 г):
Плотность цинка равна кг/м, объем получается м
Теперь определим реальный объем шара, то есть тот, который он вытесняет, по известному весу в жидкости. Вес шара Н, вес в жидкости равен , откуда объем вытесняемой жидкости (и объем шара)
мы получили больший объем, чем в первом случае, то есть шар имеет полость внутри, которая и влияет на его внешний объем.
Задача 8. Камень имеет объем 7,5 дм и массу 18,7 кг.
Какую силу придется приложить, чтобы удерживать его в воздухе и в воде?
Чтобы удержать такой камень в воздухе, нужно преодолеть силу тяжести, то есть Н.
Теперь определим, какую силу достаточно будет приложить в воде, ведь там нам поможет сила Архимеда!
Тогда сила, которую нужно приложить в воде для удержания камня (или, проще, вес этого камня в воде) равна Н
Задача 9. Сплошное однородное тело, будучи погруженным в воду, весит 170 мН, а в глицерин – 144 мН. Каким будет вес этого тела, если его погрузить в четыреххлористый углерод?
Запишем систему уравнений по тем условиям, что описаны в задаче. Вес тела в воде равен весу тела на воздухе, уменьшенному на силу Архимеда:
Вес тела в глицерине равен весу тела на воздухе, уменьшенному на силу Архимеда – только в глицерине сила Архимеда отличается от той, что действовала на тело в воде:
Из этих двух уравнений, объединив их в систему, можно найти объем тела.
Вычтем второе уравнение из первого:
Подставляем числа:
Теперь, когда мы знаем объем тела и плотность четыреххлористого углерода, можно найти силу Архимеда в нем:
Ответ: 110 мН
Задача 10. Кусок парафина толщиной 5 см плавает в воде. Он имеет форму прямоугольного параллелепипеда. Какая часть куска выступает над водой?
Если кусок парафина плавает, а не тонет, значит, сила Архимеда достаточна для того, чтобы компенсировать силу тяжести. Тогда можно записать:
Представим массу куска через его объем и плотность:
Здесь – объем всего куска, а – объем погруженной части.
Тогда:
Так как объем – это произведение площади основания на высоту, то можно сократить площадь:
Откуда делаем вывод, что , то есть из пяти см выступает 0,5 см.
Задача 11. Прямоугольная баржа после приема груза осела на 0,5 м. Принимая длину баржи 5 м, а ширину – 3 м, рассчитать вес принятого ею груза.
Рассчитаем объем воды, который был вытеснен баржей после осадки:
м
Такой объем воды весит 7,5 тонн – это легко понять, помня величину плотности воды.
То есть вес груза, принятого баржей, равен , или 75 кН.
Задача 12. Плот состоит из 12 бревен, каждое из которых имеет объем 0,8 м. Бревна сосновые. Можно ли на этом плоту переправить на другой берег автомобиль массой 1,5 тонны?
Рассчитаем вес плота: Н
К этому весу будет еще добавлен вес автомобиля: Н
Определим силу Архимеда. Если она окажется больше, чем суммарный вес плота и автомобиля, то плот выдержит (не будет затоплен при переправе), а если меньше, то переправлять автомобиль нельзя. Предположим, весь объем плота оказывается в воде при погрузке автомобиля. Тогда сила Архимеда: Н.
Так как , то делаем вывод, что плот может переправить автомобиль и даже не погрузится при переправе целиком в воду, то есть колеса не намокнут.
Задача 13.
Теплоход, вес которого вместе с оборудованием составляет 20 МН, имеет объем подводной части при погружении до ватерлинии 6000 м. Как велика грузоподъемность теплохода?
Сразу вычислим силу Архимеда, так как знаем водоизмещение судна:
Н.
Часть этой силы пойдет на компенсацию веса самого судна с оборудованием:
, или 40 МН – такого веса груз можно нагрузить на теплоход.
Задача 14. В сообщающиеся сосуды диаметром каждый налита жидкость плотностью . В один сосуд опустили тело массой , которое стало плавать в жидкости. Как и на сколько изменится уровень жидкости в сосудах?
Тело в одном из двух сосудов
Так как тело плавает, то заключаем, что сила Архимеда достаточна, чтобы скомпенсировать вес тела. Тогда запишем это формулой:
Так как сосудов два, и по закону уровень воды в них одинаков, то, если общий объем воды увеличивается на благодаря телу, то в каждом сосуде он поднимется на .
Высота подъема воды равна
Или
Вытеснение воды и принцип Архимеда в задачах по физике
Автор: The Experts at Dummies and
Обновлено: 26-03-2016
Из книги: Бесплатная онлайн-практика)
Физика I: 501 Практические задачи для чайников (+ Бесплатная онлайн-практика)
Исследовать книгу Купить на Amazon
Используя принцип Архимеда, вы можете рассчитать объем объекта, определив, сколько воды он вытесняет. Например, вы можете рассчитать массу куска дерева, исходя из того, насколько глубоко он погружен в воду.
Вот несколько практических вопросов, которые вы можете попробовать.
Практические вопросы
Деревянный брусок размером 0,12 х 0,34 х 0,43 м 3 плывет по реке самой широкой стороной вниз. Древесина погружена на высоту 0,053 метра.
Какова масса куска дерева?Вы погружаете баскетбольный мяч в воду до тех пор, пока половина его объема не окажется под водой. Если радиус баскетбольного мяча равен 12 см, какова выталкивающая сила мяча из-за воды?
Лодка массой 4000 кг плавает, треть ее объема погружена в воду. Если в лодку сядут еще два человека, каждый из которых весит 690 ньютонов, какой дополнительный объем воды вытеснится?
Какова масса куска дерева?Ответы
Ниже приведены ответы на практические вопросы:
7,75 кг
Закон Архимеда говорит вам, что вес вытесненной воды равен выталкивающей силе:
Чтобы удерживать дерево на плаву, выталкивающая сила должна иметь ту же величину, что и сила тяжести на бруске, поэтому
Объем вытесненной воды
Значит, масса вытесненной воды равна
.Таким образом, масса деревяшки 7,75 кг.
35 Н
Выталкивающая сила равна массе вытесненной воды, умноженной на ускорение свободного падения:
Объем вытесненной воды составляет половину объема баскетбольного мяча:
Здесь р = 12 см.
В метрах радиус равенИспользуя уравнение для плотности, масса вытесненной воды равна
Выталкивающая сила
0,14 м 3
Вес дополнительной вытесненной воды равен общему весу двух дополнительных людей, попавших в лодку:
Масса вытесненной воды равна
Решите уравнение плотности для объема вытесненной воды и используйте этот результат для массы вытесненной воды, чтобы найти ответ:
В метрах радиус равен Об этой статье
Эта статья из книги:
- Физика I: 501 Практические задачи для чайников (+ Бесплатная онлайн-практика) ,
Об авторе книги:
Эту статью можно найти в категории:
- Physics , Open Stax0 Physics College ,
Решение, глава 11, задача 42 (задачи и упражнения)
1PE2PE3PE4PE5PE6PE7PE8PE9PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE21PE22PE23PE24PE25PE26PE27PE28PE29PE30PE31PE32PE33PE34PE35PE36PE37PE38PE39PE40PE41PE42PE43PE44PE45PE46PE47PE48PE49PE50PE51PE52PE53PE54PE55PE56PE57PE58PE59PE60PE61PE62PE63PE64PE65PE66PE67PE68PE69PE70PE71PE72PE73PE74PE75PE76PE77PE78PE79PE80PE81PE82PE83PE84PE85PE
Изменить главуРасширенный поиск
Вопрос
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела.
Вопрос от OpenStax находится под лицензией СС BY 4.0.
Окончательный ответ
- $39,5 \textrm{g}$
- 50,0 $ \textrm{ мл} $
- $0,79 \textrm{г/мл}$. Это этиловый спирт.
Видеорешение
Зарегистрируйтесь, чтобы просмотреть это видеорешение!
Начать бесплатную неделю
Trustpilot
Рейтинг
ПлохоНе так уж плохоСреднеХорошоОчень хорошо
1 голос с рейтингом 5
Скриншоты калькулятора
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. Мы собираемся вычислить плотность неизвестной жидкости, используя измерения кажущейся массы известного куска материала, который представляет собой железо и погружен в эту жидкость.
Итак, масса железа вне жидкости равна 39.0,0 грамм, а кажущаяся масса в жидкости 350,5 грамм. Итак, первый вопрос: какая масса жидкости вытесняется? Таким образом, выталкивающая сила, которую испытывает кусок железа, является его весом… разницей между его весом вне жидкости и весом в жидкости; мы можем разложить эти
Итак, масса железа вне жидкости равна 39.0,0 грамм, а кажущаяся масса в жидкости 350,5 грамм. Итак, первый вопрос: какая масса жидкости вытесняется? Таким образом, выталкивающая сила, которую испытывает кусок железа, является его весом… разницей между его весом вне жидкости и весом в жидкости; мы можем разложить эти 
Итак, это 390,0 граммов, разделенных на 7,8 граммов на миллилитр, и мы можем сказать, что это масса железа, я имею в виду, что, строго говоря, это не совсем так, потому что есть некоторая выталкивающая сила из-за воздуха, когда это измерение было сделано, но это будет быть настолько маленьким и незначительным, что он, вероятно, влияет на какую-то десятичную точку, которая здесь даже не показана. Хорошо! Это работает до 50,0 миллилитров. А теперь часть (с)… вопрос в том, какова плотность жидкости, а затем выяснить, что это за жидкость. Таким образом, это будет его масса, деленная на его вытесненный объем, и объем вытесненной жидкости будет таким же, как объем погруженного в нее железа, поэтому мы можем заменить 