Как найти скорость зная радиус и ускорение: Период, радиус и скорость

Линейная скорость | формула и расшифровка

4356

3

20.05.2022

3 мин. на чтение

Понимание любого понятия в физике предполагает расшифровку определения связанных терминов. Таким образом, в случае линейной скорости становится необходимым определить линейную скорость и скорость по отдельности.

Линейная скорость относится к движению объекта по прямой линии или по заданной оси. С другой стороны, скорость означает расстояние, которое движущееся тело проходит в определенном направлении за определенное время. Таким образом, сочетание этих двух определений поможет вам понять основную концепцию линейной скорости.

Что такое скорость?

Термин «скорость» может использоваться в различных областях, включая физику, термодинамику, химию и т. д. Прежде чем мы перейдем к пониманию линейной и угловой скорости, мы сначала определим скорость как отдельный термин.

Скорость можно объяснить как скорость изменения положения объекта в течение определенного срока или диапазона времени, ее можно разделить на два типа: угловая скорость и линейная скорость. Чтобы определить скорость, мы возьмем пример, поэтому представьте, что вы едете по дороге и смотрите на приборную панель или любые вывески во время движения, спидометр показывает, что автомобиль движется со скоростью 65 км в час, тогда мы можем сказать, что скорость 65 км в час — это скорость, которая представляет собой скорость изменения км по отношению к часам, которые мы видим. Формула скорости равна расстоянию, деленному на время, может рассчитать линейную скорость объекта. В формуле v обозначает линейную скорость, d обозначает пройденное расстояние, а t обозначает время.

Теперь, возвращаясь к ее различным типам, линейная скорость — это просто скорость изменения положения объекта, который движется по прямому пути, поэтому любой движущийся объект имеет линейную скорость, с другой стороны, угловая скорость применяется только или может применяться к объектам, которые движутся по круговой траектории, а также может быть определена как скорость изменения углового смещения во времени. Угловая скорость, измеряемая в рад/с, которая также может быть преобразована в градусы, представляет собой изменение угла во времени. v=rω для расчета линейной скорости по угловой скорости.

V = ωr, где ω равно радианам в секунду, а r — радиус.

Если период вращения равен t, то ω=^2π/_t. Как результат, v=^2π∗r/_t.

Линейную скорость можно испытать в повседневной жизни, поскольку мы видим так много движущихся объектов, которые имеют линейную скорость, таких как человек, идущий на прогулку, вождение, бег или езду на велосипеде, всегда может быть линейная скорость, которая может наблюдаться. Кроме того, бывают случаи, когда объект может двигаться по прямому пути с заданной постоянной скоростью, это можно сказать, что объект движется с постоянной линейной скоростью, проще говоря, мы можем сказать, что скорость Лены объекта не изменяется и, следовательно, постоянный. Линейная скорость, измеряемая в м/с, — это скорость по прямой.

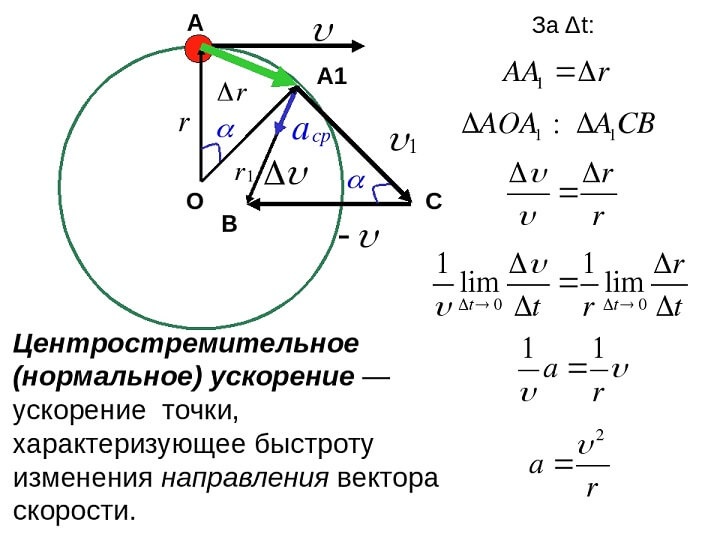
Когда мы говорим об окружности, связь между дугой на окружности и углом, на который она опирается, измеренным в излучении, позволяет нам определить величины, связанные с движением по окружности, и благодаря этому также мы можем сказать, что объекты, движущиеся по круговой траектории, относятся к типу 2. скорости, когда линейна, а другая – угловая скорость, как упоминалось выше. В дополнение к этому мы также можем понимать равномерное круговое движение. Равномерное круговое движение может определять линейную скорость, которая измеряет изменение длины дуги с течением времени.

Когда мы говорим о круговом движении, мы также говорим о направлении линейной скорости. Теперь направление скорости частицы Салина является тангенциальным к круговому пути, который мы видим в любой данной точке этого кругового движения. Направление играет очень важную роль в определении изменения характеристик, скорость является физической векторной величиной, что означает, что для ее правильного определения требуются как величина, так и направление, поэтому, если происходит изменение скорости, направления или того и другого, меняется философия объекта, и тогда мы говорим, что объект является ускоренным движением или ускоряется.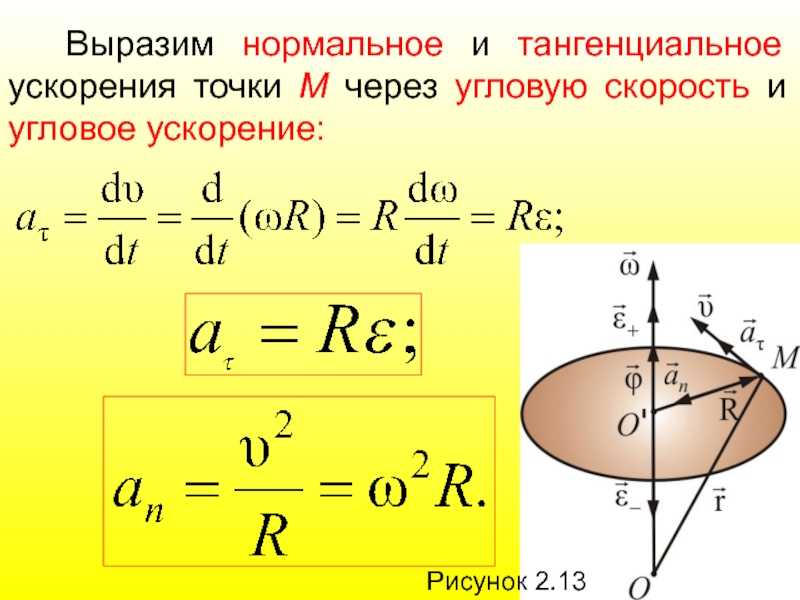

Что такое линейная скорость? 

В самом основном смысле определение линейной скорости связано с измерением скорости объекта, когда он движется в определенном направлении. Следовательно, это относится к смещению объекта во времени. 

Однако объект должен двигаться по определенной прямой линии. Единицей линейной скорости в системе СИ является метр в секунду или м/с (мс- ¹ ). 

С другой стороны, размерная формула линейной скорости имеет вид M ⁰ L ¹ T ¹

Кроме того, вы должны знать, что это векторная величина, что указывает на то, что она имеет направленный характер. 

Какая формула линейной скорости? 

Нет никаких различий между обычной скоростью и линейной скоростью, поскольку обе они являются векторными величинами. 

Следовательно, формула линейной скорости –  ν = d/t

Например, предположим, что движущийся объект преодолевает расстояние 500 метров по прямой линии за 10 секунд. В этом случае линейная скорость объекта равна – 

ν = 500 метров/10 секунд = 50 м/с или 50 мс- ¹ . 

Логически говоря, линейная скорость также применяется к объекту, который движется в круговом направлении, следуя геометрическому месту. В этом случае она называется угловой скоростью. 

Криволинейное движение

Простая физика – EASY-PHYSIC

Задача 1. За промежуток времени с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость и модуль средней скорости .

Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению. Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.

Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с

 

Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска . Найти геометрическое место всех точек диска,  скорость которых 2 м/с. Угол .

Скорость точек окружности

Решение:

Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра м/с.  Линейные скорости показаны для  точек оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга: .  В точке C скорости, напротив, сложатся, поскольку они сонаправлены: м/с.

Определим теперь скорости точек и . Понятно, что они будут равны численно, но направлены в разные стороны.

Осталось разобраться с точкой . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу . Углы, которые образуются между векторами, показаны на рисунке, в том числе угол . Тогда в параллелограмме угол , а так как

, то все углы в треугольнике равны и он равносторонний, то есть м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные , точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.

 

Пробуксовывание

Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса , если известно, что скорость нижней точки м/c, а верхней – м/c.

Решение:

Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше. Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников и запишем отношения сходственных сторон:

Тогда

Тогда

Теперь обратимся к подобным треугольникам и . Для них отношение сходственных сторон равно:

Откуда м/с.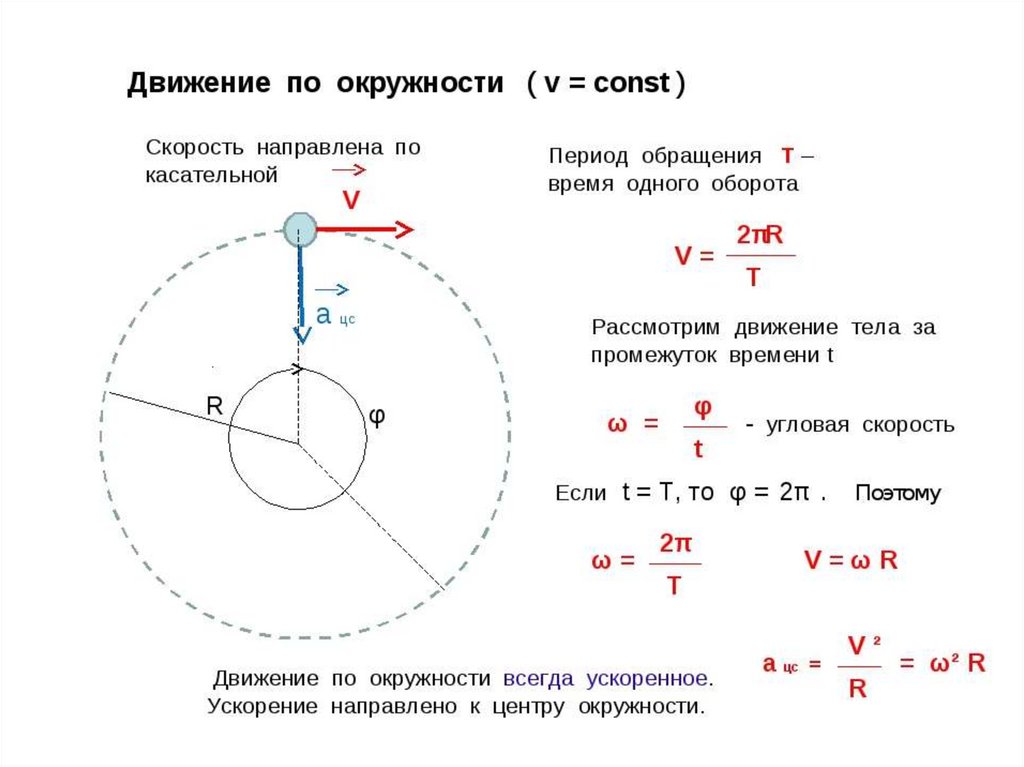

Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей и , при этом не забываем о векторном сложении скоростей, берем скорость со знаком «минус»:

м/с.

Ответ: 4 м/с.

 

Проскальзывание

Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А м/с, а нижней точки  B м/с. Определить скорость концов диаметра , перпендикулярного к , для того же момента времени. Под какими углами они направлены к горизонту?

Решение:

Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:

м/с.

Так как скорость точки есть результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра колеса , то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки , данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек и равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:

Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки можно найти как

Ответ: ,

 

Шарик катится по двум линейкам

Задача 5. Шарик радиусом см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно см, и за время с проходит см. С какими скоростями движутся верхняя и нижняя точки шарика?

На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка . Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника . Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки   будет

Таким же способом определяем скорость верхней точки :

Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.

 

Задача 6.  Автомобиль движется по закругленному шоссе, имеющему радиус кривизны м. Закон движения автомобиля имеет вид: , где м, м/с, м/с. Найти скорость автомобиля , его тангенциальное  , нормальное и полное ускорения в момент времени с.

Решение.

Путь:

Производная пути – линейная скорость:

Вторая производная – тангенциальное ускорение:

Нормальное ускорение:

Полное ускорение:

 

Задача7. Угол поворота диска радиусом см  изменяется со временем по закону . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.

Решение: угловая скорость – производная угла:

Угловое ускорение – производная угловой скорости:

Линейная скорость:

 

Задача 8.  Точка движется по окружности с постоянным угловым ускорением рад/. Найти угол между скоростью и ускорением  через 1 с после начала движения. Начальная скорость точки равна 0.

Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.

Известно, что нормальное ускорение  , тангенциальное ускорение . При этом , или . Тогда

Искомый угол:

Ответ:

Два концентрических колеса

Задача 9. Два концентрических колеса радиусами см и см вращаются с угловыми скоростями рад/c и рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси?  Проскальзывания нет.

Решение: определим радиус маленького (третьего) колеса, м:

Определим линейную скорость точек первого колеса:

Определим линейную скорость точек второго колеса:

Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:

Ответ: 20 рад/с

 

Задача 10. Гайку закручивают на болт за время . Длина болта , резьба составляет угол с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен .

Скорость вращения гайки по ходу завинчивания на болт

Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость (). Тогда .

Из рисунка видно, что

С другой стороны, так как длина болта , а гайка спускается по нему за время , то

Тогда

И можно определить :

Тогда

Ответ:

 

2}{R}$
Где
$a_c$ — центростремительное ускорение
$v$ — скорость объекта
$R$ — радиус окружности
Единица СИ центростремительного ускорения совпадает с ускорением, т.е. м/с ² . Это векторная величина

Пример нескольких вопросов, где вы можете использовать этот Калькулятор центростремительного ускорения
Вопрос 1
Рассчитайте центростремительное ускорение объекта, движущегося по кругу радиусом 10 м со скоростью 10 м/с 92}{a_c}$

Если заданы радиус и центростремительное ускорение, скорость рассчитывается как
$v= \sqrt {a_c R}$

Родственные калькуляторы

• Калькулятор ускорения
• Калькулятор движения снаряда
• Калькулятор углового ускорения
• Калькулятор кинетической энергии
• Калькулятор средней скорости

сделайте ссылку на эту страницу, скопировав следующий текст
Калькулятор центростремительного ускорения

Включите JavaScript для просмотра комментариев с помощью Disqus.

Физический калькуляторМатематический калькуляторХимический калькулятор

6.3 Центростремительная сила — University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Объясните уравнение центростремительного ускорения
• Примените второй закон Ньютона, чтобы составить уравнение для центростремительной силы
• Использование концепции кругового движения при решении задач, связанных с законами движения Ньютона

В книге “Движение в двух и трех измерениях” мы рассмотрели основные понятия кругового движения. Объект, совершающий круговое движение, например один из гоночных автомобилей, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это направленное по центру ускорение, называемое центростремительным ускорением, определяется формулой

ac=v2rac=v2r

, где v — скорость тела, направленная по касательной к кривой в любой момент времени. Если мы знаем угловую скорость ωω, то можем использовать

ac=rω2.ac=rω2.

Угловая скорость показывает скорость, с которой объект вращается по кривой, в рад/с. Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.

Ускорение должно создаваться силой. Любая сила или комбинация сил может вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросе, сила земного притяжения на Луне, трение между роликовыми коньками и полом катка, сила наката на автомобиле и силы на трубе вращающейся центрифуги. . Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Направление центростремительной силы совпадает с направлением центростремительного ускорения к центру кривизны. Согласно второму закону движения Ньютона, результирующая сила равна массе, умноженной на ускорение: Fnet=ma.Fnet=ma. Для равномерного кругового движения ускорение равно центростремительному ускорению:

_. а=а.с.а=а.с. Таким образом, величина центростремительной силы FcFc равна

Fc=mac.Fc=mac.

Подставляя выражения для центростремительного ускорения acac(ac=v2r;ac=rω2),(ac=v2r;ac=rω2), получаем два выражения для центростремительной силы FcFc через массу, скорость, угловую скорость и радиус кривизны:

Fc=mv2r;Fc=mrω2.Fc=mv2r;Fc=mrω2.

6,3

Вы можете использовать любое более удобное выражение для центростремительной силы. Центростремительная сила F→cF→c

всегда перпендикулярно пути и указывает на центр кривизны, потому что a→ca→c перпендикулярно скорости и указывает на центр кривизны. Обратите внимание, что если вы решите первое выражение для r , вы получите

r=mv2Fc.r=mv2Fc.

Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую, как на рис. 6.20.

Рисунок 6.20 Сила трения дополняет центростремительную силу и численно равна ей.

Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше Fc,Fc, тем меньше радиус кривизны r и круче кривой. Вторая кривая имеет те же самые v , но больший FcFc дает меньшее r ‘.

Пример 6.15

Какой коэффициент трения нужен автомобилям на плоской кривой?

(a) Рассчитайте центростремительную силу, действующую на автомобиль массой 900,0 кг, который движется по кривой радиусом 500,0 м со скоростью 25,00 м/с. (b) Предполагая, что кривая не имеет наклона, найдите минимальный статический коэффициент трения между шинами и дорогой, причем статическое трение является причиной, удерживающей автомобиль от проскальзывания (рис. 6.21).

Рисунок 6.21 Этот автомобиль на ровном месте удаляется и поворачивает влево. Центростремительная сила, заставляющая автомобиль поворачивать по круговой траектории, возникает из-за трения между шинами и дорогой. Необходим минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и сойдет с проезжей части.

Стратегия

1. Мы знаем, что Fc=mv2r.Fc=mv2r. Таким образом,

   Fc=mv2r=(900,0 кг)(25,00 м/с)2(500,0 м)=1125 Н.Fc=mv2r=(900,0 кг)(25,00 м/с)2(500,0 м)=1125 Н.

2. На рис. 6.21 показаны силы, действующие на автомобиль на кривой без уклона (на ровной поверхности). Трение направлено влево, удерживая автомобиль от скольжения, и, поскольку это единственная горизонтальная сила, действующая на автомобиль, трение в данном случае является центростремительной силой. Мы знаем, что максимальное статическое трение (при котором шины катятся, но не скользят) равно µsN,µsN, где µsµs — статический коэффициент трения, а Н — нормальная сила. Нормальная сила равна весу автомобиля на ровной поверхности, поэтому N=mg.N=mg. Таким образом, центростремительная сила в этом случае равна

   Fc≡f=µsN=µsmg.

   Fc≡f=µsN=µsmg.
   Теперь у нас есть связь между центростремительной силой и коэффициентом трения. Используя уравнение

   Fc=mv2r,Fc=mv2r,

   мы получаем

   mv2r=мксмг.mv2r=мксмг.

   Мы решаем это для мкс, мкс, учитывая, что масса сокращается, и получаем

   мкс=v2rg.мкс=v2rg.

   Подставляя известные,

   мкс=(25,00 м/с)2(500,0 м)(9,80 м/с2)=0,13 мкс=(25,00 м/с)2(500,0 м)(9,80 м/с2)=0,13.

   (Поскольку коэффициенты трения являются приблизительными, ответ дается только двумя цифрами.)

Значение

Коэффициент трения, показанный на рис. 6.21(b), намного меньше, чем обычно наблюдается между шинами и дорогами. Автомобиль все еще преодолевает кривую, если коэффициент больше 0,13, потому что статическое трение является реактивной силой, которая может принимать значение меньше, но не больше, чем мксН.мксН. Более высокий коэффициент также позволит автомобилю проходить поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м/с. Обратите внимание, что масса отменяется, а это означает, что в этом примере не имеет значения, насколько сильно загружена машина для преодоления поворота. Масса компенсируется, потому что предполагается, что трение пропорционально нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы больше, как обсуждается далее.

Проверьте свое понимание 6,9

Автомобиль, движущийся со скоростью 96,8 км/ч, движется по кривой окружности радиусом 182,9 м по ровной проселочной дороге. Каким должен быть минимальный коэффициент трения покоя, чтобы автомобиль не скользил?

Кривые с наклоном

Давайте теперь рассмотрим кривую с наклоном s , где наклон дороги помогает вам преодолевать кривую (рис. 6.22). Чем больше угол θθ, тем быстрее вы сможете взять кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. В «идеально наклонной кривой» угол θθ таков, что вы можете преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой. Мы выведем выражение для θθ для идеально изогнутой кривой и рассмотрим связанный с ним пример.

Рисунок 6.22 Автомобиль на этой кривой с уклоном удаляется и поворачивает влево.

Для идеального крена чистая внешняя сила равна горизонтальной центростремительной силе при отсутствии трения. Составляющие нормальной силы Н в горизонтальном и вертикальном направлениях должны быть равны центростремительной силе и весу автомобиля соответственно. В случаях, когда силы не параллельны, удобнее всего рассматривать составляющие вдоль перпендикулярных осей — в данном случае вертикального и горизонтального направлений.

На рис. 6.22 показана диаграмма свободного кузова автомобиля на кривой без трения. Если угол θθ идеален для скорости и радиуса, то чистая внешняя сила равна необходимой центростремительной силе. Единственными двумя внешними силами, действующими на автомобиль, являются его вес w→w→ и нормальная сила дороги N→.N→. (На поверхность без трения может воздействовать только сила, перпендикулярная поверхности, т. е. нормальная сила.) Эти две силы должны складываться, чтобы получить результирующую внешнюю силу, направленную горизонтально к центру кривизны и имеющую величину mv2/r.mv2/. р. Поскольку это решающая сила, и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть

Nsinθ=mv2r.Nsinθ=mv2r.

Поскольку автомобиль не отрывается от поверхности дороги, результирующая вертикальная сила должна быть равна нулю, а это означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны по направлению. Из рисунка 6.22 мы видим, что вертикальная составляющая нормальной силы равна Ncosθ,Ncosθ, а единственная другая вертикальная сила — это вес автомобиля. Они должны быть равны по величине; таким образом,

Ncosθ=мг.Ncosθ=мг.

Теперь мы можем объединить эти два уравнения, чтобы исключить N и получить желаемое выражение для θθ. Решение второго уравнения относительно N=mg/(cosθ)N=mg/(cosθ) и подстановка его в первое дает

мгsinθcosθ=mv2rmgtanθ=mv2rtanθ=v2rg.mgsinθcosθ=mv2rmgtanθ=mv2rtanθ=v2rg.

Взятие арктангенса дает

θ=загар-1(v2rg).θ=загар-1(v2rg).

6,4

Это выражение можно понять, если рассмотреть, как θθ зависит от v и r . Большое θθ получается для больших v и маленький р. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что θθ не зависит от массы транспортного средства.

Пример 6.16

Какая идеальная скорость для крутого крутого поворота?

Кривые на некоторых тестовых трассах и гоночных трассах, таких как Daytona International Speedway во Флориде, очень крутые. Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет проходить повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, с которой следует двигаться по кривой радиусом 100,0 м с наклоном 31,0°31,0°, если бы на дороге не было трения.

Стратегия

Прежде всего заметим, что все члены в выражении для идеального угла кривой с креном, кроме скорости, известны; таким образом, нам нужно только переставить его так, чтобы скорость появилась в левой части, а затем подставить известные величины.

Раствор

Начиная с

tanθ=v2rg,tanθ=v2rg,

получаем

v=rgtanθ.v=rgtanθ.

Учитывая, что tan31.0°=0.609,tan31.0°=0.609, получаем

v=(100.0м)(9.80м/с2)(0.609)=24,4 м/с.v=(100,0 м)(9,80 м/с2)(0,609)=24,4 м/с.

Значение

Это примерно 165 км/ч, что соответствует очень крутому виражу и довольно резкому повороту. Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.

Самолеты также совершают повороты по крену. Подъемная сила из-за силы воздуха, действующей на крыло, действует под прямым углом к ​​крылу. Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет его. Угол крена, показанный на рис. 6.23, определяется как θθ. Мы анализируем силы так же, как рассматривали случай, когда автомобиль огибает кривую с креном.

Рисунок 6.23 При вираже горизонтальная составляющая подъемной силы неуравновешена и ускоряет самолет. Нормальная составляющая подъемной силы уравновешивает вес самолета. Угол крена определяется как θθ. Сравните векторную диаграмму с диаграммой, показанной на рис. 6.22.

Интерактивный

Вместе с божьей коровкой исследуйте вращательное движение.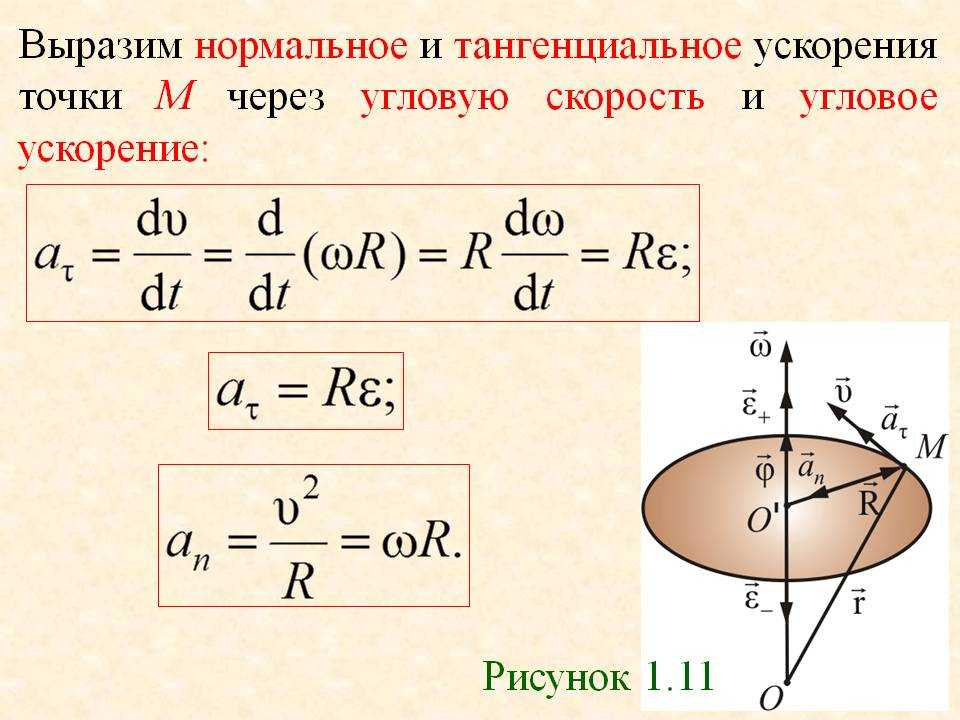 Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой xy – положение, скорость и ускорение с использованием векторов или графиков.

Интерактивный

Круговое движение требует силы, так называемой центростремительной силы, которая направлена ​​к оси вращения. Эта упрощенная модель карусели демонстрирует эту силу.

Силы инерции и неинерциальные (ускоренные) системы отсчета: сила Кориолиса

Что общего между взлетом реактивного самолета, поворотом автомобиля, катанием на карусели и круговым движением тропического циклона? Каждая проявляет силы инерции — силы, которые просто кажутся возникающими из-за движения, потому что система отсчета наблюдателя ускоряется или вращается. Большинство людей согласятся, что при взлете в реактивном самолете вас как будто вдавливают обратно в сиденье, когда самолет ускоряется на взлетно-посадочной полосе. Однако физик сказал бы, что вы склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт возникает, когда вы делаете крутой поворот на своем автомобиле, скажем, вправо (рис. 6.24). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не то, что вы испытываете силу слева.

Рисунок 6.24 а) Водитель автомобиля чувствует себя вынужденным сместиться влево относительно автомобиля при повороте направо. Это сила инерции, возникающая из-за использования автомобиля в качестве системы отсчета. б) В земной системе отсчета водитель движется прямолинейно, подчиняясь первому закону Ньютона, а машина движется вправо. Слева на водителя относительно Земли силы нет. Вместо этого справа на автомобиль действует сила, заставляющая его поворачиваться.

Мы можем согласовать эти точки зрения, изучив используемые системы отсчета. Давайте сосредоточимся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве системы отсчета, тогда как физик может использовать Землю. Физик может сделать такой выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в законах движения Ньютона. Автомобиль является неинерциальной системой отсчета, потому что он ускоряется в сторону. Сила слева, ощущаемая пассажирами автомобиля, представляет собой инерционную силу, не имеющую физического происхождения (она возникает исключительно из-за инерции пассажира, а не из-за какой-либо физической причины, такой как напряжение, трение или гравитация). Автомобиль, как и водитель, фактически ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.

Физик выберет любую систему отсчета, наиболее удобную для анализируемой ситуации. Для физика не проблема включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерциальные (ускоренные) системы отсчета используются, когда это полезно. При обсуждении движения астронавта в космическом корабле, летящего со скоростями, близкими к скорости света, необходимо учитывать различные системы отсчета, как вы оцените при изучении специальной теории относительности.

Теперь давайте мысленно прокатимся на карусели, а именно на быстро вращающейся карусели для игровой площадки (рис. 6.25). Вы принимаете карусель за систему отсчета, потому что вращаетесь вместе. При вращении в этой неинерциальной системе отсчета вы чувствуете силу инерции, которая стремится сбить вас с толку; это часто называют центробежной силой (не путать с центростремительной силой). Центробежная сила является широко используемым термином, но на самом деле его не существует. Вы должны крепко держаться, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.

Рисунок 6,25 а) Всаднику на карусели кажется, что его сбрасывают. Эту силу инерции иногда ошибочно называют центробежной силой, пытаясь объяснить движение всадника во вращающейся системе отсчета. (b) В инерциальной системе отсчета и в соответствии с законами Ньютона его увлекает инерция (у незаштрихованного всадника Fnet=0Fnet=0 и он движется прямолинейно). Сила FцентростремительнаяFцентростремительная необходима, чтобы вызвать движение по окружности.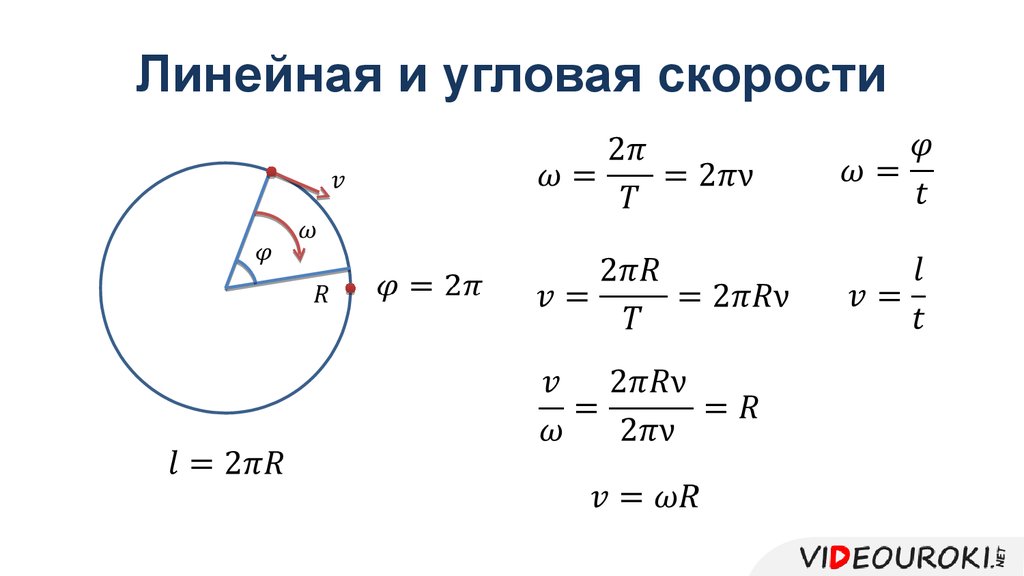

Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах (рис. 6.26). Как упоминалось ранее в этой главе, центрифуга вращает образец очень быстро. Если смотреть со стороны вращающейся системы отсчета, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц несет их вдоль линии, касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.

Рисунок 6,26 Центрифуги используют инерцию для выполнения своей задачи. Частицы в жидком осадке оседают, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет седиментацию. В конечном итоге частицы вступают в контакт со стенками пробирки, которые затем создают центростремительную силу, необходимую для их движения по окружности постоянного радиуса.

Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета. Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на рис. 6.27? Мяч движется по прямой относительно Земли (при условии пренебрежимо малого трения) и по кривой вправо на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а карусель вращается под ним. В системе отсчета карусели мы объясняем кажущуюся кривую вправо, используя силу инерции, называемую силой Кориолиса, которая заставляет мяч изгибаться вправо. Любой человек в этой системе отсчета может использовать силу Кориолиса, чтобы объяснить, почему объекты следуют кривым траекториям, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.

Рисунок 6.27 Глядя вниз на вращение карусели против часовой стрелки, мы видим, что мяч, скользящий прямо к краю, движется по кривой вправо. Человек двигает мяч к точке B , начиная с точки A .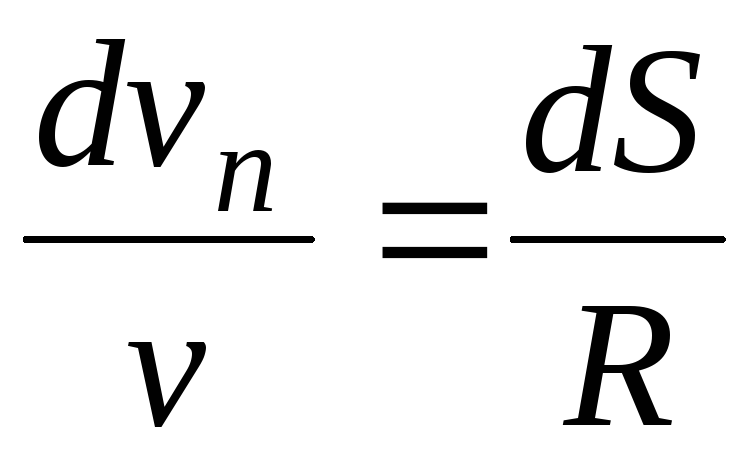 Обе точки поворачиваются в заштрихованные положения ( A ’ и B ’), показанные во времени, когда мяч движется по криволинейной траектории во вращающейся системе отсчета и по прямой траектории в системе отсчета Земли.

До сих пор мы считали Землю инерциальной системой отсчета, практически не беспокоясь о последствиях ее вращения. Тем не менее, такие эффекты do — например, в ротации погодных систем. Большинство последствий вращения Земли можно качественно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на рис. 6.27. Как и на карусели, любое движение в Северном полушарии Земли вызывает действие силы Кориолиса вправо. Как раз обратное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли невелика, сила Кориолиса обычно незначительна, но для крупномасштабных движений, таких как ветры, она оказывает существенное влияние.

Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке. (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, представляющих собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями.) На рис. 6.28 показано, как происходит это вращение. Воздух течет к любой области низкого давления, а тропические циклоны содержат особенно низкое давление. Таким образом, ветры направляются к центру тропического циклона или к погодной системе низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с восходящим воздухом, что также приводит к охлаждению и образованию облаков, что делает модели низкого давления хорошо видимыми из космоса. И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.

Рисунок 6,28 (a) Вращение этого урагана в Северном полушарии против часовой стрелки является основным следствием действия силы Кориолиса. (b) Без силы Кориолиса воздух попадал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветры вправо, вызывая вращение против часовой стрелки. (d) Ветер, идущий от зоны высокого давления, также отклоняется вправо, создавая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит a и кредит e: модификации работы НАСА)

Вращение тропических циклонов и траекторию шарика на карусели с таким же успехом можно объяснить инерцией и вращением системы под ними. Когда используются неинерциальные системы отсчета, для объяснения искривленного пути необходимо изобрести силы инерции, такие как сила Кориолиса.