Как найти t среднее физика: Средняя путевая скорость — урок. Физика, 10 класс.

Расстояние и время – основные термины, без которых невозможно определить среднюю скорость.

Прежде всего, мы должны рассчитать общую длину пути, по которому прошел объект, а затем мы должны проверить продолжительность времени, необходимого для достижения пункта назначения. Позже, чтобы найти среднюю скорость этого движения, нам нужно использовать ранее рассчитанные расстояние и время с помощью формулы.

Теперь давайте продолжим изучение, чтобы узнать больше подходов к нахождению средней скорости.

Увидев важность расстояния и времени при вычислении средней скорости. Теперь давайте, как рассчитать это за интервал.

• Если вы вычисляете среднюю скорость на графике, вам следует рассмотреть любые два интервала времени и расстояния, а затем найти значения расстояния и времени и подставить их в формулу средней скорости.

                                                                     В = С_f – S_i / т₂ – т₁

• В другом методе, если вы собираетесь напрямую использовать формулу, вы должны знать начальную и конечную точки, чтобы вам было легко вычислить V_{средний}, вы даже можете рассмотреть некоторую часть интервала, чтобы найти V_{средний} Это происходит путем деления общего расстояния на общее время.

                                    V = общее расстояние / общее время или

В = (В_f + V_i) / 2

Теперь давайте посмотрим, как рассчитать V_{средний} между двумя точками.

Среднюю скорость между двумя точками можно найти по простой формуле.

В общем, мы знаем, что Vavg тела равно среднему арифметическому начальных и конечных точек, приведенному ниже.

Vavg = [Начальная скорость (i) + Конечная скорость (v)] / 2

Пора узнать, как найти V_{средний} на графике.

Мы можем найти среднюю скорость с помощью графика смещения-времени.

• Здесь смещение будет по оси y, а время по оси x.
• Постройте точки в соответствии с осью и соедините их, чтобы создать область на графике.
• Затем найдите общую площадь на графике, взяв два интервала времени и расстояния.
• Измерьте его по линии графика и рассчитайте по формуле

                                                   V_{средний} = (V_i+V_f) / 2.

Переменные, взятые на графике, имеют характерную природу, все факторы, такие как изменение положения (между начальной и конечной точками), характер графика, т. Е. Является ли он линейным или нет, имеет значение.

При таком подходе мы можем рассчитать среднюю скорость по графику.

Линейный график иногда называют прямолинейным графиком.

Если мы хотим узнать среднюю скорость на линейном графике, тогда мы должны взять как начальную, так и конечную скорости и разделить ее на число 2. Это похоже на среднее значение, которое мы используем в математике для решения определенных задач.

Теперь давайте узнаем условие вычисления средней скорости на нелинейном графике.

Нелинейный граф также можно рассматривать как искривленный граф.

В нелинейном графике, что мы можем сделать, чтобы вычислить V_{средний} мы можем рассмотреть область под графиком, которая состоит из смещения (интегрировать его), а затем разделить на время.

Таким образом мы можем вычислить V_{средний} в нелинейном графике.

Приведенное ниже – одна из основных проблем, которую можно решить, используя подходы к вычислению средней скорости.

Представьте, что человек едет на своей машине в какой-то пункт назначения, но в течение первых 15 секунд положение машины меняется с x₁ = 80 м до x₂= 100 м. Какова средняя скорость автомобиля?

Решение: учитывая исходное положение x₁= 80m

                 Точно так же конечная позиция x₂ = 100m

Изменение водоизмещения автомобиля рассчитывается следующим образом:

Δx = х₂ – Икс₁ = 100 м – 80 м = 20 м

Δt = 15 с

По формуле мы имеем

v = Δx / Δt

v = 20/15

v = 1.33 м / с

Таким образом, средняя скорость автомобиля составляет 1. 33 м / с.

Из поставленной выше задачи мы узнали еще об одном подходе к нахождению средней скорости

Средняя скорость – заметное явление в физике.

Это векторная величина, определяемая как деление ∆x на ∆t. Где ∆x обозначает смещение, а ∆t обозначает общее время, затрачиваемое телом на завершение движения. Иногда может быть положительным или отрицательным, все зависит от направления смещения. Обозначается с помощью единицы СИ м / с.

Есть два основных типа скоростей, с которыми мы обычно сталкиваемся в физике.

Два основных типа скоростей – средние и мгновенные скорости. Как следует из их названия, среднее означает сумму скоростей каждого интервала, рассчитанную за общее время. Напротив, мгновенная скорость будет вычислением скорости в конкретный период движения.

Если мы возьмем конкретный временной интервал, тогда будет разница в измерении средней и мгновенной скорости.

Основное различие заключается в том, что для определенного периода интервала мгновенная скорость измеряется смещением и временем в определенной точке (s, t), а средняя скорость считается общим изменением положения во времени в определенном временном интервале.

Скорость не остается неизменной в конкретном движении, она продолжает изменяться.

Мы выяснили, что скорость является переменной, зависящей от многих факторов. Он не остается постоянным, но продолжает изменять свое значение с помощью перемещения и времени этого объекта. Исходя из этого, мы можем сказать, что средняя скорость движения не остается неизменной.

Есть много приложений, с помощью которых мы можем легко измерить среднюю скорость.

Первый метод – найти среднюю скорость, взяв первую и конечную точки движения, вычтя ее, а затем разделив весь член на 2.

Второй метод основан на использовании формулы, известной как уравнение средней скорости.

Уравнение средней скорости = В = (В_f + V_i) / 2

• V = средняя скорость.
• V_f = конечная скорость.
• V_i = начальная скорость

Это простое уравнение для измерения средней скорости.

Есть много способов найти смещение в кинематике.

Один из них – найти смещение с помощью формулы средней скорости, которая состоит из изменения положения / смещения. Меняя местами члены формулы, мы можем использовать ее для расчета смещения.

Оба термина означают совершенно разные друг от друга, когда мы изучаем их в физике.

Здесь мы знаем, что скорость – это скаляр, а скорость – вектор, тогда основное различие заключается в физических величинах, которые измеряют важность того, как их можно измерить.

Основные различия между этими двумя величинами приведены ниже:

• Средняя скорость говорит только о положении движущегося тела, здесь мы должны заметить, что величина будет разной для каждого положения, и определение скорости на любом временном интервале на длине курса осуществляется с помощью средней скорости.

• Средняя скорость говорит о сохранении скорости на всем пути движения. Это общая скорость, рассчитанная с учетом общей длины пути и времени, и, поскольку это скаляр, мы не можем определить направление пути.

Различные методологии и задачи –

Средняя скорость является одной из основных функций, определяемых в движении. В этой статье мы узнаем, как найти среднюю скорость.

Основным методом определения средней скорости является деление суммы изменений положения объекта на общее время, затраченное этим объектом на завершение движения. Поскольку это векторная физическая величина, направление объекта также имеет важное значение при расчете средней скорости.

Далее мы изучим другие методы, как найти среднюю скорость, так как это основная тема поста.

Основная формула, используемая для расчета V _avg , включает в себя как перемещение во времени.

Общая используемая формула выглядит следующим образом:

Она используется при решении основных задач, связанных со средней скоростью.

V = S _f – S _I / T ₂ – T ₁

V = ΔS / ΔT

, где

ΔS =

Расстояние и время являются основными условиями, без которых невозможно найти среднюю скорость.

Прежде всего, мы должны рассчитать общую длину пути, по которому прошел объект, затем мы должны проверить продолжительность времени, затраченного на достижение пункта назначения. В дальнейшем, чтобы найти среднюю скорость этого движения, нам нужно использовать ранее вычисленные расстояние и время с помощью формулы.

Теперь давайте продолжим изучение, чтобы узнать больше о подходах к нахождению средней скорости.

Увидев важность расстояния и времени при расчете средней скорости. Теперь давайте, как вычислить его на интервале.

• Если вы вычисляете среднюю скорость на графике, то вы должны рассмотреть любые два интервала времени и расстояния, а затем узнать значения расстояния и времени и подставить их в формулу средней скорости.

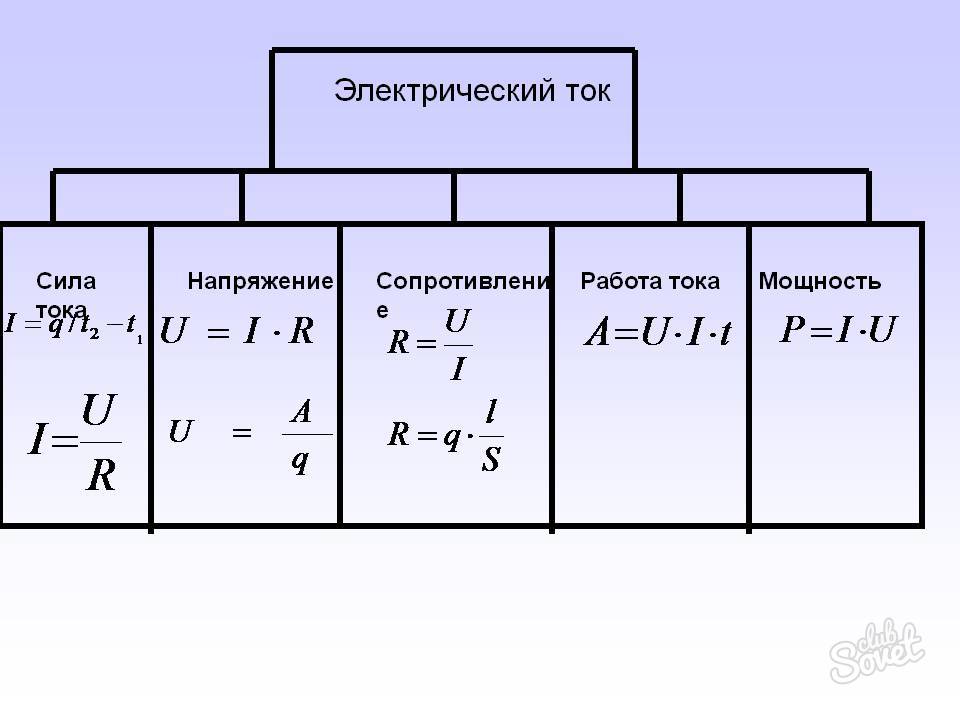
                                                                V = S _f – S _i / t ₂ – t ₁

• В другом методе, если вы собираетесь использовать формулу напрямую, то вы должны знать начальную и конечную точки, чтобы она была легко для вас вычислить V _avg , вы даже можете рассмотреть некоторую часть интервала, чтобы найти V _avg Это происходит путем деления общего расстояния на общее время.

                                   V = общее расстояние/общее время     или

V = (V _f + V _i ) / 2

Теперь давайте рассмотрим метод расчета V _avg между двумя точками.

Среднюю скорость между двумя точками можно найти по простой формуле.

В общем случае мы знаем, что Vср тела равна среднему арифметическому начальной и конечной точек, приведенному ниже

Vср = [ Начальная скорость (i) + Конечная скорость (v)] / 2

Пришло время узнать, как найти V _avg на графике.

Мы можем найти среднюю скорость с помощью графика перемещение-время.

• Здесь смещение будет по оси y, а время по оси x.
• Нанесите точки на оси и соедините их, чтобы создать область на графике.
• Затем найдите общую площадь на графике, взяв два интервала времени и расстояния.
• Измерение его вдоль линии графика и может быть рассчитана с использованием формулы

V _AVG = (V _I +V _F )/2.

Переменные, взятые на графике, имеют заметный характер, все факторы, такие как изменение положения (между начальной и конечной точками), характер графика, т. е. линейный он или нет.

При таком подходе мы можем рассчитать среднюю скорость по графику.

Линейный график иногда называют прямолинейным графиком.

Если мы хотим узнать среднюю скорость на линейном графике, то мы должны взять начальную и конечную скорости и разделить их на число 2. Это похоже на среднее значение, которое мы используем в математике для решения некоторых задач.

Теперь давайте узнаем условие для расчета средней скорости в нелинейном графике.

Нелинейный график также можно рассматривать как криволинейный график.

В нелинейном графике для расчета V _avg мы можем рассмотреть площадь под графиком, которая состоит из смещения (интегрировать ее), а затем разделить ее на время.

Таким образом, мы можем вычислить V _avg на нелинейном графике.

Приведенная ниже является одной из основных задач, которые могут быть решены с использованием подходов для расчета средней скорости.

Предположим, что человек едет на своей машине в какой-то пункт назначения, но в течение первых 15 с положение автомобиля меняется с x ₁  = 80 м на x ₂ = 100 м. Какова теперь средняя скорость автомобиля?

Решение: Начальная позиция равна x ₁ = 80M

Аналогично, конечная позиция составляет x ₂ = 100m

Изменение смещения автомобиля рассчитывается следующим образом:

Δx = X ₂ – x. ₁ = 100 м – 80 м = 20 м

ΔT = 15 с

Из формулы, которую мы имеем,

V = Δx / ΔT

V = 20/15

v= 1,33 м/с

Следовательно, средняя скорость автомобиля равна 1,33 м/с.

Из вышеприведенной задачи мы познакомились с еще одним подходом к нахождению средней скорости

Средняя скорость — важное явление в физике.

Это векторная величина, определяемая как ∆x, деленная на ∆t. Где ∆x означает перемещение, а ∆t говорит об общем времени, затраченном телом на совершение движения. Иногда это может быть положительным или отрицательным, все зависит от направления смещения. Обозначается с использованием единицы СИ м/с.

Обычно в физике встречаются два типа скоростей.

Два основных типа скоростей — это средние и мгновенные скорости. Как следует из их названия, среднее значение означает общую сумму скоростей каждого интервала, рассчитанную за общее время. Напротив, мгновенная скорость будет определять скорость в определенный период движения.

Если мы возьмем конкретный интервал времени, то будет разница в измерении средней и мгновенной скорости.

Основное различие заключается в том, что для определенного периода интервала мгновенная скорость измеряется с учетом смещения и времени в определенной точке (s,t), а средняя скорость считается общим изменением положения со временем в определенное время. интервал.

Скорость не остается неизменной в конкретном движении, она продолжает меняться.

Мы изучили, что скорость является переменной величиной, зависящей от многих факторов. Он не остается постоянным, а продолжает изменять свое значение с помощью перемещения и времени этого объекта. Отсюда мы можем сказать, что средняя скорость не остается неизменной в движении.

Существует множество приложений, с помощью которых мы можем легко измерить среднюю скорость.

Первый метод заключается в нахождении средней скорости путем взятия первой и конечной точек движения, вычитания их и последующего деления всего члена на 2.

Второй метод заключается в использовании формулы, известной как средняя скорость уравнение.

Уравнение средней скорости = V = (V _f + V _i )/2

• В = средняя скорость.
• V _f = конечная скорость.
• V _i = начальная скорость

Это простое уравнение для измерения средней скорости.

Есть много способов найти перемещение в кинематике.

Один из них – найти перемещение с помощью формулы средней скорости, состоящей из изменения положения/перемещения. Поменяв местами члены формулы, мы можем использовать ее для расчета смещения.

Оба термина означают совершенно разные значения, когда мы изучаем их в физике.

Здесь мы знаем, что скорость является скаляром, а скорость является вектором, тогда основное различие заключается в физических величинах, которые измеряют значимость того, как их можно измерить.

Основная разница между этими двумя величинами приведена ниже,

• Средняя скорость говорит только о положении тела в движении, здесь надо заметить, что величина будет разной для каждого положения и нахождение скорости на любом временном интервале на длине пути делается с помощью средней скорость.

• Средняя скорость говорит о сохранении скорости на всем пути движения. Это сумма скоростей, рассчитанная с учетом общей длины пути и времени, и, поскольку это скаляр, мы не можем определить направление пути.

1.1: Справочный материал – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Том Вайдеман
• Калифорнийский университет, Дэвис

Среднее положение

В этой лаборатории мы проведем несколько испытаний, в ходе которых на листе бумаги будут отображаться точки, измеряющие положение шарика в момент удара им об пол. Все эти точки можно рассматривать как находящиеся в начале векторов положения \(\overrightarrow r_1\), \(\overrightarrow r_2\), \(\overrightarrow r_3\) и так далее. Как это обычно бывает в экспериментах, нас будет интересовать среднее количество по многим испытаниям — в данном случае среднее положение, в котором приземляется шарик. Нахождение среднего вектора ничем не отличается от нахождения среднего числа, а именно:

\[\text{средняя позиция} = \left<\overrightarrow r\right> = \dfrac{\overrightarrow r_1 + \overrightarrow r_2 +\dots+\overrightarrow r_n}{n}\]

Мы не захотим на самом деле выберите начало координат и нарисуйте все эти векторы, поэтому полезно придумать какой-нибудь способ найти среднее положение непосредственно из положений точек. Нетрудно показать, что средняя позиция для двух испытаний — это как раз точка, расположенная посередине между позициями двух испытаний.

Рисунок 1.1.1 – Среднее двух векторов положения

Метод нахождения среднего положения более чем двух точек не такой простой, но мы воспользуемся хитростью, чтобы не допустить слишком сложно. Обратите внимание, что если у нас есть четыре точки, мы можем записать вектор среднего положения следующим образом:

\[\left<\overrightarrow r\right> = \dfrac{\overrightarrow r_1 + \overrightarrow r_2 +\overrightarrow r_3 + \overrightarrow r_4 }{4} = \dfrac{\dfrac{\overrightarrow r_1 + \overrightarrow r_2}{2} +\dfrac{\overrightarrow r_3 + \overrightarrow r_4}{2}}{2}\]

Это показывает, что мы можем получить среднее положение четырех точек, сначала найдя среднее положение двух пар точек, а затем найдя среднее значение этих средних значений. Это позволяет нам просто использовать линейку, чтобы найти промежуточные точки между парами точек, чтобы найти среднее положение всех точек. Обратите внимание, что эта процедура требует, чтобы у нас было некоторое количество точек, равное степени двойки (2, 4, 8, 16 и т. д.). Мы могли бы сделать это для другого числа, но тогда мы теряем простоту «на полпути между точками», и, поскольку мы контролируем количество испытаний, мы будем придерживаться этого метода.

Следует также отметить, что не имеет значения, как мы разделяем точки по парам – в итоге мы получаем одно и то же среднее положение:

\[\left<\overrightarrow r\right> = \dfrac{ \dfrac{\overrightarrow r_1 + \overrightarrow r_2}{2} +\dfrac{\overrightarrow r_3 + \overrightarrow r_4}{2}}{2} = \dfrac{\dfrac{\overrightarrow r_1 + \overrightarrow r_3}{2 } +\dfrac{\overrightarrow r_2 + \overrightarrow r_4}{2}}{2}\]

Рисунок 1.1.2 – Среднее положение четырех точек, найденных двумя способами

Когда мы проводим эксперимент, нас интересует больше, чем просто среднее значение, которое мы получаем из многих испытаний, мы хотим знать, в какой степени этому среднему можно доверять. То есть мы хотим знать, насколько

Всякий раз, когда экспериментальные прогоны имеют разрозненные результаты либо из-за участия человека, либо из-за того, что аппарат не может очень точно повторить прогон, мы определяем неопределенность статистически

• вычислить среднее значение всех точек данных

\[\left = \dfrac{x_1 + x_2 + \dots + x_n}{n}\]

92}{n}}\]

Это описание вычисления стандартного отклонения облегчает запоминание, поскольку мы просто вычисляем средние значения (сначала точек данных, затем квадратов отклонения значений точек данных от среднее значение), но технически в тех ситуациях, когда мы вычисляем среднее значение из фактических данных, на самом деле существует несколько более точная формула для стандартного отклонения. Он включает в себя деление суммы квадратов отклонений на \(n-1\), а не на \(n\). Мы не будем вдаваться в технические подробности того, почему это так, но важно отметить, что разница между ними может стать существенной, когда \(n\) достаточно мала, как это часто бывает в наших экспериментах.

Поэтому в дальнейшем мы будем использовать так называемую «непредвзятую» версию стандартного отклонения: 92}{n-1}}\]

То, как этот метод измерения неопределенности работает для нашего настоящего эксперимента, должно быть ясно: сначала используйте метод, описанный выше, чтобы определить место на бумаге, которое является средней точкой приземления. Во-вторых, измерьте расстояние от каждой точки до средней точки приземления. Это “отклонение от среднего” (\(\Delta x\), измеряемое в сантиметрах) каждой точки данных. Затем посчитайте оттуда.

Расчетная неопределенность

Еще одно место, где мы вносим неопределенность в наши результаты, — это измерения. Например, если мы измеряем расстояние линейкой, мы не ожидаем, что наши измерения будут точными до микрона (\(\frac{1}{1000}\) миллиметра), и мы должны оценить неопределенность этих измерения должны быть в диапазоне, возможно, нескольких миллиметров. Таким образом, в эксперименте, описанном выше, наши измерения расстояний между точками и между средними точками приземления и точками вносят неопределенность в наши результаты, потому что наш измерительный прибор не измеряет эти расстояния точно. Однако в этом случае мы обнаруживаем, что крошечная оценочная неопределенность этих измерений расстояния в несколько миллиметров незначительна по сравнению со статистической неопределенностью, связанной с прицеливанием человека (которая находится в диапазоне «несколько сантиметров»). Поэтому мы можем игнорировать предполагаемую неопределенность, связанную с измерениями линейки для этого эксперимента, поскольку она вносит незначительный вклад. Хотя оба типа неопределенности обычно встречаются в любом эксперименте, обычно верно то, что только один тип является доминирующим вариантом, что позволяет нам игнорировать другой. Самый простой способ понять это – сделать несколько повторений (которые должны быть идентичными) прогонов, чтобы понять, насколько результаты «разбросаны». Хотя в этом эксперименте этот разброс значительно превышает неопределенность измерения, чаще всего верно обратное. Это потому, что мы будем использовать аппараты, которые хорошо справляются с повторяющимися прогонами.

Так как же нам сделать достойную оценку неопределенности измерения? Не вдаваясь в детали, с которыми вы могли столкнуться на занятиях по статистике (например, нюансы центральной предельной теоремы и предположение о нормальном распределении для наших измерений), мы скажем, что диапазон неопределенности таков, что мы ожидаем, что примерно две трети точек данных попадут в пределах одного стандартного отклонения от среднего . Хотя это работает автоматически, когда мы вычисляем неопределенность статистически, мы также будем использовать это в качестве стандарта для наших оценок неопределенности измерений. То есть оцените неопределенность измерения таким образом, чтобы истинное значение измерения находилось в пределах диапазона неопределенности вашего записанного измерения примерно в двух третях случаев.

Хороший пример для запоминания

Если вы находите понятия статистической и оценочной неопределенностей запутанными, вот хорошая модель, которую следует иметь в виду. Предположим, вы проводите эксперимент, который включает измерение как расстояния между двумя четко определенными точками, так и временного интервала между двумя событиями. Так, например, прыгающий шарик имеет довольно четко определенные точки приземления, а время между приземлениями — это временной интервал. Для разделения двух точек используется линейка или рулетка, и вы можете посмотреть на маркировку на измерительном устройстве, чтобы получить представление о погрешности этого измерения. Это предполагаемая неопределенность. Временной интервал другой – устройство, которое запускало шарик, может быть непостоянным, но что более важно, если человек нажимает на секундомер, когда видит приземление шарика, то неопределенность в этом измерении больше поддается статистическому расчету – измерению временной интервал для нескольких «идентичных» случаев много раз и вычислить стандартное отклонение.

---

Эта страница под названием 1.1: Справочные материалы публикуется под лицензией CC BY-SA 4.